9 Regresión lineal

Librerías usadas

• spdep
• ggplot2
• lmtest
• RColorBrewer
• classInt
• spatialreg

En un modelo de regresión espacial, donde tenemos una variable dependiente y variables exógenas, nos debemos preguntar por fuentes de :

• Dependencia espacial: efectos indirectos espaciales (spatial spillovers), que aparecen como flujos interregionales de conocimiento, comercio o factores de producción.
• Heterocedasticidad: resultantes de límites administrativos que no son consistentes con la naturaleza de los procesos espaciales estudiados.

¿Qué data es espacial en economía?

Se trata básicamente de todos los datos recogidos por las oficinas estadísticas (INEC en Ecuador) para zonas separadas por límites administrativos (provincias, cantones, parroquias) y datos puntuales a los que se pueden asignar ubicaciones, relacionados con la vida de la población, las actividades de las empresas y los rastros en la realidad virtual (registro de teléfonos móviles, coches, ordenadores IP).

¿Cuáles son las consecuencias de omitir la dimensión espacial cuando los datos son espaciales?

• En cuanto a la variable dependiente, se rompe el supuesto clásico de independencia y los errores por lo tanto no tienen covarianza igual a cero porque muestran dependencia espacial.

• La omisión de una variable espacial significtiva, por ejemplo \(\rho Wy\) o \(\theta Wy\) se traduce en un error de especificación del modelo.

• La omisión de un rezago espacial y la estimación de los parámetros usando OLS tradicional genera estimadores sesgados e inconsistentes.

• Cuando no se trata la autocorrelación espacial de los residuos, las estimaciones OLS son ineficientes, pero asintóticamente consistentes.

Heterogeneidad

Cuando tenemos heterogeneidad, podemos tratarlo

• Usar datos en diferente escala, es decir, datos a un nivel de agregación menor o mayor.

• Es posible incluir variables que se aproximen a fenómenos espaciales no observados: pueden ser variables dummy (cero-uno) para características o ubicaciones específicas (por ejemplo, capitales regionales, pertenencia a conglomerados) o variables con una distribución espacial muy similar a la distribución del error.

• Es posible incluir coordenadas geográficas como variables explicativas.

• Es posible estimar modelos econométricos en grupos (clusters) que muestran homogeneidad interna y diversidad inte-cluster.

• Se debe elegir el método de estimación espacial correcto, seleccionando la mejor matriz de pesos espaciales posible, el tipo y la clase de modelo adecuados y una buena especificación del modelo.

9.1 Una tipología de modelos econométricos

Podemos agrupar los modelos en función de sus características. Aquí se propone, restringido a modelos de regresión lineal, una clasificación de modelos econométricos espaciales.

9.1.1 Una clasificación general

Recordemos que la característica principal de la econometría espacial es cómo los efectos espaciales son tomados en cuenta.

Esta característica presupone que el espacio ha sido formalizado de una forma u otra.

En general la matriz de pesos espaciales logra ser aplicable en varios contextos empíricos siempre que:

• los pesos recojan adecuadamente la dependencia espacial
• la heterogeneidad espacial sea tomada en cuenta en la especificación del modelo.

Una distinción importante en términos de estrategias de estimación y pruebas de hipótesis es de procesos espaciales:

• simultáneos: expresado como probabilidad conjunta
• condicionales: expresado como probabilidad condicional.

Ambos se suelen presentar de manera autor regresiva: donde el valor de una variable en un punto se relaciona con sus valores en el resto del sistema espacial.

Un modelo simultáneo se remonta al trabajo de Whittle (1954) que en notación matricial es equivalente a un modelo espacial autorregresivo de primer orden:

\[ y = \rho W y+\epsilon \] con \(y\) como el vector de la variable y \(\epsilon\) el vector del término de error, y \(W\) como la matriz de pesos espaciales correspondiente. La estimación de este modelo implica la especificación de una distribución de probabilidad conjunta y optimización no lineal.

El modelo condicional fue propuesto originalmente por Besag (1974) como alternativa a la estimación no lineal de Whittle.

En esencia, consiste en una relación lineal entre la esperanza condicional de la variable dependiente y sus valores en el resto del sistema (\(S\)):

\[ E[y_i|y_j \forall j\in S, j \neq i] = \rho W y \] La estructura condicional del modelo hace posible míninos cuadrados como técnica de estimación siempre que los datos se codifiquen de un modo particular.

La codificación consiste en eliminar observaciones tal que las variables dependientes que quedan se puedan considerar como independientes (no contiguas). Si hay pocas observaciones no se recomienda hacerlo, también debe considerarse que este proceso no es único por lo que pueden obtenerse resultados diferentes según la codificación.

Besag (1975), y Lele and Ord (1986) han desarrollado -a pseudo-máxima verosimilitud para el modelo condicional que evita la codificación; pero es más compleja matemáticamente.

La mayoría de situaciones en ciencias regionales empíricas se expresan más fácilmente en forma simultánea. Este enfoque también es más cercano al enfoque econométrico tradicional.

De forma análoga al enfoque Box-Jenkins en series de tiempo, los especificaciones de modelos espaciales combinan procesos auto regresivos y de media móvil. Un proceso espacial de media móvil tiene la forma:

\[ y =\epsilon+ \rho W \epsilon \]

donde \(y\) es un vector de variables, o un vector de términos aleatorios independientes y \(W\) es la matriz de peros espaciales.

Otro punto importante pone la diferenciación de modelos son los datos:

• En observaciones transversales (cross-sectional) hay información insuficiente en los datos para extraer un patrón simultáneo total de la interacción, y a reparametrización del modelo en términos auto regresivos es una necesidad.

• Si se tienen datos cross-sectional y de series de tiempo, la información temporal puede relajar esa necesidad.

9.1.2 Una taxonomía de Modelos de Regresión Lineal Espacial

Esta clasificación asume observaciones de unidades disponibles en corte transversal en un punto del tiempo.

Se deriven varios modelos mediante imposición de restricciones en el modelo general.

El punto de partida es:

\[ y = \rho W_1 y+X\beta+\epsilon\tag{9.1} \]

\[ \epsilon = \lambda W_2 \epsilon+\mu \]

con \(\mu\sim N(0,\Omega)\), y los elementos de la diagonal de la matriz de covarianza del error \(\Omega\) como

\[ \Omega_{jj} = h_{i}(z\alpha) \quad h_i>0 \] En esta especificación:

• \(\beta_{K\times 1}\) es el vector de parámetros de las variables exógenas (no rezagadas) \(X_{N\times K}\).
• \(\rho\) es el coeficiente de la variable dependiente espacialmente rezagada.
• \(\lambda\) es el coeficiente de la estructura autorregresiva espacial para el error \(\epsilon\).

La perturbación \(\mu\) se asume normalmente distribuida con matriz de covarianza \(\Omega\). Los elementos de la diagonal de \(\Omega\) permiten heterocedasticidad como una función de \(P+1\) variables exógenas \(z\) que incluyen el término constante.

Los \(P\) parámetros \(\alpha\) están asociados con los términos no constantes, tal que, para \(\alpha=0\), se tiene que

\[ h = \sigma^2, \]

(la situación clásica de homocedasticidad).

Las matrices \(N\times N\) (\(W_1\) y \(W_2\)) son matrices de pesos espaciales estandarizadas o no estandarizados.

\(W_1\) se asocia con el proceso autorregresivo de la variable dependiente. \(W_2\) se asocia con el proceso autorregresivo del error.

Esto sugiere que los dos procesos pueden tener diferentes estructuras espaciales. Así propuesto, los modelos pueden tener \(3+K+P\) parámetros desconocidos, en forma vectorial:

\[ \theta = [\rho,\beta',\lambda,\sigma^2,\alpha']'. \tag{9.2} \] Varias estructuras espaciales se derivan cuando sub vectores de \(\theta\) se hacen cero.

9.1.2.1 Modelo clásico de regresión lineal, sin efectos espaciales

para \(\rho=0\), \(\lambda=0\), \(\alpha=0\), (\(P+2\) restricciones):

\[ y = X\beta + \epsilon \tag{9.3} \]

9.1.2.2 Modelo autorregresivo espacial (SLM)

incluye especificaciones de factor común (con \(WX\) incluido en las variables explicativas), como caso especial (si se incluye \(WX\) se tiene el modelo de Durbin)

para \(\rho=0\), \(\alpha=0\), (\(P+1\) restricciones):

\[ y = \rho W_1 y + X\beta+\epsilon \tag{9.4} \]

9.1.2.3 Modelo de regresión lineal con error autorregresivo espacial (SEM)

para \(\rho=0\), \(\alpha=0\), (\(P+1\) restricciones):

\[ y = X\beta+(I-\lambda W_2)^{-1}\mu \tag{9.5} \] A partir del modelo (9.1), nota que:

\[ \epsilon -\lambda W_2 \epsilon = \mu \\ (I-\lambda W_2)\epsilon = \mu \\ (I-\lambda W_2)^{-1}(I-\lambda W_2)\epsilon = (I-\lambda W_2)^{-1}\mu \\ \epsilon=(I-\lambda W_2)^{-1}\mu \]

9.1.2.4 Modelo autorregresivo espacial mixto regresivo con error espacial autorregresivo (SARMA)

para \(\alpha=0\), (\(P\) restricciones):

\[ y = \rho W_1 y+X\beta+(I-\lambda W_2)^{-1}\mu \tag{9.6} \] Se puede obtener cuatro especificaciones más si se permite heterocedasticidad (una forma para \(h(z\alpha)\)) en (9.3)-(9.6).

Los modelos que estimaremos en las siguientes secciones son SAR, SEM y SDM. La figura 9.1 muestra la relación entre ellos.

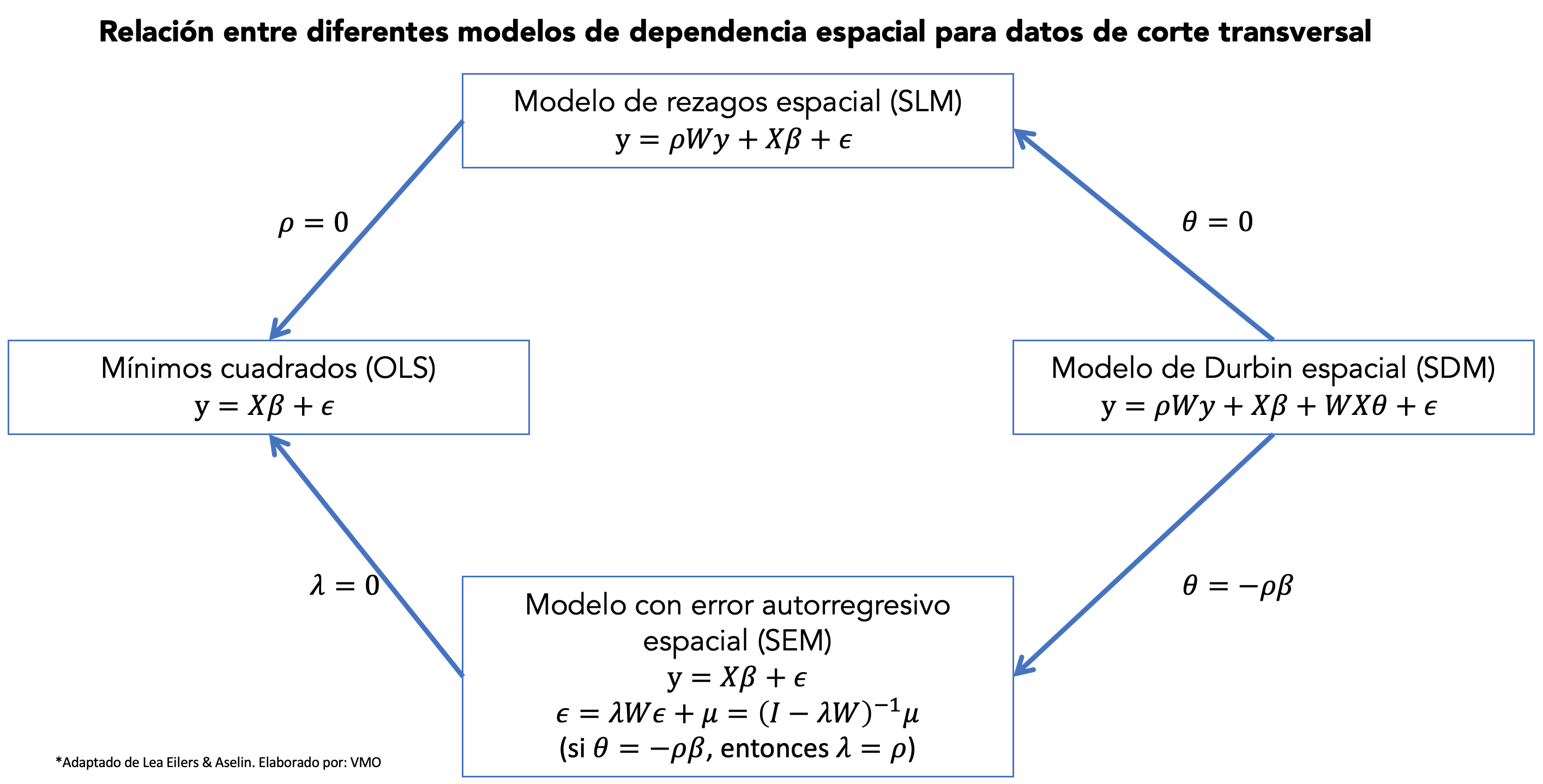
Figure 9.1: Relación entre modelos espaciales

9.2 Modelo de rezagos espacial (SLM)

El modelo de rezagos espacial (Spatial lag model o SLM) es:

\[ y = \rho Wy+X\beta+\epsilon \tag{9.7} \] donde \(y\) es un vector \(n\times 1\) de observaciones de la variable dependiente, \(X\) es una matriz \(n\times K\) de observaciones de las variables explicativas, \(\beta\) es el vector de parámetros \(K\times 1\).

La siguiente figura 9.2 representa el modelo autorregresivo espacial en (9.7) para dos regiones. Las variables (\(x_1\), \(x_2\)) y los términos no observados (\(\epsilon_1\), \(\epsilon_2\)) tienen un efecto directo sobre \(y\) para ambas regiones. Tenga en cuenta que el modelo incorpora efectos de desbordamiento espacial por el efecto de \(y_1\) sobre \(y_2\) y viceversa. Es decir, el modelo refleja la simultaneidad inherente a la autocorrelación espacial.

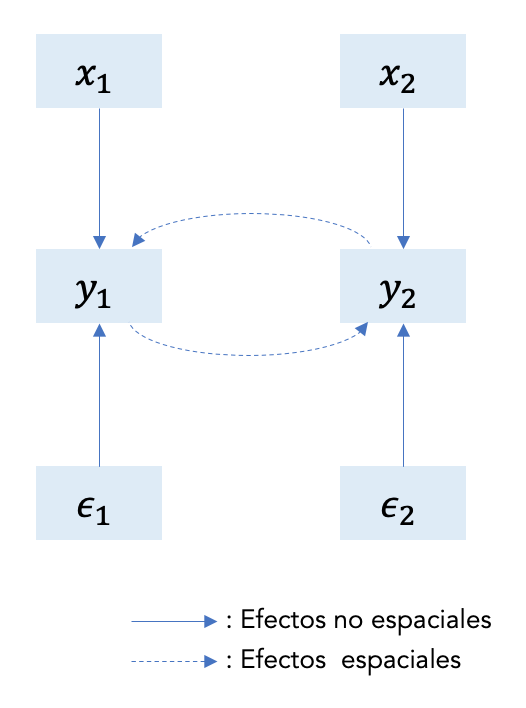
Figure 9.2: Estructura de efectos en SLM

La ecuación (9.7) expresa el modelo SLM en su forma estructural o de comportamiento donde se relaciona tanto las variables exógenas como endógenas con la dependiente \(y\).

Otra forma de expresar el modelo es en su forma reducida:

\[ y = (I-\rho W)^{-1}X\beta +(I-\rho W)^{-1}\epsilon \tag{9.8} \] que ya no contiene ninguna variable dependiente espacialmente rezagada en el lado de la derecha. La ecuación (9.8) expresa la naturaleza simultánea del proceso autorregresivo espacial.

La forma estructural es un modelo de la forma \(f(y,X,\epsilon)\), mientras la forma reducida es de la forma \(y = g(X,\epsilon)\).

Notemos que \((I-\rho W)\) debe ser invertible, es decir \(det(I-\rho W)\neq 0\). Entonces ¿qué valores de \(\rho\) hacen que \((I-\rho W)\) sea invertible? Se puede demostrar que para matrices simétricas, \((I-\rho W)\) es invertible si

\[ \omega_{min}^{-1}<\rho <\omega_{max}^{-1} \] donde \(\omega_{min}^{-1}\) y \(\omega_{max}^{-1}\) son los valores propios mínimo y máximo de \(W\).

Recuerda que es común estandarizar \(W\) por fila tal que sus filas sumen \(1\). Dado que \(W\) es no negativa, esto asegura que los pesos estén entre \(0\) y \(1\) y la estandarización se puede interpretar como promediar los valores de los vecinos.

Si \(W\) es estandarizada por filas, esto implica que \(-1<\rho <1\) pero recuerda que esto no significa que \(\rho\) sea la correlación convencional, esto solo sucede porque \(W\) es estandarizada por filas. Un problema de estandarizar por filas es que la comparación entre filas puede resultar complicado.

Otra forma de estandarizar \(W\) es multiplicarla por un número, digamos \(a\) tal que se remueva el efecto de las unidades de medida. En particular:

\[ a = min\{r,c\}\\ r = \underset{i}{max}\sum_j|w_{ij}| \quad \text{máximo de la suma for filas en valor absoluto}\\ c = \underset{j}{max}\sum_i|w_{ij}| \quad \text{máximo de la suma for columnas en valor absoluto} \] Como resultado, \((I-\rho W)\) será invertible para \(|\rho|=\frac{1}{a}\). Ten en cuenta que esta normalización tiene la ventaja de garantizar que las ponderaciones espaciales resultantes, \(w_{ij}\), estén todas entre \(0\) y \(1\) y, por lo tanto, aún puedan interpretarse como intensidades de influencia relativas.

Los momentos del modelo en forma reducida son:

Esperanza

\[ \mathbb{E}(y|X,W) = \mathbb{E}\left[(I-\rho W)^{-1}X\beta+ (I-\rho W)^{-1}\epsilon|X,W \right]\\ = (I-\rho W)^{-1}X\beta \]

[Expansión de Leontief]. Si \(|\rho|<1\), entonces \[(I-\rho W)^{-1}=\sum_{i=0}^{\infty}(\rho W)^i\]

• En promedio, el valor de \(y\) en una ubicación \(i\) no solo se explica por los valores de las variables explicativas asociadas a esta ubicación, sino también por las asociadas a todas las demás ubicaciones (vecinas o no) a través de la transformación espacial inversa \((I-\rho W)^{-1}\).

• Este efecto multiplicador espacial disminuye con la distancia, es decir, las potencias de \(W\) en la expansión en serie de \((I-\rho W)^{-1}\)

• Un choque aleatorio en una ubicación \(i\) no solo afecta el valor de \(y\) en esta ubicación, sino que también tiene un impacto en los valores de \(y\) en todas las demás ubicaciones a través de la misma transformación inversa espacial \((I-\rho W)^{-1}\).

Varianza

\[ Var(y|X,W) = \mathbb{E}(yy^T|W,X)\\ =(I-\rho W)^{-1}\mathbb{E}(\epsilon\epsilon^T|W,X)(I-\rho W^T) \]

• Esta matriz de varianza-covarianza es completa, lo que implica que cada ubicación está correlacionada con todas las demás ubicaciones del sistema.

• Sin embargo, esta correlación disminuye con la distancia. Esta ecuación también muestra que la covarianza entre cada par de términos de error no es nula y disminuye con el orden de proximidad.

• Además, los elementos de la diagonal de \(\mathbb{E}(\epsilon\epsilon^T|W,X)\) no son constantes. Esto implica heterocedasticidad de error de \(\epsilon\).

• Dado que no hemos asumido nada sobre la varianza del error, podemos decir que \(\mathbb{E}(\epsilon\epsilon^T|W,X)\) es una matriz completa, digamos \(\Omega_\epsilon\). Esto cubre la posibilidad de heterocedasticidad, autocorrelación espacial o ambas. En ausencia de cualquiera de estas complicaciones, la matriz de varianza se simplifica a la \(\sigma^2I\) habitual.

9.2.0.1 Ejemplo

Realizaremos una regresión donde la variable dependiente es la pobreza por NBI (personas) y la independiente es el valor agregado bruto no petrolero per cápita.

1. Preparamos los datos: esto incluye el cálculo de la matriz de ponderaciones espaciales.

# **** Importo datos: VAB no petrolero
uu <- "https://raw.githubusercontent.com/vmoprojs/DataLectures/master/SpatialData/VABNoPetroleroCantones2007-2019.csv"
datos <- read.csv(uu,sep = ",")
datos$COD_CANT[nchar(datos$COD_CANT)==3] = paste("0",datos$COD_CANT[nchar(datos$COD_CANT)==3],sep = "")

datos <- subset(datos,datos$YEAR == 2019)

# **** Importo datos: Población por cantones
uu <- "https://raw.githubusercontent.com/vmoprojs/DataLectures/master/SpatialData/proyeccion_cantonal_total_2010-2020.csv"

poblacion <- read.csv(uu,sep = ";")

poblacion$CODIGO[nchar(poblacion$CODIGO)==3] = paste("0",poblacion$CODIGO[nchar(poblacion$CODIGO)==3],sep = "")

# **** Importo datos: NBI
uu <- "https://raw.githubusercontent.com/vmoprojs/DataLectures/master/SpatialData/NBI_PER_CANT.csv"
NBI <- read.csv(uu, sep = ";")

NBI$CODIGO[nchar(NBI$CODIGO)==3] = paste("0",NBI$CODIGO[nchar(NBI$CODIGO)==3],sep = "")

datos <- merge(datos,poblacion[,c("CODIGO","A_2020","SuperficieKM2")],by.x = "COD_CANT",by.y = "CODIGO",all.x = TRUE)

datos <- merge(datos,NBI[,c("CODIGO","POBRES_P")],by.x = "COD_CANT",by.y = "CODIGO",all.x = TRUE)

datos$VAB_PC <- datos$VAB/datos$A_2020 #miles de USD / pob
datos$DensPob <- datos$A_2020/datos$SuperficieKM2 

# **** Importo datos: NBICOVID (https://www.covid19ecuador.org/cantones)

uu <- "https://raw.githubusercontent.com/andrab/ecuacovid/master/datos_crudos/positivas/por_fecha/cantones_por_dia_acumuladas.inec.csv"

c19 <- read.csv(uu, sep = ",")
c19 <- c19[,c("inec_canton_id","X24.03.2022")]
c19$inec_canton_id[nchar(c19$inec_canton_id)==3] = paste("0",c19$inec_canton_id[nchar(c19$inec_canton_id)==3],sep = "")
names(c19) <- c("COD_CANT","C19")

# names(datos)
datos <- merge(datos,c19, by.x = "COD_CANT",all.x = TRUE)
datos$C19_pc <- (datos$C19/datos$A_2020)*1000

# cor.test(datos$C19_pc,datos$DensPob,use="na.or.complete")
# cor.test(datos$C19_pc,datos$DensPob,use="na.or.complete",method = "spearman")
# cor.test(datos$C19_pc,datos$POBRES_P,use="na.or.complete",method = "spearman")
# cor.test(datos$DensPob,datos$POBRES_P,use="na.or.complete",method = "spearman")
# plot(datos$DensPob,datos$POBRES_P)


uu <- "https://github.com/vmoprojs/DataLectures/raw/master/SpatialData/2012_nxcantones.zip"
poligonos <- read_git_shp(uu)

## Reading layer `nxcantones' from data source 
##   `/private/var/folders/0p/n_r_hl095sv7nktfp_8n9n_80000gn/T/Rtmp4EHXgX/file2ca465eeb04/nxcantones.shp' 
##   using driver `ESRI Shapefile'
## Simple feature collection with 224 features and 6 fields
## Geometry type: MULTIPOLYGON
## Dimension:     XY
## Bounding box:  xmin: -732143.5 ymin: 9445216 xmax: 1147852 ymax: 10189400
## Projected CRS: WGS 84 / UTM zone 17S

poligonos <- poligonos[poligonos$DPA_PROVIN!="90",]
poligonos <- poligonos[poligonos$DPA_PROVIN!="20",]
poligonos = merge(poligonos,datos,by.x  ="DPA_CANTON",by.y = "COD_CANT",all.x=TRUE)



# Me quedo con los datos que no son perdidos:
poligonos <- poligonos[!is.na(poligonos$POBRES_P),]

library(spdep)
set.ZeroPolicyOption(TRUE)

## [1] TRUE

# Se construye la lista de vecinos
cont.nb <- poly2nb(poligonos)
# Se construye la matriz de pesos espaciales
cont.listw <- nb2listw(cont.nb, style="W",zero.policy = TRUE)

2. Revisamos si el NBI tiene autocorrelación espacial.

y <- poligonos$POBRES_P 
x <- (poligonos$VAB_PC)
# x <- poligonos$CONSUMO_INTERMEDIO/poligonos$A_2019
# x <- poligonos$PRODUCCION/poligonos$A_2019
# cor(x,y)
# plot(y~x)
MImc <- moran.mc(y, cont.listw, 999)
MImc

## 
##  Monte-Carlo simulation of Moran I
## 
## data:  y 
## weights: cont.listw  
## number of simulations + 1: 1000 
## 
## statistic = 0.29793, observed rank = 1000, p-value = 0.001
## alternative hypothesis: greater

# (Zmi <- (MImc$statistic-mean(MImc$res))/sd(MImc$res))

Se rechaza la hipótesis nula de independencia espacial.

3. Ajustamos un modelo de regresión lineal.

mod.lm <- lm(y~x)
summary(mod.lm)

## 
## Call:
## lm(formula = y ~ x)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -0.37428 -0.08681  0.00911  0.10271  0.40619 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  0.820727   0.013324  61.597  < 2e-16 ***
## x           -0.018275   0.003332  -5.484 1.17e-07 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.1284 on 213 degrees of freedom
## Multiple R-squared:  0.1237, Adjusted R-squared:  0.1196 
## F-statistic: 30.07 on 1 and 213 DF,  p-value: 1.173e-07

En promedio, por cada unidad que aumenta el VAB per cápita, la pobreza disminuye 0.018275.

4. Revisamos si los residuos de la regresión tienen autocorrelación espacial.

library(RColorBrewer)
library(classInt)

res <- mod.lm$residuals

res.palette <- colorRampPalette(c("red","orange","white", "lightgreen","green"), space = "rgb")
pal <- res.palette(5)

classes_fx <- classIntervals(round(res,2), n=5, style="fixed", fixedBreaks=as.numeric(quantile(res)), rtimes = 1)

## Warning in classIntervals(round(res, 2), n = 5, style = "fixed", fixedBreaks = as.numeric(quantile(res)), : variable
## range greater than fixedBreaks

cols <- findColours(classes_fx,pal)


plot(st_geometry(poligonos),col=cols, border="grey",main = "Residuos del modelo OLS")
legend(x="bottomleft",cex=0.8,fill=attr(cols,"palette"),bty="n",legend=names(attr(cols, "table")),ncol=5)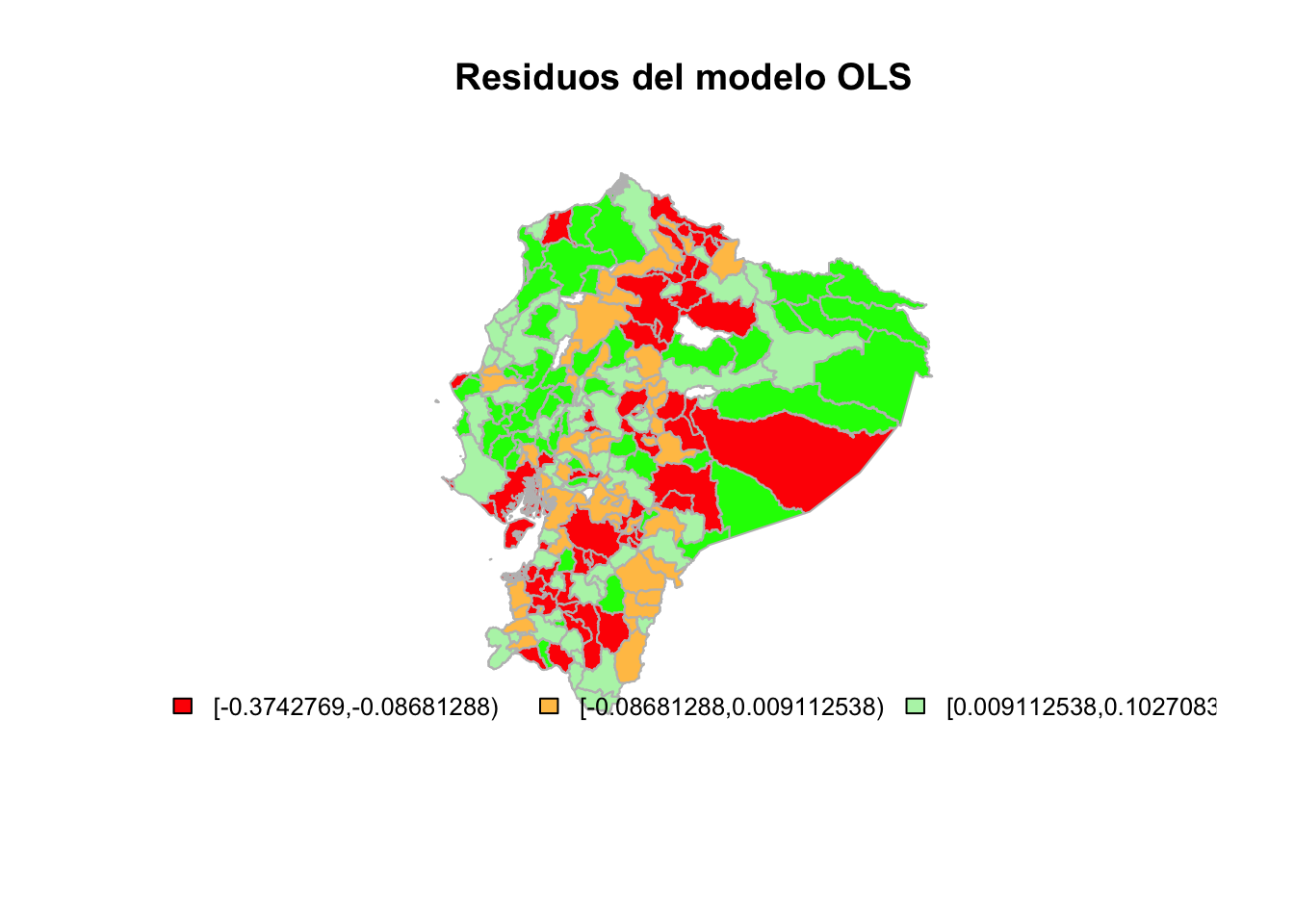

## Residual Autocorrelation

moran.mc(res, listw=cont.listw, zero.policy=T,nsim = 999)

## 
##  Monte-Carlo simulation of Moran I
## 
## data:  res 
## weights: cont.listw  
## number of simulations + 1: 1000 
## 
## statistic = 0.25128, observed rank = 1000, p-value = 0.001
## alternative hypothesis: greater

Se rechaza la hipótesis nula de independencia.

5. Caculamos el modelo SLM.

La función lagsarlm del paquete spatialreg (R. Bivand and Piras (2015)) nos permite hacer la estimación:

mod.slm <- spatialreg::lagsarlm(y~x,  listw=cont.listw, zero.policy=T, na.action=na.exclude)
summary(mod.slm,Nagelkerke= TRUE)

## 
## Call:spatialreg::lagsarlm(formula = y ~ x, listw = cont.listw, na.action = na.exclude,     zero.policy = T)
## 
## Residuals:
##        Min         1Q     Median         3Q        Max 
## -0.3592939 -0.0829217  0.0081117  0.0947552  0.3872752 
## 
## Type: lag 
## Regions with no neighbours included:
##  14 27 29 57 76 77 81 93 154 155 188 217 
## Coefficients: (asymptotic standard errors) 
##               Estimate Std. Error z value  Pr(>|z|)
## (Intercept)  0.7292456  0.0336304 21.6841 < 2.2e-16
## x           -0.0174281  0.0032459 -5.3693 7.902e-08
## 
## Rho: 0.12467, LR test value: 8.7856, p-value: 0.0030363
## Asymptotic standard error: 0.042193
##     z-value: 2.9546, p-value: 0.0031303
## Wald statistic: 8.7299, p-value: 0.0031303
## 
## Log likelihood: 141.7023 for lag model
## ML residual variance (sigma squared): 0.015611, (sigma: 0.12494)
## Nagelkerke pseudo-R-squared: 0.15881 
## Number of observations: 215 
## Number of parameters estimated: 4 
## AIC: -275.4, (AIC for lm: -268.62)
## LM test for residual autocorrelation
## test value: 14.618, p-value: 0.00013167

• LR test: test de razón de verosimilitud. Compara el modelo no espacial (con restricciones) con el espacial (sin restricciones). \(H_0: \text{OLS es mejor}\).

• Wald statistic compara las distancias entre los parámetros del modelo no espacial (con restricciones) y el espacial (sin restricciones). \(H_0: \text{OLS es mejor}\)

• Log likelihood: es la verosimilitud del modelo.

• ML residual variance: es la varianza según máxima verosimilitud.

• AIC: Akaike information criterion o criterio de información de Akaike.

• Log likelihood: es la verosomilitud del modelo.

• LM test for residual autocorrelation: test de multiplicador de lagrange para el residuo (\(H_0:\text{no autocorrelación}\)).

• Nagelkerke pseudo-R-squared se despliega solo si Nagelkerke= TRUE en el summary.

6. Revisamos si los residuos siguen presentando autocorrelación espacial:

res.sar <- resid(mod.slm)
moran.mc(res.sar, listw=cont.listw, zero.policy=T,nsim = 9999)

## 
##  Monte-Carlo simulation of Moran I
## 
## data:  res.sar 
## weights: cont.listw  
## number of simulations + 1: 10000 
## 
## statistic = 0.16673, observed rank = 9998, p-value = 2e-04
## alternative hypothesis: greater

No se rechaza la hipótesis nula de independencia.

9.3 Modelo de Durbin espacial (SDM)

El modelo de Durbin así como su forma estructural (9.9) y su forma reducida (9.10):

\[ y = \rho Wy+X\beta+WX\gamma+\epsilon \tag{9.9} \]

\[ y = (I-\rho W)^{-1}(X\beta+WX\gamma+\epsilon) \tag{9.10} \]

El SDM da como resultado un modelo espacial autorregresivo de una forma especial, que incluye no solo la variable dependiente espacialmente rezagada y las variables explicativas, sino también las variables explicativas espacialmente rezagadas, \(WX\). \(y\) depende de factores de si misma de la matriz \(X\), más los mismos factores promediados en las \(n\) regiones vecinas.

Ten en cuenta en la siguiente figura 9.3 que la Región 1 no solo ejerce un impacto en la Región 2 (y viceversa) a través de \(y\), sino también a través de la variable independiente \(x\).

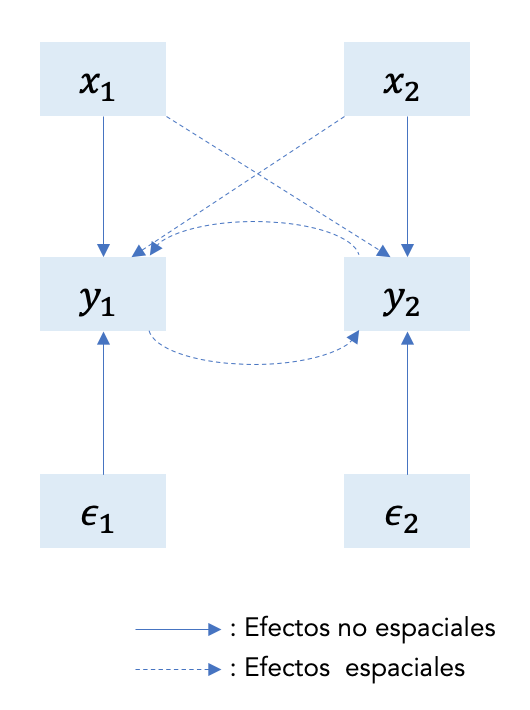
Figure 9.3: Estructura de efectos en SDM

Este modelo también tiene muy buenas propiedades en términos de cálculo de efectos marginales que exploraremos más adelante.

Siguiendo con nuestro ejemplo, la estimación de Durbin en R se puede usar el argumento type = "mixed":

mod.sdm <- spatialreg::lagsarlm(y~x,  listw=cont.listw, zero.policy=T, na.action=na.exclude,type = "mixed")
summary(mod.sdm)

## 
## Call:spatialreg::lagsarlm(formula = y ~ x, listw = cont.listw, na.action = na.exclude, 
##     type = "mixed", zero.policy = T)
## 
## Residuals:
##       Min        1Q    Median        3Q       Max 
## -0.346053 -0.083618  0.012648  0.090370  0.366270 
## 
## Type: mixed 
## Regions with no neighbours included:
##  14 27 29 57 76 77 81 93 154 155 188 217 
## Coefficients: (asymptotic standard errors) 
##               Estimate Std. Error z value  Pr(>|z|)
## (Intercept)  0.7595258  0.0339721 22.3573 < 2.2e-16
## x           -0.0167160  0.0031649 -5.2816  1.28e-07
## lag.x       -0.0182386  0.0049550 -3.6808 0.0002325
## 
## Rho: 0.15578, LR test value: 13.77, p-value: 0.00020657
## Asymptotic standard error: 0.041513
##     z-value: 3.7527, p-value: 0.00017497
## Wald statistic: 14.082, p-value: 0.00017497
## 
## Log likelihood: 148.261 for mixed model
## ML residual variance (sigma squared): 0.014656, (sigma: 0.12106)
## Number of observations: 215 
## Number of parameters estimated: 5 
## AIC: -286.52, (AIC for lm: -274.75)
## LM test for residual autocorrelation
## test value: 11.09, p-value: 0.00086803

9.4 Modelo con error espacial (SEM)

Otra forma de dependencia espacial ocurre cuando la dependencia opera a través del proceso de error, ya que los errores de diferentes áreas pueden mostrar autocorrelación espacial. El modelo SEM se formula como:

\[ y = X\beta+u \tag{9.11}\\ u = \lambda Wu+\epsilon \] donde \(\lambda\) es el parámetro autorregresivo del rezago espacial del error \(Wu\) y \(\epsilon\) es \(\text{i.i.d.}\).

En su forma estructural tenemos:

\[ y = X\beta+(I-\rho W)^{-1}\epsilon \] Esta expresión conduce a un efecto de difusión espacial global, pero no hay un efecto multiplicador espacial.

La siguiente figura 9.4 visualiza el \(SEM\) para dos regiones. Ten en cuenta que el término de error de ambas regiones está relacionado y el único efecto espacial va de \(\epsilon_1\) a \(\epsilon_2\) y viceversa.

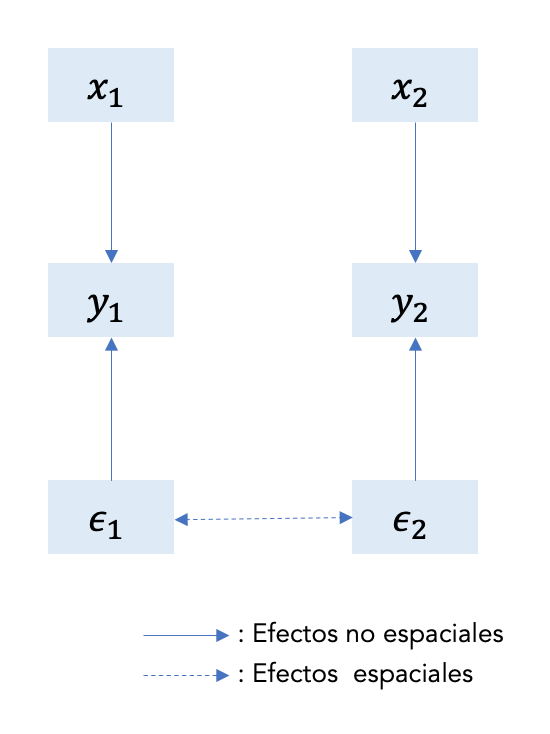
Figure 9.4: Estructura de efectos en SEM

Como afirman Luc Anselin and Bera (1998), la dependencia del error espacial puede interpretarse como una nuisance (\(\lambda\) como un parámetro de nuisance) en el sentido de que refleja la autocorrelación espacial en los errores de medición o en variables que de otro modo no son cruciales para el modelo (es decir, las variables ignoradas se propagan a través de las unidades espaciales de observación).

A diferencia de los modelos anteriores, los efectos de las interacciones entre los términos de error no requieren un modelo teórico para un proceso de interacción espacial o social, sino que son consistentes con una situación en la que los determinantes de la variable dependiente omitidos del modelo están espacialmente autocorrelacionados, o con una situación donde los choques no observados siguen un patrón espacial.

Los efectos de interacción entre los términos no observados también pueden interpretarse como un mecanismo para corregir a los políticos que buscan rentas por cambios imprevistos en la política fiscal. Ver por ejemplo, Allers and Elhorst (2005).

Siguiendo con nuestro ejemplo, la estimación de \(SEM\) en R se puede usar la función errorsarlm:

mod.sem <- spatialreg::errorsarlm(y~x,  listw=cont.listw, zero.policy=TRUE)
summary(mod.sem)

## 
## Call:spatialreg::errorsarlm(formula = y ~ x, listw = cont.listw, zero.policy = TRUE)
## 
## Residuals:
##       Min        1Q    Median        3Q       Max 
## -0.353228 -0.086281  0.017956  0.091724  0.336851 
## 
## Type: error 
## Regions with no neighbours included:
##  14 27 29 57 76 77 81 93 154 155 188 217 
## Coefficients: (asymptotic standard errors) 
##               Estimate Std. Error z value  Pr(>|z|)
## (Intercept)  0.8130830  0.0155231 52.3788 < 2.2e-16
## x           -0.0144655  0.0030446 -4.7512 2.022e-06
## 
## Lambda: 0.38912, LR test value: 22.817, p-value: 1.7814e-06
## Asymptotic standard error: 0.077092
##     z-value: 5.0474, p-value: 4.4776e-07
## Wald statistic: 25.477, p-value: 4.4776e-07
## 
## Log likelihood: 148.7183 for error model
## ML residual variance (sigma squared): 0.01411, (sigma: 0.11879)
## Number of observations: 215 
## Number of parameters estimated: 4 
## AIC: -289.44, (AIC for lm: -268.62)

Vemos la prueba de Moran sobre el residuo del modelo para evaluar si la autocorrelación ha sido removida:

set.seed(1)
moran.mc(resid(mod.sem),listw=cont.listw, zero.policy=TRUE,999)

## 
##  Monte-Carlo simulation of Moran I
## 
## data:  resid(mod.sem) 
## weights: cont.listw  
## number of simulations + 1: 1000 
## 
## statistic = -0.012407, observed rank = 452, p-value = 0.548
## alternative hypothesis: greater

Al no rechazar la hipótesis nula, podemos concluir que el residuo del modelo SEM ya no presenta autocorrelación espacial.

9.5 El mejor modelo espacial

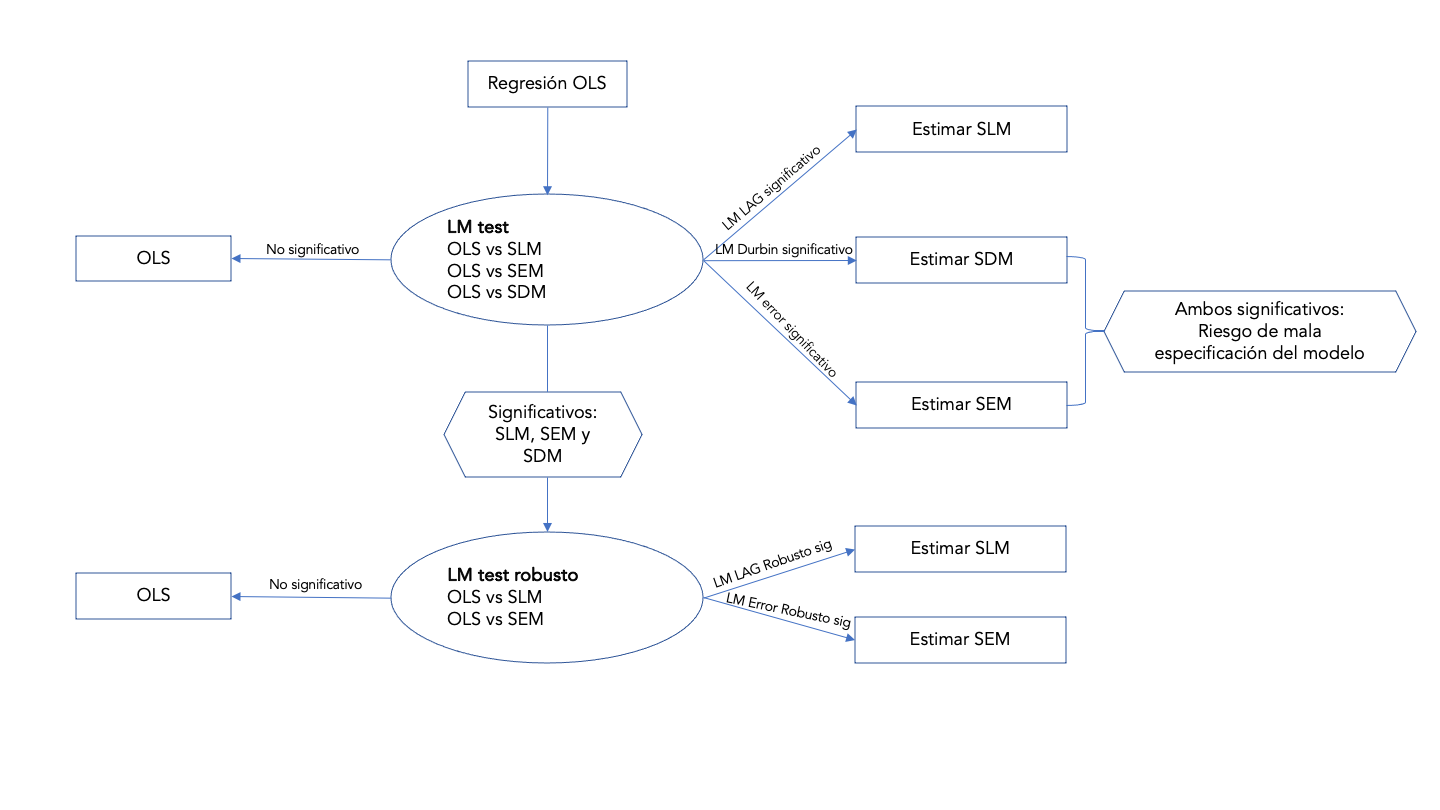
¿Cómo decidir? Para el caso simple de elegir entre una alternativa SLM o SEM, existe evidencia de que el modelo adecuado es probablemente el que tiene el valor de prueba LM significativo más grande (Luc Anselin and Rey (1991)).

• Cuando el test \(\text{LM}_{LAG}\) es significativo y el \(\text{LM}_{ERR}\) es no es significativo, el modelo más apropiado es el modelo \(\text{SLM}\);

• en la misma línea, cuando la prueba \(\text{LM}_{ERR}\) es significativa y el valor \(\text{LM}_{LAG}\) no es significativo, el modelo más apropiado es el modelo \(\text{SEM}\).

Como puede adivinar, a veces es posible encontrar que ambas pruebas estadísticas son significativas. En este caso, una regla de decisión puede ser la siguiente:

• cuando el valor \(\text{LM}_{LAG}\) de prueba es mayor que el valor \(\text{LM}_{ERR}\) de prueba, sería mejor considerar el modelo \(\text{SLM}\);

• cuando el valor \(\text{LM}_{ERR}\) de prueba es mayor que el valor \(\text{LM}_{LAG}\) de prueba, sería mejor considerar el modelo \(\text{SEM}\)

Por supuesto, si ambas estadísticas son significativas, también podría ser apropiado estimar un modelo autorregresivo general (\(\text{SAC}\)).

Siguiendo con nuestro ejemplo, la prueba del multiplicador de Lagrange en R se puede hacer con la función lm.RStests:

LM <- lm.RStests(mod.lm, cont.listw, test="all")
print(LM)

## 
##  Rao's score (a.k.a Lagrange multiplier) diagnostics for spatial dependence
## 
## data:  
## model: lm(formula = y ~ x)
## test weights: cont.listw
## 
## RSerr = 26.077, df = 1, p-value = 3.28e-07
## 
## 
##  Rao's score (a.k.a Lagrange multiplier) diagnostics for spatial dependence
## 
## data:  
## model: lm(formula = y ~ x)
## test weights: cont.listw
## 
## RSlag = 9.0494, df = 1, p-value = 0.002628
## 
## 
##  Rao's score (a.k.a Lagrange multiplier) diagnostics for spatial dependence
## 
## data:  
## model: lm(formula = y ~ x)
## test weights: cont.listw
## 
## adjRSerr = 17.568, df = 1, p-value = 2.772e-05
## 
## 
##  Rao's score (a.k.a Lagrange multiplier) diagnostics for spatial dependence
## 
## data:  
## model: lm(formula = y ~ x)
## test weights: cont.listw
## 
## adjRSlag = 0.54024, df = 1, p-value = 0.4623
## 
## 
##  Rao's score (a.k.a Lagrange multiplier) diagnostics for spatial dependence
## 
## data:  
## model: lm(formula = y ~ x)
## test weights: cont.listw
## 
## SARMA = 26.617, df = 2, p-value = 1.66e-06

Las pruebas \(LM\) robustas tienen en cuenta la posibilidad alternativa, es decir, la prueba LMerr responderá tanto a una variable dependiente rezagada espacialmente omitida como a los residuos autocorrelacionados espacialmente, mientras que la prueba RLMerr robusta está diseñada para probar residuos autocorrelacionados espacialmente en la posible presencia de una variable dependiente espacialmente rezagada omitida.

9.6 Interpretación de los modelos espaciales

9.6.1 Propagación (spillovers) espaciales

Un enfoque importante de la ciencia regional es el desbordamiento espacial. Una definición básica de derrames en un contexto espacial sería que los cambios que ocurren en una región ejercen impactos en otras regiones (J. P. LeSage and Pace (2014)). Algunos ejemplos son:

• Los cambios en la tasa impositiva por una unidad espacial podrían tener un impacto en las decisiones de fijación de la tasa impositiva de las regiones cercanas, un fenómeno que ha sido etiquetado como imitación de impuestos y competencia de criterios entre gobiernos locales.

• Situaciones en las que las mejoras a la vivienda realizadas por un propietario ejercen un impacto beneficioso en los precios de venta de las viviendas vecinas.

• La innovación de los investigadores universitarios se difunde a las empresas cercanas.

• La contaminación del aire o del agua generada en una región se extiende a las regiones cercanas.

9.6.1.1 Spillovers globales

Los efectos de propagación globales surgen cuando los cambios en una característica de una región afectan los resultados de todas las regiones. Esto se aplica incluso a la propia región, ya que los impactos pueden pasar a los vecinos y regresar a la propia región (retroalimentación). Específicamente, los spillovers globales impactan a los vecinos, los vecinos a los vecinos, los vecinos a los vecinos de los vecinos, etc.

9.6.1.2 Spillovers locales

Los efectos de propagación locales representan una situación en la que el impacto recae solo en los vecinos cercanos o inmediatos, desapareciendo antes de que afecten a las regiones vecinas de los vecinos.

Como se puede observar en las definiciones anteriores, la principal diferencia es que la retroalimentación o la interacción endógena solo es posible para los efectos de contagio globales.

9.6.2 Efectos marginales

Matemáticamente, la noción de spillover puede pensarse como la derivada \(\partial y_i/\partial x_j\). Esto significa que los cambios en las variables explicativas en la región \(i\) impactan en la variable dependiente en la región \(j \neq i\).

En general, se puede notar que el cambio de cada variable en cada región implica \(n^2\) efectos marginales potenciales. Si tenemos \(K\) variables en nuestro modelo, esto implica \(K\times n^2\) medidas potenciales. Incluso para valores pequeños de \(n\) y \(K\), puede resultar bastante difícil informar estos resultados de forma compacta.

Para superar este problema, J. LeSage and Pace (2009) (p. 36-37) proponen las siguientes medidas de resumen escalares:

9.6.2.1 Impacto directo promedio (ADI)

Sea \(S_r = A(W)^{-1}(I_n\beta_r+W\theta_r)\) para la variable \(r\) (\(A(W)=(I_n-\rho W)\)). El impacto de los cambios en la i-ésima observación de \(x_r\), denotada por \(x_{ir}\), en \(y_i\) puede ser resumida midiendo el promedio \(S_r(W)_{ii}\):

\[ \text{ADI}=\frac{1}{n}\text{tr}(S_r(W)) \tag{9.12} \]

El promedio sobre el impacto directo asociado con todas las observaciones \(i\) es similar a las interpretaciones típicas de coeficientes de regresión que representan la respuesta promedio de las variables dependientes a independientes.

Por ejemplo, si la región \(i\) aumenta el número de viajeros que usan el transporte público, ¿cuál será el impacto promedio en los tiempos de viaje en la región \(i\)? Esta medida tendrá en cuenta los efectos de retroalimentación que surgen del cambio en el uso del transporte público de la \(i\)-ésima región en los tiempos de desplazamiento de las regiones vecinas en el sistema de regiones espacialmente dependientes.

9.6.2.2 Impacto total promedio hacia una observación (ATIT)

Sea \(S_r = A(W)^{-1}(I_n\beta_r+W\theta_r)\) para la variable \(r\) (\(A(W)=(I_n-\rho W)\)). La suma en la \(i\)-ésima fila de \(S_r (W)\) representaría el impacto total en la observación individual \(y_i\) resultante de cambiar la \(r\)-ésima variable explicativa en la misma cantidad en todas las \(n\) observaciones. Hay \(n\) de estas sumas dadas por el vector de columna \(c_r = S_r (W)\iota_n\), por lo que un promedio de estos impactos totales es:

\[ \text{ATIT} = \frac{1}{n}\iota'_nc_r \tag{9.13} \]

donde \(\iota_n\) denota un vector columna compuesto de unos, esto es: \(\iota_n = (1,1,\ldots,1)'\).

9.6.2.3 Impacto total promedio desde una observación (ATIF)

Sea \(S_r = A(W)^{-1}(I_n\beta_r+W\theta_r)\) para la variable \(r\) (\(A(W)=(I_n-\rho W)\)). La suma de la \(j\)-ésima columna de \(S_r (W)\) produciría el impacto total sobre todo \(y_i\) al cambiar la \(r\)-ésima variable explicativa en una cantidad en la \(j\)-ésima observación. Hay \(n\) de estas sumas dadas por el vector fila \(r_r\iota'_nS_r(W)\), por lo que un promedio de estos impactos totales es:

\[ \text{ATIF} = \frac{1}{n}r_r\iota_n \tag{9.14} \]

La ecuación (9.14) relaciona cómo los cambios en una sola observación \(j\) influyen en todas las observaciones. Por el contrario, la ecuación (9.13) considera cómo los cambios en todas las observaciones influyen en una sola observación \(i\). En ambos casos, promediar todas las \(n\) observaciones conduce al mismo resultado numérico. La implicación de este interesante resultado es que el impacto total promedio es el promedio de todas las derivadas de \(y_i\) con respecto a \(x_{jr}\) para cualquier \(i\), \(j\).

Entonces

\[ \bar{M}(r)_{\text{directo}} = n^{-1}\text{tr}(S_r(W)) \] \[ \bar{M}(r)_{\text{total}} = n^{-1}\iota'_n\text{tr}(S_r(W))\iota_n \]

\[ \bar{M}(r)_{\text{indirecto}} = \bar{M}(r)_{\text{total}}-\bar{M}(r)_{\text{directo}} \]

Para el modelo SEM, las propagaciones espaciales (spillovers) son cero por diseño, como en el caso de los modelos de regresión no espacial. Es decir, los coeficientes se interpretan como en regresión lineal clásica: la estimación del parámetro \(\beta_r\) es igual al efecto marginal promedio de la variable sobre la variable dependiente \(y\).

Siguiendo con nuestro ejemplo, el modelo elegido es el \(\text{SEM}\), en R estimamos sus impactos con la función impacts:

spatialreg::impacts(mod.slm, listw=cont.listw)

## Impact measures (lag, exact):
##        Direct    Indirect       Total
## x -0.01749413 -0.00241609 -0.01991023

Tras bastidores:

listw = cont.listw
slm <- mod.slm

rho <- slm$rho # rho estimado del modelo SLM
beta_hat <- coef(slm)[-1] # Parámtros estimados
A <- spatialreg::invIrW(listw, rho = rho) # (I - rho*W)^{-1}
X <- cbind(1, x) # Matriz de covariables
y_hat_pre <- A %*% crossprod(t(X), beta_hat) # y estimado

## Construimos: S_r(W) = A(W)^-1 (I * beta_r + W * theta_r)
Ibeta <- diag(length(listw$neighbours)) * coef(slm)["x"]
S <- A %*% Ibeta
ADI <- sum(diag(S)) / nrow(A) # Directo

n <- length(listw$neighbours)
Total <- crossprod(rep(1, n), S) %*% rep(1, n) / n

Indirect <- Total - ADI

c(Direct = ADI, Indirect=Indirect,Total = Total)

##       Direct     Indirect        Total 
## -0.017494135 -0.002277553 -0.019771688

Pruebe los modelos \(SLM\), \(SDM\) y \(SEM\), recuerde agregar covariables al modelo.

9.6.3 Una interpretación más práctica

• Difusión y efectos externos (desbordamiento): la mayoría de las veces se derivan de efectos directos e indirectos, que miden el impacto de variables exógenas en una ubicación y vecindario determinados. Muestran la interdependencia de las unidades espaciales: cuando es positivo, la mayoría de las veces se interpreta como cooperación y cuando es negativo, como separación/rivalidad/competencia.

	Efecto directo	Efecto Indirecto (spillover)
OLS/SEM	\(\beta_k\)	0
SAR/SAC	Elementos diagonales de la matriz \((I-\rho W)^{-1}\beta_k\)	Elementos NO diagonales de la matriz \((I-\rho W)^{-1}\beta_k\)
SXL/SDEM	\(\beta_k\)	\(\theta_k\)
SDM/GNS	Elementos diagonales de la matriz \((I-\rho W)^{-1}[\beta_k+W\theta_k]\)	Elementos NO diagonales de la matriz \((I-\rho W)^{-1}[\beta_k+W\theta_k]\)

donde,

• Modelos con dos componentes espaciales:

  • \(SAC\) (spatial autocorrelation model): \(Y = \beta_0+\rho W Y+X\beta+u \text{ donde } u = \lambda Wu+e\)
  • \(SDM\) (spatial Durbin model): \(Y = \beta_0+\rho W Y+X\beta+WX\theta+e\)
  • \(SDEM\) (spatial Durbin error model): \(Y = \beta_0+X\beta+WX\theta+u \text{ donde } u = \lambda Wu+e\)

• Modelos con un componente espacial

  • \(SAR\) (spatial autoregressive model): \(Y = \beta_0+\rho W Y+X\beta+e\) - \(SEM\) (spatial error model): \(Y = \beta_0+X\beta+u \text{ donde } u = \lambda Wu+e\)
    
  • \(SLX\) (explanatory variables spatially lagged): \(Y = \beta_0+X\beta++WX\theta+e\)

9.6.3.1 Signos

9.6.3.1.1 Efectos Directos positivos, Indirectos positivos

Cuando ambos efectos (directos e indirectos) son positivos, es decir, un aumento de \(x_i\) en la región \(i\) y un aumento de \(x_j\) en la vecindad de \(j\) se traducen en un aumento de \(y_i\) en la región \(i\); esto significa que existe un efecto de apoyo en los procesos, indistintamente de la ubicación.

Un aumento en la variable explicativa (por ejemplo, ingresos, inversión en infraestructura, etc.) en una región determinada potencia el resultado a nivel local (efecto directo), y este cambio positivo se transmite a las regiones cercanas, creando un impacto positivo allí también (efecto indirecto).

Caso de ejemplo:

Consideremos un modelo econométrico espacial que evalúa el impacto de la inversión en parques públicos sobre los valores de las propiedades:

• Efecto directo (positivo): la inversión en parques públicos aumenta directamente los valores de las propiedades en la región donde se ubica el parque.

• Efecto indirecto (positivo): la mejora en una región también influye positivamente en los valores de las propiedades en las regiones circundantes debido a los beneficios compartidos, como un mayor atractivo o mejores servicios regionales.

Implicaciones de política:

• Beneficios amplificados: una intervención de política (como el desarrollo de infraestructura o mejoras ambientales) en una región puede generar un efecto multiplicador, donde los beneficios no solo afectan el área objetivo sino también a las regiones vecinas.

• Planificación coordinada: la presencia de efectos indirectos positivos resalta la necesidad de una planificación espacial coordinada, ya que las mejoras en un área pueden tener impactos regionales más amplios.

9.6.3.1.2 Efectos Directos negativos, Indirectos negativos

• Cuando ambos efectos son negativos, es decir, un aumento de \(x_i\) en la región \(i\) y un aumento de \(x_j\) en la vecindad de \(j\) se traducen en una disminución de \(y_i\) en la región \(i\) – esto significa que existe un efecto de debilitamiento mutuo de los procesos, independientemente de la ubicación.

Esto indica que la variable en estudio tiene consecuencias adversas tanto dentro de la región de interés como en las regiones vecinas:

Un aumento en la variable explicativa provoca una disminución local del resultado (efecto directo). Este cambio negativo también se transmite a las regiones vecinas, lo que genera nuevas disminuciones en esas áreas (efecto indirecto).

Caso de ejemplo:

Consideremos un modelo econométrico espacial que investiga el impacto de las tasas de criminalidad en los valores de las propiedades:

• Efecto directo (negativo): un aumento de las tasas de criminalidad en la región A reduce directamente los valores de las propiedades en la región A.

• Efecto indirecto (negativo): el aumento de la delincuencia en la región A también hace que los valores de las propiedades disminuyan en las regiones circundantes debido al temor a que la delincuencia se propague, la reputación regional o la disminución del atractivo.

Implicaciones de política:

• Impactos negativos amplificados: la presencia de efectos indirectos negativos sugiere que las consecuencias nocivas de un factor (por ejemplo, delincuencia, contaminación, declive económico) se extienden más allá del área de origen e influyen negativamente en las regiones vecinas.

• Riesgos de propagación regional: los responsables de las políticas deben considerar que abordar los problemas en una región puede no ser suficiente, ya que las consecuencias negativas pueden perpetuar los problemas en las áreas circundantes. La cooperación regional o intervenciones políticas más amplias pueden ser necesarias para mitigar los efectos generalizados.

Consideración especial:

En algunos casos, los efectos indirectos negativos pueden indicar competencia o desplazamiento entre regiones. Por ejemplo, si una región aumenta su tasa impositiva, las empresas podrían mudarse a áreas vecinas, lo que afectaría negativamente la producción económica de la región original así como de sus vecinas.

9.6.3.1.3 Efectos Directos negativos, Indirectos positivos

Cuando los efectos directos son negativos y los indirectos positivos, es decir, un aumento de \(x_i\) en la región \(i\) se traduce en una disminución de \(y_i\) en la región \(i\), mientras que un aumento de \(x_j\) en la vecindad de \(j\) se traduce en un aumento de \(y_i\) en la región \(i\), esto significa que los factores interactúan de manera diferente, muchas veces debido a la aparición de desventajas/distorciones en la escala o a la aparente heterogeneidad de las áreas de estudio y vecinas.

Este patrón de efectos directos negativos y efectos indirectos positivos puede interpretarse como impactos negativos localizados con beneficios regionales:

La región que experimenta un aumento en la variable explicativa sufre un impacto negativo directo, pero las regiones vecinas pueden beneficiarse de los efectos indirectos o de la redistribución de los impactos negativos.

Caso de ejemplo:

Consideremos un modelo de regresión espacial que examina los efectos de la congestión urbana:

• Efecto directo (negativo): un aumento de la congestión del tráfico en la región A conduce directamente a una disminución de la calidad de vida local (por ejemplo, mayor contaminación, tiempos de viaje más largos y menores valores de las propiedades).

• Efecto indirecto (positivo): las regiones vecinas (regiones B y C) podrían beneficiarse de la congestión en la región A. Por ejemplo, las empresas o los residentes pueden trasladarse de la congestionada región A a regiones vecinas, lo que aumenta los valores de las propiedades o mejora la actividad económica en esas áreas.

Implicaciones de política:

• Distribución desigual de los efectos: las políticas destinadas a abordar cuestiones como la contaminación, la congestión o la actividad industrial pueden tener que considerar tanto los efectos locales como los regionales. Un efecto directo negativo sugiere daños o costos localizados, mientras que los efectos indirectos positivos implican que algunas regiones podrían beneficiarse a expensas del área afectada.

• Redistribución espacial: la combinación de efectos directos negativos e indirectos positivos podría indicar efectos indirectos o spillover en los que las regiones vecinas se benefician a medida que las personas, las empresas o los recursos se alejan de la región afectada.

Casos específicos:

• Shocks económicos: una región que experimenta una recesión económica (por ejemplo, pérdidas de empleos en la región A debido al cierre de fábricas) podría sufrir efectos directos negativos, pero las regiones vecinas podrían beneficiarse del desplazamiento de trabajadores o empresas, lo que daría lugar a efectos indirectos positivos para esas áreas.

• Regulación ambiental: supongamos que una región endurece las regulaciones ambientales, lo que hace que las industrias locales sufran (efecto directo negativo). Las regiones vecinas podrían beneficiarse a medida que las empresas se reubican, lo que lleva empleos y actividad económica a las áreas circundantes (efecto indirecto positivo).

9.6.3.1.4 Efectos Directos positivos, Indirectos negativos

• Cuando los efectos directos son positivos y los efectos indirectos son negativos, es decir, un aumento de \(x_i\) en la región \(i\) se traduce en un aumento de \(y_i\) en la región \(i\), mientras que un aumento de \(x_j\) en el vecindario \(j\) se traduce en una disminución de \(y_i\) en la región \(i\) – esta es la relación de lixiviación, cuando los recursos de una ubicación trabajan a favor de otra ubicación, debilitando su propia ubicación.

9.7 Evaluación del modelo de regresión espacial

La evaluación de la calidad de los modelos espaciales tiene reglas ligeramente diferentes a la evaluación de otros tipos de modelos econométricos.

1. La normalidad o heterocedasticidad típica de los residuos y las variables no se estudia generalmente, ya que los modelos espaciales no tienen tales supuestos (Baltagi and Yang (2013) desarrollaron una versión de la prueba LM resistente a la falta de normalidad y heterocedasticidad de los residuos).

2. Cuando se detectan valores atípicos, no se eliminan en los modelos sobre datos de área, sino que se modelan, por ejemplo, con variables ficticias (cero-uno). Su eliminación podría causar discontinuidad espacial y deficiencias en los datos en las áreas del mapa relacionado y, como consecuencia, una matriz de ponderaciones espaciales incompatible W.

3. Un elemento importante del diagnóstico es la evaluación de la autocorrelación espacial de los residuos utilizando las estadísticas I de Moran, que permiten determinar si es necesario un modelo espacial cuando se prueban residuos que se originan en MCO o si el modelo espacial ha filtrado con éxito la relación espacial cuando se examinan los residuos del modelo espacial.

4. En la evaluación del ajuste de los modelos espaciales, debido a la estimación MLE, se utiliza con mayor frecuencia el criterio de información de Akaike, el criterio bayesiano (BIC) o el criterio LogLik, mientras que el pseudo-R2 se utiliza en mucha menor medida.

5. La búsqueda del mejor modelo consiste en encontrar dicha especificación y tener en cuenta la clase de modelo, el método de estimación y la selección de variables para que la significancia de los coeficientes sea la más ventajosa. Son aplicables las recomendaciones de la Asociación Estadounidense de Estadística de 2016 con respecto a la comprensión del valor p y su uso en la evaluación de la calidad de la regresión (Wasserstein and Lazar (2016)).

6. Las pruebas de heterocedasticidad espacial basadas en estadísticas de escaneo (scan test) para datos puntuales (Le Gallo, López, and Chasco (2020)) o las denominadas LOSH son una extensión de las medidas de autocorrelación espacial G local (Ord and Getis (1995), Ord and Getis (2012)). Permiten rastrear la formación de agrupaciones espaciales de residuos a partir de modelos y así inferir características locales no observadas.

9.7.1 Ajuste del modelo: criterios de información y pseudo \(R^2\)

Las siguientes medidas están disponibles para los modelos espaciales: Akaike, Bayesiano, logLik y pseudo-\(R^2\).

Akaike

Tiene por fórmula

\[ AIC = -2\text{logLik}+2k = A+N\log(\frac{RSS}{N})+2k \]

donde \(N\) es el número de observaciones, RSS es la suma de los residuos al cuadrado, \(k\) es el número de parámetros estimados y \(A\) es una constante.

BIC

Tiene por fórmula

\[ BIC = -2\text{logLik}+k\log N = A+N\log(\frac{RSS}{N})+2k+k\log N \]

Tanto AIC como BIC dependen del tamaño de la muestra; por lo tanto, son incomparables para la misma especificación estimada en diferentes tamaños de conjuntos de datos.

Utilizando los criterios de información, se elige un modelo para el cual el AIC y/o el BIC sean los más bajos (también para valores negativos).

En R:

#AIC:
AIC(mod.slm)

## [1] -275.4047

mod.slm$AIC_lm.model

## [1] -268.6191

#BIC:
BIC(mod.slm)

## [1] -261.9221

# loglik:
logLik(mod.slm)

## 'log Lik.' 141.7023 (df=4)

mod.slm$LL

##          [,1]
## [1,] 141.7023

Pseudo \(R^2\)

Tiene por fórmula

\[ R^2_{\text{Nagelkerke}} = \frac{R^2_{\text{Cox and Snell}}}{1 - (L_0)^{\frac{2}{N}}} \]

donde

• \(L_0\) es la verosimilitud del modelo nulo (solo intercepto).
• \(N\) es el tamaño de la muestra.
• \(R^2_{\text{Cox and Snell}} = 1 - \left(\frac{L_0}{L_1}\right)^{\frac{2}{N}}\)
• \(L_1\) es la verosimilitud del modelo ajustado (el modelo con predictores).

Al examinar el pseudo-\(R^2\), como en el caso del \(R^2\) tradicional, se busca un modelo con el valor más alto de esta medida.

9.7.2 Test de heterocedasticidad

En el diagnóstico de modelos lineales y espaciales se puede comprobar la heterocedasticidad de los residuos. Se puede utilizar

1. Prueba de Breusch-Pagan (prueba BP): supone en \(H_0\) que la varianza de los residuos es constante (homocedastasticidad) y en \(H_1\) que la varianza de los residuos es inestable (heterocedasticidad).

2. Prueba LOSH relacionada con G local: Mide la varianza de una variable de vecindad, indicando áreas con variabilidad uniforme y variada. Valores altos de \(H_i\) indican un entorno heterogéneo, mientras que los valores bajos indican homogeneidad local.

En el caso de heterocedasticidad estadísticamente significativa, se deben utilizar modelos de heterogeneidad espacial.

La heterogeneidad espacial significa que los procesos son inestables en el espacio.

La heterogeneidad puede ser resultado de:

• Una especificación funcional deficiente del modelo o de una especificación incorrecta del modelo, por ejemplo, al omitir una variable. En ese caso, la distribución espacial de los errores del modelo es como la distribución de la variable omitida.

• Inestabilidad de los parámetros, por ejemplo, la inestabilidad estructural o los patrones heterocedásticos de grupo (por ejemplo, regiones del sur/no sur, aldea/ciudad). Estos patrones se denominan regímenes espaciales (Luc Anselin (1988)).

En R:

library(lmtest)

bptest(mod.lm)

## 
##  studentized Breusch-Pagan test
## 
## data:  mod.lm
## BP = 82.94, df = 1, p-value < 2.2e-16

spatialreg::bptest.Sarlm(mod.sdm)

## 
##  studentized Breusch-Pagan test
## 
## data:  
## BP = 73.937, df = 2, p-value < 2.2e-16

spatialreg::bptest.Sarlm(mod.slm)

## 
##  studentized Breusch-Pagan test
## 
## data:  
## BP = 83.53, df = 1, p-value < 2.2e-16

spatialreg::bptest.Sarlm(mod.sem)

## 
##  studentized Breusch-Pagan test
## 
## data:  
## BP = 67.548, df = 1, p-value = 2.22e-16

LOSH1 <- function (x, listw, a = 2, var_hi = TRUE, zero.policy = NULL, 
          na.action = na.fail, spChk = NULL) 
{
  if (is.null(zero.policy)) 
    zero.policy <- get("zeroPolicy", envir = .spdepOptions)
  stopifnot(is.logical(zero.policy))
  n <- length(listw$neighbours)
  if (n != length(x)) 
    stop("Different numbers of observations")
  NAOK <- deparse(substitute(na.action)) == "na.pass"
  NAOK <- TRUE
  if (var_hi) {
    res <- matrix(nrow = n, ncol = 6)
    colnames(res) <- c("Hi", "E.Hi", "Var.Hi", "Z.Hi", "x_bar_i", 
                       "ei")
  }
  else {
    res <- matrix(nrow = n, ncol = 3)
    colnames(res) <- c("Hi", "x_bar_i", "ei")
  }
  Wi <- vapply(listw$weights, sum, FUN.VALUE = 0)
  res[, "x_bar_i"] <- lag.listw(listw, x, zero.policy = zero.policy, 
                                NAOK = NAOK)/Wi
  res[, "ei"] <- abs(x - res[, "x_bar_i"])^a
  denom_hi <- mean(res[, "ei"],na.rm = TRUE) * Wi
  res[, "Hi"] <- lag.listw(listw, res[, "ei"], zero.policy = zero.policy, 
                           NAOK = NAOK)/denom_hi
  if (var_hi) {
    var_ei <- (sum(res[, "ei"]^2,na.rm = TRUE)/n) - mean(res[, "ei"],na.rm = TRUE)^2
    res[, "Var.Hi"] <- (n - 1)^(-1) * denom_hi^(-2) * var_ei * 
      (n * vapply(listw$weights, function(y) sum(y^2), 
                  FUN.VALUE = 0) - Wi^2)
    res[, "Z.Hi"] <- (2 * res[, "Hi"])/res[, "Var.Hi"]
    res[, "E.Hi"] <- 1
  }
  res
}

lt.lm <- LOSH1(mod.lm$residuals, cont.listw, a=2, var_hi=TRUE, zero.policy=TRUE, na.action=na.exclude)
lt.spatial <- LOSH1(mod.sdm$residuals, cont.listw, a=2, var_hi=TRUE, zero.policy=TRUE, na.action=na.exclude)
summary(lt.spatial)

##        Hi               E.Hi       Var.Hi            Z.Hi              x_bar_i               ei          
##  Min.   :0.00193   Min.   :1   Min.   :0.1338   Min.   : 0.002094   Min.   :-0.23397   Min.   :0.000001  
##  1st Qu.:0.41510   1st Qu.:1   1st Qu.:0.3000   1st Qu.: 1.827028   1st Qu.:-0.06789   1st Qu.:0.001370  
##  Median :0.91230   Median :1   Median :0.4543   Median : 4.100446   Median :-0.02074   Median :0.007292  
##  Mean   :1.06572   Mean   :1   Mean   :0.5520   Mean   : 5.384723   Mean   :-0.01252   Mean   :0.016435  
##  3rd Qu.:1.55128   3rd Qu.:1   3rd Qu.:0.6086   3rd Qu.: 8.149815   3rd Qu.: 0.04778   3rd Qu.:0.021116  
##  Max.   :5.42973   Max.   :1   Max.   :1.8432   Max.   :21.419139   Max.   : 0.22144   Max.   :0.128267  
##  NA's   :12                    NA's   :12       NA's   :12          NA's   :12         NA's   :12

summary(lt.spatial[,"Hi"])

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max.    NA's 
## 0.00193 0.41510 0.91230 1.06572 1.55128 5.42973      12

library(ggplot2)
ggplot() + 
  geom_sf(data = poligonos, aes(fill = lt.spatial[,"Hi"]))+
  ggtitle("Distribución espacial de las estadísticas LOSH para los residuos del modelo SDM")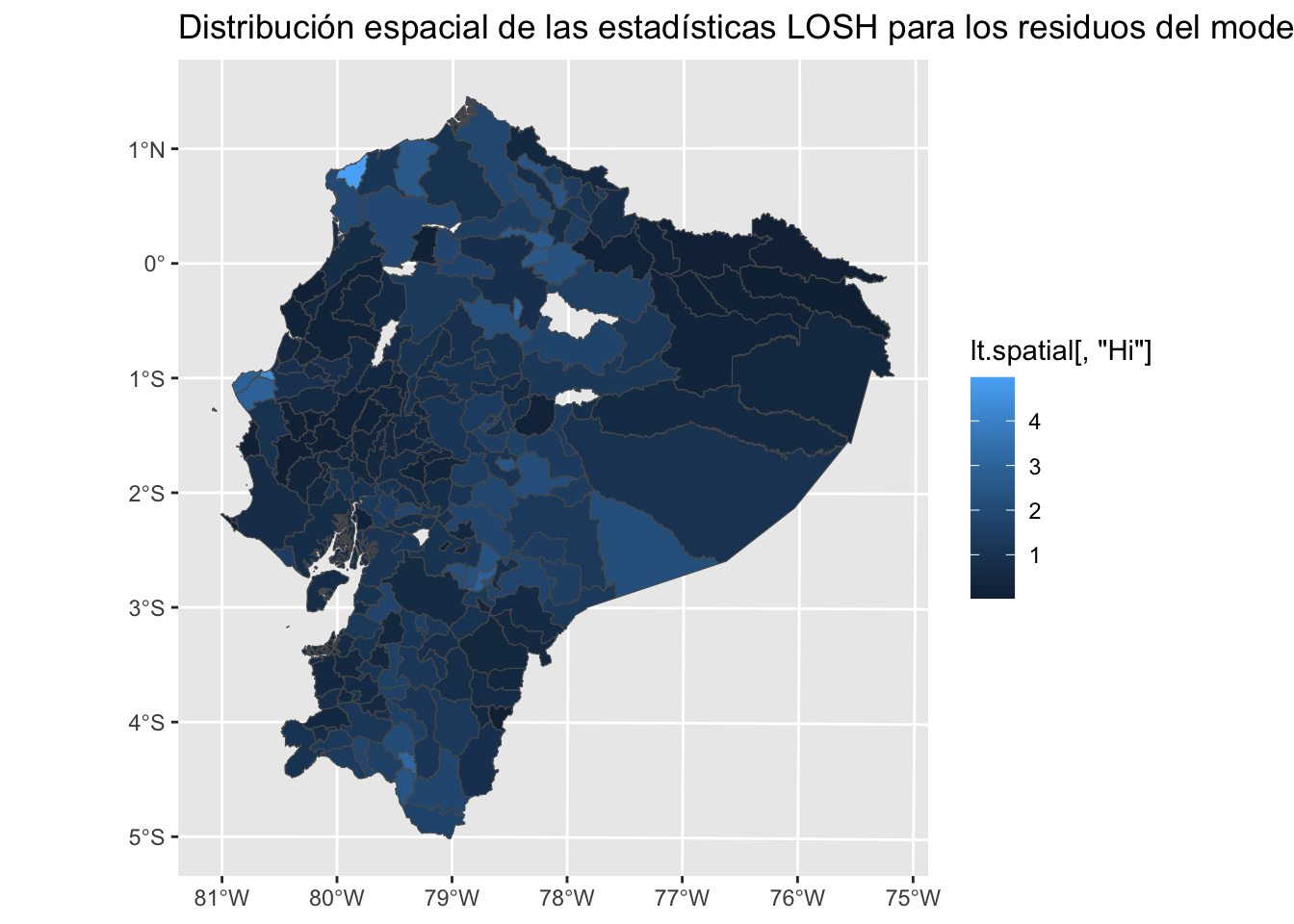

# ggplot() + 
#   geom_sf(data = poligonos, aes(fill = lt.lm[,"Hi"]))+
#   ggtitle("Distribución espacial de las estadísticas LOSH para los residuos del modelo OLS")

9.7.3 Autocorrelación de residuos

En econometría espacial, el primer paso para el diagnóstico del modelo es estudiar los residuos de un modelo lineal para detectar la ocurrencia de autocorrelación espacial. Para este propósito, se utiliza el I de Moran para residuos, así como las estadísticas join-count.

La existencia de autocorrelación espacial en los residuos no implica necesariamente el uso de modelos espaciales, sino que puede ser resultado del efecto de estimar una relación no lineal con un modelo lineal.

En esta situación, conviene comprobar los residuos del modelo estimado por MCO sobre logaritmos de las variables (Cliff and Ord (1981)). Si a pesar de ello persiste la autocorrelación espacial, la razón de este estado puede ser la omisión de variables en el modelo.

En una situación en la que se produce autocorrelación espacial a pesar de la regresión sobre logaritmos y la adición de una variable que explica la variabilidad espacial (variable omitida), es necesario estimar modelos espaciales.

moran.test(mod.lm$residuals,cont.listw)

## 
##  Moran I test under randomisation
## 
## data:  mod.lm$residuals  
## weights: cont.listw  
## n reduced by no-neighbour observations  
## 
## Moran I statistic standard deviate = 4.9682, p-value = 3.38e-07
## alternative hypothesis: greater
## sample estimates:
## Moran I statistic       Expectation          Variance 
##       0.251276078      -0.004950495       0.002659856

moran.test(mod.sem$residuals,cont.listw)

## 
##  Moran I test under randomisation
## 
## data:  mod.sem$residuals  
## weights: cont.listw  
## n reduced by no-neighbour observations  
## 
## Moran I statistic standard deviate = -0.14455, p-value = 0.5575
## alternative hypothesis: greater
## sample estimates:
## Moran I statistic       Expectation          Variance 
##      -0.012406650      -0.004950495       0.002660820

9.7.4 Test de la Lagrange para selección del modelo

En una situación donde la prueba de autocorrelación espacial de los residuos del modelo MCO muestra la existencia de una relación espacial, se puede utilizar la prueba del multiplicador de Lagrange (LM) para encontrar a priori una mejor especificación de los modelos espaciales, el rezago y/o el error espacial.

9.7.5 Test de razón de verosimilitud y de Wald

Las pruebas LR, Wald y LM (también llamadas pruebas de puntuación) pueden ayudar a elegir el mejor modelo. Cada una de ellas se basa en una comparación de la función de verosimilitud; es decir, funciona para resultados de estimación para los que se determina el logLik.

La prueba LR se utiliza para probar los modelos anidados. Suponiendo que el modelo logLik sin restricciones es mayor que el modelo limitado, la prueba LR prueba si la diferencia logLik es significativa. Si es así, entonces el modelo restringido debe descartarse. Si la diferencia es insignificante, elija un modelo más simple o limitado, porque el modelo ilimitado no aporta valor agregado.

La prueba de Wald, al igual que la prueba LR, compara las distancias entre los parámetros de ambos modelos, aunque en la prueba misma se utiliza solo un modelo limitado. \(H_0\) supone que las distancias entre los parámetros de los modelos son pequeñas; por lo tanto, el modelo limitado es mejor. En \(H_1\), se supone que la distancia entre los parámetros es grande, y cuanto mayor sea la distancia entre los parámetros, menos probable es que las restricciones sean apropiadas; es decir, el modelo ilimitado es mejor. El modelo restringido es el modelo MCO, que supone que los coeficientes espaciales son iguales a 0.

9.7.6 Selección de la matriz de pesos espaciales

La elección de la matriz de pesos espaciales \(W\) es importante para el resultado del modelado espacial, ya que la matriz \(W\) determina qué regiones y en qué medida se estudian los vecinos de las regiones.

Con base en esta información se determinan los rezagos espaciales, es decir, el promedio de los valores en las regiones vecinas, ponderados con pesos espaciales.

Por este motivo, junto con otra matriz de pesos espaciales, los rezagos espaciales con diferentes valores entran de manera diferente en el modelo, lo que se traduce en estimaciones de parámetros diferentes, con variables explicativas y componentes espaciales.

9.7.7 Predicción en modelos espaciales

La predicción espacial es un intento de determinar el valor de una variable en lugares vecinos, conociendo el valor del proceso en una región dada o estimando el valor de una variable dependiente basándose en valores conocidos de variables explicativas basadas en el modelo estimado y la estructura adoptada de dependencias espaciales.

Hay tres componentes de la predicción: tendencia, señal y ruido.

• La tendencia es un factor de suavizado no-espacial y se expresa mediante \(X\beta\).

• La señal es un factor espacial y se expresa mediante una fórmula \(\lambda Wy-\lambda WX\beta\) para modelos de error y \(\rho Wy\) para modelos de rezago. La suma de los factores de tendencia y señal se llama ajuste.

• El error de predicción es ruido.

Forecast Bias (FB)

\[ FB = \sum_i^n(y_i-\hat{y_i}) \]

Forecast Bias (FB)

\[ FB = \sum_i^n(y_i-\hat{y_i}) \]

Mean deviation (MD)

\[ MAD = \sum_i^n |y_i-\hat{y_i}| \]

MAE (MAE)

\[ MAE = \sum_i^n \frac{|y_i-\hat{y_i}|}{n} \]

Mean absolute percentage error (MAPE)

\[ MAPE = \frac{1}{n}\sum_i^n \frac{|y_i-\hat{y_i}|}{y_i} \]

mean square error (RMSE)

\[ RMSE = \sqrt{\frac{\sum_i^n(y_i-\hat{y_i})^2}{n}} \]

?predict.Sarlm

mod.slm.pred <- predict(mod.slm)

## This method assumes the response is known - see manual page

mod.sdm.pred <- predict(mod.sdm)

## This method assumes the response is known - see manual page

mod.sem.pred <- predict(mod.sem)

## This method assumes the response is known - see manual page

library(Metrics)
vec<-c("mod.slm.pred", "mod.sdm.pred", "mod.sem.pred")
metrics<-matrix(0, nrow=3, ncol=5)
rownames(metrics)<-vec
colnames(metrics)<-c("bias", "bias%", "MAE","MAPE", "RMSE")
for(i in 1:3){
  # i = 1
  metrics[i,1]<-bias(y, get(vec[i]))
  metrics[i,2]<-percent_bias(y, get(vec[i]))
  metrics[i,3]<-mae(y, get(vec[i]))
  metrics[i,4]<-mape(y, get(vec[i]))
  metrics[i,5]<-rmse(y, get(vec[i]))
  }
metrics

##                      bias       bias%        MAE      MAPE      RMSE
## mod.slm.pred 5.423028e-18 -0.03527089 0.10067132 0.1492630 0.1249443
## mod.sdm.pred 3.090039e-18 -0.03336969 0.09691912 0.1439706 0.1210607
## mod.sem.pred 4.580035e-04 -0.03296074 0.09614415 0.1426417 0.1187855

9.8 Ejercicios

1. Realizar un modelo de regresión entre NBI personas (2010) y el número de robos totales 2019 en Ecuador a nivel cantonal.

2. Usando un análisis de regresión espacial completo usando datos a nivel provincial de la Encuesta Nacional de Actividades de Innovación (AI) 2012-2014:

https://raw.githubusercontent.com/vmoprojs/DataLectures/master/SpatialData/ACTIprov.csv

Contiene las siguientes variables:

• DPAprov: DPA de la provincia
• exitoso: Porcentaje de innovaciones exitosas. Igual a 1 cuando la innovación se realiza en procesos y productos.
• actipor: Innovación interna. Valor destinado hacia actividades de investigación y desarrollo al interior de la empresa
• ImasD: Porcentaje de empresas que cooperaron en actividades de Investigación y Desarrollo.
• IngDis: Porcentaje de empresas que cooperaron en actividades de Ingeniería y Diseño.
• Capa: Porcentaje de empresas que cooperaron en actividades de Capacitación.
• Asistec: Porcentaje de empresas que cooperaron en actividades de Asistencia Técnica.
• Info: Porcentaje de empresas que cooperaron en actividades de Información.
• Pruebas: Porcentaje de empresas que cooperaron en actividades de Pruebas de Productos.
• Público: Porcentaje de gasto en Investigación y Desarrollo financiado por el Gobierno sobre el total de gasto en I+D.
• Apoyo: Monto de apoyo no reembolsable en Investigación y Desarrollo.
• Financiero: Promedio de financiamiento realizado por la Banca Privada.
• GDPP: Logaritmo del valor agregado bruto

Estime el modelo base:

\[ exitoso = \beta_0+\beta_1ImasD+\beta_2IngDis+\beta_3Capa+\beta_4AsisTec+\beta_5Info+\beta_6Pruebas+\beta_7Publico+\beta_8Apoyo+\beta_9Financiero+\beta_10log(GDPP) \] Pruebe los modelos \(SLM\), \(SDM\) y \(SEM\).

uu <- "https://raw.githubusercontent.com/vmoprojs/DataLectures/master/SpatialData/ACTIprov.csv"