STA 570 - Statistical Tables

library(tidyverse)

Dr. Sonderegger’s Video Companion: video

Statistics makes use of a wide variety of distributions and before the days of personal computers, every statistician had books with hundreds and hundreds of pages of tables allowing them to look up particular values. Fortunately in the modern age, we don’t need those books and tables, but we do still need to access those values. To make life easier and consistent for R users, every distribution is accessed in the same manner.

Example Distributions

These distributions are native to R. If you are looking for a distribution not listed below, there is likely a package available that will provide the distribution.

Distribution	R Stem	Parameters	Parameter Interpretation
Binomial	`binom`	`size` `prob`	Number of Trials Probability of Success (per Trial)
Exponential	`exp`	`rate`	Mean of the distribution
Normal	`norm`	`mean=0` `sd=1`	Center of the distribution Standard deviation
Uniform	`unif`	`min=0` `max=1`	Minimum of the distribution Maximum of the distribution
t	`t`	`df`	Degrees of freedom
F	`f`	`df1` `df2`	Numerator Degrees of freedom Denominator Degrees of freedom

All of the functions in R to manipulate distributions have a similar naming scheme. They begin with a d,p,q, or r and then the stem of the distribution. For example, I might use a function called pnorm(). The above table lists the most common distributions you might see in an introductory statistics course.

Base R functions

All the probability distributions available in R are accessed in exactly the same way, using a d-function, p-function, q-function, and r-function. For the rest of this section that \(X\) is a random variable from the distribution of interest and \(x\) is some possible value that \(X\) could take on. Notice that the p-function is the inverse of the q-function.

Function `d`-function(x)	Result The distance from the x-axis to the curve at a given \(x\).
Function `d`-function(x)
`p`-function(x)	Probability of an outcome less than or equal to `x`
`q`-function(q)	The x-value with the input probability to the left. This is the inverse question as the `p`-function. Often referred to as the ‘quantiles’
`r`-function(n)	Generate \(n\) random observations from the distribution

For each distribution in R, there will be this set of functions but we replace the “-function” with the distribution name or a shortened version. norm, exp, binom, t, f are the names for the normal, exponential, binomial, T and F distributions, respectively. Furthermore, most distributions have additional parameters that define the distribution and will also be passed as arguments to these functions, although, if a reasonable default value for the parameter exists, there will be a default. For example, we often work with the standard normal distribution in a statistics course, so the normal distribution has defaults mean = 0 and sd = 1.

d-function

The purpose of the d-function is to calculate the distance from the x-axis to the density curve or height of a probability mass function. The “d” actually stands for density. This relates to the probability density function (pdf) or probability mass function (pmf) taught in introductory statistics classes. Notice that for discrete distributions, this is the probability of observing that particular value, while for continuous distributions, the height doesn’t have a nice physical interpretation, but is related to the statistical concept of density, which can be integrated to obtain a probability.

We start with an example of the Binomial distribution. For \(X\sim Binomial\left(n=10,p=.2\right)\), suppose we wanted to know \(P(X=0)\). We know the probability mass function is

\[ P\left(X=x\right)={n \choose x}p^{x}\left(1-p\right)^{n-x} \]

thus

\[ P\left(X=0\right) = {10 \choose 0}\,0.2^{0}\left(0.8\right)^{10} = 1\cdot1\cdot0.8^{10} \approx 0.107 \]

but that calculation is fairly tedious. To get R to do the same calculation, we just need the height of the probability mass function at \(0\). To do this calculation, we need to know the x value we are interested in along with the distribution parameters \(n\) (related to sample size) and \(p\) (the probability of success). The first thing we should do is check the help file for the binomial distribution functions to see what parameters are needed and what they are named.

?dbinom

The help file shows us the parameters \(n\) and \(p\) are called size and prob respectively. So to calculate the probability that \(X=0\) we would use the following command:

dbinom(0, size=10, prob=.2)

## [1] 0.1073742

p-function

Often we are interested in determining the probability less than or equal to a given outcome. This is a statistical term known as the cumulative density, and is important for ideas such as p-values. The corresponding p-functions in R provide the cumulative density functions (CDFs) for given distributions.

To continue our binomial distribution example, again let \(X\sim Binomial\left(n=10,p=0.2\right)\). Suppose I want to know the probability of observing a 0, 1, or 2. That is, what is \(P\left(X\le2\right)\)? I could just find the probability of each and add them up.

dbinom(0, size=10, prob=.2)   +       #   P(X==0) +
  dbinom(1, size=10, prob=.2) +       #     P(X==1) +
  dbinom(2, size=10, prob=.2)         #     P(X==2)

## [1] 0.6777995

This could get tedious for binomial distributions with a large number of trials. The shortcut is to use the pbinom() function.

pbinom(2, size=10, prob=.2)

## [1] 0.6777995

For discrete distributions, you must be careful because R will give you the probability of less than or equal to 2. If you wanted less than two, you should use dbinom(1,10,.2). That is, for a discrete distribution like the binomial given above, we must always recall that

\[ P(X < 2) = P(X \leq 1) \]

The normal distribution works similarly. Suppose for \(Z\sim N\left(0,1\right)\) and we wanted to know \(P\left(Z\le-1\right)\)?

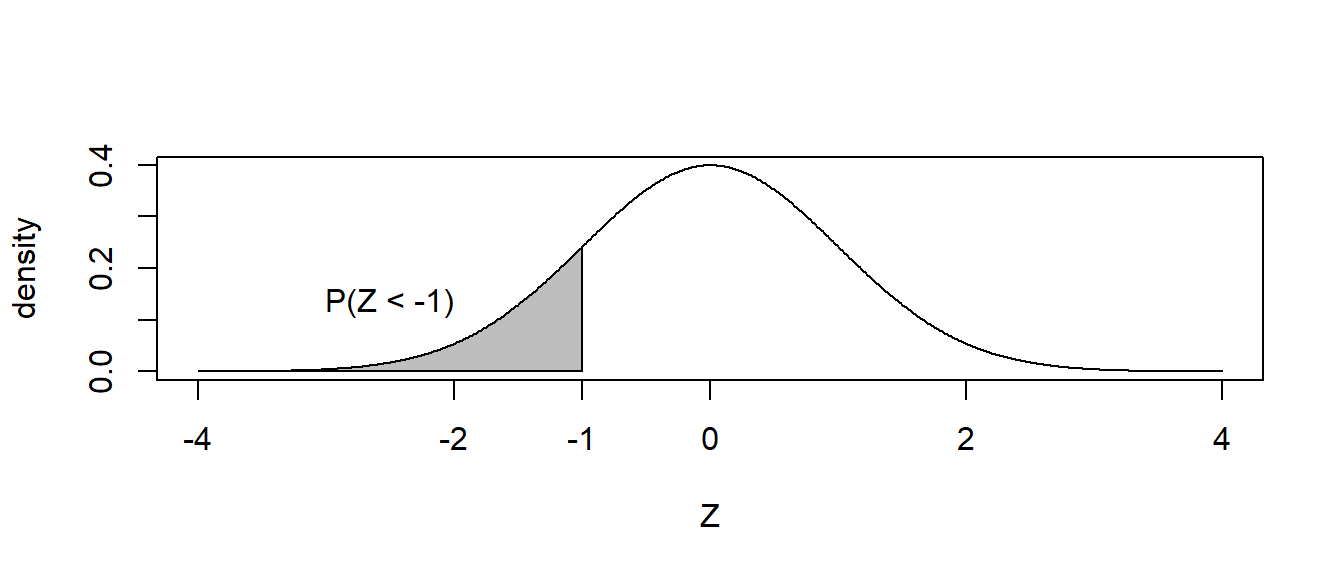
The answer is easily found via pnorm().

pnorm(-1)

## [1] 0.1586553

Notice for continuous random variables, the probability \(P\left(Z=-1\right)=0\) so we can ignore the issue of “less than” vs “less than or equal to”. That is, for a continuous distribution \(P(Z < -1) = P(Z \leq -1)\). These are important concepts frequently covered when studying distributional theory and differentiation of discrete vs. continuous distributions!

Often times we will want to know the probability of greater than some value. That is, we might want to find \(P\left(Z \ge -1\right)\). For the normal distribution, there are a number of tricks we could use. Notably

\[ P\left(Z\ge-1\right) = P\left(Z\le1\right)=1-P\left(Z<-1\right) \]

but sometimes I’m lazy and would like to tell R to give me the area to the right instead of area to the left (which is the default). This can be done by setting the argument lower.tail=FALSE. I encourage you take the complement probability yourselves, but this option does exist.

The mosaic package includes an augmented version of the pnorm() function called xpnorm() that calculates the same number but includes some extra information and produces a pretty graph to help us understand what we just calculated and do the tedious “1 minus” calculation to find the upper area. Fortunately this x-variant exists for the Normal, Chi-squared, F, Gamma continuous distributions and the discrete Poisson, Geometric, and Binomial distributions.

mosaic::xpnorm(-1)

##

## If X ~ N(0, 1), then

##  P(X <= -1) = P(Z <= -1) = 0.1587

##  P(X >  -1) = P(Z >  -1) = 0.8413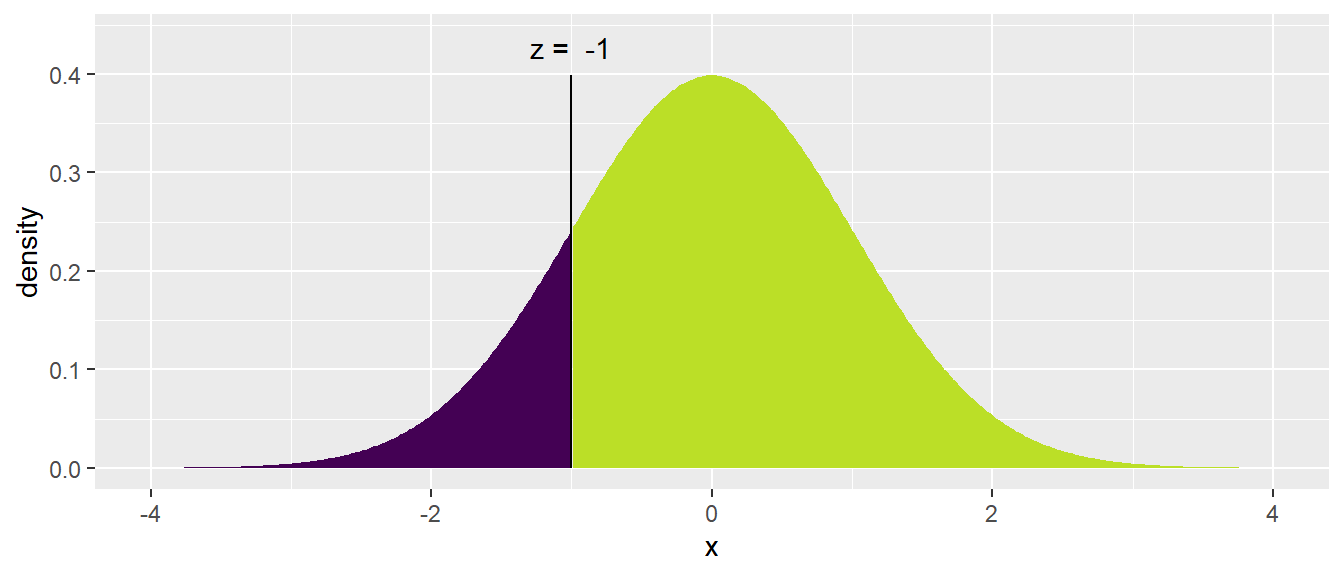

##

## [1] 0.1586553

`q`-function

We will also sometimes find ourselves asking for the quantiles of a distribution. Percentiles are by definition \(1/100\), \(2/100\), etc but if I am interested in something that isn’t an even division of 100, we get fancy and call them quantiles. This is a small semantic quibble, but we ought to be precise. That being said, I won’t correct somebody if they call these percentiles. For example, I might want to find the \(0.30\) quantile, which is the value such that \(30\%\) of the distribution is less than it, and \(70\%\) is greater. Mathematically, I wish to find the value \(z\) such that \(P(Z<z)=0.30\).

To find this value in the tables in a book, we use the table in reverse. R gives us a handy way to do this with the qnorm() function and the mosaic package provides a nice visualization using the augmented xqnorm(). Below, I specify that I’m using a function in the mosaic package by specifying it via PackageName::FunctionName() format because I haven’t loaded the mosaic package because some of its functions conflict with dplyr.

mosaic::xqnorm(0.30)   # Give me the value along with a pretty picture

##

## If X ~ N(0, 1), then

##  P(X <= -0.5244005) = 0.3

##  P(X >  -0.5244005) = 0.7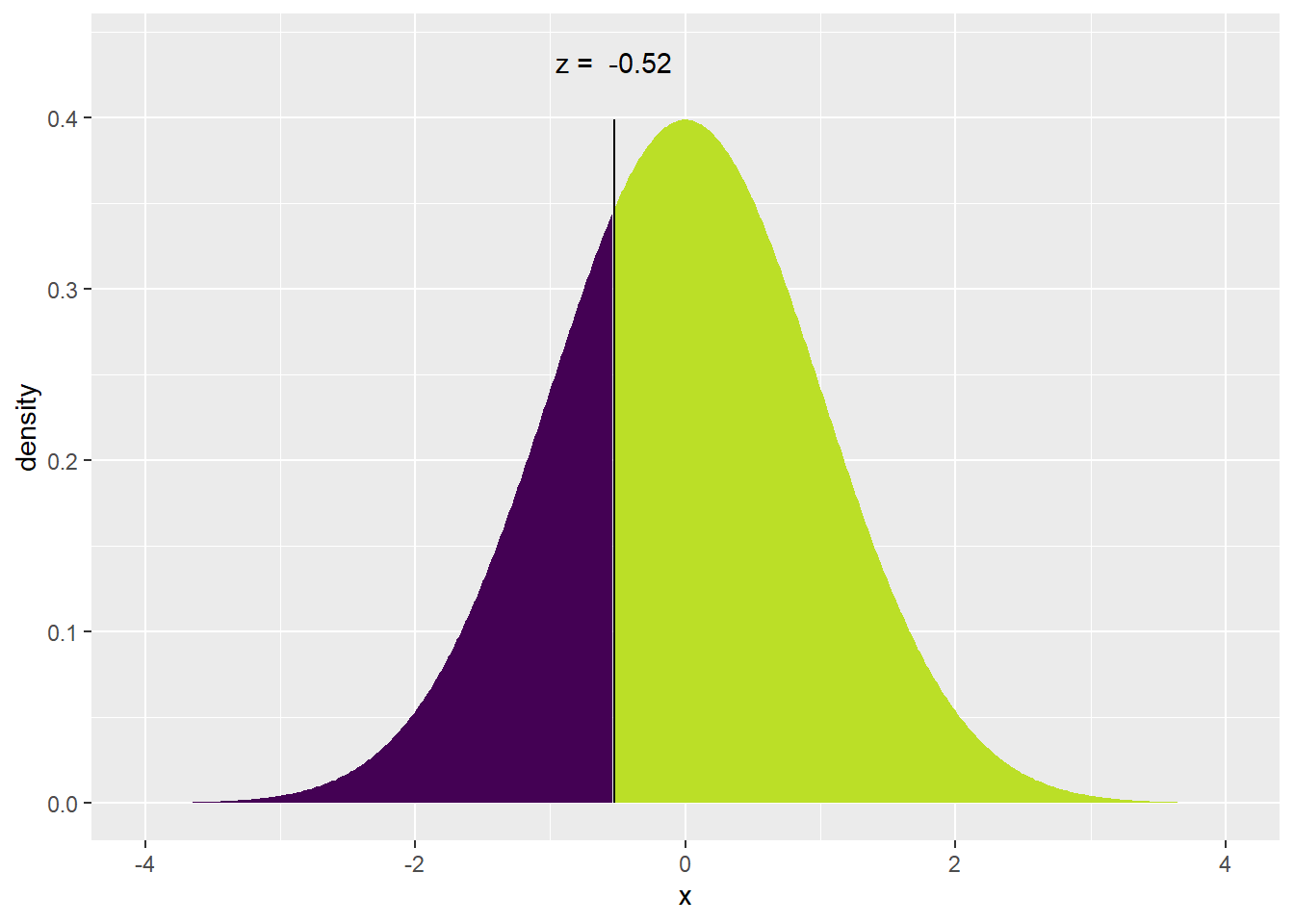

##

## [1] -0.5244005

qnorm(.30)             # No pretty picture, just the value

## [1] -0.5244005

r-function

Finally, I often want to be able to generate random data from a particular distribution. R does this with the r-function. The first argument to this function the number of random variables to draw and any remaining arguments are the parameters of the distribution. Below are examples of drawing \(n = 5\) samples from a normal distribution, and \(n = 4\) samples from a binomial distribution, whose parameters are given in the additional sub-function arguments.

rnorm(5, mean=20, sd=2)

## [1] 17.19842 17.32009 17.47477 21.60018 18.34705

rbinom(4, size=10, prob=.8)

## [1] 9 8 9 8

mosaic::plotDist() function

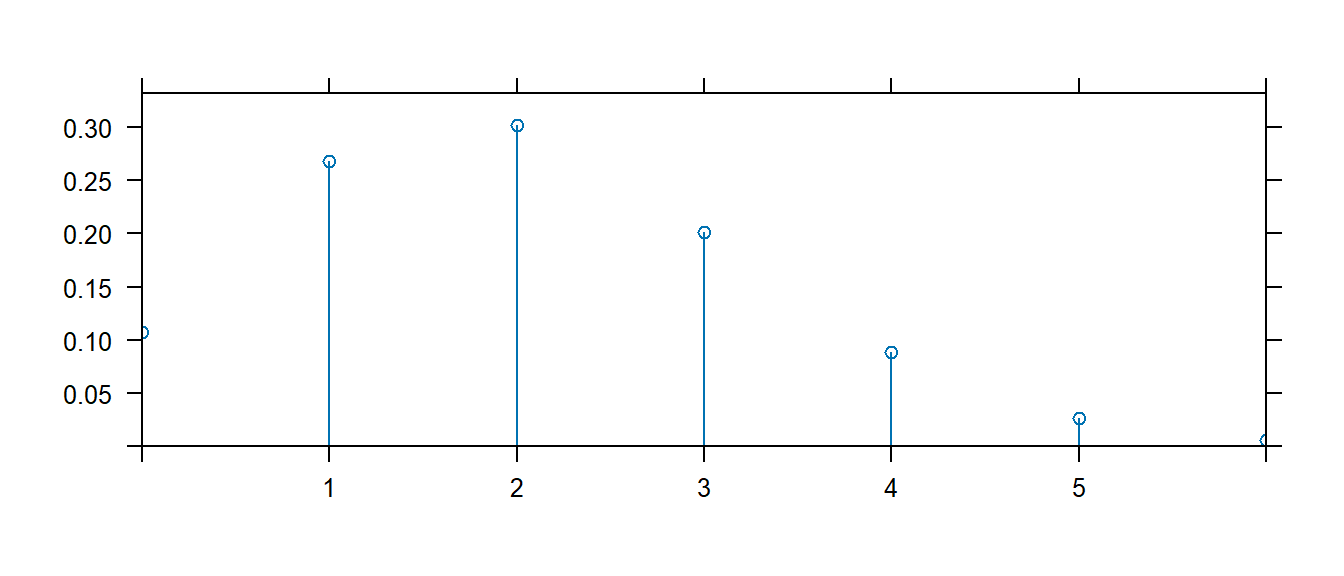
The mosaic package provides a very useful routine for understanding a distribution. The plotDist() function takes the R name of the distribution along with whatever parameters are necessary for that function and show the distribution. For reference below is a list of common distributions and their R name and a list of necessary parameters.

For example, to see the normal distribution with mean \(\mu=10\) and standard deviation \(\sigma=2\), we use

mosaic::plotDist('norm', mean=10, sd=2)

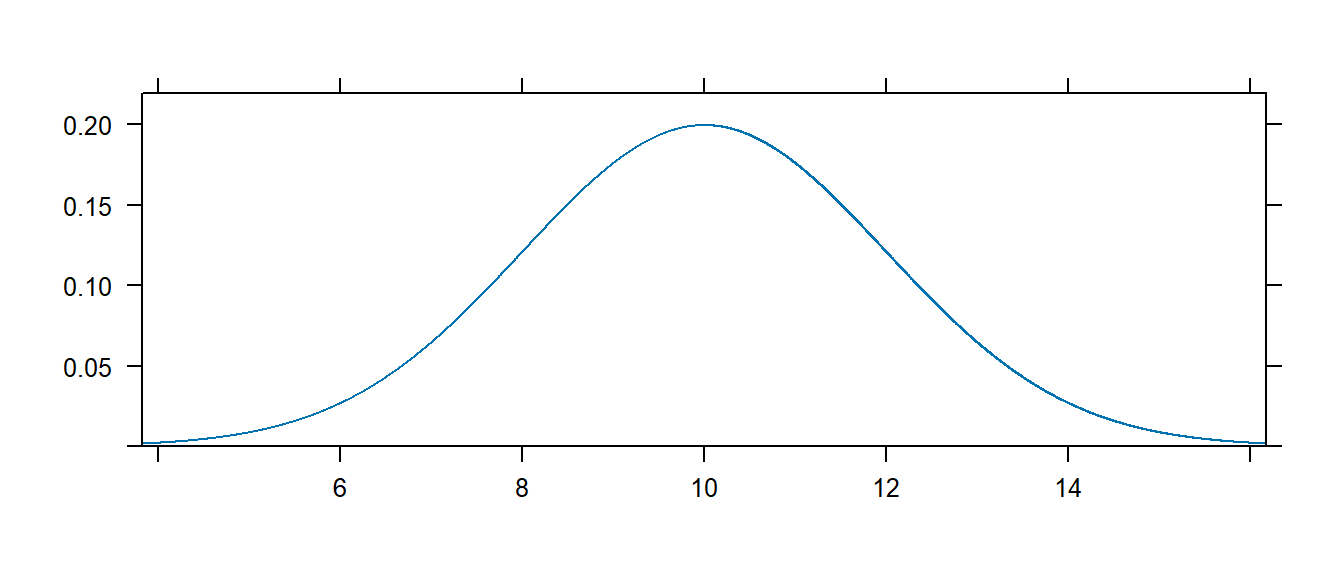
This function works for discrete distributions as well.

mosaic::plotDist('binom', size=10, prob=.2)

Exercises

Exercise 1

We will examine how to use the probability mass function (a.k.a. d-function) and cumulative probability function (a.k.a. p-function) for the Poisson distribution.

a) Create a graph of the distribution of a Poisson random variable with rate parameter \(\lambda=2\) using the mosaic function plotDist().

b) Calculate the probability that a Poisson random variable (with rate parameter \(\lambda=2\)) is exactly equal to 3 using the dpois() function. Be sure that this value matches the graphed distribution in part (a).

c) For a Poisson random variable with rate parameter \(\lambda=2\), calculate the probability it is less than or equal to 3, by summing the four values returned by the Poisson d-function.

d) Perform the same calculation as the previous question but using the cumulative probability function ppois().

Exercise 2

We will examine how to use the cumulative probability functions (a.k.a. p-functions) for the normal and exponential distributions.

a) Use the mosaic function plotDist() to produce a graph of the standard normal distribution (that is a normal distribution with mean \(\mu=0\) and standard deviation \(\sigma=1\).

b) For a standard normal, use the pnorm() function or its mosaic augmented version xpnorm() to calculate

\(P\left(Z<-1\right)\)
\(P\left(Z\ge1.5\right)\)

c) Use the mosaic function plotDist() to produce a graph of an exponential distribution with rate parameter 2.

d) Suppose that \(Y\sim Exp\left(2\right)\), as above, use the pexp() function to calculate \(P\left(Y \le 1 \right)\). (Unfortunately there isn’t a mosaic augmented xpexp() function.)

Exercise 3

We next examine how to calculate quantile values for the normal and exponential distributions using R’s q-functions.

a) Find the value of a standard normal distribution (\(\mu=0\), \(\sigma=1\)) such that 5% of the distribution is to the left of the value using the qnorm() function or the mosaic augmented version xqnorm().

b) Find the value of an exponential distribution with rate 2 such that \(60\%\) of the distribution is less than it using the qexp() function.

Exercise 4

Finally we will look at generating random deviates from a distribution.

a) Generate a single value from a uniform distribution with minimum \(0\) and maximum \(1\) using the runif() function. Repeat this step several times and confirm you are getting different values each time.

b) Generate a sample of size 20 from the same uniform distribution and save it as the vector x using the following:

x <- runif(20, min=0, max=1)

Then produce a histogram of the sample using the function hist() or geom_histogram

data.frame(x=x) %>% 
    ggplot(aes(x=x)) + 
    geom_histogram(bins=10)

c) Generate a sample of 2000 from a normal distribution with mean=10 and standard deviation sd=2 using the rnorm() function. Create a histogram of the resulting sample.