4.3 One-Sample Median Wilcoxon Test

The Wilcoxon one-sample median test (aka Wilcoxon signed rank test) is a non-parametric alternative to the t-test for cases when the the sampling distribution of the population mean is not normally distributed, but is at least symmetric.

Under the Wilcoxon test, the measured median, \(\eta_x\), approximates the population median, \(\eta\). The method calculates the difference between each value and the hypothesized median, \(\eta_0\), ranks the difference magnitudes, then sums the ranks for the negative and the positive differences, \(W+\) and \(W-\). The test compares the smaller of the two sums to a table of critical values.

Here is a case study. A store claims their checkout wait times are \(\le\) 4 minutes. You challenge the claim by sampling 6 checkout experiences. The mean wait time was 4.6, but the data may violate normality.

data.frame(wait = wait) %>%
  ggplot(aes(sample = wait)) +
  stat_qq() +
  stat_qq_line(col = "goldenrod") +
  theme_minimal() +
  labs(title = "Normal Q-Q Plot")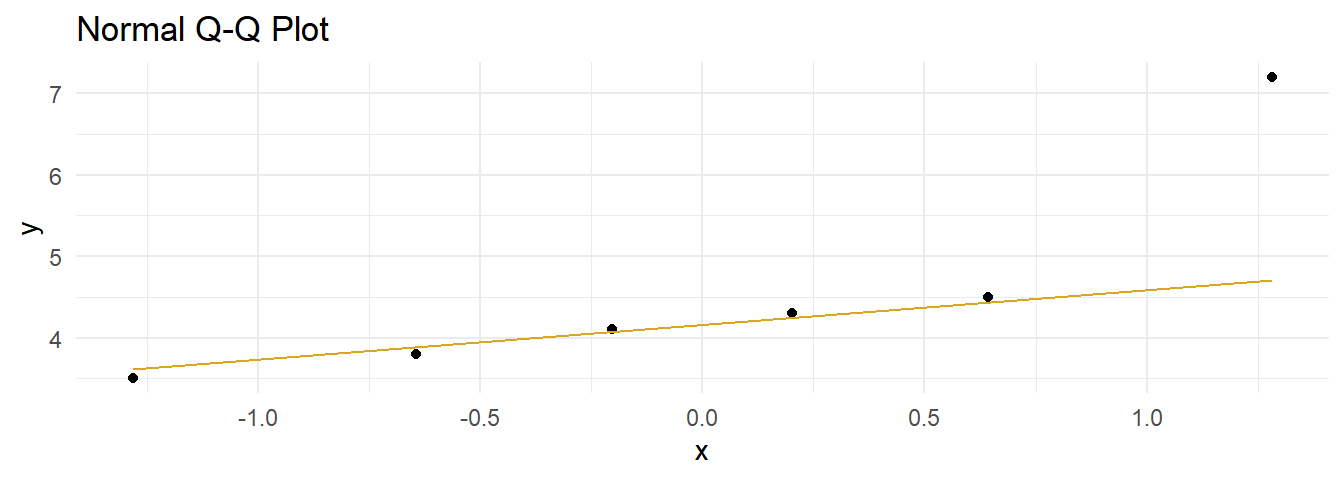

Shapiro-Wilk rejects the null hypothesis of a normally distributed population.

shapiro.test(wait)

## 
##  Shapiro-Wilk normality test
## 
## data:  wait
## W = 0.75105, p-value = 0.0204

Use the Wilcoxon test instead.

(wt <- wilcox.test(wait, mu = 4, alternative = "greater"))

## Warning in wilcox.test.default(wait, mu = 4, alternative = "greater"): cannot
## compute exact p-value with ties

## 
##  Wilcoxon signed rank test with continuity correction
## 
## data:  wait
## V = 14.5, p-value = 0.2309
## alternative hypothesis: true location is greater than 4

A Wilcoxon Signed-Ranks Test indicated that wait times were not statistically significantly higher than the 4-minute claim, z = 14.5, p = 0.231.