Case Study 4

The case study below uses a data set from Laerd and a second modified version. The first data set passes the chi-square test of homogeneity requirements. The second (in parentheses), fails the n-sizes test.

A researcher recruits 100 (50) patients who have a “high” classification of cholesterol and who currently have a poor lifestyle. The researcher randomly assigns 50 (25) of them to a drug intervention and 50 (25) to a lifestyle intervention. After six months, a doctor reclassifies the patients as either still having a “high” classification of cholesterol or now having a “normal” classification of cholesterol.

The chi-sq data set has the following summary statistics.

The Fisher data set has the following summary statistics.

Conditions

n-Size

The chi-square test of homogeneity applies with the CLT conditions hold.

• the sample is independently drawn,
• there are at least 5 successes (Normal) and failures (High) for each group \(i\),
• the sample sizes for both groups are >=30, and
• the probability of success for each group is not extreme, \(0.2 < \pi_i < 0.8\).

The conditions hold for the chi-sq data set, but not for the Fisher data set.

Test

Chi-Square

(ind_discrete$chisq_test <- ind_discrete$chisq_dat %>%
  tabyl(intervention, risk_level) %>%
  chisq.test(correct = FALSE))

## 
##  Pearson's Chi-squared test
## 
## data:  .
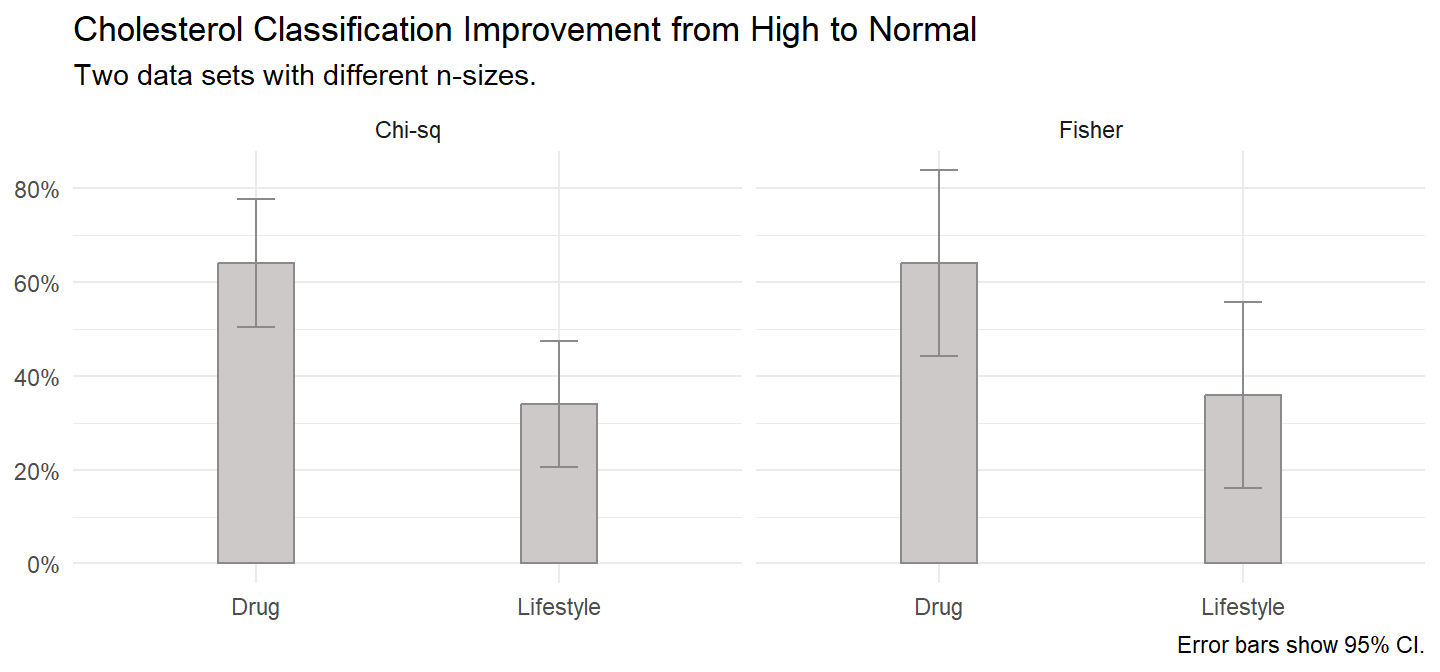
## X-squared = 9.0036, df = 1, p-value = 0.002694

100 patients with a high cholesterol classification were randomly assigned to either a drug or lifestyle intervention, 50 in each intervention. The test of two proportions used was the chi-square test of homogeneity. At the conclusion of the drug intervention, 32 patients (64%) had improved their cholesterol classification from high to normal compared to 17 patients (34%) in the lifestyle intervention, a difference in proportions of 0.30, p = 0.0027.

Fisher

(ind_discrete$fisher_test <- ind_discrete$fisher_dat %>%
  tabyl(intervention, risk_level) %>%
  fisher.test())

## 
##  Fisher's Exact Test for Count Data
## 
## data:  .
## p-value = 0.08874
## alternative hypothesis: true odds ratio is not equal to 1
## 95 percent confidence interval:
##  0.08497039 1.15362199
## sample estimates:
## odds ratio 
##  0.3241952

50 patients with a high cholesterol classification were randomly assigned to either a drug or lifestyle intervention, 25 in each intervention. At the conclusion of the drug intervention, 16 patients (64%) had improved their cholesterol classification from high to normal compared to 9 patients (36%) in the lifestyle intervention. Due to small sample sizes, Fisher’s exact test was run. There was a non-statistically significant difference in proportions of 0.28, p = 0.0887.