13 Tables and Statistics

For this class, we’ll be using some new packages, gt, gtsummary, and broom. Install and load them before we begin.

install.packages("gt")
install.packages("gtsummary")
install.packages("broom")
install.packages("broom.helpers")
install.packages("webshot2")
library(gt)
library(gtsummary)
library(broom)
library(tidyverse)
library(gapminder) # Interesting data set about life expectancy, population, gdp, etc.
library(sf)

13.1 Making nice tables

Sometimes, our visualizations just won’t cut it, and we need to just make a table out of the data. To start out, we’ll once again use the gapminder data set.

gapminder |> glimpse()
## Rows: 1,704
## Columns: 6
## $ country   <fct> "Afghanistan", "Afghanistan", "Afghanistan", "Afghanistan", "Afghanistan", "Afghanistan", "Afghanistan", "Afghanistan", "Afghanistan", "Afghanistan", "Afghanistan", "Afghanistan", "Albania", "Albania", "Albania", "Albania", "Albania", "Albania", "Al…
## $ continent <fct> Asia, Asia, Asia, Asia, Asia, Asia, Asia, Asia, Asia, Asia, Asia, Asia, Europe, Europe, Europe, Europe, Europe, Europe, Europe, Europe, Europe, Europe, Europe, Europe, Africa, Africa, Africa, Africa, Africa, Africa, Africa, Africa, Africa, Africa, A…
## $ year      <int> 1952, 1957, 1962, 1967, 1972, 1977, 1982, 1987, 1992, 1997, 2002, 2007, 1952, 1957, 1962, 1967, 1972, 1977, 1982, 1987, 1992, 1997, 2002, 2007, 1952, 1957, 1962, 1967, 1972, 1977, 1982, 1987, 1992, 1997, 2002, 2007, 1952, 1957, 1962, 1967, 1972, 197…
## $ lifeExp   <dbl> 28.801, 30.332, 31.997, 34.020, 36.088, 38.438, 39.854, 40.822, 41.674, 41.763, 42.129, 43.828, 55.230, 59.280, 64.820, 66.220, 67.690, 68.930, 70.420, 72.000, 71.581, 72.950, 75.651, 76.423, 43.077, 45.685, 48.303, 51.407, 54.518, 58.014, 61.368, 6…
## $ pop       <int> 8425333, 9240934, 10267083, 11537966, 13079460, 14880372, 12881816, 13867957, 16317921, 22227415, 25268405, 31889923, 1282697, 1476505, 1728137, 1984060, 2263554, 2509048, 2780097, 3075321, 3326498, 3428038, 3508512, 3600523, 9279525, 10270856, 1100…
## $ gdpPercap <dbl> 779.4453, 820.8530, 853.1007, 836.1971, 739.9811, 786.1134, 978.0114, 852.3959, 649.3414, 635.3414, 726.7341, 974.5803, 1601.0561, 1942.2842, 2312.8890, 2760.1969, 3313.4222, 3533.0039, 3630.8807, 3738.9327, 2497.4379, 3193.0546, 4604.2117, 5937.029…

To make a table, simply use the gt() function. This creates a tidy looking table that we’ll be able to export.

gapminder |> 
  gt()

For our purposes, though, we’ll want to filter the data to only show Mongolia, so that our table will fit on a single page.

gapminder |>
  filter(country == "Mongolia") |>
  gt()
country continent year lifeExp pop gdpPercap
Mongolia Asia 1952 42.244 800663 786.5669
Mongolia Asia 1957 45.248 882134 912.6626
Mongolia Asia 1962 48.251 1010280 1056.3540
Mongolia Asia 1967 51.253 1149500 1226.0411
Mongolia Asia 1972 53.754 1320500 1421.7420
Mongolia Asia 1977 55.491 1528000 1647.5117
Mongolia Asia 1982 57.489 1756032 2000.6031
Mongolia Asia 1987 60.222 2015133 2338.0083
Mongolia Asia 1992 61.271 2312802 1785.4020
Mongolia Asia 1997 63.625 2494803 1902.2521
Mongolia Asia 2002 65.033 2674234 2140.7393
Mongolia Asia 2007 66.803 2874127 3095.7723

13.2 Exporting tables

Similarly to ggsave(), we can use gtsave() to save our tables to a file. We can save them as a Word document, an HTML file, or a PNG image. This is going to make it easy to share with your collaborators and include in your reports.

gapminder |>
  filter(country == "Mongolia") |>
  gt() |> 
  gtsave("mongolia_table.docx")
gapminder |>
  filter(country == "Mongolia") |>
  gt() |> 
  gtsave("mongolia_table.html")
gapminder |>
  filter(country == "Mongolia") |>
  gt() |> 
  gtsave("mongolia_table.png")

13.3 Classwork: Export a table

  1. Use some filtering, grouping, and summarizing to create a table that shows the average life expectancy by country in Europe.
  2. Export this table to a Word document.

13.4 Summary statistics

Traditionally, a scientific paper will have two tables: one for the descriptive statistics and one for the regression results. The descriptive statistics table will show the mean, median, and standard deviation for continuous variables, and the count and percentage for categorical variables. The tbl_summary() function from the gtsummary package will do this for us automatically.

gapminder |> 
  select(-country) |> 
  tbl_summary()
Characteristic N = 1,7041
continent
    Africa 624 (37%)
    Americas 300 (18%)
    Asia 396 (23%)
    Europe 360 (21%)
    Oceania 24 (1.4%)
year 1,980 (1,965, 1,995)
lifeExp 61 (48, 71)
pop 7,023,596 (2,792,776, 19,593,661)
gdpPercap 3,532 (1,202, 9,326)
1 n (%); Median (Q1, Q3)

There are a lot of options that we can change in the tbl_summary() function. For example, we can change the type of variable, the label, the number of digits to round to, and the statistics to show.

Here, we’ll change the type of the year variable to categorical, change the label of the year variable, round the lifeExp variable to two digits, and change the statistics to show for continuous and categorical variables.

Gt is a very new package, so the way things work changes all the time. Don’t put too much brain power into memorizing this stuff, and just read the docs here:

GT

GTSummary

gapminder |> 
  select(-country) |> 
  tbl_summary(
    type = list(year ~ "categorical"), # Change between continuous and categorical
    label = list(year ~ "Year"), # Change the label without having to rename the column
    digits = list(lifeExp ~ 2, pop ~ 0), # Change the number of digits to round to
    statistic = list(
      all_continuous() ~ c("{min}, {mean}, {max}"), # Change the statistics to show for continuous variables
      all_categorical() ~ "{n} / {N} ({p}%)" # Change the statistics to show for categorical variables
    ),
    )
Characteristic N = 1,7041
continent
    Africa 624 / 1,704 (37%)
    Americas 300 / 1,704 (18%)
    Asia 396 / 1,704 (23%)
    Europe 360 / 1,704 (21%)
    Oceania 24 / 1,704 (1.4%)
Year
    1952 142 / 1,704 (8.3%)
    1957 142 / 1,704 (8.3%)
    1962 142 / 1,704 (8.3%)
    1967 142 / 1,704 (8.3%)
    1972 142 / 1,704 (8.3%)
    1977 142 / 1,704 (8.3%)
    1982 142 / 1,704 (8.3%)
    1987 142 / 1,704 (8.3%)
    1992 142 / 1,704 (8.3%)
    1997 142 / 1,704 (8.3%)
    2002 142 / 1,704 (8.3%)
    2007 142 / 1,704 (8.3%)
lifeExp 23.60, 59.47, 82.60
pop 60,011, 29,601,212, 1,318,683,096
gdpPercap 241, 7,215, 113,523
1 n / N (%); Min, Mean, Max

13.5 How to read a regression model

Next, in a scientific paper, we often run a regression model to see how different variables are related to each other. The lm() function in R will run a linear regression model for us. We can then use the summary() function to see the results.

Here, I’m looking at the effect of the year on life expectancy. The lm() function takes the formula y ~ x, where y is the dependent variable and x is the independent variable. The summary() function will show us the results of the regression model.

regression_model <- lm(lifeExp ~ year, data = gapminder)
regression_model |> summary()
## 
## Call:
## lm(formula = lifeExp ~ year, data = gapminder)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -39.949  -9.651   1.697  10.335  22.158 
## 
## Coefficients:
##               Estimate Std. Error t value            Pr(>|t|)    
## (Intercept) -585.65219   32.31396  -18.12 <0.0000000000000002 ***
## year           0.32590    0.01632   19.96 <0.0000000000000002 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 11.63 on 1702 degrees of freedom
## Multiple R-squared:  0.1898, Adjusted R-squared:  0.1893 
## F-statistic: 398.6 on 1 and 1702 DF,  p-value: < 0.00000000000000022

But what does this mean? The Estimate column shows the effect of the independent variable on the dependent variable. In this case, the year variable has a coefficient of 0.325, which means that for every year, the life expectancy increases by 0.325 years. The Pr(>|t|) column shows the p-value of the coefficient. In this case, the p-value is less than 0.05, which means that the effect of the year on life expectancy is statistically significant. R-squared is a measure of how well the model fits the data. It ranges from 0 to 1, with 1 being a perfect fit. In this case, the R-squared is 0.1898, which means that the year explains 19% of the variation in life expectancy.

You can include multiple regressors, separated by a +, and this will condition on the other variables. Here, we condition on each continent, which is a categorical variable.

regression_model <- lm(lifeExp ~ year + continent, data = gapminder)
regression_model |> summary()
## 
## Call:
## lm(formula = lifeExp ~ year + continent, data = gapminder)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -29.3401  -4.3842   0.1598   4.5875  20.6759 
## 
## Coefficients:
##                     Estimate Std. Error t value            Pr(>|t|)    
## (Intercept)       -596.26130   20.32816  -29.33 <0.0000000000000002 ***
## year                 0.32590    0.01027   31.74 <0.0000000000000002 ***
## continentAmericas   15.79341    0.51400   30.73 <0.0000000000000002 ***
## continentAsia       11.19957    0.47005   23.83 <0.0000000000000002 ***
## continentEurope     23.03836    0.48421   47.58 <0.0000000000000002 ***
## continentOceania    25.46088    1.52184   16.73 <0.0000000000000002 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 7.316 on 1698 degrees of freedom
## Multiple R-squared:  0.6801, Adjusted R-squared:  0.6792 
## F-statistic: 722.1 on 5 and 1698 DF,  p-value: < 0.00000000000000022

Take a statistics class to learn more about this.

Remember back when we did some geom_smooth() stuff? the method argument can be set to "lm" to show the regression line. This is a quick and dirty way to show the regression line on a scatter plot.

gapminder |> ggplot(aes(x = year, y = lifeExp)) +
  geom_point() +
  geom_smooth(method = "lm", se = FALSE) +
  theme_minimal()
## `geom_smooth()` using formula = 'y ~ x'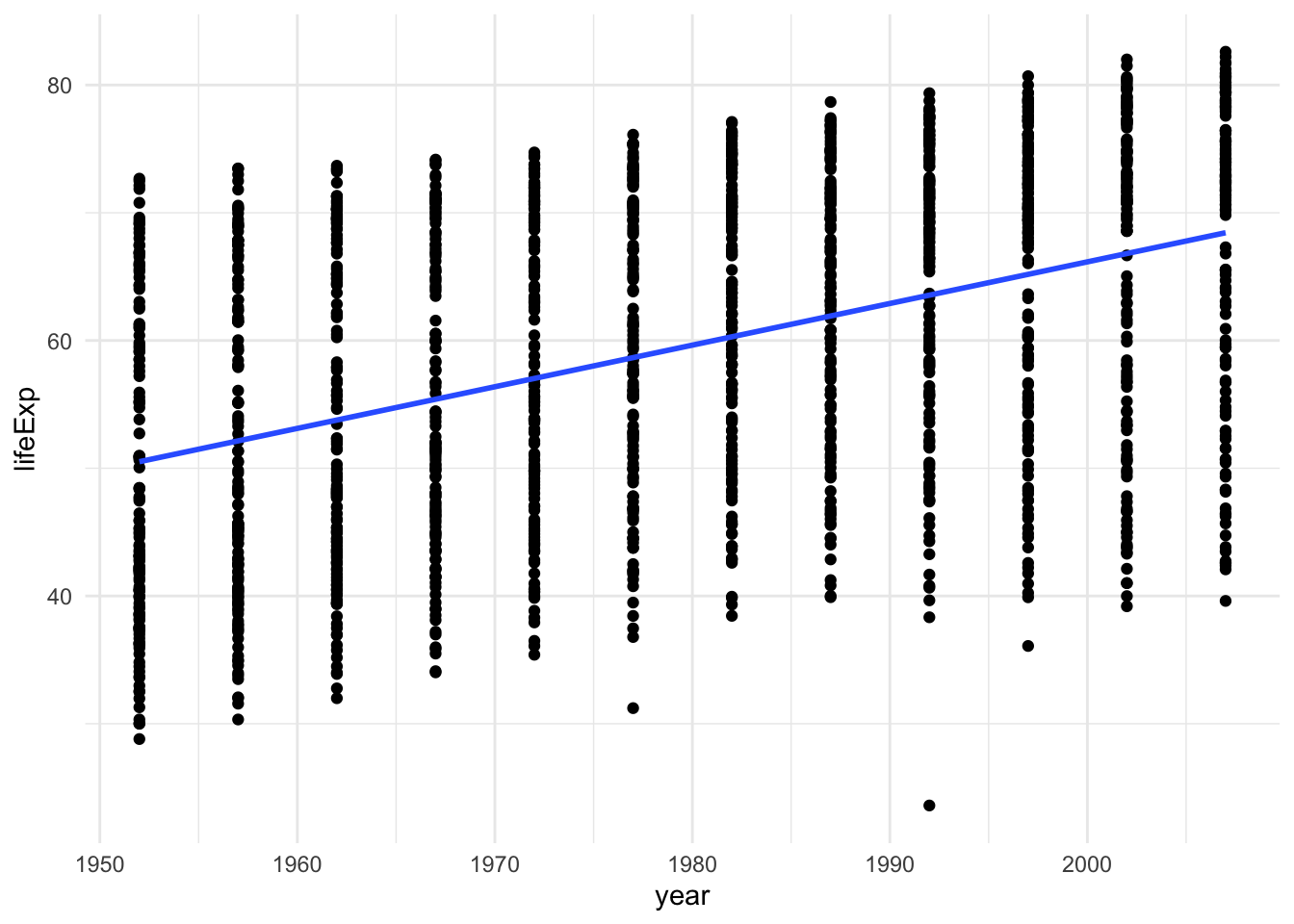

These regression tables can be exported as well, using the tbl_regression() function from the gtsummary package.

regression_model |> tbl_regression()
Characteristic Beta 95% CI1 p-value
year 0.33 0.31, 0.35 <0.001
continent


    Africa — —
    Americas 16 15, 17 <0.001
    Asia 11 10, 12 <0.001
    Europe 23 22, 24 <0.001
    Oceania 25 22, 28 <0.001
1 CI = Confidence Interval

To save it, you have to first convert it to a gt table using the as_gt() function, and then use the gtsave() function to save it to a file.

regression_model |> tbl_regression() |> as_gt() |> gtsave("regression_model.docx")

13.6 Classwork: Do a whole scientific study

For our final classwork, you’re going to be a social scientist, and find the relationship between some statistics about European countries. You’ll need to find some data, clean it, and run a regression model to see how different variables are related to each other. You’ll then need to make a table of the descriptive statistics and a table of the regression results.

This will bring together stuff we’ve learned throughout the course, so you’ll want to also look back at the previous lessons.

  1. First, load some data about a continent of your choice.
library(rnaturalearth)

europe <- ne_countries(continent = "Europe", returnclass = "sf")
  1. Now, think of two things that might be related to each other. For example, you could look at the relationship between health spending and life expectancy. Use the wbsearch() function to find the indicators that you need.
library(wbstats)
wbsearch("health expenditure")
wbsearch("life expectancy")
  1. Next, load and clean the data, as we did before.
health_expenditure <- wb_data(indicator = "SH.XPD.CHEX.GD.ZS", start_date = 2020, end_date = 2020)
health_expenditure <- health_expenditure |> rename(spending = SH.XPD.CHEX.GD.ZS)
health_expenditure |> glimpse()
## Rows: 217
## Columns: 9
## $ iso2c        <chr> "AW", "AF", "AO", "AL", "AD", "AE", "AR", "AM", "AS", "AG", "AU", "AT", "AZ", "BI", "BE", "BJ", "BF", "BD", "BG", "BH", "BS", "BA", "BY", "BZ", "BM", "BO", "BR", "BB", "BN", "BT", "BW", "CF", "CA", "CH", "JG", "CL", "CN", "CI", "CM", "CD", "CG", …
## $ iso3c        <chr> "ABW", "AFG", "AGO", "ALB", "AND", "ARE", "ARG", "ARM", "ASM", "ATG", "AUS", "AUT", "AZE", "BDI", "BEL", "BEN", "BFA", "BGD", "BGR", "BHR", "BHS", "BIH", "BLR", "BLZ", "BMU", "BOL", "BRA", "BRB", "BRN", "BTN", "BWA", "CAF", "CAN", "CHE", "CHI", "…
## $ country      <chr> "Aruba", "Afghanistan", "Angola", "Albania", "Andorra", "United Arab Emirates", "Argentina", "Armenia", "American Samoa", "Antigua and Barbuda", "Australia", "Austria", "Azerbaijan", "Burundi", "Belgium", "Benin", "Burkina Faso", "Bangladesh", "B…
## $ date         <dbl> 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2020, …
## $ spending     <dbl> NA, 15.533614, 3.220706, 7.519203, 8.786739, 5.824770, 10.347015, 12.240000, NA, 5.921462, 10.683737, 11.390000, 5.850000, 10.718372, 11.197513, 2.469704, 6.501933, 2.270639, 8.480000, 4.716848, 7.647008, 9.700000, 6.410000, 5.309744, NA, 8.02258…
## $ unit         <chr> NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA…
## $ obs_status   <chr> NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA…
## $ footnote     <chr> NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA…
## $ last_updated <date> 2024-11-13, 2024-11-13, 2024-11-13, 2024-11-13, 2024-11-13, 2024-11-13, 2024-11-13, 2024-11-13, 2024-11-13, 2024-11-13, 2024-11-13, 2024-11-13, 2024-11-13, 2024-11-13, 2024-11-13, 2024-11-13, 2024-11-13, 2024-11-13, 2024-11-13, 2024-11-13, 2024-…
life_expectancy <- wb_data(indicator = "SP.DYN.LE00.IN", start_date = 2020, end_date = 2020)
life_expectancy <- life_expectancy |> rename(years_to_live = SP.DYN.LE00.IN)
life_expectancy |> glimpse()
## Rows: 217
## Columns: 9
## $ iso2c         <chr> "AW", "AF", "AO", "AL", "AD", "AE", "AR", "AM", "AS", "AG", "AU", "AT", "AZ", "BI", "BE", "BJ", "BF", "BD", "BG", "BH", "BS", "BA", "BY", "BZ", "BM", "BO", "BR", "BB", "BN", "BT", "BW", "CF", "CA", "CH", "JG", "CL", "CN", "CI", "CM", "CD", "CG",…
## $ iso3c         <chr> "ABW", "AFG", "AGO", "ALB", "AND", "ARE", "ARG", "ARM", "ASM", "ATG", "AUS", "AUT", "AZE", "BDI", "BEL", "BEN", "BFA", "BGD", "BGR", "BHR", "BHS", "BIH", "BLR", "BLZ", "BMU", "BOL", "BRA", "BRB", "BRN", "BTN", "BWA", "CAF", "CAN", "CHE", "CHI", …
## $ country       <chr> "Aruba", "Afghanistan", "Angola", "Albania", "Andorra", "United Arab Emirates", "Argentina", "Armenia", "American Samoa", "Antigua and Barbuda", "Australia", "Austria", "Azerbaijan", "Burundi", "Belgium", "Benin", "Burkina Faso", "Bangladesh", "…
## $ date          <dbl> 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2020,…
## $ years_to_live <dbl> 75.72300, 62.57500, 62.26100, 76.98900, NA, 78.94600, 75.89200, 72.17300, NA, 78.84100, 83.20000, 81.19268, 66.86800, 61.56600, 80.69512, 60.08800, 59.73100, 71.96800, 73.65854, 79.17400, 72.67700, 76.22500, 72.45722, 72.85400, 81.13600, 64.4670…
## $ unit          <chr> NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, N…
## $ obs_status    <chr> NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, N…
## $ footnote      <chr> NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, N…
## $ last_updated  <date> 2024-11-13, 2024-11-13, 2024-11-13, 2024-11-13, 2024-11-13, 2024-11-13, 2024-11-13, 2024-11-13, 2024-11-13, 2024-11-13, 2024-11-13, 2024-11-13, 2024-11-13, 2024-11-13, 2024-11-13, 2024-11-13, 2024-11-13, 2024-11-13, 2024-11-13, 2024-11-13, 2024…
  1. Now, join the data together and save it as a new data frame.
europe_data <- europe |>
  left_join(health_expenditure, by = c("iso_a3" = "iso3c")) |> 
  left_join(life_expectancy, by = c("iso_a3" = "iso3c"))
  1. Now, make a table of the descriptive statistics.
Country Current health expenditure (% of GDP) Life expectancy at birth, total (years)
Albania 7.519203 76.98900
Austria 11.390000 81.19268
Belarus 6.410000 72.45722
Belgium 11.197513 80.69512
Bosnia and Herz. 9.700000 76.22500
Bulgaria 8.480000 73.65854
Croatia 7.720000 77.72439
Czechia 9.213688 78.17561
Denmark 10.560000 81.60244
Estonia 7.579065 78.59512
Finland 9.630000 81.93171
France NA NA
Germany 12.692553 81.04146
Greece 9.503638 81.28780
Hungary 7.290000 75.56829
Iceland 9.610000 83.06341
Ireland 7.109147 82.55610
Italy 9.630000 82.19512
Kosovo NA NA
Latvia 7.250000 75.18537
Lithuania 7.480000 74.97805
Luxembourg 5.740000 82.14390
Moldova 7.000000 70.16600
Montenegro 11.420000 75.93171
Netherlands 11.210000 81.35854
North Macedonia 7.730000 74.39512
Norway NA NA
Poland 6.500000 76.50000
Portugal 10.550000 80.97561
Romania 6.230000 74.25366
Russia 7.570000 71.33878
Serbia 8.700421 74.47805
Slovakia 7.130000 76.86585
Slovenia 9.430000 80.53171
Spain 10.745660 82.33171
Sweden 11.330000 82.35610
Switzerland 11.732068 83.00000
Ukraine 7.560000 71.18512
United Kingdom 12.158634 80.35122
  1. This is probably too much information, so let’s just do a table of the basic summary statistics.
Characteristic N = 391
GDP (in million USD) 209,852 (51,475, 533,097)
Current health expenditure (% of GDP) 8.96 (7.39, 10.65)
    Unknown 3
Life expectancy at birth, total (years) 78.4 (75.1, 81.5)
    Unknown 3
1 Median (Q1, Q3)
  1. If you want, make a map of the data. We’ve done enough of this, so you can skip it if you like.

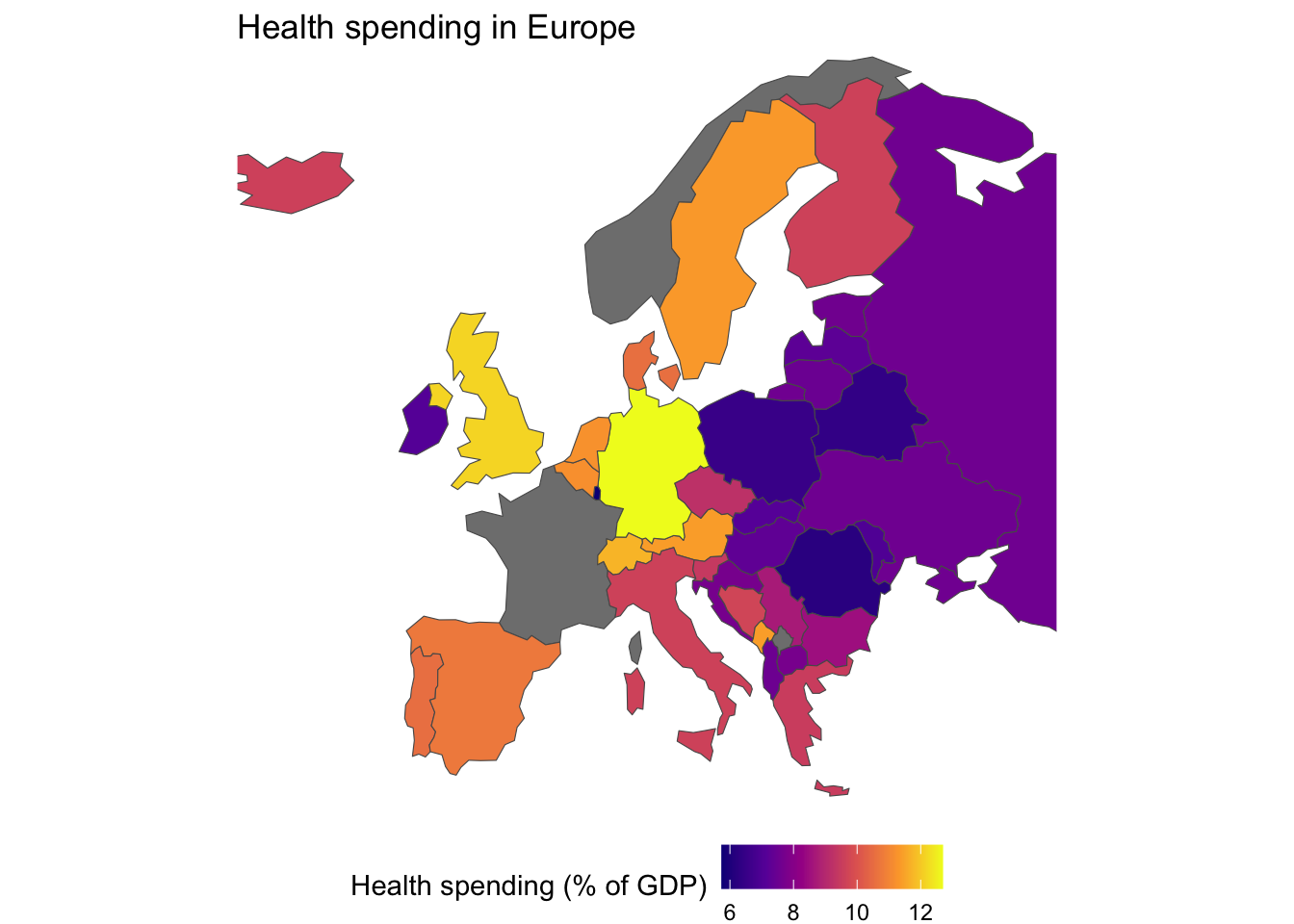
  1. Before running the regression model, drop any missing values. You can do this with the drop_na() function.
europe_data <- europe_data |> drop_na(spending, years_to_live)
  1. Now, run the regression model and make a table of the results.
regression <- lm(years_to_live ~ spending + gdp_md, data = europe_data)
regression |> tbl_regression(
  label = list(spending = "Health spending (% of GDP)",
               gdp_md = "GDP (in million USD)")
  )
Characteristic Beta 95% CI1 p-value
Health spending (% of GDP) 1.2 0.53, 1.9 <0.001
GDP (in million USD) 0.00 0.00, 0.00 0.9
1 CI = Confidence Interval
  1. Plot each relationship in the regression model using geom_smooth().
## `geom_smooth()` using formula = 'y ~ x'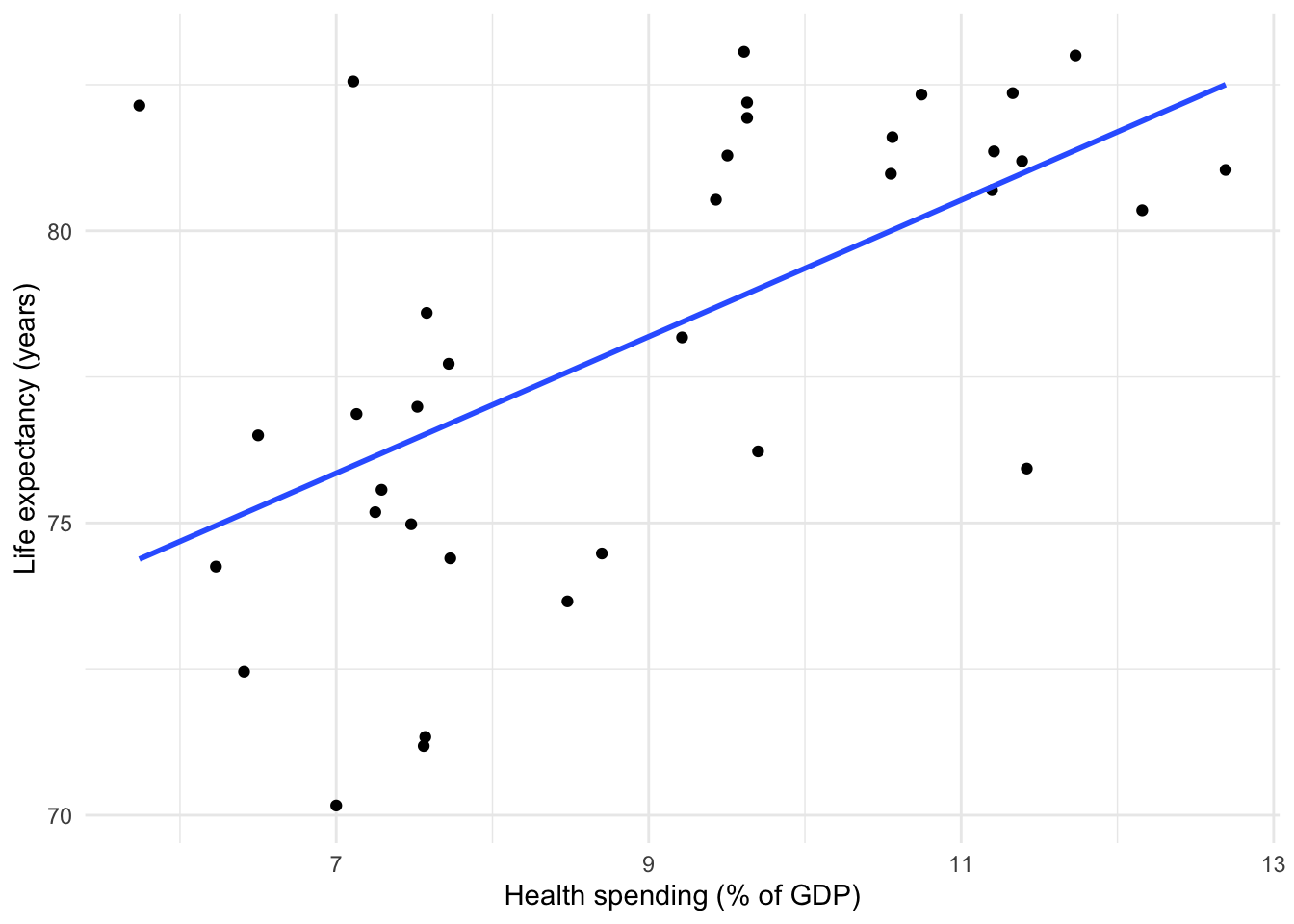

europe_data |> ggplot(aes(x = gdp_md, y = years_to_live)) +
  geom_point() +
  geom_smooth(method = "lm", se = FALSE) +
  labs(
    x = "GDP (in million USD)",
    y = "Life expectancy (years)"
  ) +
  theme_minimal()
## `geom_smooth()` using formula = 'y ~ x'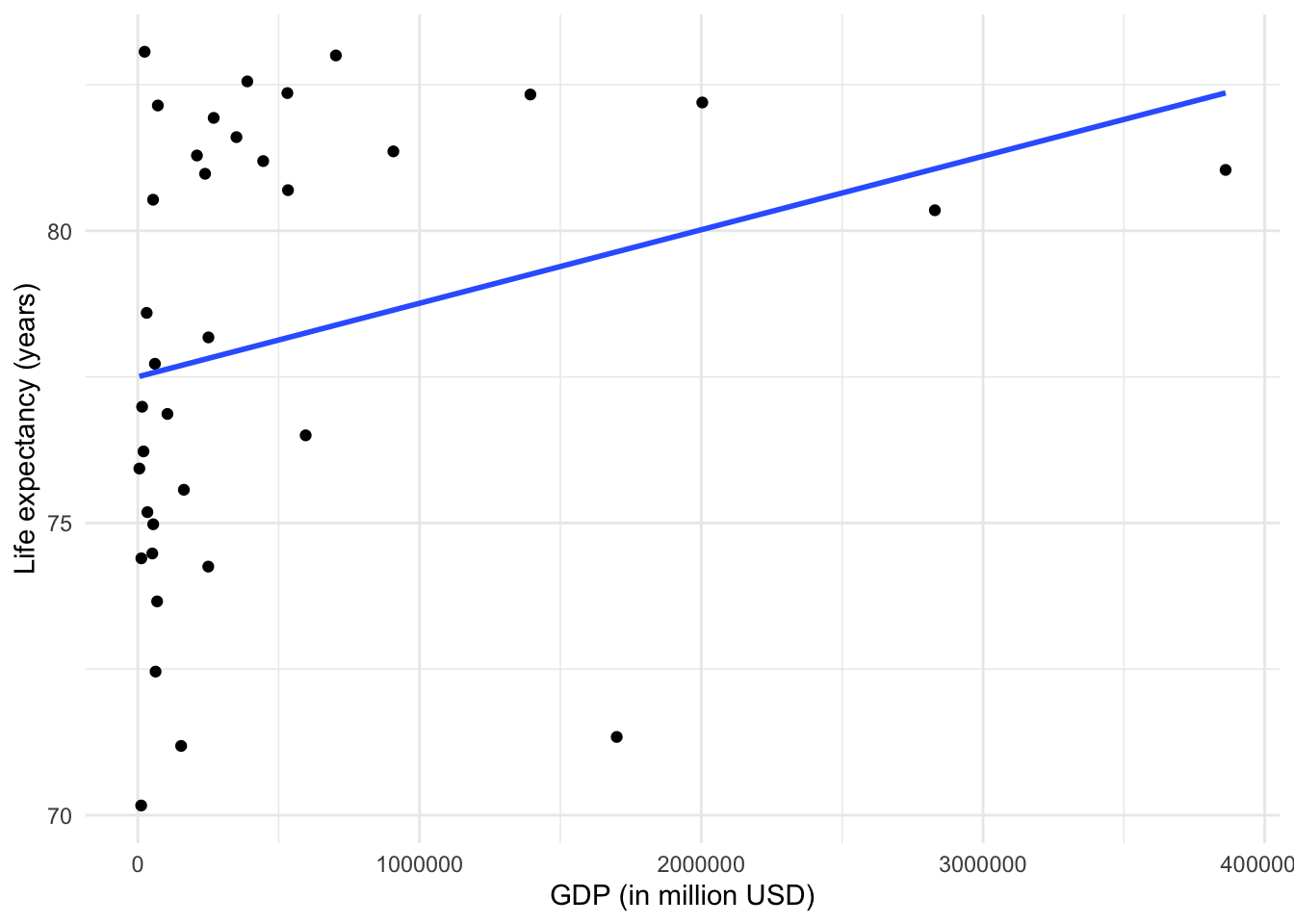

And that’s science! All that would be left for you to do is write up your results and submit them to a journal.