Chapter 9 Censored and Count Data
We now turn to methods that are appropriate for dependent variables that are either censored or count data. This will include the Tobit and Heckman models for censored data and the Poisson and Negative Binomial models for count data.
This chapter makes use of some packages that have not yet been used in this text, so you should ensure that you have censReg and sampleSelection installed.
Next, I will load in the data that will be used in this chapter, which comes from the AER and wooldridge packages.
data(charity)
data(fringe)
data(mroz)
data(affairs)
data(Medicaid1986)
data(DoctorVisits)
data(EquationCitations)
data(NMES1988)
data(wagepan)
data(murder)
data(NaturalGas)
data(HealthInsurance)9.1 Censored Models
The first part of this chapter looks at models designed to fit a regression to a dependent variable that is censored. A variable is said to be censored if we only have partial information about some of the observations; specifically, there is some upper or lower boundary on the observations. If the variable cannot take on a value below some threshold level it is said to be left-censored, and if it cannot take on a value above some threshold level it is said to be right-censored. It is possible for data to be both left- and right-censored at the same time!
Censoring is often due to the presence of “corner solutions” or top/bottom coding. Some examples might help make more clear the type of variables we are talking about.
Let’s say you are trying to estimate the demand for tickets to a hockey arena. In this case, there is a maximum limit for how many tickets can be sold–the stadium capacity. This data is likely to be right-censored. Let’s take a deeper look to see why taking this into account matters.
Suppose our arena seats 10,000 people and over the course of the season we vary our prices by game to get a feel for how many tickets we sell at a range of prices. Those data look like:
| Price | Tickets |
|---|---|
| 45 | 4700 |
| 40 | 5600 |
| 35 | 6100 |
| 30 | 6900 |
| 25 | 7500 |
| 20 | 8700 |
| 15 | 9400 |
| 10 | 10000 |
| 5 | 10000 |
| 0 | 10000 |
Once we drop to a price of $10, we sell out the arena. Dropping the price to $5 or $0 can’t possible result in more tickets being sold (or given away!) because there are no more seats to sell. This presents a problem, because at a price $5, there is a good chance that we could have sold more tickets if they existed to sell! At a price of $0, we probably could have given away a lot more than 10,000 tickets!
For the sake of continuing the explanation, let’s assume that there was no cap on tickets available to sell, and we have access to this “true” data. The number of hypothetical tickets that would be sold at each of these prices are as follows:
| Price | Actual Tickets | Hypothetical Tickets |
|---|---|---|
| 45 | 4700 | 4700 |
| 40 | 5600 | 5600 |
| 35 | 6100 | 6100 |
| 30 | 6900 | 6900 |
| 25 | 7500 | 7500 |
| 20 | 8700 | 8700 |
| 15 | 9400 | 9400 |
| 10 | 10000 | 10100 |
| 5 | 10000 | 11400 |
| 0 | 10000 | 12600 |
From $45 down to a price of $15, the two series are the same. Beyond that, however, we can see that the the hypothetical sales exceed actual sales. To see why this might pose an issue, we can graph the estimated demand curves for both of these data series in the same plot. In the graph below, the purple dots show where true sales and hypothetical sales would be the same for any price above $15. For prices below $10, pink dots show the actual ticket sales, while the blue dots show the hypothetical true sales were it not for the stadium seating capacity. The pink and blue lines show the respective demand curves based on both actual sales and hypothetical sales:
hockeydat %>% ggplot(aes(y = price, x = quantity)) +
geom_point(aes(y = price, x = quantity_a),
color = "deeppink",
size = 3,
alpha = .5) +
geom_smooth(aes(y = price, x = quantity_a),
method = lm,
color = "deeppink4",
linetype = 2,
se = FALSE) +
geom_point(aes(y = price, x = quantity),
color = "cornflowerblue",
size = 3,
alpha = .5) +
geom_smooth(aes(y = price, x = quantity),
method = lm,
color = "blue",
linetype = 2,
se = FALSE) +
theme_classic() +
labs(
y = "Price",
x = "Tickets Sold")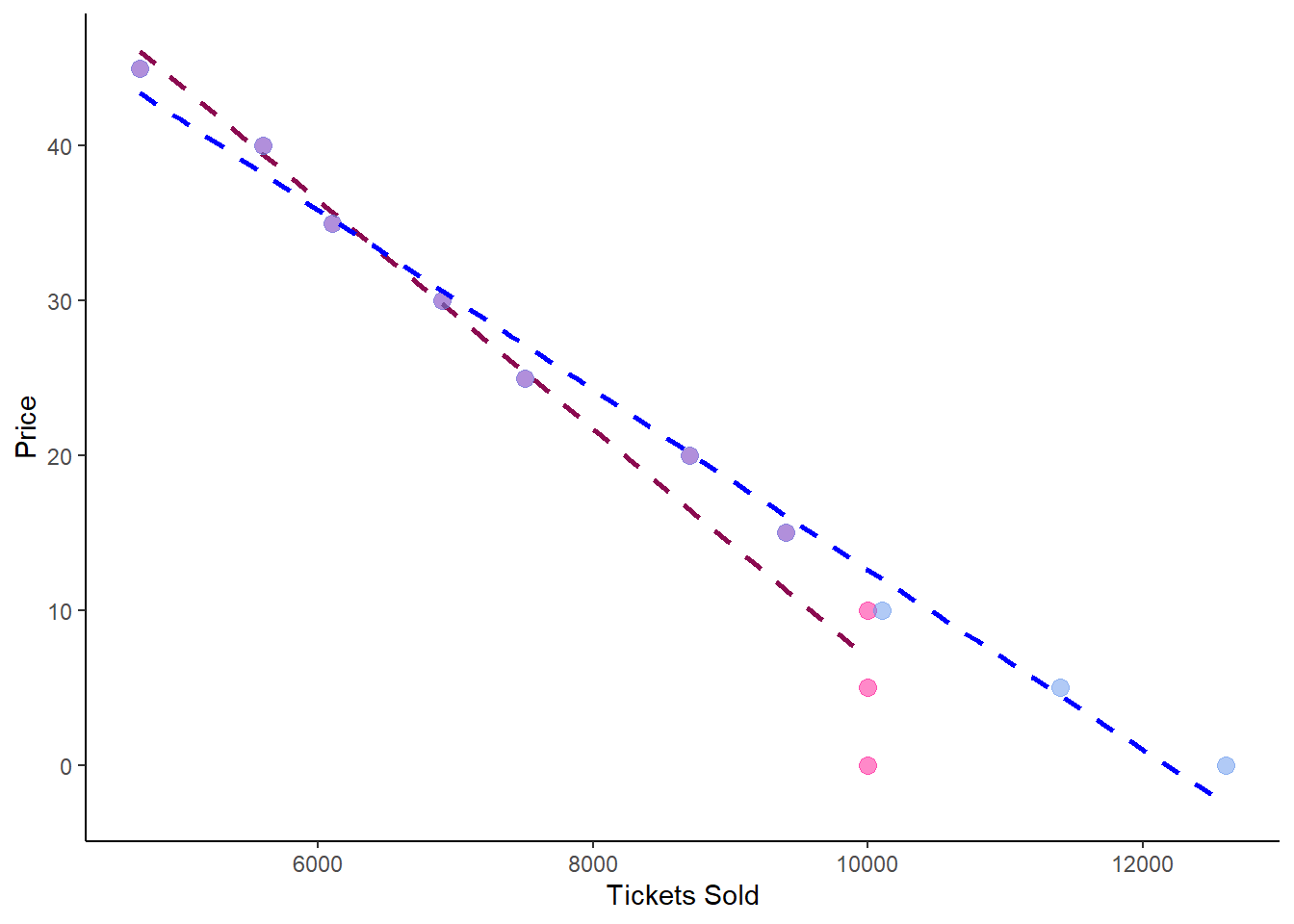
The blue line is the better line. However, in the real world, we would never get access to the blue data, only the pink data. This is why censored models are useful, because they allow us to approximate something much closer to the blue line than the actual data we have would enabled.
Looking at the OLS estimates on the censored data (\(quantity\_a\)) v. the hypothetical data (\(quantity\)), we see a big difference between the slopes of the two regression lines, indicating that the demand curve estimated from the real world data (column 2) is quite far off from the “true” demand curve (column 1) that came from the hypothetical data:
##
## =========================================================
## Dependent variable:
## ----------------------------
## quantity quantity_a
## (1) (2)
## ---------------------------------------------------------
## price -170.182*** -129.333***
## (6.354) (9.690)
##
## Constant 12,129.090*** 10,800.000***
## (169.608) (258.656)
##
## ---------------------------------------------------------
## Observations 10 10
## R2 0.989 0.957
## Adjusted R2 0.988 0.952
## Residual Std. Error (df = 8) 288.570 440.076
## F Statistic (df = 1; 8) 717.328*** 178.139***
## =========================================================
## Note: *p<0.1; **p<0.05; ***p<0.01Using the censored techniques we will learn later in this chapter on this data, I obtain a coefficient on price of -156.4 using the \(quantity\_a\) variable, a clear improvement over the simple OLS method!
Is this data not also left-censored? After all, you can’t sell negative tickets! Yes, but since there are not likely to be any zeroes in the data set (unless this hockey team is really bad at pricing!), you don’t need to worry about it. Basically, you don’t need to worry about censoring if it could happen, only if it exists in the data.
Here’s a couple more examples of where you might find censored data:
If you are trying to predict student performance on tests or standardized tests, you often run into data that is top and/or bottom coded. SAT scores, for example, are top-coded at 800 and bottom-coded at 200 on each section. Why does this matter? If two students with very different levels of math skills take the SAT, the one with better math skills is likely to perform much better on the SAT. But what if those two students are both very good at math in objective terms, so they both get 800?
Corner solutions are often common when the dependent variable is a percentage, so observations get bunched at 0% and/or 100%. For example, maybe you are looking at individual investment decisions and want to predict what percent of people’s portfolios they invest in equity v. fixed income investments. Most people likely have a mix of both, but you might find in the data that there are a bunch of people invest all their assets in stocks and none in bonds AND a bunch of people who invest all of their assets in bonds and none in stocks.
Data may not exist for some observations in your data set, and you think that the reason the data does not exist can be modeled. For example, you might have data on incomes for a large group of women, and many of them have 0 income because they don’t have a job. Do they not have a job because they have little education and can’t find a job? Or do they not have a job because they are voluntarily staying home with small children?
We will look at two types of models to fit censored data: the Tobit model and the Heckman model. Unlike the Probit and Logit models encountered in Chapter 8, these model types are not interchangeable, and which one you use depends on the type of censoring involved. Of the examples above, the first three cases (hockey tickets, SAT scores, investment modeling) would call for a Tobit model, whereas the last one (women’s wages) would be a situation for a Heckman model.
9.1.1 Tobit Regression
Let’s illustrate the Tobit model using the fringe dataset in the wooldridge package. The variable \(annbens\) contains the dollar value of annual benefits for the 616 individuals in the data set.
summary(fringe$annbens)## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.0 826.8 1614.4 1894.4 3161.2 5129.1Here, we can see that the minimum is $0 and the maximum is $5129.1. Let’s think about this a little further:
- Does the maximum have to be $5129.1? Could it be higher?
- Does the minimum have to be $0? Could it be lower?
While it seems possible that somebody could have more than $5129.1 in fringe benefits per year, how could somebody have negative valued fringe benefits? This suggests that there is a good chance of $0 being a “corner solution.” We can more closely at the data to see if this is in fact true. Let’s take a look at the \(annbens\) variable graphically:
fringe %>% ggplot(aes(x = annbens)) +
geom_histogram(binwidth = 100, color = "#00573C", fill = "#00573C") +
theme_classic() +
scale_x_continuous(expand = c(0, 0)) +
scale_y_continuous(expand = c(0, 0))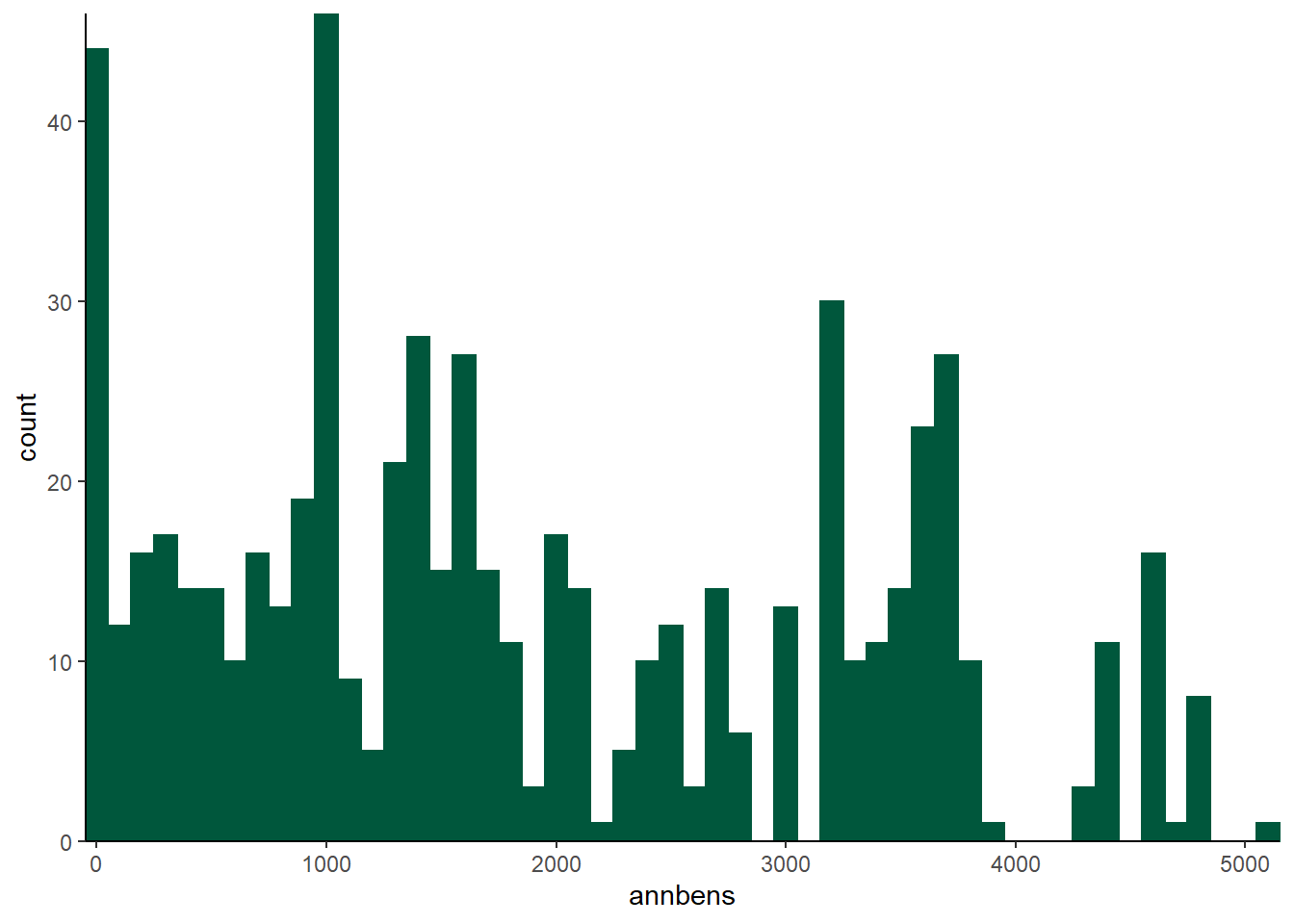 
There are two pretty big spikes - one at zero, and another around 1000. But these spikes are different in nature. The presence of the big spike at 0 is suggestive of a corner solution. This next command is a little tricky, but it will ask R to list the 10 most common values for the \(annbens\) variable.
sort(table(fringe$annbens),decreasing=TRUE)[1:10]##
## 0 3669.919921875 3161.18994140625 4550.240234375
## 41 19 18 15
## 2491.2900390625 4442.65966796875 1444.76000976562 2405.31005859375
## 12 11 10 10
## 2969.92993164062 1639.53002929688
## 10 9Not only is 0 the most common value, it is twice as likely as any other value for this variable! This is a pretty good indication that if we want to model \(annbens\), we should probably use a Tobit model. Intuitively, the Tobit model is kind of a hybrid of OLS regression and the probit model. In fact, it gets its name as a combination of its inventor, Nobel Laureate economist James Tobin, and the probit model. The math behind the Tobit is essentially estimating a probit on whether or not the dependent variable is censored or not, a linear regression on the data that is not censored, and combining them into one estimate.
A Tobit model is estimated with the censReg() function, which is part of the censReg package. This function works a lot like the lm() and glm() commands we have been using, but we need to specify a couple extra options. We need to tell the censReg function how the data is censored with the left = 0 and right = Inf arguments. The Inf is short for infinite, so this argument simply tells R that the data is not right-censored. The left = 0 tells R that the dependent variable is left censored at 0; were we dealing with right-censored data, we would use left = -Inf and set our right censoring with the right option.
reg1a <- censReg(annbens ~ tenure + annearn, left = 0, right = Inf, data = fringe)
stargazer(reg1a, type = "text")##
## ===============================================
## Dependent variable:
## ---------------------------
## annbens
## -----------------------------------------------
## tenure 55.486***
## (6.155)
##
## annearn 0.072***
## (0.005)
##
## logSigma 7.064***
## (0.030)
##
## Constant 497.035***
## (92.486)
##
## -----------------------------------------------
## Observations 616
## Log Likelihood -4,920.289
## Akaike Inf. Crit. 9,848.579
## Bayesian Inf. Crit. 9,866.272
## ===============================================
## Note: *p<0.1; **p<0.05; ***p<0.01The model estimates the value of fringe benefits as a function of an individual’s tenure with their current employer and annual earnings. We interpret the coefficients in roughly the same way as we would an OLS coefficient–technically it’s a weighted average of the OLS and a probit estimates, but that’s getting too much in the weeds for this book. The \(logSigma\) term is a model parameter.
As another example, we can examine the charity data in the wooldridge package. This data has a variable, \(\mathit{gift}\), that is clearly left censored at zero. In this dataset, \(\mathit{gift}\) measures the amount of money donated by 4268 potential donors. As the histogram shows, this is a case where there are a ton of zeroes:
charity %>% ggplot(aes(x = gift)) +
geom_histogram(binwidth = 5, color = "#00573C", fill = "#00573C") +
theme_classic() +
scale_x_continuous(expand = c(0, 0)) +
scale_y_continuous(expand = c(0, 0))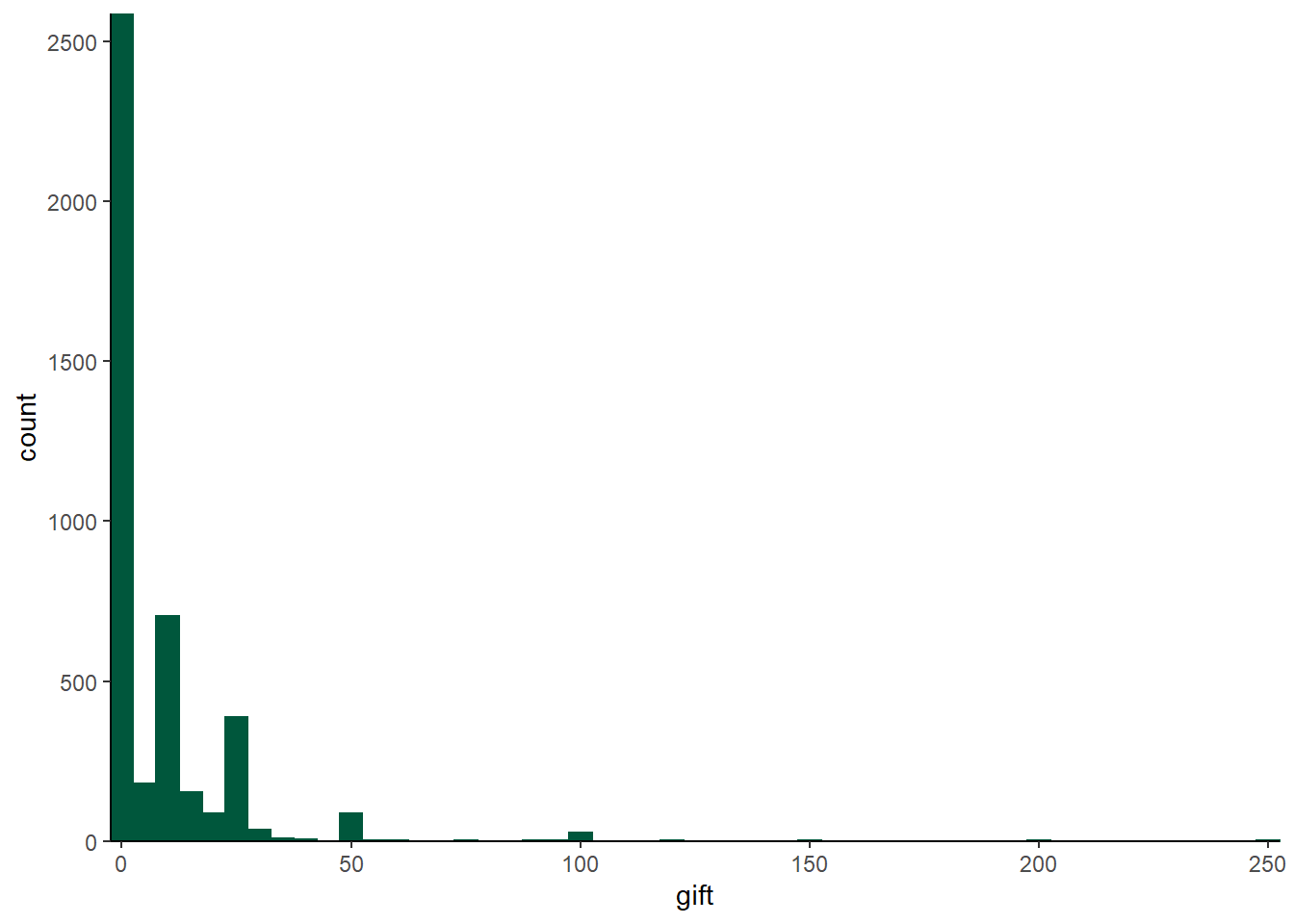 
Of the 4268 observations in the dataset, over half are zero! Here are the 10 most common gift sizes in the data:
sort(table(charity$gift),decreasing=TRUE)[1:10]##
## 0 10 25 5 15 20 50 30 2 100
## 2561 702 387 158 152 86 86 36 25 25With this many left censored observations, Tobit is probably going to be a good model to use.
reg2a <- censReg(gift ~ mailsyear + avggift, left = 0, right = Inf, data = charity)
stargazer(reg2a, type = "text")##
## ===============================================
## Dependent variable:
## ---------------------------
## gift
## -----------------------------------------------
## mailsyear 6.618***
## (0.782)
##
## avggift 0.022***
## (0.006)
##
## logSigma 3.367***
## (0.019)
##
## Constant -22.658***
## (1.786)
##
## -----------------------------------------------
## Observations 4,268
## Log Likelihood -9,626.172
## Akaike Inf. Crit. 19,260.340
## Bayesian Inf. Crit. 19,285.780
## ===============================================
## Note: *p<0.1; **p<0.05; ***p<0.01Let’s push our analysis a bit further by estimating the same model with an OLS regression using the lm() command. We can compare these models side-by-side with stargazer:
reg2b <- lm(gift ~ mailsyear + avggift, data = charity)
stargazer(reg2a, reg2b, type = "text")##
## =======================================================
## Dependent variable:
## -----------------------------------
## gift
## censored OLS
## regression
## (1) (2)
## -------------------------------------------------------
## mailsyear 6.618*** 2.602***
## (0.782) (0.342)
##
## avggift 0.022*** 0.019***
## (0.006) (0.003)
##
## logSigma 3.367***
## (0.019)
##
## Constant -22.658*** 1.769**
## (1.786) (0.737)
##
## -------------------------------------------------------
## Observations 4,268 4,268
## R2 0.023
## Adjusted R2 0.023
## Log Likelihood -9,626.172
## Akaike Inf. Crit. 19,260.340
## Bayesian Inf. Crit. 19,285.780
## Residual Std. Error 14.889 (df = 4265)
## F Statistic 51.066*** (df = 2; 4265)
## =======================================================
## Note: *p<0.1; **p<0.05; ***p<0.01The coefficients on these models are very different; the AIC and BIC are useful tools for comparing models of different types like this. We can obtain these measures for our OLS model with the AIC() and BIC() commands, respectively.
AIC(reg2b)## [1] 35169.5BIC(reg2b)## [1] 35194.94As lower values of AIC and BIC indicate better models, it seems clear that the Tobit model outperforms the OLS model by a fairly large margin.
9.1.2 Heckman Selection Model
The Heckman Selection Model (sometimes simply called the Heckman model) shares many similarities with the Tobit model. Like the Tobit model, the Heckman model is named for an Economics Nobel Laureate: James Heckman. At its core, it is the same combination of estimating a probit on whether or not the dependent variable is censored or not and a linear regression on the data that is not censored. There are two key difference here. First, in the Heckman model, the data are not “piled-up” at some value (typically on the left), they are truly unobserved. The second difference is that we have some theory or explanation as to why some are observed and some are not.
Let’s look at some wage data, where the Heckman model is commonly used. The mroz data in the wooldridge package looks at the wages of married women in the mid 1970s, and contains a the \(repwage\) variable, which is the reported wage of the women in the data set. If we look at at the variable more closely, we see that over half of the women have a wage of 0!
summary(mroz$repwage)## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.00 0.00 0.00 1.85 3.58 9.98While they report their wage as $0, this is not a case of these women working for free; rather, many of these women have simply opted out of the labor force. In a sense, then, we actually don’t know what their wage would have been had they chosen to work. Thus, their wages can be said to be “unobserved,” which is the first thing we need to estimate a Heckman model. The second thing we need is something that influences whether or not we observe their data that is not correlated with the variable we are trying to explain; in this case, their wages. We will use the \(kidslt6\) variable for this – we would suspect that having more pre-school aged kids make someone less likely to work, but shouldn’t necessarily reduce their wages should they choose to work.
The selection() command is a bit tricky, as we need to specify two models, one for the probit model to see if wages are observed or not, and a second for the regression model to actually predict wages. We also need to edit our dataset a bit to put some NA values in for the zeroes.
mroz2 <- mroz
mroz2$repwage[mroz2$repwage == 0] <- NA Now that the missing values are coded as NA we specify the selection model as:
reg3a <- selection(!is.na(repwage) ~ kidslt6 + educ + city + exper, repwage ~ educ + city + exper, data = mroz2)This line of code might seem to be a little tricky at first. The first equation models whether or not the \(repwage\) variable is missing or not using the!is.na() command – is.na(repwage) returns a yes/no on if \(repwage\) is missing (NA), and the ! in front of it serves as a “not” function. This is modeled as a function of the number of children, education, experience, and a city dummy. The second equation models \(repwage\) as a function of education, experience, and the city dummy. It is essential in a Heckman model that at least one of the variables in the selection equation is not in the OLS model.
If we use the summary() command, we can see both the first and second stages of the model:
summary(reg3a)## --------------------------------------------
## Tobit 2 model (sample selection model)
## Maximum Likelihood estimation
## Newton-Raphson maximisation, 6 iterations
## Return code 8: successive function values within relative tolerance limit (reltol)
## Log-Likelihood: -1074.942
## 753 observations (417 censored and 336 observed)
## 11 free parameters (df = 742)
## Probit selection equation:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -2.018059 0.278046 -7.258 9.93e-13 ***
## kidslt6 -0.149159 0.063947 -2.333 0.0199 *
## educ 0.114519 0.021676 5.283 1.67e-07 ***
## city 0.014163 0.095353 0.149 0.8820
## exper 0.045549 0.005654 8.055 3.16e-15 ***
## Outcome equation:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -4.85420 0.65514 -7.409 3.46e-13 ***
## educ 0.39926 0.04938 8.085 2.53e-15 ***
## city 0.54199 0.22749 2.383 0.0174 *
## exper 0.12916 0.01436 8.992 < 2e-16 ***
## Error terms:
## Estimate Std. Error t value Pr(>|t|)
## sigma 2.43194 0.13646 17.82 <2e-16 ***
## rho 0.97004 0.01284 75.57 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## --------------------------------------------The selection model is in the top table, the regression on the observed data is in the bottom table. The \(kidslt6\) variable is significant at the 2% level in the selection equation; the negative coefficient indicates the expected result that women with young children are less likely to have an observed wage.
Let’s compare these estimates with a Tobit model and an OLS regression: note that the OLS and Tobit models are using the version of \(repwage\) that has zeroes as opposed to \(NA\) values.
reg3b <- censReg(repwage ~ kidslt6 + educ + city + exper, left = 0, right = Inf, data = mroz)
reg3c <- lm(repwage ~ kidslt6 + educ + city + exper, data = mroz)
stargazer(reg3a, reg3b, reg3c, type = "text")##
## =======================================================================
## Dependent variable:
## ---------------------------------------------------
## repwage
## selection censored OLS
## regression
## (1) (2) (3)
## -----------------------------------------------------------------------
## kidslt6 -1.376*** -0.469***
## (0.379) (0.157)
##
## educ 0.399*** 0.472*** 0.268***
## (0.049) (0.077) (0.036)
##
## city 0.542** 0.241 0.199
## (0.227) (0.362) (0.169)
##
## exper 0.129*** 0.186*** 0.091***
## (0.014) (0.022) (0.010)
##
## logSigma 1.408***
## (0.044)
##
## Constant -4.854*** -7.804*** -2.426***
## (0.655) (1.018) (0.445)
##
## -----------------------------------------------------------------------
## Observations 753 753 753
## R2 0.189
## Adjusted R2 0.184
## Log Likelihood -1,074.942 -1,205.004
## Akaike Inf. Crit. 2,422.008
## Bayesian Inf. Crit. 2,449.753
## rho 0.970*** (0.013)
## Residual Std. Error 2.185 (df = 748)
## F Statistic 43.489*** (df = 4; 748)
## =======================================================================
## Note: *p<0.1; **p<0.05; ***p<0.01We can get the AIC and BIC from the Heckman and LM models with the AIC() and BIC() functions:
AIC(reg3a) # Heckman## 'log Lik.' 2171.885 (df=11)AIC(reg3b) # Tobit## 'log Lik.' 2422.008 (df=6)AIC(reg3c) # OLS## [1] 3321.357BIC(reg3a) # Heckman## [1] 2222.749BIC(reg3b) # Tobit## [1] 2449.753BIC(reg3c) # OLS## [1] 3349.102The Heckman model seems to be substantially better here than the Tobit model, and both are a ton better than OLS for this data.
9.2 Count Models
The last type of data we will look at in this notebook is count data; dependent variables that can only take on whole number values. For example:
- The number of children an individual has
- The number of doctor’s visits a person makes in a year
Typically we only use count models in cases where the counts are relatively low numbers – a decent ballpark number is that the mean of the dependent variable should be under 10 – We would not use a count model if our dependent variable was the number of McDonalds hamburgers sold annually at each restaurant or the number of puppies born each month by state, even though hamburgers and puppies are fundamentally countable.
The two primary models used for count data are the Poisson and the Negative Binomial models. The poisson model is a bit easier to estimate, so we will begin there.
We have used the binary measure from the affairs dataset in the wooldridge package before; let’s now turn to the \(\mathit{naffairs}\) variable, a count variable that measures the number of affairs an individual had in the past year. First, let’s look at a graph and some summary statistics of \(\mathit{naffairs}\):
summary(affairs$naffairs)## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.000 0.000 0.000 1.456 0.000 12.000table(affairs$naffairs)##
## 0 1 2 3 7 12
## 451 34 17 19 42 38affairs %>% ggplot(aes(x = naffairs)) +
geom_histogram(binwidth = 1, fill = "darkblue") +
theme_classic() +
scale_x_continuous(expand = c(0, 0), breaks = 0:12) +
scale_y_continuous(expand = c(0, 0))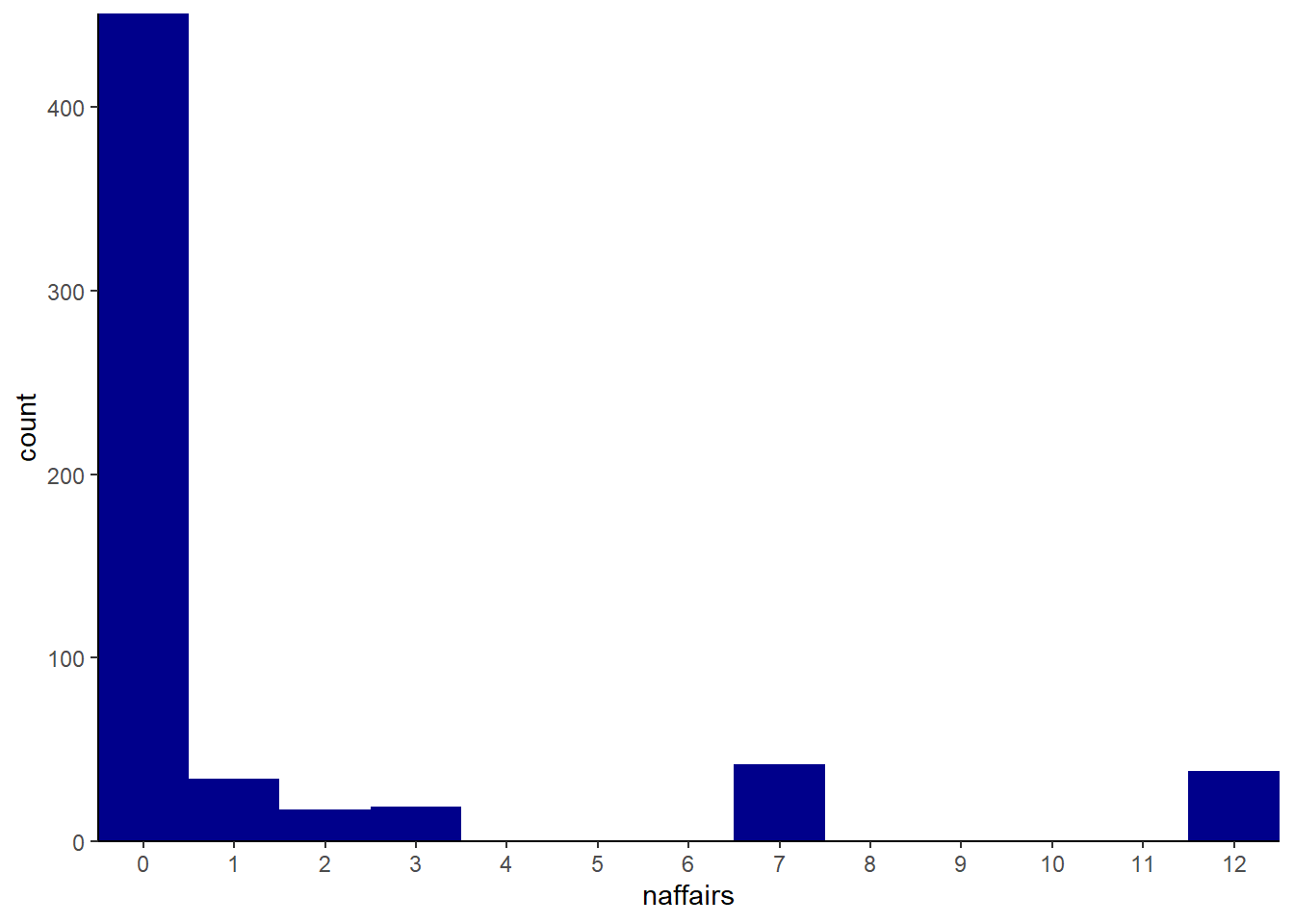 
The mean is 1.5, and the both the table and histogram show that the \(\mathit{affairs}\) variable is indeed a count variable. This suggests that a poisson model is likely indicated. We estimate the poisson model with the glm() function and set use the family = poisson() option. Because this is a glm() type model, to make the coefficients easier to interpret we need to filter the results through margins() and display the results using export_summs() rather than stargazer().
reg4a <- glm(naffairs ~ male + yrsmarr + kids + relig + educ + ratemarr, data = affairs, family = poisson())
reg4amargins <- margins(reg4a)
huxtable::set_width(export_summs(reg4amargins,
number_format = "%.4f",
stars = c(`***` = 0.01, `**` = 0.05, `*` = 0.1)),
.4)| Model 1 | |
|---|---|
| educ | 0.0233 |
| (0.0215) | |
| kids | -0.0276 |
| (0.1493) | |
| male | 0.0756 |
| (0.1080) | |
| ratemarr | -0.5968 *** |
| (0.0453) | |
| relig | -0.5255 *** |
| (0.0484) | |
| yrsmarr | 0.1115 *** |
| (0.0120) | |
| nobs | 0 |
| null.deviance | 2925.4552 |
| df.null | 600.0000 |
| logLik | -1446.4158 |
| AIC | 2906.8316 |
| BIC | 2937.6218 |
| deviance | 2398.8417 |
| df.residual | 594.0000 |
| nobs.1 | 601.0000 |
| *** p < 0.01; ** p < 0.05; * p < 0.1. | |
For the sake of comparison, we can look at these results side-by-side with an OLS estimated with the same data:
reg4b <- lm(naffairs ~ male + yrsmarr + kids + relig + educ + ratemarr, data = affairs)
huxtable::set_width(export_summs(reg4amargins, reg4b,
model.names = c("Poisson", "OLS"),
number_format = "%.4f",
stars = c(`***` = 0.01, `**` = 0.05, `*` = 0.1)),
.6)| Poisson | OLS | |
|---|---|---|
| educ | 0.0233 | 0.0092 |
| (0.0215) | (0.0583) | |
| kids | -0.0276 | -0.1719 |
| (0.1493) | (0.3447) | |
| male | 0.0756 | 0.0317 |
| (0.1080) | (0.2779) | |
| ratemarr | -0.5968 *** | -0.7078 *** |
| (0.0453) | (0.1203) | |
| relig | -0.5255 *** | -0.4941 *** |
| (0.0484) | (0.1119) | |
| yrsmarr | 0.1115 *** | 0.1069 *** |
| (0.0120) | (0.0288) | |
| (Intercept) | 4.8635 *** | |
| (1.0599) | ||
| N | 0 | 601 |
| R2 | 0.1227 | |
| *** p < 0.01; ** p < 0.05; * p < 0.1. | ||
Again, as a means of comparing models we look at the AIC:
AIC(reg4a) # Poisson## [1] 2906.832AIC(reg4b) # OLS## [1] 3076.498THe AIC is quite a bit lower for the poisson than for the OLS estimate, indicating a better fit.
summary(reg4a)##
## Call:
## glm(formula = naffairs ~ male + yrsmarr + kids + relig + educ +
## ratemarr, family = poisson(), data = affairs)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -4.1159 -1.5897 -1.1474 -0.7298 7.3642
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 1.914067 0.265349 7.213 5.46e-13 ***
## male 0.051942 0.074163 0.700 0.484
## yrsmarr 0.076602 0.007824 9.791 < 2e-16 ***
## kids -0.018948 0.102553 -0.185 0.853
## relig -0.360938 0.030893 -11.683 < 2e-16 ***
## educ 0.016015 0.014779 1.084 0.279
## ratemarr -0.409897 0.027886 -14.699 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for poisson family taken to be 1)
##
## Null deviance: 2925.5 on 600 degrees of freedom
## Residual deviance: 2398.8 on 594 degrees of freedom
## AIC: 2906.8
##
## Number of Fisher Scoring iterations: 7Looking at the summary() of the poisson object shows us that the poisson model assumes the “(d)ispersion parameter for poisson family taken to be 1.” The AER package has a command called dispersiontest() which allows us to see if the dispersion paramener is in fact 1:
AER::dispersiontest(reg4a)##
## Overdispersion test
##
## data: reg4a
## z = 6.4475, p-value = 5.687e-11
## alternative hypothesis: true dispersion is greater than 1
## sample estimates:
## dispersion
## 6.538199The dispersion paramenter very clearly is not equal to 1. The dispersion is 6.54, which, according to the dispersion test, is significantly different from 1. This means that the model is overdispersed, which is just a fancy way of saying that the dependent variable has more variation than the Poisson model would like it to have, so we probably need to choose a different technique. Poisson models are almost always overdispersed, and the primary alternatives are either the Zero Inflated Poisson (ZIP) or the Negative Binomial. We will discuss the Negative Binomial, but the ZIP model will be left for the interested student to investigate further on his/her own.
The Negative Binomial model, often referred to as a “Negbin” model, is estimated with the glm.nb() function in the MASS package. The glm.nb() function works pretty much the same way as glm, but we don’t need to specify a family since the family is negative binomial. We also need to run these results through the margins() function:
reg4c <- glm.nb(naffairs ~ male + yrsmarr + kids + relig + educ + ratemarr, data = affairs)
reg4cmargins <- margins(reg4c)
huxtable::set_width(export_summs(reg4cmargins,
model.names = c("Negbin"),
number_format = "%.4f",
stars = c(`***` = 0.01, `**` = 0.05, `*` = 0.1)),
.4)| Negbin | |
|---|---|
| educ | -0.0050 |
| (0.0807) | |
| kids | 0.1167 |
| (0.4880) | |
| male | 0.0827 |
| (0.3872) | |
| ratemarr | -0.6283 *** |
| (0.2167) | |
| relig | -0.6613 *** |
| (0.2112) | |
| yrsmarr | 0.1250 *** |
| (0.0481) | |
| nobs | 0 |
| null.deviance | 389.7536 |
| df.null | 600.0000 |
| logLik | -728.5533 |
| AIC | 1473.1066 |
| BIC | 1508.2954 |
| deviance | 339.3364 |
| df.residual | 594.0000 |
| nobs.1 | 601.0000 |
| *** p < 0.01; ** p < 0.05; * p < 0.1. | |
Again, we can look at all 3 models together.
huxtable::set_width(export_summs(reg4cmargins, reg4amargins, reg4b,
model.names = c("Negbin", "Poisson", "OLS"),
number_format = "%.4f",
stars = c(`***` = 0.01, `**` = 0.05, `*` = 0.1)),
.8)| Negbin | Poisson | OLS | |
|---|---|---|---|
| educ | -0.0050 | 0.0233 | 0.0092 |
| (0.0807) | (0.0215) | (0.0583) | |
| kids | 0.1167 | -0.0276 | -0.1719 |
| (0.4880) | (0.1493) | (0.3447) | |
| male | 0.0827 | 0.0756 | 0.0317 |
| (0.3872) | (0.1080) | (0.2779) | |
| ratemarr | -0.6283 *** | -0.5968 *** | -0.7078 *** |
| (0.2167) | (0.0453) | (0.1203) | |
| relig | -0.6613 *** | -0.5255 *** | -0.4941 *** |
| (0.2112) | (0.0484) | (0.1119) | |
| yrsmarr | 0.1250 *** | 0.1115 *** | 0.1069 *** |
| (0.0481) | (0.0120) | (0.0288) | |
| (Intercept) | 4.8635 *** | ||
| (1.0599) | |||
| N | 0 | 0 | 601 |
| R2 | 0.1227 | ||
| *** p < 0.01; ** p < 0.05; * p < 0.1. | |||
The coefficients in the negbin model are similar to those in the poisson model, and the AIC is much lower for the negbin than it is for the poisson, indicating it is likely the preferred model:
AIC(reg4a) # Poisson AIC## [1] 2906.832AIC(reg4c) # Nebgin AIC## [1] 1473.107It is my experience that negbin is almost always a better choice than poisson.
9.3 Wrapping Up
While models for censored and count variables are a little more niche than the OLS and probit/logit models we encountered earlier, there are some types of data for which they are indispensable; health economics and labor economics have notable examples of each, as we saw above.
We next move on to time series modeling.
9.4 End of Chapter Exercises
Censored Data: For each of the following, examine the data (and the help file for the data) to try and build a good multivariate model. Think carefully about the variables you have to choose among to explain your dependent variable with. Consider strongly the use of non-linear or interaction effects in your model. For 1 and 2, do not use the same model as in the example in the text!
Use the
wooldridge:fringedata from the Tobit discussion. Build a model using Heckman, and compare it with the same model using Tobit. Discuss your results.Use the
wooldridge:charitydata from the Tobit discussion. Build a model using Heckman, and compare it with the same model using Tobit. Discuss your results.Use either
wooldridge:jtrain2orwooldridge:jtrain3to build Tobit and Heckman models. Think carefully about the specification for the Heckman model: is there a variable that is correlated with the censoring that is not correlated with the dependent variable? Interpret and present the results of each.
Count Data: For each of the following, examine the data (and the help file for the data) to try and build a good multivariate model. Think carefully about the variables you have to choose among to explain your dependent variable with. Consider strongly the use of non-linear or interaction effects in your model. Start with estimating both a basic lm and a Poisson model and discuss the differences. Test the dispersion assumption of the Poisson model. If the model is overdispersed, estimate the same model using negative binomial and compare the results of each.
Look at hospital vistation rates using one of the following 3 datasets:
AER:Medicaid1986,AER:DoctorVisits, andAER:NMES.Can you predict student attendance in
wooldridge:attend? This might be tricky – don’t include as independent variables anything that attendance might cause! Also, are the counts high enough that anlm()model is just as good?The
AER:EquationCitationdata includes citation counts as a variable; try your hand at some basic bibliometrics!