Kapitel 2 Servomotoren

2.1 Grundlegende Anforderungen

Da Servomotoren häufig dazu verwendet werden hochdynamische Positionieraufgaben in einem weiten Drehzahlbereich zu übernehmen, besitzen diese grundlegend eine hohe Dynamik, hohe Positioniergenauigkeit sowie hohe Überlastfähigkeit. Um Brems- und Beschleunigungsvorgänge während einer sogenannten Bahnkurve gewährleisten zu können, ist ein Betrieb in allen Quadranten des Drehzahl-Drehmoment-Diagrammes notwendig. Gleichzeitig soll der Servomotor über den gesamten Betriebsbereich hinweg ein möglichst lineares Regelverhalten aufweisen, was eine einfache und präzise Regelbarkeit ermöglicht. Brems- und Beschleunigungsvorgänge wechseln sich kontinuierlich ab, wodurch in kurzen Intervallen sehr hohes Drehmoment benötigt wird, welches in Konstantphasen meist deutlich abfällt. Diese Forderung bedingt ein geringes Massenträgheitsmoment. Aufgrund ihres vielfältigen Anwendungsbereiches zeichnen sich entsprechende Servomotoren somit durch folgende Merkmale aus:

• hohe Drehzahlgenauigkeit
• weiter Drehzahl-Stellbereich
• kompakte Bauweise
• hohes Stillstandmoment
• kurze Hochlaufzeiten
• kurze Drehmoment-Anregelzeit (Zeitkonstanten)
• geringes Gewicht
• geringes Massenträgheitsmoment
• hoher Wirkungsgrad
• geringer Wartungsaufwand

2.2 Grobeinteilung

Grundsätzlich unterscheidet sich ein Servomotor nicht von den gängigen Motortypen. Die prinzipiellen Komponenten sind:

• Rotor
• Stator
• Leistungsanschluss, welcher als Stecker oder Klemmenkasten ausgeführt werden kann
• Anschluss des integrierten Feedback-Systems

Abbildung 2.1: Beispiel eines Servomotors (Quelle: www.siemens.com)

Zum Einsatz als Servomotoren kommen grundsätzlich eine Vielzahl unterschiedlicher Motorentypen, wobei in der Vergangenheit häufig bürstenlose, permanenterregte Gleichstrommotoren verwendet wurden. Aufgrund der technologischen Fortschritte im Bereich der Leistungshalbleiter und Mikroprozessoren befinden sich heutzutage eher Wechselstrommaschinen im Einsatz. Gleichzeitig wird dabei den AC-Synchronmotoren, aufgrund der speziellen Eigenschaften, häufig der Vorrang gegeben. Eine Einteilung der unterschiedlichen, im Einsatz befindlichen, Servomotoren liefert Abbildung 2.2.

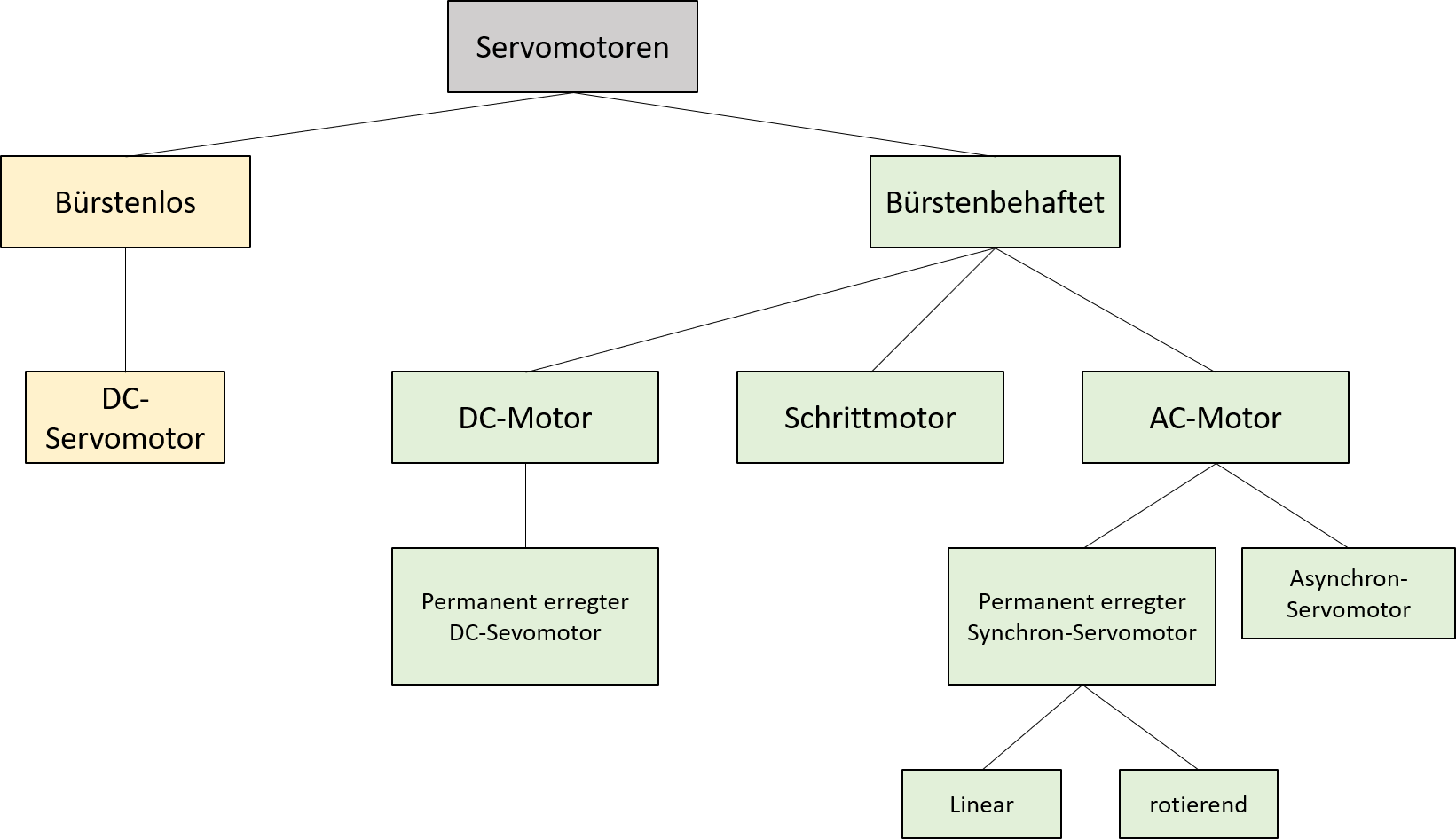
Abbildung 2.2: Unterteilung der verwendeten Servomotoren

2.3 Synchron-Servomotor (permanenterregt)

2.3.1 Aufbau

Da es sich, wie oben erwähnt, vorwiegend um permanenterregte Synchronmotoren handelt, lässt sich ein solcher Motortyp in folgende Komponenten unterteilen:

• Rotor mit Permanentmagneten
• Stator mit Drehstromwicklung
• Leistungsanschluss
• Drehzahlgeber

Je nach Hersteller wird weiterhin häufig unterschieden, ob es sich um einen gehäusebehafteten oder einen gehäuselosen Motor handelt. Dabei bedeutet gehäuselos, dass das Statorblechpaket sowohl die Aufgabe des magnetischen Rückschlusses als auch die Funktionalität des eigentlichen Gehäuses übernimmt. Dies wirkt sich positiv auf das Gewicht des Motors aus und der gesamte Eisenquerschnitt kann ausgenutzt werden.

Die auf dem Rotor befindlichen Permanentmagneten bestehen dabei in der Regel aus Seltenen Erden (häufig Neodym-Eisen-Bor), welche die magnetischen Eigenschaften der herkömmlichen Ferrit-Magnete bei weitem übertreffen und somit höhere Momentendichten ermöglichen.

2.3.2 Funktionsweise

Der Servoumrichter, welcher den Motor mit Drehstrom versorgt, erzeugt in den Wicklungen des Motors ein sogenanntes Drehfeld, welches eine magnetische Kraft auf den Rotor ausübt. Diese Kraftwirkung entsteht dabei durch die Verkopplung des, vom Rotor ausgehenden, Rotorfeldes mit dem Statordrehfeld. Diese Kraftwirkung resultiert, bei entsprechender Regelung der Winkelgeschwindigkeit des Drehfeldes, in ein entsprechendes Drehmoment, welches wiederum zur Beschleunigung des Rotors führt. Die Winkelgeschwindigkeiten von Drehfeld und Rotor unterscheiden sich dabei nicht, sie verlaufen also synchron, was zur Namensgebung dieses Motortyps geführt hat. Eine Belastung des Motors mit einem entsprechenden Lastmoment führt zu einer Verschiebung des vom Rotor (rotierend) ausgehenden Drehfeldes in Bezug auf das Statordrehfeld. Diese winkelmässige Verschiebung beider Drehfelder zueinander wird als Polradwinkel \(\alpha\) bezeichnet. Das Lastmoment führt dabei zu einem Nacheilen des Rotors bezogen auf das Statordrehfeld. Mit steigendem Polradwinkel, welcher durch Erhöhung des Lastmomentes hervorgerufen wird, nimmt das vom Motor abgegebene Drehmoment zu. Das maximale Drehmoment ist erreicht sobald der Polradwinkel einen Wert von \(\alpha = 90^\circ\) beträgt, wobei die Rotorpole in diesem Fall genau zwischen den Statorpolen liegen. Dieser Zusammenhang lässt sich folgendermassen beschreiben.

\[M = M_{Max}\cdot sin(\alpha)\]

Sollte dieses maximale Drehmoment vom Lastmoment überschritten werden und sich somit ein Polradwinkel \(\alpha > 90^\circ\) einstellen, nimmt das vom Motor abgegebene Drehmoment ab, was wiederum eine weitere Erhöhung des Polradwinkels nach sich zieht. Der Motor befindet sich somit in einer instabilen Betriebslage und bleibt somit stehen, was als "Ausser Tritt fallen" bezeichnet wird. Sollte es in diesem Fall nicht zur Abschaltung kommen, ist eine thermische Schädigung des Motors die Folge.

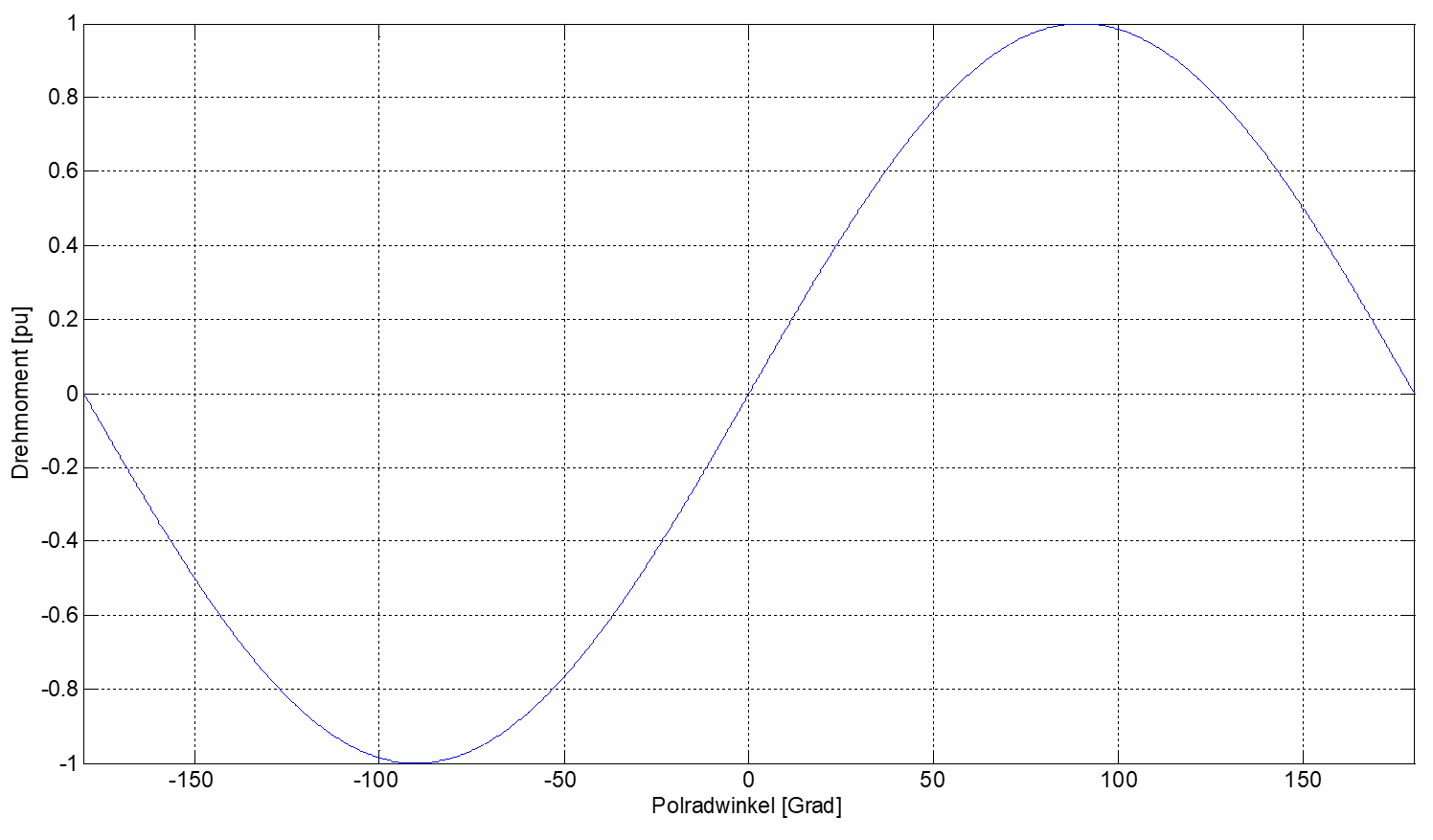
Abbildung 2.3: Abhängigkeit des Motormomentes vom Polradwinkel

2.3.3 Thermische und dynamische Grenzen

Die dynamischen Grenzen des Servoantriebs werden hauptsächlich vom Umrichter bestimmt, da dieser einen ausreichend hohen Strom zur Verfügung stellen muss, um das maximale Drehmoment erreichen zu können. Desweiteren gilt es zu berücksichtigen, dass das maximale Drehmoment oberhalb der Bemessungsdrehzahl abfällt. Dieser Abfall ist durch die im Motor erzeugte induzierte Spannung (aufgrund des rotierenden Rotors) zu begründen. Da die auf dem Rotor befindlichen Permanentmagnete mit dem Rotor rotieren, induzieren sie in der dreisträngigen Statorwicklung sinusförmige Spannungen, welche der vom Umrichter zur Verfügung gestellten Spannung entgegenwirken. Durch die Gegenspannungen kann der Umrichter ab einer bestimmten Drehzahl nicht mehr den für das maximale Drehmoment notwendigen Strom liefern. Bei der Dimensionierung eines Servoantriebes gilt es somit zu beachten, dass das maximal benötigte Drehmoment in allen Drehzahlbereichen unterhalb bzw. auf der dynamischen Grenzlinie des Motors liegt.

Zur Bestimmung der thermischen Auslastung des Motors werden die mittlere Drehzahl sowie das effektive Drehmoment benötigt. Der sich ergebende Arbeitspunkt muss dabei unterhalb der thermischen Grenzkennlinie des verwendeten Motors liegen. Wird dies nicht berücksichtigt, kommt es zur thermischen Überlastung des Motors. Auch die thermische Grenzlinie zeigt eine Abhängigkeit von der Drehzahl, wobei auch hier die Kennlinie mit der Drehzahl abnimmt. Diese Abnahme lässt sich hauptsächlich durch Wirbelstrom-, Eisen- und Ummagnetisierungsverluste begründen. Je nach verwendeter Kühlart (fremd-, eigen- oder selbstbelüftet) unterscheidet ich der Verlauf der thermischen Grenzlinie.

2.4 Asynchron-Servomotor

Der Asynchronmotor ist der am häufigsten eingesetzte Elektromotor. Circa 85% der in der Industrie verwendeten Antriebe bestehen aus Asynchronmotoren.

2.4.1 Aufbau

Ein Servo-Asynchronmotor ist in Abbildung 2.4 dargestellt.

Abbildung 2.4: Servo-Asynchronmotor der Firma Lenze (Quelle: www.lenze.com)

Der Asynchron-Servomotor besteht prinzipiell aus folgenden Komponenten:

• Rotor mit kurzgeschlossener Wicklung (Kurzschlussläufer)
• Stator mit Statorwicklung
• Leistungsanschluss
• Gebersystem

Die Statoren von Synchron- und Asynchron-Servomotoren unterscheiden sich nicht. Die Rotoren hingegen unterscheiden sich grundlegend, da der Rotor, im Gegensatz zur Synchronmaschine, ohne Magnete oder Spulen auskommt. Beim Asynchron-Servomotor entsteht der Rotorfluss durch Induktion im kurzgeschlossenen Rotor.

Die Komponenten einer Standard-Asynchronmaschine (ohne Gebersystem) sind in Abbildung 2.5 dargestellt.

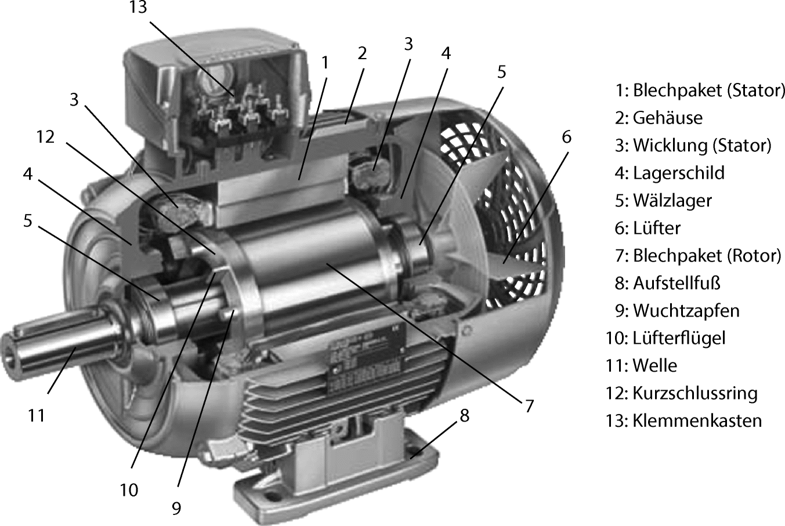
Abbildung 2.5: Grundlegener Aufbau eines Standard Asynchronmotors (Hering E., Martin R., Gutekunst J., Kempkes J. (2018) Elektrische Maschinen.)

Der Rotor besteht normalerweise aus einem geblechten Eisenkörper, welcher im Falle von hochdrehenden Motoren auch als Vollstahlkörper ausgeführt werden kann. Um die Wirbelströme und somit die Wirbelstromverluste, hervorgerufen durch das magnetische Drehfeld, zu vermeiden, werden aber normalerweise sowohl der stillstehende Stator als auch der Läufer geblecht ausgeführt. Beide sind durch einen kleinen Luftspalt voneinander getrennt. Sowohl die Läufer als auch die Ständerwicklungen sind in gleichmässig über den Umfang verteilten Nuten untergebracht (siehe Abbildung 2.6).

Abbildung 2.6: Blechschnitt einer ASM (Quelle: www.wikipedia.org)

Die Ständerwicklung wird in Stern- oder in Dreieickschaltung an das Drehstromnetz oder einen Frequenzumrichter angeschlossen. Die Käfigwicklung eines Asynchronmotors mit Kurzschlussläufer kann in eine dreisträngige Ersatzwicklung umgerechnet werden, indem die Anzahl der Läufernuten \(N_{R}\) bzw. Läuferstäbe berücksichtigt werden.

\[ W_{R} = \frac{N_{R}}{6} \]

Die Vorteile der Asynchronmaschine bestehen massgeblich in der robusten Bauweise und dem, aufgrund des einfachen Aufbaus, niedrigen Preis. Gleichzeitig treten keinerlei Rohstoffprobleme aufgrund von Seltenen-Erden-Magneten (z.B. Neodym) auf.

2.4.2 Funktionsweise

Wird der Stator des Motors mit drei um 120 Grad versetzten sinusförmigen Strömen beaufschlagt, bildet sich eine ein rotierendes Magnetfeld im Luftspalt aus, welches den Rotor durchsetzt. Rotiert der Rotor mit einer Winkelgeschwindigkeit, welche von der Winkelgeschwindigkeit des Statorfeldes abweicht, kommt es zur Induktion von Spannungen im Rotorkreis. Diese Spannungen rufen im Rotor wiederum sinusförmige Ströme hervor, da die Rotorwicklungen kurzgeschlossen sind. Diese Ströme erzeugen ebefalls ein Magnetfeld im Luftspalt. Sind beide Magnetfelder versetzt zueinander orientiert, erfährt der Läufer eine tangential wirkende Kraftwirkung (Lorentz-Kraft-Prinzip), die ein Drehmoment hervorruft. Dieses Drehmoment treibt den Läufer in Richtung der Drehfeldbewegung an. Die dadurch auftretende Rotation des Läufers verringert die Relativgeschnwindigkeit zwischen Drehfeld und Läufer, wodurch die Induktionswirkung verringert wird. Somit stellt sich schlussendlich ein Gleichgewicht zwischen dem Belastungsmoment und dem von der Asynchronmaschine zur Verfügung gestellten Drehmoment ein. Die relative Differenz der Drehzahl des Statordrehfeldes und der Rotordrehzahl bezeichnet man dabei als Schlupf (\(s\)). Da die Wirkungsweise der Maschine auf der Spannungsinduktion im Rotorkreis basiert, wird dieser Maschinentyp häufig auch als Induktionsmaschine bezeichnet. Die synchrone Drehzahl \(n_{s}\) bezeichnet die Drehzahl des Statordrehfeldes, welche lediglich von der Frequenz des Drehstromsystems \(f_{s}\) und der Polpaarzahl \(p\) der Maschine abhängt.

\[ n_{s} = \frac{60\cdot f_{s}}{p} \]

Wird die unbelastete und verlustlose Maschine betrachtet, entspricht die Drehzahl der Maschine \(n\) der Drehzahl des Statordrehfeldes \(n_{s}\). Die mechanische Winkelgeschwindigkeit des Rotors \(\omega_{mech}\) kann dabei aus der Rotordrehzahl berechnet werden:

\[ \omega_{mech} = 2\pi\cdot n \]

Wird die Maschine hingegen belastet, entsteht ein Schlupf:

\[ s = \frac{n_{s}-n}{n_{s}} = \frac{\omega_{s}-p\cdot\omega_{mech}}{\omega_{s}} = \frac{f_{Rot}}{f_{s}} \]

Die Frequenz \(f_{Rot}\) beschreibt dabei die Frequenz der induzierten Spannungen und Ströme im Rotorkreis. Mit Hilfe des Induktionsgesetzes lässt sich nachweisen, dass die Amplitude der induzierten Spannungen \(U_{ind}\) im Rotorkreis direkt proportional zum Schlupf sind (siehe Abbildung 2.7

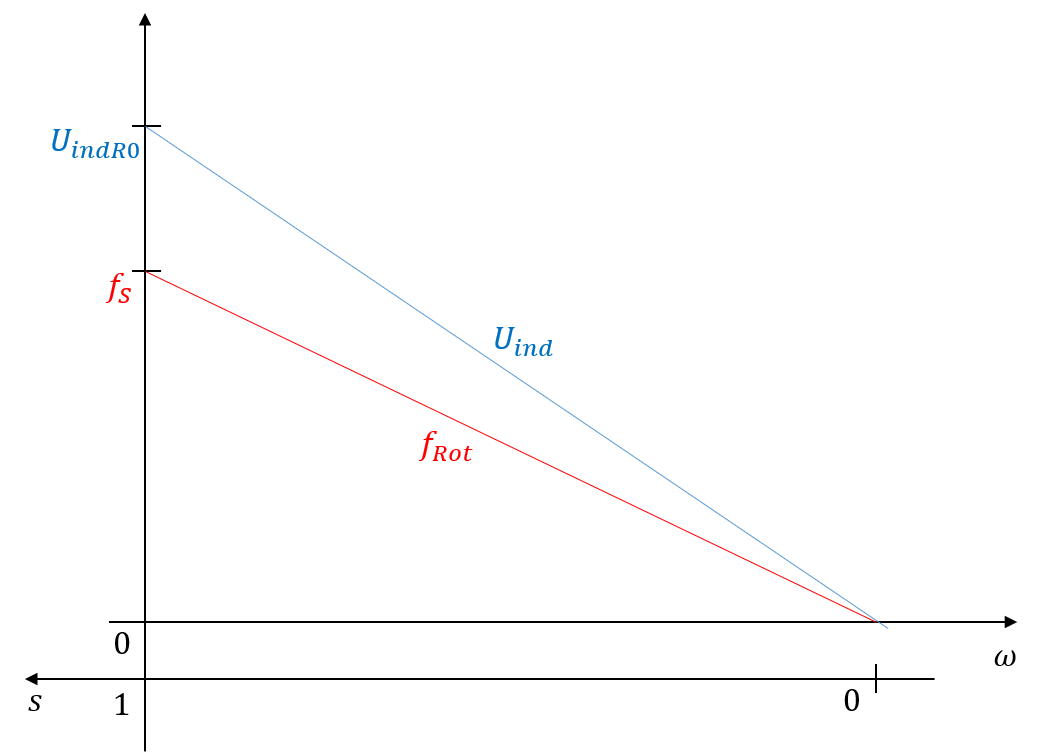
Abbildung 2.7: Amplitude der induzierten Rotorspannung und Rotorfrequenz in Abhängigkeit vom Schlupf

Der Maximalwert der induzierten Spannungen \(U_{indR0}\) im Motorbetrieb wird bei stillstehendem Läufer, bei einem Schlupfwert in Höhe von \(s=1\) erreicht. In diesem Betriebspunkt entspricht die Rotorfrequenz der Statorfrequenz. Rotiert der Rotor hingegen mit der synchronen Drehzahl (\(s=0\)), wird keinerlei Spannung im Rotorkreis mehr induziert. Bei stillstehendem Rotor wird somit eine Spannung induziert, deren Frequenz mit der Frequenz des Statordrehfeldes übereinstimmt. Folglich kann die Amplitude der induzierten Spannungen im Läuferkreis bestimmt werden:

\[ U_{ind}(s) = s\cdot U_{indR0} \]

Die induzierten Spannungen im Läufer rufen wiederum Stromflüsse hervor, deren Amplitude und Phasenlage vom Läuferwiderstand und der Läuferinduktivität des Rotorkreises beeinflusst werden.

\[ \underline{I}_{Rot}(s) = \frac{\underline{U}_{ind}(s)}{Z_{Rot}} = \frac{\underline{U}_{ind}(s)}{R_{Rot}+jX_{Rot}} = \frac{\underline{U}_{ind}(s)}{R_{Rot}+j\cdot s\cdot \omega_{Rot} L_{Rot}} \]

Die im Läufer fliessenden Ströme rufen Spannungsabfälle über dem Läuferwiderständen und den Streublindwiderständen der Läuferwicklungen hervor, wie dies in der Ersatzschaltung in Abbildung 2.8 dargestellt ist.

Abbildung 2.8: Einsträngiges Ersatzschaltbild des Läufers

Da der Blindwiderstand der Rotorimpedanz eine frequenzabhängige Grösse ist, sind sowohl Amplitude als auch Phasenlage des Rotorstromes schlupf- und somit belastungsabhängige Grössen. Der Betrag des Läuferstromes kann folgendermassen bestimmt werden:

\[ |I_{R}(s)| = \frac{U_{ind}(s)}{\sqrt{R^{2}_{Rot}+s^{2}X^{2}_{\sigma R}}} = \frac{U_{indR0}(s)}{\sqrt{\Bigl(\frac{R_{Rot}}{s}\Bigr)^{2}+X^{2}_{\sigma R}}} \]

Somit wird die Amplitude des Rotorstromes bei hohen Rotorfrequenzen reduziert, was eine Reduktion des Drehmomentes nach sich zieht. Einen ähnlichen Effekt bewirkt die Beeinflussung der Phasenlage des Rotorstromes aufgrund der stromverzögernden Wirkung der Läuferinduktivität, die auch im Zeigerdiagramm (siehe Abbildung 2.9) der Läuferspannungsgleichung sichtbar wird.

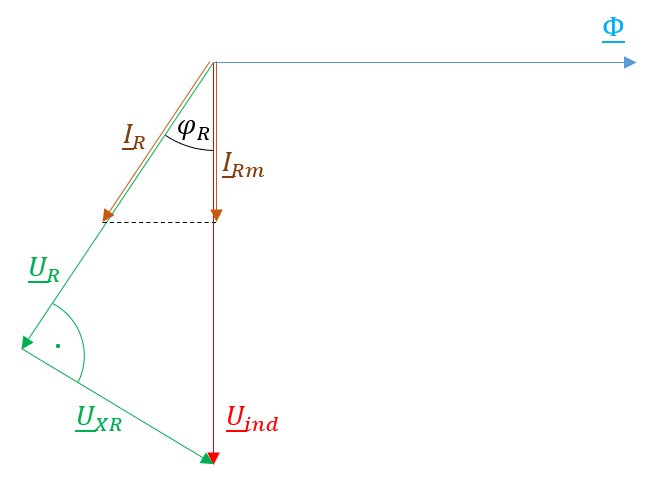
Abbildung 2.9: Zeigerdiagramm des Läuferstromes und der Läuferspannung

Dieser Effekt sorgt dafür, dass das zeitliche Maximum des Rotorstromes in den Rotorstäben nicht mit dem Flussdichtemaximum im Luftspalt zusammenfällt. Aufgrund dessen variiert das zur Verfügung stehende Drehmoment einer Asynchronmaschine mit dem Schlupf. Es stellt sich ein Drehmomentverlauf, wie in Abbildung 2.13 dargestellt ein. Im Zeigerdiagramm wurde ausserdem die mit der induzierten Spannung \(U_{ind}\) in Phase liegende Stromkomponente \(I_{Rm}\) dargestellt, welche proportional zum entwickelten Drehmoment der ASM ist. Auch in den Ständerwicklungen werden aufgrund des Drehfeldes Spannungen induziert, die aufgrund des räumlichen Versatzes der drei Wicklungen ebenfalls um jeweils 120 Grad phasenverschoben sind. Der Effektivwert der im Ständer induzierten Spannungen ist proportional zur Drehzahl des Drehfeldes und des magnetischen Flusses in der Maschine.

\[ U_{is} = k\cdot \Phi \cdot n_{s} \]

Gleichzeitig fallen aufgrund des Ständerstromes \(I_{S}\) Spannungen über dem ohmschen Widerstand \(R_{S}\) und dem Streublindwiderstand \(X_{\sigma S}\) ab. Somit ergibt sich für einen einzelnen Strang der Ständerwicklung das in Abbildung 2.10 dargestellte Ersatzschaltbild.

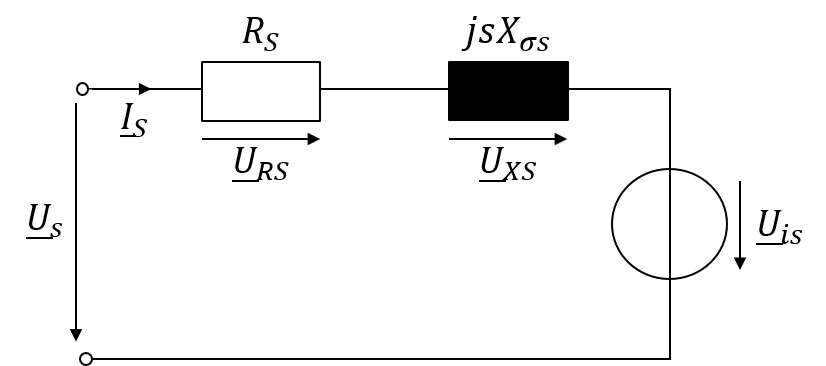
Abbildung 2.10: Einsträngiges Ersatzschaltbild des Ständers der Asynchronmaschine

Basierend auf diesem Ersatzschaltbild lässt sich die Maschengleichung aufstellen:

\[ \underline{U}_{S}=-\underline{U}_{iS}+\underline{U}_{RS}+\underline{U}_{XS} \]

Sieht man von Asynchronmotoren sehr kleiner Leistung ab, sind die Spannungsabfälle über dem Ständerwiderstand und dem Ständerblindwiderstand sehr klein im Vergleich zur induzierten Spannung \(U_{iS}\). Aufgrund dessen können diese Spannungen vernachlässigt werden, wodurch sich die Maschengleichung massgeblich vereinfacht:

\[ \underline{U}_{S}=-\underline{U}_{iS} \]

Das zugehörige Zeigerdiagramm ist in Abbildung 2.11 dargestellt.

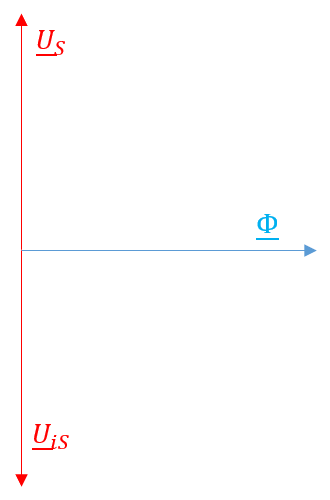
Abbildung 2.11: Zeigerdiagramm der vereinfachten Spannungsgleichung

Da sowohl die Ständer- als auch die Läuferwicklungen von Strömen durchflossen werden, kommt es zur Überlagerung des Ständer- und Läuferflusses bzw. deren magnetischer Durchflutungen (\(\Theta_{S}\) bzw \(\Theta_{R}\)). Die resultierende Durchflutung \(\underline{\Theta}_{ges}\) kann somit berechnet werden:

\[ \underline{\Theta}_{ges} = \underline{\Theta}_{S}+\underline{\Theta}_{R} = N_{S}\cdot \underline{I}_{S} + N_{R}\cdot \underline{I}_{R} \] Je nach Belastung der Maschine rufen die Läuferströme somit ein Läuferdrehfeld hervor, welches wiederum das Fliessen von Ständerströmen nach sich zieht. Die dadurch hervorgerufenen Durchflutungen überlagern sich und bewirken eine resultierende Durchflutung \(\Theta_{ges}\), welche dazu führt, dass die oben genannte Bedingung

\[ \underline{U}_{S}=-\underline{U}_{iS} \] erfüllt wird. Betrachtet man die unbelastete Maschine, erreicht der Läufer nahezu die synchrone Drehzahl, wodurch keine Läuferströme induziert werden. In diesem Fall fliesst somit lediglich der Magnetisierungsstrom \(I_{\mu}\) in den Ständerwicklungen, welcher benötigt wird um das magnetische Feld aufzubauen. Der Magnetisierungsstrom fällt im Vergleich zum Transformator deutlich grösser aus, da der magnetische Widerstand, aufgrund des Luftspaltes, erheblich grösser ausfällt.

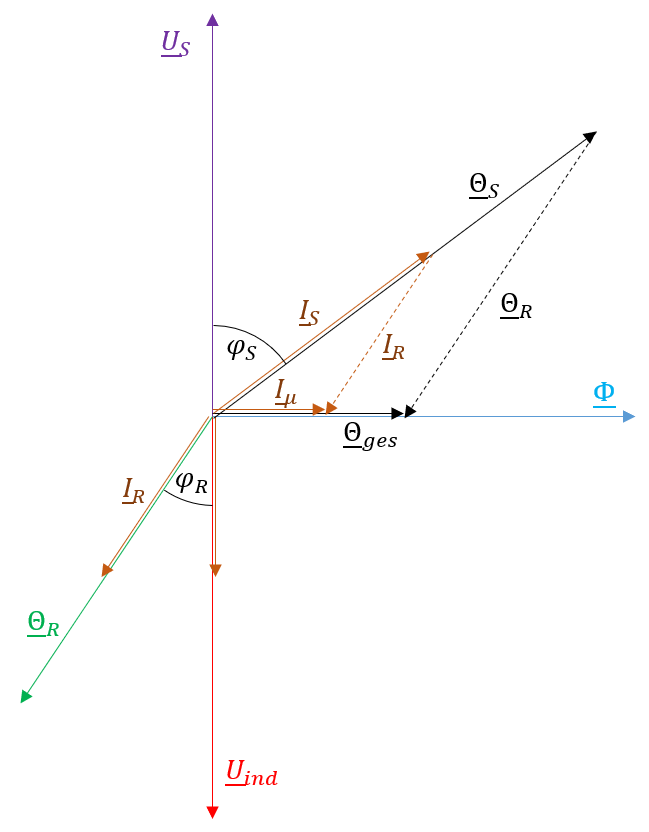
Abbildung 2.12: Zeigerdiagramm der Ströme und Durchflutungen der ASM

Das zugehörige Zeigerdiagramm der Ströme und Durchflutungen ist in Abbildung 2.12 dargestellt.

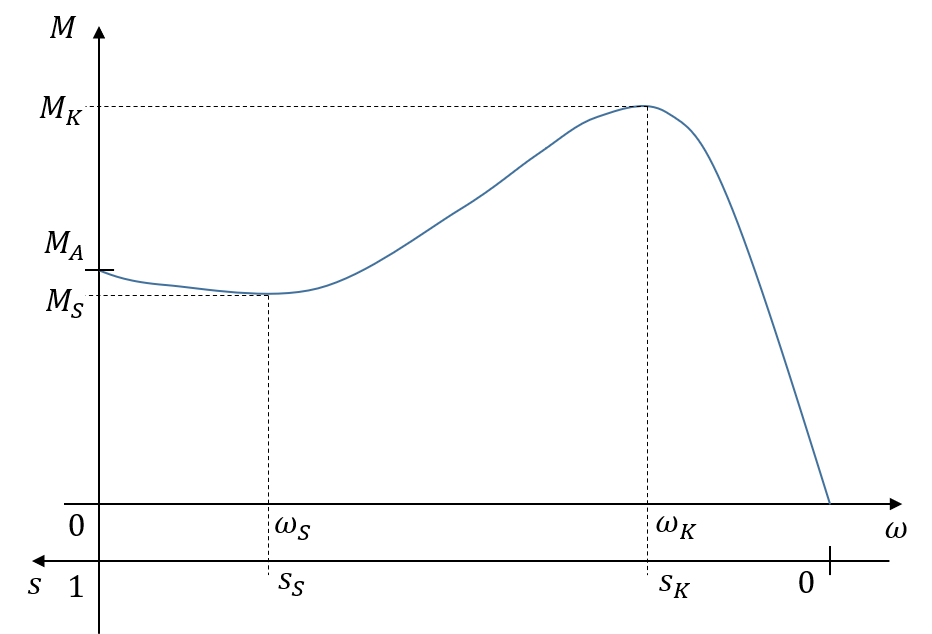
Abbildung 2.13: Typischer Verlauf der Drehzahl-Drehmoment-Kennlinie einer Asynchronmaschine bei Speisung mit fester Spannung und Frequenz

Abbildung 2.13 zeigt mehrere charakteristische Punkte der Drehmomentkurve. Das Anzugsdrehmoment \(M_{A}\) stellt das Drehmoment dar, welches bei Stillstand und Anlauf am Netz zur Verfügung gestellt werden kann. Das Sattelmoment \(M_{S}\) beschreibt ein lokales Minimum im Drehmomentverlauf und kann durch bauliche Massnahmen (z.B. Design der Rotorstäbe) beeinflusst werden. Nicht alle Asynchronmaschinen weisen ein solches Minimum auf. Das Kippmoment \(M_{K}\) stellt das maximal zur Verfügung zu stellende Drehmoment dar, tritt bei der Kippdrehzahl \(n_{K}\) bzw. \(\omega_{K}\) auf und besitzt in diesem Punkt den Kippschlupf \(s_{K}\). Der Arbeitsbereich der Asynchronmaschine beschränkt sich üblicherweise auf den Bereich \(s<\frac{s_{K}}{2}\). Dieser Bereich kann näherungsweise als linear betrachtet werden. Die Reduktion der Drehzahl bei Belastung fällt bei ASM grosser Leistung weniger stark aus als bei Maschinen kleiner Leistungen. Aufgrund dessen weisen leistungsstärkere Motoren einen geringeren Nennschlupf auf als Motoren geringer Leistung. Der Nennschlupf liegt, je nach Leistung des Motors, im Bereich unterhalb von \(s=10%\) (z.B. ca. 6% bei einem Motor mit einer Leistung von 1kW und ca. 1.5% bei einem Motor mit einer Leistung von 100kW).

Durch entsprechende feldorientierte Regelverfahren, kann die Orientierung beider Drehfelder so beeinflusst werden, dass der Asynchron-Servomotor sehr dynamisch betrieben werden kann.

2.4.3 Ersatzschaltung

Betrachtet man eine stillstehende dreisträngige Asynchronmaschine deren Rotorwicklungen herausgeführt werden, kann deren Verhalten mit dem eines Drehstromtransformators beschrieben werden. Somit kann das einphasige Ersatzschaltbild der Asynchronmaschine für den stationären Betrieb mit dem eines Einphasentransformators beschrieben werden, welches sich aus den physikalischen Gesetzmässigkeiten ergibt, die in Abbildung 2.14 veranschaulicht werden.

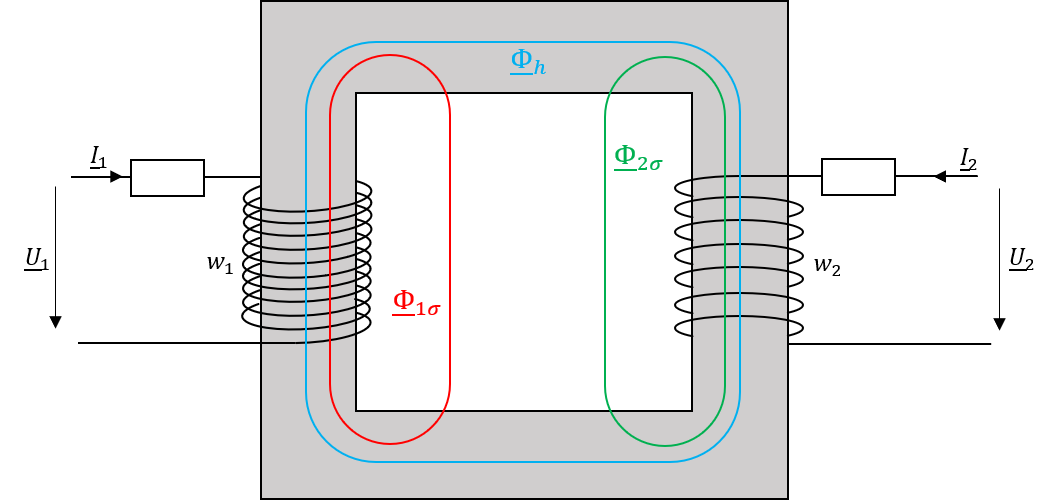
Abbildung 2.14: Modell eines Einphasentrafos

Die ohmschen Widerstände \(R_{1}\) bzw. \(R_{2}\) repräsentieren die Wicklungswiderstände der zwei Wicklungssysteme. Der magnetische Fluss, der beide Wicklungen durchsetzt wird als Hauptfluss \(\Phi_{h}\) bezeichnet und stellt die eigentliche magnetische Kopplung der beiden Wicklungen dar. Die Flüsse \(\Phi_{1\sigma}\) bzw. \(\Phi_{2\sigma}\) tragen nicht zur Energieübertragung zwischen beiden Wicklungen bei und werden aufgrund dessen als Streuflüssen bezeichnet. Diese Zusammenhänge resultieren schlussendlich im sog. T-Ersatzschaltbild, welches in Abbildung 2.15 dargestellt ist.

Abbildung 2.15: T-Ersatzschaltbild der stillstehenden ASM (links: mit herausgeführten Rotorwicklungen, rechts: mit Kurzschlusskäfig)

Wie auch beim Transformator üblich, werden die sekundärseitigen bzw. rotorseitigen Grössen, unter Berücksichtigung des Übersetzungsverhältnisses, auf die Primärseite bzw. Statorseite umgerechnet. Diese Umrechnung ermöglicht die Betrachtung eines einzelnen Stromkreises, welcher mit den Mitteln der Wechselstromrechnung berechnet werden kann. Zur Umrechnung wird das Übersetzungsverhältnis \(ü\) verwendet, welches sich aus dem Quotienten der Wicklungszahlen ergibt:

\[ ü=\frac{w_{1}}{w_{2}}=\frac{w_{S}}{w_{R}} \]

2.4.4 Grenzkennlinien

Ein signifikanter Punkt in der Drehmomentkennlinie des Motors ist die sogenannte Bemessungsdrehzahl. Wird der Motor oberhalb dieser Drehzahl eingesetzt, fällt das zur Verfügung stehende Drehmoment deutlich ab. Auch im Fall des Asynchron-Servomotors gilt, dass das effektive Motordrehmoment bei mittlerer Drehzahl maximal auf der sogenannten S1-Kennlinie liegen darf. Im Falle von Servomotoren werden häufig Kurvenscharen unter Angabe der Servoumrichterleistung aufgeführt. Diese geben Auskunft darüber, welche Drehmomente bei entsprechenden Drehzahlen verfügbar sind. Allerdings ist die S1-Kennlinie unentbehrlich bei der Beurteilung, ob das entsprechende Drehmoment auch dauerhaft abgegeben werden kann.

2.5 Synchroner Linearmotor

Grundsätzlich unterscheidet sich die Funktionsweise des synchronen Linearmotors nicht von der eines rotierenden Synchron-Servomotors. Werden höchste Anforderungen an die Dynamik bzw. Positioniergenauigkeit gestellt, wird häufig ein Linearmotor verwendet. Die Vortiele eines Lineramotors im Vergleich zum rotativen Synchron-Servomotor lassen sich folgendermassen zusammenfassen:

• höhere Geschwindigkeiten
• höhere Beschleunigungen
• Spielfrei (keine Getriebe, Zahnriemen oder Ähnliches)
• praktisch verschleissfrei
• höhere Positioniergenauigkeit

Synchrone Linearmotoren ersetzen in verschiedenen Branchen häufig traditionelle, nicht direkt angetriebene Lösungen, wie zum Beispiel Zahnstangen-, Spindel-, Ketten- und Riemenantriebe. Vom Aufbau her unterscheidet man beim Linearmotor ähnlich wie beim rotierenden Synchronmotor zwischen einem bewegten (üblicherweise Rotor) und einem feststehenden Teil (üblicherweise Stator). Im Falle des Linearmotors bezeichnet man diese zwei Teile als Primär- bzw. Sekundärteil. Diese Unterscheidung bezieht sich dabei auf die Funktionsweise:

• Der Primärteil entspricht dem Stator des rotierenden permanenterregten Synchronmotors, welches das Blechpaket sowie die Motorwicklung enthält.
• Das Sekundärteil des Motors entspricht dem Rotor des rotierenden permanenterregten Synchronmotors, welcher aus einem Trägermaterial aus Stahl und aufgeklebten Permanentmagneten besteht.

Die prinzipiell gleiche Funktionsweise des Linearen und rotativen Motors zeigt sich am deutlichsten, wenn man sich den rotativen Motor aufgeschnitten und gerade gebogen vorstellt, wie dies in Abbildung 2.16 dargestellt ist.

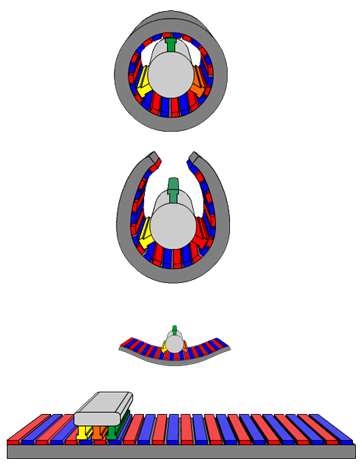
Abbildung 2.16: Prinzipieller Aufbau des Linearmotors (www.wikipedio.org)

Im Gegensatz zum rotativen Synchronmotor ist es beim Linearmotor hingegen möglich sowohl das Primär- als auch das Sekundärteil zu bewegen. Aufrgund dessen unterscheidet man bei synchronen Linearmotoren zwischen Langstator und Kurzstatorprinzip. Da die Kraftwirkung eines Linearmotors auf der Lenzschen Regel basiert, ist es essentiell wichtig einen exakten Luftspalt zwischen Primär- und Sekundärteil einzuhalten. Wird der Luftspalt vergrössert, verringert sich die Leistung des Motors und im schlimmsten Fall bleibt er stehen. Ein einwandfrei arbeitendes System setzt somit eine exakte Vorbereitung der Montagefläche voraus, da der Luftspalt über das Linearführungssystem und die Montageplatte eingestellt wird. Um einen möglichst konstanten Luftspalt gewährleisten zu können, werden Räder, Luftkissen verwendet oder man erreicht dies durch Schweben auf einem geregelten Elektromagneten.

2.5.1 Langstatorprinzip

Beim Langstatorprinzip ist der Verfahrweg durch mindestens einen Primärteil vorgegeben, welcher länger ist als die Magnetleiste, welche sich am bewegten Fahrschlitten befindet. Dieser bewegte Fahrschlitten wird als Sekundärteil bezeichnet. Da der Fahrschlitten somit lediglich Permanentmagnete aufweist, ist keine Energiezufuhr nötig, wodurch sich theoretisch unbegrenzte Verfahrwege ergeben.

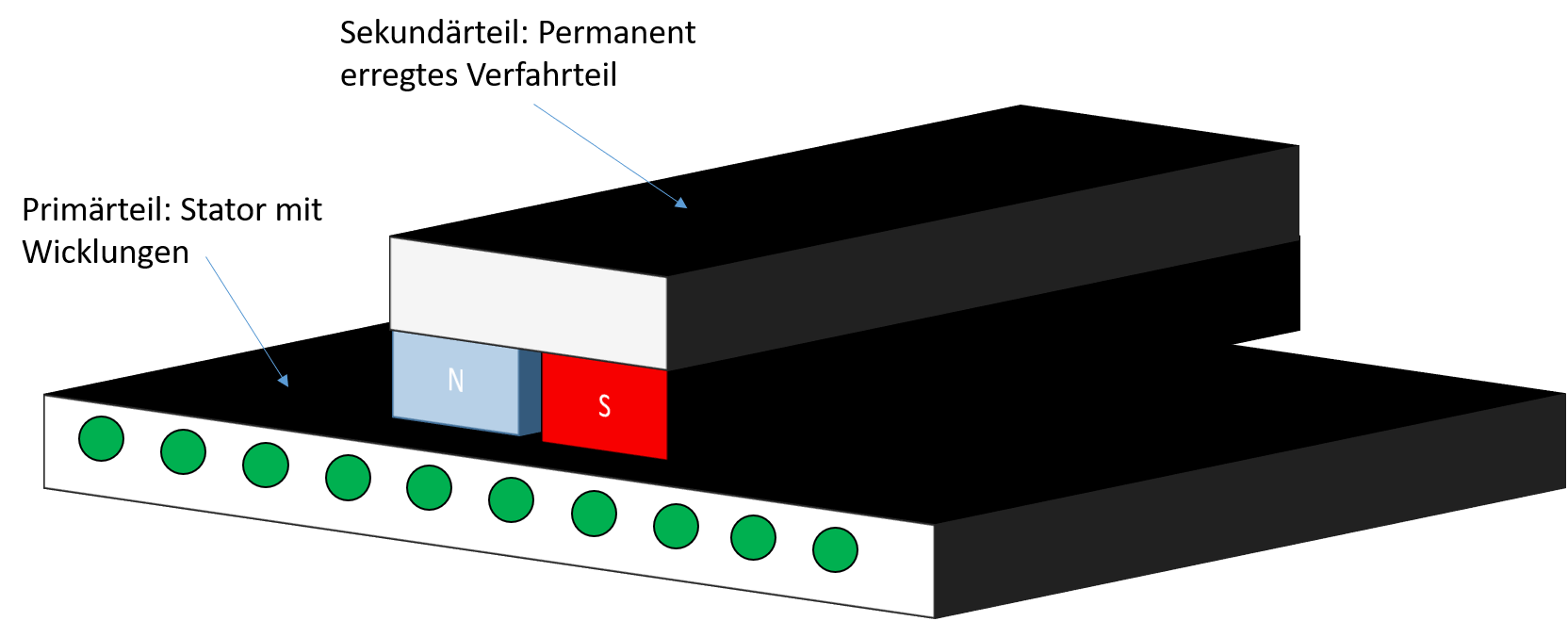
Abbildung 2.17: Aufbau eines synchronen Linearmotors nach Langstatorprinzip

Dieses Prinzip kommt hauptsächlich bei Logistik- und Transportapplikationen zum Einsatz.

2.5.2 Kurzstatorprinzip

Beim Kurzstatorprinzip wird im Gegensatz zum Langstatorprinzip das im Vergleich zur Magnetleiste kurze Primärteil verfahren. Da dem Primärteil Energie zugeführt werden muss, sind die Verfahrwege bei diesem Motortyp durch entsprechende Kabellängen begrenzt.

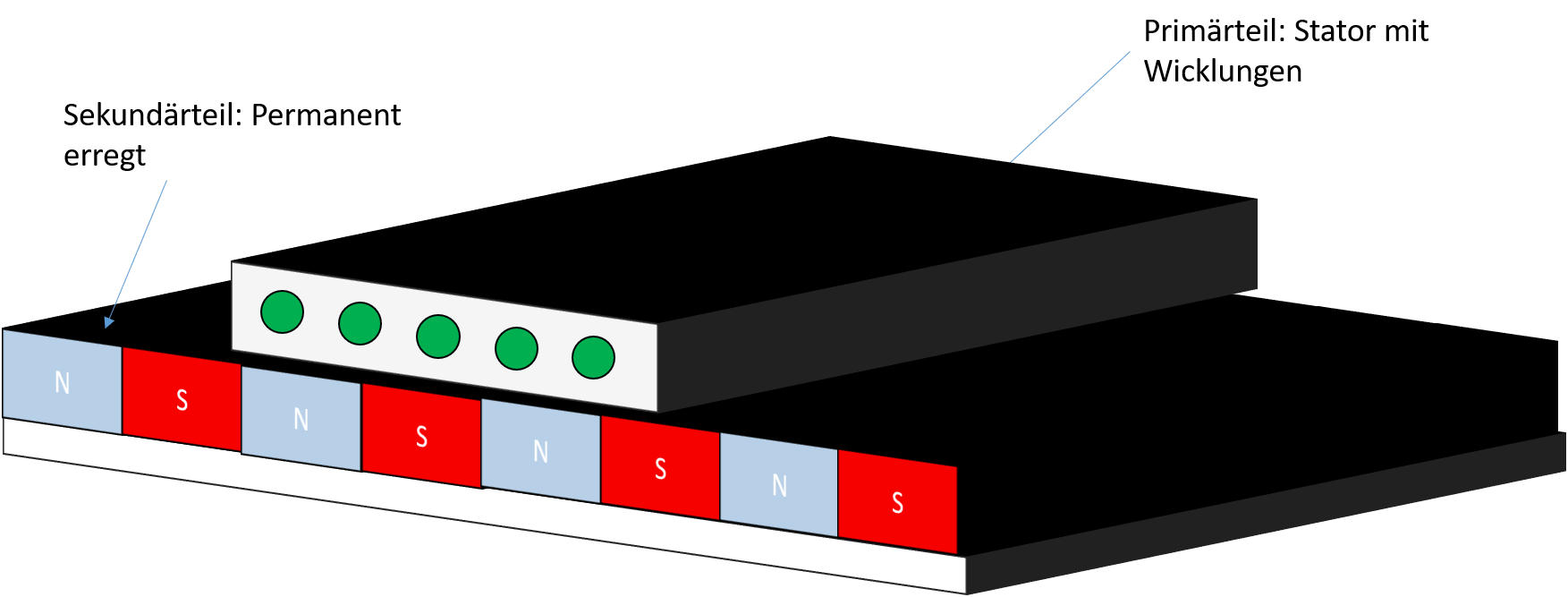
Abbildung 2.18: Aufbau eines synchronen Linearmotors nach Kurzstatorprinzip

2.5.3 Geschwindigkeits-Kraft-Diagramm (Motorkennlinie)

Eine typische Motorkennlinie ist in Abbildung 2.19 dargestellt.

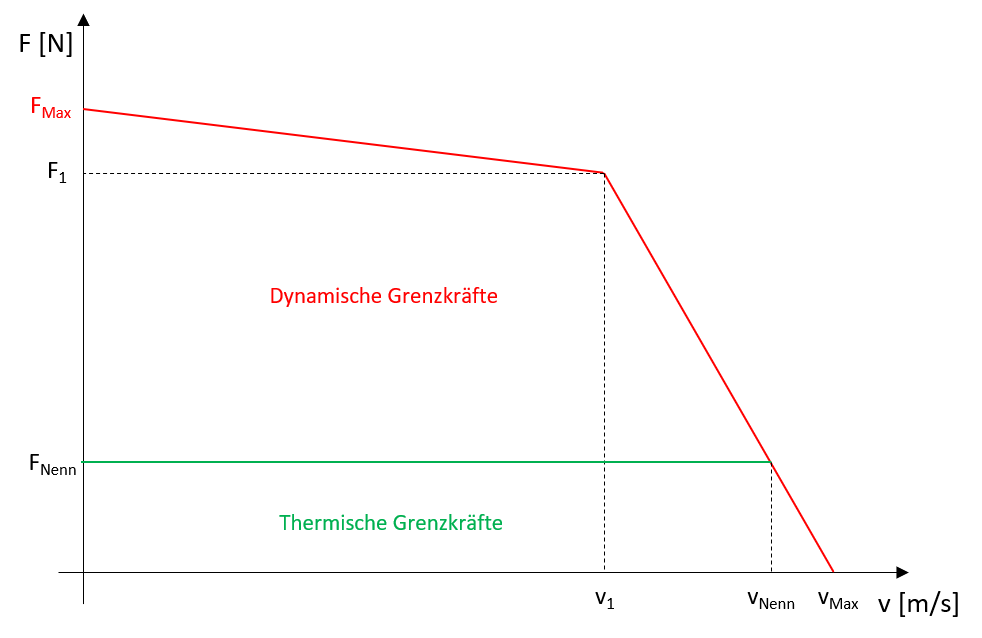
Abbildung 2.19: Typische Motorkennlinie eines Linearmotors

Das Geschwindigkeits-Kraft-Diagramm gibt Auskunft über die vom Motor aufzubringenden Spitzenkräfte \(F_{Max}\) bzw. \(F_{Nenn}\) in Abhängigkeit von der zugehörigen Verfahrgeschwindigkeit. Dabei gelten folgende Definitionen:

• \(F_{Nenn}\): Dauerkraft
• \(F_{1}\): Maximalkraft, die bis Erreichen der Geschwindigkeit \(v_{1}\) zur Verfügung steht
• \(F_{Max}\): Maximalkraft
• \(v_{Max}\): Maximale Verfahrgeschwindigkeit
• \(v_{1}\): Geschwindigkeit bis zu der die Kraft \(F_{1}\) zur Verfügung steht
• \(v_{Nenn}\): Bemessungsgeschwindigkeit, bis zu der die Nennkraft zur Verfügung steht

Die Nennkraft \(F_{Nenn}\) des Motors ist dabei von gewissen Parametern abhängig:

• Grösse der Flanschfläche des Primärteils
• Stärke der Flanschfläche des Primärteils
• Umgebungstemperatur
• Aufstellungshöhe

Weiterhin gilt es zu beachten, dass bei der thermischen Auslastung des Motors ebenfalls ein gewisser Wärmetransport vom Kern des Primärteils zur Umgebung vorhanden sein muss, damit eine ausreichende Kühlung gewährleistet werden kann.

2.5.4 Kühlarten

Da auch im Falle eines Linearmotors eine thermische Überlastung vermieden werden muss, muss für ausreichende Kühlung gesorgt werden. Die Grösse der Kühlfläche wird dabei massgeblich durch die Flanschfläche und die Dicke des Primärteils bestimmt. Man unterscheidet dabei generell zwischen zwei Kühlarten:

• Konvektionskühlung
• Wasserkühlung

Bei der Konvektiosnkühlung erfolgt die Kühlung durch Abstrahlung und durch Erwärmung der Umgebungsluft. Dabei muss gewährleistet sein, dass die Oberfläche des Motors einen ausreichenden Wärmetransport ermöglicht. Je nach Anwendungsfall ist es jedoch möglich, dass zusätzliche Massnahmen ergriffen werden müssen. In diesem Fall wird häufig auf zusätzliche Fremdlüfter zurückgegriffen, welche einen konstanten Luftstrom sicherstellen und somit die Wärmeenergie verstärkt abführen. Durch die Erwärmung kommt es ausserdem zu einer gewissen Wärmeausdehnung, die durch entsprechendes Know How im Aufbau des Motors berücksichtigt wird und sich von Hersteller zu Hersteller unterscheidet. Bei Wasserkühlung werden im Primärteil zusätzliche Kühlkanäle untergebracht, die mit einem Wasserkreislauf verbunden werden. Diese Kühlart zeichnet sich durch folgende Eigenschaften aus:

• hoher technischer Aufwand
• kostenintensiv
• hohe Kühlleistung
• bei Ausfall der Wasserkühlung deutliche Leistungseinbussen
• geringere Wärmeabgabe an die Umgebungsluft

In speziellen Fällen wird auch auf Wasserkühlung mit thermischer Kapselung zurückgegriffen, wobei der Primärteil in einem Kühlmantel verkapselt wird und somit praktisch vollständig von der restlichen Maschinenkonstruktion getrennt wird. Diese Mantelung ist von Kühlkanälen durchzogen. Die Eigenschaften dieser Kühlart lassen sich folgendermassen zusammenfassen:

• sehr hohe Kühlleistung
• sehr hoher technischer Aufwand
• grosses Bauvolumen
• sehr kostenintensiv
• thermische Entkoppelung des Motors von der Maschinenkonstruktion und somit keine Wärmeausdehnung