Kapitel 5 Betriebsarten und Regelstrukturen

Wie bei vielen elektrischen Antrieben ist auch der Regelkreis von Servoumrichter kaskadenförmig aufgebaut, wobei sich die einzelnen Regelkreise überlagern. Die grundlegende Struktur eines solchen Regelkreises ist in Abbildung 5.1 gegeben.

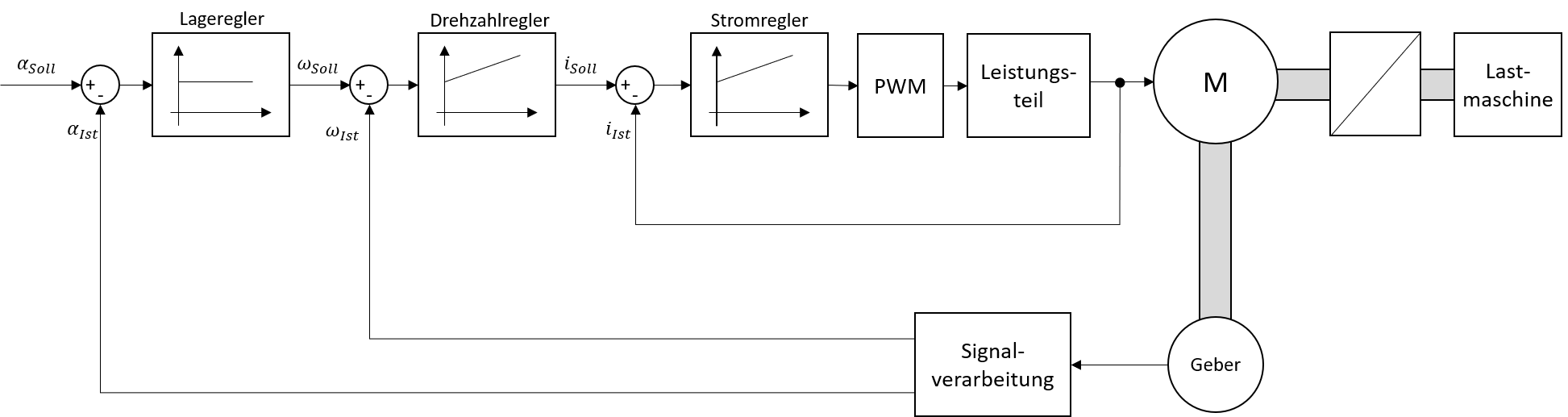
Abbildung 5.1: Grundsätzlicher Aufbau des kaskadierten Regelkreises eines Servoumrichters

Wie Abbildung 5.1 erkennen lässt, beinhaltet die Regelkreisstruktur drei überlagerte Regelkreise (von innen nach aussen):

• Stromregelkreis, welcher das Drehmoment des Motors beeinflusst (basierend auf z.B. FOR oder DSR)
• Drehzahlregelkreis um die Drehzahl des Motors zu regeln
• Lageregelkreis zur Regelung der Winkellage des Rotors

Heutzutage kommen in der Antriebsregelung auch hin und wieder Methoden der modernen Regelungstechnik, wie zum Beispiel Zustandsregelung und Beobachter zum Einsatz, allerdings wird im überwiegenden Teil der Antriebe auf die klassische Kaskadenregelung zurückgegriffen. Die Parametrierung der Regelkreise erfolgt dabei von innen nach aussen. Durch die Kaskadenregelung können die unterlagerten Regelgrössen durch Begrenzung der zugehörigen Sollwerte limitiert werden, wodurch zum Beispiel die Wicklungsströme begrenzt werden können und somit eine thermische Überlastung des Stromrichters bzw. des Motors vermieden wird. Sind alle Daten der zu regelnden Strecken bekannt, ist eine Berechnung der Regelparameter möglich. Gleichzeitig bieten heutige Antriebe auch die Möglichkeit der Selbsteinstellung. Die Bandbreite der einzelnen Regelkreise nimmt von innen nach aussen ab, was damit zu begründen ist, dass die Zeitkonstanten der inneren Strecken kleiner ausfallen als die äusseren.

5.1 Der Stromregelkreis

Die Aufgabe des Stromregelkreises besteht darin das Drehmoment des Motors möglichst dynamisch an die Lastverhältnisse anzupassen, um damit die Drehzahl beeinflussen zu können. Im Gegensatz zu kostengünstigen Umrichtern, die lediglich die Spannungsamplitude sowie die Frequenz variieren (Spannungs-Frequenz-Steuerung) kommen verschiedene Verfahren (z.B. Feldorientierte Regelung bzw. Raumzeigermodulation) zum Einsatz. Unabhängig davon, ob es sich um eine Gleichstrommaschine oder eine Drehfeldmaschine handelt, ist das Drehmoment proportional zum Motorstrom. Somit kann für beide Motorarten ein vergleichbares Regelkonzept verwendet werden. Die eigentliche Stellgrösse des Stromreglers ist die Motorspannung. Aufgrund des integrierenden Verhaltens der Motorinduktivitäten lässt sich die Stromamplitude jeder einzelnen Motorphase durch gepulstes Ein- bzw. Ausschalten der Leistungshalbleiter des Wechselrichters beeinflussen.

\[ i(t) = \frac{1}{L} \cdot \int{u(t)\cdot d(t)} \]

Die typische Stromregelstrecke ist in Abbildung 5.2 dargestellt und setzt sich aus einem Stellglied (dem Umrichter), einem Verzögerungsglied (Wicklungsinduktivität und Wicklungswiderstand) sowie eine häufig verwendete Messwertglättung zusammen.

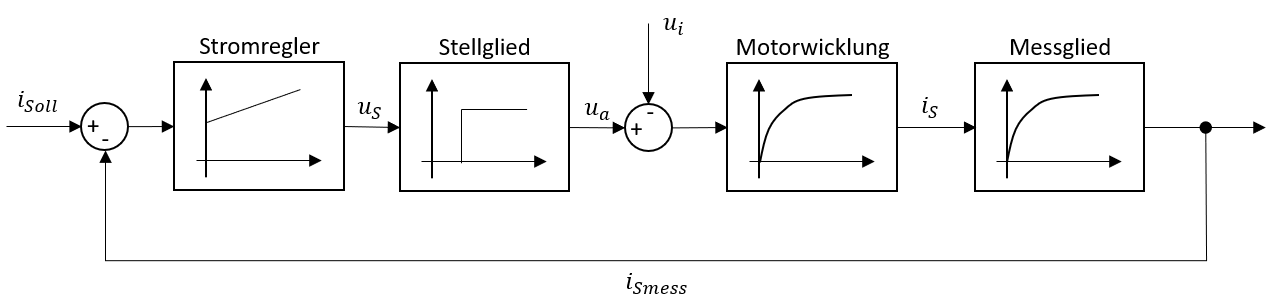
Abbildung 5.2: Grundsätzlicher Aufbau des Stromregelkreises eines elektrischen Antriebes

Als Regler wird nahezu immer ein PI-Regler verwendet, welcher sich durch eine Verstärkung \(K_{P}\) und eine Nachstellzeit \(T_{n}\) charakterisieren lässt und folgende Übertragunsfunktion beschrieben werden kann.

\[ G_{R}(s) = K_{P}\cdot\frac{1+s\cdot T_{n}}{s\cdot T_{n}} \]

Um aus aus der Steuerspannung \(u_{s}\) die Ausgangsspannung \(u_{a}\) zu erzeugen kommt ein leistungselektronisches Stellglied zum Einsatz, welches mit einer gewissen Zeitverzögerung auf eine Änderung der Steuerspannung reagiert. Diese Verzögerung lässt sich als Totzeit darstellen und kann mit folgender Übertragungsfunktion \(G_{SR}(s)\) beschrieben werden.

\[ G_{SR}(s) = \frac{u_{a}}{u_{s}} = K_{SR}\cdot e^{-sT_{SR}} \]

Als treibende Spannung über dem Wicklungswiderstand \(R_{A}\) und der Wicklungsinduktivität \(L_{A}\) wirkt die Differenz zwischen der Ausgangsspannung \(u_{a}\) und der induzierten Spannung \(u_{i}\). Die Reihenschaltung von \(R_{A}\) und \(L_{A}\) wirkt als PT1-Glied mit der Zeitkonstante \(T_{A}=\frac{L_{A}}{R_{A}}\).

\[ G_{S}(s)=\frac{i_{s}}{u_{a}-u_{i}} = \frac{1}{R_{A}+s\cdot L_{A}}=\frac{1}{R_{A}}\cdot \frac{1}{1+s\cdot \frac{L_{A}}{R_{A}}}=K_{A}\cdot \frac{1}{1+s\cdot T_{A}} \]

Die Strommessung erfolgt üblicherweise mit einem geeigneten Stromsensor, dessen Signal meist mit einem zusätzlichen PT1-Glied und einer entsprechenden Zeitkonstante \(T_{MG}\) geglättet wird. Die entsprechende Übertragungsfunktion \(G_{MG}\) lautet somit.

\[ G_{MG}(s)=\frac{i_{Smess}}{i_{s}}=\frac{1}{1+s\cdot T_{MG}} \]

Somit lässt sich die Übertragungsfunktion des offenenen Stromregelkreises \(G_{OI}(s)\) bestimmen.

\[ G_{OI}(s)=G_{R}(s)\cdot G_{SR}(s)\cdot G_{S}(s)\cdot G_{MG}(s) \]

Das Totzeitglied kann durch ein PT1-Glied angenähert werden, dessen Zeitkonstante, aufgrund der Schaltfrequenzen im Kilohertzbereich, sehr gering ausfällt. Die Daten des Motors und des Stromrichters bestimmen folglich die Parameter des Stromreglers. Die Auslegung des Stromreglers erfolgt dabei, indem seine Nachstellzeit die massgebliche Streckenzeitkonstante kompensiert und der Proportionalanteil nach dem Betragsoptimum bestimmt wird. Der geschlossenen Regelkreis verhält sich unter diesen Bedingungen wie ein PT2-Glied mit einer Dämpfung von 0.7, dessen zeitliches Verhalten für den überlagerten Drehzahlregelkreis als PT1-Glied beschrieben werden kann.

5.1.1 Feldorientierte Regelung

Bei der Stromregelung von Drehfeldmaschinen müssen sinusförmige Wechselgrössen geregelt werden, was aus regelungstechnischer Sicht eine Herausforderung darstellt. Aufgrund dessen wurde die feldorientierte Regelung entwickelt, welche unter Verwendung von Raumzeigern eine Regelung zweier Gleichgrössen ermöglicht. Mit Hilfe dieses Ansatzes kann die Stromregelung einer Drehfeldmaschine auf die Regelung zweier Gleichgrössen reduziert werden, wie dies bereits von der Gleichstrommaschine bekannt ist.

5.1.1.1 Symmetriebedingung des Dreiphasensystems

Voraussetzung für die Beschreibung eines symmetrischen Dreiphasensystems als Raumzeiger ist die Symmetriebedingung selbst. Dazu müssen die Amplituden aller Phasen gleich gross sein:

\[ \forall t \geq 0: \hat y(t):= \hat y_{a}(t)=\hat y_{b}(t)=\hat y_{c}(t) \]

Gleichzeitig müssen die Phasenwinkel aller Phasen um einen Winkel von \(\frac{2\pi}{3}\) zueinander versetzt sein:

\[ \forall t \geq 0: \phi(t):= \phi_{a}(t)=\phi_{b}(t)=\phi_{c}(t) \] Sind diese Bedingungen erfüllt, beträgt die Summe aller drei Grössen zu jedem Zeitpunkt Null:

\[ y_{a}(t) + y_{b}(t) + y_{c}(t)=\hat y \bigg[cos\big(\phi(t)\big)+cos\bigg(\phi(t)-\frac{2\pi}{3}\bigg)+cos\bigg(\phi(t)-\frac{4\pi}{3}\bigg)\bigg] \] Mit Hilfe des Additionstheorems \(cos(a)+cos(b)=2\cdot cos\bigg(\frac{a+b}{2}\bigg)cos\bigg(\frac{a-b}{2}\bigg)\) folgt daraus:

\[ y_{a}(t) + y_{b}(t) + y_{c}(t) = \hat y \bigg[2\cdot cos\bigg(\phi(t)-\frac{\pi}{3}\bigg)cos\bigg(\frac{\pi}{3}\bigg) + cos\bigg(\phi(t)-\frac{4\pi}{3}\bigg)\bigg] \] Wird weiterhin berücksichtigt, dass \(cos\big(\frac{\pi}{3}\big)=\frac{1}{2}\) gilt, lässt sich dieser Ausdruck durch erneute Verwendung des Additionstheorems weiter vereinfachen:

\[ y_{a}(t) + y_{b}(t) + y_{c}(t) = \hat y \bigg[cos\big(\phi(t)\big)\cdot cos\bigg(\frac{\pi}{2}\bigg)\bigg] \] Mit \(cos\big(\frac{\pi}{2}\big) = 0\) lässt sich diese Nullbedingung somit mathemtisch beweisen:

\[ y_{a}(t) + y_{b}(t) + y_{c}(t) = 0 \]

5.1.1.2 Entstehung eines Drehfeldes

Damit sich ein entsprechendes Drehfeld im Luftspalt einer Drehfeldmaschine einstellt, müssen mehrere Bedingungen erfüllt sein (siehe Abbildung 5.3):

• Alle Wicklungsstränge besitzen die gleiche Windungszahl
• Pro Phase \(2p\) Pole
• Die Wicklungsanfänge sind um \(\Delta \varphi_{1}=\frac{2\pi}{3p}\) zueinander verschoben
• Der Versatz von Wicklungsanfang zu Wicklungsende beträgt \(\Delta \varphi_{12}=\frac{\pi}{p}\)
• sinusförmiger Strom- und Spannungsverlauf

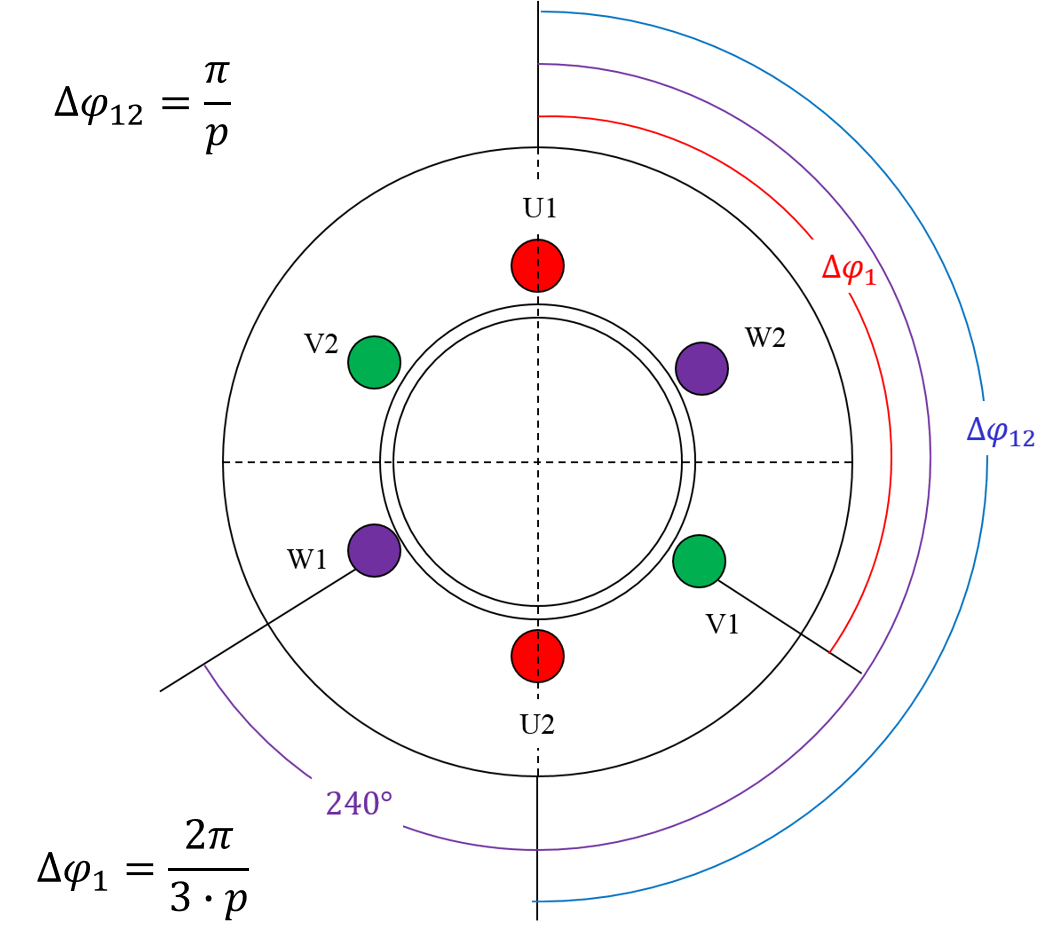
Abbildung 5.3: Grundsätzlicher Aufbau einer zweipoligen Drehfeldmaschine

Grundsätzlich ist es möglich ein Drehfeld auf verschiedene Arten zu erzeugen:

• Rotation eines Polrades im Stator
• Bestromung einer Drehfeldwicklung mit Drehstrom

Um die Entstehung eines Drehfeldes mit Hilfe einer Drehfeldwicklung zu begründen, kann von anfänglich von einer einzelnen Wicklung, wie im Abbildung 5.4 dargestellt, ausgegangen werden (unter Vernachlässigung von Sättigungserscheinungen).

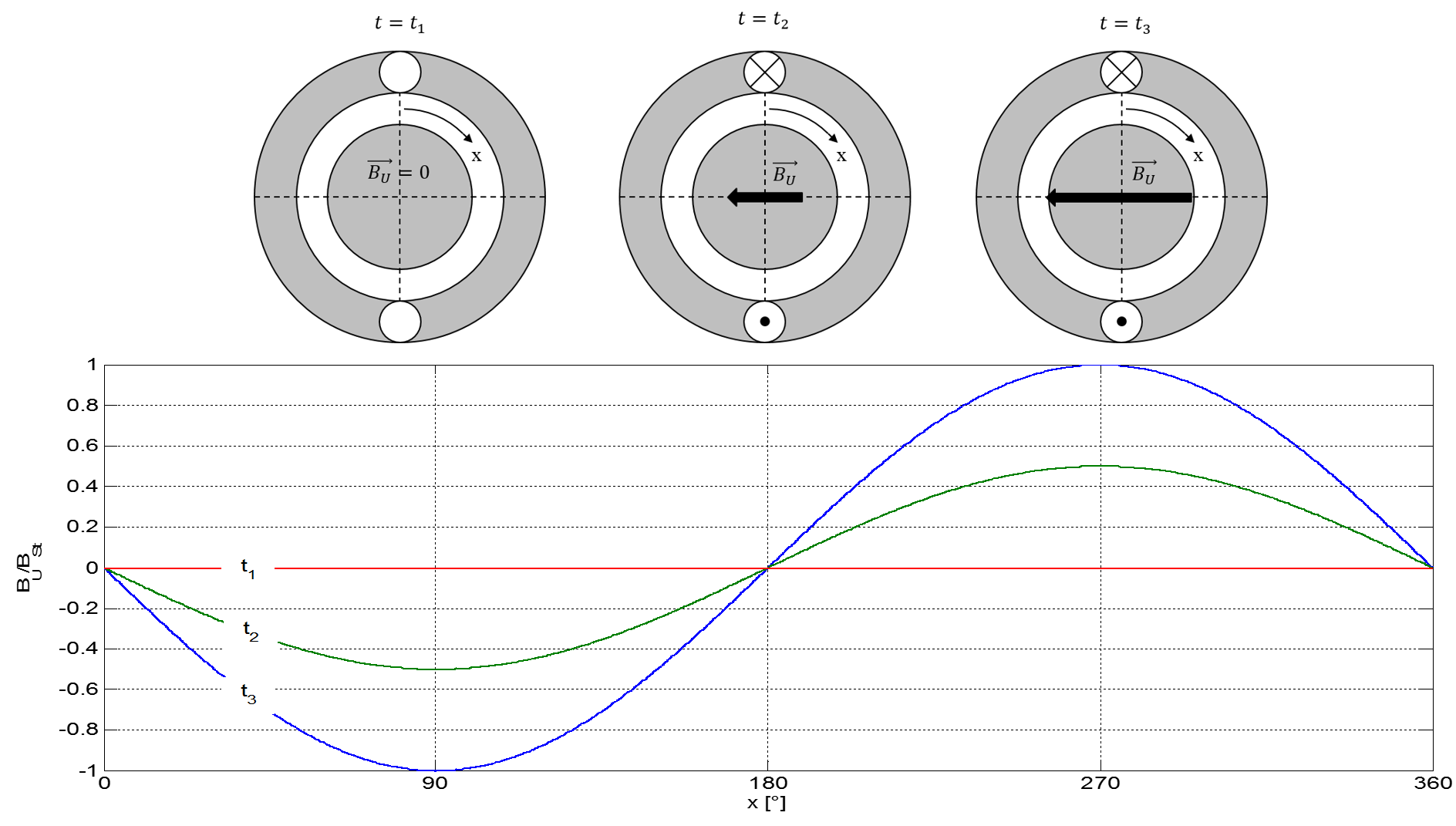
Abbildung 5.4: Flussdichteverteilung einer einzelnen Wicklung mit dem Strom als Parameter

Die Abbildung 5.4 zeigt die unterschiedlichen Flussdichteverteilungen einer einzelnen, unterschiedlich stark bestromten Wicklung im Stator einer elektrischen Maschine. Es zeigt sich eine direkte Proportionalität zwischen dem Wicklungsstrom und der Amplitude der Flussdichte, solange man sich im linearen Bereich der Magnetisierungskennlinie befindet. Die Nulldurchgänge sowie die Maxima sind von der Stromamplitude unabhängig. Die zugehörige Flussdichte dieses Stranges U kann anhand der folgenden Gleichung beschrieben werden.

\[ B_{U}(x,t)=-\hat{B}\cdot \sin{(x)}\cdot \sin{(\omega t)} \]

Da es sich bei einer dreisträngigen Drehstromwicklung um drei Strangwicklungen handelt, die um \(120^{\circ}\) zueinander versetzt am Umfang des Stators in Nuten untergebracht werden und diese gleichzeitig mit um \(120^{\circ}\) zeitlich verschobener Spannung versorgt werden, können die von diesen zwei zusätzlichen Wicklungen ausgehenden Flussdichteverteilungen anhand der Gleichungen:

\[ B_{V}(x,t)=-\hat{B}\cdot \sin{(x-\frac{2\pi}{3})}\cdot \sin{(\omega t-\frac{2\pi}{3})} \]

bzw.

\[ B_{W}(x,t)=-\hat{B}\cdot \sin{(x-\frac{4\pi}{3})}\cdot \sin{(\omega t-\frac{4\pi}{3})} \]

beschrieben werden. Somit lässt sich die räumliche Flussdichteverteilung im Luftspalt durch Addition aller drei Flussdichteverteilungen beschreiben:

\[ B_{Ges}(x,t)=B_{U}(x,t)+B_{V}(x,t)+B_{W}(x,t) \] Je nach Anordnung des gedanklichen Koordinatensystems in Bezug zu den Wicklungsachsen variiert die mathematische Beschreibung der entsprechenden physikalischen Grössen.

5.1.1.3 Raumzeigerdarstellung

Mit Hilfe eines Raumzeigers werden physikalische Grössen eines Dreiphasensystems als Zeiger in einer komplexen Ebene dargestellt, wobei eine Verwechslung mit der Zeigerdarstellung in der Wechselstromlehre vermieden werden sollte. Sie werden dazu verwendet Magnetfelder sowie Ströme und Spannungen von Drehfeldmaschinen zu beschreiben.

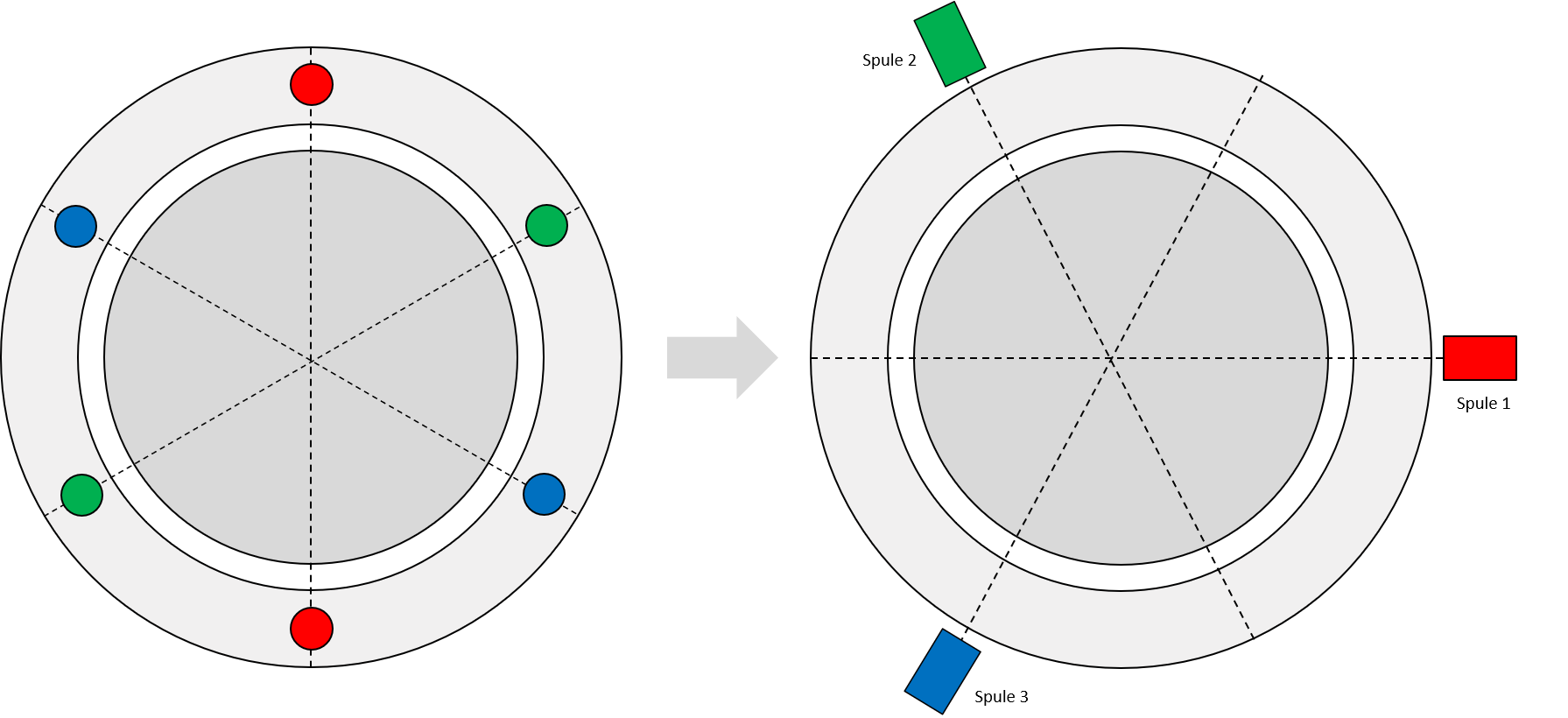
Abbildung 5.5: Modell einer Drehfeldmaschine (links: Darstellung mit örtlich konzentrierten Spulen; rechts: mit wirkungsorientierter Spulenanordnung)

Überträgt man die Erkenntnisse aus dem Kapitel 5.1.1.2 auf das in Abbildung 5.5 dargestellte Modell einer Drehfeldmaschine, lassen sich die physikalischen Grössen (Strom, Spannung, etc.) der einzelnen Wicklungen (Spule 1-3) mit Hilfe eines Vektors darstellen, dessen Betrag mit der Amplitude der physikalischen Grösse variiert. Hierbei gilt es zu berücksichtigen, dass die Flussdichteverteilung im Luftspalt einer Maschine, aufgrund der Verteilung der Wicklungen nicht ideal sinusförmig verläuft.

Durch Überlagerung (Vektoraddition) der drei Vektoren, deren Betrag bei sinusförmiger Speisung variiert, kann der zugehörige Raumzeiger, wie in Abbildung 5.6 gezeigt, dargestellt werden.

Abbildung 5.6: Entstehung des rotierenden Spannungs-Raumzeigers (schwarz) einer symmetrischen Drehfeldmaschine

Der so enstandene Raumzeiger, der in der Schnittebene der Maschine verläuft (somit zweidimensional) kann mit Hilfe eines orthogonalen Koordinatensystems mathematisch dargestellt werden. Bei der Wahl der Lage des Koordinatensystems ist man grundsätzlich frei. Je nach Literatur bzw. betrachtetem Modell wird zwischen statorfestem, rotorfestem bzw. beliebigem Koordinatensystem unterschieden.

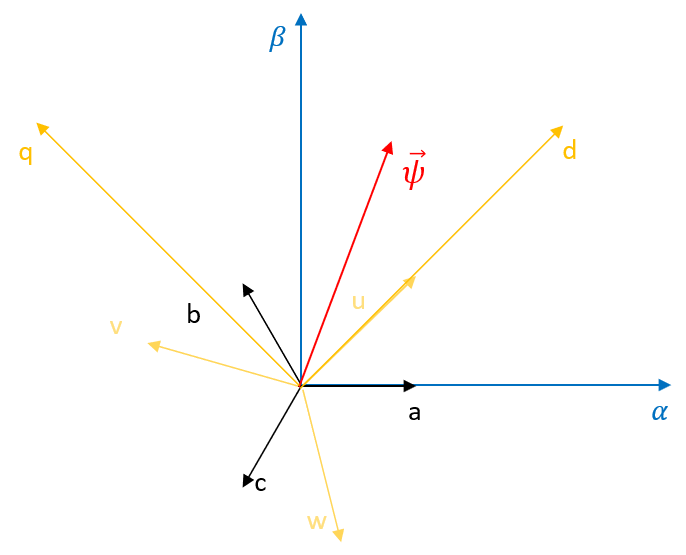
Abbildung 5.7: Darstellung eines Raumzeigers in unterschiedlichen Koordinatensystemen

Das statorfeste Koordinatensystem (Index \(S\)) wird dabei folgendermassen definiert:

\[ \vec{x}^{S}=(x_{\alpha},x_{\beta})^{T}=\begin{pmatrix}x_{\alpha}\\x_{\beta}\end{pmatrix} \]

Das statorfeste Koordinatensystem ist ein ortsfestes Koordinatensystem, welches üblicherweise so angeordnet wird, dass die \(\alpha\)-Achse mit einer der drei Wicklungsachsen des Stators (üblicherweise U) zusammenfällt. Beim rotorfesten Koordinatensystem (Index \(R\)) hingegen handelt es sich um ein rotierendes Koordinatensystem, welches so angeordnet wird, dass es mit einer Wicklungsachse des Rotors (welcher rotiert) zusammenfällt.

\[ \vec{x}^{R}=(x_{d},x_{q})^{T}=\begin{pmatrix}x_{d}\\x_{q}\end{pmatrix} \]

Folglich rotiert das rotorfeste Koordinatensystem mit der mechanischen Winkelgeschwindigkeit \(\Omega_{mech}\) um das statorfeste Koordinatensystem. Je nach Verwendung ist es ebenfalls möglich ein beliebig rotierendes Koordinatensystem zu definieren, welches beispielsweise mit dem Statorfluss, dem Rotorfluss bzw. dem Luftspaltfluss rotiert. Vor allem in der Vergangenheit wurden die Raumzeiger mit Hilfe der komplexen Zahlen dargestellt, wobei berücksichtigt werden muss, dass die reele Achse der komplexen Zahlenebene mit der Spulenachse U zusammenfällt. Die Berechnung des Raumzeigers basiert in diesem Fall auf der Gleichung:

\[ \vec{x}=\frac{2}{3}\big(x_{U}+a\cdot x_{V} + a^{2}\cdot x_{W} \big) \]

Wobei der komplexe Drehoperator \(a\) verwendet wird:

\[ a=e^{j\frac{2\pi}{3}}=-\frac{1}{2}+j\frac{\sqrt{3}}{2} \] \[ a^{2}=e^{j\frac{4\pi}{3}}=-\frac{1}{2}-j\frac{\sqrt{3}}{2} \]

In moderneren Veröffentlichungen wird stattdessen immer öfter die oben dargestellte Vektornotation verwendet.

Um Grössen des Dreiphasen-Systems \(\vec{x}^{a,b,c}\) in das statorfeste Koordinatensystem umwandeln zu können, wird die Allgemeine Clarke Transformation herangezogen:

\[ \begin{pmatrix}x_{\alpha}(t) \\ x_{\beta}(t) \\ x_{0}(t) \end{pmatrix} = c\cdot \begin{bmatrix} 1 & -\frac{1}{2} & -\frac{1}{2}\\ 0 & \frac{\sqrt{3}}{2} & -\frac{\sqrt{3}}{2} \\ \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{bmatrix} \cdot \vec{x}^{a,b,c} = c \cdot T_{C}\cdot \vec{x}^{a,b,c} \]

Der Skalierungsfaktor \(c\) variiert, je nachdem ob eine amplitudenkorrekte \((c=\frac{2}{3})\) oder eine leistungskorrekte \((c=\sqrt{\frac{2}{3}})\) Transformation gewünscht ist. Bei der leistungskorrekten Transformation kann die Leistungberechnung durch Multiplikation des Strom- und Spannungsraumzeigers im statorfesten Koordinatensystem erfolgen. Die Drehmatrix \(T_{C}\) kann bei symmetrischen Dreiphasensystemen noch weiter vereinfacht werden, da die Nullkomponente \(x_{0}(t)\) in diesem Fall entfällt:

\[ \begin{pmatrix}x_{\alpha}(t) \\ x_{\beta}(t)\end{pmatrix} = c\cdot \begin{bmatrix} 1 & -\frac{1}{2} & -\frac{1}{2}\\ 0 & \frac{\sqrt{3}}{2} & -\frac{\sqrt{3}}{2} \end{bmatrix} \cdot \vec{x}^{a,b,c} = c \cdot T_{C}\cdot \vec{x}^{a,b,c} \]

Die inverse Clarke-Transformation wird verwendet, um eine Umrechnung vom statorfesten in das dreiphasige Koordinatensystem zu ermöglichen.

\[ \vec{x}^{a,b,c}=\frac{1}{c}\cdot \begin{bmatrix} \frac{2}{3} & 0 \\ -\frac{1}{3} & \frac{1}{\sqrt{3}} \\ -\frac{1}{3} & -\frac{1}{\sqrt{3}} \end{bmatrix} \cdot \begin{pmatrix}x_{\alpha}(t) \\ x_{\beta}(t)\end{pmatrix} = \frac{1}{c} \cdot T^{-1}_{C}\cdot \vec{x}^{S} \]

Da alle betrachteten Koordinatensystem den gleichen Ursprung besitzen, kann eine Drehung des Koordinatensystems durch eine entsprechende Drehmatrix \(T_{P}(\varphi_{k})\) in Abhängigkeit des unter Umständen zeitabhängigen Winkels \(\varphi_{k}\) vorgenommen werden. Durch eine solche Drehung ist der Raumzeiger somit in beliebig rotierten bzw. beliebig rotierenden Koordinaten darstellbar.

\[ T_{P}(\varphi_{k}) = \begin{bmatrix} cos\big(\varphi_{k}(t)\big) & -sin\big(\varphi_{k}(t)\big) \\ sin\big(\varphi_{k}(t)\big) & cos\big(\varphi_{k}(t)\big) \end{bmatrix} \]

Diese Umrechnung der physikalischen Grössen einer Drehfeldmaschine vom statorfesten Koordinatensystem in beliebige Koordinatensysteme \((\vec{x}^{k}\) wird in der Antriebstechnik als Park-Transformation bezeichnet (Index \(P\)). Die Anwendung der Drehmatrix \(T_{P}(\varphi_{k})\) ist gleichbedeutend mit einer Drehung des statorfesten Koordinatensystems um den Winkel \(\varphi_{k}\), wie es in Abbildung 5.8 dargstellt ist.

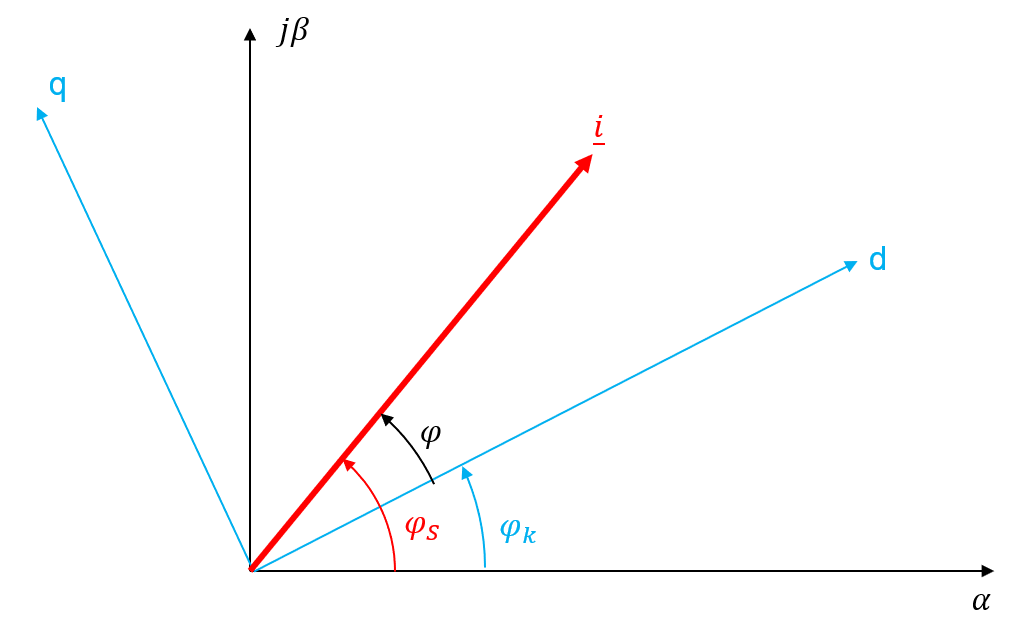
Abbildung 5.8: Darstellung eines Raumzeigers im statorfesten und k-Koordinatensystem

Der Winkel \(\varphi_{S}\) repräsentiert hierbei den Winkel des Strom-Raumzeigers \(\vec{i}\) im statorfesten Koorrdinatensystem. Der Winkel \(\varphi_{k}\) hingegen repräsentiert den Winkel, der notwendig ist, um das statorfeste KOS in die Position des beliebigen k-KOS zu drehen. Der eigentliche Winkel des Strom-Raumzeigers im k-KOS wird durch den Winkel \(\varphi\) zum Ausdruck gebracht. Für die Winkelbeziehungen in der Abbildung 5.8 ergibt sich somit folgender Zusammenhang.

\[ \varphi=\varphi_{S} - \varphi_{k} \]

Um einen beliebigen Raumzeiger \(\vec{x}^{S}\), gegeben im statorfesten KOS (Index \(S\)), in das beliebige k-KOS (Index \(k\)) zu überführen \(\vec{x}^{k}\) muss die inverse Park-Transformation angewandt werden, was gleichbedeutend ist mit der Park-Transformation mit negativem Winkel \(\varphi_{k}\).

\[ \vec{x}^{k}=T_{P}^{-1}(\varphi_{k})\cdot \vec{x}^{S}=T_{P}(-\varphi_{k})\cdot \vec{x}^{S}= \begin{bmatrix} cos\big(\varphi_{k}\big) & sin\big(\varphi_{k}\big) \\ -sin\big(\varphi_{k}\big) & cos\big(\varphi_{k}\big) \end{bmatrix}\cdot \vec{x}^{S} \]

Begründen lässt sich dies damit, dass ein beliebiger Raumzeiger, welcher im statorfesten KOS dargestellt wird, einen grösseren Winkel \(\varphi_{S}\) aufweist als der gleiche Raumzeiger im beliebigen k-KOS, nachdem dieses um den Winkel \(+\varphi_{k}\) gedreht wurde. Der gleiche Raumzeiger weist somit im beliebigen k-KOS einen, um den Wert \(\varphi_{k}\) kleineren, Winkel auf als im statorfesten KOS.

Auch die Park-Transformation sowie deren Inverse lassen sich mit Hilfe von komplexen Zahlen äquivalent darstellen.

\[ \vec{x}^{k}=\vec{x}^{S}\cdot e^{-j\varphi_{k}} \]

\[ \vec{x}^{S}=\vec{x}^{k}\cdot e^{j\varphi_{k}} \]

5.1.2 Motivation der Feldorientierung bei Drehfeldmaschinen

Die Motivation der Feldorientierung bei Drehfeldmaschinen liegt darin begründet, die Regelung von Drehmoment und Maschinenfluss auf ein Mass, ähnlich wie bei der DC-Maschine zu vereinfachen. Abbildung 5.9 stellt dieses Prinzip am Beispiel einer permanentmagneterregten Synchronmaschine dar.

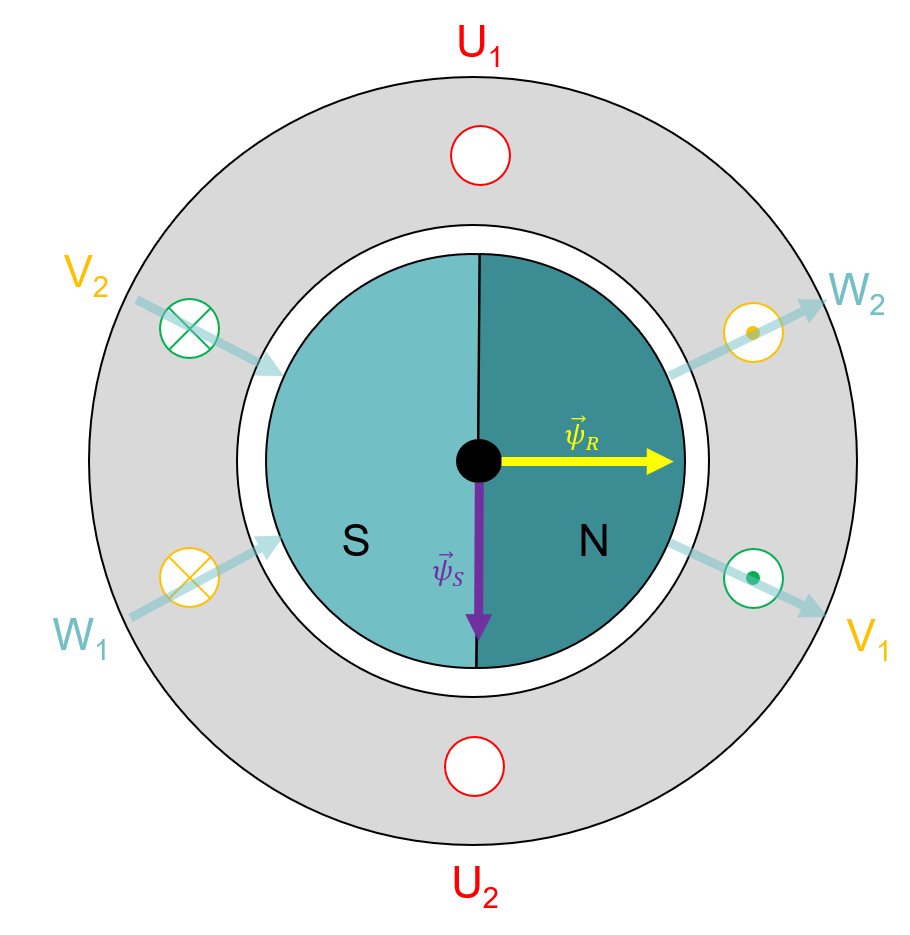
Abbildung 5.9: Stator- und Rotorflussvektor am Beispiel der PMSM

Das maximale Drehmoment wird erzeugt sobald sich der Rotorfluss-Raumzeiger \(\vec{\psi}_{R}\), wie in der Abbildung gezeigt, orthogonal zum Statorfluss-Raumzeiger \(\vec{\psi}_{S}\) angeordnet befindet. Im Falle der Gleichstrommaschine wird dafür mit Hile des Kommutators, also mechanisch, gesorgt. Bei der Drehfeldmaschine wird ein ähnliches Verhalten durch die Einführung eines mit dem Rotor rotierenden Koordinatensystems erreicht, welches auf die aktuelle Rotorposition ausgerichtet wird, wie dies in Abbildung 5.10 dargestellt ist.

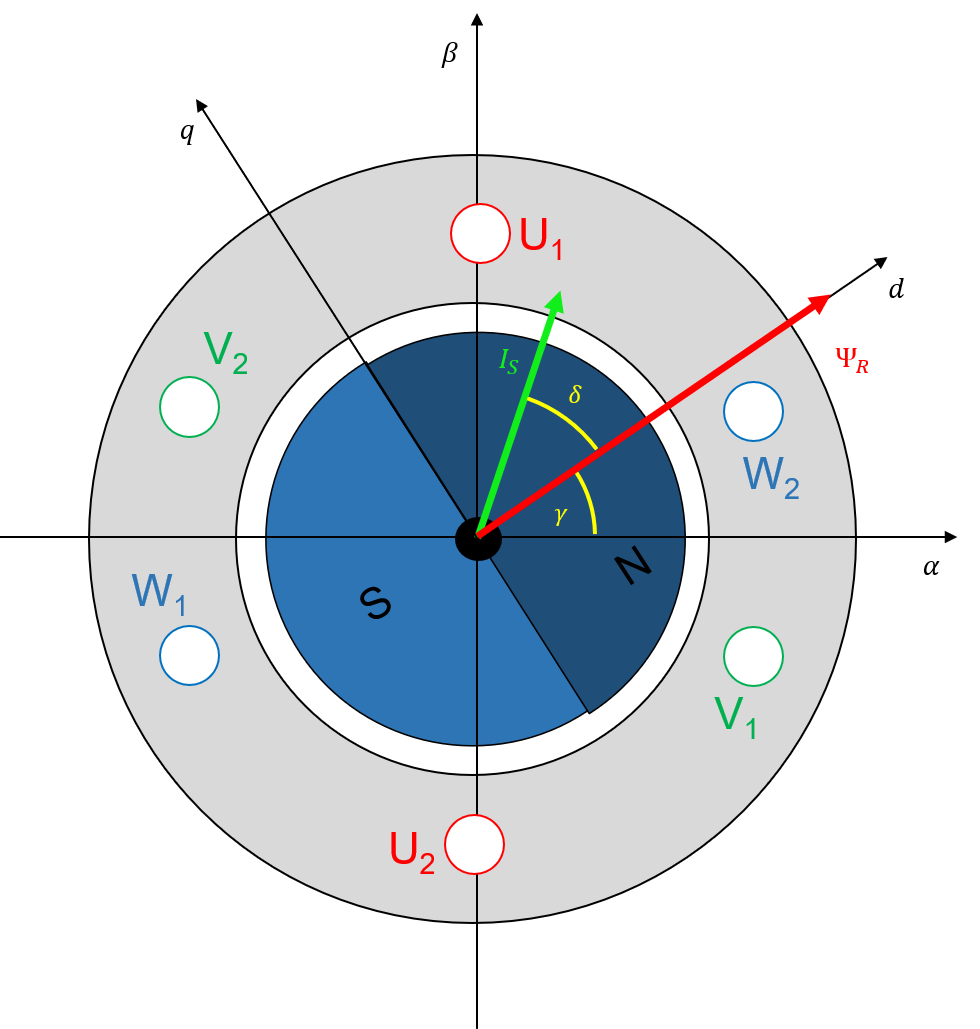
Abbildung 5.10: Prinzip der Feldorientierung am Beispiel der PMSM

Ausgehend von diesem Modell lässt sich das resultierende Drehmoment mit Hilfe des Vektorproduktes des Statorstrom- und des Rotorflussvektors im Statorkoordinatensystem bestimmen.

\[ M=|\Psi_{R}\times I_{S}| = |\Psi_{R}| \cdot |I_{S}|\cdot sin(\delta) \] Dies lässt sich auch durch Berechnung der folgenden Determinante bewerkstelligen.

\[ M = \begin{vmatrix} \Psi_{R\alpha} & \Psi_{R\beta} \\ I_{S\alpha} & I_{S\beta} \end{vmatrix} = \Psi_{R\alpha} \cdot I_{S\beta} - \Psi_{R\beta} \cdot I_{S\alpha} \]

Durch die Einführung des rotierenden, am Rotorfluss orientierten Koordinatensystems, wird gleichzeitig die Berechnung des Drehmomentes vereinfacht, da der Rotorfluss immer in Richtung der d-Achse der KOS ausgerichtet wird. In diesem Fall kann das Drehmoment lediglich durch die q-Komponente des Statorstromvektors beeinflusst werden und das Drehmoment lässt sich somit folgendermassen berechnet werden.

\[ M = \frac{3}{2}\cdot \Psi_{R} \cdot i_{q} \]

Allerdings muss berücksichtigt werden, dass bei hochpoligen Maschinen alle Polpaare zur Drehmomentbildung beitragen, wodurch obige Gleichung korrekterweise noch mit der Polpaarzahl multipliziert werden muss.

\[ M = \frac{3}{2}\cdot p \cdot \Psi_{R} \cdot i_{q} = k_{T} \cdot i_{q} \] Der Faktor \(k_{T}\) wird dabei sehr häufig als Motorkonstante bzw. Drehmomentkonstante bezeichnet. Um das rotorfeste KOS korrekt ausrichten zu können, ist die Kenntnis der aktuelle Rotorposition notwendig. Diese kann entweder mit Hilfe von im Stator eingebetteten Hallsensoren (heutzutage eher weniger verbreitet), mit Hilfe eines entsprechenden Encoders gemessen werden oder sie wird durch Messung der Statorspannungen und der Statorströme basierend auf einem entsprechenden Motormodell berechnet (sensorlose Variante). Ausgehend von der Darstellung in Abbildung 5.10 ist ausserdem zu erkennen, dass der Maschinenfluss durch Variation der d-Komponente des Statorstromvektors in seiner Amplitude beeinflusst werden kann, da diese eine Statorflusskomponente hervorruft, die in die gleiche Richtung zeigt, wie der Rotorfluss. Somit ist es, ähnlich wie bei der Gleichstrommaschine, möglich den Maschinenfluss und das Drehmoment getrennt voneinander zu beeinflussen. Eine Variation der Amplitude der q-Komponente des Statorstromvektors \(i_{q}\) bewirkt eine Variation des elektrischen Drehmomentes und eine Variation der d-Komponente des Statorstromvektors \(i_{d}\) beeinflusst den Maschinenfluss. Da es sich beim rotorfesten KOS um ein rotierendes KOS handelt, werden aus den zwei Komponenten des Statorstromvektors \(i_{d}\) bzw. \(i_{q}\) Gleichkomponenten, welche getrennt voneinander mit Hilfe von PI-Reglern geregelt werden können. Ausgehend von dieser Überlegung sind folgende, grundlegenden Schritte zur Umsetzung einer Feldorientierten Regelung einer PMSM notwendig:

1. Messung der aktuellen Phasenströme
2. Überführung der Phasenströme in das statorfeste KOS mit Hilfe der Clarke Transformation, wodurch sich ein Strom-Raumzeiger ergibt
3. Überführung des Strom-Raumzeigers in das rotorfeste KOS mit Hilfe der Park Transformation, wodurch sich Gleichgrössen ergeben (im stationären Betrieb)
4. Regelung der fluss- und. drehmomentbildenden Stromkomponenten mit Hilfe zweier PI-Regler.
5. Der sich einstellende Strom-Raumzeiger wird mit Hilfe der inversen Park Transformation in das statorfeste KOS überführt
6. Mittels entsprechender Modulationsverfahren (z.B. Raumzeigermodulation) werden die drei Phasenströme eingeprägt

Basierend auf dieser Vorgehensweise ergibt sich ein Blockschaltbild, wie es in Abbildung 5.11 dargestellt ist.

Abbildung 5.11: Blockdiagramm der feldorientierten Regelung einer PMSM (vereinfacht)

Der Sollwert \(i_{qSoll}\) wird dabei vom übergeordneten Drehzahlregler und der Sollwert \(i_{dSoll}\) wird vom Flussregler vorgegeben.

5.1.3 Modulationsverfahren

Im Laufe der Zeit haben sich mehrere unterschiedliche Verfahren der Pulsweitenmodulation (PWM) entwickelt. Die wesentlichen Unterschiede bestehen in ihrem Oberschwingungsspektrum, der erreichbaren Ausgangssapnnungsamplitude und dem Implementierungsaufwand. Eine einfache Unterscheidung kann in die Gruppe der trägerbasierten und der trägerlosen PWM-Verfahren erfolgen.

5.1.3.1 Trägerbasierte PWM-Methoden

Bei trägerbasierten PWM-Verfahren wird grundsätzlich ein Refernzsignal, welches zum Beispiel die Spannungsamplitude repräsentiert, mit ein periodischen Trägersignal (z.B. Sägezahnsignal) verglichen. Aus diesem Vergleich entsteht schlussendlich aus dem Vergleich dieser beiden Signale. Das es sich bei dem Trägersignal um ein periodisches Signal handelt, entsteht somit ein PWM-Signal mit fester Frequenz und gleichzeitig ein fest definiertes Oberschwingungsspektrum.

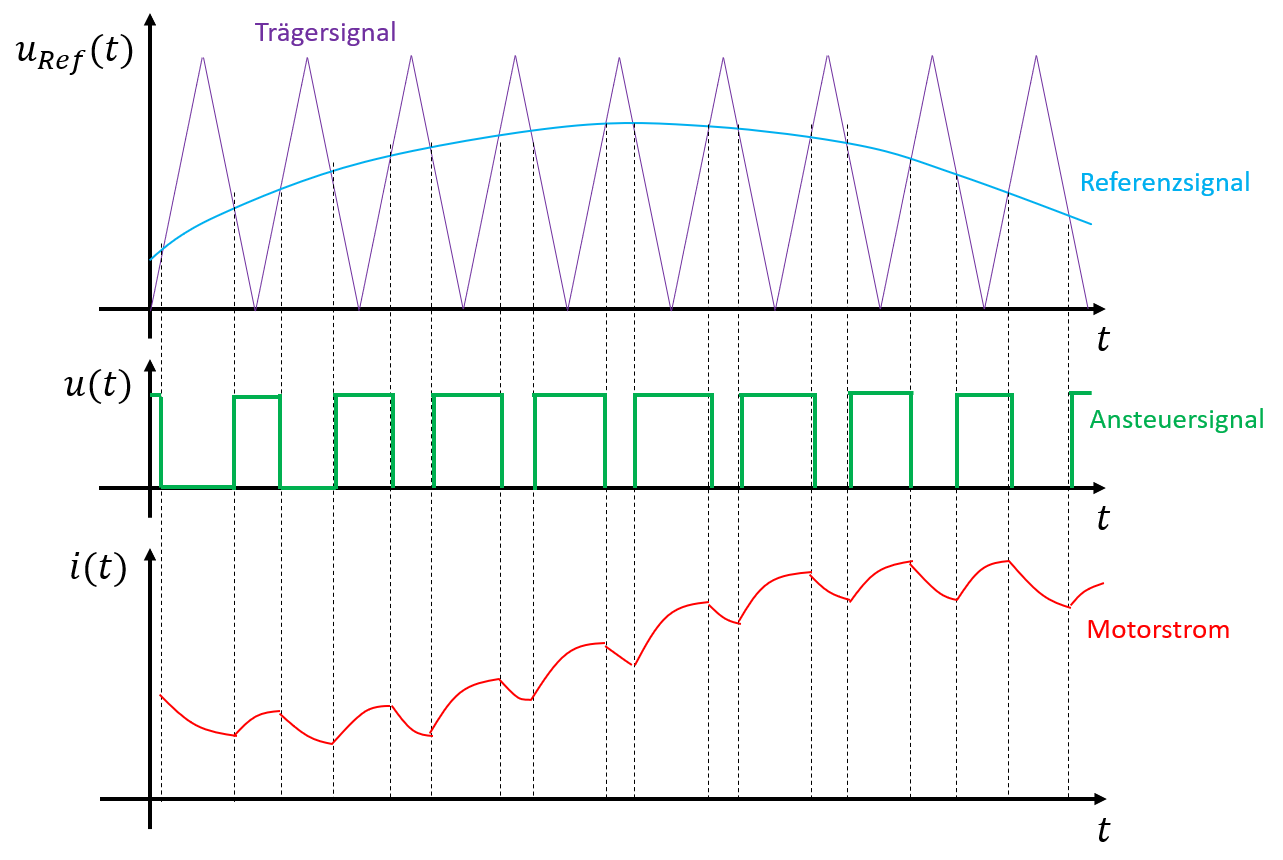
Abbildung 5.12: Einphasige PWM bei Verwendung der Unterschwingungsverfahrens

Ein Beispiel für das Unterschwingungsverfahren (häufig auch als Sinus-Dreieck-Modulation bezeichnet) ist in Abbildung 5.12 dargestellt. Um Doppelpulse bei der Ansteuerung der Leistungshalbleiter zu vermeiden muss darauf geachtet werden, dass eine Anpassung des Referenzsignals bei Erreichen des Maximus des Referenzsignals erfolgt. Das hier dargestellte Unterschwingungsverfahren wird häufig noch modifiziert angewandt (z.B. durch Injektion der dritten Harmonischen), wobei sich diese modifizierten Verfahren im Wesentlichen in der erreichbaren Ausgangsspannung (Modulationsindex), der Summe des Oberschwingungsspektrums und im Implementierungsaufwand unterscheiden.

5.1.3.2 Raumzeigermodulation

Die Raumzeigermodulation ist ein Steuerverfahren für elektrische Antriebssysteme welches auf der Pulsweitenmodulation basiert. Vorraussetzung ist das eine Halbbrücke für jede der drei Phasen vorhanden ist, die es ermöglicht jede einzelne Motorphase (U, V, W) auf entweder positive oder negative Zwischenkreisspannung zu legen. Jede Halbbrücke hat zwei mögliche Schaltzustände, wodurch sich für alle drei Halbbrücken insgesamt \(2^{3}=8\) mögliche Schaltzustände ergeben. In Abhängigkeit dieser Schaltzutände ergeben sich unterschiedliche Spannungswerte zwischen den Motorphasen und somit auch unterschiedliche Spannungsraumzeiger. Eine Ausnahme dieser Regel bilden die zwei Schaltzustände, bei der alle drei Motorphasen entweder auf das negative oder das positive Zwischenkreispotenzial des Zwischenkreises gelegt werden. In diesem Fall werden alle drei Motorphasen kurzgeschlossen und es ist keine Motorspannung messbar. Aufgrund dessen werden diese zwei Spannungsraumzeiger als Nullspannungszeiger bezeichnet. Sowohl die benötigte Leistungsendstufe sowie das zugehörige Raumzeigerdiagramm sind der Abbildung 5.13 dargestellt.

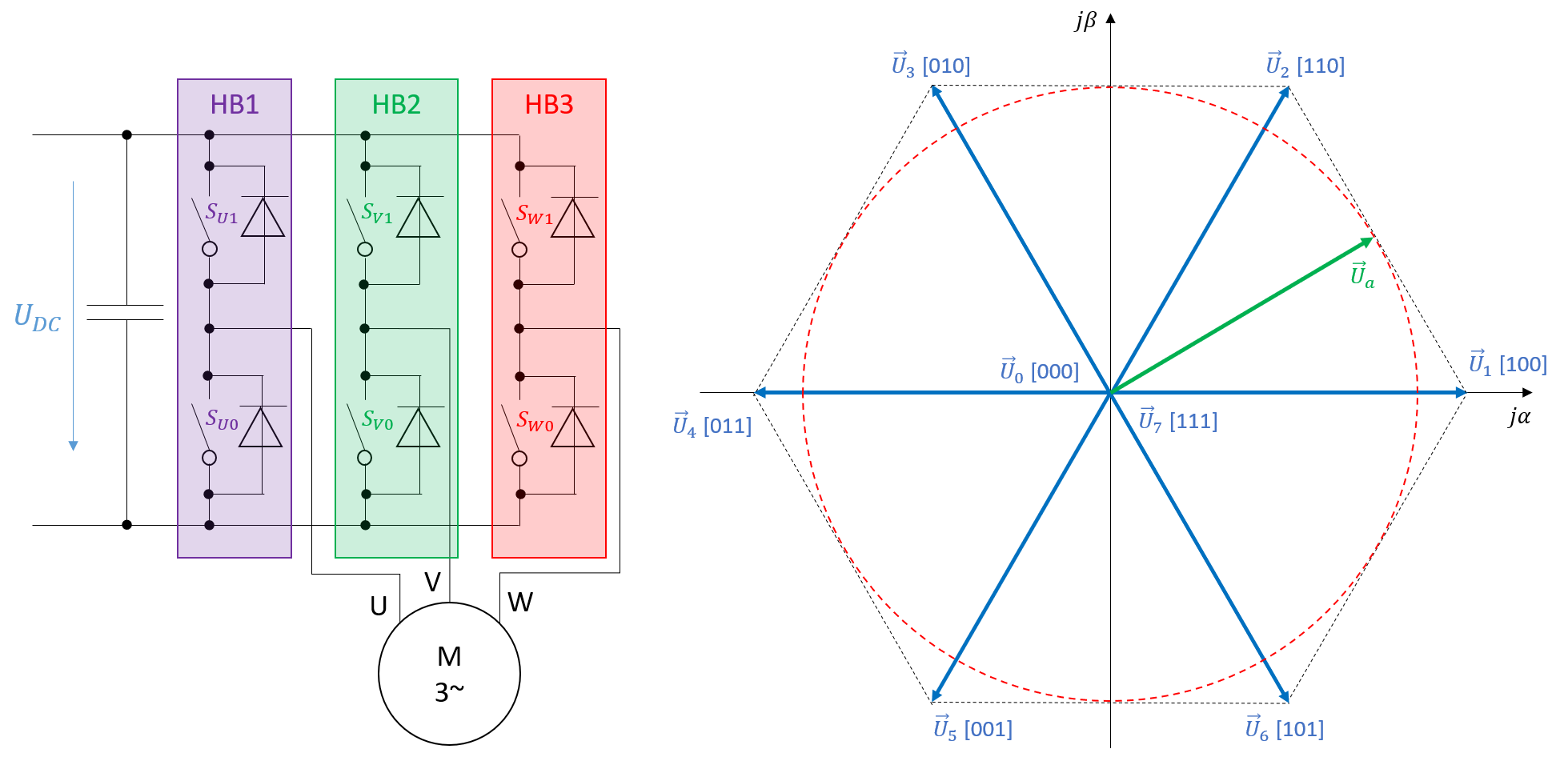
Abbildung 5.13: Zur Raumzeigermodulation benötigte Leistungsendstufe sowie zugehöriges Raumzeigerdiagramm

Wie das obige Diagramm erkennen lässt, sind die 6 aktiven Spannungsraumzeiger nicht ausreichend, um einen sinusförmigen Verlauf der Motorspannung zu gewährleisten, da es auf diese Weise nicht möglich ist Spannungsraumzeiger mit beliebigen Beträgen und Winkeln zu erzeugen. Um dieser Forderung dennoch gerecht werden zu können, wird auf das Prinzip der Pulsweitenmodulation zurückgegriffen und mit den zur Verfügungs stehenden Spannungsraumzeigern kombiniert. Soll beispielsweise der Spannungsraumzeiger \(\vec{U_{\alpha}}\) in Abbildung 5.13 erzeugt werden, dann wird abwechselnd der links- und rechtsseitig begrenzende Spannungsraumzeiger (in diesem Beispiel \(\vec{U_{1}}\) und \(\vec{U_{2}}\)) erzeugt und an den Motorklemmen ausgegeben. Die Dauer mit welcher der jeweilige Spannungsraumzeiger aktiv ist, hängt von der Schaltfrequenz des Umrichters ab. Da die Motorwicklungen eine Tiefpasswirkung (induktiver und ohmscher Anteil) besitzen, werden die hochfrequenten Anteile der Motorspannung gefiltert und es ergibt sich ein mittlerer Strom, welcher den gewünschten Flussraumzeiger nach sich zieht. Durch entsprechende Bestimmung der Einschaltdauer der jeweiligen, links und rechts vom gewünschten Spannungsraumzeiger befindlichen, Spannungsraumzeiger kann somit der Winkel des erzeugten Spannungsraumzeigers beeinflusst werden. Eine Modifikation der Amplitude ist auf diese Weise hingegen nicht möglich. Um gleichzeitig die Amplitude aktiv beeinflussen zu können, werden die Nullspannungszeiger in die obige Überlegung mit einbezogen. Dies bedeutet, dass bei gleichzeitiger Modifikation der Amplitude und der Winkellage des gewünschten Spannungsraumzeigers, sowohl die links- und rechtsseitig begrenzenden Spannungsraumzeiger als auch die Nullspannungszeiger in die Modulation einbezogen werden müssen. Die grundlegende Funktionsweise der Raumzeigermodulation besteht somit darin, den Sektor zu bestimmen, in welchem sich der gewünschte Spannungsraumzeiger befindet und anschliessend die drei Einschaltdauern der zwei Spannungsraumzeiger sowie des jeweiligen Nullspannnungszeigers zu bestimmen. Dieses Prinzip entspricht dem Prinzip der Pulsweitenmodulation. Dieser Zusammenhang kann auch als grafische Repräsentation in einem schiefwinkligen Koordinatensystem repräsentiert werden, wie es in Abbildung dargestellt ist.

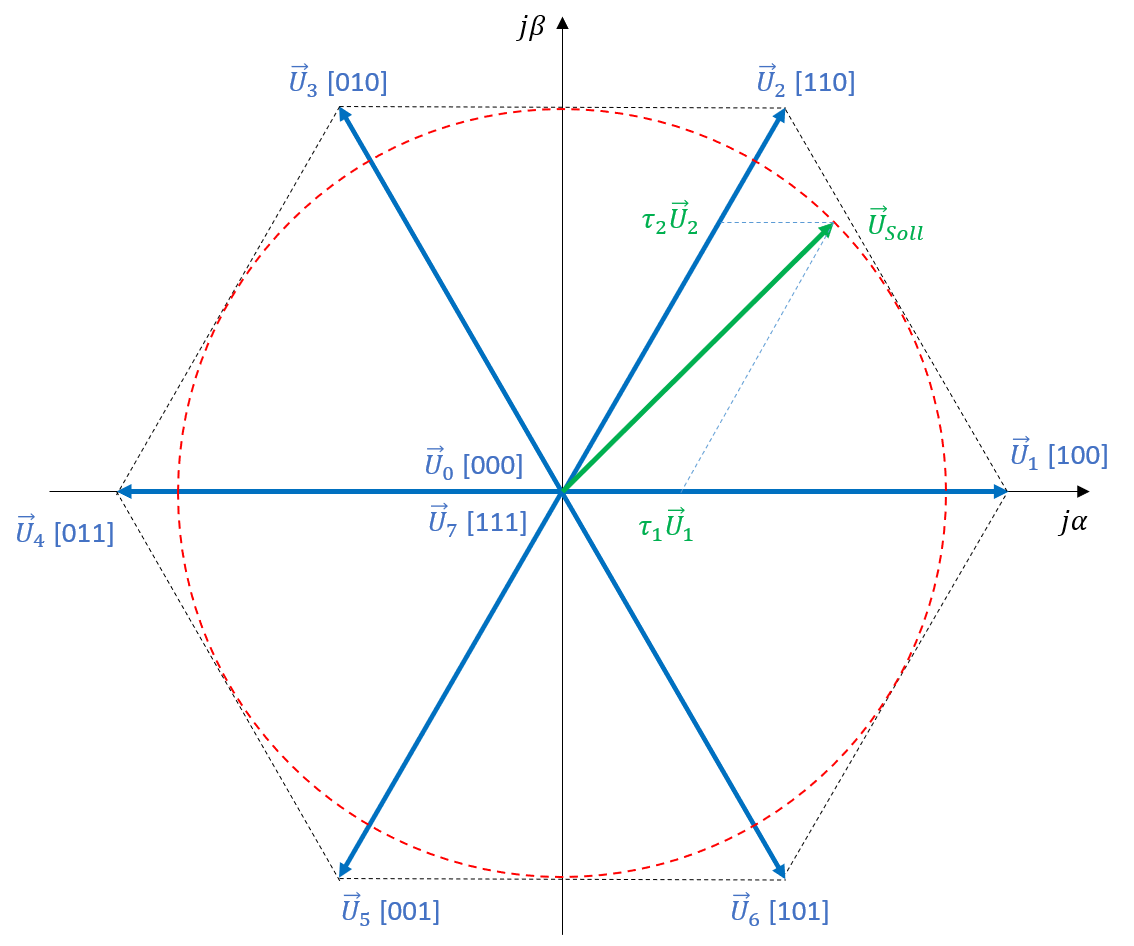
Abbildung 5.14: Grafische Repräsentation der Raumzeigermodulation

Die maximale Ausgangsspannung, die dem Radius des Kreises in Abbildung 5.14 entspricht, kann mit Hilfe der Spannungs im Zwischenkreis \(U_{DC}\) bestimmt werden.

\[ \hat{U}=U_{DC}\cdot \cos(30^{\circ})=\frac{\sqrt{3}}{2}\cdot U_{DC} \] Je nach aktuellem Schaltzustand der drei Halbbrücken ergeben sich unterschiedliche Spannungsverhältnisse an den Motorwicklungen, was dazu führt, dass jeweils zwei Motorphasen parallel geschalten werden. Dieser Umstand führt dazu, dass sich die Spannungsabfälle an den Motorwicklungen unterscheiden, was beispielhaft in Abbildung 5.13 dargestellt ist.

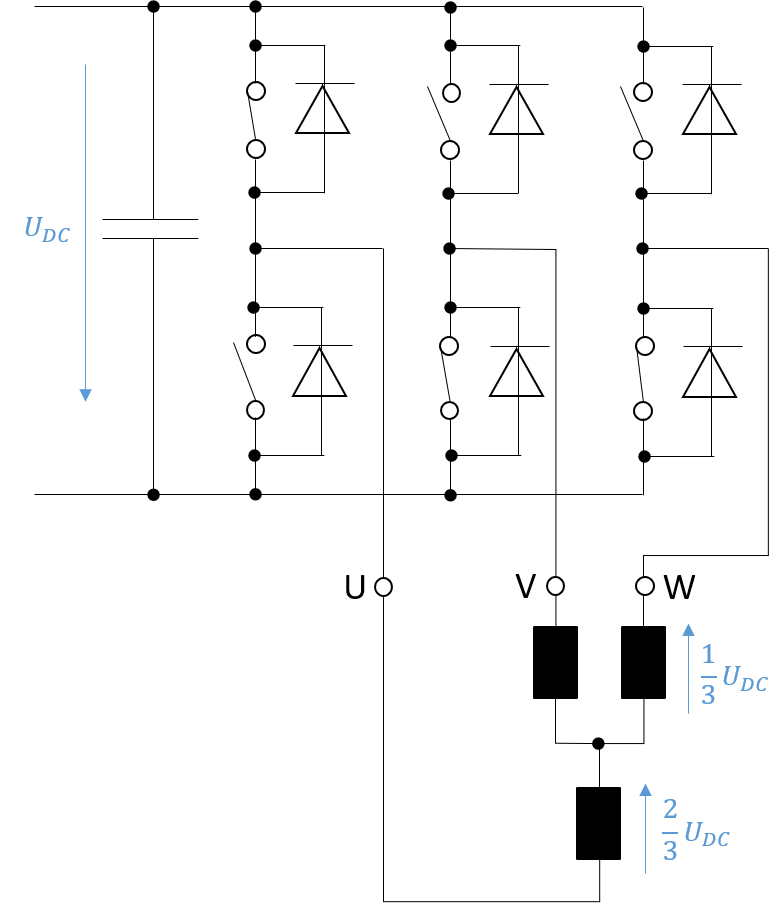
Abbildung 5.15: Unterschiedliche Spannunsgverteilung an den Motorwicklungen

Die maximale Strangspannung, die an die Motorwicklungen angelegt werden kann ergibt sich somit anhand folgender Gleichung.

\[ \hat{U}_{Str}=\frac{2}{3}\cdot \frac{\sqrt{3}}{2}\cdot U_{DC}=\frac{\sqrt{3}}{3}\cdot U_{DC} \]

Soll beispielsweise ein Spannungsraumzeiger im ersten Sektor (zwischen \(\vec{U_{1}}\) und \(\vec{U_{2}}\)) erzeugt werden, kann dies anhand der folgenden Gleichung dargestellt werden.

\[ \underline{u}_{soll}=\frac{1}{T_{a}}\bigl(\tau_{0}\cdot T_{a}\cdot \underline{u}_{0/7} + \tau_{1}\cdot T_{a}\cdot \underline{u}_{1} + \tau_{2}\cdot T_{a}\cdot \underline{u}_{2}\bigr) \] In diesem Fall repräsentiert die Konstante \(T_{a}\) einen Schaltzyklus und die Konstante \(\tau_{x}\) repräsentieren die Zeitauer für welche die jeweiligen Spannungsraumzeiger aktiv sind. Die entsprechenden Zeitdauern werden anhand des schiefwinkligen Koordinatensystems in Abbildung 5.14 bestimmt.

\[ \tau_{2} = \sqrt{3}T_{a}\frac{|U_{Soll}|}{\hat{U}_{Str}}\sin({\alpha_{Soll}}) \]

\[ \tau_{1} = \sqrt{3}T_{a}\frac{|U_{Soll}|}{\hat{U}_{Str}} sin\biggl(\frac{\pi}{3}-\alpha_{Soll}\biggr) \]

Dieses Prinzip kann auch für andere Sektoren des Spannungsraumzeiger-Hexagons angewandt werden.

5.2 Der Drehzahlregelkreis

Die grundlegende Funktion des Drehzahlregelkreises besteht darin, die aktuelle Motordrehzahl einem entsprechenden Sollwert nachzuführen. Dabei besagt das dynamische Grundgesetz der Rotation, dass zwischen dem an einem Körper angreifenden Drehmoment \(M\), seinem Trägheitsmoment \(J\) und der Winkelbeschleunigung \(\alpha\) folgender Zusammenhang besteht.

\[ M = M_{el}-M_{L}=J\cdot \alpha = J\cdot \frac{d\omega}{dt}=J\cdot 2\pi\cdot \frac{dn}{dt} \]

Im Falle eines elektrischen Antriebes wird ein Motordrehmoment \(M_{el}\) zur Verfügung gestellt, welches einem Lastmoment \(M_{L}\) entgegenwirkt. Dieses physikalische Grundgesetz entspricht im Grundsätz dem der Translation, wobei lediglich das Trägheitsmoment durch die träge Masse \(m\), die Winkelbeschleunigung durch die Beschleunigung \(a\) und das Drehmoment durch die Kraft \(F\) ersetzt werden.

\[ F = m\cdot a = m \cdot \frac{dv}{dt} \]

Beide, diesem Prinzip zugrundeliegenden Modelle sind in der Abbildung 5.16 dargestellt.

Abbildung 5.16: Modelle zum dynamischen Grundgesetz der Rotation und Translation

Das den Modellen zugrunde liegende Bezugssystem entspricht dabei dem Verbraucherzählpfeilsystem, welches dadurch gekennzeichnet ist, dass sich bei einer Leistungsabgabe an die Last eine positive Leistung einstellt. Bei elektrischen Antrieben gilt ausserdem die Seite der Leistungsabgabe als Abtriebsseite und die Drehrichtungsangabe erfolgt im mathematisch positiven Sinn, entgegen dem Uhrzeigersinn, mit Blick von der Antriebs- zur Abtriebsseite. Unter Berücksichtigung der in Kapitel 5.1 dargestellten Berechnung des Drehmomentes (feldorientierte Regelung der PMSM) ist es möglich das Solldrehmoment in eine drehmomentbildende Soll-Stromkomponente \(i_{qSoll}\) umzurechnen.

\[ i_{qSoll} = \frac{2\cdot M_{Soll}}{3\cdot p\cdot \Psi_{R}} = \frac{M_{Soll}}{k_{T}} \]

Neben dem Motormoment \(m_{el}\) muss gleichzeitig das Lastmoment \(m_{L}\) berücksichtigt werden, welches mit negativem Vorzeichen zu berücksichtigen ist (bei Leistungsabgabe). Basierend auf diesen Überlegungen lässt sich der Drehzahlregelkreis ableiten, wie er in Abbildung 5.17 dargestellt ist.

Abbildung 5.17: Prinzipieller Aufbau des Drehzahlregelkreises

Die aktuelle Drehzahl wird über einen Motorgeber und eine entsprechende Berechnung erfasst und dem Istwertfilter zugeführt. Zur Erfassung der Lage- bzw. Drehzahl des Rotors kommen grundsätzlich unterschiedliche Gebersysteme zum Einsatz. Dabei wird unterschieden, ob diese Geber Absolutwertinformationen (aktueller Winkelwert) oder lediglich inkrementelle Informationen über die Rotorlage bereitstellen. Je nach Servoumrichter und dessen Funktionsweise ist es notwendig absolute Lageinformation zur Ansteuerung des Leistungsteils zu erhalten. In diesem Fall ist der Einsatz eines Absolutwergebers unerlässlich. Aus der Information zur Lage des Rotors wird im Umrichter selsbt die aktuelle Drehzahl bestimmt, indem die Lageinformation in regelmässigen Abständen abgetastet wird und sowohl Lagedifferenz und die bekannten Zeitdifferenz zur Berechnung herangezogen werden. Die Drehzahl steht folglich nicht als Momentanwert zur Verfügung, sondern repäsentiert stattdessen den Mittelwert der Drehzahl über das entsprechende Abtastintervall. Um eine hohe Dynamik zu erreichen, ist es notwendig das Abtastintervall möglichst kurz zu wählen. Gleichzeitig spielt auch die Auflösung des verwendeten Gebersystems eine entscheidende Rolle. Somit kommt es, je nach Gebersystem zu unterschiedlichen Quantisierungsfehlern, welcher sich in einer Drehzahlschwankung (Drehzahl-Ripple) äussert. Um zu vermeiden, dass diese Schwankung über den Drehzahlregler auf den unterlagerten Strom- bzw. Drehmomentregelkreis übertragen wird, wird ein Istwertfilter verwendet, dessen Zeitkonstante von folgenden Parametern abhängt:

• Gebertyp
• Verstärkung des Drehzahlreglers
• Massenträgheit des mechanischen Systems

Die Filterzeitkonstante sollte so klein wie möglich gewählt werden, um die Dynamik des Drehzahlregelkreises nicht negativ zu beeinflussen.

5.2.1 Vorsteuerung des Drehmomentes

Bei hohen Ansprüchen an die Dynamik wird ausserdem häufig eine Vorsteuerung implementiert, die der Kompensation des zur Änderung der Winkelgeschwindigkeit notwendigen Drehmomentes dient. Somit ergibt sich der Drehzahlregelkreis mit Vorsteuerung, wie er in Abbildung 5.18 dargestellt ist.

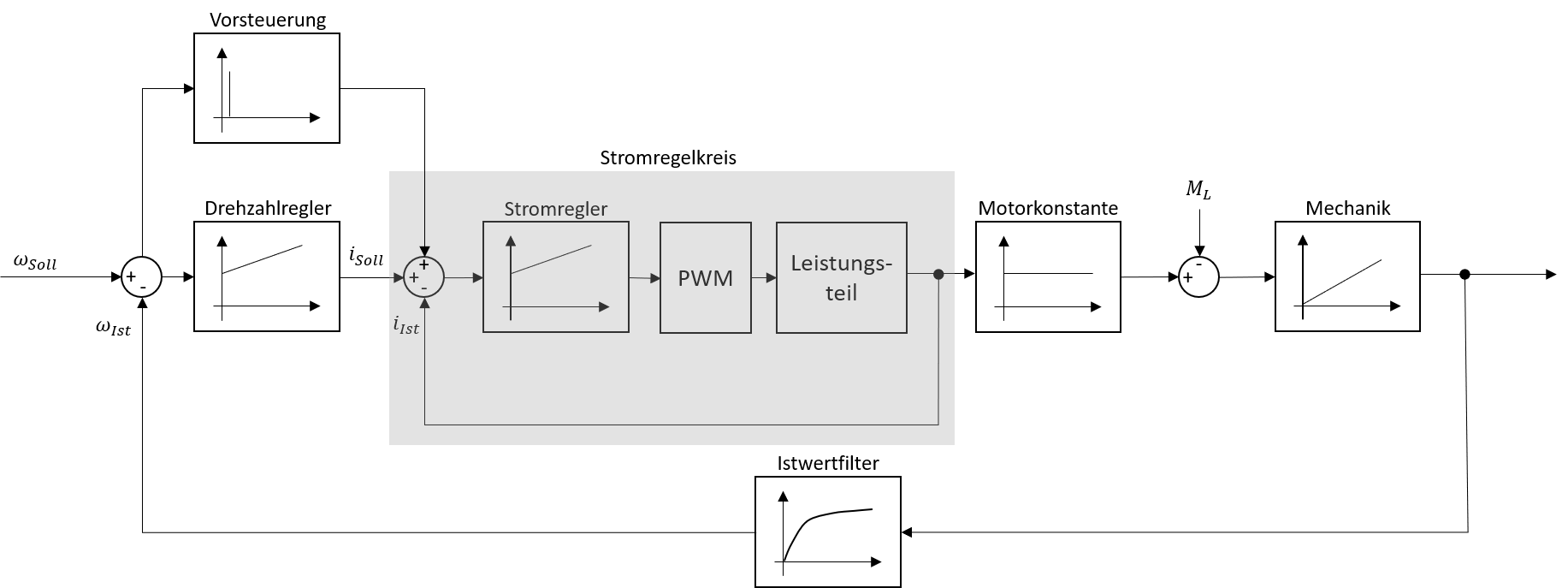
Abbildung 5.18: Prinzipieller Aufbau des Drehzahlregelkreises mit Vorsteuerung

Hierbei gilt es zu berücksichtigen, dass die verwendete Vorsteuerung keinen Einfluss auf das Störgrössenverhalten des Drehzahlregelkreises hat. Die Beschleunigungs-Vorsteuerung ergibt sich lediglich aus dem Anstieg des Drehzahl-Sollwertes durch Verwendung eines D-Gliedes. Somit wird ein anstiegsproportionaler Wert zur Stellgrösse des Drehzahlreglers addiert, wodurch der Regler lediglich auf Störgrössen (Lastmomentänderungen) reagieren muss. Wird der Drehzahl-Sollwert als Analogsignal übertragen und ist somit unter Umständen stark verrauscht, muss der Drehzahlsollwert gefiltert werden. Ein solcher Sollwertfilter hat allerdings gleichzeitig einen Einfluss auf die Vorsteuerung und beeinflusst somit ebenfalls die Dynamik des Drehzahlregelkreises im Führungsverhalten.

5.2.2 Lastankopplung

Das mechanische Verbinden der eigentlichen Last (häufig translatorisch zu bewegende Massen) wird als Ankoppeln bezeichnet. Diese Ankopplung, kann je nach mechanischer Verbindung spielfrei oder spielbehaftet erfolgen. Die Unterscheidung besteht dabei darin, ob die gekoppelte Last jeder Bewegung (Rotation) des Motors unmittelbar (spielfrei) oder nicht zu jedem Zeitpunkt unmittelbar (spielbehaftet) folgt. Spielfreie Lastankopplungen werden häufig auch als Direktantrieb bezeichnet. Beispiele für spielfreie Lastankopplungen sind:

• Klauenkupplungen
• Lamellenkupplungen
• Scheibenkupplungen

Das Beispiel einer spielfreien Klauenkupplung ist in Abbildung 5.19 dargestellt.

Abbildung 5.19: Beispiel einer spielfreien Klauenkupplung (Quelle: www.reiff-tpshop.de)

Beispiele für spielbehaftete Kopplung sind unter anderen:

• Strinradgetriebe
• Riemenantriebe
• Zahnradgetriebe

In beiden Fällen hat die Kopplung der Last mit dem Motor einen Einfluss auf die mechanische Zeitkonstante \(T_{mech}\), da diese massgeblich von der Massenträgheit abhängig ist.

\[ T_{mech} = \frac{J_{Ges}}{c_{Reib}} \]

Da eine Kopplung der Last mit dem Motor immer mit einer Erhöhung des Gesamträgheitsmomentes \(J_{Ges}\) einhergeht kommt es zu einer Erhöhung der mechanischen Zeitkonstante.

\[ J_{Ges} = J_{Mot} + J_{Last} \]

Aufgrund dessen hat eine solche Veränderung der mechanischen Zeitkonstante einen Einfluss auf den oben beschriebenen Drehmoment-Ripple und wird diesen im Vergleich zum leer laufenden Motor erhöhen. Überschreitet dieser die zulässigen Grenzen, wird diesem Effekt damit begegnet die Zeitkonstante des Drehzahl-Istwertfilter zu erhöhen und gleichzeitig die Verstärkung des Drehzahlregler zu reduzieren. Aus diesem Grund wirken sich Gebersystem mit einem geringen Drehmoment-Ripple positiv auf die Dynamik des Drehzahlregelkreises aus. Im Falle einer spielbehafteten Kopplung, welche aus regelungstechnischer Sicht einer Totzeit entspricht, wird der Drehzahlregler in den Momenten in denen kein Kraftschluss zwischen Motorwelle und Last besteht zu hohe Stellwerte erzeugen. Dies führt zu Instabilität des Drehzahl-Regelkreises, was sich wiederum im Drehzahlschwankungen äussert. Üblicherweise wird auch in diesem Fall die die Zeitkonstante des Istwertfilters erhöht und die Verstärkung des Reglers reduziert.

5.3 Lageregelung

Der Lageregelkreis besteht aus dem Lageregler und der Regelstrecke. Die Regelstrecke enthält den drehzahlgeregelten Motor mit der angekoppelten Mechanik der Arbeitsmaschine. Die Ausgangsgrösse des Lagereglers und damit Eingangsgrösse der Regelstrecke ist der Drehzahlsollwert. Der unterlagerte Drehzahlregelkreis sorgt für eine dynamische Verstellung der Drehzahl. Er kann für die grundlegende Betrachtung der Lageregelung vereinfacht und durch ein PT1-Glied mit einer kleinen Verzögerungszeitkonstante nachgebildet werden. Die vom Drehzahlregelkreis bereitgestellte Drehzahl führt zu Lageänderungen an der Motorwelle und an den mechanischen Komponenten der angeschlossenen Arbeitsmaschine. Der Zusammenhang zwischen Drehzahl bzw. Winkelgeschwindigkeit und mechanischer Lage wird durch ein I-Glied beschrieben. Als Integrationszeitkonstante zwischen Drehzahl und gemessenem Lageistwert wird die Getriebeübersetzung wirksam.

Abbildung 5.20: Vereinfachte Darstellung des Lageregelkreises

Der Lageregler eines Servoantriebs wird üblicherweise als P-Regler ausgeführt, der den Drehzahlsollwert ausgibt. Der Drehzahlsollwert muss dabei entsprechend den Gegebenheiten des Antriebes und der angeschlossenen Arbeitsmaschine auf einen Maximalwert begrenzt werden. Der P-Regler dient zur unverzögerten Reaktion auf Sollwertänderungen bzw. das Einwirken von Störgrössen. Treten aufgrund dieser Vorgänge Regelabweichungen auf, bewirkt das P-Glied eine sofortige Änderung der Solldrehzahl und damit eine unverzögerte Reaktion des Lagereglers. Die Dynamik des Lageregelkreises hängt von der Proportionalverstärkung des Lagereglers, dem \(k_{v}\)-Faktor ab. Es wird angestrebt, diesen so gross wie möglich einzustellen.

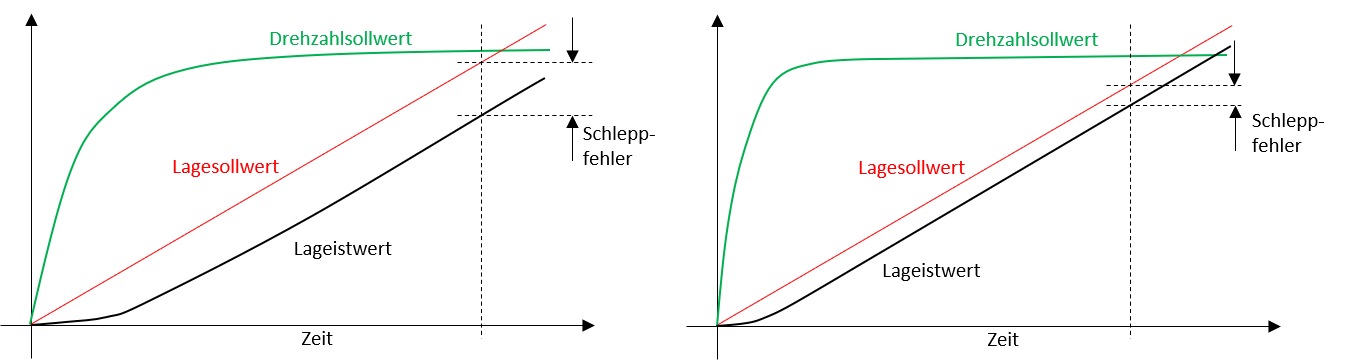
Abbildung 5.21: Einfluss der Proportionalverstärkung auf den Schleppfehler (links:geringe Verstärkung, rechts: grosse Verstärkung)

Der \(k_{v}\)-Faktor beeinflusst unmittelbar die Grösse des Schleppfehler bzw. Schleppabstandes, der beim Anfahren einer neuen Position auftritt. Je grösser der \(k_{v}\)-Faktor ist, umso kleiner ist der sich einstellende Schleppfehler.

5.3.1 Vorsteuerung der Drehzahl

Ähnlich wie bereits am Beispiel des Drehzahlreglers ist es möglich den Lageregler zu entlasten und durch Differentiation des Lagesollwertes den Drehzahlsollwert zu berechnen. Somit steht dieser Sollwert viel schneller zur Verfügung, als wenn er erst durch die Reaktion des Lagereglers gebildet werden müsste. Auch in diesem Fall ist es möglich die Maximalwerte der Drehzahl zu berücksichtigen und den Sollwert so vorzugeben, dass die Maximalwertbegrenzungen nicht aktiv werden müssen.

5.4 Sollwertaufbereitung

Da Lageregler im allgemeinen Bestandteil einer Bewegungssteuerung darstellen, weist der Lagesollwert in Abhängigkeit von der zu lösenden Bewegungsaufgabe unterschiedliche zeitliche Verläufe auf. Bei jeder Positionsänderung ändert sich somit der Lagesollwert, welcher dabei sehr grosse Sprünge aufweisen kann. Eine ungefilterte Weitergabe dieses Wertes an den Lageregler würden die unterlagerten Drehzahl bzw. Stromregler sehr schnell die entsprechenden Begrenzungen erreichen. Gleichzeitig würde die Mechanik der angeschlossenen Arbeitsmaschine mit starken Drehmomentstössen belastet und einen sehr hohen Verschleiss aufweisen. Aufgrund dessen wird der Lagesollwert über einen speziellen Rampengenerator geführt und von diesem stark geglättet. Die Art und Weise der Verrundungfunktion im Rampengenerator ist je nach Optimierungsfunktion (z.B. Ruckbegrenzung) variabel. Handelt es sich hingegen um Synchronisierungsanwendungen (z.B. x-y-Tische) ändert sich der Lagesollwert fortlaufend. Aufgrund dieses kontinuierlichen Verlaufes ist in diesem speziellen Fall auf eine weitere Glättung durch einen Rampengenerator zu verzichten, da dieser die Synchronisiergenauigkeit verschlechtern würde.