Kapitel 7 Mechanische Bewegungsgleichungen
Ein elektrischer Antrieb fungiert schlussendlich als elektromechanischer Energiewandler, dessen Aufgabe darin besteht elektrische Energie möglichst verlustlos in mechanische Energie umzuwandeln. Die mechanische Energie kann dabei durch Drehmomente und Drehzahlen mathematisch beschrieben werden. Unter Berücksichtigung der Vorzeichen dieser zwei physikalischen Grössen, ergeben sich vier verschiedene Betriebszustände, die wiederum in einer Drehmoment-Drehzahl-Ebene dargestellt werden können.
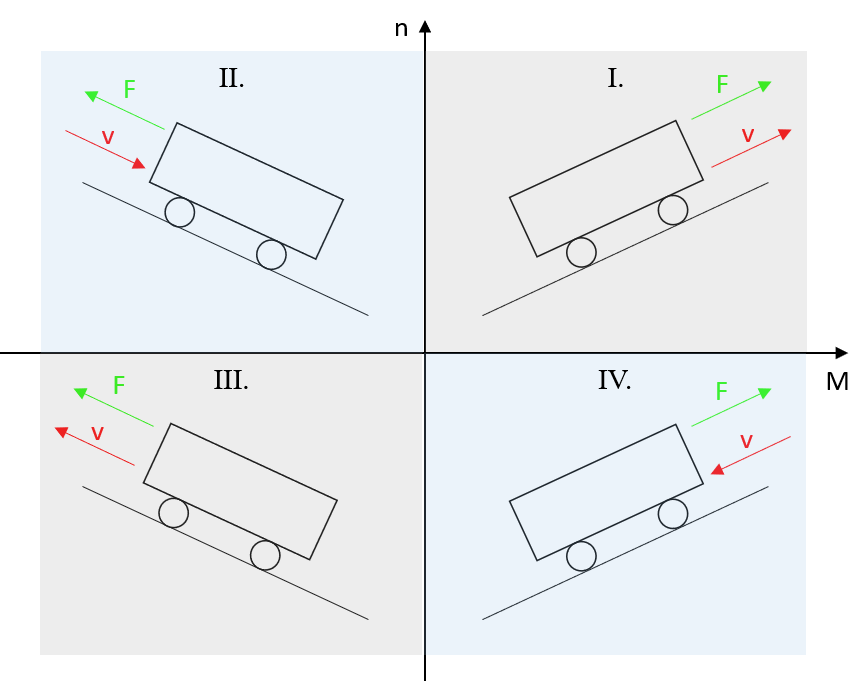
Abbildung 7.1: Die vier Quadranten der Drehmoment-Drehzahl-Ebene
Wird hierbei das Verbraucherzählpfeilsystem angewandt, welches sich dadurch auszeichnet, dass bei positiven Leistungswerten eine Leistungsabgabe an die Last erfolgt, dann können Betriebspunkte, die sich sowohl im ersten als auch im dritten Quadranten befinden als motorische Betriebszustände (Leistungsaufnahme der Last) betrachtet werden. Betriebspunkte im zweiten und vierten Quadranten hingegen werden als generatorische Betriebszustände (Leistungsabgabe der Last) betrachtet. Die mechanische Leistung ergibt sich, je nach Art der Bewegung (Rotation oder Translation) aus dem Produkt von Kraft und Geschwindigkeit bzw. dem Produkt aus Drehmoment und Winkelgeschwindigkeit \(\omega\).
\[ P_{mech} = F\cdot v = M\cdot \omega = M\cdot 2\pi\cdot n \]
7.1 Grundgleichungen
Die Aufgabe eines elektrischen Antriebes besteht darin Kräfte bzw. Drehmomente zu erzeugen, um Massen oder Trägheitsmomente zu beschleunigen.

Abbildung 7.2: Kräfteverhältnisse bei der translatorischen Bewegung
Wie in Abbildung 7.2 dargestellt wirkt eine antreibende Kraft \(F\) auf eine Masse \(m\) und beschleunigt diese. Die Summe aller Kräfte muss laut Newtonschem Grundgesetz null ergeben.
\[ \sum_{i}{F_{i}} = F-m\cdot a-F_{Reib}\cdot v = F-m\cdot \dot{v}-\mu_{Reib}\cdot v \]
Der Faktor \(\mu_{Reib}\) repräsentiert dabei einen Reibkoeffizienten, der eine geschwindigkeistproportionale Reibkraft erzeugt. Somit führt diese Gleichung zu einer Differentialgleichung erster Ordnung zur Beschreibung des Systemverhaltens.
\[ F=m\cdot \dot{v}+\mu_{Reib}\cdot v \]
Ein ähnliches Bild ergibt sich bei der Betrachtung der rotatorischen Bewegung (siehe Abbildung 7.3). Ein Körper mit einem Trägheitsmoment \(J\) erfährt eine Beschleunigung durch das antreibende Drehmoment \(M\).
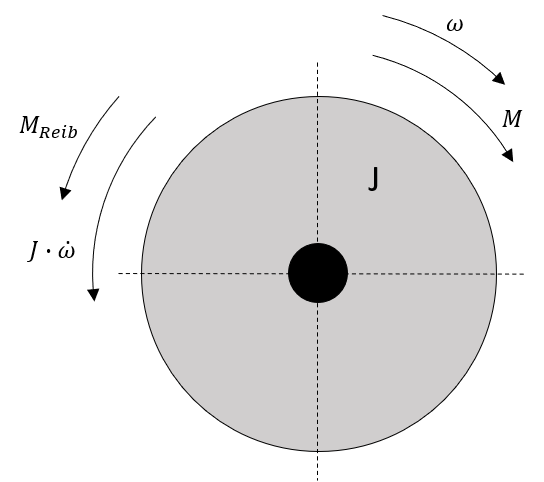
Abbildung 7.3: Momentenverhältnisse bei der rotatorischen Bewegung
In diesem Fall muss die Summe aller Drehmomente null ergeben.
\[ \sum_{i}{M_{i}} = M-J\cdot \alpha-M_{Reib}\cdot v = M-J\cdot \dot{\omega}-\mu_{Reib}\cdot \omega \]
Es ergibt sich auch für diesen Fall eine systembeschreibende DGL erster Ordnung.
\[ M=J\cdot \frac{d\omega}{dt}+\mu_{Reib}\cdot \omega \]
7.1.1 Lösung der Bewegungsgleichung im Zeitbereich
Diese DGL lässt sich, für den Fall eines konstanten Drehmomentes, durch die Methode zur Trennung der Variablen analytisch lösen.
\[ \frac{d\omega}{M-\mu_{Reib}\cdot \omega} = \frac{dt}{J} \]
Dadurch können beide Seiten der Gleichung integriert werden, was eine, bis auf die Konstante \(c\) eindeutige Lösung liefert.
\[ \int{\frac{d\omega}{M-\mu_{Reib}\cdot \omega}} = \int{\frac{dt}{J} + c} \]
\[ -\frac{1}{\mu_{Reib}}\cdot \ln(M-\mu_{Reib}\cdot \omega) = \frac{t}{J}+c \]
\[ \ln(M-\mu_{Reib}\cdot \omega)) = -t\frac{\mu_{Reib}}{J}-\mu_{Reib}\cdot c \]
Der natürliche Logarithmus kann durch beidseitige Anwendung der inversen Funktion (e-Funktion) aufgelöst werden.
\[ M-\mu_{Reib}\cdot \omega = e^{-t\frac{\mu_{Reib}}{J}-\mu_{Reib}\cdot c} \] Da die Eingangsrösse des mechanischen Systems durch das Drehmoment \(M\) und die Ausgangsgrösse durch die Drehzahl \(\omega\) repräsentiert wird, ist es sinnvoll die Gleichung nach \(\omega\) umzustellen.
\[ \omega=\frac{M}{\mu_{Reib}}-e^{-t\frac{\mu_{Reib}}{J}}\cdot \frac{e^{-\mu_{Reib}\cdot c}}{\mu_{Reib}}=\frac{M}{\mu_{Reib}}-x\cdot e^{-t\frac{\mu_{Reib}}{J}} \]
Die Konstante \(x\) kann bestimmt werden, indem der Anfangswert für \(\omega\) null gesetzt wird (\(\omega(t=0)=0\)).
\[ \omega(t=0)=0=\frac{M}{\mu_{Reib}}-x \]
Somit kann die eindeutige Lösung der DGL angeben.
\[ \omega = \frac{M}{\mu_{Reib}} \biggl(1-e^{-t\frac{\mu_{Reib}}{J}}\biggr) = \frac{M}{\mu_{Reib}} \biggl(1-e^{\frac{-t}{T_{mech}}}\biggr) \]
Der Faktor \(\frac{J}{\mu_{Reib}}\) wird dabei als mechanische Zeitkonstante \(T_{mech}\) bezeichnet, da dieser Faktor die Dimension der Zeit aufweist.
\[ \biggl[\frac{J}{\mu_{Reib}} \biggr] = \frac{kg\cdot m^{2}}{Nm\cdot s} = \frac{kg\cdot m^{2}}{\frac{kg\cdot m^{2}}{s}} = s \]
Abbildung 7.4 zeigt die Sprungantwort des mechanischen Systems für verschiedene Trägheitsmomente bei einem Faktor \(\frac{M}{\mu_{Reib}}=1\).
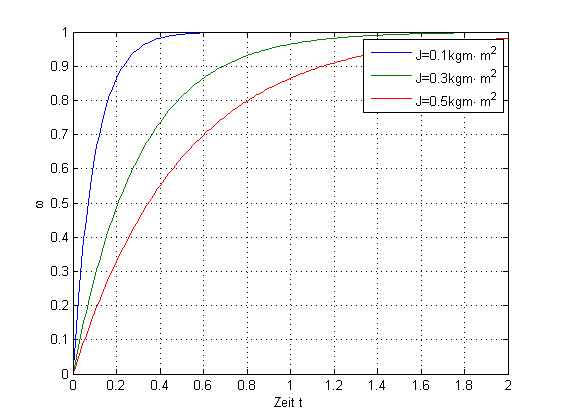
Abbildung 7.4: Qualitativer Drehzahlverlauf bei einem Drehmomentsprung und unterschiedlichem Trägheitsmoment (Anfangswert null)
Wie die Abbildung zeigt, ist das zeitliche Verhalten des Drehzahlverlaufes vom Trägheitsmoment abhängig. Die anfängliche Steigung der Drehzahl kann über die Ableitung der Drehzahlgleichung bestimmt werden.
\[ \frac{d\omega}{dt} = \frac{M}{\mu_{Reib}\cdot T_{mech}} = \frac{M}{J} \]
Der Endwert der Drehzahl hingegen wird nur vom Reibkoeffizienten \(\mu_{Reib}\) beeinflusst. Durch Messung der Sprungantwort lässt sich somit sowohl das Trägheitsmoment als auch der Reibkoeffizient bestimmen.
7.1.2 Systemtheoretische Betrachtung
In der Regelungstechnik wird zur Lösung von DGL und zur Beurteilung verschiedenen Systemverhaltens häufig die Laplace-Transformation herangezogen. Auch bei der mechanischen Grundgleichung ist dieser Ansatz zielführend. Ausgehend von der DGL
\[ M=J\cdot \frac{d\omega}{dt}+\mu_{Reib}\cdot \omega \]
kann eine einfache Überführung in den Laplacebereich erfolgen.
\[ M(s)=J(s\cdot\omega(s)-\omega_{0})+\mu_{Reib}\cdot \omega(s) \]
Wird auch hier der Anfangswert \(\omega_{0}=\omega(0)\) null gesetzt, kann die Gleichung weiter umgeformt werden und liefert die Darstellung der DGL im Laplacebereich.
\[ \omega(s) = \frac{M(s)}{\frac{J}{\mu_{Reib}}s+1} \]
Der Quotient
\[ G(s) = \frac{Ausgangsgrösse}{Eingangsgrösse} \]
liefert die Übertragungsfunktion \(G(s)\), die das statische und dynamische Verhalten des Systems im Laplace-Bereich beschreibt.
\[ G(s) = \frac{\omega(s)}{M(s)} = \frac{1}{\frac{J}{\mu_{Reib}}s+1} \]
Mit Hilfe der Übertragungsfunktion kann die Ausgangsgrösse \(X_{aus}(s)\), bei Kenntnis der Eingangsgrösse \(X_{ein}(s)\) berechnet werden (\(X_{aus}(s)=G(s)\cdot X_{ein}(s)\)).
Die Übertragungsfunktion des betrachteten mechanischen Systems beschreibt somit ein Verzögerungsglied erster Ordnung, was das Verhalten, welches in Abbildung 7.4 dargestellt ist, bestätigt.
7.2 Mechanische Übertragungselemente
In der Antriebstechnik spielen auch mechanische Übertragungselemente eine massgeblich Rolle, da sie das Verhalten des Antriebsstranges beeinflussen. Insbesondere bei Positionierantrieben ist eine Kenntnis der mechanischen Gegenheiten im Antriebsstrang von Bedeutung, da die Widerstandskräfte und -momente hauptsächlich durch die verwendete Mechanik und die damit einhergehende Reibung bestimmt werden. Sie bestimmen somit in weiten Teilen die Dimensionierung des Antriebssystems selbst und beeinflussen die Regelung des Systems.
7.2.1 Gewindespindeln
Bei Positionierantrieben müssen sehr häufig Dreh- in Längsbewegungen umgewandelt werden, wobei häufig Gewindespindeln zum Einsatz kommen. Dabei wird häufig zwischen Trapezgewindetriebe und Kugelgewindetrieben unterschieden. Bei Trapezgewindespindeln wird das Prinzip der Gleitreibung verwendet, was dazu führt, dass diese Spindelart einen geringen Wirkungsgrad aufweist. es handelt sich dabei allerdings um eine kostengünstige Lösung.

Abbildung 7.5: Trapezgewindespindel (Quelle: www.bornemann-gewindetechnik.de)
Kugelgewindespindeln werden auch als Kugelumlaufspindeln bezeichnet und zeichnen sich dadurch aus, dass, ähnlich wie bei einem Kugellager, Rollreibung zwischen Spindel und Mutter auftritt. Dies wird dadurch erreicht, dass Wälzkörper (Kugeln) zwischen der Spindel und der Spindelmutter aufgefädelt werden. Bei hochgenauen Kugelumlaufspindeln laufen diese Kugeln in einem geschlossenen System innerhalb der Spindelmutter um.

Abbildung 7.6: Kugelumlaufspindel (Quelle: www.bs-wiki.de)
Kugelumlaufspindeln erreichen damit einen relativ hohen Wirkungsgrad. Da sich die Last während einer Umdrehung der Spindel um die Steigung \(k\) vorwärts bewegt, kann somit die lineare Geschwindigkeit \(v\) aus der Winkelgeschwindigkeit \(\omega\) der Gewindestange berechnet werden:
\[\begin{equation} v= n\cdot \frac{k}{60} = \frac{k\cdot \omega}{2\pi} \tag{7.1} \end{equation}\]
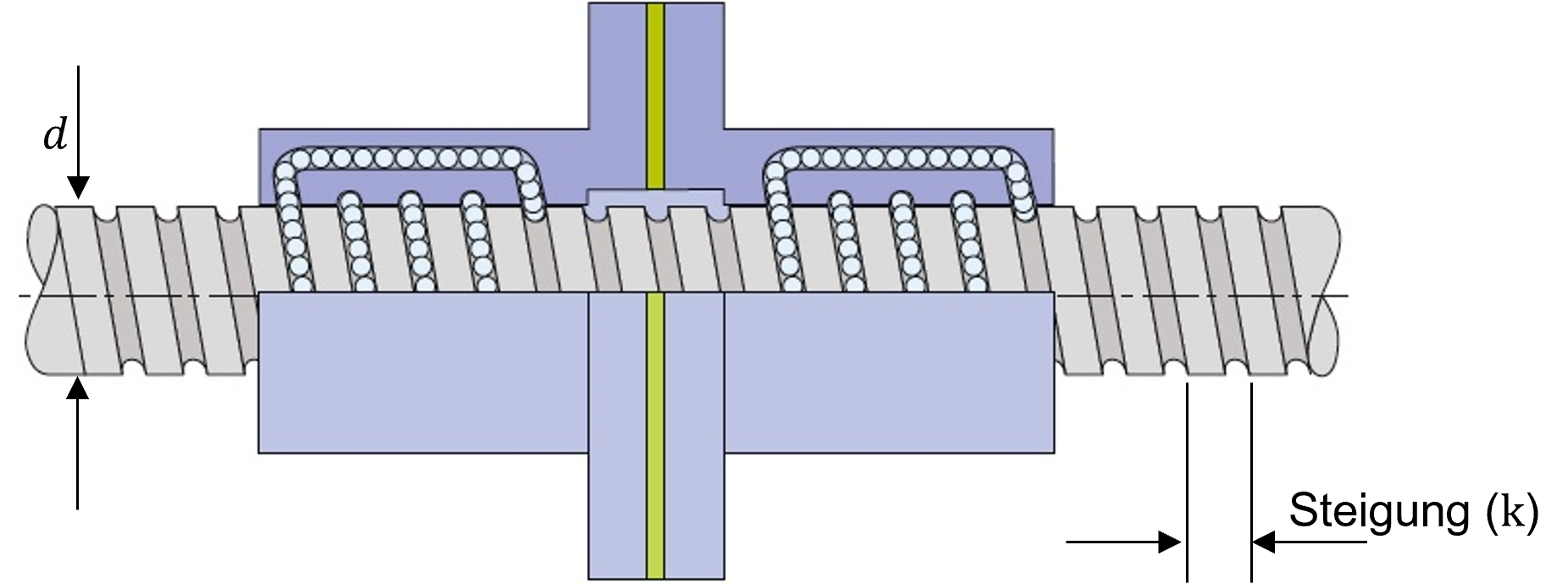
Abbildung 7.7: Wichtige Parameter am Beispiel der Kugelumlaufspindel (Quelle: www.ludwigmeister.de; modifiziert)
Die Umrechnung zwischen der auf die Last wirkenden Kraft und dem entsprechenden Drehmoment kann einerseits über die Leistungsbilanz erfolgen:
\[\begin{equation} P_{Rot} = M\cdot \omega = P_{Lin} = F\cdot v = F\cdot \frac{k\cdot \omega}{2\pi} \Rightarrow F=M\cdot \frac{2\pi}{k} \Longleftrightarrow M=F\frac{k}{2\pi} \tag{7.2} \end{equation}\]
Andererseits ergibt sich dieses Ergebnis auch, wenn man die geometrischen Verhältnisse der durch die Gewindesteigung entstehenden Kraftvektoren berücksichtigt. Um die notwendigen Antriebsmomente bestimmen zu können, muss die Kraft bestimmt werden, die notwendig ist, um einen Körper (Masse der zu bewegenden Last) eine schiefe Ebene nach oben zu bewegen. Diese schiefe Ebene entspricht dabei der Steigung, die durch die Steigung des Gewindes hervorgerufen wird (vgl. Abb. 7.8).
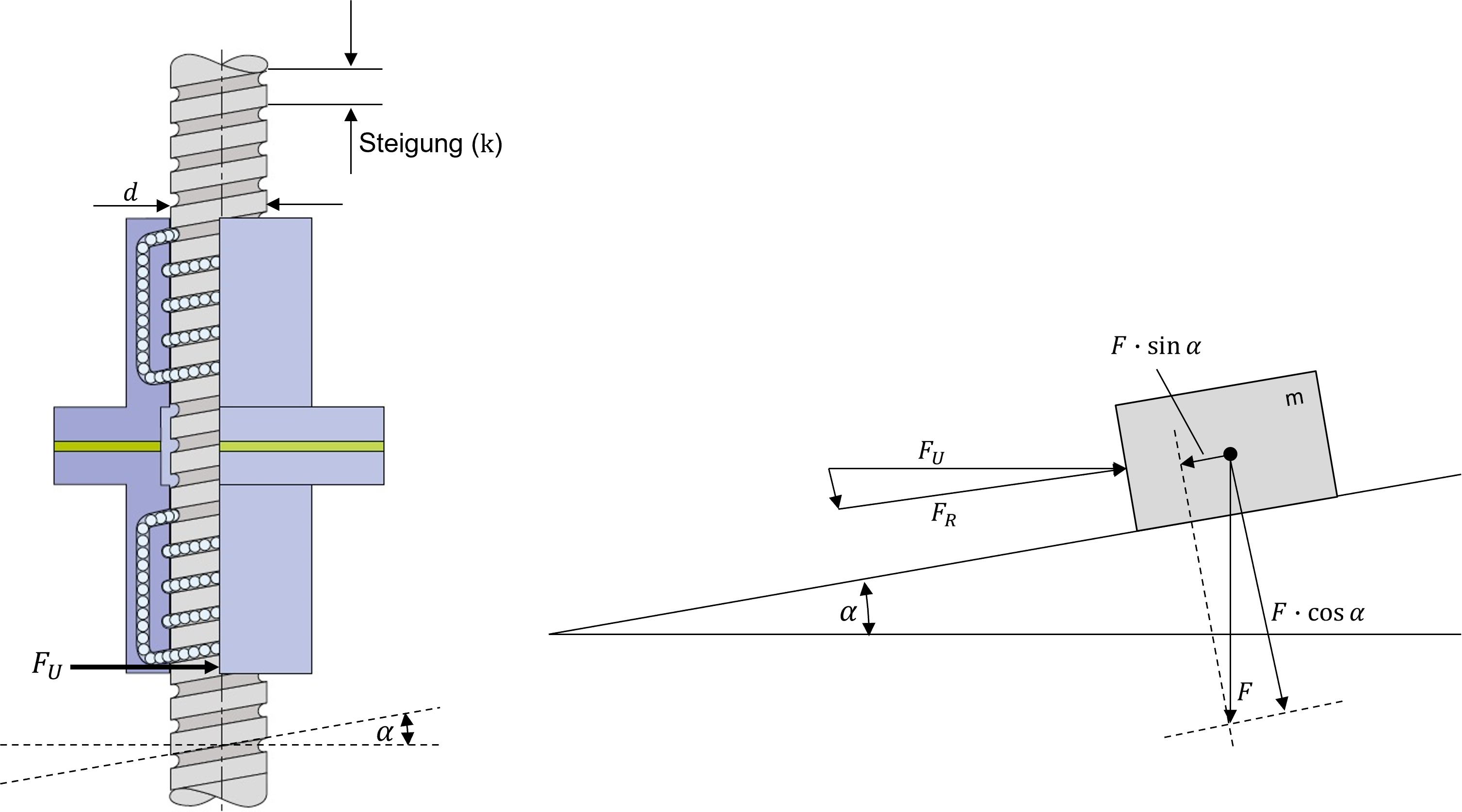
Abbildung 7.8: Kraftwirkungen an einer Gewindespindel ohne Reibung (Quelle: www.ludwigmeister.de; modifiziert)
Die Steigung \(k\) beschreibt dabei um wieviel das Gewinde über eine Umdrehung hinweg steigt und \(d\) stellt den Durchmesser der Gewindespindel dar. Für die resultierende Kraft (\(F_{R}\)), um einen Körper auf der schiefen Ebene nach oben zu bewegen, wenn dieser mit der Kraft F senkrecht nach unten wirkt, gilt (Garbrecht 2019):
\[\begin{equation} F_{R}=F\cdot sin (\alpha) \tag{7.3} \end{equation}\]
Der Steigungswinkel der schiefen Ebene kann dabei mit Hilfe der Winkelverhältnisse am rechtwinkligen Dreieck bestimmt werden (vgl. Abb. 7.9).
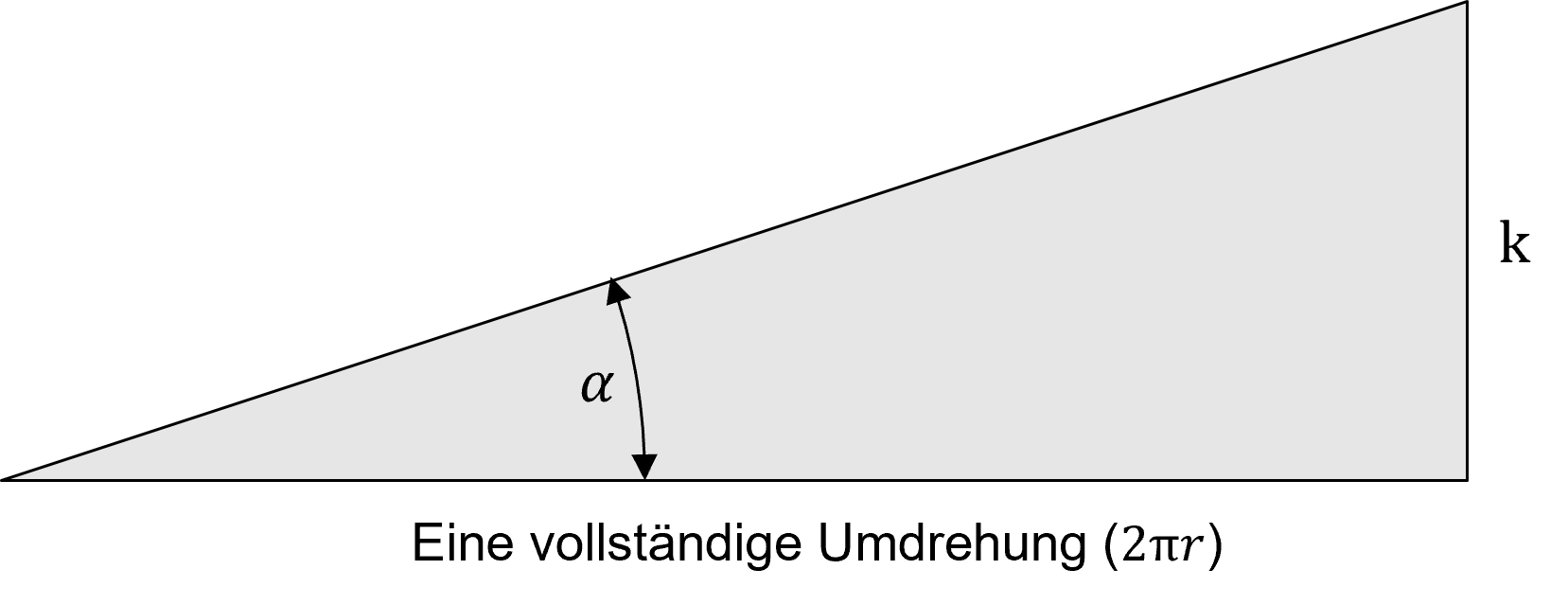
Abbildung 7.9: Winkelverhältnisse an einer schiefen Ebene
Da mit der Steigung und der auf der schiefen Ebene zurückgelegte Winkelweg bekannt sind, kommt der Tangens bei der Berechnung zur Anwendung:
\[\begin{equation} \alpha=\arctan \left(\frac{k}{2\pi\cdot r}\right) \tag{7.4} \end{equation}\]
Bei dem Paramter \(r\) handelt es sich dabei um den Radius der Gewindestange. Die Umfangskraft \(F_{U}\) (vgl. Abb. 7.8), ist die Kraft die vom Antrieb aufgebracht werden muss, da diese orthogonal zur Mittellinie der Spindel angreift. Die eigentlich zum Bewegen einer Masse \(m\) auf der schiefen Ebene resultierende Kraft \(F_{R}\) die parallel zur schiefen Ebene verläuft, ist somit kleiner als die orthogonal zur Mittellinie der Spindel angreifende Umfangskraft \(F_{U}\).
\[\begin{equation} F_{U}=\frac{F_{R}}{cos(\alpha)}=F\cdot \frac{\sin \alpha}{\cos \alpha} = F\cdot \tan \left(\alpha\right) \tag{7.5} \end{equation}\]
Setzt man die Formel zur Berechnung des Winkels \(\alpha\) (Formel (7.4)) in die Gleichung zur Berechnung der Umfangskraft ein, kann unter Berücksichtigung des Radius \(r\) der Gewindestange das entsprechende Drehmoment bestimmt werden:
\[\begin{equation} M=F\cdot r\cdot \tan \alpha = F\cdot r\cdot \tan \left(\arctan \left(\frac{k}{2\pi\cdot r}\right)\right) = F\cdot r\cdot\frac{k}{2\pi\cdot r} \tag{7.6} \end{equation}\]
Bei beiden obigen Gleichungen ((7.2) und (7.6)) zur Bestimmung des Drehmomentes gilt es zu beachten, dass dabei die Reibung nicht berücksichtigt wurde. Bei hochgenauen und hochdynamischen Antriebssystemen, wie sie häufig bei Positionierantrieben gefordert werden, wird die Reibung sehr häufig in der Antriebsdimensionierung und der Einstellung der Regelparameter berücksichtigt.
7.2.1.1 Berücksichtigung der Reibung
Gilt es die Reibung bei der Dimensionierung zu berücksichtigen, so wird die bereits erwähnte schiefe Ebene, die sich durch die Gewindesteigung ergibt, mit einem zusätzlichen Reibwert versehen (siehe Parameter \(\mu\) in Abbildung 7.10).
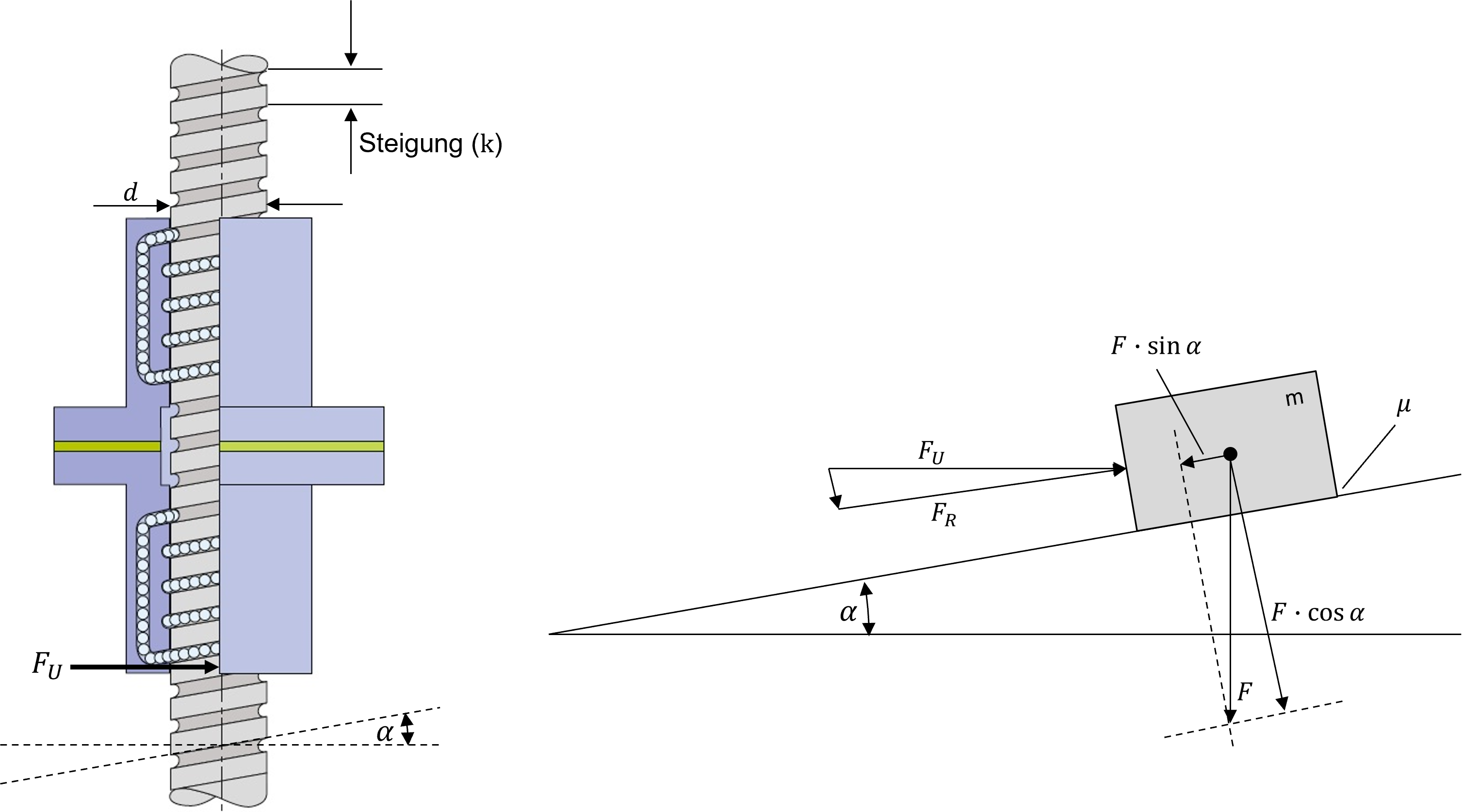
Abbildung 7.10: Kraftwirkungen an einer Gewindespindel (Quelle: www.ludwigmeister.de; modifiziert)
Die resultierende Kraft (\(F_{R}\)), um den Körper auf der schiefen Ebene nach oben zu bewegen, wird somit um eine zusätzliche, winkelabhängige Komponente erweitert (Garbrecht 2019):
\[ F_{R}=F\cdot sin (\alpha) + F \cdot \mu \cdot cos (\alpha) \]
Der Reibwert \(\mu\) quantifiziert die Reibung zwischen Gewindebolzen und Spindelmutter. Auf diese Art und Weise wird es möglich zwischen Spindelantrieben mit Trapezgewinde und Kugelumlaufspindel zu unterscheiden. Wird auch hier der allgemeine Ansatz zur Berechnung der Umfangskraft verwendet (Teil 1 Formel (7.5)), ergibt sich für die Umfangskraft \(F_{U}\) unter Berücksichtigung der Spindelreibung:
\[ F_{U} = \frac{F_{R}}{\cos {\alpha}} = \frac{F\cdot sin (\alpha) + F \cdot \mu \cdot cos (\alpha)}{\cos \left(\alpha\right)} =F\cdot tan(\alpha) + \mu \cdot F \]
In (Garbrecht 2019) wird dabei für den Reibwert \(\mu\) ein fiktiver Reibungswinkel \(\rho\) eingeführt, der die zusätzliche Reibkraft zum Ausdruck bringt:
\[ \rho = arctan(\mu) \]
Diese Modifikation erlaubt es die Gleichung für die Umfangskraft weiter zu vereinfachen:
\[ F_{U} = F\cdot tan(\alpha \pm \rho) \]
Somit wird der eigentliche Steigungswinkel \(\alpha\) angepasst und berücksichtigt neben der Steigung auch die Reibung im Gewinde selbst. Da die Reibung beim Senken einer Last der Abwärtsbewegung hemmend entgegenwirkt, wird dies durch das negative Vorzeichen des Reibungswinkels berücksichtigt. Basierend auf der benötigten, reibungsbehafteten Umfangskraft lässt sich somit das notwendige Drehmoment bestimmen:
\[ M=F\cdot r\cdot \tan\left(\alpha \pm \rho\right) \]