Kapitel 9 Servogetriebe
Die grundsätzliche Aufgabe eines Getriebes besteht in der Wandlung von Drehmoment und Drehzahl, was gleichzeitig der Unterschied zu Kupplungen darstellt, die im Allgemeinen ein konstantes Moment bei konstanter Drehzahl übertragen. Aufrgund dessen spielt eine Servogetriebe eine fundamentale Rolle als Einheit eines Servo-Getriebemotors. Hin und wieder wird ein Getriebe auch als Rotations-Rotations-Umformer bezeichnet.
9.1 Grundsätzliche Anforderungen
Aufgrund der steigenden Anforderungen bzgl. kurzer Taktzeiten an moderne Servoanwendungen ergeben sich sehr hohe Beschleunigungswerte, die mit folgenden Anforderungen an Servogetriebe einhergehen:
- hoher Wirkungssgrad
- niedriges Massenträgheitsmoment
- hohe Verdrehsteifigkeit
- geringes Verdrehspiel
- Übertragung sehr hoher Drehmomente
- Schwingungsarmut
- lange Lebensdauer
- geringer Wartungsaufwand
- Kompakte Bauweise
- geringes Gewicht
Insbesondere bei hohchdynamischen Antrieben spielt das Massenträgheitsmoment sowie der Wirkungsgrad des Getriebes eine massgebliche Rolle.
9.2 Getriebeübersicht
Eine Möglichkeit zur Einteilung verschiedener Getriebearten bietet die Richtung des Kraftschlusses. In diesem Fall kann folgende Einteilung erfolgen:
- Winkelgetriebe
- Koaxialgetriebe
- Parallelwellengetriebe
Im Falle von Winkelgetrieben stehen die an- und die abtreibende Welle im rechten Winkel zueinander, wodurch eine rechtwinklige Umlenkung des Kraftschlusses erfolgt. Bei Koaxial- und Parallelwellengetrieben hingegen liegen die an- und die abtreibende Welle in einer Ebene, was einen geradlinien Kraftschluss bedingt.
Desweiteren ist es möglich die Getriebe nach Ihren Komponenten bzw. ihrem Aufbau zu unterteilen. Eine solche Grobeinteilung wird in Tabelle 9.1 dargestellt.
| Raedergetriebe | Riemengetriebe | Kettengetriebe |
|---|---|---|
| Stirnrad | Zahnriemen | Rollenkette |
| Planeten | Flachriemen | Zahnkette |
| Kegelrad | Keilriemen |
9.2.1 Servo-Planetengetriebe
Planetengetriebe sind in der Lage sehr hohe Drehmomente bei gleichzeitig vergleichsweise kleinem Bauraum übertragen. Sie werden meistens mit drei umlaufenden Planetenrädern ausgestattet. Die Lastverteilung auf die (meist) drei Planetenräder führt zu einer höheren Leistungsdichte im Vergleich zu Strinradgetrieben, was die geringere Baugrösse begründet.
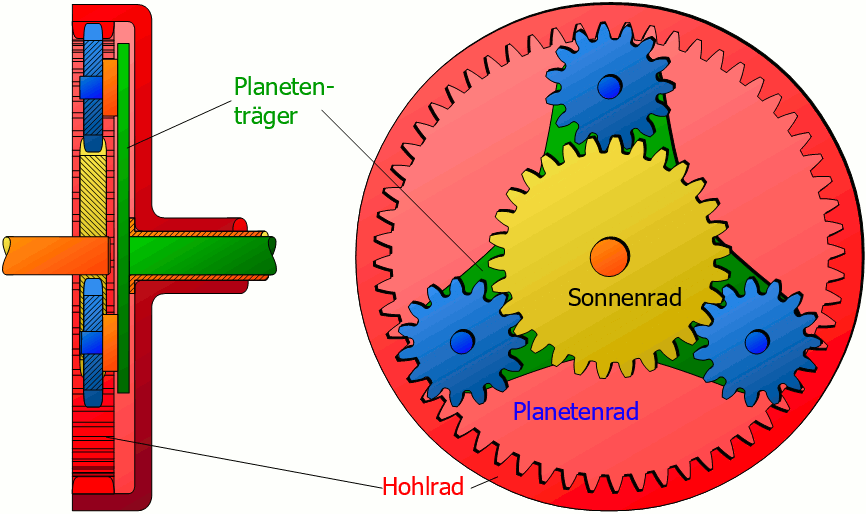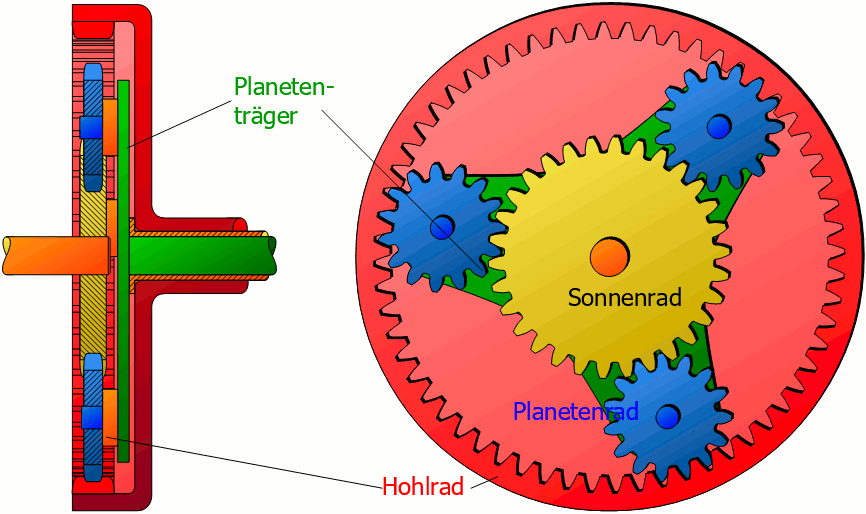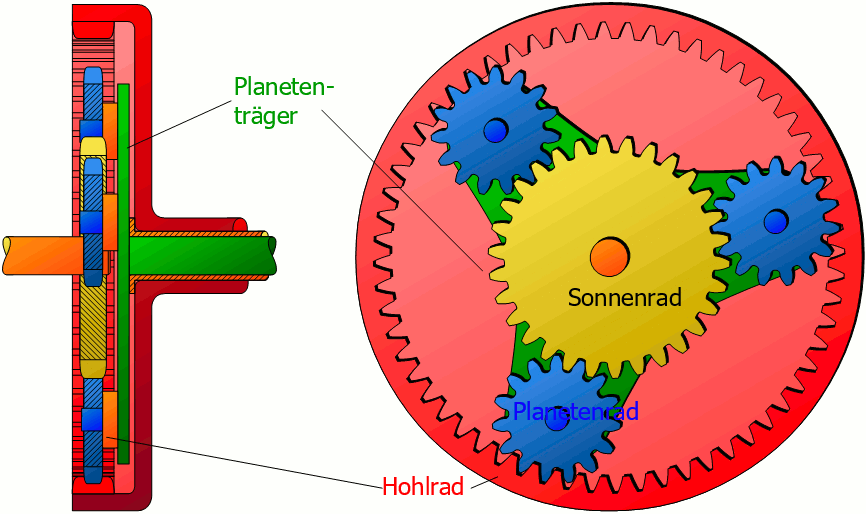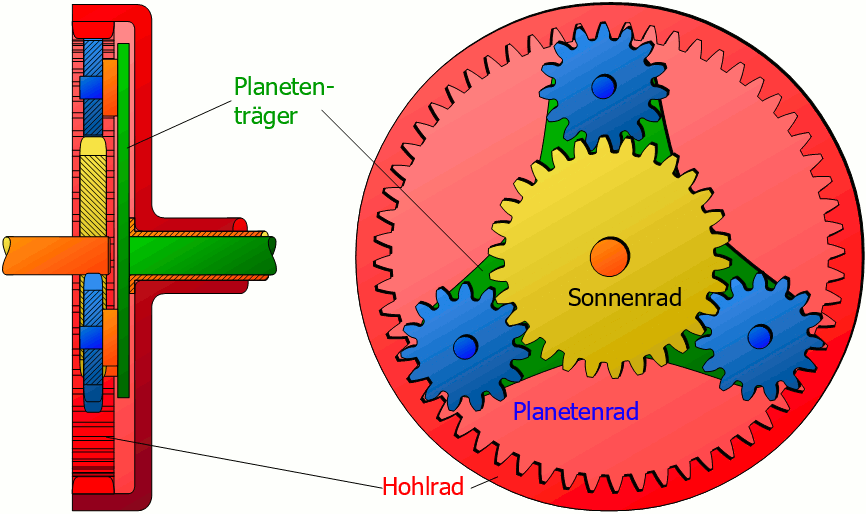
Abbildung 9.1: Funktionsweise des Planetengetriebes (Quelle: www.ahoefler.de)
Geringe Fertigungstoleranzen gewährleisten bei Planetengetrieben geringe Verdrehwinkel von 3-6 Winkelminuten. Bei gleichzeitig grosszügig bemessenen Wellendurchmessern garantieren Planetengetriebe gleichzeitig eine hohe Verdrehsteifigkeit was eine hohe Positioniergenauigkeit mit sich bringt. Ausserdem weisen Planetengetriebe einen hohen Wirkungsgrad, geringe Geräuschemissionen und gleichzeitige Wartungsarmut mit sich. Aufgrund des recht komplizierten Aufbaus sind Planetengetriebe relativ teuer.
9.2.2 Servo-Kegelradgetriebe
Kegelradgetriebe (Bevel gears, siehe Abb. 9.2) bestehen aus einem kleineren Kegelrad , welches wiederum in ein Tellerrad mit einem grösseren Durchmesser eingreift. Je nach Form der Verzahnung (gerade, spiralförmig oder hypoid) können Kegelradgetriebe unterschieden werden. Die An- und Abtriebswelle treiben meist im 90\(^\circ\) Winkel aus. Im Falle von Servogetrieben werden Kegelradgetriebe meist mehrstufig ausgeführt.
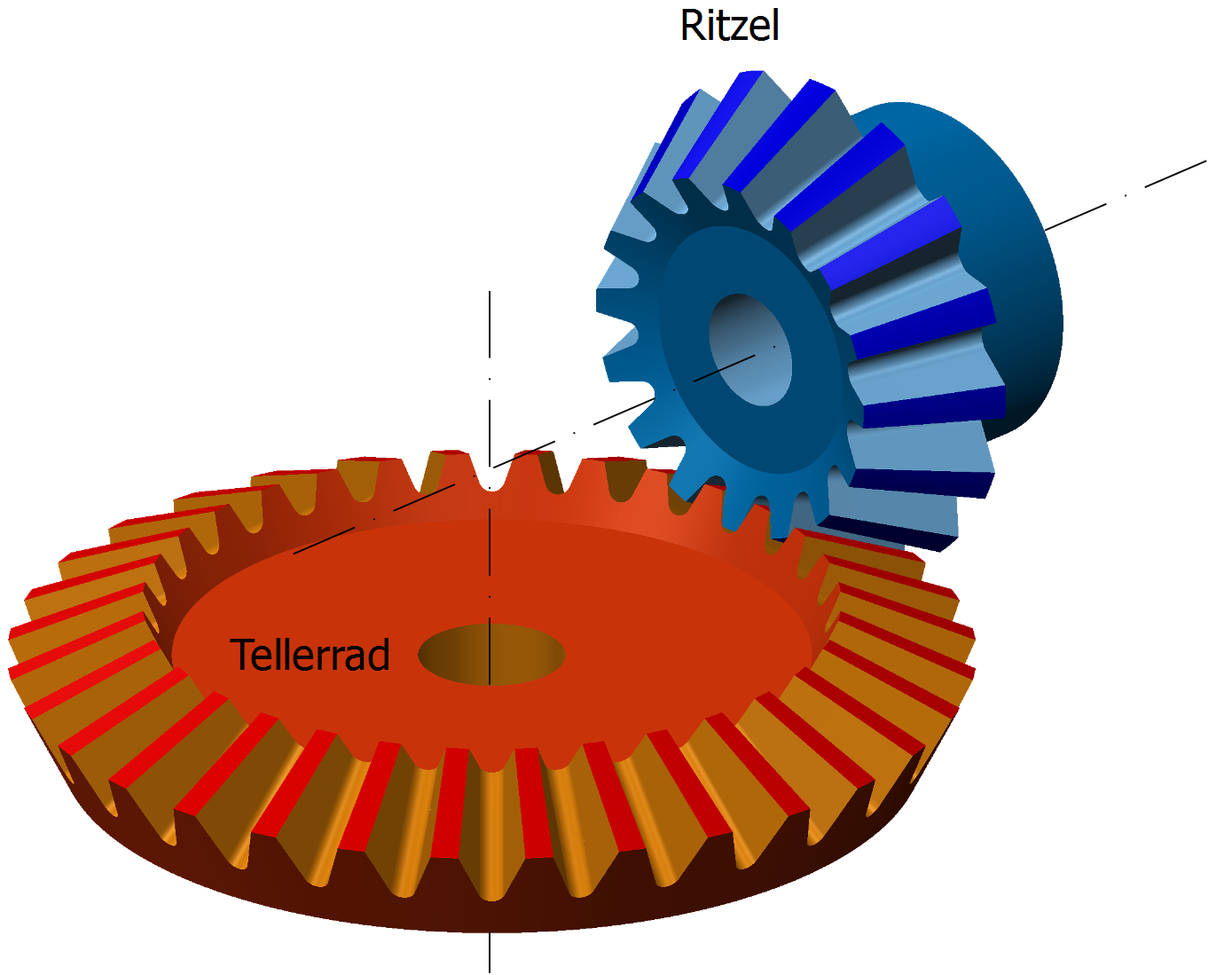
Abbildung 9.2: Aufbau des Kegelradgetriebes (Quelle: www.ahoefler.de)
Kegelradgetriebe werden auch als Winkelgetriebe bezeichnet.
9.2.3 Stirnradgetriebe
Stirnradgetriebe (Helical gear, Aufbau siehe Abb. 9.3) ist eine der gebräuchlisten Getriebearten, bei der pro Stufe Übersetzungen von \(i=4-8\) bei sehr guten Wirkungsgraden erreicht werden.
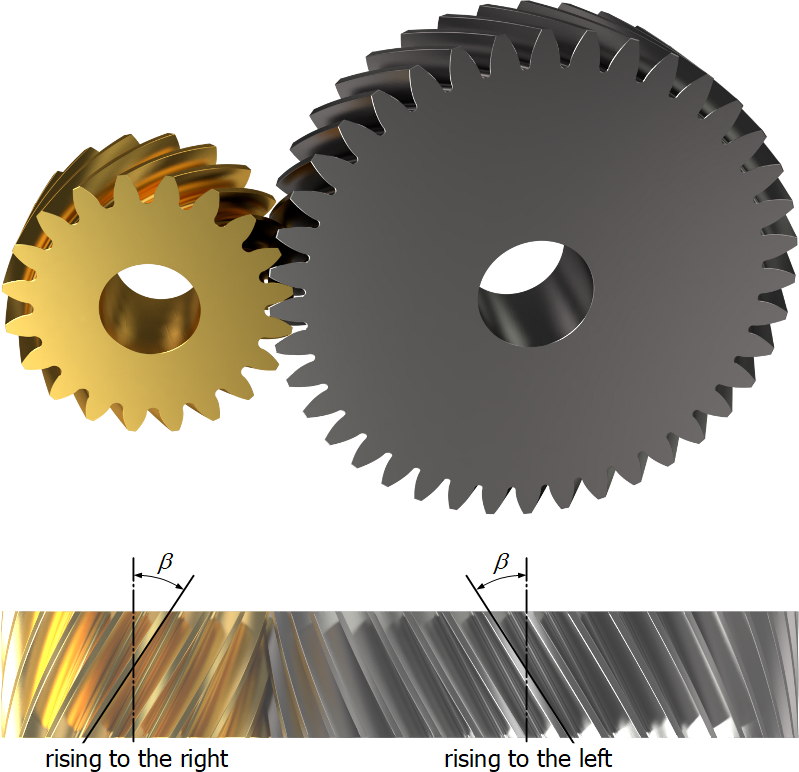
Abbildung 9.3: Aufbau eines schräg aussenverzahnten Stirnradgetriebes (Quelle: www.ahoefler.de)
Der Wirkungsgrad variiert zwischen ca. 80% (sehr kleine Getriebe) und ca.98% (grosse Getriebe). Stirnradgetriebe sind in unterschiedlichen Vertahnungsarten (gerade bzw. schräg verzahnt) erhältlich. Sie weisen ein gutes Preis-Leistungsverhältnis, bei gleichzeitig grösserem Bauraum im Vergleich zu Planetengetrieben auf. Stirnradgetriebe können zwischen innen- und aussenverzahnt unterschieden werden. Bei einer Aussenverzahnung befinden sind die Zähne am Umfang des Rades nach aussen gerichtet. Bei Inneverzahnung hingegen sind die Zähne nach innen gerichtet. Ein Zahnrad mit Innenverzahnung wird auch als Hohlrad bezeichnet. Bei der Verwendung zweier aussenverzahnter Zahnräder dreht sich die Drehrichtung zwischen An- und Abtriebsseite um. Werden hingegen aussneverzahnte Zahnräder mit Hohlrädern kombiniert wird die Drehrichtung beibehalten und es ist möglich den Bauraum etwas zu verringern. Es werden gerade und schräg verzahnte Zahnräder verwendet. Bei schräg verzahnten Zahnrädern weisen die Zahnräder eine schräge Anordung der Zähne in Achsrichtung auf. Die Schrägverzahnung führt dazu, dass die Kraftübertragung nicht plötzlich über die komplette Zahnbreite hinweg, sondern sich punktförmig verläuft. Diese Eigenschaft betrifft auch das Ende des Zahneingriffvorgang und die Kraftübertragung bricht nicht abrupt ab. Aufrgund dieses Verhaltens fällt die Geräuschemission in diesem Fall weniger stark aus. Da sich die Kraftübertragung bei Beginn und am Ende des Zahneingriffsvorganges auf einen sehr kleinen Bereich beschränkt, muss konstruktiv Sorge dafür getragen werden, dass sich mehrere Zähne gleichzeitig im Eingriff befinden, wodurch eine Verteilung der Kraft auf mehrere Zähne erfolgt. Im Gegensatz zu gerade varzahnten Zahnrädern treten bei schräg verzahnten Zahnrädern nicht nur radial wirkende Kraftkomponenten, sondern auch Axilakräfte auf, die zu einer stärkeren Belastung der Lager der Getriebewellen führen und deren Lebensdauer negativ beeinflussen. In einigen Fällen werden auch Strinradgetriebe mit Pfeilverzahnung verwendet, die die Vorteile von schräg verzahnten Zahnrädern (geringere Geräuschbelastung und höhere Drehmomente) bei gleichzeitiger Elimination der Axialkräfte aufweisen. Dies ist allerdings aufgrund der höheren Komplexität nur durch einen höheren Preis zu erreichen.
9.2.4 Gegenüberstellung
Die folgende Tabelle stellt typische Kennwerte verschiedener Getriebearten gegenüber.
| Kenngrösse | Stirnradgetriebe | Planetengetriebe | Harmonic Drive | Schneckengetriebe |
|---|---|---|---|---|
| Gesamtübersetzung | 4-100000 | 4-6000 | 50-320 | 4-100 |
| Stufenübersetzung | 4-8 | 4 | 50-320 | 4-100 |
| Stufen-Wirkungsgrad [%] (grosse Getriebe) | 92-95 | 90-94 | 80-90 | 18-90 (bei Selbsthemmung unter 50) |
| Stufen-Wirkungsgrad [%] (kleine Getriebe) | 90 | 80-90 | 80-90 | 18-90 (bei Selbsthemmung unter 50) |
| Radialspiel [um] | 40-50 | 40-80 | lagerabhängig | lagerabhängig |
| Axialspiel [um] | 20-200 | 20-80 | lagerabhängig | lagerabhängig |
| Verdrehspiel [’] (je Stufe, unbelastet) | kleiner 2 | kleiner 3 | kleiner 2 | einstellbar |
9.2.5 Getriebebemessung
Die Auslegung des Getriebes richtet sich in starkem Masse nach der entsprechenden Applikation. Reine Positionier- bzw. Beschleunigungsantriebe beispielsweise werden lediglich dazu verwendet die beteiligten Massenträgheiten zu beschleunigen. Ein zusätzliches Last-Drehmoment tritt in diesem Fall nicht auf. Aufgrund dessen werden entsprechende Getriebe so bemessen, dass sich kürzeste Hochlaufzeiten ergeben, indem die Winkelbeschleunigung ihr Maximum erreicht.
9.2.5.1 Getriebebemessung für Positionierantriebe
Manche Antriebe laufen gegen ein sehr geringes, vernachlässigbares Lastmoment an. Dies sind die Beschleunigungsantriebe, wie z.B. beim Schleifstein oder einer Zentrifugen. Dort spricht man dann auch von einem Leeranlauf (\(M_{2}=0\)). Wird vereinfachend angenommen, dass keine weiteren Last-Drehmomente berücksichtigt werden, wird das Antriebsmoment dazu verwendet die beteiligten Massenträgheiten (\(J_{1}\) und \(J_{2}\)) zu beschleunigen. Um die maximale Winkelbeschleunigung bestimmen zu können, muss die Winkelbeschleunigung auf der Abtriebsseite (\(\dot{\omega}_{2}\)) bestimmt werden.
\[ M_{2} = i_{G}\cdot M_{1} \]
Dieses Drehmoment wird dazu verwendet die Gesamtträgheit zu beschleunigen.
\[ J_{Ges}\dot{\omega}_{2} = i_{G}\cdot M_{1} \]
Wird die Gesamtträgheit auf die Lastseite bezogen, gilt
\[ J_{Ges} = J_{2}+J^{'}_{1} \]
Wobei \(J^{'}_{1}\) das auf die Lastseite umgerechnete motorseitige Trägheitsmoment darstellt.
\[ J^{'}_{1} = i_{G}^{2}\cdot J_{1} \]
Damit ergibt sich folgende Gleichung:
\[ \bigl(i_{G}^{2}\cdot J_{1}+J_{2}\bigr) \dot{\omega}_{2}=i_{G}\cdot M_{1} \]
Die lastseitige Winkelbeschleunigung ergibt sich somit folgendermassen:
\[ \alpha_{2}=\dot{\omega}_{2}=\frac{i_{G}}{i_{G}^{2}\cdot J_{1}+J_{2}}M_{1} \]
Einen beispielhaften Verlauf der Winkelbeschleunigung in Abhängigkeit von der Getriebeübersetzung liefert Abbildung 9.4.
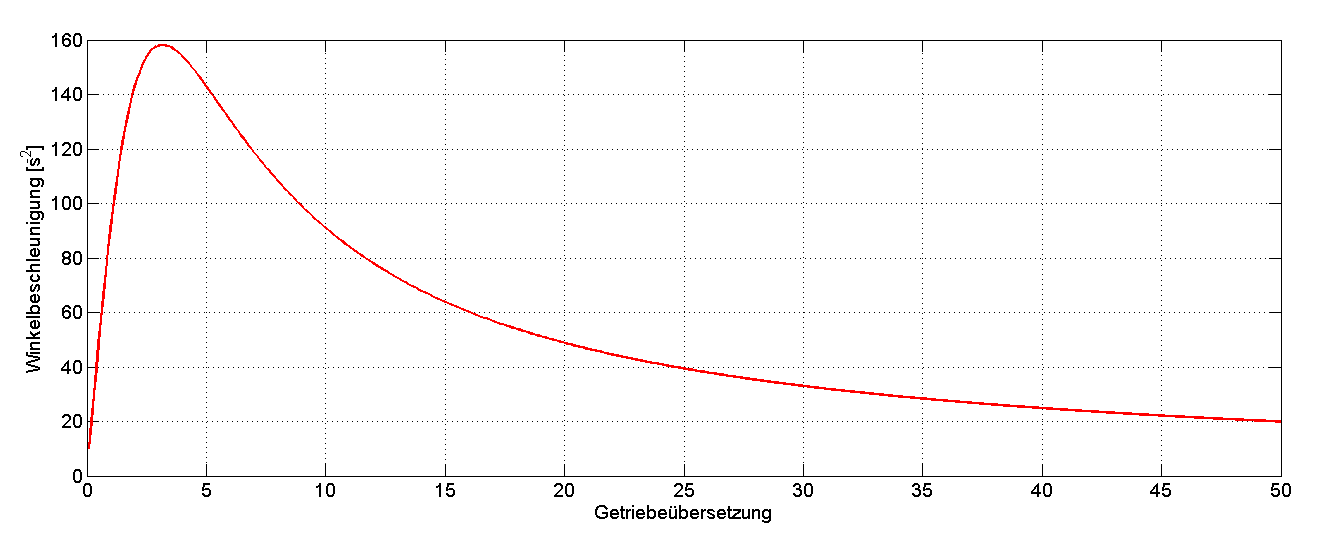
Abbildung 9.4: Typischer Verlauf der Winkelbeschleunigung
Die maximale Winkelbeschleunigung ergibt sich somit aus der Extremwertaufgabe
\[ 0=\frac{d\alpha_{2}}{i_{G}}=\frac{i_{G}^{2}J_{1}+J_{2}-2i_{G}^{2}J_{1}}{\bigl(i_{G}^{2}J_{1}+J_{2}\bigr)^{2}} \]
die folgendes Ergebnis liefert:
\[ i_{G}^{2}J_{1}=J_{2} \]
Geringste Hochlaufzeiten bei Beschleunigungsantrieben sind somit zu erwarten, wenn das Übersetzungsverhältnis \(i_{G}\) entsprechend der folgenden Formel gewählt wird:
\[ i_{G,opt}=\sqrt{\frac{J_{2}}{J_{1}}} \]
Die auf eine Seite umgerechneten Drehträgheiten sind in diesem speziellen Fall gleich gross.
\[ J^{'}_{1}=J_{2} \]
Aufrgund dessen lässt sich bei gegebenem Antriebsdrehmoment auch die maximale Lastbeschleunigung bestimmen.
\[ \alpha_{2,opt}=\frac{M_{1}}{2\sqrt{J_{1}J_{2}}} \]
9.2.6 Getriebebemessung für Positionierantriebe mit zusätzlichem Lastmoment
Für den Fall das das Lastmoment nicht vernachlässigt werden kann, ergibt sich durch ähnliche Überlegungen folgende Gleichung für die dynamische Grundgleichung auf der Lastseite.
\[ \bigl(i_{G}^{2}\cdot J_{1}+J_{2}\bigr) \dot{\omega}_{2}=i_{G}\cdot M_{1}-M_{2} \]
Die Winkelbeschleunigung ergibt sich somit zu:
\[ \alpha_{2}=\dot{\omega}_{2}=\frac{i_{G}M_{1}-M_{2}}{i_{G}^{2}\cdot J_{1}+J_{2}} \]
Auch in diesem Fall ermöglicht das Lösen der entsprechenden Extremwertaufgabe die Bestimmung der grösstmöglichen Lastbeschleunigung.
\[ 0=\frac{d\alpha_{2}}{i_{G}}=\frac{M_{1}\bigl(i^{2}_{G}J_{1}+J_{2}\bigr) - (i_{G}M_{1}-M_{2})2i_{G}J_{1}}{\bigl(i_{G}^{2}J_{1}+J_{2}\bigr)^{2}} \]
\[ 0=i^{2}_{G}J_{1}+J_{2}-\bigl(i_{G}-\frac{M_{2}}{M_{1}}\bigr)2i_{G}J_{1} \]
\[ 0=i^{2}_{G}-2\frac{M_{2}}{M_{1}}i_{G}-\frac{J_{2}}{J_{1}} \]
Bei dieser Gleichung handelt es sich um eine quadratische Gleichung, welche zwei Lösungen besitzt. Für die Bemessung der Getriebeübersetzung ist allerdings nur die positive Lösung relevant.
\[ i_{G,opt}=\frac{M_{2}}{M_{1}}+\sqrt{\bigl(\frac{M_{2}}{M_{1}}\bigr)^{2}+\frac{J_{2}}{J_{1}}} \]
Abbildung 9.5 zeigt den qualitativen Verlauf der Winkelbeschleunigung in Abhängigkeit der Getriebeübersetzung für unterschiedliche zusätzliche Lastmomente.
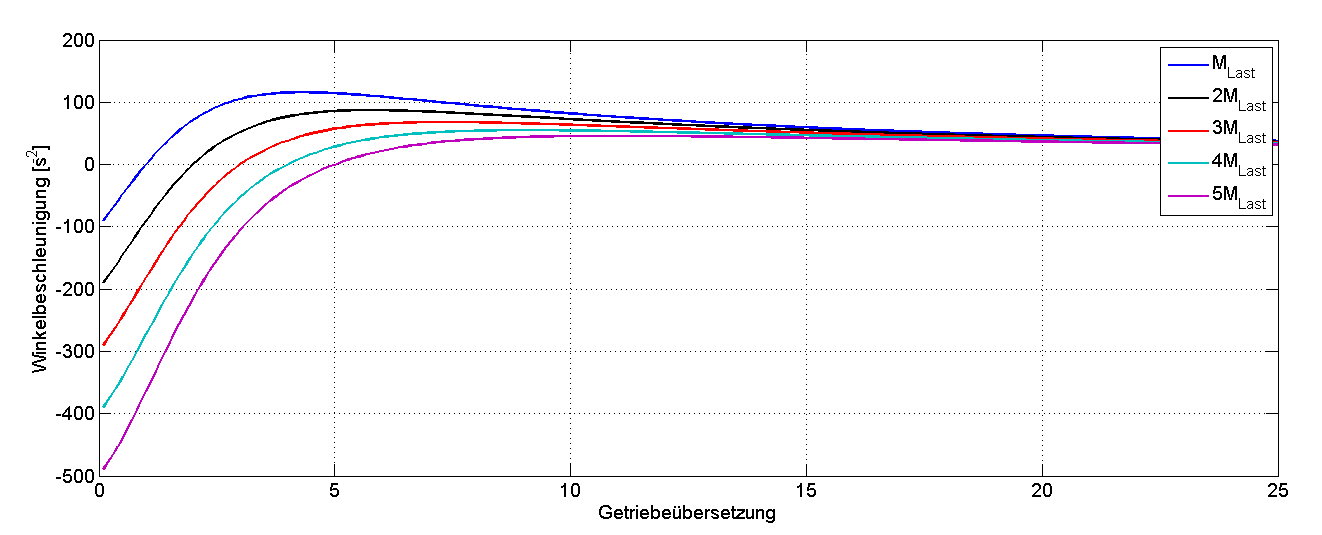
Abbildung 9.5: Typischer Verlauf der Winkelbeschleunigung für unterschiedliche zusätzliche Lastmomente
Das Diagramm zeigt, dass sich die optimale Getriebeübersetzung bei zusätzlichem Lastmoment im Vergleich zur unbelasteten Beschleunigung hin zu grösseren Werten verschiebt. Das Minimum der entsprechenden Kurven verläuft allerdings sehr flach, so dass bei kleinen Abweichungen keine grossen Fehler gemacht werden. Sinnvollerweise wird das minimale Drehmoment an der Maschinenwelle erreicht, wenn deren Drehzahlbereich vollständig ausgenutzt wird und das Übersetzungsverhältnis grösstmöglich gewählt wird.