15 Lineare Regression
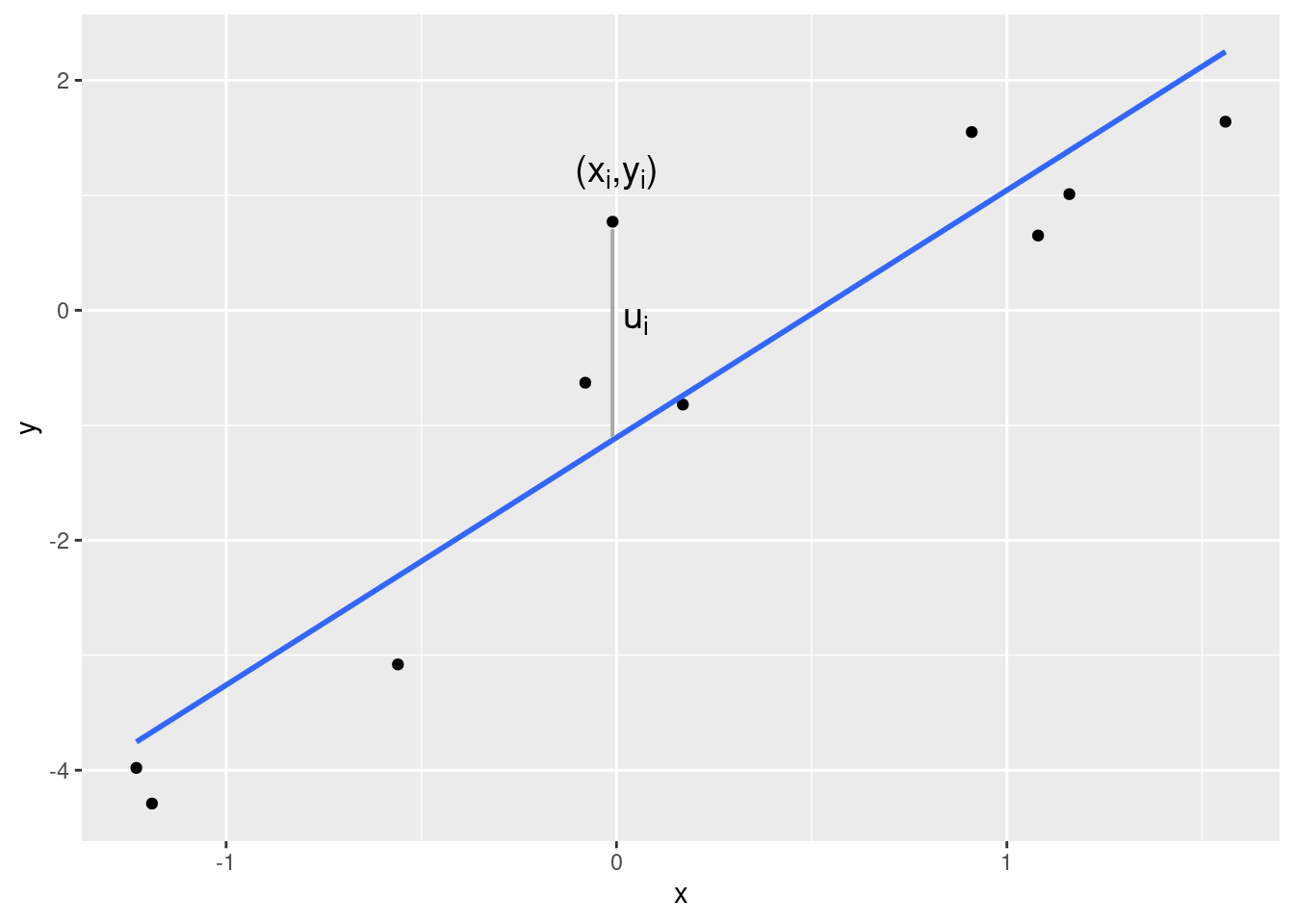
Das Ziel der linearen Regression besteht darin, den Zusammenhang zwischen zwei (oder später auch mehr als zwei) Variablen \(X\) und \(Y\) durch eine lineare Funktion möglichst gut zu erfassen. Da die Punktewolke \((x_1,y_1),\ldots,(x_n,y_n)\) aber nie exakt auf einer Geraden liegt, fügt man der linearen Funktion Größen \(u_1,\ldots,u_n\) hinzu, die die Abweichungen von der Geraden repräsentieren. \[ y_i = a+ b x_i+u_i \] für \(i=1,\ldots,n\). Man nennt die \(u_i\) Residuen (engl. residuals). Die folgende Abbildung zeigt ein (positives) Residuum. Es ist der vertikale Abstand des beobachteten Punkts von der Geraden.
Die Frage ist nun: Welche Gerade passt sich am besten der Punktewolke an? Anders gefragt: Wie soll man den Achsenabschnitt (engl. intercept) \(a\) und den Steigungskoeffizienten (engl. slope) \(b\) der linearen Funktion wählen?
Noch ein Hinweis zur Sprechweise: Wenn \(Y\) auf der \(y\)-Achse abgetragen wird und \(X\) auf der \(x\)-Achse, dann sagt man, dass \(Y\) auf \(X\) regressiert wird (engl. to regress \(Y\) on \(X\)).
15.1 Herleitungen

Um die Frage nach der optimalen Anpassung zu beantworten, braucht man ein Kriterium, mit dem beurteilt werden kann, wie gut sich eine Gerade an die Punktewolke anpasst. Das gängige Kriterium ist die Summe der quadrierten Residuen, also die Summe aller \(u_i^2\). Die Zielfunktion hängt von dem Achsenabschnitt und dem Steigungskoeffizienten ab. Um deutlich zu machen, dass diese beiden Werte frei gewählt werden können, nennen wir die Argumente der Zielfunktion \(\alpha\) und \(\beta\), \[\begin{align*} Z(\alpha, \beta) &=\sum_{i=1}^n u_i^2 \\ &= \sum_{i=1}^n (y_i - \alpha -\beta x_i)^2 \end{align*}\] Diese Funktion wird nun bezüglich \(\alpha\) und \(\beta\) minimiert. Man spricht daher auch von der Methode der kleinsten Quadrate. Um das Minimum zu finden, bilden wir zunächst die partiellen Ableitungen.
Wie müssen \(\alpha\) und \(\beta\) gewählt werden, um die Summe der quadrierten Residuen zu minimieren? Es handelt sich offenbar um ein Optimierungsproblem in zwei Variablen (\(\alpha\), \(\beta\)) ohne Nebenbedingungen. Wir gehen in drei Schritten vor: Ableiten, Nullsetzen, Auflösen.
Die beiden partiellen Ableitungen der Zielfunktion sind \[\begin{align*} \frac{\partial Z(\alpha,\beta)}{\partial\alpha} &= \sum_{i=1}^n 2(y_i-\alpha-\beta x_i)\cdot(-1)\\ &= -2\sum_{i=1}^n (y_i-\alpha-\beta x_i)\\ \frac{\partial Z(\alpha,\beta)}{\partial\beta} &= \sum_{i=1}^n 2(y_i-\alpha-\beta x_i)\cdot(-x_i)\\ &= -2\sum_{i=1}^n (x_i y_i-\alpha x_i-\beta x_i^2) \end{align*}\] Setzt man die Ableitung nach \(\alpha\) auf Null, so ergibt sich \[\begin{align*} &&-2\sum_{i=1}^n (y_i-\alpha-\beta x_i) &= 0 \\ \Leftrightarrow&&\sum_{i=1}^n (y_i-\alpha-\beta x_i) &= 0 \\ \Leftrightarrow&&\alpha n+ \beta\sum_{i=1}^n x_i &= \sum_{i=1}^n y_i \end{align*}\] Eine alternative Darstellung dieser Gleichung, die wir im nächsten Abschnitt benötigen, lautet \[ \sum_{i=1}^n u_i=0, \] in anderen Worten: Im Optimum müssen Achsenabschnitt und Steigungskoeffizient so gewählt werden, dass die Summe der Residuen 0 ergibt.
Nullsetzen der Ableitung nach \(\beta\) ergibt \[\begin{align*} &&-2\sum_{i=1}^n (x_i y_i-\alpha x_i-\beta x_i^2)&=0\\ \Leftrightarrow&&\sum_{i=1}^n (x_i y_i-\alpha x_i-\beta x_i^2) &= 0 \\ \Leftrightarrow&&\alpha\sum_{i=1}^n x_i + \beta\sum_{i=1}^n x_i^2 &= \sum_{i=1}^n x_i y_i \end{align*}\] Auch hier gibt es eine alternative Darstellung, in der die Residuen vorkommen. Dazu formen wir die mittlere Gleichung um, \[\begin{align*} &&\sum_{i=1}^n (x_i y_i-\alpha x_i-\beta x_i^2) &= 0 \\ \Leftrightarrow&&\sum_{i=1}^n x_i(y_i-\alpha-\beta x_i) &= 0\\ \Leftrightarrow&&\sum_{i=1}^n x_i u_i &= 0 \end{align*}\] Im Optimum müssen Achsenabschnitt und Steigungskoeffizient so gewählt werden, dass nicht nur \(\sum_{i=1}^n u_i=0\), sondern außerdem auch noch \(\sum_{i=1}^n x_i u_i=0\) gilt.
Wir kehren aber nun zu der Schreibweise ohne die Residuen zurück. Für das Optimum müssen diese beiden Gleichungen simultan erfüllt sein: \[\begin{align*} \alpha n+ \beta\sum_{i=1}^n x_i &= \sum_{i=1}^n y_i \\ \alpha\sum_{i=1}^n x_i + \beta\sum_{i=1}^n x_i^2 &= \sum_{i=1}^n x_i y_i \end{align*}\] Es handelt sich um ein lineares Gleichungssystem mit zwei Gleichungen und zwei Unbekannten, nämlich \(\alpha\) und \(\beta\). Die Lösung des Gleichungssystems kann man auf verschiedenen Wegen finden, z.B. mit Cramérs Ansatz. Die optimalen Werte von \(\alpha\) und \(\beta\) nennen wir \(a\) und \(b\). Zuerst leiten wir \(b\) her. \[\begin{align*} b &= \frac{ \left|\begin{array}{cc} n & \sum_{i=1}^n y_i \\ \sum_{i=1}^n x_i & \sum_{i=1}^n x_i y_i \end{array}\right|} {\left|\begin{array}{cc} n & \sum_{i=1}^n x_i \\ \sum_{i=1}^n x_i & \sum_{i=1}^n x_i^2 \end{array}\right|} \\[5mm] &= \frac{n\sum_{i=1}^n x_i y_i -\sum_{i=1}^n x_i \sum_{i=1}^n y_i} {n\sum_{i=1}^n x_i^2 -(\sum_{i=1}^n x_i)^2} \end{align*}\] Multipliziert man Zähler und Nenner mit \(1/n^2\), dann vereinfacht sich der Ausdruck zu \[ b=\frac{s_{XY}}{s_X^2}. \] Der optimale Steigungskoeffizient ist also der Quotient aus der Kovarianz von \(X\) und \(Y\) und der Varianz von \(X\). Diesen Wert können wir nun in die erste Gleichung des obigen Gleichungssystem einsetzen. Der optimalen Achsenabschnitt \(a\) muss folgende Bedingung erfüllen, \[ a n+ b\sum_{i=1}^n x_i = \sum_{i=1}^n y_i \] bzw. nach Teilen beider Seiten durch \(n\) und Umstellen \[ a=\bar y - b\bar x. \] Fassen wir zusammen: Die Methode der kleinsten Quadrate liefert einen Achsenabschnitt \(a\) und einen Steigungskoeffizienten \(b\), so dass die Gerade \(y=a+bx\) sich optimal an eine Punktewolke anpasst: \[\begin{align*} a &= \bar y-b\bar x\\ b &= \frac{s_{XY}}{s_X^2}. \end{align*}\] Die durch \(y=a+bx\) beschriebene Gerade nennt man Regressionsgerade.
15.2 Anpassungsgüte
Die minimierte Summe der quadrierten Residuen beträgt \[ \sum_{i=1}^n u_i^2 = \sum_{i=1}^n (y_i - a - bx_i)^2. \] Ist diese Summe nun groß oder klein? Kann durch die Regression die Streuung der \(Y\)-Werte eher schlecht oder eher gut erfasst werden? Um das zu beurteilen, müssen wir die Streuung der \(Y\)-Werte genauer analysieren.
Zu jeden \(x_i\) gehört ein \(Y\)-Wert, der genau auf der Regressionsgeraden liegt, nämlich \[ \hat y_i=a+bx_i. \] Die \(\hat y_1,\ldots,\hat y_n\) nennt man Prognosen, auch wenn dieser Begriff umgangssprachlich für echte Vorhersagen besetzt ist, also für Aussagen über die Zukunft. Die englische Bezeichnung “fitted values” trifft den Sachverhalt besser.
Aus der Definition der Prognosen folgt: Die tatsächlich beobachteten \(Y\)-Werte sind die Summe aus den Prognosen und den Residuen, \[ y_i = \hat y_i+u_i. \] Summiert man über alle \(i\) und dividiert beide Seiten durch \(n\), ergibt sich \[ \frac{1}{n}\sum_{i=1}^n y_i = \frac{1}{n}\sum_{i=1}^n \hat y_i +\frac{1}{n}\sum_{i=1}^n u_i. \] Wir wissen aber aus dem letzten Abschnitt, dass \(\sum_{i=1}^n u_i=0\) ist. Darum gilt, dass der Mittelwert der \(Y\)-Werte gleich ist dem Mittelwert der \(\hat Y\)-Werte, \[ \overline y=\overline{\hat y}. \] Nun betrachten wir die Varianz der \(Y\)-Werte und formen sie gezielt um. Dabei benutzen wir die Definition der prognostizierten Werte \(\hat y_i\) und die Eigenschaft, dass die Mittelwerte der \(Y\)-Werte und der \(\hat Y\)-Werte gleich sind. \[\begin{align*} s_Y^2 &= \frac{1}{n}\sum_{i=1}^n (y_i-\overline y)^2 \\ &= \frac{1}{n}\sum_{i=1}^n (\hat y_i -\overline{\hat y}+u_i )^2 \\ &= \frac{1}{n}\sum_{i=1}^n \left((\hat y_i -\overline{\hat y})+u_i \right)^2 \\ &= \frac{1}{n}\sum_{i=1}^n \left((\hat y_i -\overline{\hat y})^2 +2(\hat y_i -\overline{\hat y})u_i+u_i^2 \right) \\ &= \frac{1}{n}\sum_{i=1}^n (\hat y_i -\overline{\hat y})^2 +2\frac{1}{n}\sum_{i=1}^n(\hat y_i -\overline{\hat y})u_i +\frac{1}{n}\sum_{i=1}^n u_i^2. \end{align*}\] Der erste Summand ist die Varianz der \(\hat Y\)-Werte, also \(s_{\hat Y}^2\). Der dritte Summand ist die Varianz der Residuen \(s_U^2\), weil der Mittelwert (bzw. die Summe) der Residuen 0 ist. Der Term in der Mitte nimmt den Wert 0 an, was man nicht ohne weiteres erkennen kann, sondern herleiten muss. Dazu schauen wir uns die Summe genauer an, \[\begin{align*} \sum_{i=1}^n (\hat y_i-\overline{\hat y}) u_i &= \sum_{i=1}^n \hat y_i u_i- \sum_{i=1}^n\overline{\hat y}u_i \\ &= \sum_{i=1}^n \hat y_i u_i- \overline{\hat y}\sum_{i=1}^nu_i \\ &= \sum_{i=1}^n \hat y_i u_i, \end{align*}\] denn die Summe der Residuen ist 0. Nun ersetzen wir \(\hat y_i\) durch \(a+bx_i\) und erhalten \[\begin{align*} \sum_{i=1}^n \hat y_i u_i &= \sum_{i=1}^n (a+bx_i) u_i\\ &= \sum_{i=1}^n a u_i+\sum_{i=1}^n b x_i u_i\\ &= a\sum_{i=1}^n u_i+ b\sum_{i=1}^n x_i u_i. \end{align*}\] Wir wissen aber bereits, dass diese beiden Summen 0 ergeben. Damit ist der Streuungszerlegungssatz gezeigt: \[ s_Y^2=s_{\hat Y}^2+s_U^2. \] Die Streuung (Varianz) der tatsächlichen \(Y\)-Werte kann exakt zerlegt werden in die Summe der Streuung der gefitteten Werte (\(\hat Y\)-Werte) und der Streuung der Residuen. Das Besondere der linearen Regression besteht darin, dass diese Zerlegung sehr elegant und gut interpretierbar ist. Die Größe \(s_{\hat Y}^2\) bezeichnet die durch die Regression “erklärte Streuung”, und \(s_U^2\) ist die “unerklärte Streuung”.
Der Anteil der erklärten Streuung \(s_{\hat Y}^2\) an der gesamten Streuung \(s_Y^2\) heißt Bestimmtheitsmaß und wird in der Literatur meist mit \(R^2\) (engl. R squared) notiert, \[ R^2 = \frac{s_{\hat Y}^2}{s_Y^2}. \] Da Varianzen niemals negativ sein können, liegt das Bestimmtheitsmaß immer in dem Intervall \([0,1]\). Werte in der Nähe von 0 zeigen, dass (fast) kein linearer Zusammenhang zwischen den Variablen \(X\) und \(Y\) besteht. Werte in der Nähe von 1 zeigen, dass es zwischen \(X\) und \(Y\) einen (fast) exakten linearen Zusammenhang gibt.
Achtung: Wenn zwischen zwei Variablen \(X\) und \(Y\) ein deutlicher linearer Zusammenhang gefunden wird, zieht man leicht den Schluss, dass \(X\) einen kausalen Einfluss auf \(Y\) hat. Wie schon bei den Zusammenhangsmaßen ist das leider eine unzulässige Schlussfolgerung, denn Regression impliziert keine Kausalität!
Wenn \(X\) und \(Y\) in einem linearen Zusammenhang stehen, kann das zwar daran liegen, dass \(X\) tatsächlich einen kausalen Einfluss auf \(Y\) hat, aber es kann auch andere Ursachen haben. So kann der kausale Effekt in die andere Richtung verlaufen, d.h. \(Y\) hat einen kausalen Effekt auf \(X\). Oder es kann eine oder mehrere Hintergrundvariablen geben, die sowohl auf \(X\) als auch auf \(Y\) wirken. Wie man kausale Effekte ökonometrisch sauber aufdecken kann, lernen Sie in dem Modul Empirical Economics (allerdings nur im VWL-Studiengang).
15.3 Lineare Modelle in R
Die Regression \(y_i=a+bx_i+u_i\) gehört zu den sogenannten linearen Modellen. Sie spielen so eine große Rolle in Data Science, dass es in R eine eigene Syntax gibt, mit der lineare Modelle dargestellt werden können. Die Syntax der linearen Regression von \(Y\) auf \(X\) lautet allgemein wie folgt:
regr <- lm(Y~X, data=DATAFRAME)Dabei ist DATAFRAME der Name des Dataframes, in dem die Variablen \(X\) und \(Y\) gespeichert sind. Die Notation Y~X wird in R “formula” genannt. Sie bedeutet, dass die Variable links von der Tilde (also hier \(Y\)) erklärt wird durch das, was rechts von der Tilde steht (hier also \(X\)). In dem hier gezeigten einfachsten Fall steht rechts nur eine einzelne Variable, es ist jedoch möglich auf der rechten Seite mehrere Variablen oder auch Transformationen der Variablen aufzulisten, die dann gemeinsam \(Y\) erklären sollen.
Als Ergebnis der linearen Regression wird ein recht komplexes Objekt ausgegeben. In dem obigen Befehl wird dieses Objekt unter dem Namen regr gespeichert (und erscheint auch im Environment-Pane).
Das Objekt regr enthält
den Achsenabschnitt \(a\) und den Steigungskoeffizienten \(b\); sie können durch
coefficients(regr)als Vektor ausgelesen werden oder durchregrbzw.print(regr)angezeigt werden,die Residuen \(u_1,\ldots,u_n\); sie können durch
residuals(regr)ausgelesen werden,die Prognosen \(\hat y_1,\ldots,\hat y_n\); sie können durch
fitted.values(regr)ausgelesen werden,weitere Informationen, die uns jedoch (noch) nicht interessieren.
Beispiel:

Wir betrachten den Auszug aus der Internet-Movie-Database imdb und schränken den Datensatz auf Filme nach 2015 ein. Den Datensatz mit den neuen Filmen speichern wir als Dataframe neuefilme.
imdb <- read_csv("../data/imdb.csv",
col_types = "ccnfnnnnnn")
neuefilme <- filter(imdb, year > 2015)Nun regressieren wir das Bruttoeinspielergebnis grossinc auf das Filmbudget budget und speichern das lm-Objekt unter dem Namen regr.
regr <- lm(grossinc~budget, data=neuefilme)Der Achsenabschnitt und der Steigungskoeffizient der optimal angepassten Regressionsgeraden sind
regr
Call:
lm(formula = grossinc ~ budget, data = neuefilme)
Coefficients:
(Intercept) budget
-17.932 3.809 Eine Erhöhung des Budgets um 1 Mio. Dollar hat also in diesem Datensatz im Mittel zu einer Erhöhung des Bruttoergebnisses von etwa 3.81 Mio. Dollar geführt.
Das Bestimmtheitsmaß \(R^2\) wird in der Zusammenfassung der Regressionsergebnisse angezeigt. Den größten Teil des Outputs können Sie hier ignorieren.
summary(regr)
Call:
lm(formula = grossinc ~ budget, data = neuefilme)
Residuals:
Min 1Q Median 3Q Max
-709.25 -46.28 1.34 17.25 1459.84
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -17.93197 5.42557 -3.305 0.000981 ***
budget 3.80868 0.08889 42.849 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 146.1 on 1060 degrees of freedom
Multiple R-squared: 0.634, Adjusted R-squared: 0.6336
F-statistic: 1836 on 1 and 1060 DF, p-value: < 2.2e-16Das “Multiple R-squared” (also \(R^2\)) beträgt 0.634.
Die Funktion summary berechnet neben dem \(R^2\) auch viele andere Größen, die uns hier aber (noch) nicht interessieren. Wenn man ausschließlich das \(R^2\) wissen will, lässt es sich aus dem Output der summary-Funktion mit dem Dollarzeichen herausziehen:
summary(regr)$r.squared[1] 0.633978115.4 Grafische Darstellung
Die Regressionsgerade wird häufig in ein Streudiagramm eingefügt. Das ist empfehlenswert, weil (a) es den Verlauf leichter erkennbar macht, (b) Ausreißer und unplausible Werte in den Daten leicht erkennbar sind und (c) die Streuung der Punkte um die Regressionsgerade herum visualisiert wird. Die Funktion ggplot bietet eine einfache Möglichkeit, die Regressionsgerade in ein Streudiagramm einzufügen.
Beispiel:
In einem Streudiagramm wird das Bruttoeinspielergebnis grossinc gegen das Filmbudget budget abgetragen.
ggplot(neuefilme, aes(x=budget, y=grossinc)) +
geom_point()
In diese Abbildung fügen wir nun die Regressionsgerade ein. Dazu ergänzen wir mit einem weiteren Pluszeichen ein Geom, und zwar geom_smooth. Dieses Geom fügt eine geglättete Kurve in ein Streudiagramm ein, und eine mögliche Kurve ist die Regressionsgerade. Die Optionen dafür ist method="lm" (für lineares Modell).
ggplot(neuefilme, aes(x=budget, y=grossinc)) +
geom_point() +
geom_smooth(method="lm")`geom_smooth()` using formula = 'y ~ x'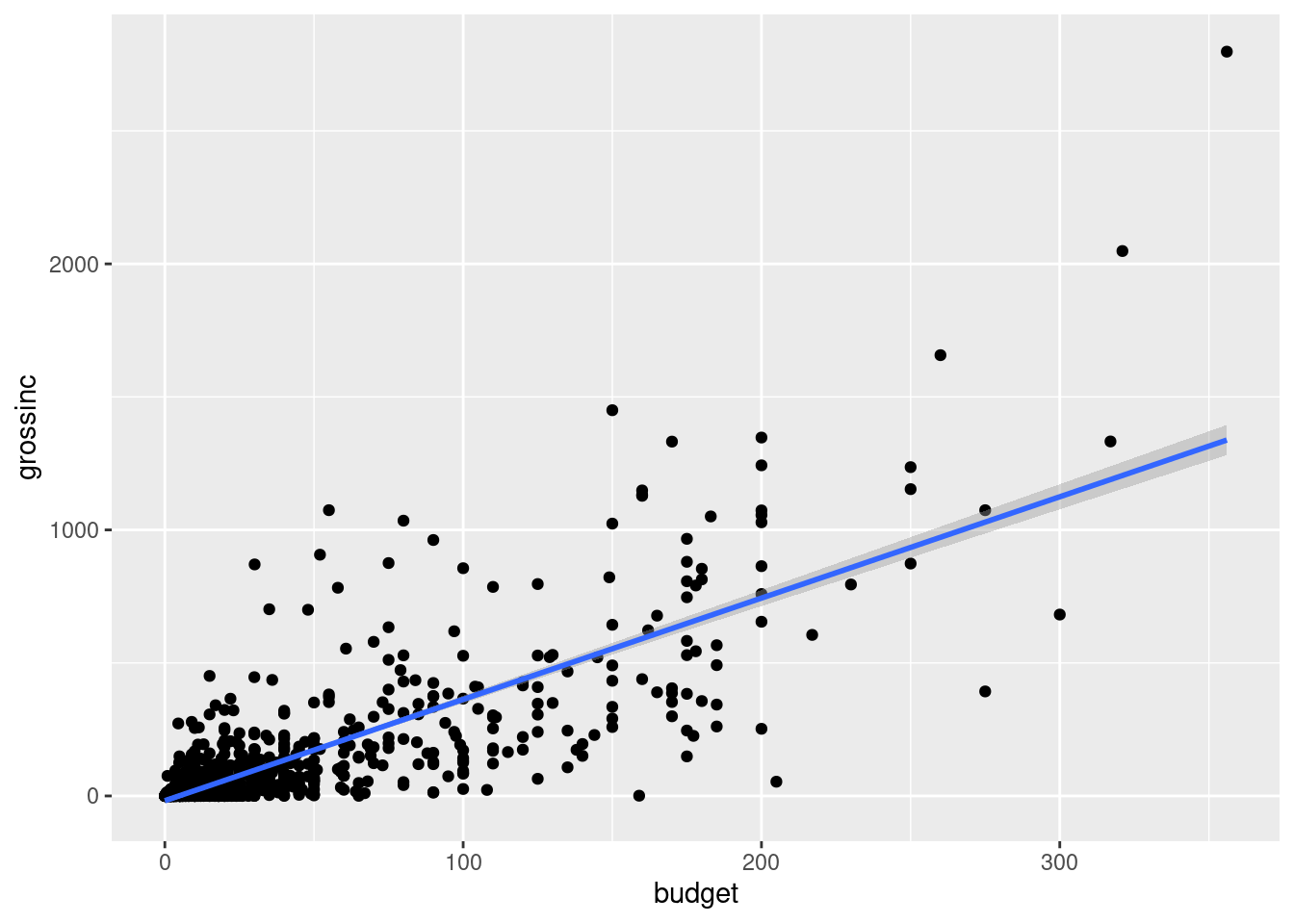
Zwei Kleinigkeiten können noch verbessert werden: Erstens, es gibt eine Benachrichtigung, dass für die Regression die \(Y\)-Variable auf die \(X\)-Variable regressiert wurde. Um diese Benachrichtigung zu vermeiden, können wir die Option formula=y~x (wie im lm-Befehl) hinzufügen. Zweitens erkennt man in der Grafik einen grauen Bereich um die Regressionsgerade herum. Dieser Bereich gibt die Unsicherheit der Anpassung an, ein Thema, das Sie (zumindest wenn Sie Volkswirtschaftslehre studieren) später in dem englischsprachigen Modul Empirical Economics kennen lernen werden. Der graue Bereich kann durch die Option se=FALSE ausgeschaltet werden. Damt ergibt sich insgesamt:
ggplot(neuefilme, aes(x=budget, y=grossinc)) +
geom_point() +
geom_smooth(method="lm", formula=y~x, se=FALSE)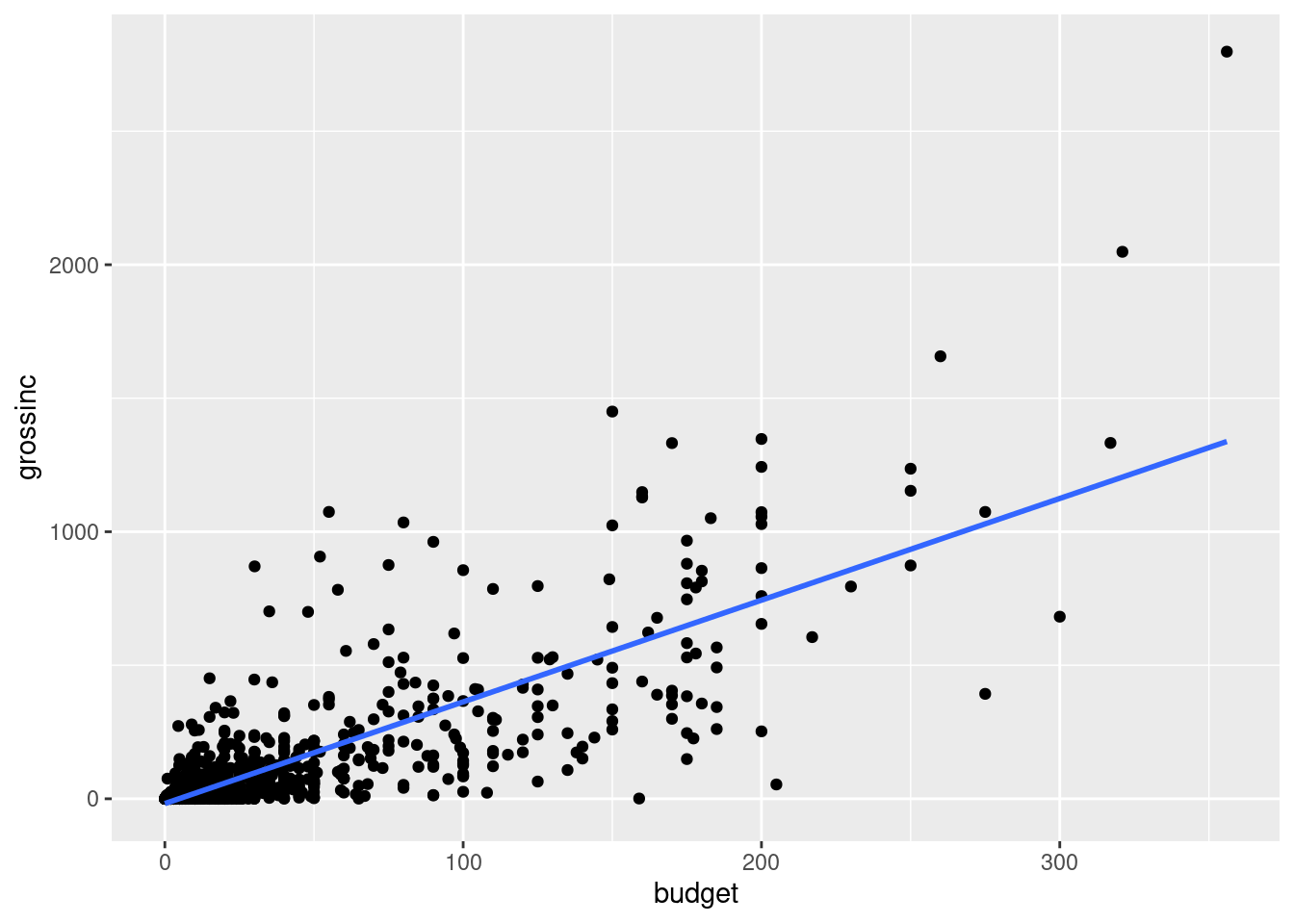
15.5 Multiple lineare Regression
In vielen Fällen ist es plausibel, dass man eine Variable \(Y\) nicht nur durch eine einzelne Variable \(X\) erklärt, sondern durch mehr als eine Variable, z.B. \(X_1, X_2,\ldots,X_k\). Man spricht dann von einer multiplen linearen Regression. Die Vorgehensweise ist sehr ähnlich zu dem Fall mit einer einzigen Variablen \(X\), er kann nur nicht mehr so einfach grafisch dargestellt werden.
Die Beobachtungen sind die Punkte \[ (x_{1,1},x_{2,1},\ldots,x_{k,1},y_1),\ldots,(x_{1,n},x_{2,n},\ldots,x_{k,n},y_n) \] wobei \(x_{j,i}\) den Wert der Variable \(j=1,\ldots,k\) in Beobachtung \(i=1,\ldots,n\) bezeichnet.
Zusammen mit den Residuen \(u_1,\ldots,u_n\) lautet nun die Regressionsgerade \[ y_i = a + b_1 x_{1,i}+ b_2 x_{2,i}+\ldots+b_k x_{k,i}+u_i. \] Es gibt also weiterhin einen Achsenabschnitt, aber nun \(k\) Steigungskoeffizienten, nämlich einen für jede erklärende Variable. Die Koeffizienten werden wiederum so gewählt, dass die Summe der quadrierten Residuen minimiert wird.

Für die Herleitung, die wir hier überspringen, sind die Methoden der linearen Algebra notwendig, die in dem Wahlpflicht-Modul Mathematik 2: Lineare Algebra für Wirtschaftswissenschaften gründlich eingeführt werden. Ausführlich wird die multiple lineare Regression in dem Wahlpflicht-Modul Econometrics und dem Pflicht-Modul Empirical Economics (nur für VWL) behandelt. An dieser Stelle wird daher nur ein kurzer Ausblick auf diese Methode gegeben. Worauf man achten muss und wo die Fallstricke der multiplen linearen Regression liegen, lernen Sie später in den anderen Modulen.
In R ist die Schätzung einer multiplen linearen Regression genauso einfach wie eine Regression mit nur einer erklärenden Variablen. Die Syntax der multiplen linearen Regression von \(Y\) auf \(X_1,X_2,\ldots,X_k\) lautet allgemein wie folgt:
regr <- lm(Y ~ X1 + X2 + ... + Xk, data=DATAFRAME)wobei DATAFRAME der Name des Dataframes ist, in dem die Variablen enthalten sind.
Beispiel:
Wir betrachten weiterhin den Datensatz neuefilme, also alle Filme aus der Internet Movie Database, die nach 2015 erschienen sind. Das Bruttoergebnis wird nun jedoch nicht nur auf das Budget regressiert, sondern zusätzlich auf die Filmdauer duration und die durchschnittliche Bewertung avgvote.
regr2 <- lm(grossinc ~ budget + duration + avgvote,
data=neuefilme)Das Ergebnis der Regression wird in dem Objekt regr2 gespeichert. Es enthält den Achsenabschnitt \(a\) und die Steigungskoeffizienten \(b_1,\ldots,b_k\). Diese Koeffizienten können durch coefficients(regr) als Vektor ausgelesen werden. Sie werden auch angezeigt, wenn man einfach regr2 oder print(regr2) eingibt.
regr2
Call:
lm(formula = grossinc ~ budget + duration + avgvote, data = neuefilme)
Coefficients:
(Intercept) budget duration avgvote
-127.6586 3.7185 -0.5515 28.3814 Das Ergebnis zeigt, dass das Bruttoergebnis eines Films im Mittel um 3.72 Mio. Dollar höher ausfällt, wenn das Budget um 1 Mio. Dollar erhöht wird. Längere Filme spielen etwas niedrigere Ergebnisse ein: Wenn die Filmlänge um eine Minute steigt, sinkt das Bruttoergebnis im Mittel um 0.55 Mio. Dollar. Auch mit der Bewertung der Zuschauer hängt das Ergebis zusammen. Eine bessere Bewertung geht mit einem höheren Bruttoergebnis einher. Eine Erhöhung um 1 Punkt (auf der Bewertungsskala) geht im Mittel mit einer Erhöhung des Bruttoergebnisses um 28.4 einher.
In dem Objekt regr2 findet man außerdem die Residuen und die Prognosen. Sie können durch residuals(regr2) bzw. fitted.values(regr) ausgelesen werden.
Auch bei der multiplen linearen Regression gibt das Bestimmtheitsmaß \(R^2\) an, wie hoch der Anteil der erklärten Streuung ist. Es wird auf die gleiche Weise wie oben von der summary-Funktion berechnet. In diesem Beispiel ergibt sich
summary(regr2)
Call:
lm(formula = grossinc ~ budget + duration + avgvote, data = neuefilme)
Residuals:
Min 1Q Median 3Q Max
-722.52 -45.73 -6.62 33.51 1463.09
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -127.65858 30.93375 -4.127 3.97e-05 ***
budget 3.71847 0.09435 39.410 < 2e-16 ***
duration -0.55146 0.30066 -1.834 0.0669 .
avgvote 28.38143 4.41329 6.431 1.92e-10 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 143.4 on 1058 degrees of freedom
Multiple R-squared: 0.6481, Adjusted R-squared: 0.6471
F-statistic: 649.6 on 3 and 1058 DF, p-value: < 2.2e-16Das Bestimmtheitsmaß beträgt also 0.6481.