soep <- read_csv("../data/mocksoep.csv",
col_types = "nnnnfnnnffnnncnnnnn") %>%
filter(empllev=="voll" & year==2020)
n <- dim(soep)[1]9 Additionssätze
Wenn man die Population in Gruppen zerlegt, lässt sich der Mittelwert für jede Gruppe einzeln oder für die gesamte Population berechnen. Natürlich können die Mittelwerte in den Gruppen sich voneinander unterscheiden. Zwischen den Gruppenmittelwerten und dem Gesamtmittelwert besteht aber eine Beziehung. Auch die Varianz lässt sich für jede Gruppe oder für die gesamte Population berechnen. Im folgenden untersuchen wir, wie man aus den Gruppenmittelwerten oder den Gruppenvarianzen den Gesamtmittelwert und die Gesamtvarianz berechnen kann.
9.1 Aggregation von Mittelwerten
Wie errechnet man aus Gruppenmittelwerten den Gesamtmittelwert? Die Zahl der Gruppen, in die wir die Population zerlegen, nennen wir \(J\). Die Zerlegung muss so erfolgen, dass jede Beobachtung genau einer Gruppe zugeordnet wird. Eine solche Zerlegung nennt man auch Partition oder vollständige Zerlegung. Den Umfang der Gruppe \(j\) bezeichnen wir mit \(n_j\), den Umfang der gesamten Population mit \(n\). Es muss gelten \[ n=\sum_{j=1}^J n_j. \] Die Gruppenmittelwerte werden mit \(\bar x_1,\ldots, \bar x_j\) bezeichnet, der Gesamtmittelwert ist \(\bar x\).
Für den Mittelwert der Gruppe \(j\) gilt \[\begin{align*} \bar x_j &= \frac{1}{n_j}\sum_{i\in I_j} x_i. \end{align*}\]
Der Ausdruck unter dem Summenzeichen zeigt an, dass die Summation über alle Beobachtungen läuft, die in die Gruppe \(j\) gehören. \(I_j\) ist also die Menge aller Indizes der Gruppe \(j\).
Die Beziehung zwischen \(\bar x_1,\ldots, \bar x_J\) und \(\bar x\) ergibt sich aus folgender Formel, \[\begin{align*} \bar x&=\sum_{j=1}^J \bar x_j \frac{n_j}{n}\\ &=\sum_{j=1}^J \bar x_j f_j \end{align*}\] Der Additionssatz für Mittelwerte besagt also: Der Gesamtmittelwert ist die Summe der Gruppenmittelwerte, wobei jeder Gruppenmittelwert mit der relativen Häufigkeit der Gruppe gewichtet wird.
Dass dieser Zusammenhang gilt, lässt sich leicht herleiten, wenn man die Definition der Gruppenmittelwerte einsetzt: \[\begin{align*} \sum_{j=1}^J \bar x_j \frac{n_j}{n} &= \sum_{j=1}^J \frac{1}{n_j}\sum_{i\in I_j} x_i \frac{n_j}{n}\\ &= \frac{1}{n} \sum_{j=1}^J \sum_{i\in I_j} x_i\\ &= \frac{1}{n} \sum_{i=1}^n x_i\\ &= \bar x. \end{align*}\]
Der Schritt von der zweiten zur dritten Zeile gilt, weil die Summation \(\sum_{j=1}^J\sum_{i\in I_j}\) über alle Beobachtungen aller Gruppen läuft - und das sind schlicht und einfach alle Beobachtungen \(\sum_{i=1}^n\).
Beispiel:
Wir laden wieder den Beispieldatensatz mocksoep.csv und beschränken uns auf vollzeitbeschäftigte Personen im Jahr 2020. Die Anzahl an Beobachtungen \(n\) ist die Zeilenzahl des Datensatzes.
Für die Gruppeneinteilung verwenden wir das Geschlecht sex. Die beiden Gruppenmittelwerte der Lohneinkommen earn für Männer und Frauen und die absoluten und relativen Häufigkeiten bestimmen wir mit Hilfe der Funktionen group_by und summarise. Die Werte schreiben wir in einen Dataframe, den wir unter dem Namen lohn speichern.
soep %>%
group_by(sex) %>%
summarise(xj = mean(earn),
nj = n(),
fj = n()/n) -> lohn
print(lohn)# A tibble: 2 × 4
sex xj nj fj
<fct> <dbl> <int> <dbl>
1 F 42617. 3570 0.351
2 M 62558. 6614 0.649Als Gesamtmittelwert \(\bar x\) erhalten wir aus dem gesamten Datensatz
xquer <- mean(soep$earn)
xquer[1] 55567.84Wenn die Daten für die gesamte Population vorliegen, ist es natürlich am einfachsten, den Gesamtmittelwert auf diese Weise direkt auszurechnen.
Der Additionssatz besagt nun, dass man den Gesamtmittelwert auch aus den Gruppenmittelwerten und den (absoluten oder relativen) Gruppengrößen errechnen kann, selbst wenn die Populationsdaten nicht vorliegen. Zur Kontrolle berechnen wir das Gesamtmittel aus dem Dataframe lohn:
summarise(lohn, xquer=sum(xj*nj/n))# A tibble: 1 × 1
xquer
<dbl>
1 55568.9.2 Aggregation von Varianzen
Die Aggregation von Varianzen ist etwas komplexer. Das liegt daran, dass die gesamte Varianz nicht nur durch die Streuung innerhalb der Gruppen beeinflusst wird, sondern auch durch die Streuung zwischen den Gruppen. Selbst wenn in allen Gruppen die Gruppenvarianzen Null sind, ist die Gesamtvarianz nicht Null, sobald sich die Werte zwischen den Gruppen unterscheiden.
Wir übernehmen die Notation für die Gruppenumfänge \(n_j\) und die Gruppenmittelwerte \(\bar x_j\). Die Varianz der Beobachtungen in Gruppe \(j\) bezeichnen wir mit \(s_j^2\).
Wie verhält sich nun die Gesamtvarianz \(s^2\) zu den Gruppenvarianzen \(s_1^2,\ldots,s_J^2\) ? Die Antwort auf diese Frage liefert der sogenannte Streuungszerlegungssatz (oder Additionssatz für Varianzen): \[\begin{align*} s^2 &= \underbrace{\sum_{j=1}^{J}s_j^2\frac{n_j}{n}}_{=s_{int}^2}+ \underbrace{\sum_{j=1}^J\left( \bar{x}_j-\bar{x}\right)^2\frac{n_j}{n}}_{=s_{ext}^2}. \end{align*}\]
Die Gesamtvarianz ergibt sich als Summe der internen Streuung \(s^2_{int}\) und der externen Streuung \(s^2_{ext}\). Die interne Streuung ist (analog zum Additionssatz für Mittelwerte) die gewichtete Summe der Gruppenvarianzen. Sie misst also, wie stark die Streuung in den einzelnen Gruppen ist. Die externe Streuung ist die (gewichtete) Varianz der Gruppenmittelwerte um das Gesamtmittel herum. Sie misst also, wie stark die Streuung zwischen den Gruppen ist.
Die Aufteilung in interne und externe Varianz erlaubt es uns, Aussagen über die Homogenität von Gruppen zu treffen. Wenn die interne Streuung nur einen kleinen Anteil an der Gesamtvarianz hat, sind die Gruppen sehr homogen. Wenn der Anteil der internen Streuung hingegen groß ist, handelt es sich um relativ heterogene Gruppen.
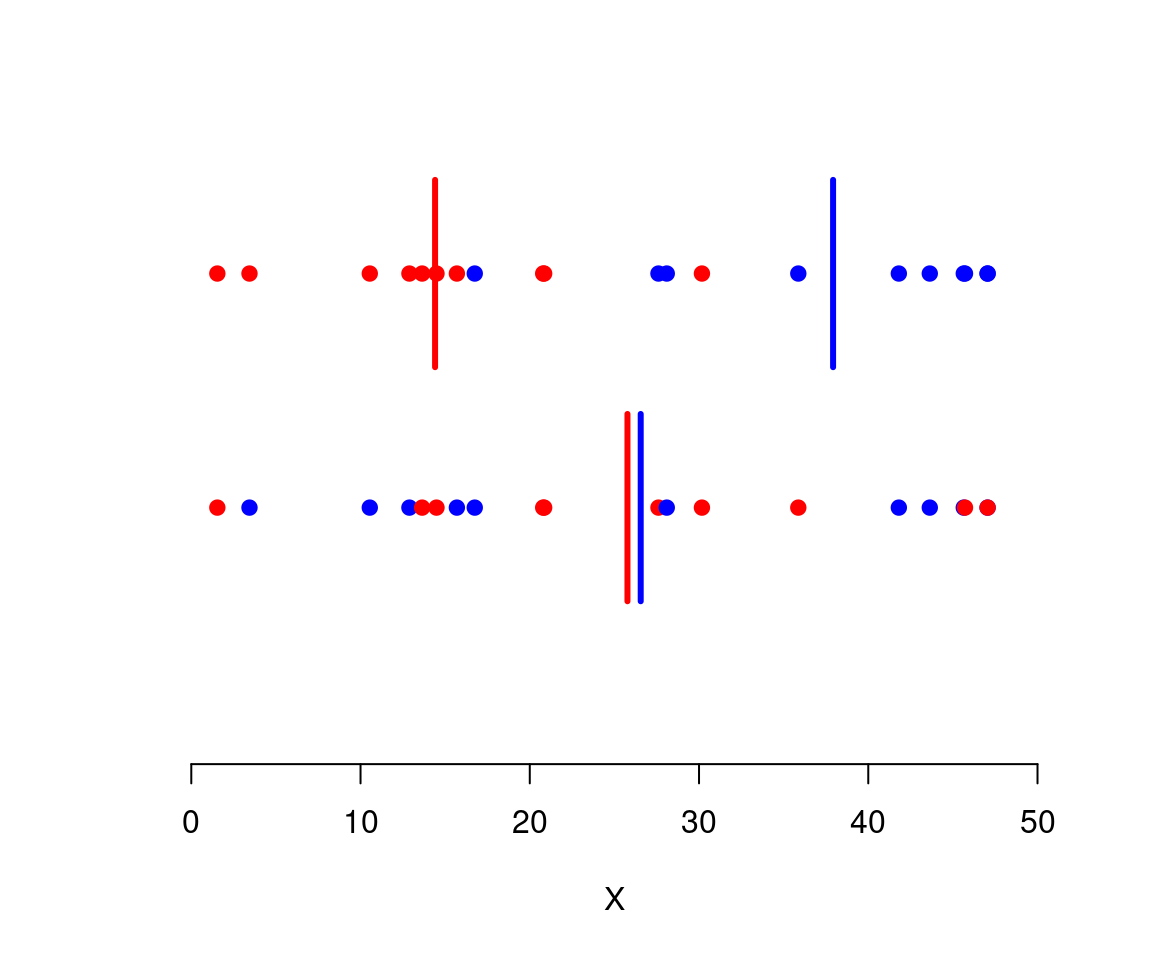
Das lässt sich an einer einfachen Grafik gut erkennen. Die folgenden Punkte zeigen \(n=20\) Werte einer Variablen \(X\). Alle Punkte gehören entweder in die rote oder in die blaue Gruppe. Bei der oberen Gruppeneinteilung ist die interne Varianz klein (homogene Gruppen), im unteren Fall ist die interne Varianz groß (heterogene Gruppen). Die senkrechten Striche zeigen jeweils die beiden Gruppenmittelwerte.
Die Herleitung des Streuungszerlegungssatzes ist etwas komplizierter als der Additionssatz für Mittelwerte, aber die einzelnen Schritte sind trotzdem gut nachvollziehbar. Wir starten mit der Definition der Varianz: \[\begin{align*} s^2 &= \frac{1}{n}\sum_{i=1}^n (x_i-\bar x)^2 \\ &= \frac{1}{n}\sum_{j=1}^J\sum_{i\in I_j}(x_i-\bar x)^2\\ &= \frac{1}{n}\sum_{j=1}^J\sum_{i\in I_j}((x_i-\bar x_j)+(\bar x_j-\bar x))^2 \end{align*}\]
Nun wenden wir die binomische Formel an: \[\begin{align*} s^2 &= \frac{1}{n}\sum_{j=1}^J\sum_{i\in I_j}[(x_i-\bar x_j)^2+(\bar x_j-\bar x)^2 +2(x_i-\bar x_j)(\bar x_j-\bar x)]\\ &= \frac{1}{n}\sum_{j=1}^J\sum_{i\in I_j}(x_i-\bar x_j)^2 +\frac{1}{n}\sum_{j=1}^J\sum_{i\in I_j}(\bar x_j-\bar x)^2 \\ &\qquad +2\frac{1}{n}\sum_{j=1}^J\sum_{i\in I_j}(x_i-\bar x_j)(\bar x_j-\bar x). \end{align*}\]
Schauen wir uns die drei Summanden genauer an. Der erste Summand lässt sich so umformen: \[\begin{align*} \frac{1}{n}\sum_{j=1}^J\sum_{i\in I_j}(x_i-\bar x_j)^2 &= \sum_{j=1}^J\frac{n_j}{n}\frac{1}{n_j}\sum_{i\in I_j}(x_i-\bar x_j)^2\\ &= \sum_{j=1}^J\frac{n_j}{n}s_j^2, \end{align*}\] d.h. es handelt sich hierbei um die interne Streuung.
In dem zweiten Summanden hat die innere Summe (über \(i\)) \(n_j\) Summanden, die nicht von \(i\) abhängen und alle gleich sind. Darum gilt \[\begin{align*} \frac{1}{n}\sum_{j=1}^J\sum_{i\in I_j}(\bar x_j-\bar x)^2 &= \sum_{j=1}^J\frac{n_j}{n}(\bar x_j-\bar x)^2. \end{align*}\]
Der dritte Summand summiert sich zu Null. Um das zu sehen, formen wir den Ausdruck so um: \[\begin{align*} 2\frac{1}{n}\sum_{j=1}^J\sum_{i\in I_j}(x_i-\bar x_j)(\bar x_j-\bar x) &=2\frac{1}{n}\sum_{j=1}^J(\bar x_j-\bar x)\sum_{i\in I_j}(x_i-\bar x_j). \end{align*}\]
In der hinteren Summe gilt für alle \(j\) \[\begin{align*} \sum_{i\in I_j}(x_i-\bar x_j)&=\sum_{i\in I_j}x_i-\sum_{i\in I_j}\bar x_j\\ &= n_j\bar x_j-n_j\bar x_j\\ &=0, \end{align*}\] weshalb auch der gesamte dritte Summand Null ergibt. Damit ist der Streuungszerlegungssatz gezeigt.
Beispiel:
Wir betrachten wieder die Variable Arbeitseinkommen (earn) im Datensatz soep. Die Gruppen sind wieder Männer und Frauen (sex). Zuerst bestimmen wir die Gruppenmittelwerte und -varianzen. Bei der Berechnung der Varianz muss hier beachtet werden, dass die R-Funktion var die sogenannte Stichprobenvarianz berechnet. Um die Populationsvarianz zu erhalten, müssen wir den Wert umskalieren, vgl. Abschnitt @ref(varianz). Für die Gruppe \(j\) ist der Skalierungsfaktor \((n_j-1)/n_j\).
soep %>%
group_by(sex) %>%
summarise(xj = mean(earn),
s2j = var(earn)*(n()-1)/n(),
nj = n()) -> lohn
print(lohn)# A tibble: 2 × 4
sex xj s2j nj
<fct> <dbl> <dbl> <int>
1 F 42617. 2155554800. 3570
2 M 62558. 24167151248. 6614Die Populationsvarianz aller Arbeitseinkommen beträgt
s2 <- var(soep$earn)*(n-1)/n
print(s2)[1] 16541526142Gemäß dem Streuungszerlegungssatz berechnen wir nun aus den Gruppenangaben die interne und externe Varianz:
s2int <- sum(lohn$s2j * lohn$nj / n)
print(s2int)[1] 16450988706s2ext <- sum(lohn$nj / n * (lohn$xj - xquer)^2)
print(s2ext)[1] 90537436Der Anteil der externen Streuung an der Gesamtstreuung ist eher gering, nämlich nur
print(round(s2ext/s2,4))[1] 0.0055Offensichtlich spielt die externe Varianz keine große Rolle. Die Streuung der Arbeitseinkommen in Deutschland wird also trotz der starken Unterschiede in den Mittelwerten überwiegend durch die Streuung innerhalb der Geschlechtergruppen erklärt, nicht durch die unterschiedlich hohen Durchschnittslöhne zwischen Männern und Frauen.
9.3 Gewichtete Mittelwerte
Eine sehr häufige und wichtige Anwendung des Additionssatzes für Mittelwerte sind gewichtete Mittelwerte. In vielen Datensätzen repräsentieren die Beobachtungen nicht nur eine Einheit der Population (z.B. eine Person oder ein Unternehmen), sondern mehrere Populationseinheiten. Das muss bei der Berechnung des Mittelwerts berücksichtigt werden.
Beispiel:
Um das Problem zu verdeutlichen, betrachten wir ein einfaches Beispiel: Ein fiktiver Datensatz enthält Angaben zum Lohn mehrerer Personen. Nicht alle Beobachtungen sind in diesem Datensatz gleich wichtig. Manche Beobachtungen repräsentieren mehr als eine Person. Für wie viele Personen eine Beobachtung steht, wird durch das Gewicht w (engl. weight) angegeben.
D <- data.frame(id = 1:9,
lohn = c(1500,2000,7400,3200,8500,3500,3300,9000,1100),
w = c(3,2,1,1.5,1,1.5,1.5,1,3))
D id lohn w
1 1 1500 3.0
2 2 2000 2.0
3 3 7400 1.0
4 4 3200 1.5
5 5 8500 1.0
6 6 3500 1.5
7 7 3300 1.5
8 8 9000 1.0
9 9 1100 3.0Die erste Beobachtung repräsentiert also nicht nur eine Person mit einem Lohn von 1500, sondern 3 Personen mit einem Lohn von 1500. In diesem Beispiel haben die niedrigen Einkommen tendenziell ein höheres Gewicht. Gewichte müssen nicht ganzzahlig sein. Wie hoch ist der durchschnittliche Lohn, wenn man die Gewichtung berücksichtigt?
Zur Beantwortung dieser Frage können wir den Additionssatz für Mittelwerte benutzen. Dazu interpretieren wir jede Beobachtung als eine “Gruppe”, jeden Lohn als “Gruppendurchschnitt” und das Gewicht als die “Gruppengröße”. Damit ergibt sich der gewichtete Mittelwert \[
\bar x=\sum_{i=1}^n x_i \frac{w_i}{W},
\] wobei \(W\) die Summe alle Gewichte ist, \[
W=\sum_{i=1}^n w_i.
\] In R gibt es zur Berechnung des gewichteten Mittelwerts die Funktion weighted.mean. Sie hat als erstes Argument den Vektor der Beobachtungen der Variable (x), deren Mittelwert bestimmt werden soll. Das zweite Argument (w) ist der Vektor der zugehörigen Gewichte.
Für das Beispiel ergibt sich
weighted.mean(D$lohn, w=D$w)[1] 3335.484Zum Vergleich: Das ungewichtete Mittel (also der normale Mittelwert) beträgt
mean(D$lohn)[1] 4388.889Auch andere Lagemaße (und auch Streuungsmaße) können mit einer Gewichtung versehen werden, aber das vertiefen wir in diesem Kurs nicht.
9.4 Preisindex
Es gibt noch andere Arten von Gewichtung. In den Wirtschaftswissenschaften ist es oft interessant, Aussagen über die Entwicklung des “Preisniveaus” zu machen. Dieses Kapitel ist ein Exkurs, in dem es um die Messung des Preisniveaus geht. Wenn das Preisniveau insgesamt ansteigt, spricht man von Inflation. Dass Inflation für den sozialen Frieden eines Landes gefährlich werden kann, wenn sie zu hoch steigt, wird durch ein Zitat unterstrichen, das Lenin zugeschrieben wird:
Wer die Kapitalisten vernichten will, muss ihre Währung zerstören.
Was genau ist aber unter “Inflation” bzw. unter einem “steigenden Preisniveau” zu verstehen? Wie kann man Inflation messen? Die Antwort auf diese Frage wäre ziemlich einfach, wenn alle Preise sich (prozentual) gleich stark verändern würden. Wenn beispielsweise alle Preise um 5 Prozent steigen, dann beträgt die Inflationsrate natürlich 5 Prozent. So einfach ist es aber in der Realität nicht. Manche Preise steigen stark, manche nur ein wenig, einige Preise fallen vielleicht sogar. Wie lassen sich die vielen verschiedenen Preisveränderungen aggregieren?
Offensichtlich ist ein einfacher Mittelwert aller Preisveränderungen nicht für die Aggregation geeignet, weil manche Güter für die Haushalte eine viel wichtigere Rolle spielen als andere. Wenn der Preis für Brot um 15 Prozent steigt, der Preis für Bügeleisen hingegen um 5 Prozent fällt, dann sollte die Preissteigerung bei Brot ein höheres Gewicht bekommen als die Preisverringerung bei Bügeleisen, denn für praktisch alle Haushalte ist Brot ein viel wichtigeres Gut als Bügeleisen.

Auf welche Weise können die Preisveränderungen der einzelnen Güter sinnvoll gewichtet werden? Wie lassen sich die Preisveränderungen sinnvoll zu einem Preisindex aggregieren? Diese Frage ist schon vor langer Zeit behandelt worden. Im Jahr 1871 erschien der Aufsatz “Die Berechnung einer mittleren Waarenpreissteigerung” des Ökonomen Ernst Louis Etienne Laypeyres in den “Jahrbüchern für Nationalökonomie und Statistik”. Der Preisindex von Laspeyres ist heutzutage der am meisten verwendete Verbraucherpreisindex.
Um die Gewichtung zu erklären, brauchen wir ein wenig Notation. Mit \(p_i^0\) wird der Preis von Gut \(i\) in der Ausgangsperiode bezeichnet (in Geldeinheiten pro Mengeneinheit, z.B. Euro/Stk). Die Ausgangsperiode heißt in der Preismessung auch Basisperiode. Mit \(p_i^1\) wird der Preis von Gut \(i\) in der Betrachtungsperiode bezeichnet. Die Preisveränderung von Gut \(i\) von der Basisperiode bis zur Betrachtungsperiode wird durch den Quotienten \[ \frac{p_i^1}{p_i^0} \] gemessen. Beispielsweise bedeutet \(p_i^1/p_i^0=1.05\), dass der Preis von Gut \(i\) um 5 Prozent gestiegen ist.
Laspeyres schlug 1871 vor, die Preisveränderungen mit dem Wert bzw. den Ausgabenanteilen der Güter zu gewichten. Je mehr Geld der typische Haushalt für ein Gut ausgibt, desto höher sollte das Gewicht dieses Gutes sein. Um dieses Gewicht zu finden, braucht man Angaben über die Mengen, die der typische Haushalt von jedem Gut verbraucht. Die Mengen sind in den beiden Perioden nicht unbedingt gleich, vor allem dann nicht, wenn die Preise sich verändern. Man muss sich also entscheiden, welche Mengen für die Berechnung verwendet werden sollen. Dem Preisindex von Laspeyres werden die Mengen der Basisperiode zugrunde gelegt. Wir bezeichnen sie mit \(q_i^0\).
In der Basisperiode gibt der typische Haushalt \[ w_i=p_i^0\cdot q_i^0 \] für Gut \(i\) aus. Die Gesamtausgaben betragen folglich \[ W=\sum_{i=1}^n p_i^0\cdot q_i^0, \] wobei \(n\) die Anzahl der betrachteten Güter ist. Die einzelnen Preisveränderungen werden nun mit der Gewichtung \(w_i/W\) aggregiert. Die gesamte Preisveränderung (die Veränderung des “Preisniveaus”) lautet \[ I_{0,1}^{Laspeyres}=\sum_{i=1}^n \frac{p_i^1}{p_i^0}\frac{w_i}{W}. \] Der Preisindex \(I_{0,1}^{Laspeyres}\) gibt also an, wie hoch das Preisniveau in Periode 1 im Vergleich zu Periode 0 ist. Man erkennt, dass es sich um den gewichteten Mittelwert der Preisquotienten handelt. Formal ist dieser Ausdruck vollkommen analog aufgebaut zu dem gewichteten Mittelwert aus dem letzten Abschnitt.
Der Ausdruck lässt sich so umformen, dass sich eine elegante ökonomische Interpretation ergibt.
\[\begin{align*} I_{0,1}^{Laspeyres} &= \sum_{i=1}^n \frac{p_i^1}{p_i^0}\frac{w_i}{W}\\ &= \sum_{i=1}^n \frac{p_i^1}{p_i^0}\frac{p_i^0\cdot q_i^0}{\sum_{j=1}^n p_j^0\cdot q_j^0}\\ &= \sum_{i=1}^n \frac{p_i^1\cdot q_i^0}{\sum_{j=1}^n p_j^0\cdot q_j^0}\\ &= \frac{\sum_{i=1}^n p_i^1\cdot q_i^0}{\sum_{i=1}^n p_i^0\cdot q_i^0}. \end{align*}\]
Der Laspeyres-Preisindex kann also als Quotient geschrieben werden. Im Nenner steht, wie viel der typische Haushalt in der Basisperiode für alle Güter ausgegeben hat. Im Zähler steht, wie viel er in der Berichtsperiode für die gleichen Mengen ausgegeben hätte (auch wenn er in Periode 1 tatsächlich andere Mengen als in Periode 0 gekauft hat).
Das Mengengerüst nennt man in der Preismessung auch anschaulich den Warenkorb. Das statistische Bundesamt befragt regelmäßig alle paar Jahre eine große Zahl von Haushalten nach ihren Einkäufen. Auf diese Weise wird der Warenkorb ermittelt, den der “typische Haushalt” in Deutschland einkauft und der für die Berechnung des sogenannten Verbraucherpreisindex genutzt wird. Der Begriff “Warenkorb” ist zwar anschaulich, aber nicht ganz passend, weil wir für den Preisindex gar nicht unbedingt alle eingekauften Mengen benötigen, sondern nur ihre Gewichtung.
Beispiel:
Der folgende Dataframe D zeigt, wie hoch die Preise der fünf Güter A, B, C, D, E in den Jahren 2022 und 2023 waren. Außerdem ist angegeben, welche Mengen von den Gütern im Basisjahr gekauft wurden.
Gut Preis2022 Preis2023 Menge2022
1 A 100.0 108.00 3.00
2 B 10.0 11.00 23.00
3 C 0.5 0.48 420.00
4 D 7.0 7.10 21.00
5 E 800.0 810.00 0.15Aus diesen Angaben ergibt sich der Wert des Warenkorbs im Jahr 2022 (d.h. in Periode 0) als
sum(D$Preis2022 * D$Menge2022)[1] 1007Der gleiche Warenkorb hätte im Jahr 2023 (also in Periode 1)
sum(D$Preis2023 * D$Menge2022)[1] 1049.2gekostet. Der Laspeyres-Preisindex beträgt also gerundet
I_2022_2023 <- sum(D$Preis2023 * D$Menge2022) /
sum(D$Preis2022 * D$Menge2022)
round(I_2022_2023, 3)[1] 1.042Das Preisniveau ist also um 4.2 Prozent gestiegen.
Die Inflationsrate von Periode 0 nach Periode 1 ergibt sich als \[ \text{Inflationsrate}=(I_{0,1}^{Laspeyres}-1)\times 100 \%. \]
Mit Hilfe des Preisindex bzw. der Inflationsrate kann man nominale Größen in reale Größen umrechnen, also den Preiseffekt herausrechnen.
Beispiel:
In dem oben gezeigten Beispiel beträgt die Inflationsrate 4.2 Prozent. Wenn der durchschnittliche Monatslohn einer Firma von 3500 Euro im Jahr 2022 auf 3600 Euro im Jahr 2023 gestiegen ist, dann bedeutet das für die Angestellten der Firma, dass ihr Lohn nominal um rund
round((3600 / 3500 - 1) * 100, 1)[1] 2.9Prozent gestiegen ist. Die Kaufkraft eines Euros ist jedoch gesunken, weil man für 1 Euro im Jahr 2023 weniger kaufen kann als für 1 Euro im Jahr 2022. Der reale Monatslohn beträgt im Jahr 2023 (bezogen auf das Basisjahr 2022) nur noch
round(3600 / I_2022_2023)[1] 3455Real ist der Lohn also gar nicht gestiegen, sondern gefallen.
Es gibt noch weitere Ansätze zur Aggregation von Preisveränderungen. Der Preisindex von Paasche wird beispielsweise mit den Mengen der Berichtsperiode berechnet, also mit \(q_i^1\). In diesem Kurs gehen wir auf diese alternativen Ansätze jedoch nicht näher ein.
Beispiel:
Das statistische Bundesamt veröffentlicht für unterschiedliche Aggregationsniveaus die Preise von Gütern. Die feinste verfügbare Aufgliederung bietet der Datensatz 61111BM007 mit fast 700 verschiedenen Gütern. Mit dem folgenden Code lässt sich der vollständige Datensatz für die Monatsdaten der letzten 5 Jahre über die API des Bundesamts in R einlesen (sofern man sich dort kostenlos als Nutzer registriert hat).
library(wiesbaden)
preise <- retrieve_data("61111BM007",
genesis=c(db='de',
user="xxxxxxxxxx",
password="xxxxxxxxxxxxxxxx"))Die ersten Zeilen sehen so aus:
head(preise) id61111 DINSG CC13Z1 MONAT JAHR PREIS1_val PREIS1_qual
1 D DG CC13-0111101100 MONAT01 2020 99.6 e
2 D DG CC13-0111101100 MONAT01 2021 101.2 e
3 D DG CC13-0111101100 MONAT01 2022 102.7 e
4 D DG CC13-0111101100 MONAT01 2023 127.6 e
5 D DG CC13-0111101100 MONAT01 2024 141.0 e
6 D DG CC13-0111101100 MONAT02 2020 99.1 eDie Spalte CC13Z1 bezeichnet das Gut. Die Codeliste für diese Variable erhält man durch den folgenden Code.
codelist <- retrieve_valuelabel("CC13Z1",
genesis=c(db='de',
user="xxxxxxxxxx",
password="xxxxxxxxxxxxxxxx"))head(codelist) CC13Z1 description
1 CC13-0111101100 Reis
2 CC13-0111109100 Reiszubereitung
3 CC13-0111201100 Weizenmehl
4 CC13-0111203100 Grieß, Roggenmehl oder Ähnliches
5 CC13-0111311100 Weißbrot
6 CC13-0111312100 Roggenbrot oder MischbrotAls Beispielanwendung suchen wir das Produkt, das im Zeitraum vom Januar 2020 bis zum Januar 2024 den stärksten Preisrückgang verzeichnete.
I_2020_2024 <- preise %>%
filter(MONAT=="MONAT01") %>%
group_by(CC13Z1) %>%
summarise(Index=last(PREIS1_val)/first(PREIS1_val)) %>%
arrange(Index)Die Funktionen first und last suchen (bei gruppierten Daten) den ersten bzw. letzten Wert heraus. In diesem Fall handelt es sich dabei um die Werte vom Januar 2020 (erster Wert) und Januar 2024 (letzter Wert). Durch die arrange-Funktion werden die Werte aufsteigend nach dem Index sortiert. Der ersten Werte (also die stärksten Preisrückgänge) sind
head(I_2020_2024)# A tibble: 6 × 2
CC13Z1 Index
<chr> <dbl>
1 CC13-0731112100 0.383
2 CC13-0735015000 0.62
3 CC13-0733100200 0.743
4 CC13-0733200620 0.778
5 CC13-0731121200 0.789
6 CC13-0911210200 0.824Die Codeliste können wir mit Hilfe der Funktion left_join rechts an den Dataframe anfügen.
left_join(I_2020_2024, codelist, by="CC13Z1") %>% head()# A tibble: 6 × 3
CC13Z1 Index description
<chr> <dbl> <chr>
1 CC13-0731112100 0.383 Bahnfahrt, Nahverkehr, Job- oder Schülerticket
2 CC13-0735015000 0.62 Monatskarte Verbundverkehr, Erwachsene
3 CC13-0733100200 0.743 Flugticket, Inland, Business
4 CC13-0733200620 0.778 Flugticket, Mittelamerika, Economy
5 CC13-0731121200 0.789 Bahnfahrt, Allgemeiner Fernverkehr
6 CC13-0911210200 0.824 Fernsehgerät Die Preise für Fahrkarten und Flugtickets sind also in dem Betrachtungszeitraum besonders stark gefallen.