14  Zusammenhangsmaße

In den Wirtschaftswissenschaften interessieren wir uns sehr oft für den Zusammenhang zwischen Variablen. Gibt es einen Zusammenhang? Wenn ja, ist er stark oder schwach? Und ist der Zusammenhang gleichgerichtet oder gegenläufig? Um solche Fragen zu beantworten, gibt es Zusammenhangsmaße. Wir behandeln in diesem Kapitel drei Maße, nämlich die Kovarianz, den Korrelationskoeffizienten und den Rangkorrelationskoeffizienten.

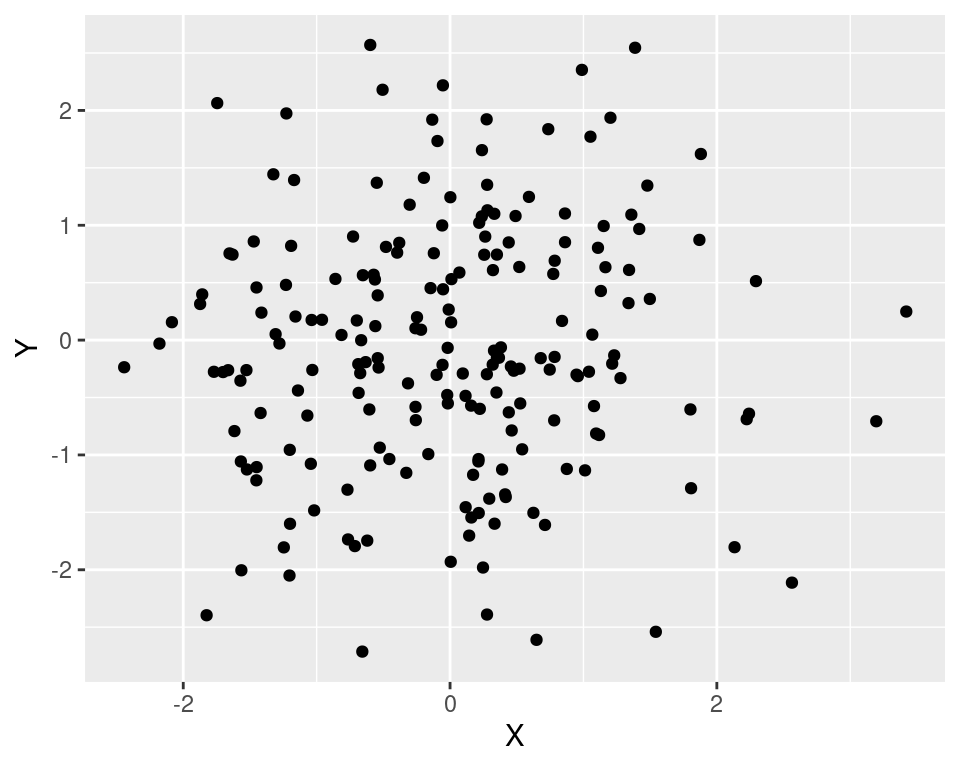
Bevor wir diese Maße im Detail ansehen, sei daran erinnert, dass auch die grafische Darstellung von bivariaten Verteilungen - vor allem als Streudiagram - hilfreich ist. Beispielsweise kann man an dem folgenden Plot erkennen, dass zwischen den Variablen \(X\) und \(Y\) kaum ein Zusammenhang besteht.

In dem nächsten Plot ist ein starker gleichläufiger Zusammenhang zu sehen.

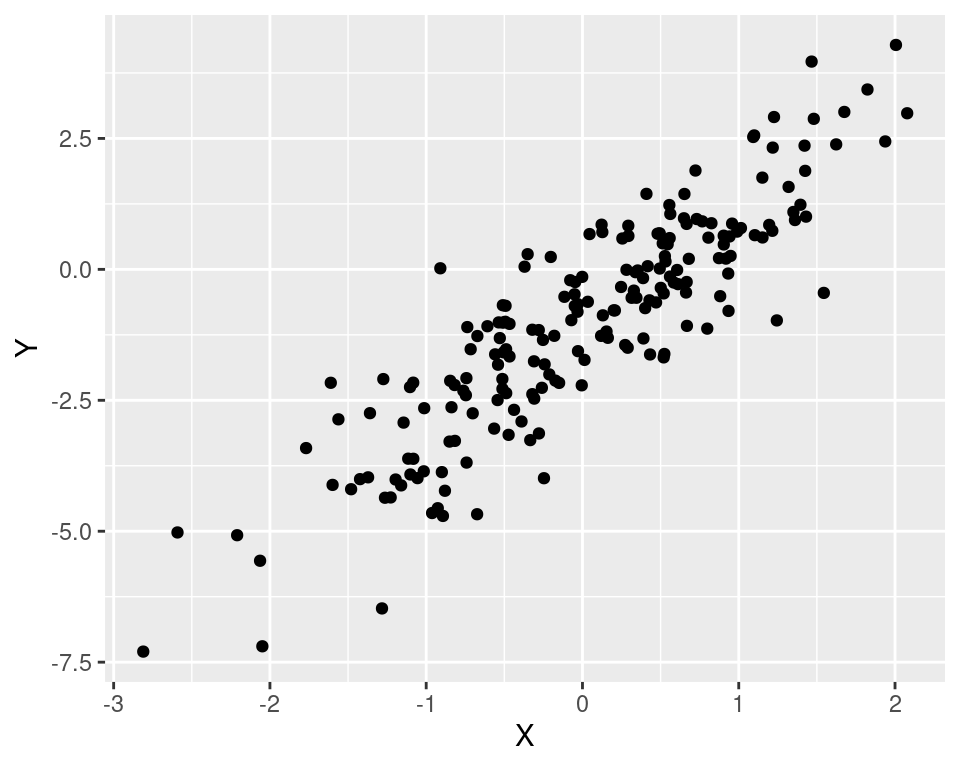
Und der folgende Plot zeigt einen schwachen gegenläufigen Zusammenhang.

14.1 Kovarianz

Wir schreiben die Beobachtungen allgemein wieder als \[ (x_1,y_1), (x_2,y_2), ..., (x_n,y_n). \] Die Kovarianz (engl. covariance, mit der Betonung auf der zweiten Silbe) von \(X\) und \(Y\) ist so ähnlich definiert, wie die Varianz. Und zwar \[ s_{XY} = \frac{1}{n}\sum_{i=1}^n (x_i-\bar x)(y_i - \bar y) \] Schauen wir uns diesen Ausdruck genauer an. Summiert werden die Produkte aus \((x_i-\bar x)\) und \((y_i-\bar y)\), die Faktoren sind also die Abweichungen der beiden Variablen von ihrem Mittelwert. Wenn \(x_i\) kleiner ist der der Mittelwert \(\bar x\), ist der Ausdruck \((x_i-\bar x)\) negativ. Wenn \(x_i\) größer ist, ist er positiv. Analog für \(Y\).

Wenn nun kleine \(x_i\) tendenziell mit kleinen \(y_i\) zusammen auftreten und große \(x_i\) mit großen \(y_i\), dann sind die Produkte in der Summe tendenziell positiv. Wenn hingegen kleine \(x_i\) tendenziell zusammen mit großen \(y_i\) auftreten und große \(x_i\) mit kleinen \(y_i\), dann werden positive Faktoren mit negativen Faktoren multipliziert, so dass die Summe tendenziell negativ ist.

Ähnlich wie für die Varianz gibt es auch für die Kovarianz eine alternative Schreibweise. Man erhält sie, indem man das Produkt ausmultipliziert und die Terme geeignet zusammenfasst. Es ergibt sich \[ s_{XY}=\left(\frac{1}{n}\sum_{i=1}^n x_i y_i\right) - \bar x\bar y \] Zwei weitere Schreibweisen, die manchmal nützlich sind, lauten \[ s_{XY}=\frac{1}{n}\sum_{i=1}^n (x_i-\bar x)y_i \] oder \[ s_{XY}=\frac{1}{n}\sum_{i=1}^n x_i (y_i-\bar y). \] Ein Sonderfall ist die Kovarianz einer Variablen mit sich selber. In diesem Fall ist \(X=Y\) und es gilt \(s_{XX}=s_X^2\). Die Kovarianz mit sich selbst ist also gerade die Varianz einer Variable.

Die Kovarianz kann nur für metrisch skalierte Variablen sinnvoll berechnet werden, weil u.a. die Mittelwerte in die Berechnung eingehen.

Zusammenfassend gilt:

• Eine positive Kovarianz zeigt einen gleichläufigen linearen Zusammenhang zwischen \(X\) und \(Y\).

• Eine negative Kovarianz zeigt einen gegenläufigen linearen Zusammenhang zwischen \(X\) und \(Y\).

• Eine Kovarianz von (fast) 0 zeigt (fast) keinen linearen Zusammenhang.

Vorsicht: Eine Kovarianz von 0 zeigt nicht unbedingt an, dass es keinerlei Zusammenhang zwischen den Variablen gibt, sondern nur, dass es keinen linearen Zusammenhang gibt. Es ist durchaus möglich, dass andere Formen von Zusammenhängen vorliegen, z.B. quadratische. Das folgende Bild zeigt eine Punktewolke für die Variablen \(X\) und \(Y\), deren Kovarianz 0 ergibt. Hier liegt zwar kein linearer, aber offensichtlich ein sehr deutlicher quadratischer Zusammenhang vor. Man darf also aus einer Kovarianz von 0 nicht schließen, dass die Variablen unabhängig voneinander sind.

In R gibt es die Funktion cov zur Berechnung der Kovarianz. In der Definition dieser Funktion steht (wie schon bei der Varianz) in dem Bruch vor der Summe nicht \(n\) im Nenner, sondern \(n-1\). Wir ignorieren diesen Unterschied, weil er bei einem großen Umfang \(n\) sehr klein ist. Wenn Sie den Wert exakt berechnen wollen, muss die Kovarianz analog zur Varianz mit dem Faktor \((n-1)/n\) umskaliert werden.

Beispiel:

Wir laden den Datensatz aktienkurse.

K <- read.csv("../data/aktienkurse.csv")
head(K)

        date   BMW    VOW    ALV    MUV
1 2014-03-03 81.65 183.20 125.45 154.20
2 2014-03-04 82.78 187.15 126.90 156.90
3 2014-03-05 82.48 185.60 126.20 156.20
4 2014-03-06 83.08 186.25 126.65 156.00
5 2014-03-07 81.86 183.55 124.20 153.35
6 2014-03-10 80.52 178.90 122.85 152.50

Der Datensatz enthält die Kursverläufe der Autoaktien BMW und Volkswagen (VOW) sowie der Versicherungsaktien Allianz (ALV) und Münchner Rückversicherung (MUV) vom 03. März 2014 bis zum 01. März 2024. Nun berechnen wir die Tagesrenditen der vier Aktien (vgl. Kapitel 8.1) und fügen sie an den Dataframe an. Für den ersten Tag kann keine Rendite berechnet werden, weil der Kurs des Vortags fehlt. Am 03. März 2014 sind die vier Tagesrenditen fehlende Werte. Darum wird der erste Tag aus dem Dataframe entfernt.

K <- K %>%
     mutate(r_BMW = (BMW-lag(BMW))/lag(BMW)*100,
            r_VOW = (VOW-lag(VOW))/lag(VOW)*100,
            r_ALV = (ALV-lag(ALV))/lag(ALV)*100,
            r_MUV = (MUV-lag(MUV))/lag(MUV)*100) %>%
     filter(date > min(date))

Die Kovarianz zwischen den Renditen der beiden Autoaktien bzw. zwischen den beiden Versicherungsaktien beträgt

cov(K$r_BMW, K$r_VOW)

[1] 2.867872

cov(K$r_MUV, K$r_ALV)

[1] 1.708416

Beide Werte sind positiv. Eine hohe Tagesrendite von BMW geht also tendenziell mit einer hohen Tagesrendite von VW einher. Für die Versicherungsaktien gilt das auch.

Die Kovarianz zwischen den Renditen der Autoaktie VW und der Versicherungsaktie Allianz beträgt

cov(K$r_ALV, K$r_VOW)

[1] 1.894598

Mit der Funktion cov kann man auch die Kovarianzen von mehr als zwei Variablen bestimmen. In diesem Fall wird die Matrix der paarweisen Kovarianzen ausgegeben. Da die Kovarianz symmetrisch ist (d.h. \(s_{XY}=s_{YX}\)), ist die Matrix der paarweisen Kovarianzen symmetrisch, also identisch zur transponierten Kovarianzmatrix.

Für die Berechnung der Kovarianzmatrix speichern wir die vier Spalten mit den Tagesrenditen in einem separaten Dataframe (renditen).

renditen <- select(K, r_BMW, r_VOW, r_ALV, r_MUV)
cov(renditen)

         r_BMW    r_VOW    r_ALV    r_MUV
r_BMW 3.091846 2.867872 1.701101 1.423023
r_VOW 2.867872 4.721933 1.894598 1.637306
r_ALV 1.701101 1.894598 2.182399 1.708416
r_MUV 1.423023 1.637306 1.708416 2.281522

Leider ist die Kovarianz nicht normiert. Darum kann man ihre Höhe nicht gut interpretieren. Man kann also an diesen Kovarianzen nicht erkennen, ob die Renditen von zwei Autoaktien stärker zusammenhängen als zwischen einer Autoaktie und einer Versicherungsaktie. Dieses Interpretationsproblem lösen wir im nächsten Abschnitt.

14.2 Korrelation

Der Korrelationskoeffizient (engl. coefficient of correlation, oft auch einfach correlation) ist eine normierte Kovarianz. Der Korrelationskoeffizient zwischen \(X\) und \(Y\) ist definiert als \[ r_{XY}=\frac{s_{XY}}{s_Xs_Y} \] Der Korrelationskoeffizient ist also die Kovarianz von \(X\) und \(Y\) dividiert durch die beiden Standardabweichungen. Da die Kovarianz nur für zwei metrisch skalierte Variablen sinnvoll berechnet werden kann, gilt das auch für den Korrelationskoeffizienten.

Ersetzt man \(s_{XY}\), \(s_X\) und \(s_Y\) durch ihre Definitionen, so erhält man \[ r_{XY}=\frac{\frac{1}{n}\sum_{i=1}^n (x_i-\bar x)(y_i-\bar y)} {\sqrt{\frac{1}{n}\sum_{i=1}^n (x_i-\bar x)^2} \sqrt{\frac{1}{n}\sum_{i=1}^n (y_i-\bar y)^2}} \] bzw. nach Kürzen von \(1/n\) \[ r_{XY}=\frac{\sum_{i=1}^n (x_i-\bar x)(y_i-\bar y)} {\sqrt{\sum_{i=1}^n (x_i-\bar x)^2} \sqrt{\sum_{i=1}^n (y_i-\bar y)^2}}. \] Der Korrelationskoeffizient hat einige Eigenschaften, die seine Interpretation erleichtern:

• Der Wert liegt immer zwischen -1 und 1.

• Die Stärke des linearen Zusammenhangs wird durch den Betrag ausgedrückt. Ein Wert von -1 zeigt einen perfekten gegenläufigen linearen Zusammenhang an, ein Wert von +1 einen perfekten gleichläufigen linearen Zusammenhang.

• Wenn kein linearer Zusammenhang vorliegt, ist der Korrelationskoeffizient 0. Wie bei der Kovarianz darf man jedoch aus einem Korrelationskoeffizienten von 0 nicht auf Unabhängigkeit der beiden Variablen schließen. Es könnte nicht-lineare Formen des Zusammenhangs geben.

• Der Korrelationskoeffizient ist (wie auch die Kovarianz) symmetrisch, d.h. \(r_{XY}=r_{YX}\).

• Die Korrelation einer Variablen mit sich selbst ist 1.

Beispiel:

In R wird der Korrelationskoeffizient mit der Funktion cor errechnet. Die Korrelation zwischen der Tagesrendite von VW und der Tagesrendite von BMW beträgt

cor(K$r_VOW, K$r_BMW)

[1] 0.7505697

Der Wert ist recht groß, es liegt also ein deutlicher Zusammenhang vor. Eine große Rendite von VW geht tendenziell einher mit einer großen Rendite von BMW. Das deutet auf einen Brancheneffekt hin. Die Korrelation zwischen den beiden Versicherungsaktien ist sogar noch etwas größer.

cor(K$r_ALV, K$r_MUV)

[1] 0.7656216

Nun bestimmen wir die Korrelationen für Paare von jeweils einer Auto- und einer Versicherungsaktie.

cor(K$r_BMW, K$r_ALV)

[1] 0.6548687

cor(K$r_BMW, K$r_MUV)

[1] 0.535785

cor(K$r_VOW, K$r_ALV)

[1] 0.5901875

cor(K$r_VOW, K$r_MUV)

[1] 0.4988357

Diese Werte sind immer noch recht groß, wenn auch niedriger als die Korrelationen innerhalb einer Branche. Es gibt also nicht nur einen Brancheneffekt, sondern auch einen großen Markteffekt, der alle (vier) Aktien ähnlich beeinflusst.

Mit der Funktion cor kann man auch die Korrelationskoeffizienten von mehr als zwei Variablen bestimmen. In diesem Fall wird die Matrix der paarweisen Korrelationskoeffizienten ausgegeben. Für die Berechnung verwenden wir wieder den weiter oben definierten Dataframe renditen.

cor(renditen)

          r_BMW     r_VOW     r_ALV     r_MUV
r_BMW 1.0000000 0.7505697 0.6548687 0.5357850
r_VOW 0.7505697 1.0000000 0.5901875 0.4988357
r_ALV 0.6548687 0.5901875 1.0000000 0.7656216
r_MUV 0.5357850 0.4988357 0.7656216 1.0000000

Korrelationsmatrizen sind symmetrisch und haben auf der Diagonale überall eine 1 stehen.

14.3 Rangkorrelation

Der Korrelationskoeffizient kann nur für metrisch skalierte Merkmale sinnvoll berechnet werden. Wie kann man vorgehen, wenn eine (oder beide) Variablen ordinal skaliert sind?

14.3.1 Ränge

Bei ordinal skalierten Variablen sind die Abstände zwischen den Ausprägungen (bis auf ihr Vorzeichen) bedeutungslos. Man kann also ohne Informationsverlust die Werte transformieren, solange Werte, die vor der Transformation größer waren, nach der Transformation immer noch größer sind.

Eine einfache Lösung dieses Problems besteht darin, nicht die letztlich beliebigen Werte der ordinal skalierten Variablen selbst zu betrachten, sondern ihre Ränge (engl. ranks). Der kleinste Wert bekommt den Rang 1, der zweitkleinste den Rang 2, und der größte Wert den Rang \(n\). Der Übergang von den Werten zu den Rängen erfolgt für beide Variablen, auch wenn nur eine der beiden Variablen ordinal skaliert ist und die andere metrisch skaliert ist.

In R lassen sich die Ränge der Elemente eines Vektors mit der Funktion rank bestimmen.

Beispiel:

Der Vektor x hat sieben Werte, nämlich (6.6, 1.7, 2, 99, -3.2, 0, 8). Die Ränge sind:

x <- c(6.6, 1.7, 2, 99, -3.2, 0, 8)
rank(x)

[1] 5 3 4 7 1 2 6

Das erste Element des Vektors ist also der fünftkleinste Wert, den kleinsten Wert (nämlich -3.2) findet man an der fünften Position, den zweitkleinsten an der sechsten Position und den größten (Rang 7) in der Mitte auf Position 3.

14.3.2 Bindungen

Wenn ein Wert mehrfach vorkommt, spricht man von Bindungen (engl. ties). In diesen Fällen ist nicht eindeutig klar, wie die Ränge vergeben werden sollen. Die Funktion rank hat die Option ties.method, mit der man festlegen kann, wie die Ränge im Fall von Bindungen vergeben werden sollen. Die Standardeinstellung ist average, d.h. es wird allen Positionen der Durchschnittsrang zugewiesen. In diesem Kurs nutzen wir nur diese Standardeinstellung, so dass man die Option einfach weglassen kann.

Beispiel:

Der Vektor y hat sieben Werte, nämlich (6, 6, 2, 8, -3.2, 0, 2). Die Ränge sind mit der Methode average folgende:

y <- c(6, 6, 2, 8, -3.2, 0, 2)
rank(y)

[1] 5.5 5.5 3.5 7.0 1.0 2.0 3.5

14.3.3 Rangkorrelation

Der Rangkorrelationskoeffizient (engl. rank correlation coefficient) ist der Korrelationskoeffizient der Ränge. Man ersetzt die \(x_i\) und \(y_i\) durch die Ränge \(R(x_i)\) und \(R(y_i)\), sonst ändert sich nichts.

In R ist die Funktion zur Berechnung des Rangkorrelationskoeffizienten cor, also die gleiche Funktion wie für den normalen Korrelationskoeffizienten. Um anzuzeigen, dass die Rangkorrelation berechnet werden soll, gibt man die Option method="spearman" an (der Statistiker Charles Spearman hat dieses Maß 1904 vorgeschlagen). Im Fall von Bindungen werden Durchschnittsränge vergeben.

Einige Eigenschaften des Rangkorrelationskoeffizienten:

• Der Rangkorrelationskoeffizient ist symmetrisch und liegt immer im Intervall \([-1,1]\).

• Er nimmt den Wert 1 an, wenn ein perfekter gleichläufiger monotoner Zusammenhang besteht.

• Er nimmt den Wert -1 an, wenn ein perfekter gegenläufiger monotoner Zusammenhang besteht.

• Wenn es keinen Zusammenhang gibt, liegt der Wert bei 0. Auch hier gilt: Ein Wert von 0 ist kein Beweis für Unabhängigkeit der beiden Variablen. Es könnte einen nicht-monotonen Zusammenhang geben, der zu einem Rangkorrelationskoeffizienten von 0 führt.

Beispiel:

In dem Datensatz mocksoep sind die beiden Variablen lifesat für die allgemeine Lebenszufriedenheit und healthsat für die subjektive Zufriedenheit mit dem Gesundheitszustand einer Person enthalten. Beide Variablen sind ordinal skaliert, denn es ist nicht sinvoll zu sagen, dass eine Zufriedenheit von 8 doppelt so groß ist wie von 4. Man kann nur sagen, dass 8 eine höhere Zufriedenheit als 4 widerspiegelt.

Wir laden den Datensatz und berechnen den Rangkorrelationskoeffizienten zwischen den beiden Variablen.

soep <- read_csv("../data/mocksoep.csv", 
                 col_types = "nnnnfnnnffnnncnnnnn") 
cor(soep$lifesat, 
    soep$healthsat, 
    method="spearman")

[1] 0.4677158

Dieser Wert ist recht hoch. Zwischen der allgemeinen Lebenszufriedenheit und der Zufriedenheit mit der Gesundheit besteht offenbar ein enger Zusammenhang. Zum Vergleich berechnen wir den Rangkorrelationskoeffizienten zwischen der Lebenszufriedenheit und dem (metrisch skalierten) Nettoeinkommen postgov.

cor(soep$lifesat, 
    soep$postgov, 
    method="spearman")

[1] 0.2202521

Auch hier besteht ein deutlicher gleichläufiger Zusammenhang, aber er ist viel niedriger.

14.4 Kontingenzkoeffizient

Wie lässt sich die Stärke des Zusammenhangs zweier Variablen messen, wenn (mindestens) eine davon nominal skaliert ist? In diesem Fall kann man nicht mehr von einer Richtung des Zusammenhangs sprechen, nur noch von seiner Stärke.

Ein gängiges Maß zur Messung der Stärke des Zusammenhangs ist der Kontingenzkoeffizient. Er basiert auf der sogenannten \(\chi^2\)-Statistik (sprich: chi-Quadrat, wobei das “ch” von “chi” wie in “ich” ausgesprochen wird, im Englischen ist die Aussprache “kai-squared”). Die \(\chi^2\)-Statistik ist \[ \chi^2= \sum_{j=1}^J \sum_{k=1}^K \frac{\left(n_{jk}-\frac{n_{j\cdot}n_{\cdot k}}{n}\right)^2}{\frac{n_{j\cdot}n_{\cdot k}}{n}}. \] Dieser Ausdruck sieht auf den ersten Blick komplex aus, aber bei genauerer Betrachtung ist er eigentlich recht einfach aufgebaut. Zum Verständnis ist es nützlich, den Begriff der Unabhängigkeit aus Kapitel 13.2 zu wiederholen. Zwei Variablen heißen unabhängig, wenn sich aus den beiden Randverteilungen die gemeinsame Verteilung wie folgt ergibt: \[ n_{jk}=\frac{n_{j\cdot}n_{\cdot k}}{n}. \] Wenn die Variablen unabhängig sind, besteht keinerlei Zusammenhang zwischen ihnen. Die \(\chi^2\)-Statistik aggregiert nun alle quadrierten Abweichungen von der Unabhängigkeit. Dabei werden die Abweichungen immer in Relation gesetzt zu der Größe, die sich im Fall der Unabhängigkeit ergäbe.

Kurz gesagt, misst die \(\chi^2\)-Statistik, wie stark die gemeinsame Verteilung zweier Variablen von der Unabhängigkeit abweicht. Wenn \(\chi^2=0\) ist, liegt Unabhängigkeit vor. In allen anderen Fällen ist \(\chi^2\) positiv.

Der Kontingenzkoeffizient ist eine Transformation der \(\chi^2\)-Statistik, so dass der Wert zwischen 0 (Unabhängigkeit) und 1 (vollständige Abhängigkeit) liegt. Die Definition lautet \[ C=\sqrt{\frac{\chi^2}{\chi^2+n}\cdot \frac{\min\{J,K\}}{\min\{J,K\}-1}}, \] wobei \(\min\{J,K\}\) entweder die Zeilenzahl oder die Spaltenzahl ist, je nachdem, welcher Wert kleiner ist.

In R gibt es standardmäßig keine Funktion zur Berechnung von \(C\), aber das Paket DescTools bietet eine solche Funktion. Das Paket muss einmalig installiert werden und kann dann mit

library(DescTools)

aktiviert werden. Anschließend gibt es die Funktion ContCoef. Die Syntax dieser Funktion ist naheliegend: die ersten beiden Argumente sind die Variablen; um die Korrektur der Zeilen- bzw. Spaltenzahl zu erhalten, muss man als drittes Argument die Option correct=TRUE setzen.

Beispiel:

Wir betrachten wieder die beiden Variablen sex und empllev aus dem SOEP-Datensatz mocksoep. Wie stark ist der Zusammenhang zwischen dem Geschlecht und dem Ausmaß der Erwerbstätigkeit im Jahr 2020?

jahr <- 2020
soep <- read_csv("../data/mocksoep.csv", 
                 col_types = "nnnnfnnnffnnncnnnnn") %>%
        filter(year == jahr)
ContCoef(soep$sex, soep$empllev, correct=TRUE)

[1] 0.390046

Der Wert liegt zwar weit von der 1 entfernt, weicht aber auch sehr deutlich von der Unabhängigkeit ab. Man kann die Stärke des Zusammenhangs durchaus als recht hoch bezeichnen.

Zum Vergleich berechnen wir die Stärke des Zusammenhangs zwischen dem Geschlecht sex und der Lebenszufriedenheit lifesat im Jahr 2018,

ContCoef(soep$sex, soep$lifesat, correct=TRUE)

[1] 0.02539486

Hier kann man nur einen sehr schwachen Zusammenhang erkennen.

14.5 Korrelation und Kausalität

Wenn zwei Variablen miteinander zusammenhängen, zieht man leicht den Schluss, dass eine der Variablen einen kausalen Einfluss auf die andere Variable hat. Das ist leider eine unzulässige Schlussfolgerung. Korrelation impliziert keine Kausalität! Und das gilt natürlich nicht nur für Korrelation im Sinne des Korrelationskoeffizienten, sondern auch für den Rangkorrelationskoeffizienten. Wenn wir einen Zusammenhang zwischen zwei Variablen feststellen, dürfen wir nicht automatisch einen kausalen Zusammenhang schlussfolgern. (Eine Ausnahme ist hier der Kontingenzkoeffizient, denn ein Wert von \(C=0\) impliziert, dass die beiden Variablen unabhängig voneinander sind.)

Wenn \(X\) und \(Y\) miteinander korreliert sind, kann das zwar daran liegen, dass \(X\) einen kausalen Einfluss auf \(Y\) hat, aber es kann auch andere Ursachen haben. So kann der kausale Effekt in die andere Richtung verlaufen, d.h. \(Y\) hat einen kausalen Effekt auf \(X\). Oder es kann eine Hintergrundvariable \(Z\) geben (confounder, vgl. Kapitel 13.4), die sowohl auf \(X\) als auch auf \(Y\) wirkt.

Leider sind Korrelationen meist weniger interessant als Kausalitäten, denn nur wenn wir einen kausalen Effekt gefunden haben, können wir eine Politikmaßnahme daraus ableiten. Wenn wir wissen, dass der Absatz steigt, weil wir den Preis senken, können wir eine gute Preispolitik entwickeln. Wenn wir wissen, dass die Inflation sinkt, weil die Zentralbank die Zinsen erhöht, kann eine stabilitätsorientierte Geldpolitik durchgeführt werden. Wenn wir wissen, dass Studierende erfolgreicher lernen, weil sie regelmäßig Hausarbeiten abgeben müssen, können wir produktivere Vorlesungen anbieten. Es reicht nicht aus, Zusammenhänge oder Korrelationen zu beobachten.

Wie man kausale Effekte ökonometrisch sauber ermitteln kann, lernen Sie in dem Modul Empirical Economics (wenn Sie VWL studieren).