absTab <- table(soep$sex, soep$empllev)
absTab
nicht voll teil
F 4710 3433 5172
M 3843 6086 198613 Bedingte Verteilungen
Bedingte Verteilungen (engl. conditional distributions) einer Variable geben die (meist relativen) Häufigkeiten an, die sich ergeben, wenn die andere Variable auf einen bestimmten Wert fixiert wird. Welche Werte nimmt \(X\) wie oft an, wenn wir wissen oder annehmen, dass \(Y\) den Wert \(y\) hat?
13.1 Definitionen
Formal: Die bedingte relative Häufigkeit von \(\xi_j\) unter der Bedingung \(Y=\eta_k\) ist für \(j=1,\ldots,J\) definiert als \[ f_{j|Y=\eta_k}=\frac{f_{jk}}{f_{\cdot k}}=\frac{n_{jk}}{n_{\cdot k}}. \] Der senkrechte Strich in \(f_{j|Y=\eta_k}\) wird meist ausgesprochen als “unter der Bedingung”, “wenn” oder “gegeben”.
Zusammen ergeben die bedingten relativen Häufigkeiten die bedingte Verteilung von \(X\) gegeben \(Y=\eta_k\), \[ f_{1|Y=\eta_k},f_{2|Y=\eta_k},\ldots,f_{J|Y=\eta_k}. \] Es gibt \(K\) verschiedene bedingte Verteilungen von \(X\), nämlich eine für jeden Wert \(\eta_1,\ldots,\eta_K\). Jede dieser bedingten Verteilungen ist eine univariate Verteilung.
Wenn wir die beiden Variablen vertauschen, erhalten wir die bedingten relativen Häufigkeiten von \(\eta_k\) unter der Bedingung \(X=\xi_j\), \[
f_{k|X=\xi_j}=\frac{f_{jk}}{f_{j\cdot}}=\frac{n_{jk}}{n_{j\cdot}}.
\] Und die bedingte Verteilung von \(Y\) gegeben \(X=\xi_j\) ist \[
f_{1|X=\xi_j},f_{2|X=\xi_j},\ldots,f_{K|X=\xi_j}.
\] Wie kann man bedingte Verteilungen in R berechnen? Der einfachste Weg besteht darin, durch den filter-Befehl sicherzustellen, dass die Bedingung für die eine Variable erfüllt ist, und anschließend die relativen Häufigkeiten für die andere Variable zu berechnen.
Beispiel:
Als Beispiel betrachten wir wieder den Datensatz mocksoep. Die Variable empllev steht für den Erwerbsumfang. Sie hat die drei Ausprägungen “nicht” für Leute, die keiner bezahlten Erwerbstätigkeit nachgehen (oder arbeitslos sind), “voll” für Vollzeitbeschäftigte und “teil” für Teilzeitbeschäftigte. Wie sieht die bedingte Verteilung der Variable empllev für Männer bzw. Frauen aus?
Um das zu bestimmen, erstellen wir zuerst die absolute Häufigkeitstabelle mit der Funktion table. Wir speichern die Tabelle unter dem Namen absTab.
Die bedingten relativen Häufigkeiten kann man leicht bestimmen mit der Funktion proportions, die wir schon zur Berechnung der relativen Häufigkeitstabelle verwendet haben. Durch die zusätzliche Angabe der Option margin wird erreicht, dass in R die bedingten relativen Häufigkeiten berechnet werden. Für margin=1 werden die bedingten relativen Häufigkeiten zeilenweise ermitteln, d.h. jede Zeile addiert sich auf 1. Für margin=2 erfolgt die Berechnung spaltenweise, d.h. jede Spalte addiert sich zu 1.
Da wir den Erwerbsumfang für das gegebene Geschlecht bestimmen möchten, gehen wir hier zeilenweise vor:
proportions(absTab, margin=1)
nicht voll teil
F 0.3537364 0.2578295 0.3884341
M 0.3225346 0.5107847 0.1666807Man erkennt, dass der größte Anteil der Frauen (über 39 Prozent) teilzeitbeschäftigt ist, nur etwa ein Viertel der Frauen ist vollzeitbeschäftigt. Bei den Männern ist gut die Hälfte vollzeitbeschäftigt und nur knapp 17 Prozent sind teilzeitbeschäftigt. Es gibt also einen deutlichen Unterschied in den bedingten Verteilungen.
Um die Verteilung des Geschlechts für einen gegebenen Erwerbsumfang zu erhalten, ändern wir die Option margin.
proportions(absTab, margin=2)
nicht voll teil
F 0.5506840 0.3606471 0.7225482
M 0.4493160 0.6393529 0.2774518Jetzt addieren sich alle drei Spalten jeweils zu 1. Man sieht, dass fast Dreiviertel der Teilzeitbeschäftigten weiblich sind, aber nur knapp 36 Prozent der Vollzeitbeschäftigten. Auch hier ist klar erkennbar, dass die bedingten Verteilungen sich sehr stark unterscheiden.
Als nächstes Beispiel untersuchen wir die bedingten Verteilungen der Lebenszufriedenheit gegeben das Geschlecht.
proportions(table(zufried, geschl), margin=2) geschl
zufried F M
1 0.003154337 0.003105329
2 0.007585430 0.007889215
3 0.017198648 0.017876626
4 0.024708975 0.023164079
5 0.079233947 0.075618968
6 0.076380023 0.085270667
7 0.192264363 0.203441041
8 0.352084116 0.352580781
9 0.173713857 0.162736047
10 0.073676305 0.068317247Beide Spalten addieren sich zu 1. Vergleicht man die Einträge, stellt man fest, dass es nur sehr kleine Unterschiede zwischen der bedingten Verteilung der Lebenszufriedenheit der Frauen und Männer gibt. Wenn alle bedingten Verteilungen exakt gleich sind, nennt man die beiden Variablen unabhängig oder deskriptiv unabhängig (siehe nächsten Abschnitt). Hier liegt zwar keine exakte Unabhängigkeit vor, aber man sieht, dass die Variablen zumindest fast unabhängig sind.
13.2 Unabhängigkeit
Wenn alle bedingten Verteilungen gleich sind, spricht man von Unabhängigkeit oder deskriptiver Unabhängigkeit. In diesem Fall ergibt sich das innere der Häufigkeitstabelle aus den beiden Randverteilungen - wohingegen sich im Allgemeinen nur die Ränder aus dem Inneren der Tabelle errechnen lassen. Konkret gilt bei Unabhängigkeit, dass für alle \(j=1,\ldots,J\) und \(k=1,\ldots,K\) \[ n_{jk} = \frac{n_{j\cdot}n_{\cdot k}}{n}. \] Die Häufigkeitstabelle sieht also im Fall der Unabhängigkeit so aus: \[ \begin{array}{|cc|cccc|c|}\hline &&&Y=&&\\ &&\eta_1&\eta_2&\ldots&\eta_K&\sum \\\hline &\xi_1& \frac{n_{1\cdot}n_{\cdot 1}}{n}& \frac{n_{1\cdot}n_{\cdot 2}}{n}&\ldots& \frac{n_{1\cdot}n_{\cdot K}}{n}&n_{1\cdot}\\ &\xi_2& \frac{n_{2\cdot}n_{\cdot 1}}{n}& \frac{n_{2\cdot}n_{\cdot 2}}{n}&\ldots& \frac{n_{2\cdot}n_{\cdot K}}{n}&n_{2\cdot}\\ X=&\vdots&\vdots&\vdots&&\vdots\\ &\xi_J& \frac{n_{J\cdot}n_{\cdot 1}}{n}& \frac{n_{J\cdot}n_{\cdot 2}}{n}&\ldots& \frac{n_{J\cdot}n_{\cdot K}}{n}&n_{J\cdot}\\ \hline &\sum&n_{\cdot 1}&n_{\cdot 2}&\ldots&n_{\cdot K}&n\\\hline \end{array} \] Tatsächlich kommt es in der Praxis nur sehr selten vor, dass eine exakte Unabhängigkeitstabelle vorliegt. Wir werden in Kapitel 14.4 einen Weg kennen lernen, wie man das Ausmaß der Abhängigkeit messen kann.
13.3 Bedingte Mittelwerte
Bedingte Verteilungen sind univariate Verteilungen. Sie werden zwar aus einer gemeinsamen Verteilung errechnet, aber die bedingten Verteilung, die wir betrachten, sind Verteilungen von nur einer Variablen (gegeben die Ausprägung einer anderen Variablen).
Da bedingte Verteilungen univariat sind, kann man alle Maße bestimmen, die wir bereits kennen gelernt haben, also z.B. Lagemaße oder Streuungsmaße. Um die bedingten Mittelwerte sinnvoll interpretieren zu können, muss die bedingte Variable metrisch skaliert sein, die bedingende Variable (also die Variable, auf die bedingt wird) darf hingegen beliebig skaliert sein. Die bedingten Mittelwerte von \(X\) gegeben \(Y=\eta_k\) sind (für alle \(k=1,\ldots,K\)) \[ \bar x_k=\frac{1}{n_{\cdot k}}\sum_{j=1}^J n_{jk}\xi_j \] bzw. wenn man direkt auf die Werte der Urliste zugreift \[ \bar x_k=\frac{1}{n_{\cdot k}}\sum_{i:y_i=\eta_k}x_i. \] Hierbei läuft die Summe über alle Beobachtungen \(i\), bei denen die Variable \(Y\) den Wert \(\eta_k\) annimmt. Summiert werden von diesen Beobachtungen die Werte der Variable \(X\). Offensichtlich gibt es nicht nur einen bedingten Mittelwert, sondern mehrere, nämlich \(K\) (wobei \(K\) die Anzahl der Ausprägungen von \(Y\) ist).
Tatsächlich haben wir im Kapitel 7 schon bedingte Mittelwerte kennen gelernt. Es sind nicht anderes als die gruppierten Mittelwerte, die man erhält, wenn man die Befehle group_by und summarise kombiniert. Die bedingende Variable ist das Argument der Funktion group_by, die bedingte Variable wird in der Funktion summarise angegeben. Der Dataframe, der als Output von group_by und summarise erzeugt wird, sieht also in der Notation der bedingten Mittelwerte so aus:
| \(Y=\eta_k\) | \(\bar x_k\) |
|---|---|
| \(\eta_1\) | \(\bar x_1\) |
| \(\eta_2\) | \(\bar x_2\) |
| \(\vdots\) | \(\vdots\) |
| \(\eta_K\) | \(\bar x_K\) |
Beispiel:
Wir untersuchen, wie im Datensatz mocksoep das Nettoeinkommen vom Erwerbsumfang abhängt. Dazu gruppieren wir den Datensatz zuerst nach der Variable, auf wir bedingen, also auf den Erwerbsumfang. Danach wird mit der Funktion summarise für jede Ausprägung der Mittelwert des metrisch skalierten Nettoeinkommens postgov berechnet.
soep %>%
group_by(empllev) %>%
summarise(m = mean(postgov))# A tibble: 3 × 2
empllev m
<fct> <dbl>
1 nicht 31297.
2 voll 52485.
3 teil 44802.Wenn eine Person keiner bezahlten Arbeit nachgeht, ist das Durchschnittsnettoeinkommen rund 33000 Euro, bei Vollzeitbeschäftigung ist es rund 54000 Euro. Wenig überraschend hängt das Nettoeinkommen also sehr deutlich vom Erwerbsumfang ab.
13.4 Simpsons Paradox
Bei der Berechnung von bedingten Mittelwerten (oder auch bedingten Anteilen) kann es zu einem scheinbaren Paradox kommen, wenn die Population nach zwei Variablen untergliedert wird (z.B. nach dem Geschlecht und dem Beruf). Im Gegensatz zu der Abbildung rechts ist das Simpson-Paradox jedoch nicht wirklich ein Paradox, sondern lässt sich mit etwas Überlegung erklären. Das Simpson-Paradox lässt sich am besten anhand eines Beispiels verstehen. Wir starten mit einem Beispiel, das auf künstlich erzeugten fiktiven Daten beruht. Zunächst laden wir den Datensatz und speichern ihn als Objekt X.
X <- read.csv("../data/simpson1.csv")Der Datensatz enthält Angaben zum Geschlecht (geschlecht mit den zwei Ausprägungen M=männlich, F=weiblich), zum ausgeübten Beruf (beruf mit den Ausprägungen A oder B) und zum Lohn von 5000 Personen. Wir untersuchen nun, wie hoch der Durchschnittslohn der Männer und der Frauen ist. Dazu berechnen wir die bedingten Mittelwerte (gegeben das Geschlecht) mit Hilfe der Befehle group_by und summarise.
X %>%
group_by(geschlecht) %>%
summarise(dlohn = mean(lohn))# A tibble: 2 × 2
geschlecht dlohn
<chr> <dbl>
1 F 2483.
2 M 3246.Offenbar verdienen in diesem Datensatz die Frauen im Durchschnitt erheblich weniger als die Männer.
Nun untersuchen wir die Durchschnittslöhne von Männern und Frauen in den beiden Berufen getrennt voneinander, d.h. als Bedingung werden nun sowohl das Geschlecht als auch der Beruf gesetzt, es gibt also nun vier bedingte Mittelwerte.
X %>%
group_by(beruf, geschlecht) %>%
summarise(dlohn = mean(lohn),
.groups="drop")# A tibble: 4 × 3
beruf geschlecht dlohn
<chr> <chr> <dbl>
1 A F 1000.
2 A M 496.
3 B F 5991.
4 B M 3994.Ein technischer Hinweis: Die Option .groups="drop" ist nicht unbedingt notwendig. Wenn sie entfällt, wird ein Dataframe als Output erzeugt, der nach der Variable beruf gruppiert ist. Da der Dataframe hier aber nur für die Darstellung des Output dient, brauchen wir diese Gruppierung nicht.
Wie man sieht, verdienen Frauen sowohl in Beruf A als auch in Beruf B im Durchschnitt deutlich mehr als die Männer. Obwohl die Frauen in beiden Berufen durchschnittlich mehr als die Männer verdienen, verdienen die Frauen in der Gesamtpopulation weniger als die Männer. Dies ist ein Beispiel für Simpsons Paradox.
Wie kann es zu so einem Effekt kommen? Um das zu verstehen, sehen wir uns an, wie hoch die Durchschnittlöhne in den beiden Berufen sind und wie hoch der Anteil der Frauen in den beiden Berufen ist. Eine sehr einfache Art, den Anteil zu berechnen, ist die Funktion mean mit einem logischen Ausdruck als Argument. Der logische Ausdruck hat den Wert 1, wenn er wahr ist, sonst hat er den Wert 0. Um den Anteil der Frauen zu bestimmen, ist die logische Bedingung geschlecht=="F".
X %>%
group_by(beruf) %>%
summarise(dlohn=mean(lohn),
anteilfrauen=mean(geschlecht=="F"))# A tibble: 2 × 3
beruf dlohn anteilfrauen
<chr> <dbl> <dbl>
1 A 883. 0.767
2 B 4543. 0.275Die Durchschnittslöhne in den beiden Berufen sind sehr unterschiedlich. In Beruf A ist der Lohn im Schnitt viel niedriger als in Beruf B. Auch der Anteil der Frauen hängt stark vom Beruf ab. In dem schlecht bezahlten Beruf A arbeiten überwiegend Frauen, in dem gut bezahlten Beruf B überwiegend Männer.
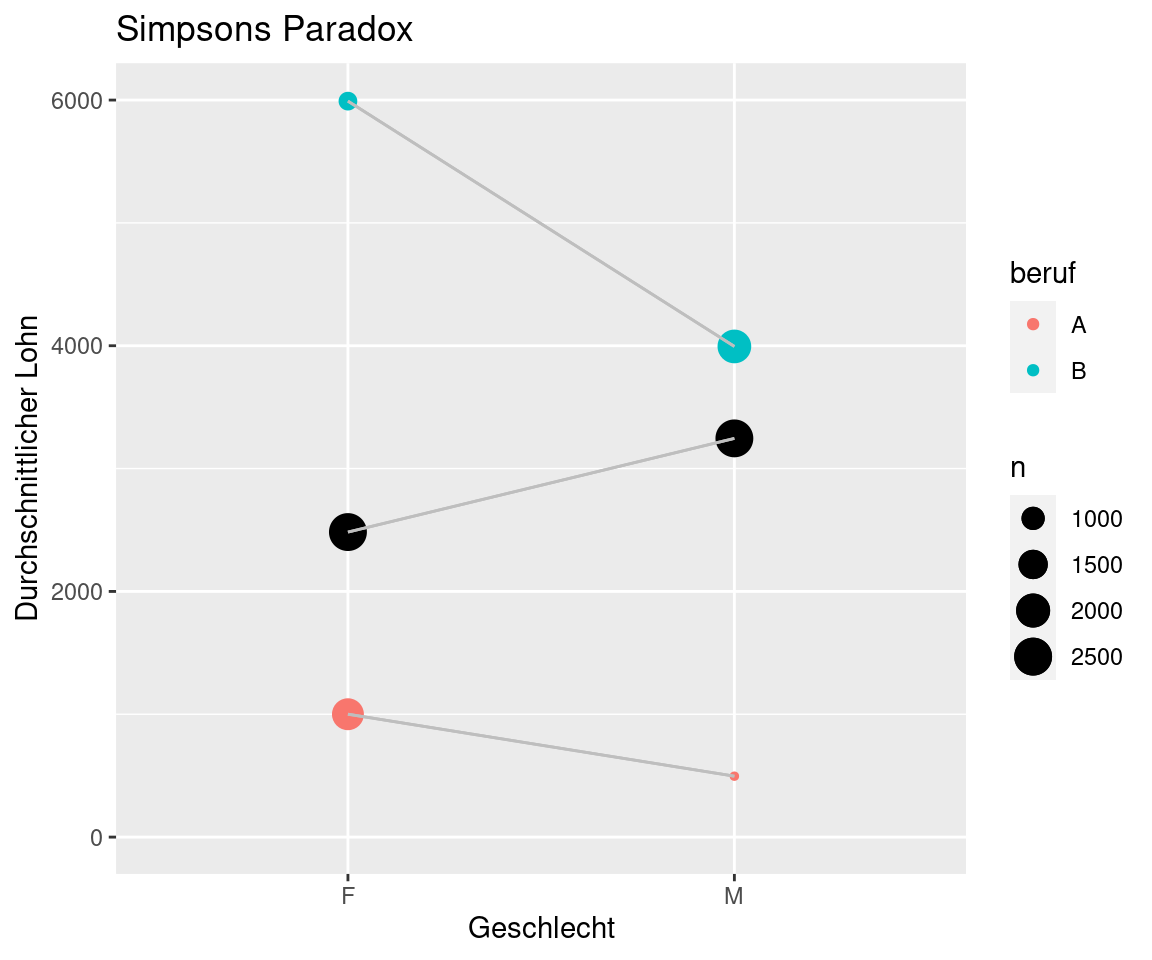
Die folgende Abbildung zeigt, wie das Paradox zustande kommt. Auf der linken Seite sieht man die Durchschnittslöhne der Frauen für die Berufe A und B (farbige Kreise) und insgesamt (schwarzer Kreis). Das gleiche ist rechts für die Männer angegeben. Die Größe der Kreise symbolisiert die Gruppengrößen. Der sehr kleine Kreis für Männer in Beruf A zeigt also, dass nur wenige Männer im Beruf A arbeiten.
Der Gesamtdurchschnitt wird durch die Gruppengrößen bestimmt (wie wir aus Kapitel 9 wissen). Daher ist der Gesamtdurchschnitt für die Männer größer als für die Frauen, obwohl in beiden Berufen ihr Durchschnitt niedriger ist.
Dieses künstliche Beispiel zeigt, dass es nicht immer klar ist, wie zwei Variablen miteinander zusammenhängen. Haben in diesem Beispiel die Männer höhere Löhne oder die Frauen? Gibt es Lohndiskriminierung? Die Antwort auf diese Frage hängt davon ab, ob man die Variable beruf in die Analyse mit einbezieht oder nicht. Die “richtige” Antwort lässt sich also nicht alleine durch statistische Untersuchungen ermitteln, sondern man braucht inhaltlichen ökonomischen Sachverstand und Urteilsfähigkeit - und natürlich eine klar formulierte Fragestellung!
Der Beruf ist in diesem Beispiel eine sogenannte Hintergrundvariable, (auch confounding variable oder confounder genannt), die je nach Fragestellung wichtig für die Datenanalyse ist. Wird die Hintergrundvariable weggelassen, kann das die Ergebnisse der Datenanalyse stark verändern. Für das Verständnis der Ergebnisse ist es darum immer wichtig zu überlegen, ob es möglicherweise relevante Hintergrundvariablen gibt und welche das sein könnten. Sehr häufig ist die Zeit eine Hintergrundvariable. Es kann dann vorkommen, dass sich der Mittelwert in jeder Gruppe erhöht, aber in der gesamten Population verringert (oder umgekehrt). Aus diesem Grund ist ein gründliches inhaltliches Verständnis der Daten und der Fragestellung unumgänglich. Eine rein statistische Analyse ohne Wissen über die inhaltlichen ökonomischen Zusammenhänge - ohne domain knowledge - reicht für eine gute Datenanalyse nicht aus.