11  Quantile

Die empirische Verteilungsfunktion, die im letzten Kapitel eingeführt wurde, gibt an, wie hoch der Anteil \(p\) der Daten ist, der einen bestimmten Wert \(x\) nicht überschreitet. Die Fragestellung lässt sich auch umkehren: Welcher Wert \(x\) teilt die Beobachtungen so auf, dass ein Anteil von \(p\) unter (oder auf) diesem Wert liegt und der Rest darüber? Der Wert, der diese Eigenschaft hat, heißt \(p\)-Quantil (engl. quantile).

11.1 Definition

Die formale Definition von Quantilen ist etwas komplizierter, damit die Definition des \(p\)-Quantils eindeutig ist. Sie lautet: Für \(0<p<1\) heißt der Wert \[ \tilde x_p=\min_{x\in\mathbb{R}} \{x|F(x)\ge p \} \] das \(p\)-Quantil. Es ist also der kleinste Wert \(x\in\mathbb{R}\) mit der Eigenschaft, dass \(F(x)\ge p\) ist.

Das \(p\)-Quantil \(\tilde x_p\) ist für jeden Wert von \(p\) in dem Intervall \((0,1)\) definiert. Um deutlich zu machen, dass der Wert von \(p\) beliebig gewählt werden kann, spricht man darum auch manchmal von der Quantilfunktion und schreibt \(Q(p)=\tilde x_p\).

Für einen Datenvektor x lässt sich das \(p\)-Quantil in R berechnen durch den Befehl

quantile(x, prob=p)

Es ist auch möglich, für mehrere Werte von \(p\) gleichzeitig die Quantile zu bestimmen, wenn nämlich p ein Vektor von Werten zwischen 0 und 1 ist. Will man beispielsweise das 0.1-Quantile, das 0.5-Quantil und das 0.9-Quantil berechnen, dann lautet der Befehl

quantile(x, prob=c(0.1,0.5,0.9))

Die Hilfefunktion zur quantile-Funktion zeigt Ihnen, dass es mehrere Varianten der Quantilsberechnung gibt. Die Unterschiede zwischen ihnen sind praktisch immer vernachlässigbar. Wenn Sie sicher gehen wollen, dass R das Quantil exakt nach der obigen Definition bestimmt, dann geben Sie in dem Funktionsaufruf zusätzlich die Option type=1 an.

quantile(x, prob=p, type=1)

Sollten in dem Datenvektor x fehlende Werte (NAs) vorkommen, können Quantile trotzdem aus den vorhandenen Werten errechnet werden, wenn die Option na.rm=TRUE gesetzt wird.

Der Median, den wir im Kapitel zu den Lagemaßen bereits kennen gelernt haben, ist ein spezielles Quantile, nämlich das 0.5-Quantil. Es gibt einige weitere, oft verwendete Quantile, für die sich eigene Bezeichnungen eingebürgert haben:

Name	\(p\)
Median (Zentralwert)	0.5
Quartile	0.25, 0.5, 0.75
Quintile	0.2, 0.4, 0.6, 0.8
Dezile	0.1, 0.2, …, 0.9
Perzentile	0.01, 0.02, …, 0.99

Der Median teilt die Daten in zwei (etwa) gleich große Scheiben ein, die Quartile teilen sie in vier, die Quintile in fünf, die Dezile in zehn und die Perzentile in 100 (etwa) gleich große Scheiben ein.

Die englischen Übersetzungen sind naheliegend: median, quartiles, quintiles, deciles, percentiles.

Beispiel:

Wir berechnen die Variable des Pro-Kopf-Nettoeinkommens im Jahr 2020 im Datensatz mocksoep. Das Nettoeinkommen wird - vereinfacht ausgedrückt - berechnet als die Summe aller Einkommensarten (z.B. Löhne, Zinseinkommen, Mieteinnahmen, Unternehmensgewinne) abzüglich Steuern. Bei Haushalten werden die Einkommen auf die Haushaltsmitglieder verteilt, um auf die Pro-Kopf-Größen zu kommen.

jahr <- 2020
soep <- read_csv("../data/mocksoep.csv", 
                 col_types = "nnnnfnnnffnnncnnnnn") 
netto <- soep %>% 
             mutate(netto = postgov/npers) %>%
             filter(year == jahr) %>%
             pull(netto)

Das 0.1-Quantil, der Median und das 0.9-Quantil sind:

quantile(netto, c(0.1,0.5,0.9))

    10%     50%     90% 
 7139.2 16511.0 35602.8 

Hieran sieht man, dass 10% der Personen 2020 ein Pro-Kopf-Nettoeinkommen von weniger als 7139 Euro hatten, jeweils die Hälfte der Personen lag unter bzw. über dem Median von 16511 Euro. Und 10% der Personen hatten ein Pro-Kopf-Nettoeinkommen von mehr als 35603 Euro.

Normalerweise bestimmt man Quantile mit Hilfe der Funktion quantile. Quantile lassen sich jedoch auch grafisch aus der empirischen Verteilungsfunktion ermitteln. Das ist in der praktischen Anwendung zwar unüblich, für das Verständnis der Quantile und ihrem Zusammenhang mit der empirischen Verteilungsfunktion aber trotzdem hilfreich.

Beispiel:

Wir betrachten als Beispiel wieder die empirische Verteilungsfunktion der jährlichen Arbeitsstunden aus dem Dataframe soep. Um auf grafischem Wege das 0.75-Quantil zu ermitteln, ziehen wir eine waagerechte Linie auf der Höhe 0.75 von der y-Achse nach rechts, bis wir auf die Verteilungsfunktion treffen. Dort knicken wir nach unten ab und bestimmen den zugehörigen Wert auf der x-Achse. Dieser Wert ist das 0.75-Quantil. In diesem Beispiel beträgt das tatsächliche 0.75-Quantil der Arbeitsstunden 2123, aber das lässt sich aus der Grafik natürlich nicht exakt ablesen.

q75 <- quantile(soep$hours, 0.75)
ggplot(soep, aes(hours)) + 
    geom_step(stat="ecdf") +
    ylab("F(hours)")+
    ggtitle("Emp. Verteilungsfunktion der Arbeitsstunden") +
    geom_segment(aes(x=0, xend=q75, y=0.75, yend=0.75),
                 arrow=arrow(length=unit(0.5,"cm")),
                 colour="red") +
    geom_segment(aes(x=q75, xend=q75, y=0.75, yend=0),
                 arrow=arrow(length=unit(0.5,"cm")),
                 colour="red") +
    annotate("text", x=2200, y=-0.02, label=paste("x=",q75))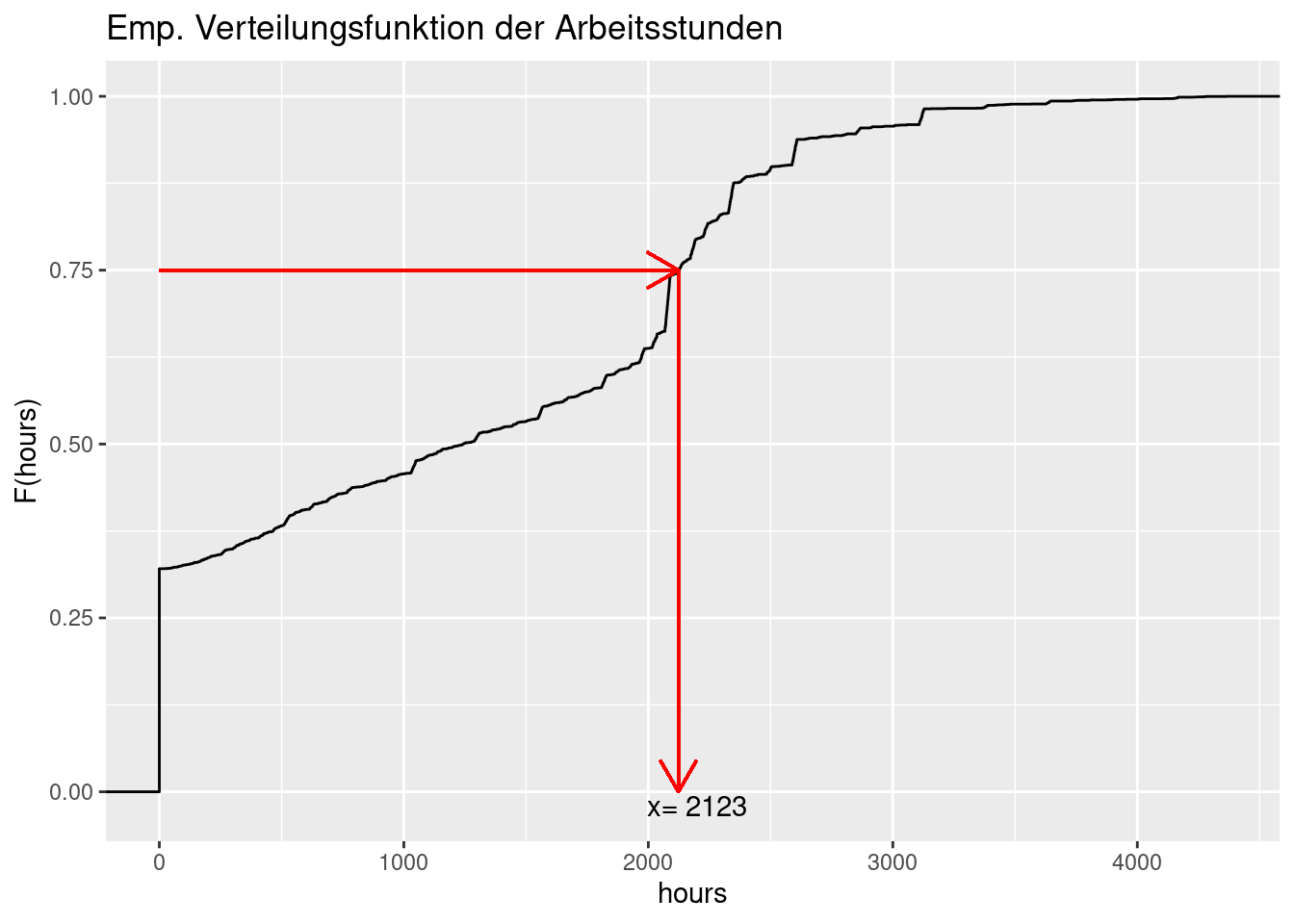

11.2 Boxplots

Eine oft verwendete grafische Darstellungsweise, die auf Quantile beruht, sind Boxplots. Der Boxplot der Datenpunkte \(x_1,\ldots,x_n\) sieht in allgemeiner Form etwa so aus:

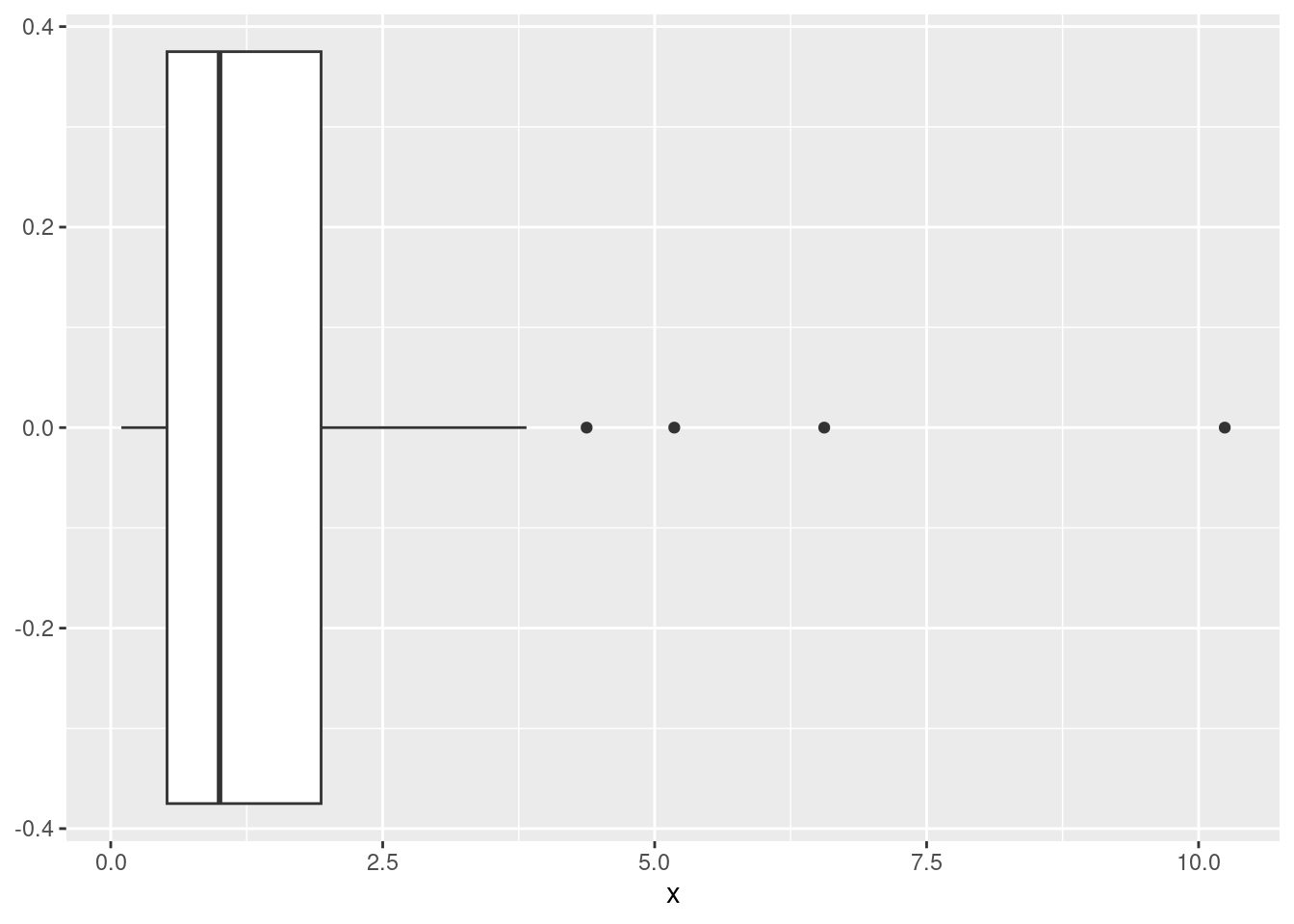
Der dick gezeichnete Strich in der Mitte der Box ist der Median der Daten. Der linke Rand der Box ist das 0.25-Quantil, der rechte Rand das 0.75-Quantil. Die dünnen Striche nach links und rechts (“whiskers”) verlaufen vom linken Rand bis zum kleinsten Wert und vom rechten Rand bis zum größten Wert. Wenn das Minimum bzw. Maximum jedoch weiter als das 1.5-fache der Boxbreite (d.h. als der Interquartilabstand) sind, wird der entsprechende Whisker auf das 1.5-fache begrenzt. Werte, die noch weiter außen liegen (Ausreißer, outliers), werden durch einzelne Punkte repräsentiert.

Boxplots sind besonders nützlich, wenn man auf die Schnelle mehrere Verteilungen miteinander vergleichen möchte.

In R kann man mit ggplot Boxplots erzeugen. Wenn nur für eine Verteilung ein Boxplot gezeichnet werden soll, lautet der Befehl

ggplot(DATAFRAME, aes(VARIABLE)) + 
    geom_boxplot()

wobei DATAFRAME der Name des Dataframes ist, in dem die zu zeichnende Variable VARIABLE liegt.

Wenn mehrere Boxplots in einer Grafik erscheinen sollen, lautet der Befehl

ggplot(DATAFRAME, aes(VARIABLE, GROUPVAR)) + 
    geom_boxplot()

Die Variable GROUPVAR muss ebenfalls im Dataframe DATAFRAME enthalten sein. Sie sollte nur wenige Ausprägungen haben, am besten nicht viel mehr als fünf. Für jede Ausprägung von GROUPVAR wird nun ein separater Boxplot erzeugt.

Beispiel:

Wir erzeugen die Boxplots des (logarithmierten) Nettoeinkommens log(postgov) für die Personen, die in Teilzeit (“teil”) oder Vollzeit (“voll”) arbeiten oder keiner bezahlten Tätigkeit nachgehen (“nicht”). Die Gruppierungsvariable ist also der Erwerbsumfang empllev. Die Logarithmierung ist sinnvoll, damit die sehr hohen Einkommen nicht die Grafik verzerren.

ggplot(soep, aes(log(postgov), empllev)) + 
    geom_boxplot()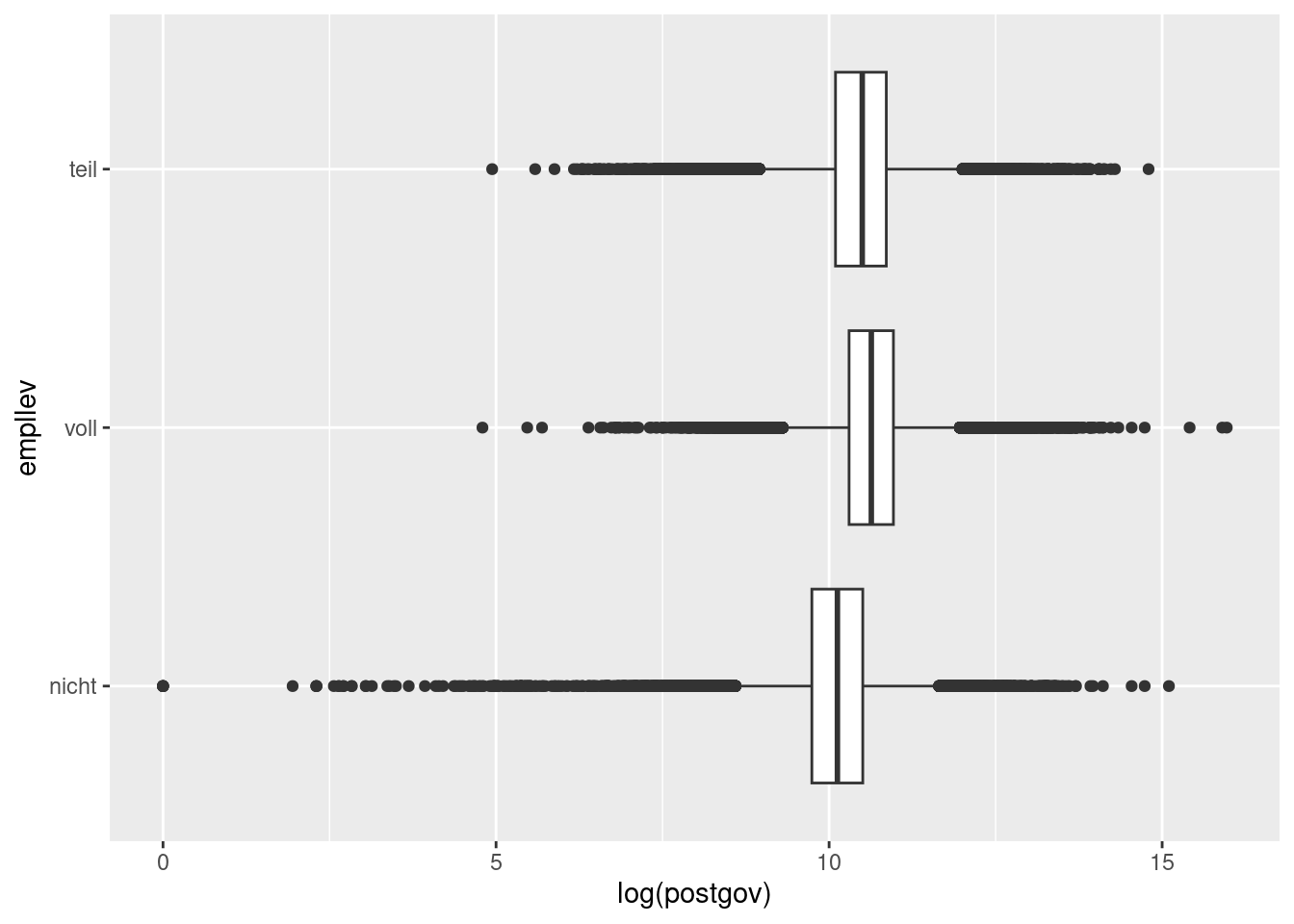

Man erkennt an den Boxplots, dass die Nettoeinkommen sehr breite Ränder haben, ein großer Teil der Beobachtungen liegt jedoch in einem recht engen Bereich: Die Hälfe aller Werte liegt innerhalb der Boxen. Man sieht ferner, dass die Verteilung des Nettoeinkommens bei Personen ohne bezahlte Tätigkeit niedriger liegt als in den anderen beiden Gruppen. Die Verteilung für die Vollzeitbeschäftigten ist am höchsten.

11.3 Violin-Plots

Eine Alternative zu Boxplots sind die sogenannten Violin-Plots. Sie symbolisieren die Verteilung oder die Verteilungen durch eine Art von symmetrischer Dichteschätzung. Besonders dicke Stellen zeigen, dass in dem Bereich viele Beobachtungen liegen, dünne Stellen stehen für wenige Beobachtungen.

Beispiel:

Als Beispiel reproduzieren wir den Boxplot aus dem letzten Beispiel in Form eines Violin-Plots:

ggplot(soep, aes(log(postgov), empllev)) + 
    geom_violin()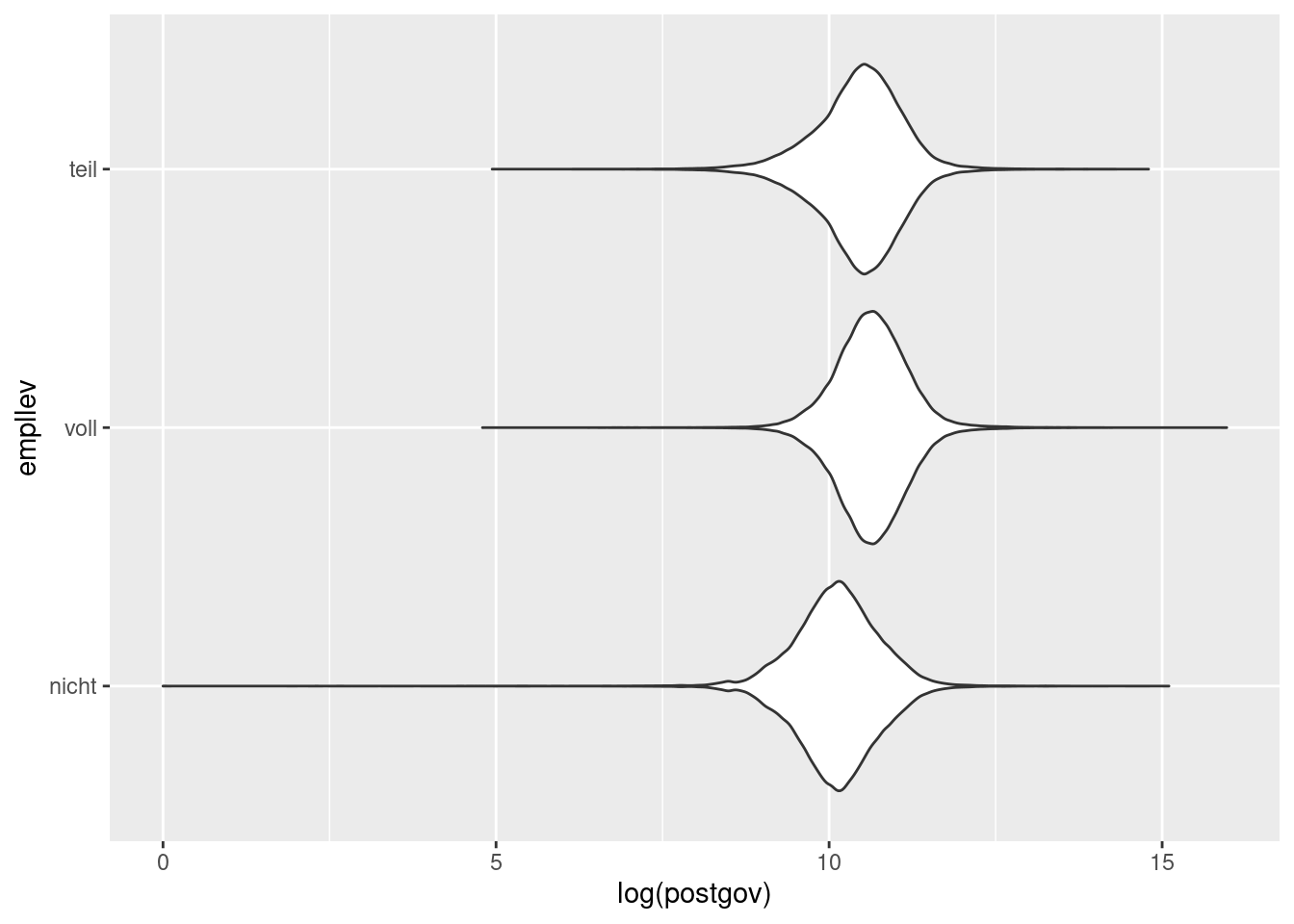

11.4 Interquartilsabstand

Quantile können auch dafür eingesetzt werden, die Streuung einer Verteilung zu messen - als Alternative zu den Maßen aus Kapitel Kapitel 8, d.h. Varianz, Standardabweichung, Median der absoluten Abweichungen oder Spannweite. Das übliche quantil-basierte Streuungsmaß ist der Interquartilsabstand (engl. interquartile range, IQR). Das Maß gibt den Abstand zwischen mit 25-Prozent-Quantil und dem 75-Prozent-Quantil an, also zwischen dem ersten und dem dritten Quartil: \[ IQR=\tilde x_{0.75}-\tilde x_{0.25}. \] Etwas vereinfacht gesagt gibt das Maß an, wie breit das Intervall ist, in dem die mittleren 50 Prozent der Daten liegen. Ob die Daten im unteren Bereich (unterhalb des ersten Quartils) und im oberen Bereich (oberhalb des dritten Quartils) sehr weit oder nur wenig streuen, spielt für den Interquartilsabstand keine Rolle.

In R lautet der Befehl IQR. Als Beispiel wird der Interquartilsabstand des Nettoeinkommens von 2020 berechnet:

IQR(netto)

[1] 13192.5

Die mittleren 50 Prozent der Nettoeinkommen liegen also in einem Intervall der Breite 13192.5.