
12 Mehrdimensionale Häufigkeiten
Bisher haben wir immer nur eine Variable zur Zeit betrachtet. Viel spannender ist es jedoch meistens, mehrere Variablen gemeinsam zu untersuchen, denn gerade die Zusammenhänge zwischen den Variablen sind aus ökonomischer Sicht interessant, z.B.:
Wie ist das Verhältnis zwischen dem Preis, die für ein Gut verlangt wird, und dem Absatz dieses Gutes?
Wie hängt die Wachstumsrate einer Volkswirtschaft mit dem Zinssatz zusammen, den die Zentralbank setzt?
Kommt es zu Diskriminierung auf dem Arbeitsmarkt, d.h. sind die Einstellungschancen, die Aufstiegsmöglichkeiten oder das Gehalt abhängig vom Geschlecht, der sexuellen Orientierung oder einem möglichen Migrationshintergrund?
Wie wichtig sind die institutionellen Rahmenbedingungen (wie z.B. ein funktionierendes Rechtssystem) für den Wohlstand einer Nation?
Wovon hängt die Lebenszufriedenheit der Menschen ab? Ändert sie sich mit dem Alter, dem Beziehungsstatus, dem Einkommen?
Um die formale Darstellung möglichst übersichtlich zu halten, beschränken wir uns auf den bivariaten Fall, also auf zwei Variablen bzw. Merkmale. Die beiden nennen wir allgemein \(X\) und \(Y\). Es handelt sich normalerweise um zwei Spalten eines Dataframes. Wenn mehr als zwei Variablen in die Untersuchung eingehen, spricht man vom multivariaten Fall. Die Variablen werden dann oft mit \(X_1,X_2,\ldots,X_k\) notiert.
Um deutlich zu machen, dass \(X\) und \(Y\) gemeinsam untersucht werden, schreiben wir \((X,Y)\) und notieren die beobachteten Werte allgemein als \[ (x_1,y_1), (x_2,y_2), ..., (x_n,y_n). \] Es gibt also Informationen zu insgesamt \(n\) Merkmalsträgern, das können Individuen, Haushalte, Firmen, Länder etc. sein. Jede Information besteht nun aus zwei Werten, nämlich \(x_i\) und \(y_i\) für die \(i\)-te Einheit.
Oftmals ist es übersichtlicher, wenn die Daten in Form einer Matrix dargestellt werden, auch wenn der Informationsgehalt sich dadurch natürlich nicht ändert. \[ \left[ \begin{array}{cc} x_1 & y_1\\ x_2 & y_2\\ \vdots & \vdots\\ x_n & y_n \end{array} \right] \] In R handelt es sich um zwei Spalten eines Dataframes.
Beispiel:
Wir laden den SOEP-Beispiel-Dataframe mocksoep und beschränken die Betrachtung auf das Jahr 2020. Den Populationsumfang speichern wir als n.
jahr <- 2020
soep <- read_csv("../data/mocksoep.csv",
col_types = "nnnnfnnnffnnncnnnnn") %>%
filter(year == jahr)
n <- dim(soep)[1]Wir interessieren uns für die beiden Variablen Lebenszufriedenheit lifesat und Geschlecht sex.
Der Anfang der Urliste sieht folgendermaßen aus. Die erste Beobachtung ist eine Frau (F) mit einer hohen Zufriedenheit (9), die zweite Person ist männlich (M) und etwas unzufriedener (7) usw. Insgesamt gibt es 24505 Beobachtungen in dem Datensatz für das Jahr 2020.
soep %>% select(lifesat, sex) %>% head()# A tibble: 6 × 2
lifesat sex
<dbl> <fct>
1 9 F
2 7 M
3 3 M
4 7 F
5 7 M
6 7 M Die Variablen kann man auf mehreren Wegen aus dem Dataframe herausziehen. Drei gängige Methoden sind:
- Spaltennummer in doppelten Klammern
zufried <- soep[[1]]
geschl <- soep[[2]]- Auswahl mit dem Dollarzeichen und dem Spaltennamen
zufried <- soep$lifesat
geschl <- soep$sex- Der pull-Befehl in tidyverse
zufried <- pull(soep, lifesat)
geschl <- pull(soep, sex)Wie schon bei den univariaten Daten, so kann auch hier eine Häufigkeitsauszählung interessante Einsichten liefern.
12.1 Absolute Häufigkeitstabellen
Bei bivariaten Daten gibt die absolute Häufigkeit an, welche Kombinationen von \(X\)- und \(Y\)-Werten wie oft angenommen werden. Wenn wir wieder die möglichen \(X\)-Werte mit \(\xi_1,..., \xi_J\) bezeichnen und die möglichen \(Y\)-Werte mit \(\eta_1,\ldots,\eta_K\) (diese griechischen Buchstaben werden eta ausgesprochen), dann sind \[ n_{jk} = \#\{x_i = \xi_j\quad\text{und}\quad y_i=\eta_k\} \] für \(j=1,\ldots, J\) und \(k=1,\ldots,K\) die absoluten Häufigkeiten. Das Hashtag-Zeichen steht für “Anzahl”. Die absolute Häufigkeit \(n_{jk}\) gibt also an, bei wie vielen Merkmalsträgern die Variable \(X\) den Wert \(\xi_j\) und die Variable \(Y\) den Wert \(\eta_k\) annimmt. Die Tabelle \[ \begin{array}{|cc|cccc|}\hline &&&Y=&&\\ &&\eta_1&\eta_2&\ldots&\eta_K\\\hline &\xi_1&n_{11}&n_{12}&\ldots&n_{1K}\\ &\xi_2&n_{21}&n_{22}&\ldots&n_{2K}\\ X=&\vdots&\vdots&\vdots&&\vdots\\ &\xi_J&n_{J1}&n_{J2}&\ldots&n_{JK}\\\hline \end{array} \] heißt (absolute) Häufigkeitstabelle, Kontingenztabelle (engl. contingency table) oder Kreuztabelle. Die Summe aller absoluten Häufigkeiten ergibt den gesamten Populationsumfang, da es hier zwei Subindizes gibt, braucht man eine Doppelsumme: \[ \sum_{j=1}^J \sum_{k=1}^K n_{jk} = n. \]
In R bestimmt man die absoluten Häufigkeiten mit dem Befehl table.
table(zufried, geschl) geschl
zufried F M
1 24 22
2 80 92
3 208 184
4 251 225
5 805 707
6 912 896
7 2392 2330
8 4408 4242
9 2482 2276
10 1013 956An dieser (zugegeben nicht sehr schön formatierten) Tabelle erkennt man, dass es nur wenige Frauen und Männer gibt, die extrem unzufrieden sind, nämlich 24 Frauen und 22 Männer. Hingegen haben 1013 Frauen und 956 Männer den höchsten Zufriedenheitswert angegeben.
Innerhalb der tidyverse-Umgebung ist eine bivariate Häufigkeitsauszählung zwar möglich, aber sie wird nicht als Tabelle mit der Lebenszufriedenheit und dem Geschlecht entlang den Zeilen und Spalten angezeigt. Stattdessen wird untereinander für jede Kombination der Merkmalsausprägungen die absolute Häufigkeit ausgegeben (was ja manchmal durchaus gewünscht sein mag).
soep %>%
group_by(lifesat, sex) %>%
summarise(n=n(),
.groups="drop")# A tibble: 20 × 3
lifesat sex n
<dbl> <fct> <int>
1 1 F 24
2 1 M 22
3 2 F 80
4 2 M 92
5 3 F 208
6 3 M 184
7 4 F 251
8 4 M 225
9 5 F 805
10 5 M 707
11 6 F 912
12 6 M 896
13 7 F 2392
14 7 M 2330
15 8 F 4408
16 8 M 4242
17 9 F 2482
18 9 M 2276
19 10 F 1013
20 10 M 956An dieser Tabelle erkennt man beispielsweise, dass es in dem Datensatz ingesamt 184 Personen gibt, die eine Lebenszufriedheit von 3 haben und männlich sind.
12.2 Relative Häufigkeitstabellen
Wenn die absoluten Häufigkeiten \(n_{jk}\) durch die relativen Häufigkeiten \[
f_{jk}=\frac{n_{jk}}{n}
\] ersetzt werden, ergibt sich die relative Häufigkeitstabelle. \[
\begin{array}{|cc|cccc|}\hline
&&&Y=&&\\
&&\eta_1&\eta_2&\ldots&\eta_K\\\hline
&\xi_1&f_{11}&f_{12}&\ldots&f_{1K}\\
&\xi_2&f_{21}&f_{22}&\ldots&f_{2K}\\
X=&\vdots&\vdots&\vdots&&\vdots\\
&\xi_J&f_{J1}&f_{J2}&\ldots&f_{JK}\\\hline
\end{array}
\] Die Summe aller Einträge ist \[
\sum_{j=1}^J \sum_{k=1}^K f_{jk}=1.
\] In R erzeugt man die relative Häufigkeitstabelle, indem man zunächst die absolute Häufigkeitstabelle berechnet und anschließend in die relative Tabelle umrechnen lässt. Zur Vereinfachung speichern wir in einem ersten Schritt die absolute Tabelle unter dem Namen absTab.
absTab <- table(zufried, geschl)Nun berechnet man die relativen Häufigkeiten mit Hilfe der Funktion proportions (oder synonym prop.table), die auf die absolute Häufigkeitstabelle angewendet wird. Mit einer Rundung der Ergebnisse auf vier Stellen ergibt sich
round(proportions(absTab), 4) geschl
zufried F M
1 0.0010 0.0009
2 0.0033 0.0038
3 0.0085 0.0075
4 0.0102 0.0092
5 0.0329 0.0289
6 0.0372 0.0366
7 0.0976 0.0951
8 0.1799 0.1731
9 0.1013 0.0929
10 0.0413 0.0390An dieser Tabelle lässt sich beispielsweise ablesen, dass rund 18 Prozent der betrachteten Personen weiblich mit einem Zufriedenheitswert von 8 sind. Und 3.9 Prozent sind extrem zufriedene (10) Männer.
12.3 Randverteilungen
Wenn man alle Zeilen der absoluten Häufigkeitstabelle addiert, erhält man die absoluten Häufigkeiten für die Variable \(Y\). Addiert man die Spalten auf, ergeben sich die absoluten Häufigkeiten für die Variable \(X\). Man spricht von den Randverteilungen (engl. marginal distributions) von \(Y\) bzw. \(X\).
Da es im bivariaten Fall zwei Randverteilungen gibt, können wir nicht einfach \(n_j\) als Symbol benutzen, denn es wäre nicht eindeutig klar, ob beispielsweise \(n_3\) die Anzahl der Einheiten mit \(x_i=\xi_3\) oder \(y_i=\eta_3\) ist. Darum wird zur Unterscheidung ein kleines Pünktchen eingeführt. Es steht an der Stelle der Variable, über die hinweg addiert wird.
Die absolute Randhäufigkeit von \(\xi_j\) (für die Variable \(X\)) wird also geschrieben als \[ n_{j\cdot} = \sum_{k=1}^K n_{jk} \] und analog für die absolute Randhäufigkeit von \(\eta_k\) (für \(Y\)), \[ n_{\cdot k} = \sum_{j=1}^J n_{jk}. \] Auf die gleiche Weise notieren wir die relativen Randhäufigkeiten: \[\begin{align*} f_{j\cdot} &= \frac{n_{j\cdot}}{n} \\ f_{\cdot k} &= \frac{n_{\cdot k}}{n} \end{align*}\] für \(j=1,\ldots,J\) bzw. \(k=1,\ldots,K\).
Die Randverteilungen zeigen, wie eine Variable verteilt ist, wenn die andere Variable aus der Betrachtung ausgeschlossen wird. Welche Werte nimmt die Variable \(X\) wie oft an, wenn wir die Variable \(Y\) ignorieren? Und umgekehrt: Wie sehen die absoluten oder relativen Häufigkeiten von \(Y\) aus, wenn wir \(X\) außer Acht lassen.
Sehr oft werden die Randhäufigkeiten einfach an den Rand der Häufigkeitstabelle angefügt: \[ \begin{array}{|cc|cccc|c|}\hline &&&Y=&&\\ &&\eta_1&\eta_2&\ldots&\eta_K&\sum \\\hline &\xi_1&n_{11}&n_{12}&\ldots&n_{1K}&n_{1\cdot}\\ &\xi_2&n_{21}&n_{22}&\ldots&n_{2K}&n_{2\cdot}\\ X=&\vdots&\vdots&\vdots&&\vdots\\ &\xi_J&n_{J1}&n_{J2}&\ldots&n_{JK}&n_{J\cdot}\\\hline &\sum&n_{\cdot 1}&n_{\cdot 2}&\ldots&n_{\cdot K}&n\\\hline \end{array} \] Analog kann man die Randverteilungen an die relative Häufigkeitstabelle anfügen: \[ \begin{array}{|cc|cccc|c|}\hline &&&Y=&&\\ &&\eta_1&\eta_2&\ldots&\eta_K&\sum \\\hline &\xi_1&f_{11}&f_{12}&\ldots&f_{1K}&f_{1\cdot}\\ &\xi_2&f_{21}&f_{22}&\ldots&f_{2K}&f_{2\cdot}\\ X=&\vdots&\vdots&\vdots&&\vdots\\ &\xi_J&f_{J1}&f_{J2}&\ldots&f_{JK}&f_{J\cdot}\\\hline &\sum&f_{\cdot 1}&f_{\cdot 2}&\ldots&f_{\cdot K}&1\\\hline \end{array} \] Die Randverteilungen sind univariate Verteilungen - entweder von \(X\) oder von \(Y\). Der Zusammenhang zwischen den beiden Variablen geht beim Übergang auf die Randverteilungen verloren. Anders gesagt: Es ist zwar möglich, die Randverteilungen aus der Häufigkeitstabelle zu konstruieren, aber umgekehrt ist es im Allgemeinen nicht möglich, aus den beiden Randverteilungen die Häufigkeitstabelle zu rekonstruieren.
In R lassen sich die beiden Randverteilungen mit der Funktion addmargins leicht errechnen. Da wir die absolute Häufigkeitstabelle bereits unter dem Namen absTab gespeichert haben, lautet der Befehl schlicht:
addmargins(absTab) geschl
zufried F M Sum
1 24 22 46
2 80 92 172
3 208 184 392
4 251 225 476
5 805 707 1512
6 912 896 1808
7 2392 2330 4722
8 4408 4242 8650
9 2482 2276 4758
10 1013 956 1969
Sum 12575 11930 24505Für die relativen Häufigkeiten wendet man addmargins auf die relative Häufigkeitstabelle an. Außerdem runden wir die Anteile auf 4 Stellen.
round(addmargins(proportions(absTab)),4) geschl
zufried F M Sum
1 0.0010 0.0009 0.0019
2 0.0033 0.0038 0.0070
3 0.0085 0.0075 0.0160
4 0.0102 0.0092 0.0194
5 0.0329 0.0289 0.0617
6 0.0372 0.0366 0.0738
7 0.0976 0.0951 0.1927
8 0.1799 0.1731 0.3530
9 0.1013 0.0929 0.1942
10 0.0413 0.0390 0.0804
Sum 0.5132 0.4868 1.0000Wir sehen an der Randverteilung der Variable geschl, dass gut die Hälfte der Personen weiblich ist (nämlich rund 51 Prozent). An der Randverteilung der Variable zufried fällt auf, dass mehr als ein Drittel (etwa 35 Prozent) von allen Personen einen Zufriedenheitswert von 8 angegeben haben.
12.4 Mehr als zwei Variablen
Im Prinzip lassen sich auch mehr als zwei Variablen in eine Häufigkeitstabelle bringen. Allerdings ist die Darstellung der Auszählung dann nicht mehr so einfach möglich wie im Fall von zwei Variablen.
Als Beispiel sehen wir uns die Lebenszufriedenheit, das Geschlecht und zusätzlich noch die Haushaltsgröße (npers) an.
zufried <- soep$lifesat
geschl <- soep$sex
hhgr <- soep$npersDie zusätzliche Dimension durch eine dritte Variable berücksichtigt man dadurch, dass mehrere “normale” (zweidimensionale) Tabellen untereinander gesetzt werden. Man spricht von “flachen” Tabellen (engl. flat tables). Das ist natürlich auf mehrere Arten möglich. Ein Beispiel ist
ftable(geschl, hhgr, zufried) zufried 1 2 3 4 5 6 7 8 9 10
geschl hhgr
F 1 8 27 52 66 218 189 443 753 337 183
2 5 31 68 92 270 356 889 1647 956 410
3 4 8 36 38 126 151 405 738 402 126
4 3 7 33 33 117 130 407 800 476 157
5 4 3 12 21 55 52 180 315 212 90
6 0 4 5 0 12 20 41 108 60 27
7 0 0 1 0 4 12 15 33 18 11
8 0 0 1 1 3 2 12 14 21 9
M 1 6 32 69 61 214 223 525 727 287 171
2 7 24 53 68 243 291 777 1648 877 365
3 5 14 33 39 89 136 379 630 355 127
4 3 17 11 32 91 122 396 753 457 153
5 1 5 12 10 39 80 164 324 202 89
6 0 0 5 8 20 24 52 97 67 30
7 0 0 0 5 5 15 18 46 15 10
8 0 0 1 2 6 5 19 17 16 11Eine andere, aber inhaltlich vollkommen gleichwertige, Darstellung erhalten wir durch Permutationen der drei Variablen, z.B.
ftable(hhgr, geschl, zufried) zufried 1 2 3 4 5 6 7 8 9 10
hhgr geschl
1 F 8 27 52 66 218 189 443 753 337 183
M 6 32 69 61 214 223 525 727 287 171
2 F 5 31 68 92 270 356 889 1647 956 410
M 7 24 53 68 243 291 777 1648 877 365
3 F 4 8 36 38 126 151 405 738 402 126
M 5 14 33 39 89 136 379 630 355 127
4 F 3 7 33 33 117 130 407 800 476 157
M 3 17 11 32 91 122 396 753 457 153
5 F 4 3 12 21 55 52 180 315 212 90
M 1 5 12 10 39 80 164 324 202 89
6 F 0 4 5 0 12 20 41 108 60 27
M 0 0 5 8 20 24 52 97 67 30
7 F 0 0 1 0 4 12 15 33 18 11
M 0 0 0 5 5 15 18 46 15 10
8 F 0 0 1 1 3 2 12 14 21 9
M 0 0 1 2 6 5 19 17 16 11An den Tabellen sieht man beispielsweise, dass es 0 Frauen gibt, die in einem 8-Personen-Haushalt leben und extrem unzufrieden sind. Es gibt 6 extrem unzufriedene Männer, die alleine leben.
Offensichtlich ist die tabellarische Darstellung von mehr als zwei Variablen nicht sehr übersichtlich. Man braucht viel Zeit und Geduld, um in solchen Tabellen interessante Zusammenhänge zu finden.
12.5 Sehr viele Ausprägungen
Eine Tabelle mit sehr vielen Spalten und/oder sehr vielen Zeilen ist unpraktisch und liefert keine leicht erkennbaren Informationen. Darum stellt sich die Frage: Wie geht man mit zwei Variablen um, von denen eine oder beide viele Ausprägungen haben?
Ein naheliegender Weg ist die Klassierung der Beobachtungen in Intervalle. Wir haben diese Methode im Kapitel Kapitel 6.3 bereits kennen gelernt. Durch den Übergang zu Intervallen wird die Anzahl der Ausprägungen so klein, dass Häufigkeitstabellen wieder sinnvoll sind.
Ein alternativer Weg, bivariate Daten mit vielen Ausprägungen übersichtlich zu zeigen, sind Grafiken. Die einfachste Grafik ist ein Streudiagramm (engl. scatterplott), vgl. Kapitel 5.
Beispiel:
Wir betrachten weiterhin den Dataframe mocksoep, eingeschränkt auf Beobachtungen aus dem Jahr rjahr. Uns interessieren die beiden Variablenhours(Arbeitsstunden im Jahr) undpostgov` (das Nettoeinkommen nach Steuern und Transfers). Da das Nettoeinkommen einige sehr große Ausreißer hat, logarithmieren wir die Werte. Ohne Logarithmierung würden der Bereich, der am häufigsten vorkommt, ganz an den Rand der Abbildung gequetscht werden.
In R kann ein Streudiagramm wie folgt erzeugt werden:
ggplot(soep, aes(hours, log(postgov))) +
geom_point()+
ggtitle("Streudiagramm")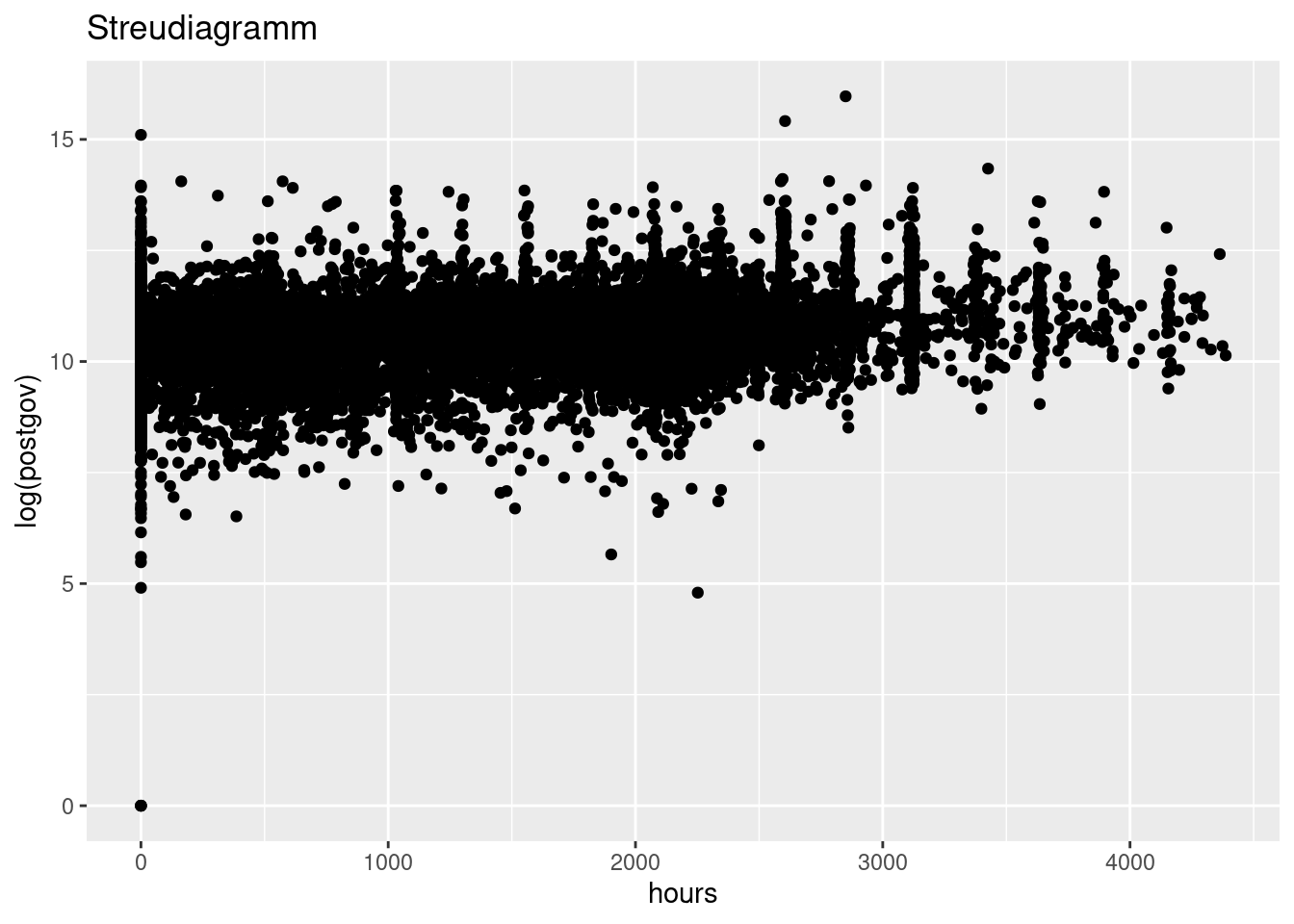
Manche Bereiche in diesem Plot sind nur schwarze Flächen, weil dort sehr viele Punkte zusammenkommen. In solchen Fällen hilft es, die Punkte etwas transparent zu machen. Die Option in geom_point für die Transparenz ist alpha. Die Option nimmt Werte zwischen 0 (total transparent, also unsichtbar) und 1 (keine Transparenz) an.
ggplot(soep, aes(hours, log(postgov))) +
geom_point(alpha=0.1)+
ggtitle("Streudiagramm")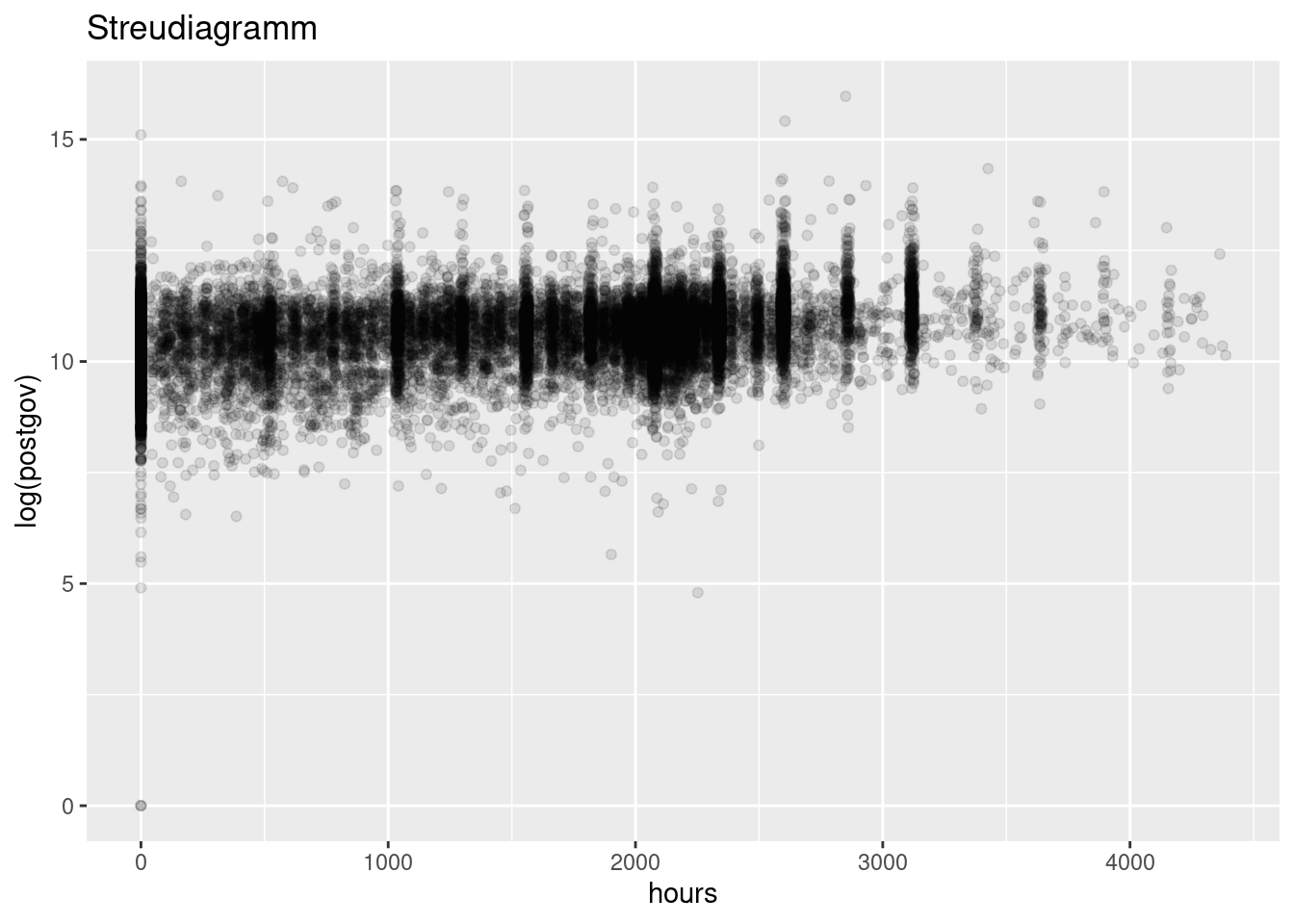
Ein alternativer Weg, bivariate Daten grafisch darzustellen, bieten zweidimensionale Histogramme. In ggplot sind 3D-Darstellungen nicht möglich. Die dritte Dimension, also die Höhe der Histogramm-Säulen wird durch die Farbe symbolisiert.
ggplot(soep,aes(hours,log(postgov))) +
geom_bin2d() +
ggtitle("Bivariates Histogramm")
Die hellblauen Bereiche sind besonders stark im Datensatz vertreten. Es gibt also viele Personen, die 0 Arbeitsstunden angegeben haben, und viele Personen mit etwas mehr als 2000 Arbeitsstunden. Außerdem ist zu erkennen, dass es tendenziell einen leicht gleichgerichteten Zusammenhang zwischen den beiden Variablen gibt. Je mehr Arbeitsstunden, desto höher ist im Schnitt das (log.) Nettoeinkommen.
Auch Kerndichten, also quasi geglättete Histogramme, sind im bivariaten Fall möglich.
ggplot(soep, aes(hours, log(postgov))) +
geom_density_2d()+
ggtitle("Kontour-Plot")
Dieser sogenannte Kontour-Plot zeigt Höhenlinien wie auf einer Landkarte. Es gibt also zwei Gipfel, einen bei 0 Arbeitsstunden und einem logarithmierten Nettoeinkommen von ungefähr 10.2, und einen zweiten Gipfel bei etwas mehr als 2000 Arbeitsstunden und einem (log.) Nettoeinkommen von rund 10.8. Wie schon oben gesehen, gibt es also viele Personen, die nicht auf dem Arbeitsmarkt tätig sind und viele Personen, die eine Vollzeitstelle haben. Nicht überraschend, ist das Nettoeinkommen für die Personen mit einer Vollzeitstelle höher.