10  Verteilungsfunktion

Die empirische Verteilungsfunktion (engl. empirical cumulative distribution function, abgekürzt edf oder ecdf) gibt an, wie hoch der Anteil der Beobachtungen kleiner oder gleich einem Wert \(x\) ist.

In den meisten Fällen wird die empirische Verteilungsfunktion als \(F(x)\) notiert. Die Definition lautet (für \(x\in\mathbb{R}\)) \[ F(x)=\frac{1}{n}\sum_{i=1}^n 1(x_i \le x), \] wobei \(1(\cdot)\) die Indikatorfunktion ist, d.h. \[ 1(A) = \left\{ \begin{array}{ll} 1 & \textsf{wenn A wahr ist}\\ 0 & \textsf{wenn A falsch ist}. \end{array}\right. \] Der Definitionsbereich der empirischen Verteilungsfunktion ist die Menge aller reellen Zahlen. Der Wertebereich ist das Intervall von 0 bis 1. Die empirische Verteilungsfunktion ist monoton steigend.

Man kann die empirische Verteilungsfunktion auch einfach als Verteilungsfunktion bezeichnen, wenn aus dem Kontext hervorgeht, dass es sich um eine empirische Verteilungsfunktion handelt (welche anderen Verteilungsfunktionen es gibt, wird in dem Modul Data Science 2 behandelt).

Für einen Datenvektor x lässt sich die empirische Verteilungsfunktion in R sehr einfach mit Hilfe der Funktion ecdf erzeugen. Im Gegensatz zu den R-Funktionen für die Berechnung von Lage- oder Streuungsmaßen braucht man in der Funktion ecdf nicht speziell auf fehlende Werte hinzuweisen, sie werden automatisch bei der Berechnung ignoriert.

Beispiel:

Aus dem Datensatz mocksoep.csv ziehen wir die Variable Lebenszufriedenheit (lifesat) heraus und speichern sie als den Vektor zufried ab. Die Lebenszufriedenheit wird auf einer Skala von 1 (miserabel) bis 10 (super) abgefragt. Da die Abstände nicht sinnvoll interpretiert werden können, sondern nur die Reihenfolge (“je höher der Wert, desto zufriedener”), handelt es sich hierbei um eine ordinal skalierte Variable.

soep <- read_csv("../data/mocksoep.csv", 
                 col_types = "nnnnfnnnffnnncnnnnn") 
zufried <- pull(soep, lifesat)

Anschließend erzeugen wir die empirische Verteilungsfunktion.

FF <- ecdf(zufried)

Hinweis: Es ist empfehlenswert, das Symbol F in R nicht für die Verteilungsfunktion zu verwenden, weil F in R auch als Abkürzung für den logischen Wert FALSE steht. Ebenso sollte man den Variablennamen T (Abkürzung für TRUE) vermeiden.

Das R-Objekt FF ist eine Funktion. Wenn wir wissen wollen, wie hoch der Anteil der Befragten ist, der eine Lebenszufriedenheit von 6 oder weniger angegeben hat, erhalten wir das Ergebnis durch:

FF(6)

[1] 0.2632941

Es ist auch möglich, mehrere Stellen auf einmal auszuwerten, z.B.

FF(0:10)

 [1] 0.000000000 0.003057153 0.012960968 0.034665480 0.064523821 0.163917499
 [7] 0.263294147 0.477927182 0.803092494 0.945437475 1.000000000

Zur Erklärung: Mit 0:10 wird ein Vektor von ganzen Zahlen von 0 bis 10 in Einerschritten erzeugt.

Offensichtlich gibt es niemanden mit einer Lebenszufriedenheit von 0 oder weniger und nicht einmal 10 Prozent mit Werten von 4 oder weniger. Da der Wert 10 die höchstmögliche Angabe ist, erreicht die Funktion an der Stelle 10 den Wert 1, d.h. alle Personen haben eine angegebene Zufriedenheit von 10 oder weniger.

Es ist durchaus möglich, die empirische Verteilungsfunktion an Stellen auszuwerten, die keinen Ausprägungen entsprechen (oder bei denen die Werte eigentlich sinnlos sind). So ist der Wert an der Stelle \(x=-5\) natürlich 0, und an der Stelle \(x=6.73\) ist es

FF(6.73)

[1] 0.2632941

Das ist der gleiche Wert wie \(F(6)\).

Die empirische Verteilungsfunktion der Lebenszufriedenheit kann mit ggplot gezeichnet werden. Die Syntax ist:

ggplot(soep, aes(lifesat)) + 
    geom_step(stat="ecdf")+
    ggtitle("Emp. Verteilungsfunktion der Lebenszufriedenheit")

Zur Erläuterung: Das erste Argument in der ggplot-Funktion (also soep) gibt an, in welchem Dataframe die Daten gespeichert sind. Danach wird durch aes festgelegt, welche Variable des Dataframes gezeigt werden soll (hier also lifesat). Durch das Pluszeichen getrennt wird angegeben, wie die Daten zu zeigen sind. Die empirische Verteilungsfunktion ist eine Treppenfunktion, daher wird als Darstellungsform geom_step ausgewählt. Schließlich wird noch festgelegt, dass nicht die Daten selber als Treppenfunktion gezeichnet werden, sondern die empirische Verteilungsfunktion, dazu dient die Angabe stat="ecdf" in den Klammern.

Die senkrechten Verbindungslinien gehören eigentlich nicht zur empirischen Verteilungsfunktion dazu. Sie dienen hier lediglich der besseren grafischen Darstellung.

Wenn die Anzahl der unterschiedlichen Ausprägungen sehr groß ist, wirkt die empirische Verteilungsfunktion glatt, obwohl sie weiterhin eine Treppenfunktion ist. Das macht das folgende Beispiel deutlich.

Beispiel:

Im sozio-ökonomischen Panel werden viele Variablen aus dem Themenbereich “Arbeit” abgefragt. Dazu gehören auch Angaben zur geleisteten Arbeitszeit in einem Jahr. Die empirische Verteilungsfunktion der Anzahl der Arbeitsstunden (pro Jahr) sieht wie folgt aus.

ggplot(soep, aes(hours)) + 
    geom_step(stat="ecdf") +
    ggtitle("Emp. Verteilungsfunktion der Arbeitsstunden")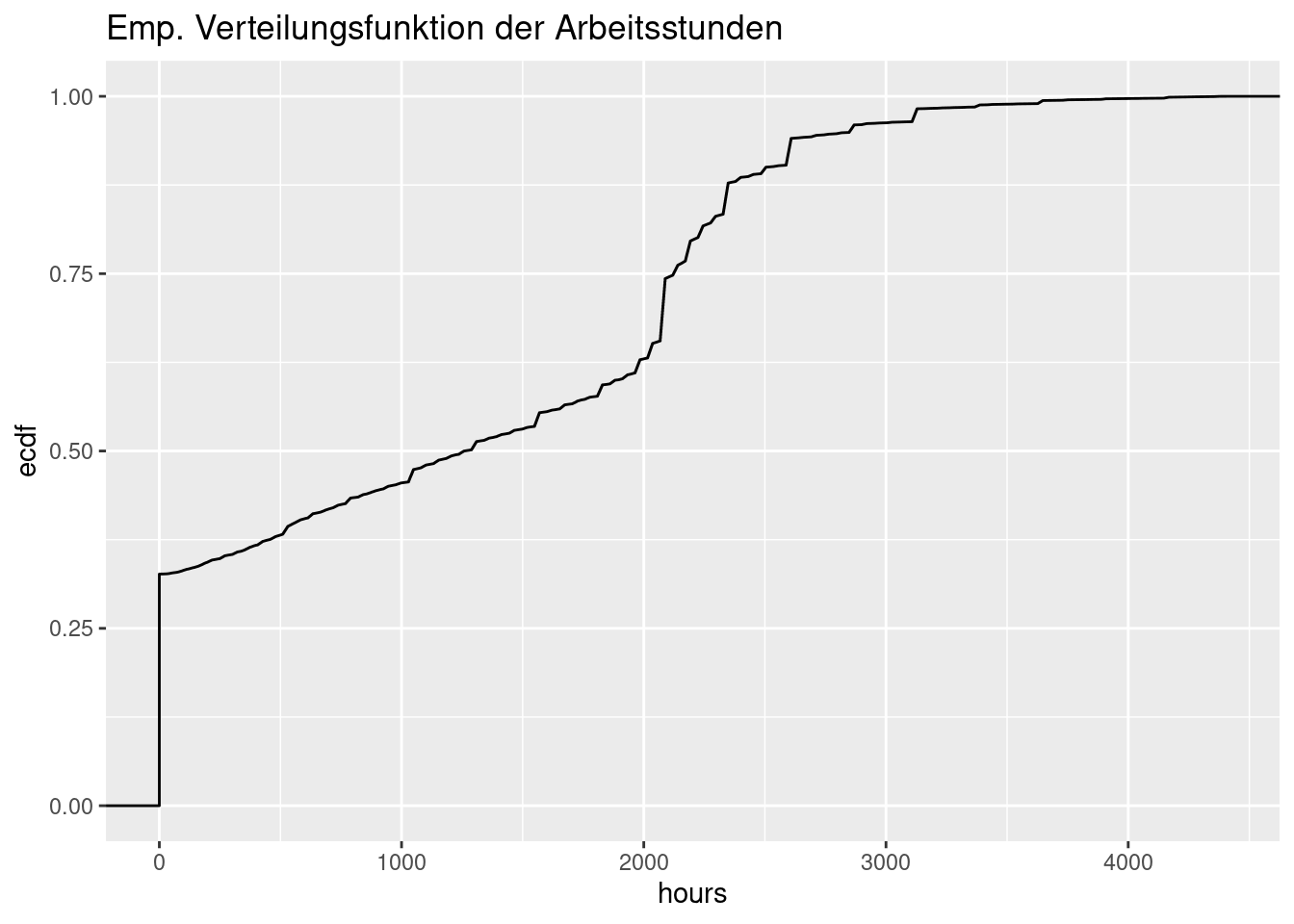

An dieser Funktion erkennt man unter anderem, dass mehr als 30 Prozent der Individuen eine Arbeitsstundenzahl von 0 hatten (dazu gehören z.B. Personen, die schon in Rente gegangen sind). Ferner kann man sehen, dass rund 90 Prozent betrachteten Personen 2500 Stunden oder weniger gearbeitet haben. Auch den Median kann man an der Grafik ablesen (oder zumindest abschätzen): 50 Prozent der Menschen hatten eine Arbeitsstundenzahl von rund 1200 oder weniger.

Empirische Verteilungsfunktionen kann man auch verwenden, um zwei Verteilungen zu vergleichen. Die folgende Abbildung zeigt die empirischen Verteilungsfunktionen der geleisteten Arbeitsstunden getrennt für Männer und Frauen.

ggplot(soep, aes(hours, colour=sex)) + 
    geom_step(stat="ecdf")+
    ggtitle("Emp. Verteilungsfunktionen der Arbeitsstunden")

Zum Verständnis ist es hilfreich nicht darauf zu achten, welche Funktion höher oder niedriger liegt, sondern darauf, welche Funktion weiter links oder weiter rechts liegt. Hier liegt die Funktion für die Frauen weiter links, also bei den niedrigeren Stundenzahlen. Wir erkennen daran, dass Frauen tendenziell weniger Arbeitsstunden hatten als Männer. Beispielsweise liegt der Median bei den Frauen deutlich unter 1000 Stunden, bei den Männern dagegen etwas über 2000 Stunden.