6  Häufigkeiten

In diesem Kapitel betrachten wir ein einzelnes Merkmal \(X\). Man spricht in diesem Fall von univariaten Daten (engl. univariate data). Es handelt sich normalerweise um eine einzelne Spalte eines Dataframes.

Die beobachteten Werte von \(X\) schreiben wir allgemein als \[ x_1, x_2, ..., x_n. \] Es gibt also Informationen zu insgesamt \(n\) Merkmalsträgern, das können Individuen, Haushalte, Firmen, Länder etc. sein. Man nennt die Daten \(x_1,...,x_n\) auch Urliste. In R handelt es sich bei der Urliste um eine Spalte eines Dataframes, und zwar in Form eines Vektors der Länge \(n\). Wir laden wieder den Beispiel-Dataframe imdb, der eine Auswahl aus der International Movie Database enthält.

imdb <- read_csv("../data/imdb.csv", col_types = "ccnfnnnnnn")
head(imdb)

# A tibble: 6 × 10
  title_id  title          year genre duration avgvote budget grossinc users_rev
  <chr>     <chr>         <dbl> <fct>    <dbl>   <dbl>  <dbl>    <dbl>     <dbl>
1 tt0035423 Kate & Leopo…  2001 Come…      118     6.4  48     76.0          341
2 tt0118589 Glitter        2001 Drama      104     2.2  22      5.27         319
3 tt0120467 Vulgar         2000 Crime       87     5.3   0.12   0.0159       119
4 tt0120630 Galline in f…  2000 Anim…       84     7    45    225.           393
5 tt0120667 I Fantastici…  2005 Acti…      106     5.7 100    334.          1029
6 tt0120679 Frida          2002 Biog…      123     7.4  12     56.3          297
# ℹ 1 more variable: critics_rev <dbl>

Es gibt in R mehrere Wege, um ein Merkmal als Vektor aus einem Dataframe heraus zu ziehen. Zwei dieser Wege haben wir im Kapitel 2.3 bereits kennen gelernt. Hier sind sie erneut, ergänzt um eine dritte Möglichkeit:

1. Spaltennummer in doppelten Klammern

x <- imdb[[4]]

2. Auswahl mit dem Dollarzeichen und dem Spaltennamen

x <- imdb$genre

3. Der pull-Befehl in tidyverse

x <- pull(imdb, genre)

oder

x <- imdb %>% pull(genre)

In diesem Beispiel ist x nun ein Vektor, der die univariaten Daten zum Ursprungsland der Filme im Dataframe imdb enthält. Wenn man den Vektor (also die Urliste) mit dem Befehl

print(x)

anzeigt, denn erhält man schlicht eine Auflistung aller Werte. Interaktiv kann man auch einfach nur x eingeben. Da der Vektor mit 5841 Elementen sehr lang ist, wird der Output hier nicht gezeigt.

Um den Umfang (engl. size) \(n\) der Population zu bestimmen, kann man entweder die erste Dimension des Dataframes auswählen,

n <- dim(imdb)[1]

oder man ermittelt die Länge des aus dem Dataframe herausgezogenen Vektors,

n <- length(x)

In beiden Fällen erhält man den Wert

print(n)

[1] 5841

Wenn eine Variable \(X\) nur relativ wenige verschiedene Werte bzw. Ausprägungen annimmt, kann eine Häufigkeitsauszählung interessante Einblicke bringen. Nominale Variablen haben oft nur recht wenige Werte, beispielsweise hat das Geschlecht nur die Ausprägungen “männlich” und “weiblich” (oder einige weitere Ausprägungen wie “divers”). Auch manche metrischen Variablen haben nur wenige Ausprägungen, z.B. die Anzahl der Personen, die in einem Haushalt leben. Für solche metrischen Variablen sind Häufigkeiten gut darstellbar und für das Verständnis der Daten hilfreich. Wenn die Anzahl der möglichen Werte dagegen sehr groß ist, wie z.B. beim Einkommen, sind Häufigkeiten nutzlos.

6.1 Absolute Häufigkeiten

Die absolute Häufigkeit (engl. absolute frequency) gibt für jeden möglichen Wert (Ausprägung) an, wie oft dieser Wert angenommen wird. Wenn wir die möglichen Werte mit \(\xi_1,..., \xi_J\) bezeichnen (diese griechischen Buchstaben werden xi ausgesprochen), dann sind \[ n_j = \#\{x_i = \xi_j\} \] für \(j=1,...J\) die absoluten Häufigkeiten. Das Hashtag-Zeichen steht für “Anzahl”. Die absolute Häufigkeit \(n_j\) gibt also an, bei wie vielen Merkmalsträgern die Variable \(X\) den Wert \(\xi_j\) annimmt. Eine Tabelle der Form \[ \begin{array}{cc}\hline \text{Ausprägung} & \text{abs. Häufigkeit}\\ \hline \xi_1 & n_1 \\ \xi_2 & n_2 \\ \xi_3 & n_3 \\ \vdots & \vdots\\ \xi_J & n_J \\\hline \end{array} \] heißt (absolute) Häufigkeitstabelle. Vorsicht: Nicht jede Tabelle ist eine Häufigkeitstabelle. Auch Urlisten, also \(x_1,\ldots,x_n\), werden oft tabellarisch dargestellt. Dann stehen in der linken Spalte die Indexwerte \(1,\ldots,n\) und in der rechten Spalte die Beobachtungen \(x_1,\ldots,x_n\). Überlegen Sie bei einer Tabelle immer, ob es sich um eine tabellarisch dargestellte Urliste oder eine Häufigkeitstabelle handelt.

Die Summe aller absoluten Häufigkeiten ergibt den gesamten Populationsumfang, \[ \sum_{j=1}^J n_j = n. \]

In R gibt es mehrere Wege, die absoluten Häufigkeiten auszuzählen.

Wenn die Daten in Form eines Vektors vorliegen, lautet der R-Befehl für die absoluten Häufigkeiten table. Er liefert folgenden Output (für einen Vektor x):

table(x)

x
   Comedy     Drama     Crime Animation    Action Biography    Horror Adventure 
     1460      1273       399       334      1426       342       326       253 
 Thriller 
       28 

Offenbar ist die Tabelle hier nicht senkrecht, sondern waagerecht angeordnet. Man erkennt, dass in dem Dataframe besonders viele Komödien und Actionfilme zu finden sind, aber nur wenige Thriller.

Die Häufigkeiten lassen sich auch ermitteln, wenn die Variable nicht als Vektor aus dem Dataframe gezogen wurden. Man verwendet für die Auszählung die Funktion group_by, um den Dataframe nach den Ausprägungen der Variable zu gruppieren, für die man die Häufigkeiten berechnen will. Anschließend kann man in der summarise-Funktion mit n() die Häufigkeiten ermitteln:

group_by(imdb, genre) %>% 
    summarise(n=n())

# A tibble: 9 × 2
  genre         n
  <fct>     <int>
1 Comedy     1460
2 Drama      1273
3 Crime       399
4 Animation   334
5 Action     1426
6 Biography   342
7 Horror      326
8 Adventure   253
9 Thriller     28

Ein Vorteil dieses Vorgehens ist, dass man den Output leicht umsortieren kann, z.B. nach der Häufigkeit absteigend:

group_by(imdb, genre) %>% 
    summarise(n=n()) %>%
    arrange(desc(n))

# A tibble: 9 × 2
  genre         n
  <fct>     <int>
1 Comedy     1460
2 Action     1426
3 Drama      1273
4 Crime       399
5 Biography   342
6 Animation   334
7 Horror      326
8 Adventure   253
9 Thriller     28

Wenn die Häufigkeiten nicht in Form einer Tabelle, sondern als Grafik dargestellt werden sollen, kann man in ggplot folgendermaßen vorgehen.

ggplot(imdb, aes(x=genre)) + geom_bar()

Zur Erklärung: Das erste Argument in ggplot (also imdb) ist der Dataframe, der die Variable enthält. Mit Hilfe von aes wird festgelegt, welche Variable als Aesthetic gezeigt werden soll. Hier wird (im Gegensatz zu einem Streudiagramm) nur eine Variable ausgewählt, die Angabe x= legt fest, dass die Ausprägungen entlang der x-Achse angezeigt werden sollen. Nach dem Pluszeichen folgt die Angabe, durch welche geometrische Form die Darstellung erfolgen soll, hier also durch ein Balkendiagramm (bar plot).

Wenn man als Aesthetic y= eingibt, werden die Ausprägungen entlang der y-Achse angezeigt, also als horizontale Balken. Das ist manchmal empfehlenswert, weil sich die Beschriftungen der Balken bei längeren Labels dann nicht überlappen.

ggplot(imdb, aes(y=genre)) + geom_bar()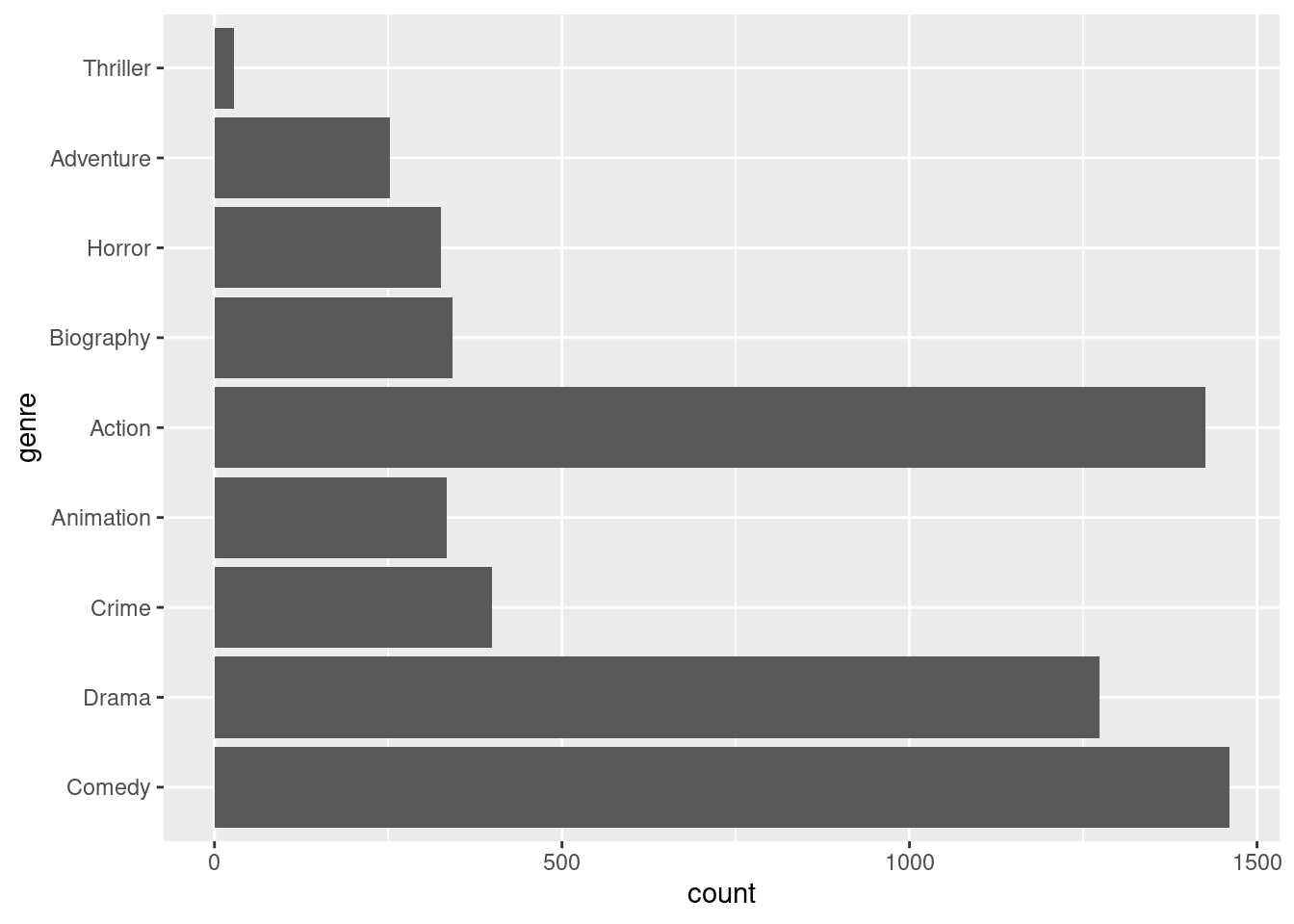

Das Lesen eines Balkendiagramms ist einfacher, wenn die Balken nach ihrer Länge geordnet werden. Das ist in R leider nicht auf elementare Weise möglich, wenn die Variable nominal skaliert und als Datentyp factor gespeichert ist. Das tidyverse-Paket forcats bietet eine Reihe von Funktionen, mit denen man Variablen vom Datentyp factor bearbeiten kann. Als Beispiel wird hier gezeigt, wie mit der Funktion fct_infreq die Ausprägungen der factor-Variable genre der Häufigkeit nach geordnet werden können.

ggplot(imdb, aes(x=fct_infreq(genre))) + geom_bar()

6.2 Relative Häufigkeiten

Neben den absoluten Häufigkeiten sind oft auch die relativen Häufigkeiten (engl. relative frequencies) von Interesse. Absolute Häufigkeiten sind Anzahlen, relative Häufigkeiten sind Anteile, sie werden durch eine Zahl zwischen 0 und 1 oder in Prozent (zwischen 0 und 100) angegeben. Die relative Häufigkeit der Ausprägung \(\xi_j\) für \(j=1,...,J\) ist \[ f_j=\frac{n_j}{n}, \] wobei \(n\) der Umfang der Population ist. Da die Summe aller absoluten Häufigkeiten dem Populationsumfang entspricht, gilt für die relativen Häufigkeiten \[ \sum_{j=1}^J f_j =1. \] In Tabellenform sieht die relative Häufigkeitsverteilung dann so aus: \[ \begin{array}{cc}\hline \text{Ausprägung} & \text{rel. Häufigkeit}\\ \hline \xi_1 & f_1 \\ \xi_2 & f_2 \\ \xi_3 & f_3 \\ \vdots & \vdots\\ \xi_J & f_J \\\hline \end{array} \] Für die Ermittlung der relativen Häufigkeiten gibt es wieder mehrere Wege in R.

Wenn die Daten als Vektor vorliegen, kann man die Anteile einer Tabelle bestimmen, indem man die Funktion proportions auf das table-Objekt wendet.

proportions(table(x))

x
    Comedy      Drama      Crime  Animation     Action  Biography     Horror 
0.24995720 0.21794213 0.06831022 0.05718199 0.24413628 0.05855162 0.05581236 
 Adventure   Thriller 
0.04331450 0.00479370 

Der Output ist nicht gut lesbar, weil die Zahl der Nachkommastellen zu groß ist. Mit der Funktion round runden wir die Ausgabe auf eine vorgegebene Anzahl von Nachkommastellen, z.B. auf vier Stellen:

round(proportions(table(x)), 4)

x
   Comedy     Drama     Crime Animation    Action Biography    Horror Adventure 
   0.2500    0.2179    0.0683    0.0572    0.2441    0.0586    0.0558    0.0433 
 Thriller 
   0.0048 

Wir sehen, dass ein Viertel der Filme Komödien sind. Der Anteil der Actionfilme ist ebenfalls fast ein Viertel. Dagegen sind nur 0.5 Prozent der Filme im Datensatz Thriller.

Mit Hilfe von group_by und summarise können wir die relativen Häufigkeiten errechnen, wenn vorher der Populationsumfang n gespeichert wurde.

n <- dim(imdb)[1]
group_by(imdb, genre) %>% 
    summarise(f = round(n()/n, 4)) %>%
    arrange(desc(f))

# A tibble: 9 × 2
  genre          f
  <fct>      <dbl>
1 Comedy    0.25  
2 Action    0.244 
3 Drama     0.218 
4 Crime     0.0683
5 Biography 0.0586
6 Animation 0.0572
7 Horror    0.0558
8 Adventure 0.0433
9 Thriller  0.0048

Die grafische Darstellung von relativen Häufigkeiten mit ggplot ist leider etwas komplizierter und sieht etwas unsystematisch aus.

ggplot(imdb, aes(x=genre)) + 
    geom_bar(aes(y=after_stat(count/sum(count))))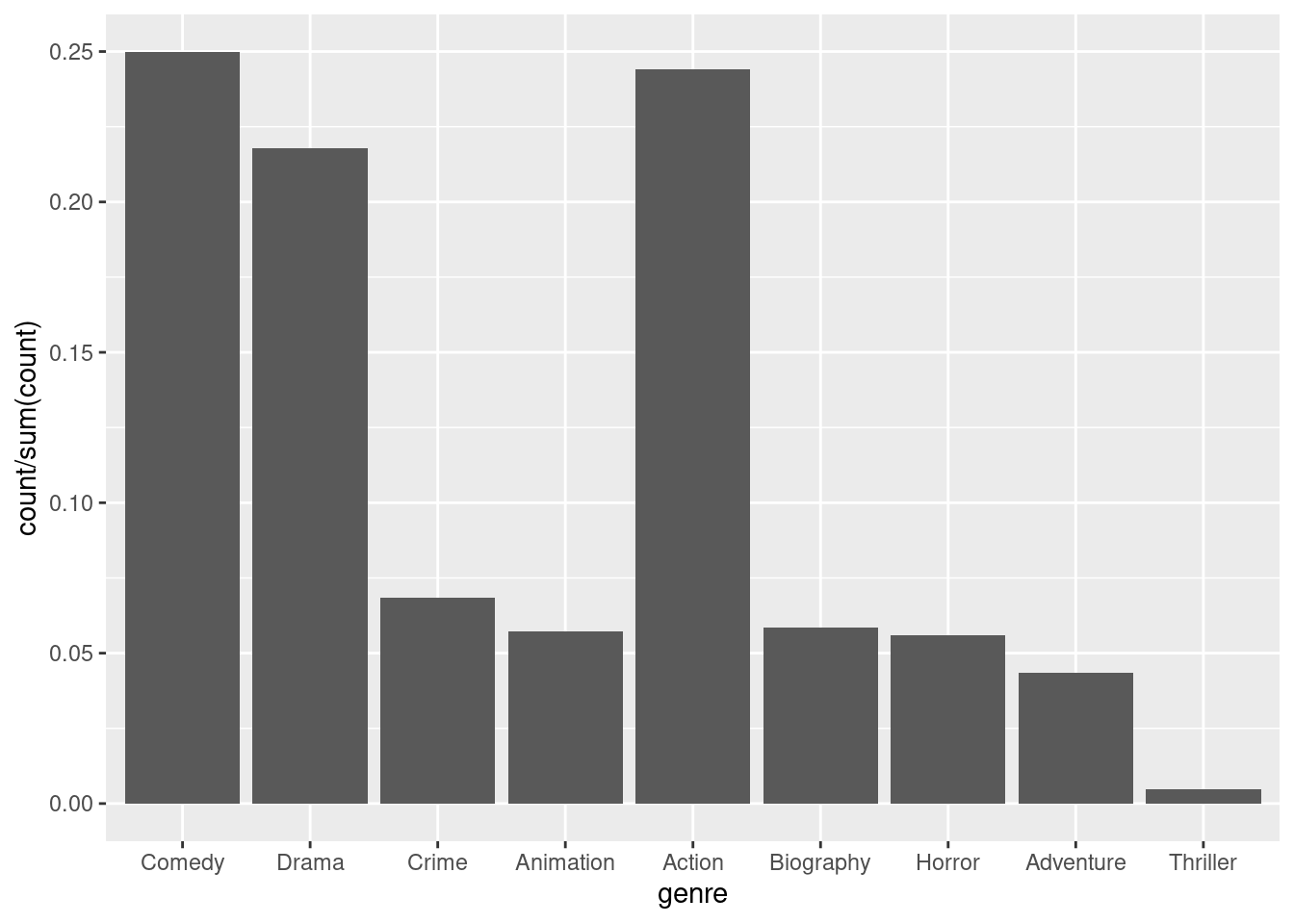

Die Angabe in geom_bar besagt, dass die relativen Häufigkeit als Aesthetic in Richtung der y-Achse interpretiert werden sollen. Die Schreibweise after_stat steht für eine Variable in ggplot, die intern aus den Daten der Variable genre berechnet wird. In diesem Fall wird die absolute Häufigkeit count durch die Summe der absoluten Häufigkeiten dividiert, es handelt sich also um die relativen Häufigkeiten.

Eine alternative Möglichkeit ist der Umweg über die relative Häufigkeitstabelle. Zunächst wird die Häufigkeitstabelle als eigener Dataframe gespeichert.

n <- dim(imdb)[1]
relTable <- group_by(imdb, genre) %>% 
    summarise(f = round(n()/n, 4))

Anschließend wird nicht der Inhalt des Dataframes imdb, sondern die Häufigkeitstabelle relTablegrafisch dargestellt. Dabei muss jedoch beachtet werden, dass die rechte Spalte die Häufigkeiten \(f_j\) enthält, nicht die einzelnen Merkmalswerte \(x_i\). Diese Information übermitteln wir an ggplot durch die Angabe stat="identity" als Argument der Funktion geom_bar:

ggplot(relTable, aes(x=genre, y=f)) + 
    geom_bar(stat="identity")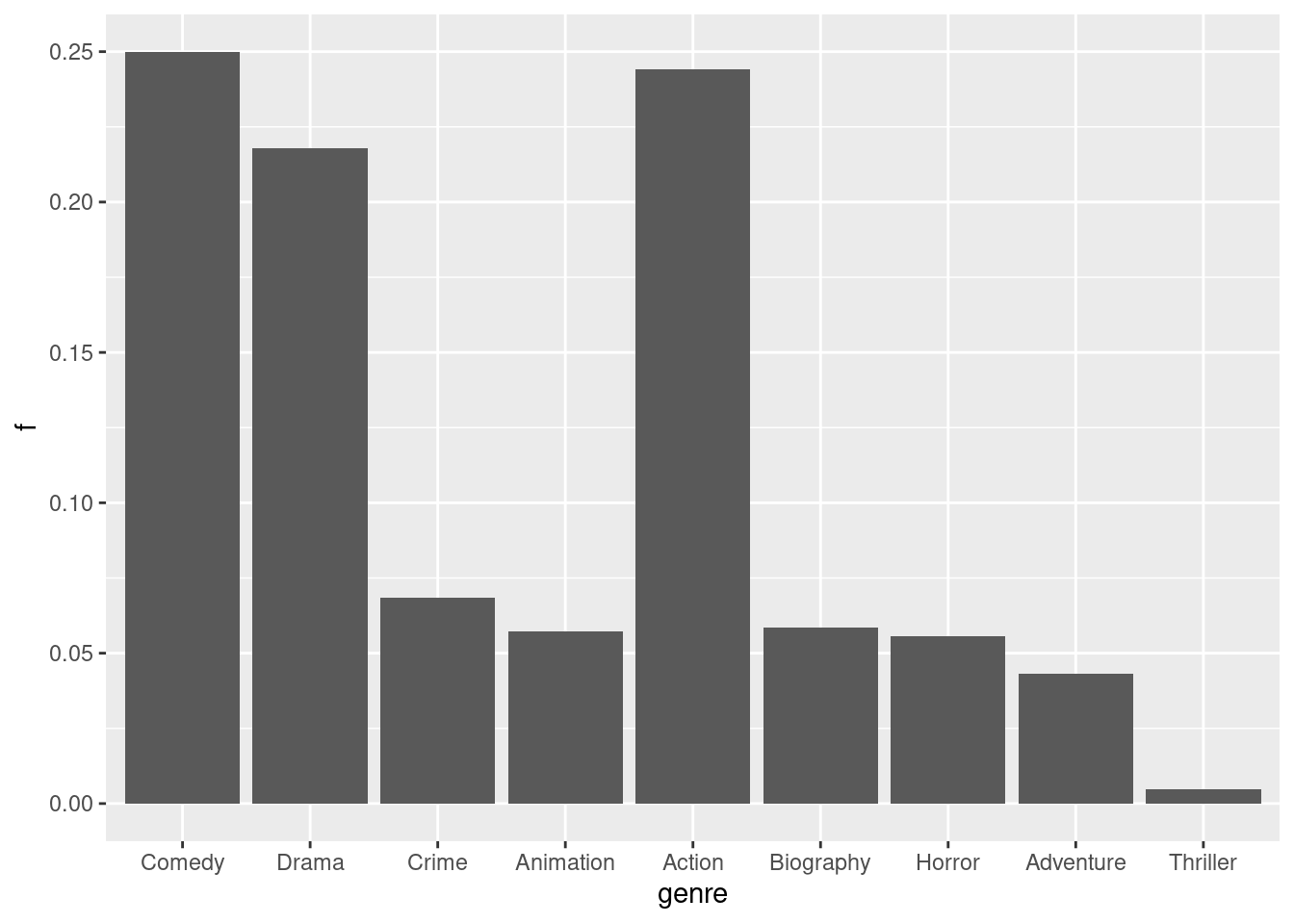

6.3 Klassierte Daten

Häufigkeiten sind für das Verständnis der Daten nur dann hilfreich, wenn die Originalinformationen ausreichend stark verdichtet werden. Das Beispiel zu den Genres in der Movie-Database ist eine deutliche Verdichtung, denn aus den 5841 Original-Ausprägungen wurde durch die Auszählung der Häufigkeiten eine übersichtliche Tabelle mit nur noch 9 Zeilen (nämlich eine für jedes Genre).

Wenn wir die Verteilung der Variable duration darstellen wollen, ist eine Häufigkeitsauszählung nicht sinnvoll, weil diese Variable 129 verschiedene Werte annimmt - viele davon nur ein einziges Mal.

Die Information über die Verteilung von Variablen, die viele verschiedene Werte annehmen, lassen sich gut verdichten und grafisch darstellen, indem man Klassen (Intervalle) bildet und dann auszählt, wie viele Werte in jeder Klasse liegen.

Wenn wir insgesamt \(J\) Klassen bilden, dann bezeichnen wir die Klassengrenzen mit \[ a_0 < a_1 < a_2 < \ldots < a_J \] Die \(i\)-te Klasse ist das Intervall \((a_{i-1}, a_i]\), d.h. die Intervallobergrenze zählen wir zum Intervall dazu, die Untergrenze nicht, sie zählt zu der nächsttieferen Klasse. Aus praktischen Gründen wird oftmals die unterste Klasse als einzige so definiert, dass auch die Untergrenze zum Intervall dazugehört, d.h. das erste Intervall ist \([a_0,a_1]\). Um die Notation im folgenden einfach zu halten, wird dieser Spezialfall nicht jedesmal extra erwähnt. Damit alle Werte \(x_1,\ldots, x_n\) abgedeckt sind, muss gelten \(a_0 \le \min_i x_i\) und \(a_J\ge \max_i x_i\).

Die absoluten Klassenhäufigkeiten sind für \(j=1,\ldots,J\) \[ n_j = \# \{x_i \in (a_{j-1},a_j]\} \] und die entsprechenden relativen Klassenhäufigkeiten sind \[ f_j = \frac{n_j}{n}. \] In R ist eine Klassierung sehr einfach möglich mit der Funktion cut. Wenn die Daten in dem Vektor x gespeichert sind, kann man mit der Funktion

x_klass <- cut(x, breaks=J)

den Vektor der zugehörigen klassierten Werte erzeugen. Dabei gibt \(J\) an, wie viele Intervalle gebildet werden sollen. Die Intervallgrenzen sind in der Standardeinstellung alle gleich weit voneinander entfernt. Das ist nicht immer sinnvoll, manchmal möchte man einige Intervalle schmaler, andere dagegen breiter haben. Oft ist es auch gewünscht, dass die Klassengrenzen keine “krummen” Werte sind. In diesen Fällen ist es möglich, mit der breaks-Option alternativ einen Vektor von Klassengrenzen in die Funktion zu übergeben. Angenommen, der Vektor a enthält die Klassengrenzen, dann lautet der Aufruf

x_klass <- cut(x, breaks=a)

Wenn einige Werte des Vektors x außerhalb aller Intervalle liegen, kommt es zu einer Fehlermeldung.

Standardmäßig gehört beim cut-Befehl die Untergrenze nicht zum Intervall dazu (sondern zum nächsttieferen Intervall). Will man für das unterste Intervall eine Ausnahme machen und \(a_0\) zum ersten Intervall gehören lassen, kann man das durch die Option include.lowest erreichen:

cut(x, breaks=a, include.lowest=TRUE)

Die klassierten Daten x_klass werden in R als Faktor (also als nominal skaliert) behandelt. Sie können ganz normal mit der Funktion table ausgezählt werden.

Beispiel:

Wir möchten die Länge (in Minuten) der Filme aus der Internet Movie Database analysieren. Dazu erstellen wir eine Tabelle mit den absoluten Häufigkeiten. Die Daten werden klassiert, weil es deutlich über 100 verschiedene Minutenwerte gibt, die in dem Datensatz imdb vorkommen.

Zuerst ziehen wir die Variable duration aus dem Dataframe heraus und speichern sie in einem Vektor mit dem Namen laenge ab.

laenge <- imdb$duration
head(laenge)

[1] 118 104  87  84 106 123

Der erste Film im Datensatz hat also eine Länge von 118 Minuten, der zweite von 104 Minuten usw.

Nun werden die Beobachtungen klassiert. Als Klassengrenzen verwenden wir den Vektor

a <- c(60,80,85,90,95,100,110,130,150,230) 

Dieser Vektor enthält die kleinste Duration, die im Datensatz vorkommt (nämlich 60), die Obergrenze des letzten Intervalls ist jedoch größer als die maximale Filmlänge (nämlich größer als 224). Der Vektor der klassierten Beobachtungen wird als laenge_kl gespeichert. Damit der kleinste Wert dem ersten Intervall zugewiesen wird, setzen wir die Option include.lowest=TRUE.

laenge_kl <- cut(laenge, breaks=a, include.lowest=TRUE)

Die absoluten Häufigkeiten können nun durch mit table ausgezählt werden.

table(laenge_kl)

laenge_kl
  [60,80]   (80,85]   (85,90]   (90,95]  (95,100] (100,110] (110,130] (130,150] 
      145       276       661       776       807      1297      1366       389 
(150,230] 
      124 

6.4 Histogramme

Die grafische Darstellung der Klassenhäufigkeiten erfolgt in Form von Histogrammen (engl. histograms). Bei einem Histogramm werden die Klassen auf der x-Achse abgetragen. Über jeder Klasse bildet man einen Balken, dessen Fläche proportional zur (absoluten oder relativen) Häufigkeit ist. Die Breite des Balkens \(j\) ist also \(a_j-a_{j-1}\), und die Höhe ist \(f_j/(a_j-a_{j-1})\) (oder \(n_j/(a_j-a_{j-1})\)). Wenn die Klassenbreiten alle gleich sind, sind die Histogrammbalken schlicht proportional zur (absoluten oder relativen) Häufigkeit.

Mit ggplot ist es sehr einfach Histogramme zu erstellen, z.B.

ggplot(imdb, aes(duration)) + geom_histogram(bins=40)

Zur Erläuterung: Das erste Argument in der Funktion ggplot ist wieder der Dataframe, der die Variable enthält, für die wir das Histogramm zeichnen wollen. Das zweite Argument gibt das Aesthetic an, also die Variable, die grafisch dargestellt werden soll, hier ist es die Dauer des Films duration. Nach dem Pluszeichen folgt das Geom, hier ist es das Histogramm. Als Argument ist die Anzahl der Balken (bins) angeben. In der Abbildung ist auf der y-Achse die absolute Zahl von Filmen in jeder Klasse abgetragen.

Man erkennt an der Abbildung, dass es sehr viele Filme gibt, die etwa 90 bis 100 Minuten dauern. Es gibt in dem Datensatz kaum Filme, die kürzer sind als 75 Minuten oder länger als 150 Minuten.

Als Alternative zur Anzahl der Klassen (bins) ist es auch möglich einen Vektor von Klassengrenzen als Argument zu übergeben. Das folgende Beispiel zeigt, wie man die Klassengrenzen vorgibt. Leider ist das Vorgehen etwas komplizierter, wenn die Klassengrenzen nicht äquidistant sind, weil zusätzlich zu den Klassengrenzen (breaks) noch sichergestellt werden muss, dass die Flächeninhalte der Balken proportional zur Klassenbreite sind. Letzteres erfolgt durch das zusätzliche Argument aes(y=..density..).

a <- c(60,75,80,85,90,95,100,110,130,150,200,230) 
ggplot(imdb, aes(duration)) + 
    geom_histogram(breaks=a, aes(y=after_stat(density)))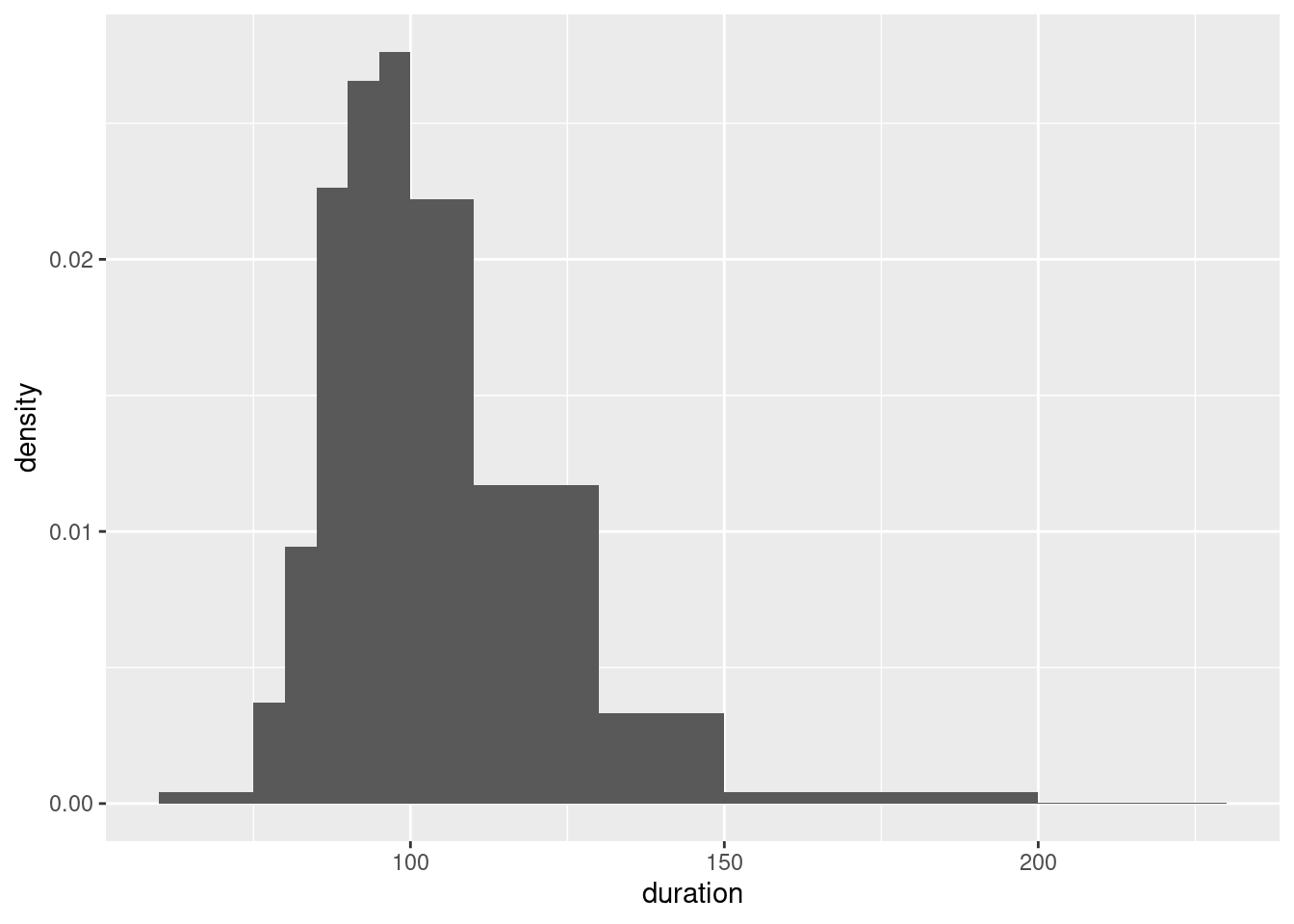

In dieser Abbildung ist auf der y-Achse die relative Häufigkeit abgetragen, und zwar so skaliert, dass die Fläche der Balken proportional zur relativen Häufigkeit ist. Daraus folgt, dass die Gesamtfläche unter dem Histogramm den Wert 1 annimmt, denn \[\begin{align*} \sum_{j=1}^J Breite_j \times Höhe_j &= \sum_{j=1}^J (a_j-a_{j-1})\frac{f_j}{a_j-a_{j-1}}\\ &= \sum_{j=1}^J f_j\\ &= 1 \end{align*}\]

(Einen knappen Überblick über die Verwendung des Summenzeichens findet man im Anhang C.)

6.5 Kerndichten

Die genaue Form eines Histogramms hängt davon ab, wie man die Klassengrenzen auswählt. Außerdem ändert sich die Höhe der Balken natürlich plötzlich, wenn man in die nächste Klasse wechselt. Man kann eine geglättete Variante des Histogramms definieren, sie wird Kerndichteschätzung (engl. kernel density estimation) genannt. Auf die genaue Definition gehen wir in diesem Kurs nicht ein.

Die Kerndichte kann in ggplot durch das Geom geom_density dargestellt werden.

ggplot(imdb, aes(duration)) + 
    geom_density()

Dass es sich tatsächlich um ein geglättetes Histogramm handelt, erkennt man gut, wenn beide Darstellungsweise gemeinsam in einer Abbildung zu sehen sind.

ggplot(imdb, aes(duration)) + 
    geom_histogram(breaks=a, aes(y=after_stat(density)))+
    geom_density()