Future and Present Value

$~$

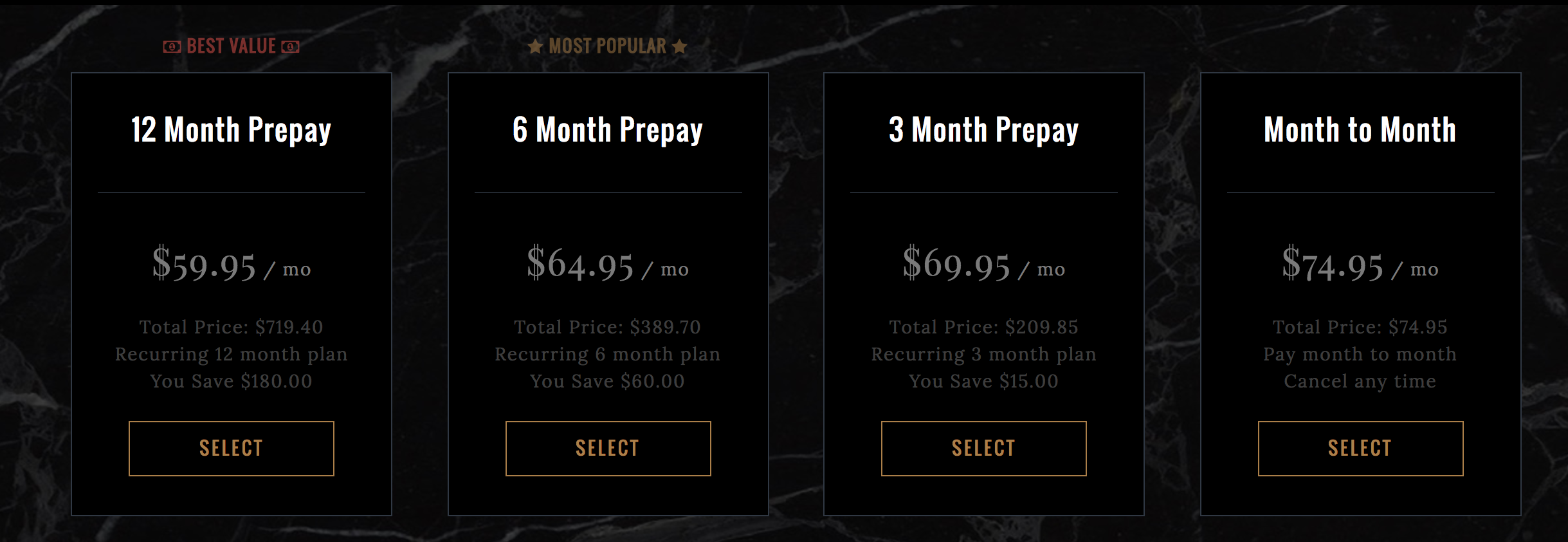
Should you let somebody else provide you with a monthly box full of vice fulfillment? The Robb Vices Box provides a monthly box of luxury products. This is luxury stuff. You can choose from a variety of subscription options as follows.

$~$

$~$

Assuming that you remain luxurious for at least the next 3 years, which of these makes the most sense? Perhaps we can look at the subscriptions price per month and what these would be for a full year.

$~$

subscriptions <- c("12 Month PrePay", "6 Month PrePay", "3 Month PrePay", "Month to Month")
monthly  <- c(59.95, 64.95, 69.95, 74.95)
yearly  <- monthly*12
robb <- data.frame(subscriptions, yearly, monthly)
kable(robb, format = "html", caption = "Different Subscription Choices for Robb Box")

Table 1: Different Subscription Choices for Robb Box
subscriptions	yearly	monthly
12 Month PrePay	719.4	59.95
6 Month PrePay	779.4	64.95
3 Month PrePay	839.4	69.95
Month to Month	899.4	74.95

$~$

Clearly, the 12 Month PrePay option is the least, however, it may be that over the course of the year you could put the extra $180 you spend by using the Month to Month option. In other words, maybe $180 dollars today is worth more than $180 a year from now. This would depend on whether or not we can use that money to make up the difference in savings. For example, maybe we can invest this money and make $1000. Then it would certainly make sense to do the month to month, but this is an unlikely scenario.

Future and Present Value

We can simplify the problem above with the following proposal – would you rather receive $1000 today or $1050 a year from now? Notice this is determined by whether or not we can make $50 or 5% on the $1000 in a year. The following definitions will help us with a further analysis here.

Future Value: Any amount of money that we possess at the moment has some future value.

Present Value: Any amound of money that we will receive in the future has a present value.

These closed formulas should be easy to make sense of for a single payment at rate r.

\[V_f = M + rM \quad \text{or} \quad V_p = \displaystyle \frac{M}{1 +r}\] $~$

Now, we can extend this to n compounding periods just as we did with simple and compound interest as follows.

\[V(n) = M(1 + r)^n \quad \text{and} \quad V(p) = \displaystyle \frac{M}{(1 + r)^n}\]