Credit Cards and Interest

Consider the Discover credit card for students, and the following two scenarios:

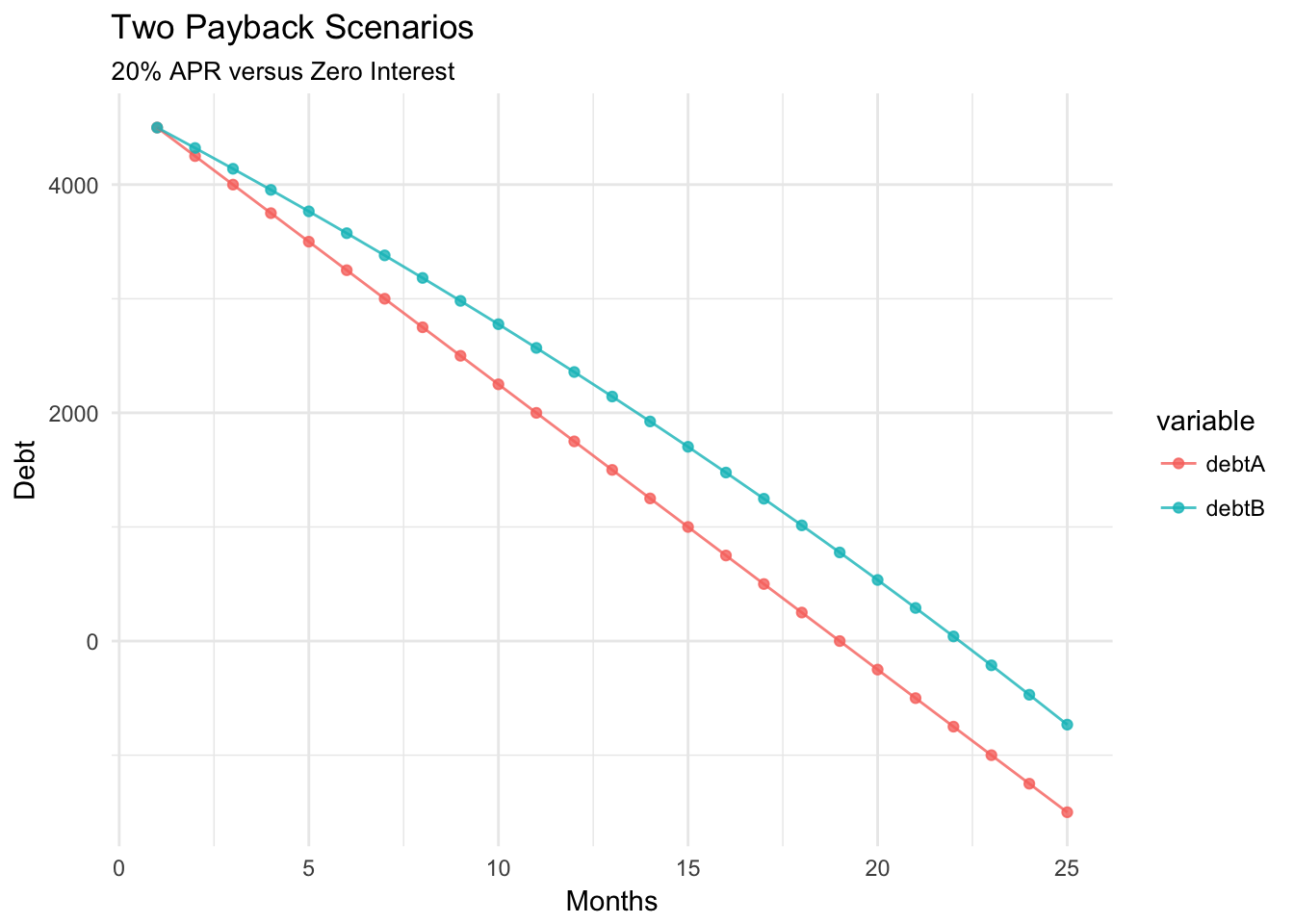
• Student A: Ran up $4500 in debt in 6 months, parents bailed him out and he pays them back $200 a month until the debt is resolved.

• Student B: Ran up $4500 in debt in 6 months, parents don’t bail them out and they will stop using card and pay back Discover at $200 a month.

We want to understand the difference in the amount of money paid back between the two. To do so, let us model these payoffs with recursively defined sequences. For Student A, we simply continually subtract the $250 dollars per month for 24 months as follows.

debtA <- 4500
for(i in 1:24){
      debtA[i+1] <- debtA[i] - 250
}

The situation for Student B is similar except that every month, the balance in the account will have interest applied to it. This will be added to the balance of the debt on a monthly basis. If we assume a 20% APR from Discovery, this works out to a 1.67% montly rate. Thus, after the first month, we pay the $250 dollars, but then we have to add back 1.67% of the $4250 still owed. We can investigate this with a similar for loop.

debtB <-  4500
for(i in 1:24){
        debtB[i+1] <- debtB[i] - 250 + 0.0167*(debtB[i] - 250)
}

Next, we can create a dataframe to display the results.

Months <- seq(length(debtB))
credit_cards <- data.frame(Months, debtA, debtB)
kable(head(credit_cards))

Months	debtA	debtB
1	4500	4500.000
2	4250	4320.975
3	4000	4138.960
4	3750	3953.906
5	3500	3765.761
6	3250	3574.474

Finally, we can melt the data in preparation for plotting.

library(reshape)
credit_plot <- melt(credit_cards, id.vars = "Months", variable.name = "series")
kable(head(credit_plot))

Months	variable	value
1	debtA	4500
2	debtA	4250
3	debtA	4000
4	debtA	3750
5	debtA	3500
6	debtA	3250

And produce our plot.

ggplot(credit_plot, aes(Months, value)) +
  geom_point(alpha = 0.8, aes(color = variable)) +
  geom_line(alpha = 0.8, aes(color = variable)) +
  theme_minimal() +
  labs(title = "Two Payback Scenarios", subtitle = "20% APR versus Zero Interest", x = "Months", y = "Debt")