8 Structural Equation Modeling (9/26)
Today, we will extend our statistical understandings regarding correlation and regression to the concept of Structural Equation Modeling (SEM).
SEM comprises a diverse set of analysis techniques, including confirmatory factor analysis and path analysis, each of which lend to the testing of theoretical models. Researchers who utilize SEM might review literature related to the constructs of interest (i.e., unobservable phenomena), and then hypothesize specific pathways within a plausible model through a set of regression equations and factor analyses, thus allowing for efficient exploration of complex relationships within and between psychological constructs. The variables within any model might include both measured variables and latent variables, or hypothetical constructs that cannot be directly observed (e.g., intelligence).
SEM utilizes maximum likelihood estimation (MLE), a statistical method which determines values for model parameters. Specifically, MLE maximizes the likelihood that the observed data will fit a theoretical model over other potential data distributions.
8.1 Differences Between Correlation and Regression
Researchers use either bivariate regression (simple—one dependent and one independent) or multiple regression (more than one independent and one dependent) as even more nuanced models of influence between two or more variables in a dataset. Dependent variables in each of these scenarios are often called criterion, outcome, or response variable, while the independent variable is often called the predictor or explanatory variable.
Regression is used to find relationships between variables—similarly to correlation analysis—however, there are three major differences between correlation and regression.
Test Purpose
“While correlation analyses are used to determine relationships and the strength of relationships between variables, researchers use regression analysis to predict, based on information from another variable or set of variables, the outcome of one variable. Otherwise, researchers can use regression analysis as a tool to explain why, based on any given predictor variables, differences exist between participants” (Russell, 2018, p. 193).
Variable Names
There must be a dependent variable in regression that a researcher is trying to predict based on other predictor (independent) variables. This concept is not used in correlation methods.
REVIEW: Regression Coefficients and Slope Intercepts
Researchers can use regression coefficients to infer beyond the direction and magnitude of relationships and discuss changes in Y due to specific changes in X (e.g., for every increase of 1 unit in Y, X increases .5)
The unstandardized regression formula is Y = a + bX where a is the intercept (where the line of best fit crosses the y-axis) and b is the slope of the regression line (½ is up 1 over 2). Put otherwise, a is the value of Y when X = 0 and b is the regression coefficient. The null hypothesis of the regression model is that independent variables are not able to significantly predict the dependent variable (i.e., the slope or standardized beta weight is 0, and that the predictor variable had no impact on the dependent variable).
Here’s how you perform simple linear regression in R. This example uses the mtcars dataset which describes several measures of a set of cars. Let’s model quarter mile time (qsec) as predicted by horsepower then examine the intercepts and coefficients before visualizing the relationship in a scatter plot.
The following code represents the unstandardized regression formula using the function lm() assigned to the object mod
mod <- lm(qsec ~ hp, data = mtcars)Use summary(mod) to display the statistical output. See the asterisks for the level of significance, and the coefficient labelled ‘estimate’ as a description of the extent to which the target variable should change as the predictor variable increases by 1 unit. The r-squared, F-statistics, degrees of freedom, and p-value provide important model fit and parsimony statistics that provide important context for the interpretation of regression coefficients.
summary(mod)##
## Call:
## lm(formula = qsec ~ hp, data = mtcars)
##
## Residuals:
## Min 1Q Median 3Q Max
## -2.1766 -0.6975 0.0348 0.6520 4.0972
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 20.556354 0.542424 37.897 < 2e-16 ***
## hp -0.018458 0.003359 -5.495 5.77e-06 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.282 on 30 degrees of freedom
## Multiple R-squared: 0.5016, Adjusted R-squared: 0.485
## F-statistic: 30.19 on 1 and 30 DF, p-value: 5.766e-06It’s helpful to store the model coefficients as objects to be referred to in plotting procedures.
beta0 <- coef(mod)[1]
beta1 <- coef(mod)[2]Use the geom_point() and geom_abline() functions to display a scatterplot with a line of best fit.
library(tidyverse) #recently added
ggplot(mtcars, aes(x = hp, y = qsec)) +
geom_point() +
geom_abline(intercept = beta0, slope = beta1, colour='red') +
ggtitle("Quarter Mile Time as a function of Horsepower") +
xlab('Horsepower') +
ylab('Quarter Mile Time')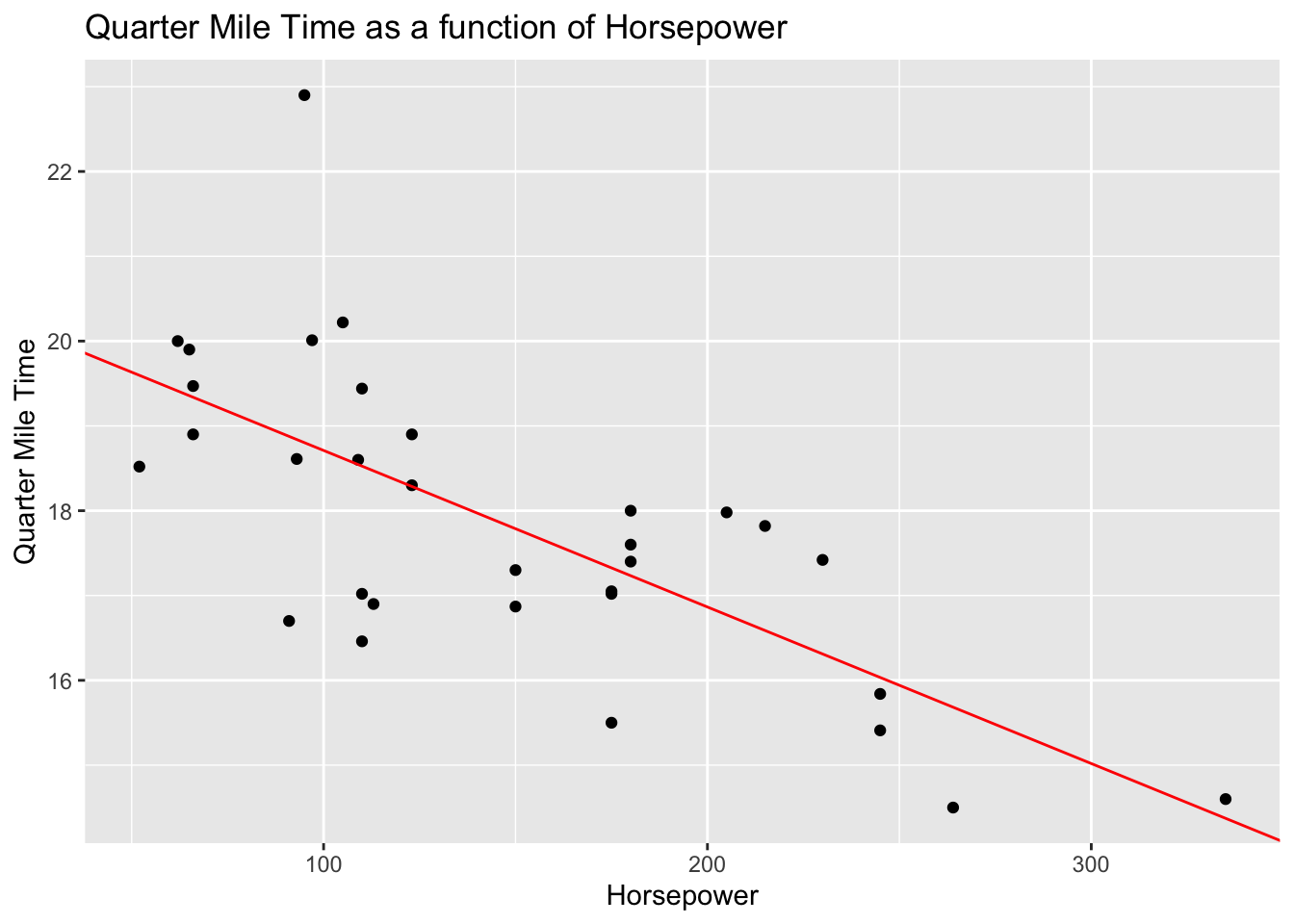
Practically, these findings suggest that horsepower is a significant predictor of quarter mile time. More specifically, the model output tells us that quarter mile time decreases by about 2 tenths of a second (.018) for each unit increase of horsepower in a given car. While statistically significant, this may seem practically insignificant. However, an increase of 100 horsepower tends to predict a loss of 1.8 seconds in quarter mile time, and a change in 300 horsepower tends to predict a loss of 5.4 seconds (which is good when the goal is speed). Is horsepower acting as a proxy for another variable? Put otherwise, would another variable (or set of variables) serve as better predictors of quarter mile time than hp?
8.2 SEM Syntax
SEM differs from multiple regression in that the individual items are allowed to contribute to the overall construct in an unequal manner, whereby in regression items are summed or averaged, thus limiting potential effects to aggregate scores of observable measures. Because of this level of specificity, latent variables can be removed in the event that items do not load appropriately on a construct. Simple regressions, as well as multiple regression are simultaneously estimated within this model. Additionally, SEM affords the calculation of both direct and indirect effects.
Like in baseR, lavaan uses tildes the regression operator ~, read as ‘is regressed on’. The dependent variable is called prior to the tilde with independent variables called after the tilde. A typical path model is defined by a set of regression formulas.
dependent1 ~ independent1 + independent2 + independent3## dependent1 ~ independent1 + independent2 + independent3dependent2 ~ independent1 + independent2## dependent2 ~ independent1 + independent2Latent variables are called with =~ which can be read as “is measured by.”
latent1 =~ item1 + item2 + item3
latent2 =~ item4 + item5 + item6Use double tildes ~~ to specify variances and covariances. This can be read as “is correlated with.”
observed1 ~~ observed1 (variance)
observed1 ~~ observed2 (covariance)Directly measure variable intercepts with the tilde ~ and the numeric value 1.
y1 ~ 1
f1 ~ 1A specified Full SEM might look like this. This code will produce a model syntax object, called model that can be called later to attain model estimates and produce visualizations.
model <- ' # regressions
targetvariable ~ construct1 + construct2 + observed1 + observed2
construct1 ~ construct2 + construct3
construct2 ~ construct3 + observed1 + observed2
# latent variable definitions
construct1 =~ item1 + item2 + item3
construct2 =~ item4 + item5 + item6
construct3 =~ item7 + item8 + item9 + item10
# variances and covariances
item1 ~~ item1
item1 ~~ item2
construct1 ~~ construct2
# intercepts
item1 ~ 1
construct1 ~ 1
'8.3 Running, Interpreting, and Visualizing Models
8.3.1 CFA
Confirmatory Factor Analysis estimates models comprised of latent variables that constitute the measurement model, which assesses how several paths might represent a theoretical assumption about the data. The measurement model only requires the =~sign to be used unless you are setting latent constructs as correlates in your CFA.
#### THIS CHUNK IS FOR TROUBLESHOOTING SEMPLOT INSTALLATION
#options(pkgType="binary")
#devtools::install_version("latticeExtra", version="0.6-28")
#install.packages('backports')
#install.packages("Hmisc")
#library(Hmisc)Model fit is assessed model using χ2, the Comparative Fit Index (CFI), and the Root Mean Square Error of Approximation (RMSEA). Each of these are examples of fit statistics, which are used to assess the extent to which a statistical model fits a set of observations. Fit statistics can also be used to compare sets of models against thresholds of good fit. For instance, a model with good fit should have a nonsignificant χ2 value, though this fit statistic is sensitive to larger sample sizes. Thus, χ2 is rarely used as a standalone measurement of model fit. The CFI compares the theoretical model to a null model and is considered to be demonstrative of good fit at or above 0.95, though models with a CFI above 0.90 are deemed to have acceptable fit. RMSEA is sensitive to parsimony of the model. In contrast with the CFI, a RMSEA value of 0.05 or below demonstrates good fit, however values below 0.1 are still considered acceptable.
We will be drawing from the lavaan package documentation for these explanatory examples. lavaan comes with three preinstalled datasets, the first of which is the “classic Holzinger and Swineford (1939) dataset [which] consists of mental ability test scores of seventh- and eighth-grade children from two different schools” (Pasteur and Grant-White). Demographic variables include an index, gender, age in years, age in months, school attended and grade level. Measured variables included assessments of visual perception, using cubes, lozenges, paragraph comprehension, sentence completion, word meaning, speeded addition, speeded counting of dots, and speeded text discrimination.
The authors hypothesized that these measured items might represent the latent constructs of visual, textual, and speed-related ability in educational contexts. The code below includes a specified model, a summary of the fit model, and a visualization of the model using the semPlot package.
#install.packages('lavaan')
#install.packages('semPlot')
library(lavaan)## This is lavaan 0.6-11
## lavaan is FREE software! Please report any bugs.##
## Attaching package: 'lavaan'## The following object is masked from 'package:psych':
##
## cor2covlibrary(semPlot)## Found more than one class "family" in cache; using the first, from namespace 'MatrixModels'## Also defined by 'lme4'## Found more than one class "family" in cache; using the first, from namespace 'MatrixModels'## Also defined by 'lme4'## Found more than one class "family" in cache; using the first, from namespace 'MatrixModels'## Also defined by 'lme4'# specify the model
HS.model <- ' visual ~ textual + speed
visual =~ x1 + x2 + x3
textual =~ x4 + x5 + x6
speed =~ x7 + x8 + x9
visual~~textual
textual~~speed
visual~~speed'
# fit the model
fit <- cfa(HS.model, data = HolzingerSwineford1939)## Warning in lav_model_vcov(lavmodel = lavmodel, lavsamplestats = lavsamplestats, : lavaan WARNING:
## Could not compute standard errors! The information matrix could
## not be inverted. This may be a symptom that the model is not
## identified.# display summary output
summary(fit, fit.measures=TRUE, standardized=TRUE)## lavaan 0.6-11 ended normally after 31 iterations
##
## Estimator ML
## Optimization method NLMINB
## Number of model parameters 23
##
## Number of observations 301
##
## Model Test User Model:
##
## Test statistic 85.306
## Degrees of freedom 22
## P-value (Chi-square) 0.000
##
## Model Test Baseline Model:
##
## Test statistic 918.852
## Degrees of freedom 36
## P-value 0.000
##
## User Model versus Baseline Model:
##
## Comparative Fit Index (CFI) 0.928
## Tucker-Lewis Index (TLI) 0.883
##
## Loglikelihood and Information Criteria:
##
## Loglikelihood user model (H0) -3737.745
## Loglikelihood unrestricted model (H1) -3695.092
##
## Akaike (AIC) 7521.490
## Bayesian (BIC) 7606.753
## Sample-size adjusted Bayesian (BIC) 7533.810
##
## Root Mean Square Error of Approximation:
##
## RMSEA 0.098
## 90 Percent confidence interval - lower 0.076
## 90 Percent confidence interval - upper 0.120
## P-value RMSEA <= 0.05 0.000
##
## Standardized Root Mean Square Residual:
##
## SRMR 0.065
##
## Parameter Estimates:
##
## Standard errors Standard
## Information Expected
## Information saturated (h1) model Structured
##
## Latent Variables:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## visual =~
## x1 1.000 0.900 0.772
## x2 0.553 NA 0.498 0.424
## x3 0.729 NA 0.656 0.581
## textual =~
## x4 1.000 0.990 0.852
## x5 1.113 NA 1.102 0.855
## x6 0.926 NA 0.917 0.838
## speed =~
## x7 1.000 0.619 0.570
## x8 1.180 NA 0.731 0.723
## x9 1.082 NA 0.670 0.665
##
## Regressions:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## visual ~
## textual 0.432 NA 0.475 0.475
## speed 0.202 NA 0.139 0.139
##
## Covariances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## .visual ~~
## textual -0.050 NA -0.066 -0.066
## textual ~~
## speed 0.173 NA 0.283 0.283
## .visual ~~
## speed 0.110 NA 0.233 0.233
##
## Variances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## .x1 0.549 NA 0.549 0.404
## .x2 1.134 NA 1.134 0.821
## .x3 0.844 NA 0.844 0.662
## .x4 0.371 NA 0.371 0.275
## .x5 0.446 NA 0.446 0.269
## .x6 0.356 NA 0.356 0.298
## .x7 0.799 NA 0.799 0.676
## .x8 0.488 NA 0.488 0.477
## .x9 0.566 NA 0.566 0.558
## .visual 0.579 NA 0.716 0.716
## textual 0.979 NA 1.000 1.000
## speed 0.384 NA 1.000 1.000inspect(fit, 'r2') #recently added## x1 x2 x3 x4 x5 x6 x7 x8 x9 visual
## 0.596 0.179 0.338 0.725 0.731 0.702 0.324 0.523 0.442 0.284#visualize output with standard estimates
semPaths(fit, "std", edge.label.cex = 1.0, curvePivot = FALSE, rotation = 3)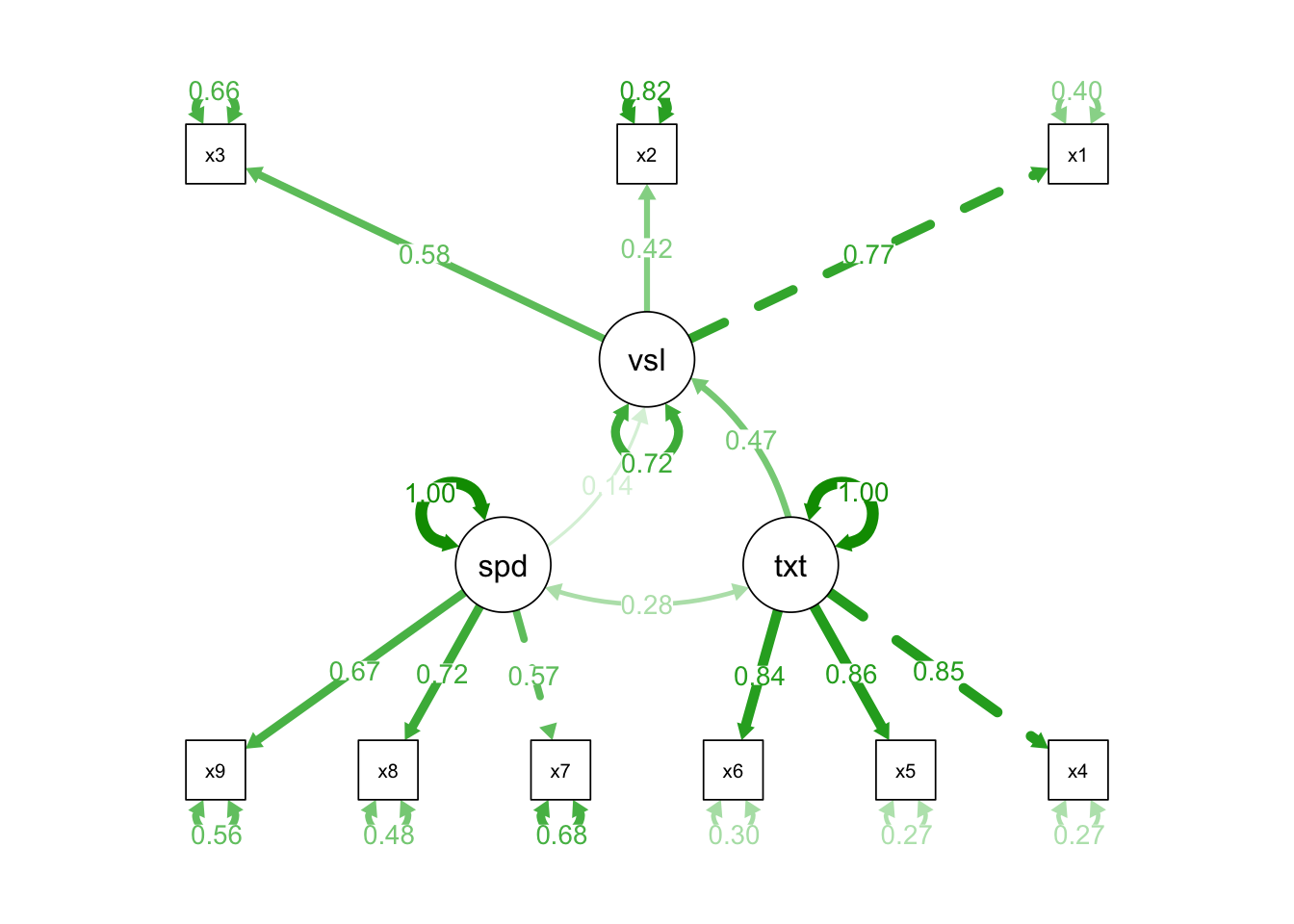
semPaths(fit, what = "path", whatLabels = "std", style = "lisrel", edge.label.cex = .9, rotation = 2, curve = 2, layoutSplit = FALSE, normalize = FALSE, height = 9, width = 6.5, residScale = 10)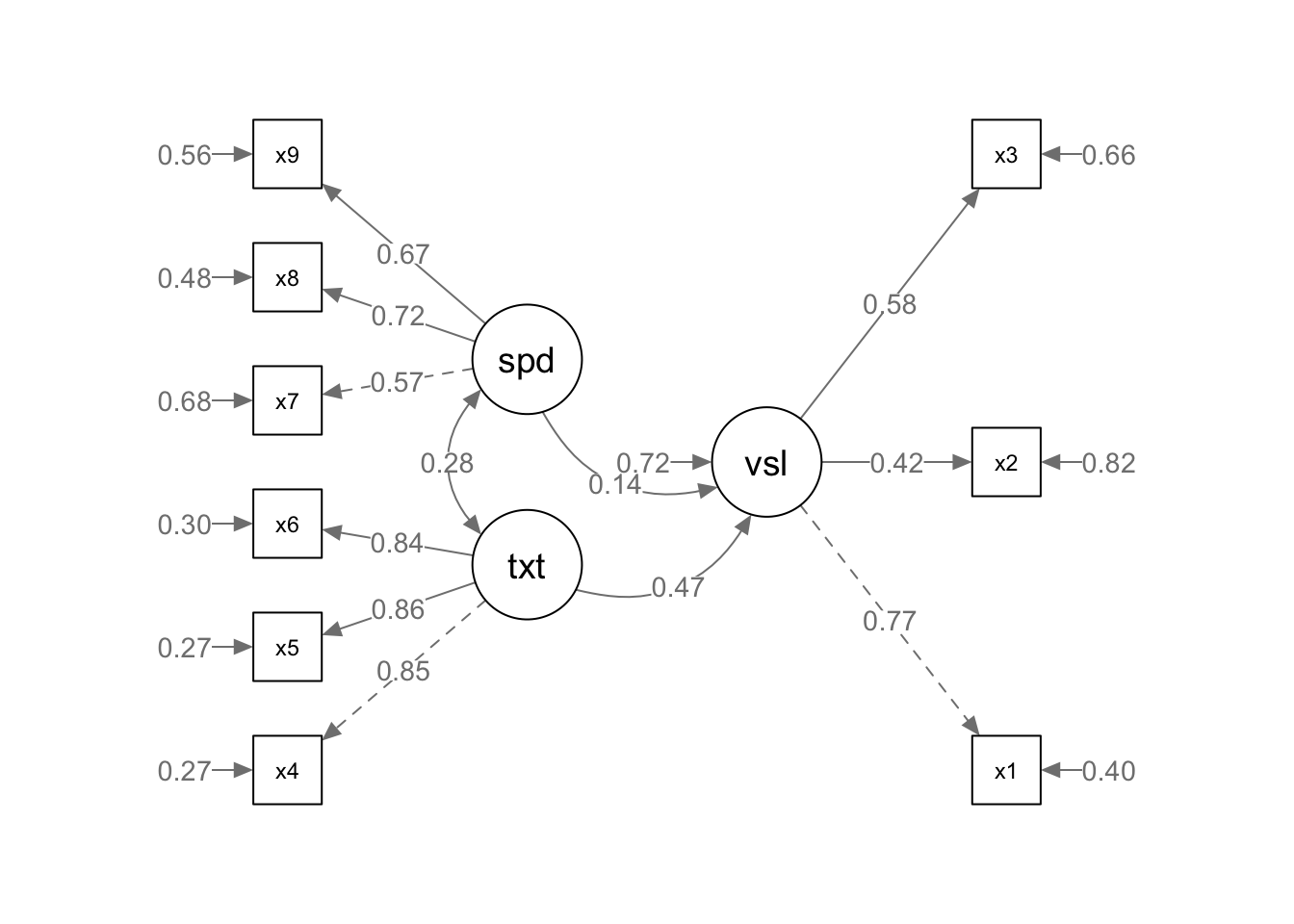
The output indicates a satisfactory fitting model despite the significant chi-square result (CFI = .93, RMSEA = .092, p = .001). Visual factors x1 and x3 loaded as expected, while x2 is approaching the lower bound for acceptable factor loading. As no items were non-significant, we might consider removing this item in a subsequent analysis to improve overall model fit. The textual and speed factor loadings were each satisfactory with the textual model holding strong consistency across each measured item (all loaded onto factor with a standardized estimate of .85 or .84). Covariances were satisfactory for this model (visual to textual is .46, visual to speed is .47, textual to speed is .28).
When we remove x2 from the model the CFI is improved at the expense of the RMSEA value. As there are no other benefits to removing this item, it should be retained. This model can be visualized using the semPlot() package. The semPath() function in particular is what we use to plot our SEM diagram. The semPaths() function takes the following arguments. For a description of each, see https://www.rdocumentation.org/packages/semPlot/versions/1.1.2/topics/semPaths
semPaths(object, what = "paths", whatLabels, style, layout = "tree",
intercepts = TRUE, residuals = TRUE, thresholds = TRUE, intStyle = "multi",
rotation = 1, curve, curvature = 1, nCharNodes = 3, nCharEdges = 3, sizeMan = 5,
sizeLat = 8, sizeInt = 2, sizeMan2, sizeLat2, sizeInt2, shapeMan, shapeLat,
shapeInt = "triangle", ask, mar, title, title.color = "black", title.adj = 0.1,
title.line = -1, title.cex = 0.8, include, combineGroups = FALSE, manifests,
latents, groups, color, residScale, gui = FALSE, allVars = FALSE, edge.color,
reorder = TRUE, structural = FALSE, ThreshAtSide = FALSE, thresholdColor,
thresholdSize = 0.5, fixedStyle = 2, freeStyle = 1,
as.expression = character(0), optimizeLatRes = FALSE, inheritColor = TRUE,
levels, nodeLabels, edgeLabels, pastel = FALSE, rainbowStart = 0, intAtSide,
springLevels = FALSE, nDigits = 2, exoVar, exoCov = TRUE, centerLevels = TRUE,
panelGroups = FALSE, layoutSplit = FALSE, measurementLayout = "tree", subScale,
subScale2, subRes = 4, subLinks, modelOpts = list(mplusStd = "std"),
curveAdjacent = '<->', edge.label.cex = 0.6, cardinal = "none",
equalizeManifests = FALSE, covAtResiduals = TRUE, bifactor, optimPoints = 1:8 * (pi/4),
...)## Error in eval(expr, envir, enclos): '...' used in an incorrect context8.3.2 Full SEM
We will be using another lavaan dataset for a Full SEM example. The PoliticalDemocracy datasets includes 75 observations of 11 variables that measure political democracy and industrialization in developing countries. Variables are labeled with the following descriptions:
Political Democracy in 1960
y1: Expert ratings of the freedom of the press in 1960
y2: The freedom of political opposition in 1960
y3: The fairness of elections in 1960
y4: The effectiveness of the elected legislature in 1960
Political Democracy in 1965
y5: Expert ratings of the freedom of the press in 1965
y6: The freedom of political opposition in 1965
y7: The fairness of elections in 1965
y8: The effectiveness of the elected legislature in 1965
Level of Industrialization in 1960
x1: The gross national product (GNP) per capita in 1960
x2: The inanimate energy consumption per capita in 1960
x3: The percentage of the labor force in industry in 1960
The bold headers represent latent, unobservable variables that are quantified by the observable bullet points. Take a quick look at the dataset using any of the methods covered thus far.
str(PoliticalDemocracy)## 'data.frame': 75 obs. of 11 variables:
## $ y1: num 2.5 1.25 7.5 8.9 10 7.5 7.5 7.5 2.5 10 ...
## $ y2: num 0 0 8.8 8.8 3.33 ...
## $ y3: num 3.33 3.33 10 10 10 ...
## $ y4: num 0 0 9.2 9.2 6.67 ...
## $ y5: num 1.25 6.25 8.75 8.91 7.5 ...
## $ y6: num 0 1.1 8.09 8.13 3.33 ...
## $ y7: num 3.73 6.67 10 10 10 ...
## $ y8: num 3.333 0.737 8.212 4.615 6.667 ...
## $ x1: num 4.44 5.38 5.96 6.29 5.86 ...
## $ x2: num 3.64 5.06 6.26 7.57 6.82 ...
## $ x3: num 2.56 3.57 5.22 6.27 4.57 ...psych::describe(PoliticalDemocracy)## vars n mean sd median trimmed mad min max range skew kurtosis se
## y1 1 75 5.46 2.62 5.40 5.46 3.11 1.25 10.00 8.75 -0.09 -1.15 0.30
## y2 2 75 4.26 3.95 3.33 4.09 4.94 0.00 10.00 10.00 0.32 -1.47 0.46
## y3 3 75 6.56 3.28 6.67 6.92 4.94 0.00 10.00 10.00 -0.59 -0.72 0.38
## y4 4 75 4.45 3.35 3.33 4.33 4.94 0.00 10.00 10.00 0.12 -1.21 0.39
## y5 5 75 5.14 2.61 5.00 5.23 3.71 0.00 10.00 10.00 -0.23 -0.78 0.30
## y6 6 75 2.98 3.37 2.23 2.51 3.31 0.00 10.00 10.00 0.89 -0.47 0.39
## y7 7 75 6.20 3.29 6.67 6.47 4.94 0.00 10.00 10.00 -0.55 -0.73 0.38
## y8 8 75 4.04 3.25 3.33 3.82 4.40 0.00 10.00 10.00 0.45 -0.96 0.37
## x1 9 75 5.05 0.73 5.08 5.03 0.82 3.78 6.74 2.95 0.25 -0.75 0.08
## x2 10 75 4.79 1.51 4.96 4.85 1.53 1.39 7.87 6.49 -0.35 -0.57 0.17
## x3 11 75 3.56 1.41 3.57 3.53 1.51 1.00 6.42 5.42 0.08 -0.94 0.16A model is specified below. Run, interpret, and visualize the model.
model <- '
# measurement model
ind60 =~ x1 + x2 + x3
dem60 =~ y1 + y2 + y3 + y4
dem65 =~ y5 + y6 + y7 + y8
# regressions
dem60 ~ ind60
dem65 ~ ind60 + dem60
# residual correlations
y1 ~~ y5
y2 ~~ y4 + y6
y3 ~~ y7
y4 ~~ y8
y6 ~~ y8
'
fit <- sem(model, data=PoliticalDemocracy)
summary(fit, fit.measures = TRUE, standardized=TRUE)## lavaan 0.6-11 ended normally after 68 iterations
##
## Estimator ML
## Optimization method NLMINB
## Number of model parameters 31
##
## Number of observations 75
##
## Model Test User Model:
##
## Test statistic 38.125
## Degrees of freedom 35
## P-value (Chi-square) 0.329
##
## Model Test Baseline Model:
##
## Test statistic 730.654
## Degrees of freedom 55
## P-value 0.000
##
## User Model versus Baseline Model:
##
## Comparative Fit Index (CFI) 0.995
## Tucker-Lewis Index (TLI) 0.993
##
## Loglikelihood and Information Criteria:
##
## Loglikelihood user model (H0) -1547.791
## Loglikelihood unrestricted model (H1) -1528.728
##
## Akaike (AIC) 3157.582
## Bayesian (BIC) 3229.424
## Sample-size adjusted Bayesian (BIC) 3131.720
##
## Root Mean Square Error of Approximation:
##
## RMSEA 0.035
## 90 Percent confidence interval - lower 0.000
## 90 Percent confidence interval - upper 0.092
## P-value RMSEA <= 0.05 0.611
##
## Standardized Root Mean Square Residual:
##
## SRMR 0.044
##
## Parameter Estimates:
##
## Standard errors Standard
## Information Expected
## Information saturated (h1) model Structured
##
## Latent Variables:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## ind60 =~
## x1 1.000 0.670 0.920
## x2 2.180 0.139 15.742 0.000 1.460 0.973
## x3 1.819 0.152 11.967 0.000 1.218 0.872
## dem60 =~
## y1 1.000 2.223 0.850
## y2 1.257 0.182 6.889 0.000 2.794 0.717
## y3 1.058 0.151 6.987 0.000 2.351 0.722
## y4 1.265 0.145 8.722 0.000 2.812 0.846
## dem65 =~
## y5 1.000 2.103 0.808
## y6 1.186 0.169 7.024 0.000 2.493 0.746
## y7 1.280 0.160 8.002 0.000 2.691 0.824
## y8 1.266 0.158 8.007 0.000 2.662 0.828
##
## Regressions:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## dem60 ~
## ind60 1.483 0.399 3.715 0.000 0.447 0.447
## dem65 ~
## ind60 0.572 0.221 2.586 0.010 0.182 0.182
## dem60 0.837 0.098 8.514 0.000 0.885 0.885
##
## Covariances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## .y1 ~~
## .y5 0.624 0.358 1.741 0.082 0.624 0.296
## .y2 ~~
## .y4 1.313 0.702 1.871 0.061 1.313 0.273
## .y6 2.153 0.734 2.934 0.003 2.153 0.356
## .y3 ~~
## .y7 0.795 0.608 1.308 0.191 0.795 0.191
## .y4 ~~
## .y8 0.348 0.442 0.787 0.431 0.348 0.109
## .y6 ~~
## .y8 1.356 0.568 2.386 0.017 1.356 0.338
##
## Variances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## .x1 0.082 0.019 4.184 0.000 0.082 0.154
## .x2 0.120 0.070 1.718 0.086 0.120 0.053
## .x3 0.467 0.090 5.177 0.000 0.467 0.239
## .y1 1.891 0.444 4.256 0.000 1.891 0.277
## .y2 7.373 1.374 5.366 0.000 7.373 0.486
## .y3 5.067 0.952 5.324 0.000 5.067 0.478
## .y4 3.148 0.739 4.261 0.000 3.148 0.285
## .y5 2.351 0.480 4.895 0.000 2.351 0.347
## .y6 4.954 0.914 5.419 0.000 4.954 0.443
## .y7 3.431 0.713 4.814 0.000 3.431 0.322
## .y8 3.254 0.695 4.685 0.000 3.254 0.315
## ind60 0.448 0.087 5.173 0.000 1.000 1.000
## .dem60 3.956 0.921 4.295 0.000 0.800 0.800
## .dem65 0.172 0.215 0.803 0.422 0.039 0.039inspect(fit, 'r2') #recently added## x1 x2 x3 y1 y2 y3 y4 y5 y6 y7 y8 dem60 dem65
## 0.846 0.947 0.761 0.723 0.514 0.522 0.715 0.653 0.557 0.678 0.685 0.200 0.961semPaths(fit, what = "path", whatLabels = "std", style = "lisrel", edge.label.cex = .9, rotation = 2, curve = 2, layoutSplit = FALSE, normalize = FALSE, height = 9, width = 6.5, residScale = 10)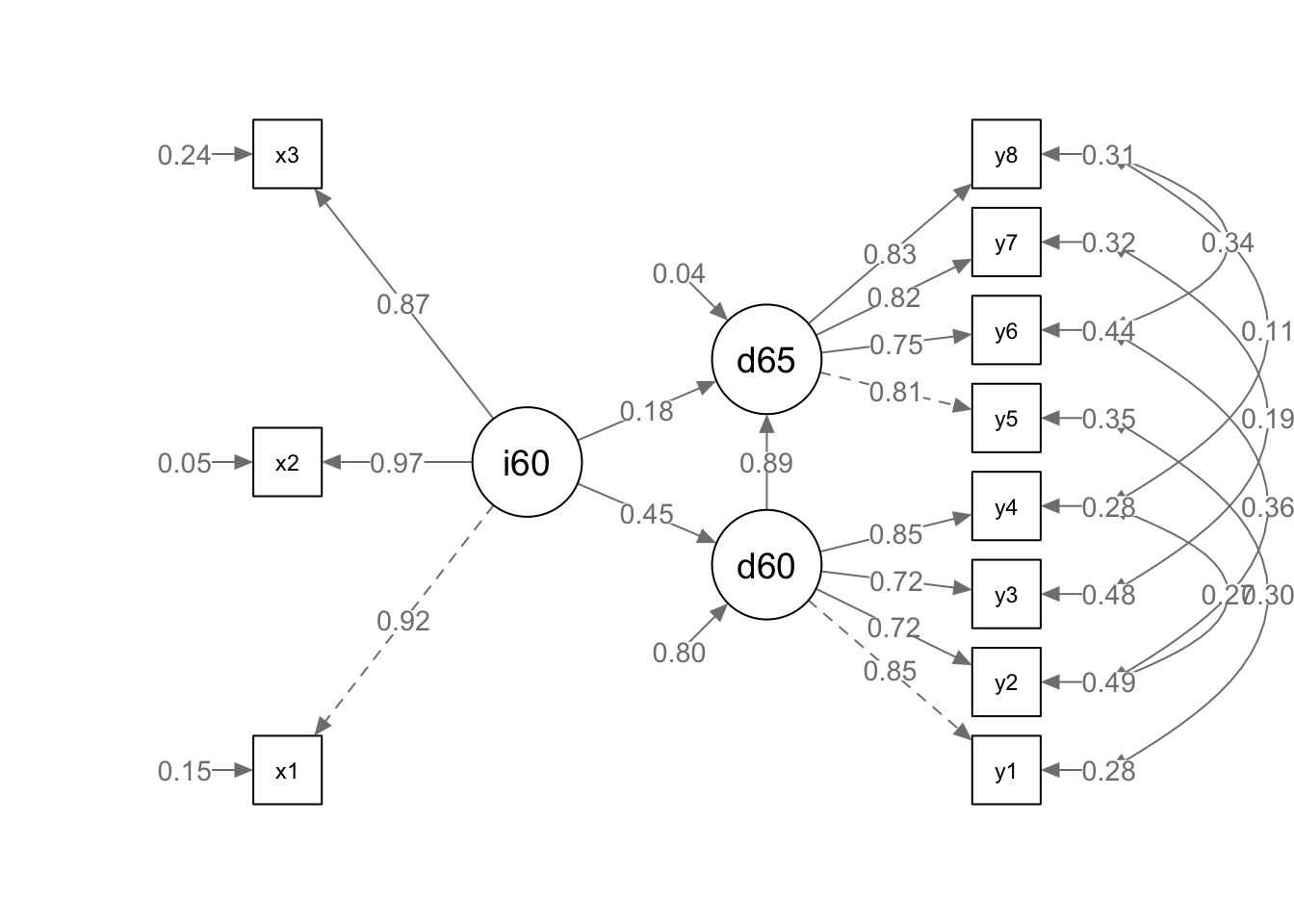
The results suggest that the model has excellent fit with a non significant chi square, a CFI of .995, and a RMSEA value .035. All factors (Ind60 x1 = .92, x2 = .97, x3 = .87; Dem60 y1 = .85, y2 = .71, y3 = .72, y4 = .85; Dem65 y5 = .81, y6 = .75, y7 = .82, y = .83) and paths (Dem60 ~ ind60 = .45; Dem65 ~ ind60(.18) + dem60(.89)) were significant and there was no evidence of colinearity in the model. Pruning would not be advisable as the model demonstrates outstanding parsimony. How do you interpret these findings on a practical level?
8.3.3 Mediation
We can create mediation models where intermediate variables are considered and called the mediator. We use these variables to attempt to explain the impact of an independent variable on an outcome. For instance, it is logical to deduce that past democratization of a country (d60) would predict future democratization (d65). However, it is questionable whether the industrialization of a country predicts a move toward democratization over time.
Let’s set up a mediation model to answer the research question: “To what extent does a country’s level of industrialization impact the development of political democracy over time?” Retain the same latent variables from the previous model. To create a mediation model, use the following formula:
direct effect Y ~ cX # mediator M ~ aX Y ~ bM # indirect effect (ab) ab := ab # total effect total := c + (ab)
The := operator “defines” new parameters which take on values that are an arbitrary function of the original model parameters” (https://lavaan.ugent.be/tutorial/mediation.html).
model <- '
# measurement model
ind60 =~ x1 + x2 + x3
dem60 =~ y1 + y2 + y3 + y4
dem65 =~ y5 + y6 + y7 + y8
# mediation
dem65 ~ c*dem60
ind60 ~ a*dem60
dem65 ~ b*ind60
# indirect effect (a*b)
ab := a*b
# total effect
total := c + (a*b)
'
fit <- sem(model, data=PoliticalDemocracy)
summary(fit, fit.measures = TRUE, standardized=TRUE)## lavaan 0.6-11 ended normally after 37 iterations
##
## Estimator ML
## Optimization method NLMINB
## Number of model parameters 25
##
## Number of observations 75
##
## Model Test User Model:
##
## Test statistic 72.462
## Degrees of freedom 41
## P-value (Chi-square) 0.002
##
## Model Test Baseline Model:
##
## Test statistic 730.654
## Degrees of freedom 55
## P-value 0.000
##
## User Model versus Baseline Model:
##
## Comparative Fit Index (CFI) 0.953
## Tucker-Lewis Index (TLI) 0.938
##
## Loglikelihood and Information Criteria:
##
## Loglikelihood user model (H0) -1564.959
## Loglikelihood unrestricted model (H1) -1528.728
##
## Akaike (AIC) 3179.918
## Bayesian (BIC) 3237.855
## Sample-size adjusted Bayesian (BIC) 3159.062
##
## Root Mean Square Error of Approximation:
##
## RMSEA 0.101
## 90 Percent confidence interval - lower 0.061
## 90 Percent confidence interval - upper 0.139
## P-value RMSEA <= 0.05 0.021
##
## Standardized Root Mean Square Residual:
##
## SRMR 0.055
##
## Parameter Estimates:
##
## Standard errors Standard
## Information Expected
## Information saturated (h1) model Structured
##
## Latent Variables:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## ind60 =~
## x1 1.000 0.669 0.920
## x2 2.182 0.139 15.714 0.000 1.461 0.973
## x3 1.819 0.152 11.956 0.000 1.218 0.872
## dem60 =~
## y1 1.000 2.201 0.845
## y2 1.354 0.175 7.755 0.000 2.980 0.760
## y3 1.044 0.150 6.961 0.000 2.298 0.705
## y4 1.300 0.138 9.412 0.000 2.860 0.860
## dem65 =~
## y5 1.000 2.084 0.803
## y6 1.258 0.164 7.651 0.000 2.623 0.783
## y7 1.282 0.158 8.137 0.000 2.673 0.819
## y8 1.310 0.154 8.529 0.000 2.730 0.847
##
## Regressions:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## dem65 ~
## dem60 (c) 0.864 0.113 7.671 0.000 0.913 0.913
## ind60 ~
## dem60 (a) 0.136 0.036 3.738 0.000 0.448 0.448
## dem65 ~
## ind60 (b) 0.453 0.220 2.064 0.039 0.146 0.146
##
## Variances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## .x1 0.082 0.020 4.180 0.000 0.082 0.154
## .x2 0.118 0.070 1.689 0.091 0.118 0.053
## .x3 0.467 0.090 5.174 0.000 0.467 0.240
## .y1 1.942 0.395 4.910 0.000 1.942 0.286
## .y2 6.490 1.185 5.479 0.000 6.490 0.422
## .y3 5.340 0.943 5.662 0.000 5.340 0.503
## .y4 2.887 0.610 4.731 0.000 2.887 0.261
## .y5 2.390 0.447 5.351 0.000 2.390 0.355
## .y6 4.343 0.796 5.456 0.000 4.343 0.387
## .y7 3.510 0.668 5.252 0.000 3.510 0.329
## .y8 2.940 0.586 5.019 0.000 2.940 0.283
## .ind60 0.358 0.071 5.020 0.000 0.799 0.799
## dem60 4.845 1.088 4.453 0.000 1.000 1.000
## .dem65 0.115 0.200 0.575 0.565 0.026 0.026
##
## Defined Parameters:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## ab 0.062 0.031 2.012 0.044 0.065 0.065
## total 0.926 0.114 8.097 0.000 0.978 0.978semPaths(fit, "std", edge.label.cex = 1.0, curvePivot = TRUE)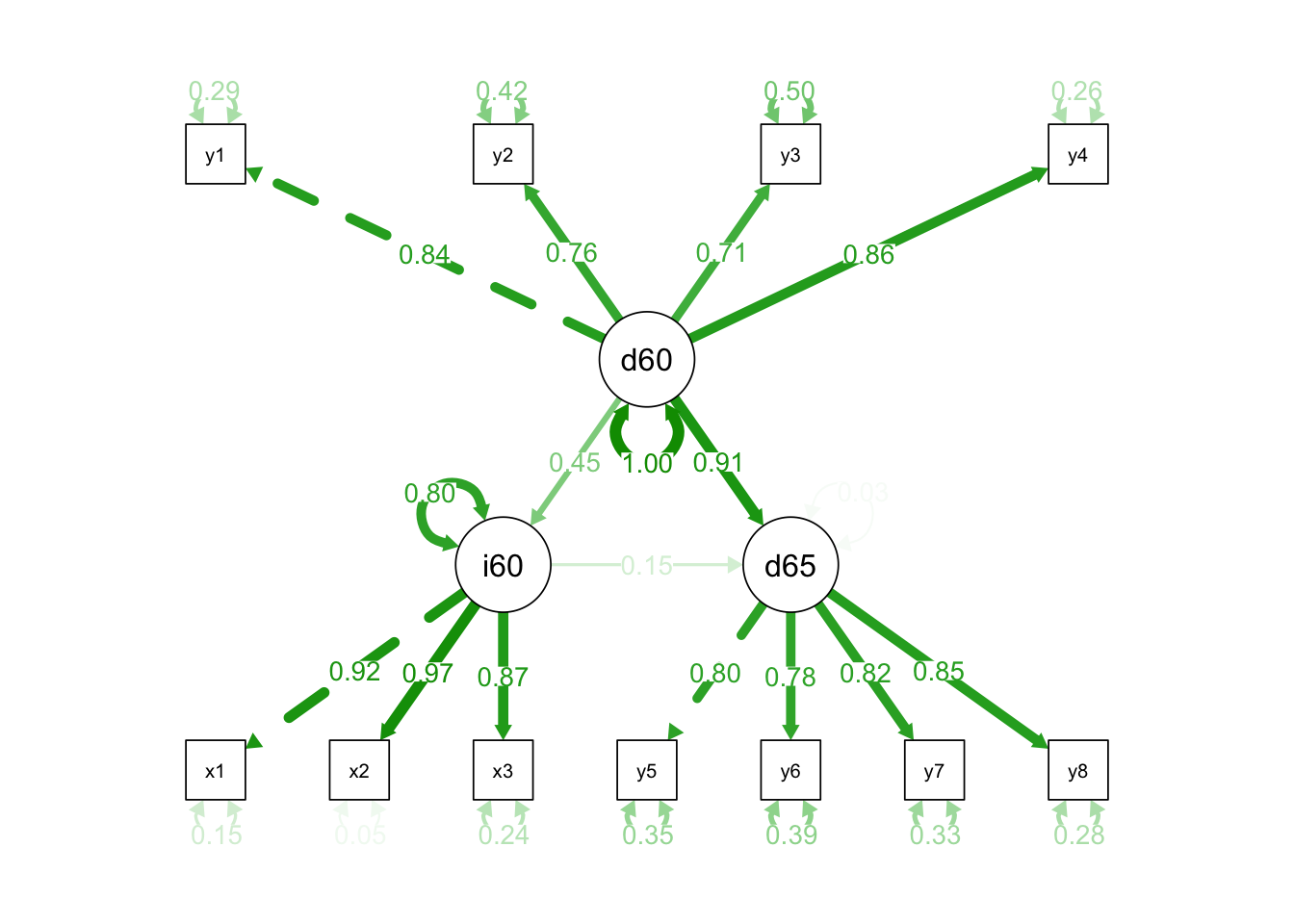
The chi-square is non significant now. The CFI is .95, and RMSEA is .101 and statistically significant. Factor structures remain intact and all paths are significant. The total effect of ind60 and dem60 explains 84% (beta weights are equivalent to r (then squared for variance explained) of the variance in dem65, however less than 1% of that variance is attributable to industrialization (p = .044). Depending on the measurement validity of this dataset, industrialization should be ruled out as a strong contributor to any change in political democracy. An additional model might be specified with other explanatory variables such as ?
8.3.4 Multiple Groups
If your sample size is large enough you can use lavaan to conduct multiple group analysis. To do this add the name of the grouping variable to group argument. The same model will be fitted to each group.
HS.model <- ' visual =~ x1 + x3
textual =~ x4 + x5 + x6
speed =~ x7 + x8 + x9
visual ~ textual'
fit <- cfa(HS.model, data = HolzingerSwineford1939, group = "school")## Warning in lav_object_post_check(object): lavaan WARNING: some estimated ov
## variances are negativesummary(fit, fit.measures = TRUE, standardized=TRUE)## lavaan 0.6-11 ended normally after 53 iterations
##
## Estimator ML
## Optimization method NLMINB
## Number of model parameters 52
##
## Number of observations per group:
## Pasteur 156
## Grant-White 145
##
## Model Test User Model:
##
## Test statistic 107.318
## Degrees of freedom 36
## P-value (Chi-square) 0.000
## Test statistic for each group:
## Pasteur 48.124
## Grant-White 59.194
##
## Model Test Baseline Model:
##
## Test statistic 893.935
## Degrees of freedom 56
## P-value 0.000
##
## User Model versus Baseline Model:
##
## Comparative Fit Index (CFI) 0.915
## Tucker-Lewis Index (TLI) 0.868
##
## Loglikelihood and Information Criteria:
##
## Loglikelihood user model (H0) -3236.131
## Loglikelihood unrestricted model (H1) -3182.472
##
## Akaike (AIC) 6576.262
## Bayesian (BIC) 6769.032
## Sample-size adjusted Bayesian (BIC) 6604.118
##
## Root Mean Square Error of Approximation:
##
## RMSEA 0.115
## 90 Percent confidence interval - lower 0.090
## 90 Percent confidence interval - upper 0.140
## P-value RMSEA <= 0.05 0.000
##
## Standardized Root Mean Square Residual:
##
## SRMR 0.079
##
## Parameter Estimates:
##
## Standard errors Standard
## Information Expected
## Information saturated (h1) model Structured
##
##
## Group 1 [Pasteur]:
##
## Latent Variables:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## visual =~
## x1 1.000 1.411 1.195
## x3 0.311 0.166 1.870 0.061 0.439 0.379
## textual =~
## x4 1.000 0.949 0.826
## x5 1.177 0.101 11.668 0.000 1.117 0.855
## x6 0.870 0.076 11.455 0.000 0.825 0.836
## speed =~
## x7 1.000 0.622 0.575
## x8 1.080 0.269 4.014 0.000 0.672 0.689
## x9 0.821 0.202 4.057 0.000 0.511 0.517
##
## Regressions:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## visual ~
## textual 0.566 0.101 5.591 0.000 0.380 0.380
##
## Covariances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## textual ~~
## speed 0.195 0.073 2.684 0.007 0.330 0.330
##
## Intercepts:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## .x1 4.941 0.095 52.249 0.000 4.941 4.183
## .x3 2.487 0.093 26.778 0.000 2.487 2.144
## .x4 2.823 0.092 30.689 0.000 2.823 2.457
## .x5 3.995 0.105 38.183 0.000 3.995 3.057
## .x6 1.922 0.079 24.320 0.000 1.922 1.947
## .x7 4.432 0.087 51.181 0.000 4.432 4.098
## .x8 5.563 0.078 71.214 0.000 5.563 5.702
## .x9 5.418 0.079 68.440 0.000 5.418 5.480
## .visual 0.000 0.000 0.000
## textual 0.000 0.000 0.000
## speed 0.000 0.000 0.000
##
## Variances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## .x1 -0.597 0.974 -0.613 0.540 -0.597 -0.428
## .x3 1.153 0.161 7.162 0.000 1.153 0.857
## .x4 0.419 0.069 6.096 0.000 0.419 0.317
## .x5 0.460 0.086 5.367 0.000 0.460 0.269
## .x6 0.293 0.050 5.862 0.000 0.293 0.301
## .x7 0.783 0.128 6.113 0.000 0.783 0.669
## .x8 0.501 0.119 4.199 0.000 0.501 0.526
## .x9 0.716 0.103 6.922 0.000 0.716 0.733
## .visual 1.704 0.994 1.715 0.086 0.855 0.855
## textual 0.901 0.150 5.998 0.000 1.000 1.000
## speed 0.387 0.135 2.867 0.004 1.000 1.000
##
##
## Group 2 [Grant-White]:
##
## Latent Variables:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## visual =~
## x1 1.000 0.777 0.676
## x3 0.885 0.210 4.217 0.000 0.687 0.663
## textual =~
## x4 1.000 0.965 0.861
## x5 0.998 0.087 11.436 0.000 0.964 0.832
## x6 0.967 0.085 11.338 0.000 0.934 0.825
## speed =~
## x7 1.000 0.727 0.705
## x8 1.155 0.175 6.594 0.000 0.839 0.802
## x9 0.927 0.145 6.399 0.000 0.673 0.657
##
## Regressions:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## visual ~
## textual 0.471 0.101 4.677 0.000 0.585 0.585
##
## Covariances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## textual ~~
## speed 0.243 0.078 3.132 0.002 0.347 0.347
##
## Intercepts:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## .x1 4.930 0.095 51.696 0.000 4.930 4.293
## .x3 1.996 0.086 23.195 0.000 1.996 1.926
## .x4 3.317 0.093 35.625 0.000 3.317 2.958
## .x5 4.712 0.096 48.986 0.000 4.712 4.068
## .x6 2.469 0.094 26.277 0.000 2.469 2.182
## .x7 3.921 0.086 45.819 0.000 3.921 3.805
## .x8 5.488 0.087 63.174 0.000 5.488 5.246
## .x9 5.327 0.085 62.571 0.000 5.327 5.196
## .visual 0.000 0.000 0.000
## textual 0.000 0.000 0.000
## speed 0.000 0.000 0.000
##
## Variances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## .x1 0.716 0.159 4.514 0.000 0.716 0.543
## .x3 0.601 0.127 4.741 0.000 0.601 0.560
## .x4 0.325 0.065 5.036 0.000 0.325 0.259
## .x5 0.413 0.072 5.770 0.000 0.413 0.308
## .x6 0.408 0.069 5.924 0.000 0.408 0.319
## .x7 0.534 0.092 5.811 0.000 0.534 0.503
## .x8 0.390 0.099 3.932 0.000 0.390 0.357
## .x9 0.598 0.091 6.537 0.000 0.598 0.569
## .visual 0.396 0.140 2.839 0.005 0.657 0.657
## textual 0.932 0.152 6.138 0.000 1.000 1.000
## speed 0.528 0.127 4.156 0.000 1.000 1.000semPaths(fit, "std", edge.label.cex = 1.0, rotation = 2, curvePivot = TRUE)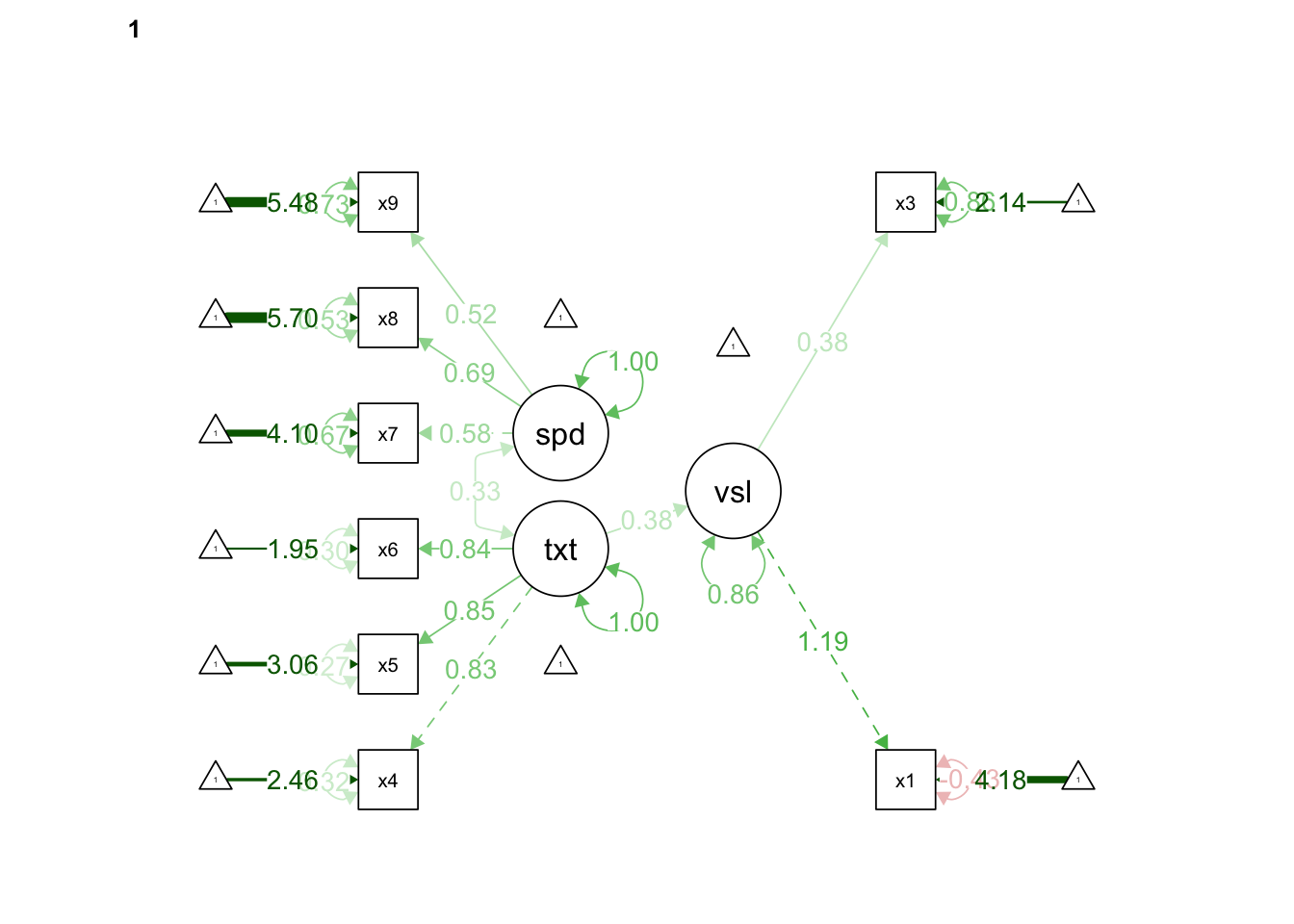
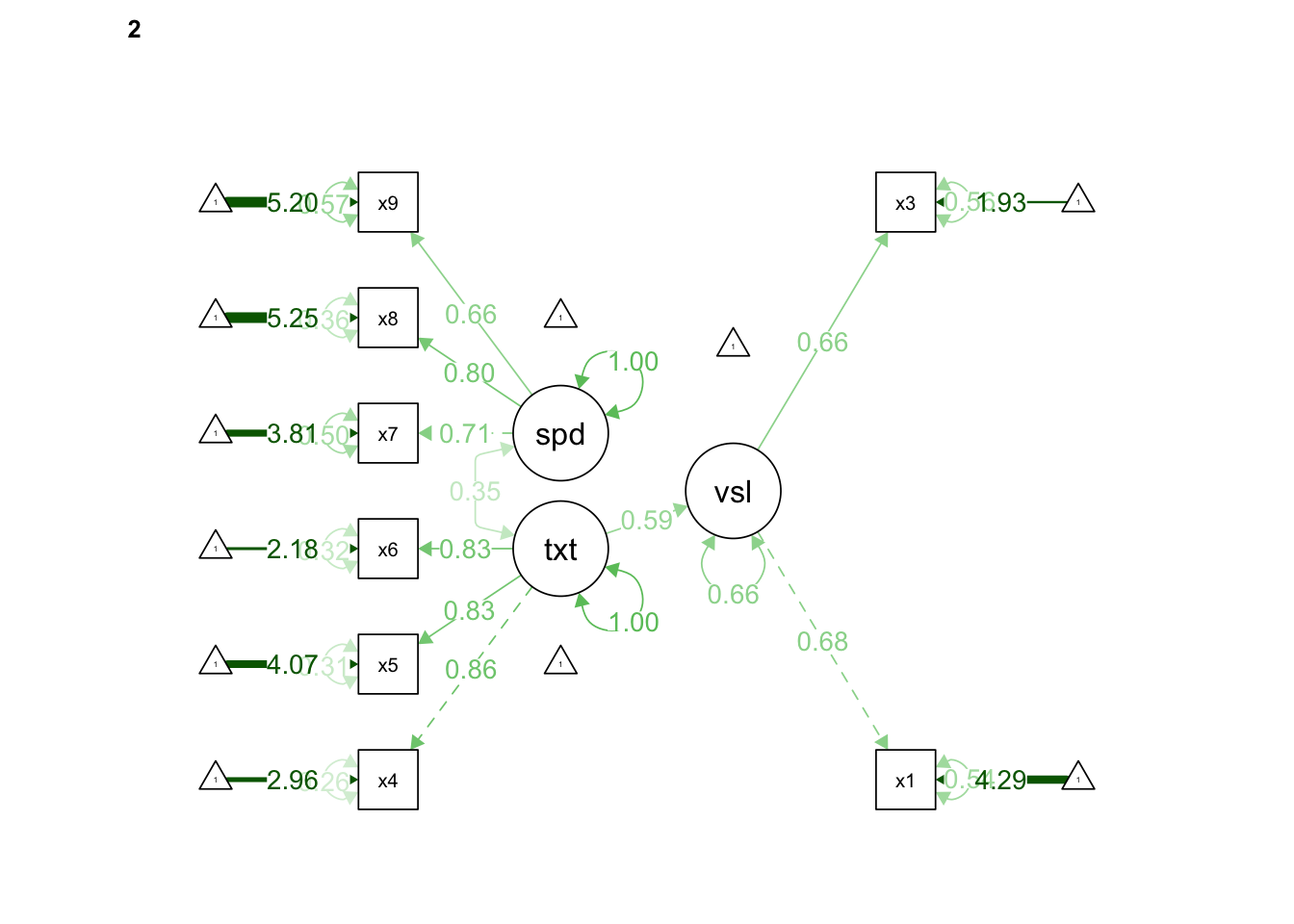
The x2 variable at the Pasteur school did not load onto the visual achievement factor. We can retool our questionnaire or consider the study validity to fix this, but for now let’s just remove it from the model again. Once we do that we can see that the x1 and x3 items are loading very differently onto the visual factor, though both items meet the threshold of .40. What would you do if this was your study?
8.3.5 Measurement Invariance
You can also test for measurement invariance across the grouping variable using the measurmentInvariance() function which “performs a number of multiple group analyses in a particular sequence, with increasingly more restrictions on the parameters”(https://lavaan.ugent.be/tutorial/groups.html). Load the semTools library to use this function.
There are four types of measurment invariance.
The first is equal form configural invariance, which assumes the factor structures (number of items) and patterns (relationships between factors) are identical across groups. The second is equal loadings (metric invariance), which assumes that factor loadings (extent which each item loads onto factors) are equal across groups. The third is equal intercepts (scalar invariance), which assumes that the intercepts of observed scores are equal across groups. Finally, equal residual variances (strict invariance) assumes that the residual variances of observed paths are equal across groups.
#install.packages('semTools')
library(semTools)
measurementInvariance(model = HS.model,
data = HolzingerSwineford1939,
group = "school")##
## Measurement invariance models:
##
## Model 1 : fit.configural
## Model 2 : fit.loadings
## Model 3 : fit.intercepts
## Model 4 : fit.means
##
## Chi-Squared Difference Test
##
## Df AIC BIC Chisq Chisq diff Df diff Pr(>Chisq)
## fit.configural 36 6576.3 6769.0 107.32
## fit.loadings 41 6576.3 6750.5 117.35 10.030 5 0.07439 .
## fit.intercepts 46 6600.7 6756.4 151.78 34.431 5 1.954e-06 ***
## fit.means 49 6638.2 6782.7 195.21 43.431 3 1.993e-09 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
##
## Fit measures:
##
## cfi rmsea cfi.delta rmsea.delta
## fit.configural 0.915 0.115 NA NA
## fit.loadings 0.909 0.111 0.006 0.003
## fit.intercepts 0.874 0.124 0.035 0.012
## fit.means 0.826 0.141 0.048 0.017This model assesses the four measurement invariance types across the grouping variable ‘school’ in the HS dataset. No model met the acceptable threshold for RMSEA. Judging by CFI alone, which is not always advisable, form, loadings, and intercept models demonstrate good fit. Thus, each school represented in the HS dataset can be assumed to be equal in these respects, but fail to demonstrate strict invariance. These statistics might be used to validate this particular measure as congruent across different groups of students.
8.4 Facial Burns Case Study
Click link to access: https://jayholster1.shinyapps.io/SEMinRAssessment/