16 Day 16 (March 23)
16.1 Announcements
- Assignment 7 is posted and due Sunday (March 26)
- Derived quantities
- Read Ch. 17 on spatial models
16.2 Gaussian process
- A Gaussian process is a probability distribution over functions
- If the function is observed at a finite number of points or “locations,” then the vector of values follows a multivariate normal distribution.
16.2.1 Multivariate normal distribution
Multivariate normal distribution
- \(\boldsymbol{\eta}\sim\text{N}(\mathbf{0},\sigma^{2}\mathbf{R})\)
- Definitions
- Correlation matrix – A positive semi-definite matrix whose elements are the correlation between observations
- Correlation function – A function that describes the correlation between observations
- Example correlation matrices
- Compound symmetry \[\mathbf{R}=\left[\begin{array}{cccccc} 1 & 1 & 0 & 0 & 0 & 0\\ 1 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 1 & 0 & 0\\ 0 & 0 & 1 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 1\\ 0 & 0 & 0 & 0 & 1 & 1 \end{array}\right]\]
- AR(1) \[\mathbf{R(\phi})=\left[\begin{array}{ccccc} 1 & \phi^{1} & \phi^{2} & \cdots & \phi^{n-1}\\ \phi^{1} & 1 & \phi^{1} & \cdots & \phi^{n-2}\\ \phi^{2} & \phi^{1} & 1 & \vdots & \phi^{n-3}\\ \vdots & \vdots & \vdots & \ddots & \ddots\\ \phi^{n-1} & \phi^{n-2} & \phi^{n-3} & \ddots & 1 \end{array}\right]\:\]
Example simulating from \(\boldsymbol{\eta}\sim\text{N}(\mathbf{0},\sigma^{2}\mathbf{R})\) in R
n <- 200 x <- 1:n I <- diag(1, n) sigma2 <- 1 library(MASS) set.seed(2034) eta <- mvrnorm(1, rep(0, n), sigma2 * I) cor(eta[1:(n - 1)], eta[2:n])## [1] -0.06408623acf(eta)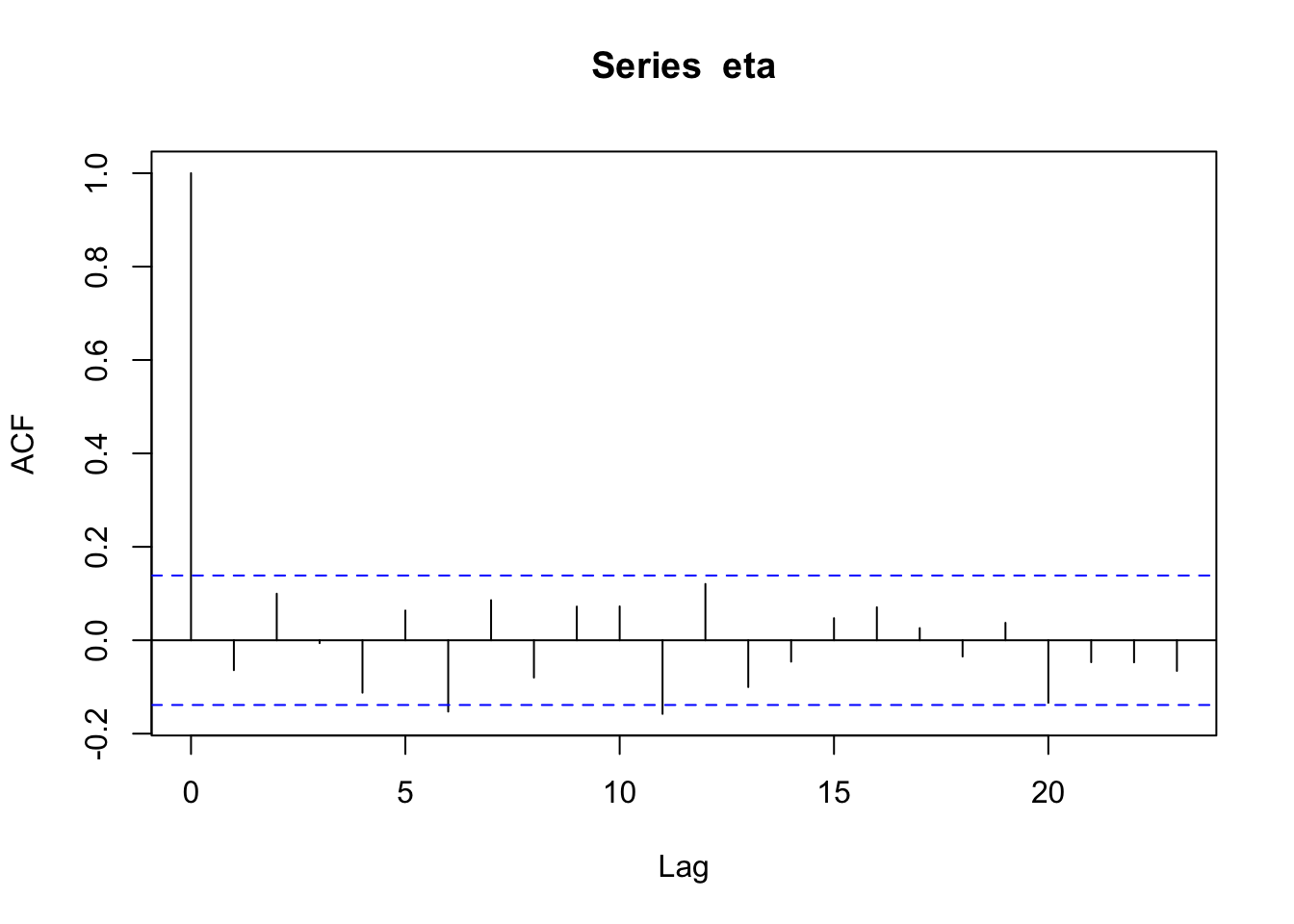
par(mfrow = c(2, 1)) par(mar = c(0, 2, 0, 0), oma = c(5.1, 3.1, 2.1, 2.1)) plot(x, eta, typ = "l", xlab = "", xaxt = "n") abline(a = 0, b = 0) n <- 200 x <- 1:n # Must be equally spaced phi <- 0.7 R <- phi^abs(outer(x, x, "-")) sigma2 <- 1 set.seed(1330) eta <- mvrnorm(1, rep(0, n), sigma2 * R) cor(eta[1:(n - 1)], eta[2:n])## [1] 0.7016662plot(x, eta, typ = "l") abline(a = 0, b = 0)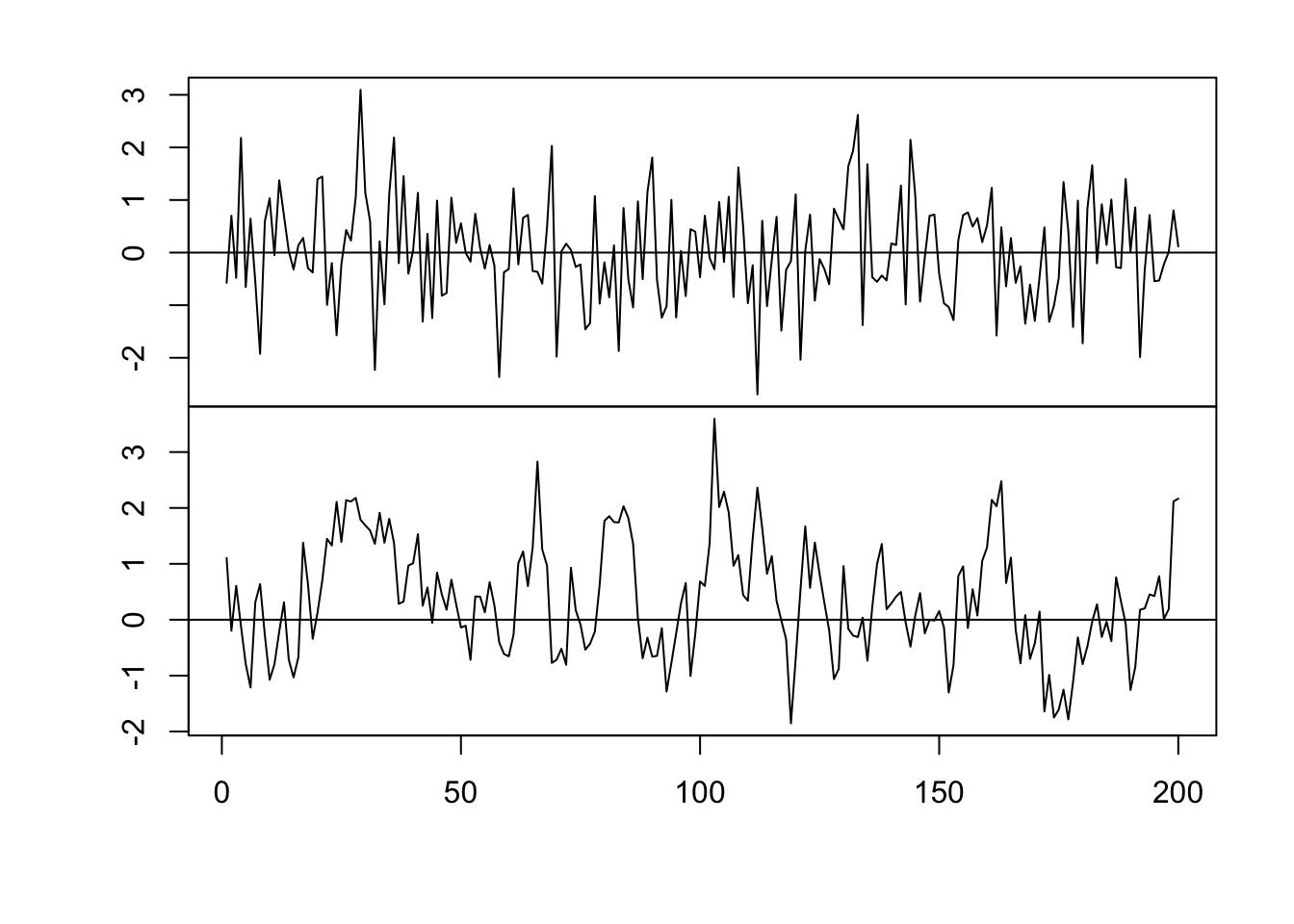
acf(eta)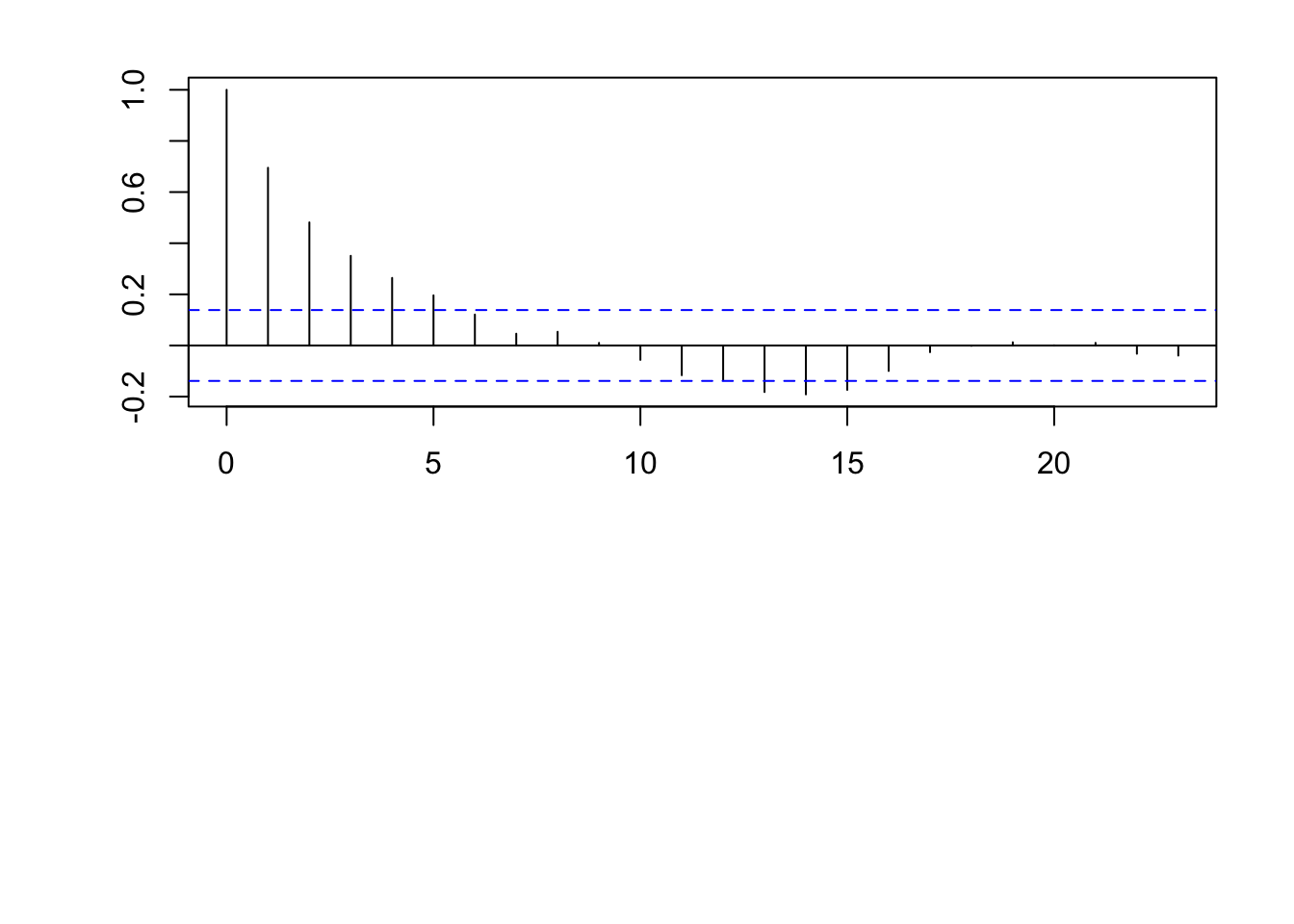
- Example correlation functions
- Gaussian correlation function \[r_{ij}(\phi)=e^{-\frac{d_{ij}^{2}}{\phi}}\] where \(d_{ij}\) is the “distance” between locations i and j (note that \(d_{ij}=0\) for \(i=j\)) and \(r_{ij}(\phi)\) is the element in the \(i^{\textrm{th}}\) row and \(j^{\textrm{th}}\) column of \(\mathbf{R}(\phi)\).
library(fields) n <- 200 x <- 1:n phi <- 40 d <- rdist(x) R <- exp(-d^2/phi) sigma2 <- 1 set.seed(4673) eta <- mvrnorm(1, rep(0, n), sigma2 * R) plot(x, eta, typ = "l") abline(a = 0, b = 0)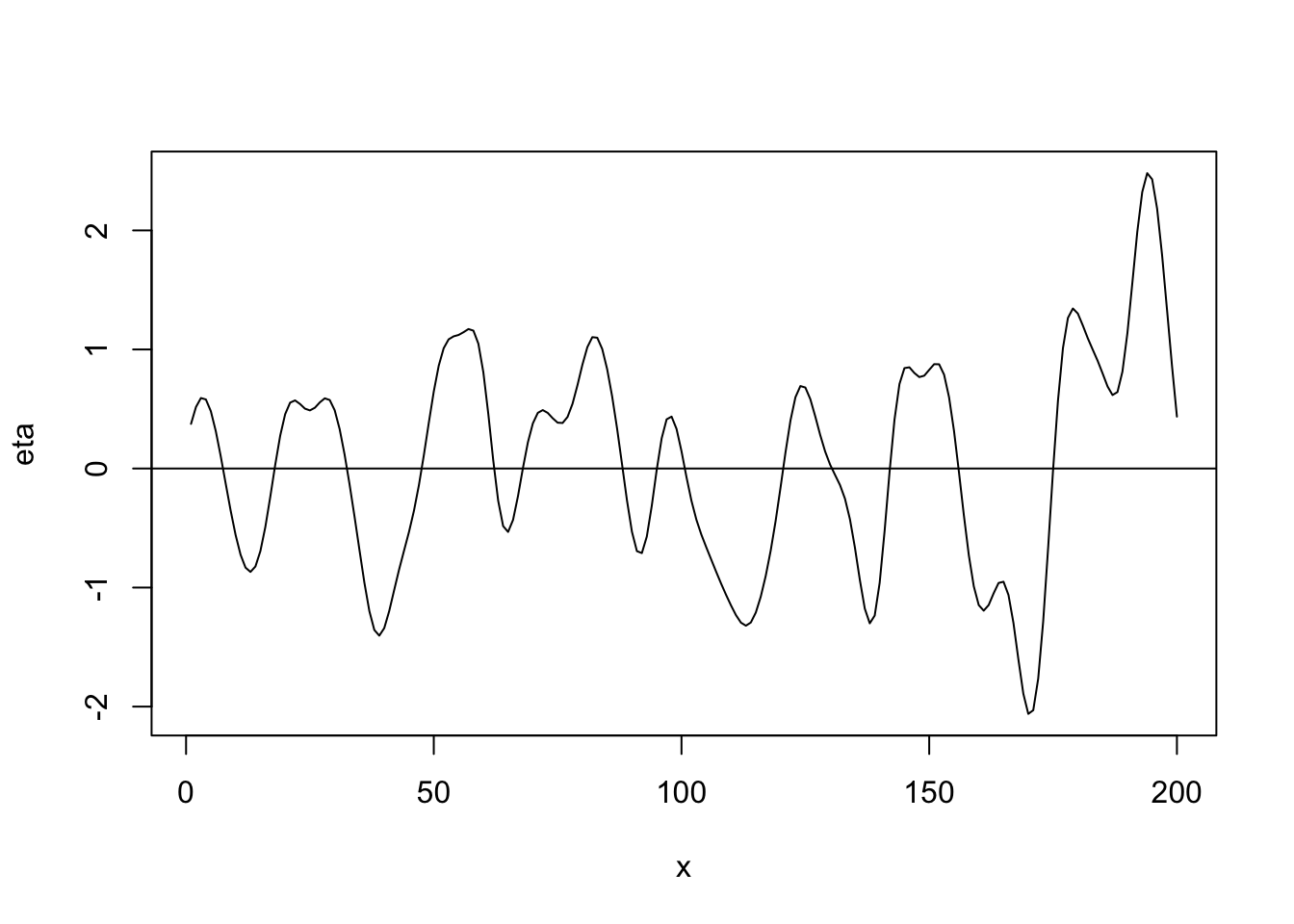
cor(eta[1:(n-1)], eta[2:n])## [1] 0.9713954- Linear correlation function \[r_{ij}(\phi)=\begin{cases} 1-\frac{d_{ij}}{\phi} &\text{if}\ d_{ij}<0\\ 0 &\text{if}\ d_{ij}>0 \end{cases}\]
library(fields) n <- 200 x <- 1:n phi <- 40 d <- rdist(x) R <- ifelse(d<phi,1-d/phi,0) sigma2 <- 1 set.seed(4803) eta <- mvrnorm(1, rep(0, n), sigma2 * R) plot(x, eta, typ = "l") abline(a = 0, b = 0)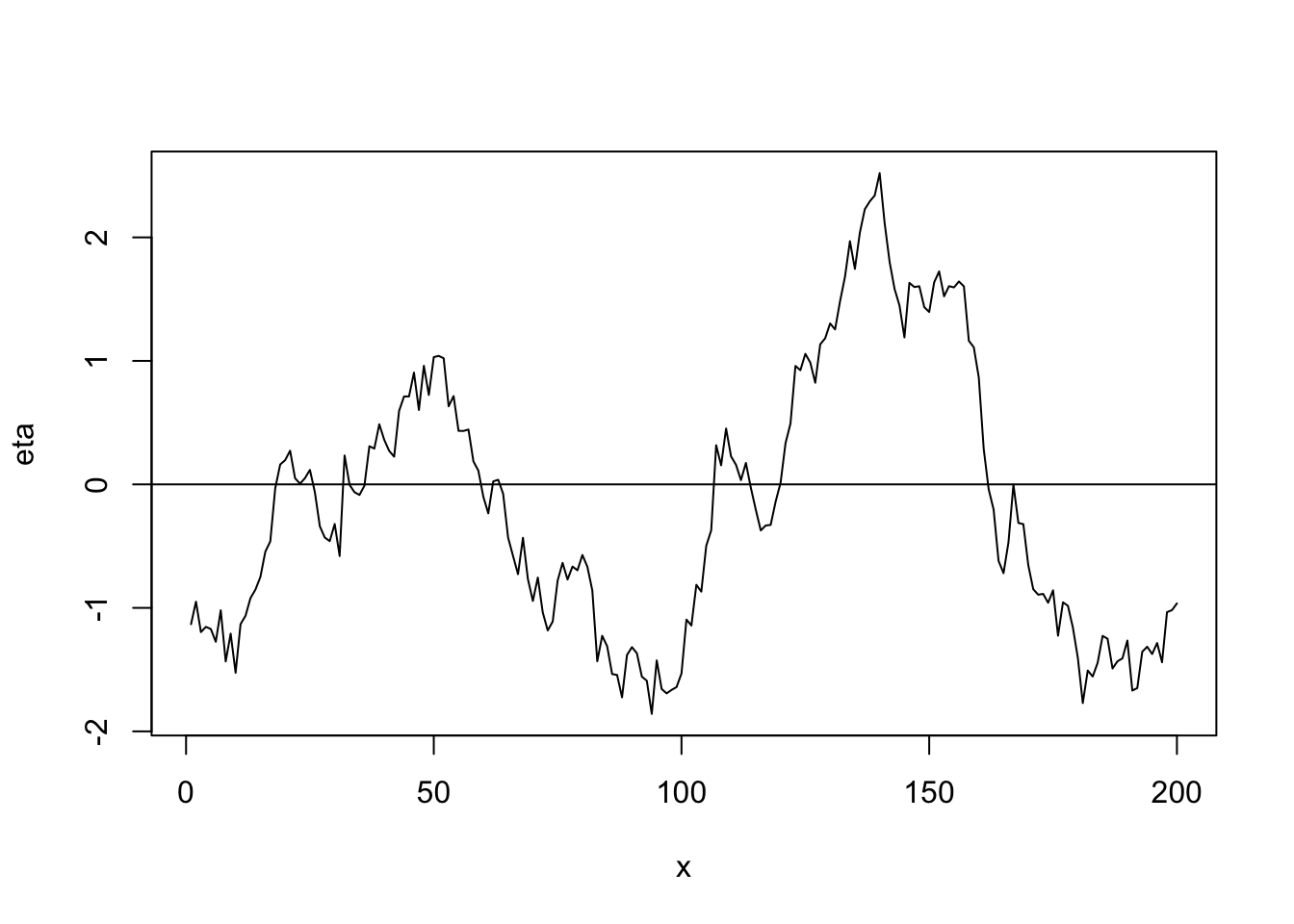
cor(eta[1:(n-1)], eta[2:n])## [1] 0.9775175- Example correlation functions
16.3 Bayesian Kriging
Read Chapter 17
Example data set
url <- "https://www.dropbox.com/s/k2ajjvyxwvsbqgf/ISIT.txt?dl=1" df <- read.table(url, header = TRUE) df <- df[df$Station == 16,c(1,2,5,6)] head(df)## Depth Sources Latitude Longitude ## 595 598 53.37 49.0322 -16.1493 ## 596 631 51.32 49.0322 -16.1493 ## 597 700 42.42 49.0322 -16.1493 ## 598 666 38.32 49.0322 -16.1493 ## 599 1317 37.29 49.0322 -16.1493 ## 600 1352 36.27 49.0322 -16.1493plot(df$Depth, df$Sources, las = 1, ylim = c(0, 65), col = rgb(0, 0, 0, 0.25), pch = 19, xlab = "Depth (m)", ylab = "Sources")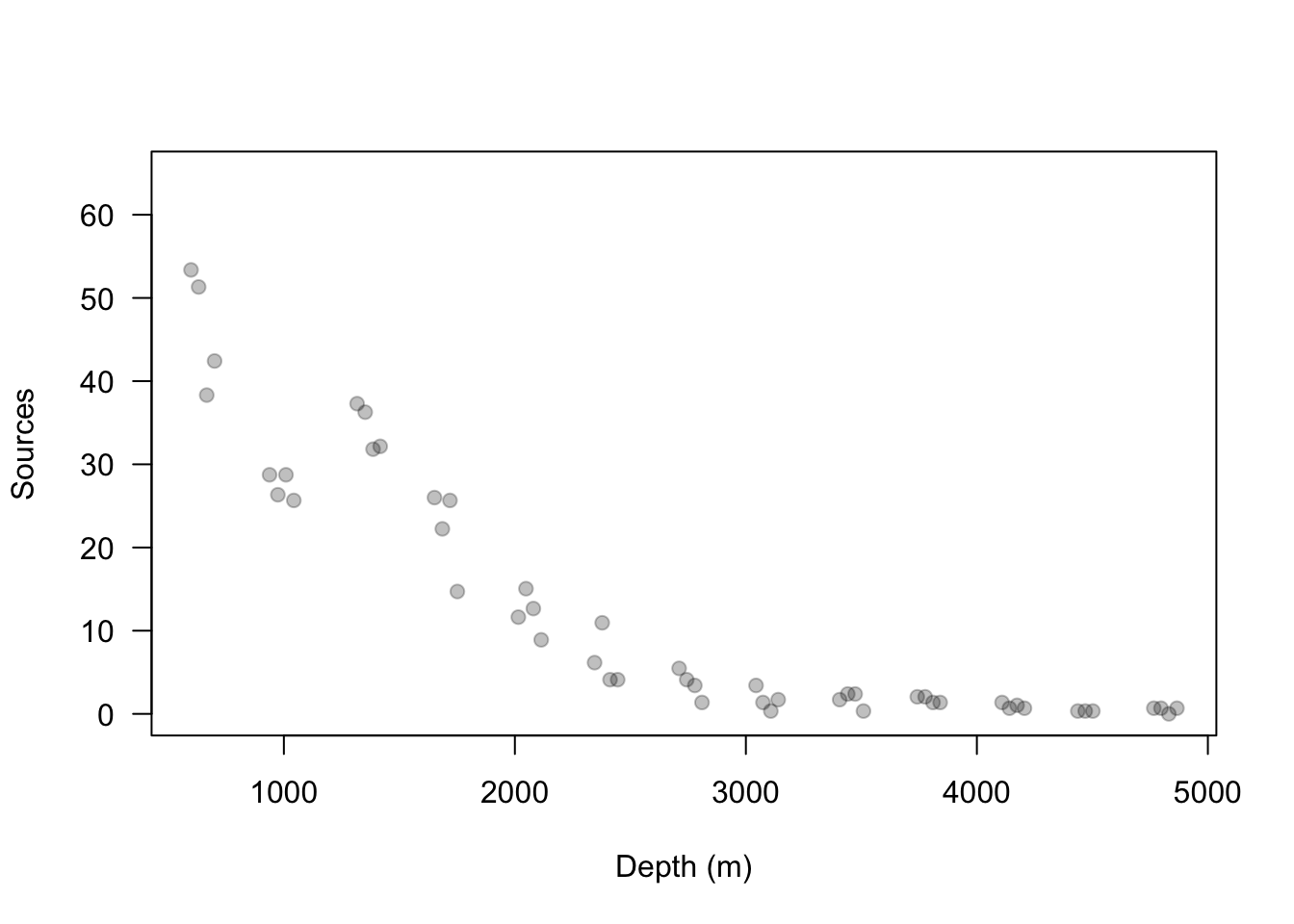
Modify the linear model
- Account for spatial autocorrelation
- Enable prediction at locations
- Write out on whiteboard
- In R
library(fields) library(truncnorm) library(mvtnorm) library(coda) library(MASS) y <- df$Sources X <- model.matrix(~I(Depth/Depth)-1,data=df) Z <- diag(1,length(y)) n <- length(y) # Distance matrix used to calculate correlation matrix D <- rdist(df$Depth) m.draws <- 10000 #Number of MCMC samples to draw samples <- as.data.frame(matrix(,m.draws+1,dim(X)[2]+3)) colnames(samples) <- c(colnames(X),"sigma2.e","sigma2.alpha","phi") samples[1,] <- c(40,10,150,250) #Starting values for beta0, sigma2.e, sigma2.alpha, and phi samples.alpha <- as.data.frame(matrix(,m.draws+1,length(y))) # Hyperparameters for priors sigma2.beta <- 100 a <- 2.01 b <- 1 c <- 2.01 d <- 1 e <- 0 f <- 10^6 accept <- matrix(, m.draws + 1, 1) # Monitor acceptance rate colnames(accept) <- c("phi") phi.tune <- 10 set.seed(3909) ptm <- proc.time() for(k in 1:m.draws){ beta <- t(samples[k,1:dim(X)[2]]) sigma2.e <- samples[k,dim(X)[2]+1] sigma2.alpha <- samples[k,dim(X)[2]+2] phi <- samples[k,dim(X)[2]+3] C <- exp(-(D/phi)^2) CI <- solve(C) # Sample alpha H <- solve((1/sigma2.e)*t(Z)%*%Z + (1/sigma2.alpha)*CI) h <- (1/sigma2.e)*t(Z)%*%(y-X%*%beta) alpha <- mvrnorm(1,H%*%h,H) # Sample beta H <- solve((1/sigma2.e)*t(X)%*%X + (1/sigma2.beta)*diag(1,dim(X)[2])) h <- (1/sigma2.e)*t(X)%*%(y-Z%*%alpha) beta <- mvrnorm(1,H%*%h,H) # Sample sigma2.alpha sigma2.alpha <- 1/rgamma(1,a+n/2,b+t(alpha)%*%CI%*%(alpha)/2) # Sample sigma2.e sigma2.e <- 1/rgamma(1,c+n/2,d+t(y-X%*%beta-Z%*%alpha)%*%(y-X%*%beta-Z%*%alpha)/2) #Sample phi phi.star <- rnorm(1,phi,phi.tune) if(phi.star > e & phi.star < f){ C.star <- exp(-(D/phi.star)^2) mh1 <- dmvnorm(alpha,rep(0,n),sigma2.alpha*C.star,log=TRUE) + dunif(phi.star,e,f,log=TRUE) mh2 <- dmvnorm(alpha,rep(0,n),sigma2.alpha*C,log=TRUE) + dunif(phi,e,f,log=TRUE) R <- min(1,exp(mh1 - mh2)) if (R > runif(1)){phi <- phi.star}} # Save samples[k+1,] <- c(beta,sigma2.e,sigma2.alpha,phi) samples.alpha[k+1,] <- alpha accept[k+1,] <- ifelse(phi==phi.star,1,0) if(k%%1000==0) print(k) } proc.time() - ptm mean(accept[-1,]) par(mfrow=c(1,1),mar=c(5,5,2,2)) plot(samples[,1],typ="l",xlab="k",ylab=expression(beta[0])) plot(samples[,2],typ="l",xlab="k",ylab=expression(sigma[epsilon]^2)) plot(samples[,3],typ="l",xlab="k",ylab=expression(sigma[alpha]^2)) plot(samples[,4],typ="l",xlab="k",ylab=expression(phi)) #Note: there is a trace plots for each of the 51 alphas plot(samples.alpha[,1],typ="l",xlab="k",ylab=expression(alpha)) burn.in <- 1000 #Effective sample size effectiveSize(samples[-c(1:burn.in),]) effectiveSize(samples.alpha[-c(1:burn.in),]) # E() of beta, sigma2.e, sigma2.alpha, phi colMeans(samples[-c(1:burn.in),]) # 95% Equal-tailed CIs apply(samples[-c(1:burn.in),],2,FUN=quantile,prob=c(0.025,0.975)) # obtain E(y) of at new depths new.depth <- seq(min(df$Depth),max(df$Depth),by=10) X.new <- model.matrix(~I(new.depth/new.depth)-1) Z.new <- diag(1,length(new.depth)) D.cross <- rdist(new.depth,df$Depth) samples.pred <- matrix(,length(burn.in:m.draws),length(new.depth)) for(k in burn.in:m.draws){ alpha <- t(samples.alpha[k,]) beta <- t(samples[k,1:dim(X)[2]]) sigma2.e <- samples[k,dim(X)[2]+1] sigma2.alpha <- samples[k,dim(X)[2]+2] phi <- samples[k,dim(X)[2]+3] C <- exp(-(D/phi)^2) C.cross <- exp(-(D.cross/phi)^2) alpha.new <- C.cross%*%solve(C)%*%alpha samples.pred[k-burn.in+1,] <- X.new%*%beta + Z.new%*%alpha.new } plot(df$Depth,df$Sources,las=1,ylim=c(0,60),col=rgb(0,0,0,0.25),pch=19, xlab="Depth (m)",ylab="Sources") points(new.depth,colMeans(samples.pred),typ="l") EV.beta <- mean(samples[-c(1:burn.in),1]) EV.alpha <- colMeans(samples.alpha[-c(1:burn.in),]) EV.e <- y - X%*%EV.beta - Z%*%EV.alpha par(mfrow=c(2,1)) plot(df$Depth, EV.e, las = 1, col = rgb(0, 0, 0, 0.25),pch = 19, xlab = "Depth (m)", ylab = expression("E("*epsilon*")")) hist(EV.e,col="grey",main="",breaks=10,xlab= expression("E("*epsilon*")"))