27 Assignment 3 (Guide)
For this assignment let \([a]\) be a beta distribution with \(\alpha=2\) and \(\beta=1\) (i.e., \(a\sim\text{beta}(\alpha=2,\beta=1)\)).
- This question was worth 5 points. The first half involves using analytical mathematics to find the Metropolis-Hastings ratio. Realize that this problem differs in format from the applications in Ch. 4 of BBM2L. The important thing to realize is that we are sampling from \([a]\) and not from the posterior distribution of a Bayesian model. The Metropolis-Hastings ratio is
\[mh = \frac{[a^{(*)}][a^{(k-1)}|a^{(*)}]}{[a^{(k-1)}][a^{(*)}|a^{(k-1)}]},\] where \(a^{(*)}\) is the proposed value of \(a\) and \(a^{(k-1)}\) is the previous (or initial) value of \(a\). Since we are using a uniform PDF for the proposal distribution, the Metropolis-Hastings ratio simplifies to
\[mh = \frac{[a^{(*)}]}{[a^{(k-1)}]},\] because \([a^{(k-1)}|a^{(*)}]=1\) and \([a^{(*)}|a^{(k-1)}]=1\). Now substitute the PDF for \(a\) into the Metropolis-Hastings ratio and you get
\[mh = \frac{2a^{*}}{2a^{(k-1)}}.\] This which simplifies to
\[mh = \frac{a^{*}}{a^{(k-1)}}.\]
The R code below implements the Metropolis-Hastings algorithm.
a.init <- 0.01
K <- 5000
samples <- matrix(,K,1)
samples[1,] <- a.init
for(k in 2:K){
a.old <- samples[k-1,]
a.try <- runif(1)
mh <- a.try/a.old
keep <- ifelse(mh>1,1,rbinom(1,1,mh))
samples[k,] <- ifelse(keep==1,a.try,a.old)
}This question was worth 2 points.
hist(samples[-c(1:1000)],freq=FALSE,xlab=expression(italic(a)),ylab=expression("["*italic(a)*"]"),main="")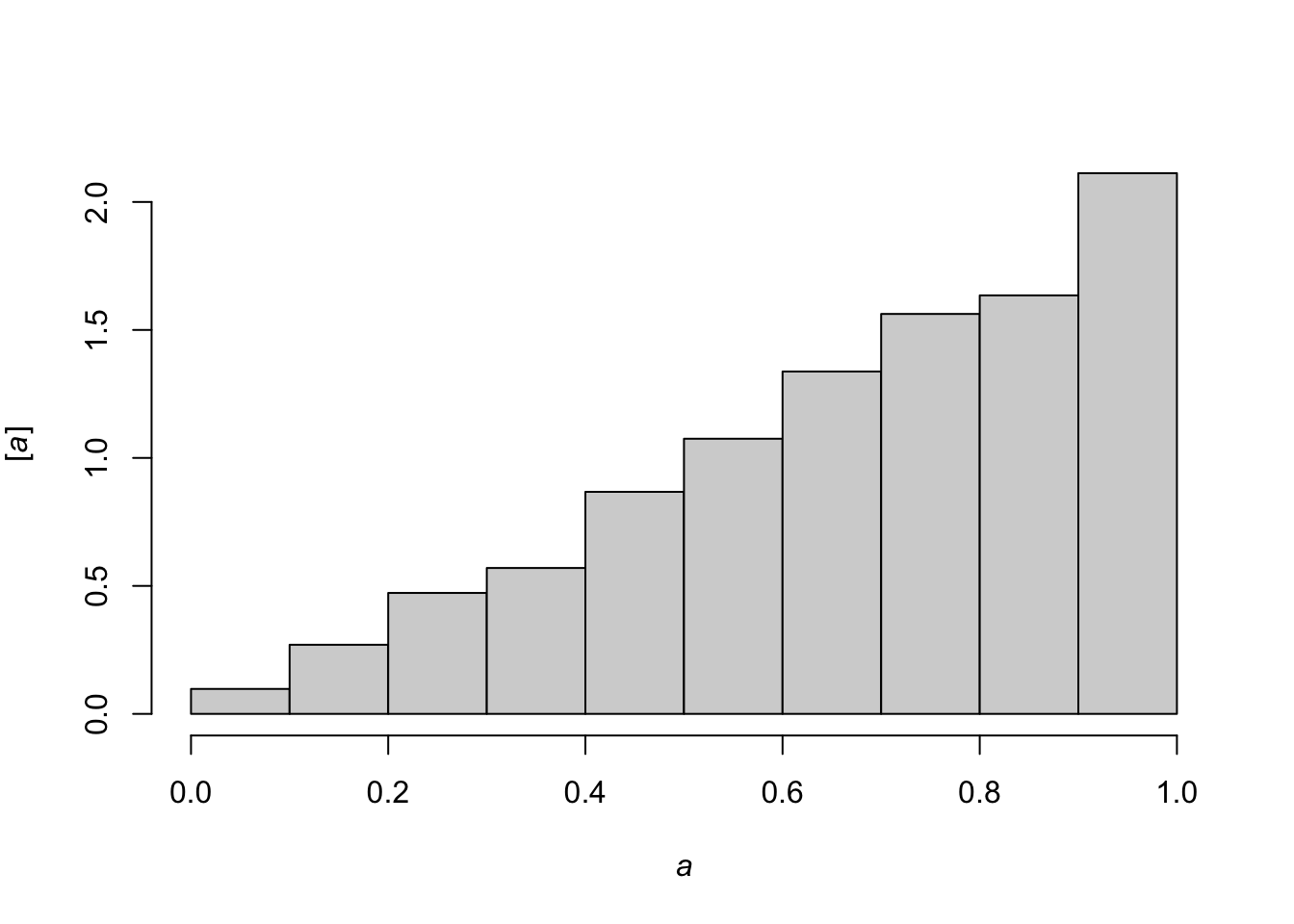
This question was worth 5 points. The R code below provides a Monte Carlo approximation to the integral
\[\int_{0}^{1}a[a]da\] where [a] is a beta(2,1) distribution with probability mass function \([a]=2a\).
mean(samples[-c(1:1000)])## [1] 0.6793755- This question was worth 5 points. The reason that values are repeated has nothing to do with the burn-in interval or the the number of samples required to reach the stationary stationary distribution (i.e., the burn-in interval). Furthermore, the reason that values are repeated is not because of autocorrelation. Autocorrelation, or correlation among sequential draws from \(a\), is partially created by the repeated values of \(a\). Many incorrect responses included some misunderstanding of the burn-in interval and autocorrelation. A deeper reading of the Metropolis-Hastings algorithm (bottom of pg. 25 in BBM2L) is needed. If you would like a revised grade for this question please re-read the Metropolis-Hastings algorithm on the bottom of pg. 25 in BBM2L and re-write your response.