5.4 Clasificación
Según (Christen 2012) Los métodos supervisados de clasificación más populares para el enlazado de registros son los árboles de decisión (Decision Trees) y las máquinas de vectores de soporte (Support Vector Machines, SVMs).
En esta prueba de concepto hemos aplicado la clasificación mediante árboles de decisión y su evolución, los bosques aleatorios (Random Forest).
5.4.1 Conjuntos de entrenamiento y de prueba
La muestra clasificada a mano se ha separado en dos subconjuntos, uno de entrenamiento, con el 70% de los registros, y otro de pruebas, con el 30% restante. Los modelos de aprendizaje máquina se han entrenado con el conjunto de datos de entrenamiento y se han probado sobre el conjunto de datos de prueba.
Este método de validación es conceptualmente simple y fácil de implementar, aunque es mejorable. Fuera de la POC, para poder evaluar mejor los resultados, se podría emplear evaluación cruzada. Para saber más sobre éstos métodos de validación, consultar la sección 5.1 del libro (James et al. 2013), ‘Cross-Validation’.
# Nos quedamos con las observaciones clasificadas manualmente.
muestra <- muestra %>% filter(!is.na(clase)) %>% filter(clase == "s" | clase == "n")
# Variables categóricas a 'as.factor'
muestra$clase <- as.factor(muestra$clase)
set.seed(666)
sample = sample.split(muestra, SplitRatio = .70)
train = subset(muestra, sample == TRUE)
test = subset(muestra, sample == FALSE)5.4.2 Clasificación de referencia
Como referencia, compararemos el resultado de la clasificación mediante aprendizaje máquina con la clasificación determinista y la clasificación probabilística.
5.4.2.1 Clasificación determinista
5.4.2.1.1 LAKORA
Se trata del algoritmo de LAKORA, que es el sistema de información de Salud que unifica sus propias bases de datos.
La clasificación es positiva si y sólo si se cumple una de estas condiciones:
- Id, Fecha de Nacimiento iguales
- Id, Apellido1 iguales
- Nombre, Apellido1, Fecha de Nacimiento iguales
- Apellidos, Fecha de Nacimiento iguales, Nombre similar (uno de los dos nombres está contenido en el otro)
- Nombre, Apellido2, Fecha de Nacimiento iguales, Apellido1 similar (uno de los apellido1 está contenido en el otro)
- Nombre, Apellido1, Fecha de Nacimiento iguales, Apellido2 similar (uno de los apellido2 está contenido en el otro)
- Id sin dígito de control, Fecha de Nacimiento iguales
- Nombre, Apellidos iguales, Fecha de Nacimiento similar (La fecha difiere en 2 dígitos a lo sumo)
- Nombre y Apellidos concatenados, Fecha de Nacimiento iguales
# Clasificación determinista 1
clasificador_determinista_1 <- function() {
determinista.pred <- vector("logical", nrow(test))
# Clasificación determinista:
determinista.pred <-
# Id, Fecha de Nacimiento iguales
(test$bdc_id_oficial.x == test$bdc_id_oficial.y &
test$bdc_fecha_nacimiento.x == test$bdc_fecha_nacimiento.y) |
# Id, Apellido1 iguales
(test$bdc_id_oficial.x == test$bdc_id_oficial.y &
test$bdc_apellido_1.x == test$bdc_apellido_1.y) |
# Nombre, Apellido1 y Fecha de Nacimiento iguales
(test$bdc_nombre.x == test$bdc_nombre.y &
test$bdc_apellido_1.x == test$bdc_apellido_1.y &
test$bdc_fecha_nacimiento.x == test$bdc_fecha_nacimiento.y) |
# Apellidos y Fecha de Nacimiento iguales, Nombre similar (incluido)
(test$bdc_apellido_1.x == test$bdc_apellido_1.y &
test$bdc_apellido_2.x == test$bdc_apellido_2.y &
test$bdc_fecha_nacimiento.x == test$bdc_fecha_nacimiento.y &
test$nombre.incluido) |
# Nombre, Apellido2 y Fecha de Nacimiento iguales, Apellido1 similar (incluido)
(test$bdc_nombre.x == test$bdc_nombre.y &
test$bdc_apellido_2.x == test$bdc_apellido_2.y &
test$bdc_fecha_nacimiento.x == test$bdc_fecha_nacimiento.y &
test$apellido_1.incluido) |
# Nombre, Apellido1 y Fecha de Nacimiento iguales, Apellido2 similar (incluido)
(test$bdc_nombre.x == test$bdc_nombre.y &
test$bdc_apellido_1.x == test$bdc_apellido_1.y &
test$bdc_fecha_nacimiento.x == test$bdc_fecha_nacimiento.y &
test$apellido_2.incluido) |
# Id sin dígito de control y Fecha de Nacimiento iguales
(test$id_oficial.dis <= 1 & # ¡Aprox!
test$bdc_fecha_nacimiento.x == test$bdc_fecha_nacimiento.y) |
# Nombre y Apellidos iguales, Fecha de Nacimiento similar (2 dígitos diferencia)
(test$bdc_nombre.x == test$bdc_nombre.y &
test$bdc_apellido_1.x == test$bdc_apellido_1.y &
test$bdc_apellido_2.x == test$bdc_apellido_2.y &
test$fecha_nacimiento.dis <= 2) |
# Nombre y Apellidos concatenados y Fecha de Nacimiento iguales
(test$nombre_completo.x == test$nombre_completo.y &
test$bdc_fecha_nacimiento.x == test$bdc_fecha_nacimiento.y)
# Los valores NA son FALSE
determinista.pred[is.na(determinista.pred)] <- FALSE
# Nuestra clasificación es una variable de tipo cadena de caracteres
determinista.pred <- as.character(determinista.pred)
determinista.pred[determinista.pred == "FALSE"] <- "n"
determinista.pred[determinista.pred == "TRUE"] <- "s"
return(determinista.pred)
}
determinista.pred<- clasificador_determinista_1()Si consultamos cuándo la predicción difiere de la realidad encontramos, como era de esperar, que todas las diferencias son casos en los que la predicción dice que dos pares no son coincidentes cuando en realidad lo son. Es decir, todas las coincidencias predichas lo son, pero hay coincidencias no predichas.
data.frame( determinista.pred, test$clase) %>%
filter(determinista.pred != test.clase) %>%
head() %>% pulcro()| determinista.pred | test.clase |
|---|---|
| n | s |
| n | s |
| n | s |
| n | s |
| n | s |
| n | s |
Es decir, no tenemos falsos positivos pero sí falsos negativos.
En la forma de matriz de confusión:
##
## determinista.pred n s
## n 50 19
## s 0 955.4.2.1.2 Cruce entre Padrón y TIS
Se trata de un cruce puntual entre los datos del Padrón y los de la Tarjeta Sanitaria TIS.
- Se normalizan las cadenas de caracteres incluyendo ciertas sustituciones.
- Se definen como
- clave completa: “NombreNormalizado-Apellido1Normalizado-Apellido2Normalizado*AñoNac-MesNac-DíaNac"
- Clave parcial: “NombreNormalizado-Apellido1Normalizado-*AñoNac-MesNac-DíaNac"
La clasificación es positiva si y sólo si se cumple una de estas condiciones:
- Matching completo por clave: cuando dos registros tienen la clave completa idéntica.
- Matching parcial por clave: cuando la clave completa de Padrón es igual a una clave parcial de TIS (sólo puede ocurrir cuando en Padrón no se tiene el segundo apellido).
- Matching similar: casos en los que la clave completa de ambos registros es parecida: si una de las dos partes es exacta y la otra contiene una partícula diferente (por ejemplo, que el día de la fecha de nacimiento sea lo único diferente de las dos claves)
- Matching por DNI: dos registros con el mismo DNI
# Clasificación determinista 2
# Funcion de normalización:
normalize <- function(cadena) {
return(
ifelse (is.na(cadena), "",
cadena %>% str_replace_all("CH", "TZ") %>% str_replace_all("TX", "TZ") %>%
str_replace_all("TS", "TZ") %>% str_replace_all("H", "") %>%
str_replace_all("Ñ", "N") %>% str_replace_all("V", "B") %>%
str_replace_all("LL", "Y") %>% str_replace_all("Y", "I") %>%
str_replace_all("CA", "KA") %>% str_replace_all("CO", "KO") %>%
str_replace_all("CU", "KU") %>% str_replace_all("CE", "ZE") %>%
str_replace_all("CI", "ZI") %>% str_replace_all("QUE", "KE") %>%
str_replace_all("QUI", "KI") %>% str_replace_all("GE", "JE") %>%
str_replace_all("GI", "JI") %>% str_replace_all("GUE", "GE") %>%
str_replace_all("GUI", "GI") %>% str_replace_all("AA", "A") %>%
str_replace_all("EE", "E") %>% str_replace_all("II", "I") %>%
str_replace_all("OO", "O") %>% str_replace_all("UU", "U") %>%
str_replace_all("NN", "N") %>% str_replace_all("\\.", " ") %>%
str_replace_all("'", "") %>% str_replace_all("\\\\", "") %>%
str_replace_all("-", " ") %>% str_replace_all("_", " ") %>%
trim()
)
)
}
# Ejemplo:
# normalize(" TXATXI CHACHI LLUVIA YES QUITO QUESO AAEEIIOOUU \\-._ X ") %>% print()
# [1] "TZATZI TZATZI IUBIA IES KITO KESO AEIOU X"
clasificador_determinista_2 <- function() {
#Normalización:
testN <- test
variablesNormalizar <- c("bdc_nombre.x", "bdc_nombre.y",
"bdc_apellido_1.x", "bdc_apellido_1.y",
"bdc_apellido_2.x", "bdc_apellido_2.y")
testN[variablesNormalizar] <- lapply(testN[variablesNormalizar], normalize)
# Clasificación:
determinista.pred <- vector("logical", nrow(test))
determinista.pred <-
( # Matching completo por clave:
paste(paste(testN$bdc_nombre.x,testN$bdc_apellido_1.x,
testN$bdc_apellido_2.x, sep="-"),
testN$bdc_fecha_nacimiento.x, sep="*") ==
paste(paste(testN$bdc_nombre.y,testN$bdc_apellido_1.y,
testN$bdc_apellido_2.y, sep="-"),
testN$bdc_fecha_nacimiento.y, sep="*")
) | (
# Matching parcial por clave:
paste(paste(testN$bdc_nombre.x,testN$bdc_apellido_1.x,
testN$bdc_apellido_2.x, sep="-"),
testN$bdc_fecha_nacimiento.x, sep="*") ==
paste(paste(testN$bdc_nombre.y,testN$bdc_apellido_1.y, sep="-"),
testN$bdc_fecha_nacimiento.y, sep="*")
) | (
# Matching similar:
(
( # primera parte exacta:
paste(testN$bdc_nombre.x,testN$bdc_apellido_1.x,
testN$bdc_apellido_2.x, sep="-") ==
paste(testN$bdc_nombre.y,testN$bdc_apellido_1.y,
testN$bdc_apellido_2.y, sep="-")
) & (
# segunda parte similar:
as.integer(year(testN$bdc_fecha_nacimiento.x)
== year(testN$bdc_fecha_nacimiento.y)) +
as.integer(month(testN$bdc_fecha_nacimiento.x)
== month(testN$bdc_fecha_nacimiento.y)) +
as.integer(day(testN$bdc_fecha_nacimiento.x)
== day(testN$bdc_fecha_nacimiento.y)) >= 2
)
) | (
( # primera parte similar:
as.integer(testN$bdc_nombre.x == testN$bdc_nombre.y) +
as.integer(testN$bdc_apellido_1.x == testN$bdc_apellido_1.y) +
as.integer(testN$bdc_apellido_2.x == testN$bdc_apellido_2.y) >= 2
) & (
# segunda parte exacta:
testN$bdc_fecha_nacimiento.x == testN$bdc_fecha_nacimiento.y
)
)
) | (
# Matching por dni
testN$bdc_id_oficial.x == testN$bdc_id_oficial.y
)
# Los valores NA son FALSE
determinista.pred[is.na(determinista.pred)] <- FALSE
determinista.2.fallos <- test[test$clase != determinista.pred,]
# Nuestra clasificación es una variable de tipo cadena de caracteres
determinista.pred <- as.character(determinista.pred)
determinista.pred[determinista.pred == "FALSE"] <- "n"
determinista.pred[determinista.pred == "TRUE"] <- "s"
return(determinista.pred)
}
determinista.pred <- clasificador_determinista_2()
# Matriz de confusión:
tabla <- table(determinista.pred, test$clase)
print(tabla)##
## determinista.pred n s
## n 50 11
## s 0 103Como era de esperar, no tenemos falsos positivos pero sí falsos negativos.
5.4.2.2 Clasificación probabilística
Con un umbral de 0.75, este es el resultado de la clasificación probabilística hecha con FastLink (Enamorado, Fifield, and Imai 2018a) en el capítulo 4.
# Clasificación probabilística
clasificador_probabilistico <- function() {
probab.pred <- vector("logical", nrow(test))
probab.pred <- test$prob > 0.75
# Nuestra clasificación es una variable de tipo cadena de caracteres
probab.pred <- as.character(probab.pred)
probab.pred[probab.pred == "FALSE"] <- "n"
probab.pred[probab.pred == "TRUE"] <- "s"
return(probab.pred)
}
probab.pred <- clasificador_probabilistico()
# Matriz de confusión:
tabla <- table(probab.pred, test$clase)
print(tabla)##
## probab.pred n s
## n 45 5
## s 5 109Tenemos tanto falsos positivos como falsos negativos.
5.4.3 Arbol de decisión
Entrenamiento y prueba de un árbol de decisión (Decision tree).
Los métodos basados en árboles buscan segmentar el espacio de predicción en regiones simples. El conjunto de reglas de división utilizado para segmentar el espacio se puede resumir en un árbol, por eso se denominan arboles de decisión. Los árboles de decisión son simples y fáciles de interpretar, aunque no son los mejores en cuanto a calidad de la predicción (James et al. 2013).
El paquete R utilizado es rpart (Therneau, Atkinson, and Ripley 2017). Las características de entrenamiento son, inicialmente, sólo las distancias que indican la similitud entre los campos a comparar.
tree <- NA
clasificador_arbol_decision_na <- function() {
# Entrenamiento del árbol de decisión
tree <<- rpart(clase ~ id_oficial.dis
+ nombre.dis + apellido_1.dis + apellido_2.dis
+ fecha_nacimiento.dis + sexo.dis + municipio_domicilio.dis
,
method='class', data = train)
# La predicción está en la forma de la probabilidad de pertenecer
# a cada una de las clases.
# Establecemos un umbral de 0.5 para la clasificación definitiva.
tree.preds <- predict(tree,test)
# Umbral de 0.5 para la clasificación
tree.preds <- as.data.frame(tree.preds)
tree.preds <- tree.preds %>% mutate(clase = ifelse(s >= 0.50, "s", "n"))
return (tree.preds)
}
tree.preds <- clasificador_arbol_decision_na()El modelo nos da una probabilidad de pertenencia a cada clase (en nuestro caso, ‘s’ y ‘n’), por lo que hay que establecer un umbral. Por ejemplo, si la probabilidad de que la clase sea ‘s’ es mayor que 0.5, el modelo predice que el par de registros pertenecen a la clase ‘s’, es decir, pertenecen a la misma persona.
| n | s | clase |
|---|---|---|
| 0.0549451 | 0.9450549 | s |
| 0.0549451 | 0.9450549 | s |
| 0.0549451 | 0.9450549 | s |
| 0.0549451 | 0.9450549 | s |
| 0.0549451 | 0.9450549 | s |
| 0.0549451 | 0.9450549 | s |
Matriz de confusión:
##
## n s
## n 42 7
## s 8 107El resultado no es demasiado bueno, pero sí que es interpretable, ya que los árboles de decisión se pueden dibujar:
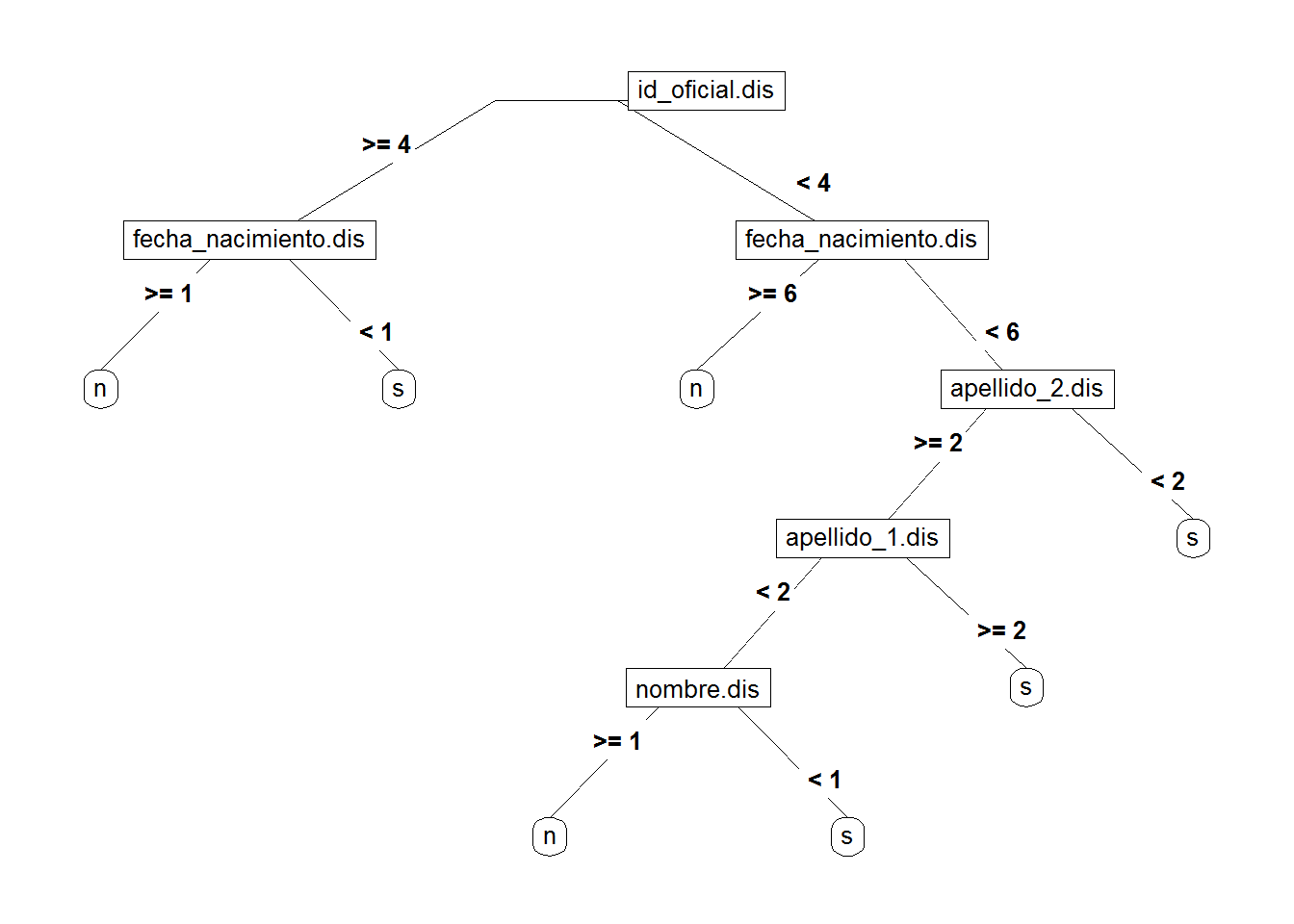
Las decisiones se toman en función de las distancias entre las variables a comparar.
5.4.3.1 Variables desconocidas
En las bases de datos a enlazar faltan datos (sobre todo en la de Registr@). Si alguna de las variables no tiene datos, la distancia es desconocida. El árbol de decisión no puede tomar decisiones sobre variables desconocidas.
Sustituimos los valores desconocidos de todas las características sintéticas por valores razonables:
- Las distancias desconocidas por la máxima distancia
- La variable desconocida que indica si es nacional o extranjero, por el valor ‘X’ (una nueva clase)
- Las variables desconocidas con la frecuencias de nombres y apellidos, por el valor 0 (frecuencia mínima)
- Las variables desconocidas que indican si una cadena está incluida en otra, por el valor FALSE (no están incluidas)
# Buscamos la máxima distancia del campo más largo:
valor_na_distancia <- max(muestra$nombre_completo.dis)
# Sustituimos todos los NA en las distancias por el valor máximo:
muestra_sin_na <- muestra
muestra_sin_na$id_oficial.dis[is.na(muestra_sin_na$id_oficial.dis)] <- valor_na_distancia
muestra_sin_na$nombre.dis[is.na(muestra_sin_na$nombre.dis)] <- valor_na_distancia
muestra_sin_na$apellido_1.dis[is.na(muestra_sin_na$apellido_1.dis)] <- valor_na_distancia
muestra_sin_na$apellido_2.dis[is.na(muestra_sin_na$apellido_2.dis)] <- valor_na_distancia
muestra_sin_na$fecha_nacimiento.dis[is.na(muestra_sin_na$fecha_nacimiento.dis)] <- valor_na_distancia
muestra_sin_na$sexo.dis[is.na(muestra_sin_na$sexo.dis)] <- valor_na_distancia
muestra_sin_na$municipio_domicilio.dis[is.na(muestra_sin_na$municipio_domicilio.dis)] <- valor_na_distancia
muestra_sin_na$nombre_completo.dis[is.na(muestra_sin_na$nombre_completo.dis)] <- valor_na_distancia
# Sustituimos todos los NA en id_nacional_extranjero por "X". Y son factores.
muestra_sin_na$id_nacional_extranjero.x[is.na(muestra_sin_na$id_nacional_extranjero.x)] <- "X"
muestra_sin_na$id_nacional_extranjero.x <- as.factor(muestra_sin_na$id_nacional_extranjero.x)
muestra_sin_na$id_nacional_extranjero.y[is.na(muestra_sin_na$id_nacional_extranjero.y)] <- "X"
muestra_sin_na$id_nacional_extranjero.y <- as.factor(muestra_sin_na$id_nacional_extranjero.y)
# Sustituimos todos los NA en ine_por_mil por 0
muestra_sin_na$ine_por_mil.x[is.na(muestra_sin_na$ine_por_mil.x)] <- 0
muestra_sin_na$ine_por_mil.y[is.na(muestra_sin_na$ine_por_mil.y)] <- 0
# Sustituimos todos los NA en *_incluido
muestra_sin_na$nombre.incluido[is.na(muestra_sin_na$nombre.incluido)] <- FALSE
muestra_sin_na$apellido_1.incluido[is.na(muestra_sin_na$apellido_1.incluido)] <- FALSE
muestra_sin_na$apellido_2.incluido[is.na(muestra_sin_na$apellido_2.incluido)] <- FALSE
muestra_sin_na$municipio_domicilio.incluido[is.na(muestra_sin_na$municipio_domicilio.incluido)] <- FALSE
muestra_sin_na$nombre_completo.incluido[is.na(muestra_sin_na$nombre_completo.incluido)] <- FALSEUna vez más, dividimos la muestra en dos conjuntos, la mayor parte para entrenar los modelos, el resto para probarlos:
# Datos de entrenamiento y prueba:
set.seed(666)
sample = sample.split(muestra_sin_na, SplitRatio = .70)
train_sin_na = subset(muestra_sin_na, sample == TRUE)
test_sin_na = subset(muestra_sin_na, sample == FALSE)Entrenamiento. Las características de entrenamiento son otra vez solo las distancias entre las variables a comparar:
clasificador_arbol_decision <- function() {
# Entrenamiento:
tree <<- rpart(clase ~ id_oficial.dis
+ nombre.dis + apellido_1.dis + apellido_2.dis
+ fecha_nacimiento.dis + sexo.dis + municipio_domicilio.dis
,method='class', data = train_sin_na)
# Prueba:
tree.preds <- predict(tree, test_sin_na)
tree.preds <- as.data.frame(tree.preds)
tree.preds <- tree.preds %>% mutate(clase = ifelse(s >= 0.5, "s", "n"))
return(tree.preds)
}
tree.preds <- clasificador_arbol_decision()
tabla <- table(tree.preds$clase, test_sin_na$clase)
print(tabla)##
## n s
## n 45 2
## s 5 112El resultado es mejor. El árbol resultante es:
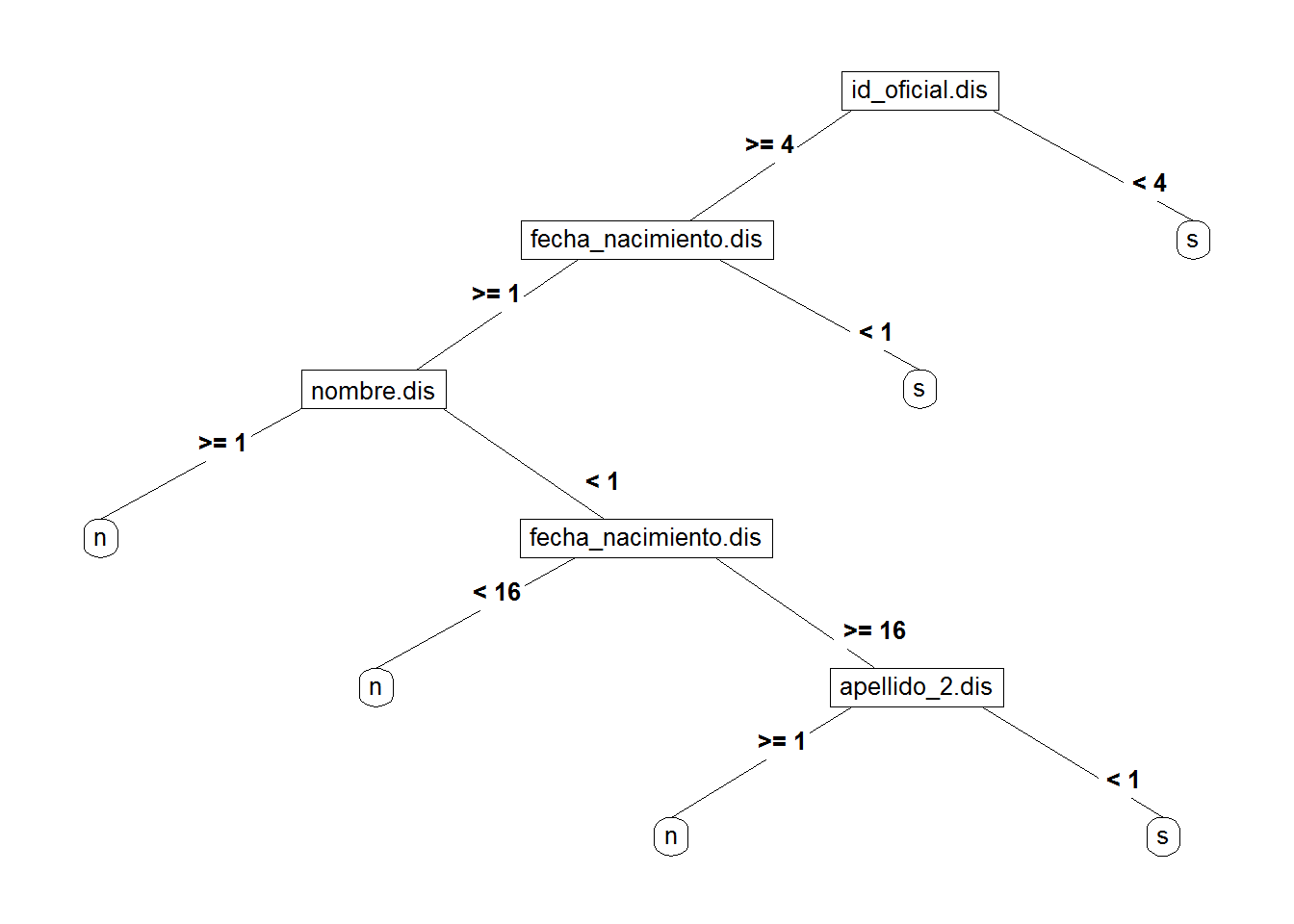
5.4.3.2 Ingeniería de características
Para mejorar el resultado añadimos al modelo las características sintéticas. Por ejemplo, añadiendo el nombre completo, tendríamos:
clasificador_arbol_fe <- function() {
# Entrenamiento:
tree <<- rpart(clase ~ id_oficial.dis
+ nombre.dis + apellido_1.dis + apellido_2.dis
+ fecha_nacimiento.dis + sexo.dis + municipio_domicilio.dis
+ nombre_completo.dis
#+ id_nacional_extranjero.x + id_nacional_extranjero.y
#+ ine_por_mil.x + ine_por_mil.y
#+ nombre.incluido + apellido_1.incluido + apellido_2.incluido
#+ municipio_domicilio.incluido + nombre_completo.incluido
,method='class', data = train_sin_na)
# Prueba:
tree.preds <- predict(tree,test_sin_na)
tree.preds <- as.data.frame(tree.preds)
tree.preds <- tree.preds %>% mutate(clase = ifelse(s >= 0.5, "s", "n"))
return(tree.preds)
}
tree.preds <- clasificador_arbol_fe()
tabla <- table(tree.preds$clase, test$clase)
print(tabla)##
## n s
## n 47 2
## s 3 112En la representación gráfica se puede ver que las variables sintéticas participan en la decisión:
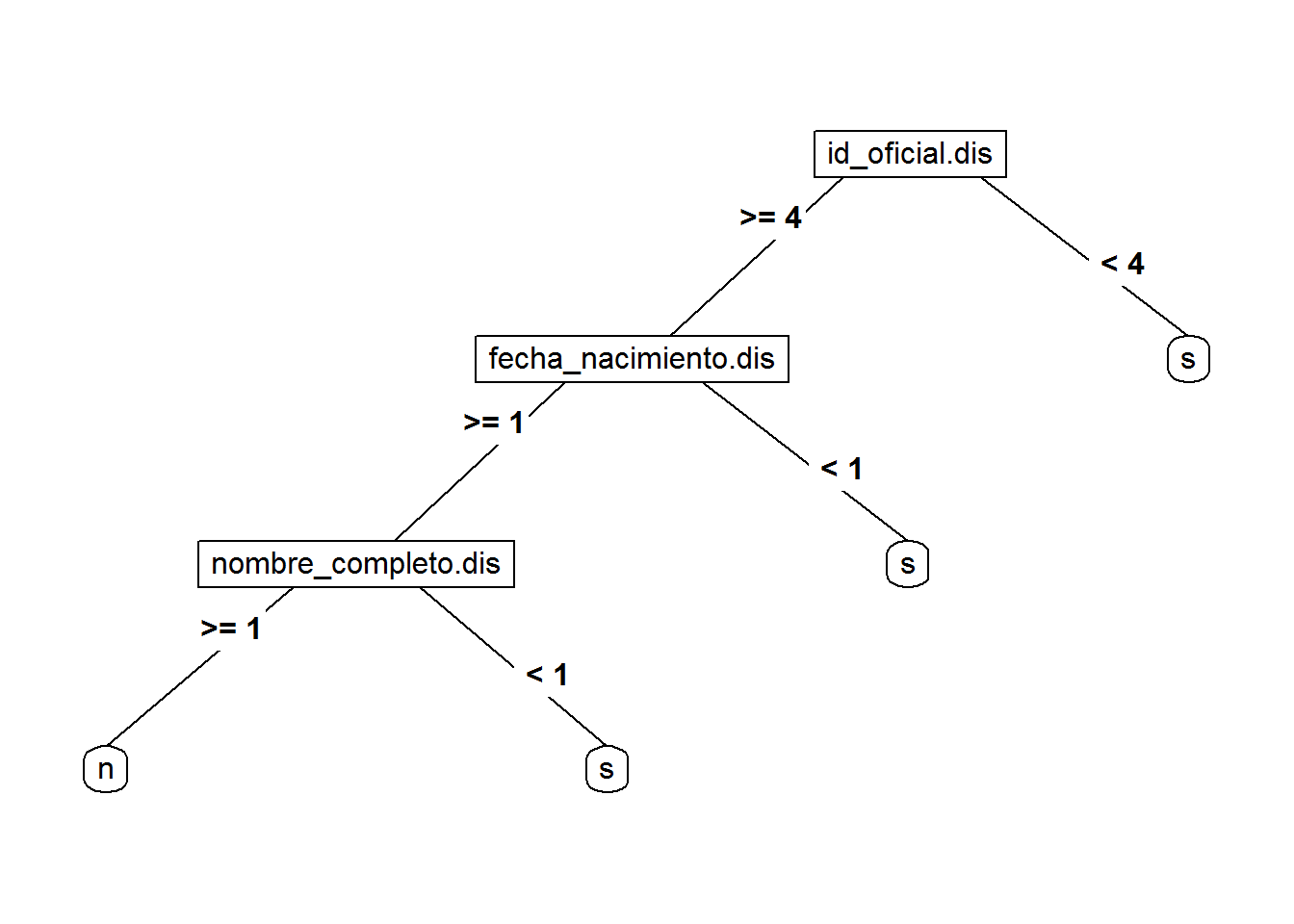
La probabilidad calculada por Fastlink (Enamorado, Fifield, and Imai 2018a) también puede utilizarse como característica sintética:
clasificador_arbol_fe <- function() {
# Entrenamiento:
tree <<- rpart(clase ~ id_oficial.dis
+ nombre.dis + apellido_1.dis + apellido_2.dis
+ fecha_nacimiento.dis + sexo.dis + municipio_domicilio.dis
+ prob
#+ nombre_completo.dis
#+ id_nacional_extranjero.x + id_nacional_extranjero.y
#+ ine_por_mil.x + ine_por_mil.y
#+ nombre.incluido + apellido_1.incluido + apellido_2.incluido
#+ municipio_domicilio.incluido + nombre_completo.incluido
,method='class', data = train_sin_na)
# Prueba:
tree.preds <- predict(tree,test_sin_na)
tree.preds <- as.data.frame(tree.preds)
tree.preds <- tree.preds %>% mutate(clase = ifelse(s >= 0.5, "s", "n"))
return(tree.preds)
}
tree.preds <- clasificador_arbol_fe()
tabla <- table(tree.preds$clase, test$clase)
print(tabla)##
## n s
## n 48 2
## s 2 112En la representación gráfica se puede ver que la probabilidad del enlazado probabilístico pasa a ser la primera variable del árbol de decisión:
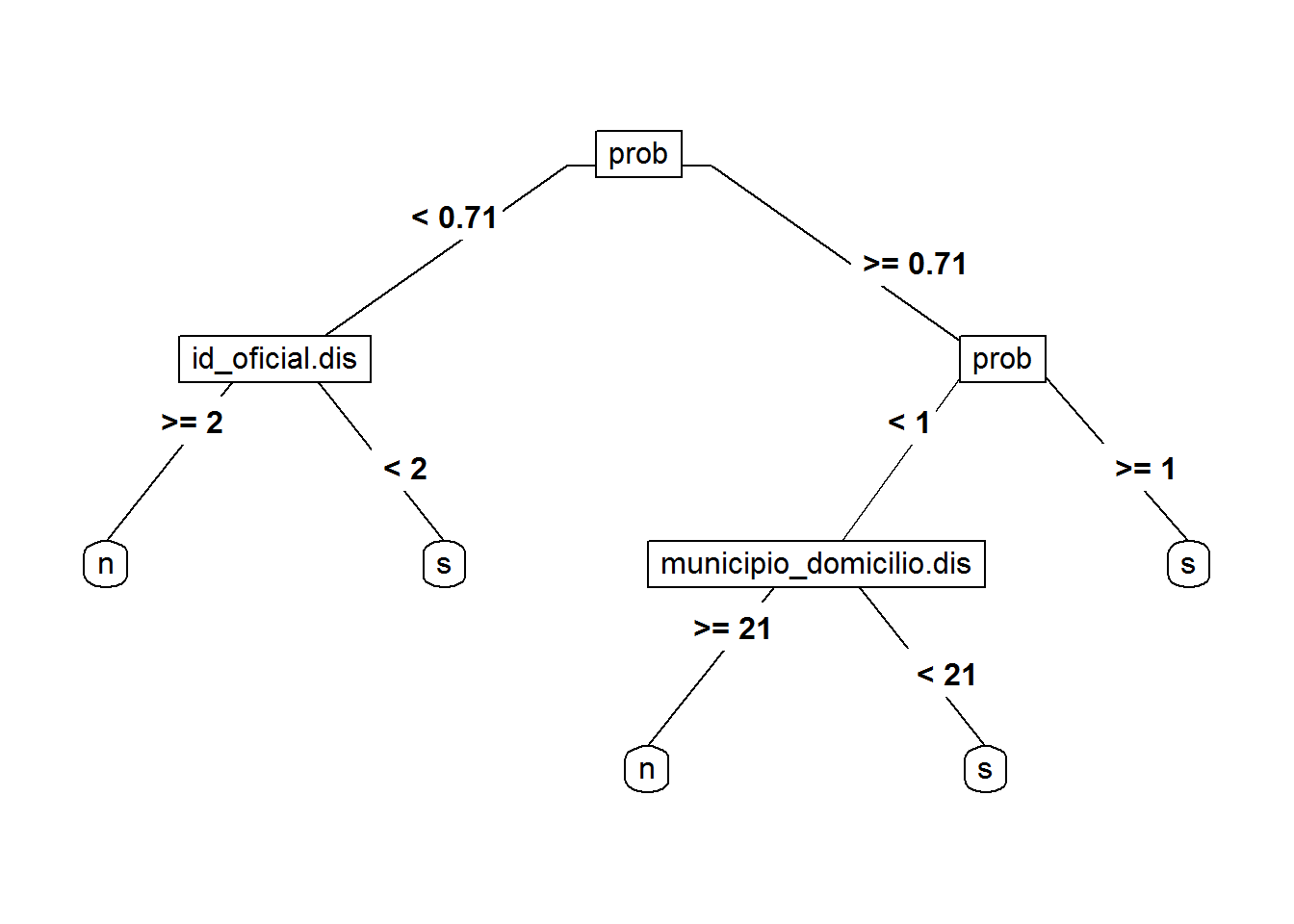
5.4.4 Bosque aleatorio
Modelado mediante un arbol aleatorio (Random forest).
Un bosque aleatorio consiste en producir múltiples árboles que luego se combinan para producir una sola predicción de consenso. La predicción mejora dramáticamente, a costa de perder la facilidad de interpretación del modelo (James et al. 2013).
El paquete utilizado es RandomForest (Breiman et al. 2018). Primero entrenamos solo con las distancias:
clasificador_bosque <- function() {
# Entrenamiento
random.forest <<- randomForest(clase ~ id_oficial.dis
+ nombre.dis + apellido_1.dis + apellido_2.dis
+ fecha_nacimiento.dis + sexo.dis + municipio_domicilio.dis
,
data = train_sin_na, importance = TRUE)
# Prueba
random.forest.preds <- predict(random.forest, test_sin_na)
return(random.forest.preds)
}
random.forest.preds <- clasificador_bosque()
tabla <- table(random.forest.preds, test_sin_na$clase)
print(tabla)##
## random.forest.preds n s
## n 49 2
## s 1 1125.4.4.1 Ingeniería de características
Finalmente entrenamos el modelo con todas las características sintéticas.
clasificador_bosque_fe <- function() {
# Entrenamiento
random.forest.fe <<- randomForest(clase ~ id_oficial.dis
+ nombre.dis + apellido_1.dis + apellido_2.dis
+ fecha_nacimiento.dis + sexo.dis + municipio_domicilio.dis
+ nombre_completo.dis
+ id_nacional_extranjero.x + id_nacional_extranjero.y
+ ine_por_mil.x + ine_por_mil.y
+ nombre.incluido + apellido_1.incluido + apellido_2.incluido
+ municipio_domicilio.incluido + nombre_completo.incluido
,
data = train_sin_na, importance = TRUE)
# Prueba
random.forest.fe.preds <- predict(random.forest.fe, test_sin_na)
return(random.forest.fe.preds)
}
random.forest.fe.preds <- clasificador_bosque_fe()
tabla <- table(random.forest.fe.preds, test_sin_na$clase)
print(tabla)##
## random.forest.fe.preds n s
## n 49 0
## s 1 114Una desventaja de los bosques aleatorios es que no tienen una representación gráfica interpretable. En su lugar tenemos una función de importancia con dos métricas que indican la importancia de cada característica en la decisión:
| n | s | MeanDecreaseAccuracy | MeanDecreaseGini | |
|---|---|---|---|---|
| id_oficial.dis | 56.5102411 | 41.434861 | 55.104009 | 59.2357990 |
| nombre.dis | 7.2689741 | 7.865708 | 9.604006 | 3.0952958 |
| apellido_1.dis | 3.2514598 | 7.250518 | 7.502929 | 1.8930463 |
| apellido_2.dis | 2.4453792 | 7.753850 | 7.619871 | 2.4674973 |
| fecha_nacimiento.dis | 31.6777822 | 20.178922 | 32.424924 | 22.7965601 |
| sexo.dis | 7.4839221 | 1.045399 | 7.426611 | 1.3646097 |
| municipio_domicilio.dis | 4.0073186 | 3.731540 | 5.386149 | 2.8295810 |
| nombre_completo.dis | 15.8321174 | 13.670422 | 18.242740 | 10.3573788 |
| id_nacional_extranjero.x | 0.4464199 | 5.565581 | 5.117908 | 1.1184379 |
| id_nacional_extranjero.y | 2.9080139 | 6.415653 | 6.676958 | 1.7034662 |
| ine_por_mil.x | 16.7498288 | 13.349142 | 20.182151 | 10.5796896 |
| ine_por_mil.y | 12.8816106 | 12.499939 | 16.620873 | 7.3601622 |
| nombre.incluido | 13.7063472 | 11.549132 | 15.502924 | 10.2245440 |
| apellido_1.incluido | 2.7964632 | 4.004313 | 4.658216 | 0.7274702 |
| apellido_2.incluido | 0.4554110 | 4.542250 | 4.230869 | 1.0646135 |
| municipio_domicilio.incluido | 4.7610935 | 2.051205 | 4.923948 | 1.8866065 |
| nombre_completo.incluido | 12.0193431 | 12.589530 | 14.956554 | 7.0805081 |
References
Christen, Peter. 2012. Data Matching, Concepts and Techniques for Record Linkage, Entity Resolution, and Duplicate Detection. https://www.springer.com/in/book/9783642311635.
James, Gareth, Daniela Witten, Trevor Hastie, and Robert Tibshirani. 2013. An Introduction to Statistical Learning with Applications in R. https://www-bcf.usc.edu/~gareth/ISL/.
Enamorado, Ted, Ben Fifield, and Kosuke Imai. 2018a. FastLink: Fast Probabilistic Record Linkage with Missing Data.
Therneau, Terry, Beth Atkinson, and Brian Ripley. 2017. Rpart: Recursive Partitioning and Regression Trees. https://CRAN.R-project.org/package=rpart.
Breiman, Leo, Adele Cutler, Andy Liaw, and Matthew Wiener. 2018. RandomForest: Breiman and Cutler’s Random Forests for Classification and Regression. https://CRAN.R-project.org/package=randomForest.