9 Varyans Analizi (ANOVA)
Varyans analizi (ANOVA) bölümünde kısaca tanıtılan konular; (a) terminoloji, (b) gruplar-arası ANOVA, ve (b) gruplar-içi ANOVA olarak üç başlıktır. Kitabın bir sonraki versiyonunda karma ANOVA (mixed ANOVA) eklenecektir.
9.1 Terminoloji
Varyans analizi kapsamında kullanılan terimler kısaca açıklanmıştır. Fakat bu bölüm bir önceki bölümde tanıtılan yaygın tasarılar (8.3) paragraflarının devamıdır.
Faktör Kategorik bağımsız değişkenler ANOVA çerçevesinde faktör olarak isimlendirilir. Önreğin bir önceki bölümde (8.3.2) rassal blok tasarısı içerisinde tanımlanan okuma hızını artırmaya yönelik yeni program ve kontrol grubu üyeliğini belirteniki kategorili (iki alt sınıflı) değişken bir faktör oluşturur. Toplumsal Cinsiyet Algısının (TCA) yüksek öğretim durumuna göre (yüksek öğretim mezunları ve yüksek öğretim mezunu olmayanlar)değişip değişmediğini test eden bir modelde TCA bağımlı değişken, yüksek öğretim durumu ise bir faktördür.
Alt sınıf Faktörü oluşturan kategorilere alt sınıf denir. TCA örneğinde faktör yüksek öğretim durumudur. Bu faktöre ait alt sınıflar yüksek öğretim mezunu ve yüksek öğretim mezunu değil olmak üzere iki tanedir.
Kesişen faktörler (Crossed factors) Bir faktöre ait alt sınıfların diğer bir faktörün bütün alt sınıfları ile kesişmesi durumudur. Tekarlanan ölçümlerin tanıtımı amaçlı bir önceki bölümde verilen örneği düşünelim,
| İlk kelime | ||
|---|---|---|
| Öğrenci | Silah | Silah Değil |
| 1 | ||
| 2 | ||
| … | ||
| 100 |
Öğrenciler de bir faktör olarak düşünüldüğünde, her öğrencinin reaksiyon süreleri ilk kelime faktörünün her iki alt sınıfında da ölçülmesi sebebi ile öğrenci ve ilk kelime faktörü kesişmiştir.
Kesişmeyen faktörler (Nesting) Bir faktöre ait bir alt sınıfın, ikinci faktörün sadece bir alt sınıfında gözlemlenmesi durumudur. Tamamen rassal tasarının tanıtımı amaçlı bir önceki bölümde verilen örneği düşünelim,
| Makine | |
|---|---|
| 1 | 2 |
| \(H_1\) | \(H_{n+1}\) |
| \(H_2\) | \(H_{n+2}\) |
| \(H_3\) | \(H_{n+3}\) |
| … | |
| \(H_n\) | \(H_{2n}\) |
Her bir hasta 1. veya 2. makine ile tedavi edildiğinden, katılımcı faktörü makine faktörünün içinde düşünülür ve faktörler kesişmemiştir.
Bağlı gözlemler faktörü (Within-subjects factor) katılımcı faktörü (öğrenci,çalışan,hasta vb.) ile kesişen faktörlerdir. Tekrarlanan ölçümler örneğinde olduğu gibi her bir katılımcı diğer bir faktörün bütün alt sınıflarında gözlemlenir. Boylamsal çalışmalarda zaman (örneğin öntest, sontest) bağlı gözlemler faktörüne örnektir.
Bağlı bloklar faktörü bloklar ile kesişen faktördür. Rassal blok tasarısını tanıtım amaçlı bir önceki bölümde verilen örneği düşünelim,
| Çift | Yeni Program | Kontrol |
| 1 | ||
| 2 | ||
| … | ||
| … | ||
| 15 |
Rassal olmayan blok, kalıtsal ve diyadik tasarılar da bağlı bloklar faktörüne örnektir.
Bağlı gözlemler faktörü ve bağlı bloklar faktörü aynı şekilde analiz edildiğinden çoğu zaman aynı isimle kullanılır, bu bölümde de her iki faktör bağlı gözlemler olarak kullanılmıştır.
Gözlemler arası faktör veya Bağlı olmayan gözlemler faktörü (Between-subjects factor) katılımcı faktörü ile kesişmeyen faktörlerdir. Toplumsal Cinsiyet Algısının (TCA) yüksek öğretim durumuna göre (yüksek öğretim mezunları ve yüksek öğretim mezunu olmayanlar)değişip değişmediğini test eden bir modelde TCA bağımlı değişken, yüksek öğretim durumu ise gözlemler arası faktördür.
9.2 Bağlı olmayan gözlemler varyans analizi (Between Subjects ANOVA)
Gözlemlerin (katılımcıların) tek bir alt sınıf kombinasyonuna ait olduğu durumlarda yapılan çözümlemelerdir.
9.2.1 Tek-yönlü bağlı olmayan gözlemler varyans analizi
Tek faktörlü bağlı olmayan gözlemler varyans çözümlemesi \(Y_{ij}=\mu+\alpha_{j}+\epsilon_{ij}\) eşitliğinde yer alan parametrelerin tahmini ile tamamlanabilir. Bu eşitlikte \(Y_{ij}\) j alt sınıfında yer alan i katılımcısına ait puanı, \(\mu\) bütün puanların ortalaması, \(\alpha_j\) j alt sınıfının etkisi ve \(\epsilon_{ij}\) hata terimidir. \(\mu_j=\mu+\alpha_j\)’dir, \(\mu_j\) j alt sınıfında yer alan katılımcıların aritmetik ortalamasıdır.
Genellikle ilgi \(\alpha_j\) üstünedir, çünkü \(\mu_j-\mu\) ’yi temsil eder. Bu ilgi \(H_0: \mu_1 = \mu_2 = \cdots = \mu_j\) boş hipotezinin test edilmesini gerektirir.Alternatif hipotez en az bir alt sınıfa ait ortalamanın farklı olduğunu belirtir. Bu boş hipotez varyansın ayrıştırılması ile test edilebilir. Myers et al. (2013) tarafından verilen notasyon kullanırsak;
| VK | sd | KT | KTO | F |
|---|---|---|---|---|
| Toplam | \(N-1\) | \(\sum_{j=1}^{J}\sum_{i=1}^{n_j}(Y_{ij} - \bar{Y}_{\cdot \cdot})^2\) | ||
| A | \(J-1\) | \(\sum_{j=1}^{J}n_j(\bar{Y}_{\cdot j}-\bar{Y{\cdot \cdot}})^2\) | \(SS_A/df_{A}\) | \(MS_A/MS_{S/A}\) |
| S/A | \(N-J\) | \(\sum_{j=1}^{J}\sum_{i=1}^{n_j}(Y_{ij} - \bar{Y}_{\cdot j})^2\) | \(SS_{S/A} / df_{S/A}\) |
| VK | BKTO |
|---|---|
| Toplam | |
| A | \(\sigma_{S/A}^2 + \frac{1}{J-1} \sum_{j} n_j (\mu_j-\mu)^2\) |
| S/A | \(\sigma_{S/A}^2\) |
VK = vayans kaynağı, sd = serbestlik derecesi, KT = kareler toplamı, KTO = kareler toplamı ortalaması, BKTO = beklenilen kareler toplamı ortalaması.
A , J adet alt sınıfa sahip gruplar arası faktörü, S/A A fatörü içerisindeki katılımcıları, N toplam örneklem sayısını, j=1,…,J faktör alt sınıflarını, i=1,…,\(n_j\) katılımcıları, \(Y_{ij}\) katılımcı puanlarını, \(\bar{Y}_{\cdot \cdot}\) genel ortalamayı, \(\bar{Y}_{\cdot j}\) j alt sınıfı katılımcı ortalamasını temsil eder.
\(MS_{A}/ MS_{S/A}\) oranı, boş hipotez doğru olduğunda ve varsayımlar ihlal edilmediğinde, J-1 ve N-J serbestlik derecesine sahip bir F dağılımını takip eder. Dolayısı ile \(MS_{A}/ MS_{S/A}\), \(F_{\alpha,J-1,N-J}\) kritik değerinden büyük ise boş hipotez terkedilir.
9.2.1.1 Etki büyüklüğü tek-yönlü bağlı olmayan gözlemler varyans analizi
Tanıtımı kolaylaştırmak amaçlı her alt sınıfın eşit sayıda gözlem içerdiğini düşünelim, \(n_1=n_2=\cdots=n_j=n\). Bu durumda A faktörü BKTO \(\sigma^2+n\theta^2_A\) ’dır ve ;
\[\theta^2_A=\sum_{j=1}^{J}\frac{(\mu-\mu_j)^2}{J-1}\].
\(\theta^2_A\) parametresinin tahmini olan \(\hat\theta^2_A\), \(\frac{MS_A-MS_{S/A}}{n}\) ile ve \(\sigma_{S/A}^2\) parametresinin tahmini olan \(\hat\sigma_{S/A}\), \(MS_{S/A}\) ile hesaplanır.
8.1.4 bölümünde değinildiği gibi, aritmetik ortalamalar arasındaki farkın büyüklüğünü yorumlamak adına etki büyüklüğü hesaplaması yapılabilir. Günümüzde varyans çözümlemesi kullanmış çoğu bilimsel makalede etki büyüklüğü de raporlanmıştır. Bu etki büyüklükleri arasında omega-kare (\(\hat\omega^2\)), eta-kare (\(\hat\eta^2\)) ve \(f\) en çok raporlananlar arasındadır.
9.2.1.1.1 Omega-kare
Omega-kare faktör tarafından açıklanan varyansın toplam varyansa oranını tahmin etmek için türetilmiştir. \(\hat\omega^2=\frac{(J-1)\hat\theta^2/J}{((J-1)\hat\theta^2/J)+\hat\sigma^2_{S/A})}\)
Omega-kare 0.01 ise küçük, 0.06 ise orta ve 0.14 ise büyük etki olarak yorumlanır Myers et al. (2013).
9.2.1.1.2 Eta-kare
Eta-kare de , \(\hat\eta^2=\frac{SS_A}{SS_{Total}}\), faktör tarafından açıklanan varyansın toplam varyansa oranını tahmin etmek için türetilmiştir.
Aynı çözümleme için, \(\hat\eta^2\) , \(\hat\omega^2\) ’den büyüktür , çünkü \(\hat\eta^2\), özellikle n küçük ise, pozitif yönde yanlı bir tahmindir. Buna rağmen \(\hat\eta^2\) bildiğimiz kadarı ile en çok raporlanan etki büyüklüğüdür. \(\hat\eta^2\), regresyon çözümlemesi çerçevesinde \(R^2\) olarak da raporlanır.
9.2.1.1.3 Etki büyüklüğü f
Cohen’in f katsayısı, \(f=\frac{\hat\theta_A}{\hat\sigma_{S/A}}\) ile hesaplanır. Bir f değeri 0.10 ise küçük, 0.25 ise orta, 0.40 ise büyük etki olarak yorumlanır.
9.2.1.1.4 Etki büyüklüğü hesaplamaları üzerine
Yukarıda verilen örneklerde tanıtımı kolaylaştırmak adına her bir alt sınıfta yer alan gözlem sayısı eşit kabul edilmiştir. Fakat pratikte alt sınıfların katılımcı sayısı genellikle eşit değildir. Aynı zamanda genellikle faktör sayısı birden fazladır. Bunlara ilave olarak, tasarı içerisinde faktörlerin manipüle edilmiş olması veya ölçülmüş (measured) olması etki büyüklüğü hesaplarını etkiler. Manipule edilen faktörler için rassal (random) ölçülen faktörler için sabit (fixed) faktör isimlendirilmesi de yaygındır. Örneğin TCA puanları rasgele seçilen 10 ilde yaşayan erkek ve kadınlar için hesaplansın. İk faktörlü bu tasarıda iller manipüle edlien faktör, cinsiyet ise ölçülen faktördür.
ezANOVA fonksiyonu (Lawrence (2016)) Bakeman (2005) tarafından bir araya getirilen genelleştirilmiş eta-kare (generalized eta-squared) formüllerini kullanarak etki büyüklüğü hesaplar. Bakeman (2005) çalışmasında Olejnik and Algina (2003) tarafından tanımlanan genelleştirilmiş eta kareyi kullanır. Etki büyüklüğünü _R paketi ezANOVA fonksiyonu ile hesaplamak isteyen kullanıcılar observed argümanını incelemeli ve ölçülmüş faktörleri bu argüman ile belirtmelidir. Etki büyüklüğünü R paketleri yerine kod yazarak hesaplamak isteyen araştırmacılar Olejnik and Algina (2003) tarafından verilen formülleri kullanabilir.
9.2.1.2 Alt sınıf ortalamalarının kıyaslanması (Testing specific contrasts)
Varyans analizi sonrasında veya varyans analizi yerine, ortalamalar ile oluşturulmuş farklı kıyaslamalar test edilebilir. Bu çerçevede kıyas, ağırlıklandırılmış aritmetik ortalamaların toplamdır ve ağırlıkların toplamı sıfırdır. İki sınıf kıyas vardır, ikili kıyaslar var karmaşık kıyaslar. Konuyu tanıtım amaşlı, tek faktörün olduğu bir tasarı düşünelim. Bu tasarıda faktöre ait 3 alt sınıf olsun, bir kontrol grubu ve iki farklı müdahele grubu, \(\mu_1\), \(\mu_2\), ve \(\mu_3\). İkili kıyaslama da bir alt grubun ağırlığı -1, diğer bir alt sınıfın ağırlığı -1 ve üçüncü alt sınıfın 0 olur. Örneğin müdahele gruplarının bir biri ile kıyaslanması için \((0)\mu_1+(1)\mu_2+(-1)\mu_3\) kullanılabilir. Kontrol grubunun diğer iki müdahele grubunun ortalaması ile kıyaslanması karmaşık kıyaslamaya örnektir ve \((-1) \mu_1+(.5)\mu_2+(.5)\mu_3\) kullanılabilir. Ortalamar arasında fark yoktur boş hipotezini test etmek için;
\[t=\frac{\sum_{j=1}^J(w_j\bar{Y})}{\sqrt{MS_{S/A}\sum_{j=1}^J(\frac{w_j^2}{n_j})}}\]
9.2.1.3 Bütün ikili kıyaslamaların test edilmesi
Bütün ikili kıyaslamaların yapılabileceği bir kaç farklı prosedür vardır. Birden çok kıyaslamanın yapılacağı durumlarda birinci tip hata oranı kontrol edilmelidir. Bu kontrol birinci tip hata oranını belirlenen bir değerde (örneğin .05) veya daha altında tutmak demektir. En çok kullanılan kontrol yöntemlerinden ikisi (a) kıyaslama bazında (per comparison) hata oranı ve (b) ortak hata oranıdır (familywise). Kıyaslama bazında kritik değer olarak \(\pm t_{(1-\alpha⁄2),N-J}\) kullanıldığında birinci tip hata oranı \(\alpha\)’dır. Ortak hata oranı en az bir kıyaslama için birinci tip hata yapılma oranıdır. Eğer bütün ikili kıyaslamalar sıfıra eşitse, ortak hata oranı \(\alpha\) ve \([J(J-1)⁄2]\alpha\) arasındadır. Örneğin 3 alt sınıfı olan bir faktör için yapılacak tüm ikili karşılaştırmalarda birinci tip hata üst limiti \(3\alpha\) ’dır. Ortak hata oranını kontrol etmek için birden fazla prosedür vardır. Bu prosdürlerin R ile tamamlanması oldukça kolaydır ve ilerleyen bölümlerde gösterimi yapılmıştır.
9.2.1.3.1 Trend analizleri
Eklenecek
9.2.1.4 Varsayımlar: tek-yönlü bağlı olmayan gözlemler varyans analizi
Tek-yönlü bağlı olmayan gözlemler varyans analizi varsayımları bağlı olmayan gruplar t testi varsayımları ile benzerdir.
Yanıtların bağımsızlığı (independence) her alt sınıfta yer alan puanlar birbirinden bağımsız olmalıdır. Yanıtların bağımsızlığını tehdit eden durumlardan biri aynı grup içeresinde yer alan bireylerin birbirlerinin yanıtlarını etkilemesidir. Eğer bir alt sınıfın içerisinde yanıtların bağımsılığını etkileyen gruplaşmalar varsa çözümleme yöntemi değiştirilmelidir. Örneğin çalışma kapsamında ulaşılan katılımcılar sınıf okul şirket gibi kümelerin içerisinde yer alıyor ve bu kümelere müdahil olmak katılımcıların yanıtlarını etkiliyor ise çok düzeyli modeller kullanılabilir. Eğer katılımcılar bir kümeden etkilenmiyorsa fakat faktöre ait alt sınıflar eşleme (matching) yöntemi ile oluşturulmuşsa oluşan bu bağlılığı göz önünde bulundurmak için rassal blok varyans analizi kullanılabilir.
Normallik. Her alt sınıfa ait puanların normal bir dağılımdan geldiği varsayılır. Eğer dağılımların uzun kuyrukları var ise muhtemelen istatistiksel güç azalacaktır. Eğer alt sınıflara ait gözlem sayısı eşit ise normal dağılımdan kopmalar birinci tip hata oranını büyük ölçüde değiştirmez. Bu durum normallikten büyük çapta kopmalar ve küçük örneklem sayıları için geçerli değildir.
Eş varyanslılık: Varyans homojenliği olarak da bilinir. J farklı alt sınıfa ait puanların J farklı evrenden geldiğini fakat J farklı evrenin eşit varyansa sahip olduğu varsayımıdır. Alt sınıflara ait gözlem sayısı eşit ve yeterince büyük değil ise, bu varsayımın ihlali birinci tip hata oranını etkiler. Bu varsayımlar sadece özet olarak değinilmiştir. Eğer yanıtların bağımsızlığı zedelenmedi ise, her alt sınıfta eşit sayıda ve en az 20 gözlem var ise ve puanların daağılımı yaklaşık olarak normal ise varyans analizi sonuçları geçerlidir. Diğer durumlarda alternatif analizler kullanılmalıdır. Eğer dirençli analizler ve geleneksel varyans analizi bütün testler için aynı sonuçları veriyorsa geleneksel analizlerin rapor edilmesi araştırmacılar arası iletişimi kolaylaştırmak adına tercih edilebilir.Varyans analizi çerçevesinde dirençli analiz yöntemleri Wilcox (2012) tarafından detaylı olarak ele alınmıştır.
9.2.1.5 R betiği: tek-yönlü bağlı olmayan gözlemler varyans analizi
Gösterim amaçlı, dataWBT’den (2.3) Kocaeli ilinde yaşayan katılımcılar seçilmiştir. TCA puanları bağımsız değişkeni, eğitim durumu 7 alt sınıflı faktörü oluşturur. Bu alt sınıflar diplomasız, ilkokul, ortaokul, lise, meslek lisesi, önlisans ve lisanstır. Fakat diplomasız katılımcı sadece bir kişi olduğu için bu katılımcı ilkokul alt sınıfına aktarılmıştır.9
Basamak 1: Veri setini hazırla ve betimsel istatistikleri rapor et
# csv yükle
urlfile='https://raw.githubusercontent.com/burakaydin/materyaller/gh-pages/ARPASS/dataWBT.csv'
dataWBT=read.csv(urlfile)
# URL sil
rm(urlfile)
#Kocaeli'yi seç
# sıralı silme uygula (listwise deletion)
dataWBT_KOCAELI=na.omit(dataWBT[dataWBT$city=="KOCAELI",
c("id","gen_att","education")])
#diplomasız katılımcıyı ilkokul alt sınıfına al
library(car)
dataWBT_KOCAELI$eduNEW <- recode(dataWBT_KOCAELI$education,
"'None'='Primary School (5 years)'")
#kozmetik, faktör etiketini kısalt
dataWBT_KOCAELI$eduNEW <- recode(dataWBT_KOCAELI$eduNEW,
"'High School (Lycee)'=
'High School (Lycee) (4 years)'")
dataWBT_KOCAELI$eduNEW <- recode(dataWBT_KOCAELI$eduNEW,
"'Vocational School'=
'Vocational High School (4 years)'")
# faktör alt sınıflarını görmek için
#table(dataWBT_KOCAELI$eduNEW)
##kozmetik, alt sınıfları sırala
#levels(dataWBT_KOCAELI$eduNEW)
dataWBT_KOCAELI$eduNEW = factor(dataWBT_KOCAELI$eduNEW,
levels(dataWBT_KOCAELI$eduNEW)[c(4,3,1,6,2,5)])
# hangi katılımcı diplomasız
#which(dataWBT_KOCAELI$education=="None")
#boş alt sınıfları kaldır
dataWBT_KOCAELI$eduNEW=droplevels(dataWBT_KOCAELI$eduNEW)
#betimsel
library(psych)
desc1BW=data.frame(with(dataWBT_KOCAELI,
describeBy(gen_att, eduNEW,mat=T,digits = 2)),
row.names=NULL)
#istenilenleri seç
# Table 1
desc1BW[,c(2,4,5,6,7,13,14)]
## group1 n mean sd median skew kurtosis
## 1 Primary School (5 years) 70 2.11 0.41 2.2 -0.19 0.81
## 2 Junior High/ Middle School (8 years) 94 2.08 0.52 2.1 -0.35 -0.37
## 3 High School (Lycee) (4 years) 158 1.84 0.58 2.0 0.29 0.64
## 4 Vocational High School (4 years) 74 2.04 0.50 2.0 -0.14 0.41
## 5 Higher education of 2 years 112 1.80 0.53 1.8 0.28 -0.36
## 6 University - Undergraduate degree 62 1.78 0.53 1.8 0.06 -0.63
# kaydet
#write.csv(desc1BW,file="onewayB_ANOVA_desc.csv")
#write.csv2(desc1BW,file="onewayB_ANOVA_desc.csv")Basamak 2 : Varsayım kontrolü
require(ggplot2)
ggplot(dataWBT_KOCAELI, aes(x = gen_att)) +
geom_histogram(aes(y = ..density..),col="black",binwidth = 0.2,alpha=0.7) +
geom_density(size=1.5) +
theme_bw()+labs(x = "Kocaeli Diploma ve TCA")+ facet_wrap(~ eduNEW)+
theme(axis.text=element_text(size=14),
axis.title=element_text(size=14,face="bold"))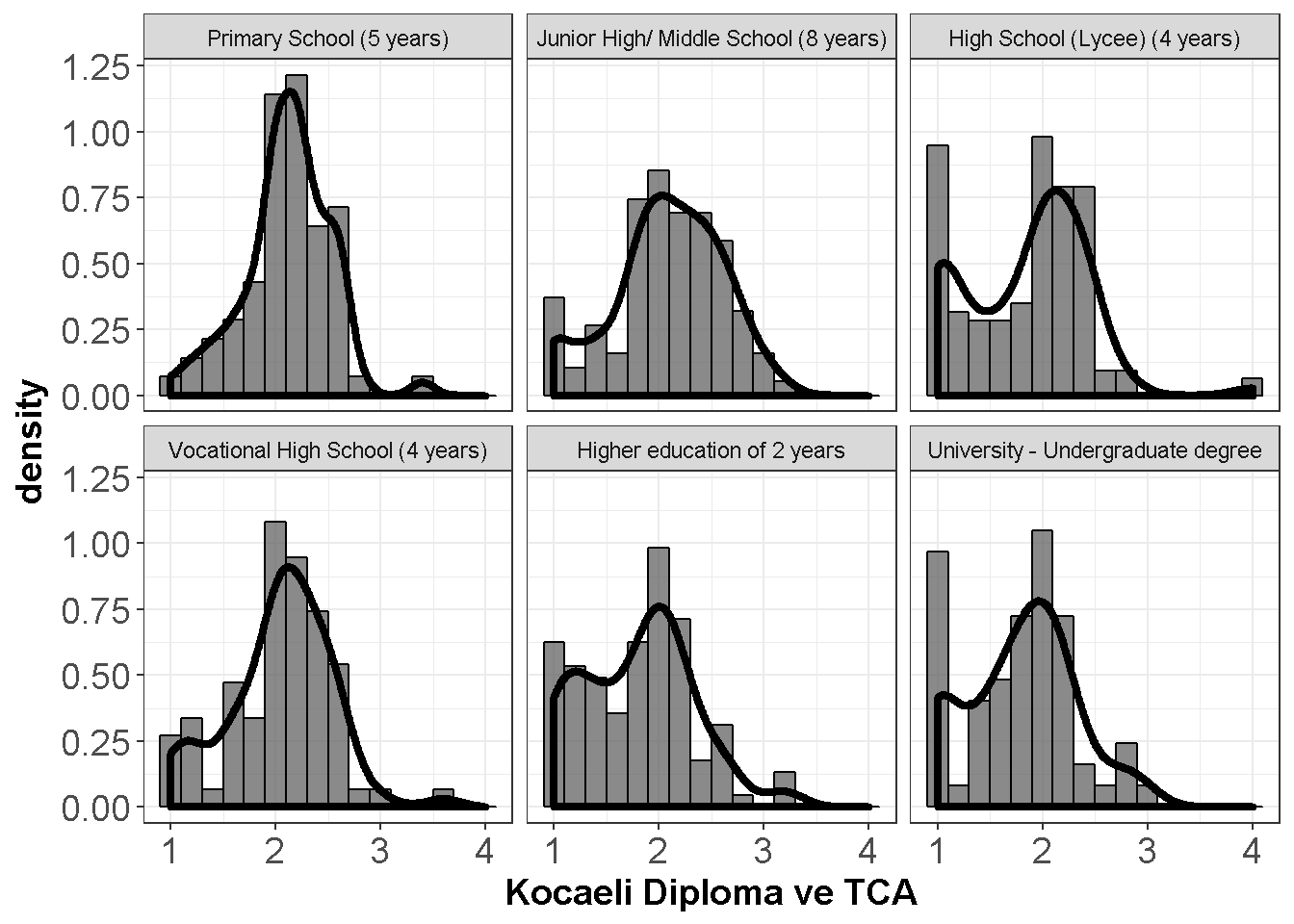
Figure 9.1: Diploma ve TCA
Normallikten kopmalar büyük ölçüde değil.
require(ggplot2)
ggplot(dataWBT_KOCAELI, aes(eduNEW,gen_att)) +
geom_boxplot() +
labs(x = "Education",y="Kocaeli Diploma ve TCA")+coord_flip()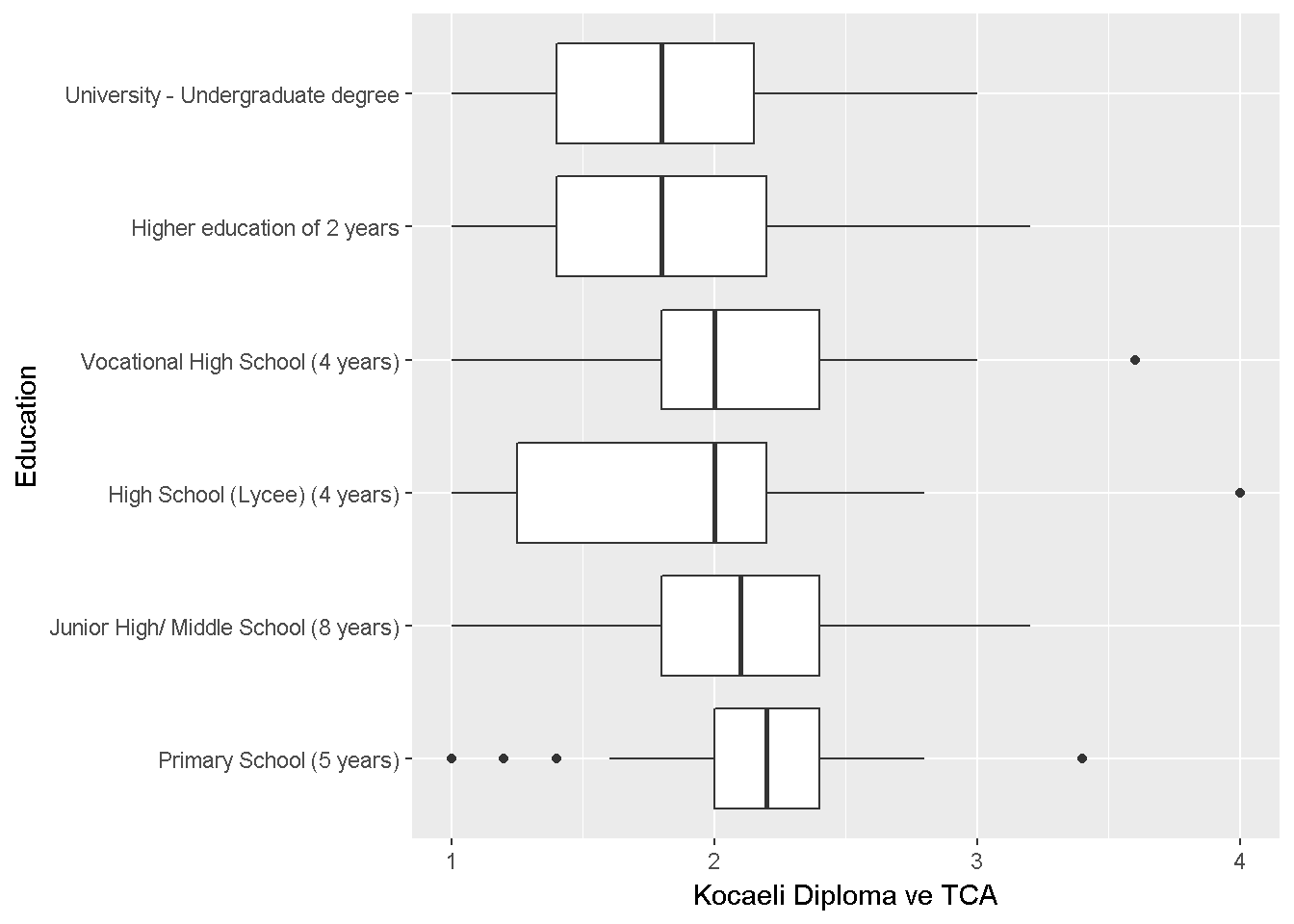
Figure 9.2: Diploma ve TCA
Varyans homojenliği sorgulanabilir fakat büyük çaplı bir farklılık yok.
Basamak 3 : varyans analizi
Gösterimin kolaylığı açısından varsayımların ihlal edilmediğini düşünelim. ezANOVA fonksiyonu (Lawrence (2016)) F testini, levene testini ve etki büyüklüğünü rapor eder. Etki büyüklüğü hesabı modele göre değişir ( Tablo 1 Bakeman (2005) veya Olejnik and Algina (2003)). Bu örnekte, Levene testi alt gruplar için varyanslar eşittir boş hipotezinin terkedilmesini destekliyor.
#ez kütüphanesini aktif hale getir
library(ez)
#katılımcı kimliğini belirten id değişkeni faktör olmazsa uyarı verir
dataWBT_KOCAELI$id=as.factor(dataWBT_KOCAELI$id)
# kozmetik, virgülden sonra kaç rakam gösterilsin?
options(digits = 3)
#birinci yol, ezANOVA fonksiyonu
alternative1 = ezANOVA(
data = dataWBT_KOCAELI,
wid=id, dv = gen_att, between = eduNEW,observed=eduNEW)
## Warning: Data is unbalanced (unequal N per group). Make sure you specified
## a well-considered value for the type argument to ezANOVA().
alternative1
## $ANOVA
## Effect DFn DFd F p p<.05 ges
## 1 eduNEW 5 564 7.27 1.31e-06 * 0.0605
##
## $`Levene's Test for Homogeneity of Variance`
## DFn DFd SSn SSd F p p<.05
## 1 5 564 1.35 63.5 2.4 0.0361 *
# kritik F değeri
qf(.95,5,564)
## [1] 2.23
ez fonksiyonu uyarısı hakkında;
#Warning: Data is unbalanced (unequal N per group). Make sure you specified
#a well-considered value for the type argument to ezANOVA().
bu fonksiyon toplam kareleri 3 farklı şekilde hesaplayabilir.
Tek yönlü varyans analizinde her 3 yöntem de aynı sonucu verir.
Dolayısıyla bu uyarı göz ardı edilebilir.R Core Team (2016b) paketinde yer alan lm fonksiyonu ile aynı sonuçlar elde edilebilir.
# ikinci yol, lm fonksiyonu
alternative2=lm(gen_att~eduNEW,data=dataWBT_KOCAELI)
#Tablo 2
anova(alternative2)
## Analysis of Variance Table
##
## Response: gen_att
## Df Sum Sq Mean Sq F value Pr(>F)
## eduNEW 5 10.13 2.02610 7.2676 1.306e-06 ***
## Residuals 564 157.24 0.27879
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1R Core Team (2016b) paketinde yer alan aov fonksiyonu da kullanılabilir.
#üçüncü yol, aov fonksiyonu
alternative3=aov(gen_att~eduNEW,data=dataWBT_KOCAELI)
summary(alternative3)
## Df Sum Sq Mean Sq F value Pr(>F)
## eduNEW 5 10.13 2.0261 7.268 1.31e-06 ***
## Residuals 564 157.24 0.2788
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1pairwise.t.test fonksiyonu ikili kıyaslama için oldukça kullanışlıdır. Hangi ortak hata kontrol prosedürünü kullanacağınızı belirledikten sonra p.adjust.method argümanını kullanabilirsiniz. Örneğin p.adjust.method =“Holm” ile Holm (1979) tarafından verilen prosedür uygulanabilir. Toplamda 6 farklı prosedür seçilebilir, detaylar için inceleyiniz; ?p.adjust
# ikili kıyaslamalar
# Tablo 3
with(dataWBT_KOCAELI, pairwise.t.test(gen_att,eduNEW,p.adjust.method ="holm"))
##
## Pairwise comparisons using t tests with pooled SD
##
## data: gen_att and eduNEW
##
## Primary School (5 years)
## Junior High/ Middle School (8 years) 1.0000
## High School (Lycee) (4 years) 0.0040
## Vocational High School (4 years) 1.0000
## Higher education of 2 years 0.0014
## University - Undergraduate degree 0.0043
## Junior High/ Middle School (8 years)
## Junior High/ Middle School (8 years) -
## High School (Lycee) (4 years) 0.0046
## Vocational High School (4 years) 1.0000
## Higher education of 2 years 0.0017
## University - Undergraduate degree 0.0057
## High School (Lycee) (4 years)
## Junior High/ Middle School (8 years) -
## High School (Lycee) (4 years) -
## Vocational High School (4 years) 0.0435
## Higher education of 2 years 1.0000
## University - Undergraduate degree 1.0000
## Vocational High School (4 years)
## Junior High/ Middle School (8 years) -
## High School (Lycee) (4 years) -
## Vocational High School (4 years) -
## Higher education of 2 years 0.0176
## University - Undergraduate degree 0.0357
## Higher education of 2 years
## Junior High/ Middle School (8 years) -
## High School (Lycee) (4 years) -
## Vocational High School (4 years) -
## Higher education of 2 years -
## University - Undergraduate degree 1.0000
##
## P value adjustment method: holm9.2.1.6 Dirençli tahminleme yöntemi: tek-yönlü bağlı olmayan gözlemler varyans analizi
Wilcox (2012) tarafından bir araya toplanan dirençli prosedürlerden bir tanesi Mair and Wilcox (2016) paketi ile kullanılabilecek t1way fonksiyonu ile tamamlanabilir. Kırpılmış ortalamalar için farklı-varyanslı(heteroscedastic) ve tek yönlü ANOVA yöntemini kullanan bu fonksiyonun detayları için inceleyiniz ;?t1way
library(WRS2)
#t1way
# 20% kırpılmış
t1way(gen_att~eduNEW,data=dataWBT_KOCAELI,tr=.2,nboot=5000)
## Call:
## t1way(formula = gen_att ~ eduNEW, data = dataWBT_KOCAELI, tr = 0.2,
## nboot = 5000)
##
## Test statistic: 7.5658
## Degrees of Freedom 1: 5
## Degrees of Freedom 2: 143.78
## p-value: 0
##
## Explanatory measure of effect size: 0.29
# 10% kırpılmış
t1way(gen_att~eduNEW,data=dataWBT_KOCAELI,tr=.1,nboot=5000)
## Call:
## t1way(formula = gen_att ~ eduNEW, data = dataWBT_KOCAELI, tr = 0.1,
## nboot = 5000)
##
## Test statistic: 9.5355
## Degrees of Freedom 1: 5
## Degrees of Freedom 2: 187.52
## p-value: 0
##
## Explanatory measure of effect size: 0.3
# 5% kırpılmış
t1way(gen_att~eduNEW,data=dataWBT_KOCAELI,tr=.05,nboot=5000)
## Call:
## t1way(formula = gen_att ~ eduNEW, data = dataWBT_KOCAELI, tr = 0.05,
## nboot = 5000)
##
## Test statistic: 9.415
## Degrees of Freedom 1: 5
## Degrees of Freedom 2: 211.55
## p-value: 0
##
## Explanatory measure of effect size: 0.31
## heteroscedastic ikili kıyaslamalar
#alt sınıfların sıralanışı
lincon(gen_att~eduNEW,data=dataWBT_KOCAELI,tr=.1)[[2]]
## [1] "Higher education of 2 years"
## [2] "Junior High/ Middle School (8 years)"
## [3] "University - Undergraduate degree"
## [4] "Vocational High School (4 years)"
## [5] "High School (Lycee) (4 years)"
## [6] "Primary School (5 years)"
#ikili kıyaslamalar
round(lincon(gen_att~eduNEW,data=dataWBT_KOCAELI,tr=.1)[[1]][,c(1,2,6)],3)
## Group Group p.value
## [1,] 1 2 0.701
## [2,] 1 3 0.000
## [3,] 1 4 0.360
## [4,] 1 5 0.000
## [5,] 1 6 0.000
## [6,] 2 3 0.000
## [7,] 2 4 0.597
## [8,] 2 5 0.000
## [9,] 2 6 0.000
## [10,] 3 4 0.004
## [11,] 3 5 0.460
## [12,] 3 6 0.467
## [13,] 4 5 0.001
## [14,] 4 6 0.003
## [15,] 5 6 0.9119.2.1.7 Örnek rapor: tek-yönlü bağlı olmayan gözlemler varyans analizi
Gösterim amaçlı seçtiğimiz dataWBT alt kümesi ile (Kocaeli şehri) tamamlanan geleneksel ANOVA ve dirençli ANOVA , aynı zamanda ikili karşılaştırma testleri aynı sonuçları vermiştir. Varsayımların ihlalleri büyük çapta olmadığı için bu sonuçlar şaşırtıcı değildir. Bu gibi geleneksel ve dirençli yöntemlerin bütün hipotez testleri için aynı karara götürdüğü durumlarda, geleneksel yöntemlerin raporlanması tercih edilebilir.
TCA puanlarının eğitim durumuna göre değişip değişmediğini test etmek amaçlı varyans çözümlemesi yapılmıştır. Tablo 1 ile bütün eğitim durumları için aritmetik ortalama, standart sapma, örenklem çarpıklığı ve örneklem basıklığı değerleri verilmiştir. Varyans analizi eğitim durumunun TCA puanları üzerinde etkisi olduğu hipotezini desteklemiştir, F(5,564) = 7.27, p < .001, \(\hat\eta^2_G=.06\). Bu analizler için ANOVA tablosu Tablo 2 ile verilmiştir. İkili kıyaslamalar ortak hata oranını Holm (1979) tarafından verilen prosedüre uygun olarak tamamlanmış sonuçlar Tablo 3 ile verilmiştir. 15 farklı ikili kıyaslamada, ortalamaların farkı 9 kıyaslama için istatistiksel olarak anlamlı bulunmuştur (tespit edilen farklılıklar detaylı olarak açıklanabilir.) Model varsayımları kontrol edilmiş, büyük çaplı bir ihlal tespit edilmemiş olmasına rağmen dirençli yöntemlerden kırpılmış ortalamalar için farklı-varyanslı ANOVA (Mair and Wilcox (2016)) prosedürü ile sonuçlar karşılaştırılmış ve bir farklılık olmadığı görülmüştür.
9.2.1.8 Kayıp data teknikleri: tek-yönlü bağlı olmayan gözlemler varyans analizi
To be added
9.2.1.9 İstatistiksel güç hesapları: tek-yönlü bağlı olmayan gözlemler varyans analizi
To be added
9.2.2 İki faktörlü bağlı olmayan gözlemler varyans analizi
Bu başlık altında iki bağlı olmayan faktörlü varyans analizi ele alınmıştır. Faktörlerden ilki J alt sınıfa sahip A faktörü, ikincisi K alt sınıfa sahip B faktörü olarak düşünülmüştür. Bu durumda JK farklı alt sınıf kombinasyonu oluşur. Her bir gözlemin bir ve yalnız bir alt sınıf kombinasyonunda yer alması ve alt sınıfların bir birine eşlenmesi söz konusu olmadığından, bu tasarı bağlı olmayan gözlemler varyans çözümlemesine uygundur.En bait halinde, her iki faktör sadece 2 alt sınıfa sahiptir. Örneğin TCA puanlarına ait varyans cinsiyet ve yüksek öğretim durumuna göre çözümlenirse aşağıda yer alan tablo oluşur.
| Lise ve altı | Yüksek öğretim | ||
|---|---|---|---|
| Kadın | \(\mu_{11}\) | \(\mu_{12}\) | \(\mu_{1\cdot}\) |
| Erkek | \(\mu_{21}\) | \(\mu_{22}\) | \(\mu_{2\cdot}\) |
| \(\mu_{\cdot 1}\) | \(\mu_{\cdot 2}\) |
Bu tasarıda hipotez testlerinde kullanılan artitmetik ortalamar \(\mu_{11}, \mu_{12}, \mu_{21},\mu_{22}\), satır ortalamaları \(\mu_{1 \cdot}\), \(\mu_{2 \cdot}\) ve sütun ortalamaları \(\mu_{\cdot 1}\), \(\mu_{\cdot 2}\) parametreleri ile gösterilmiştir. Satır veya sütun ortalamalarının genel adı marjinal ortalamadır (kenar veya köşe ortalamarı da denilebilir).
Faktörler arasında etkileşim (interaction) olup olmadığına yönelik kurulacak boş hipotez \(H_0: \mu_{11} - \mu_{12} = \mu_{21} - \mu_{22}\). Bu etkileşim aynı zamanda iki basit etkinin de karşılaştırılmasıdır, \((\mu_{21}−\mu_{11}\) ve \(\mu_{22} − \mu_{12})\) ve \(H_0: \mu_{21}−\mu_{11}= \mu_{22}- \mu_{12}\) boş hipotezi ile de gösterileblir. Bu boş hipotezlerden biri doğru ise diğeri de doğru, biri yanlış ise diğeri de yanlıştır.
Etkileşim Bu tasarıda ilk test edilen hipotez etkilesşim hipotezidir. Fakat etkileşimi tanımlamadan önce basit etkileri tanımlamak gerekir. Basit etki tek bir satırda veya tek bir sütunda yer alan ortalamarın farkıdır. Kullandığımız örnekte iki çeşit basit etki vardır, cinsiyetin basit etkisi ve yüksek öğretim durmunun basit etkisi. Her bir basit etkinin de iki çeşidi vardır; cinsiyetin yüksek öğretimliler üzerine basit etkisi (\(\mu_{12}\) ve \(\mu_{22}\)), cinsiyetin yüksek öğretim mezunu olmayanlar üzerine etkisi (\(\mu_{11}\) ve \(\mu_{21}\)). Yüksek öğretimin kadınlar üzerine etkisi (\(\mu_{11}\) ve \(\mu_{12}\)) ve yüksek öğretimin erkekler üzerine etkisi (\(\mu_{21}\) versus \(\mu_{22}\)).
Asıl etkiler marjinal ortalamar ile tanımlanan etkilerdir. Cinsiyetin asıl etkisi \(\mu_{1\cdot} - \mu_{2\cdot}\) şeklinde gösterilir ve \(H_0:\mu_{1\cdot} - \mu_{2\cdot} = 0\) boş hipotezi üzerinden test edilir. Yüksek öğretim etkisi de \(H_0:\mu_{\cdot 1} - \mu_{\cdot 2} = 0\) boş hipotezi üzerinden test edilir.
Etkileşim istatistiksel olarak anlamlı olduğunda:
- Eğer basit etkilerin yönü aynı değil ise asıl etkiyi yorumlamak yanıltıcı olur.
- Eğer basit etkilerin yönü aynı ise asıl etkiyi yorumlamanın yanıltıcı olup olmadığına araştırmacı karar verir.
Etkileşim istatistiksel olarak anlamlı ve asıl etkileri yorumlamak yanıltıcı ise araştırmacı hücre bazında aritmetik ortalamaları yorumlamalıdır.
Eşitlik İki bağlı olmayan faktör varyans analizi için çözümleme modeli \(Y_{ijk}=\mu+\alpha_{j}+\beta_k + \alpha\beta_{jk}+ \epsilon_{ij}\), olarak verilebilir. \(Y_{ijk}\) birinci faktörün j alt sınıfı, ikinci faktörün k alt sınıfında yer alan i katılımcısının puanını; \(\mu\) genel ortalamayı; \(\alpha_j\) ilk faktöre ait j alt sınıfının etkisini; \(\beta_k\) ikinci faktöre ait k alt sınıfının etkisini; \(\alpha\beta_{jk}\) etkileşimi ve \(\epsilon_{ij}\) hata terimini temsil eder.
| SV | df | F |
|---|---|---|
| A | \(J-1\) | \(\frac{MS_A}{MS_{S/AB}}\) |
| B | \(K-1\) | \(\frac{MS_B}{MS_{S/AB}}\) |
| AB | \((J-1)(K-1)\) | \(\frac{MS_{AB}}{MS_{S/AB}}\) |
| S/AB | \(N-JK\) | |
| Total | \(N-1\) |
9.2.2.1 R betiği: İki faktörlü bağlı olmayan gözlemler varyans analizi
Gösterim amaçlı dataWBTde yer alan Kayseri ili katılımcıları seçilmiştir. TCA puanlarına ait varyans cinsiyet ve yüksek öğretim durumuna göre ayrıştırılmıştır.
Basamak 1 Veriyi hazırla ve betimsel istatistikleri raporla
# CSV yükle
urlfile='https://raw.githubusercontent.com/burakaydin/materyaller/gh-pages/ARPASS/dataWBT.csv'
dataWBT=read.csv(urlfile)
#URL sil
rm(urlfile)
#Kayseri ilini seç
# sıralı silme uygula
dataWBT_Kayseri=na.omit(dataWBT[dataWBT$city=="KAYSERI",c("id","gen_att","higher_ed","gender")])
# Yüksek öğretim etiketlerini değiştir
dataWBT_Kayseri$HEF=droplevels(factor(dataWBT_Kayseri$higher_ed,
levels = c(0,1),
labels = c("non-college", "college")))
#table(dataWBT_Kayseri$gender)
#table(dataWBT_Kayseri$HEF)
#boş alt sınıfları düşür
dataWBT_Kayseri$gender=droplevels(dataWBT_Kayseri$gender)
with(dataWBT_Kayseri,
table(gender,HEF))
## HEF
## gender non-college college
## Female 99 50
## Male 67 36
# kozmetik, virgülden sonra kaç rakam gösterilsin?
options(digits = 3)
#betimsel analizler
library(doBy)
library(moments)
desc2BW=as.matrix(summaryBy(gen_att~HEF+gender, data = dataWBT_Kayseri,
FUN = function(x) { c(n = sum(!is.na(x)),
mean = mean(x,na.rm=T), sdv = sd(x,na.rm=T),
skw=moments::skewness(x,na.rm=T),
krt=moments::kurtosis(x,na.rm=T)) } ))
# Tablo 4
desc2BW
## HEF gender gen_att.n gen_att.mean gen_att.sdv gen_att.skw
## 1 "non-college" "Female" "99" "1.93" "0.424" "-0.548"
## 2 "non-college" "Male" "67" "2.32" "0.419" "-0.191"
## 3 "college" "Female" "50" "1.80" "0.346" " 0.263"
## 4 "college" "Male" "36" "2.13" "0.543" " 0.159"
## gen_att.krt
## 1 "2.51"
## 2 "3.18"
## 3 "1.94"
## 4 "2.25"
#write.csv(desc2BW,file="twowayB_ANOVA_betimsel.csv")Basamak 2: Varsayım kontrolü
require(ggplot2)
ggplot(dataWBT_Kayseri, aes(x = gen_att)) +
geom_histogram(aes(y = ..density..),col="black",binwidth = 0.2,alpha=0.7) +
geom_density(size=1.5) +
theme_bw()+labs(x = "Kayseri Diploma ve TCA")+ facet_wrap(~ HEF+gender)+
theme(axis.text=element_text(size=14),
axis.title=element_text(size=14,face="bold"))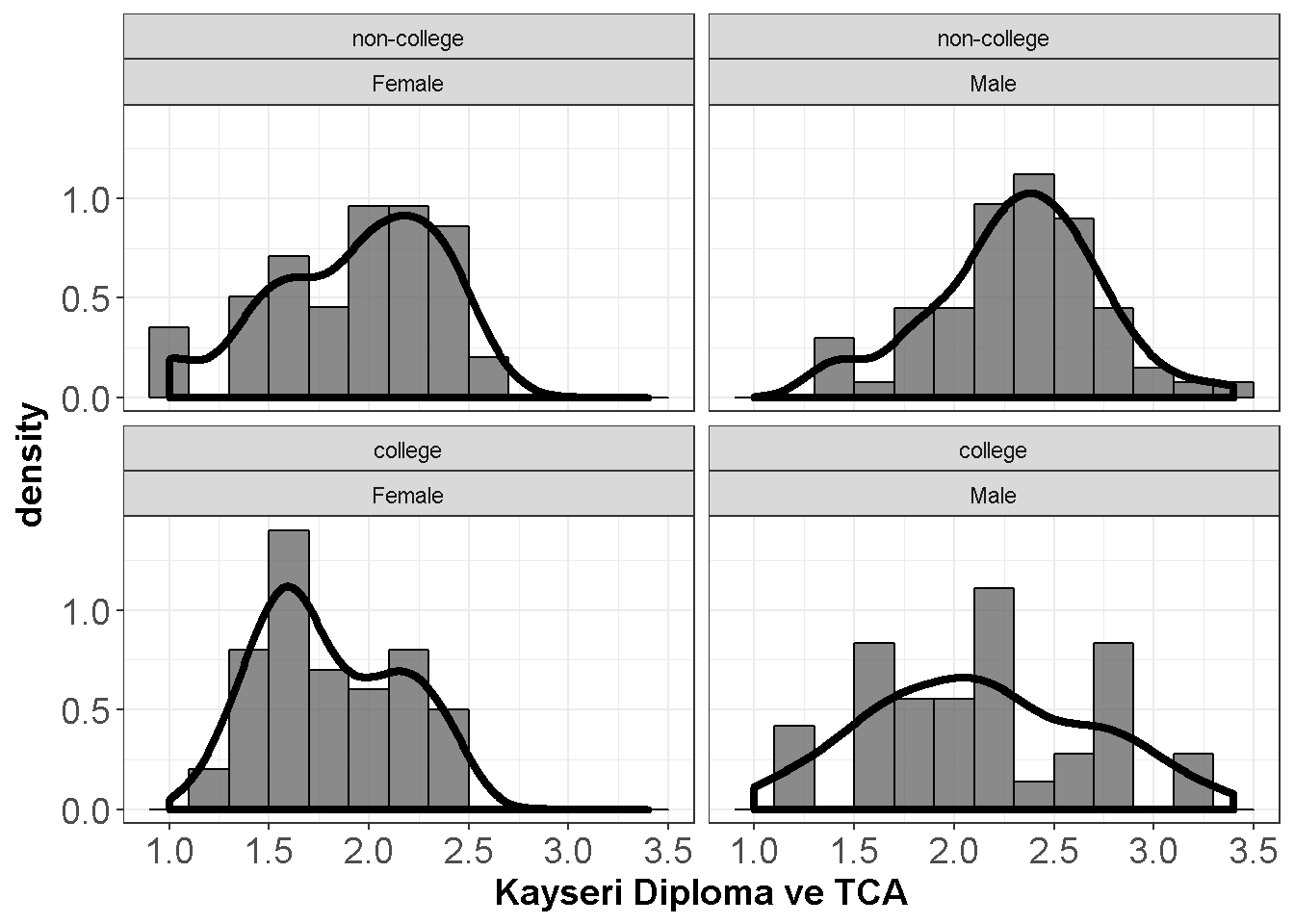
Figure 9.3: Kayseri Diploma ve TCA
Normallikten kopmalar büyük ölçüde değil.
require(ggplot2)
ggplot(dataWBT_Kayseri, aes(x=gender, y=gen_att))+
geom_boxplot()+
facet_grid(.~HEF)+
labs(x = "Gender",y="Kayseri Diploma ve TCA")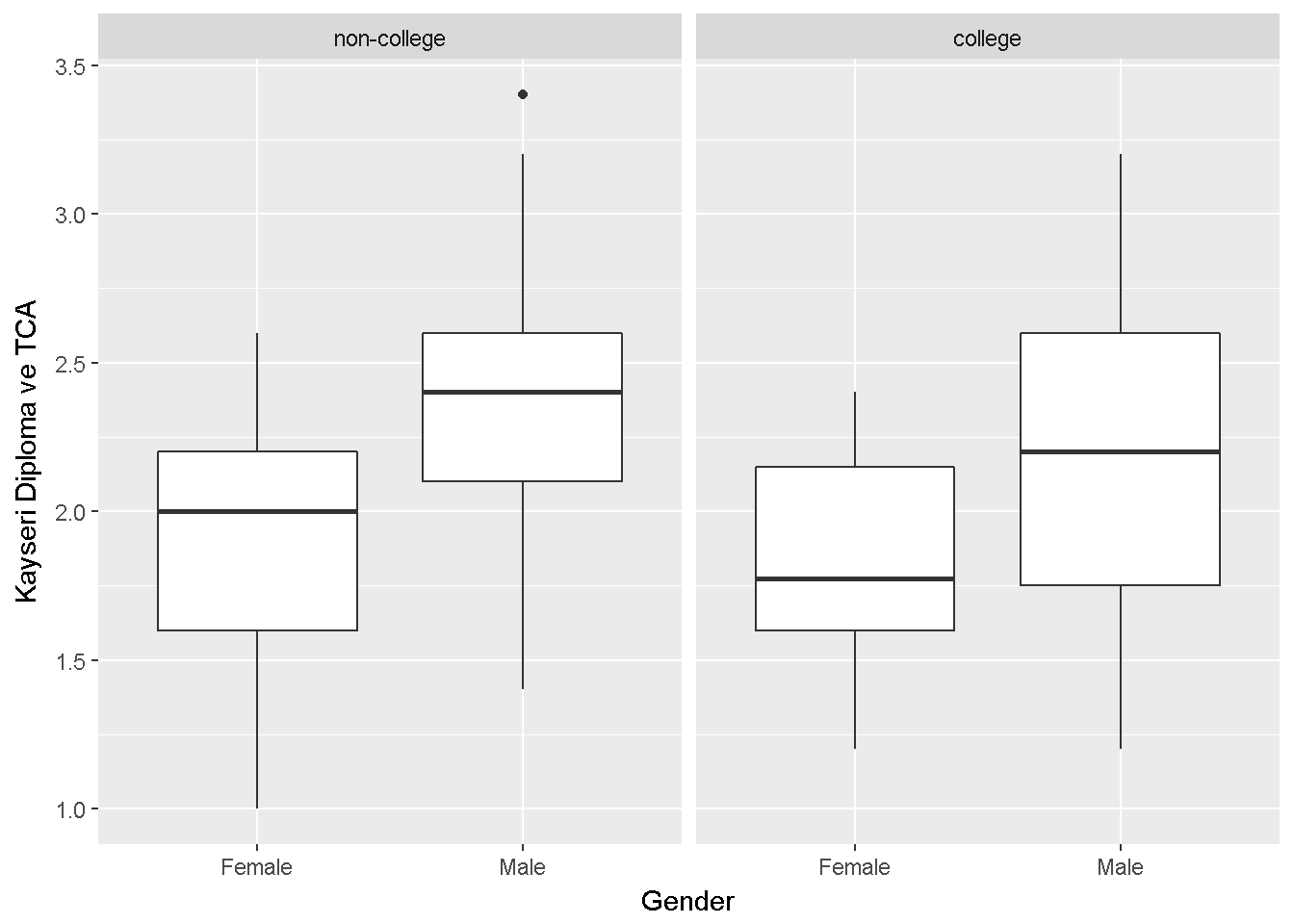
Figure 9.4: Kayseri Diploma ve TCA
Varyanslar benzer görünüyor.
Basamak 3: Varyans analizi
ezANOVA fonksiyonu (Lawrence (2016)) F testini, Levene testini ve etki büyüklüğünü rapor eder. Etki büyüklüğü hesabı kullanılan modele göre (Bakeman (2005) veya Olejnik and Algina (2003)) ve toplam kareler hesaplama yöntemine göre değişir. type argümanı hangi tip toplam kareler hesabı kullanılacağını belirler.
library(ez)
#katılımcı kimliğini belirten id değişkeni faktör olmazsa uyarı verir
dataWBT_Kayseri$id=as.factor(dataWBT_Kayseri$id)
#birinci yol ezANOVA
alternative1 = ezANOVA(
data = dataWBT_Kayseri,
wid=id, dv = gen_att, between = .(HEF,gender),observed=.(HEF,gender),type=2)
## Warning: Data is unbalanced (unequal N per group). Make sure you specified
## a well-considered value for the type argument to ezANOVA().
alternative1
## $ANOVA
## Effect DFn DFd F p p<.05 ges
## 1 HEF 1 248 6.739 9.99e-03 * 0.022436
## 2 gender 1 248 45.389 1.12e-10 * 0.151106
## 3 HEF:gender 1 248 0.251 6.17e-01 0.000837
##
## $`Levene's Test for Homogeneity of Variance`
## DFn DFd SSn SSd F p p<.05
## 1 3 248 0.469 17.5 2.22 0.0867
# Tip III toplam kareler
# alternative1b = ezANOVA(
# data = dataWBT_Kayseri,
# wid=id, dv = gen_att, between = HEF+gender,type=3)
#
# alternative1b
# kritik F değeri
qf(.95,1,248)
## [1] 3.889.2.2.2 Dirençli tahminleme yöntemi: iki-yönlü bağlı olmayan gözlemler varyans analizi
Wilcox (2012) tarafından bir araya toplanan dirençli prosedürlerden bir tanesi Mair and Wilcox (2016) paketi ile kullanılabilecek t2way fonksiyonu ile tamamlanabilir. Kırpılmış ortalamalar için farklı-varyanslı(heteroscedastic) ve iki yönlü ANOVA yöntemini kullanan bu fonksiyonun detayları için inceleyiniz ;?t2way
library(WRS2)
#t2way
# 20% kırpılmış
t2way(gen_att~HEF*gender,data=dataWBT_Kayseri,tr=.2)
## Call:
## t2way(formula = gen_att ~ HEF * gender, data = dataWBT_Kayseri,
## tr = 0.2)
##
## value p.value
## HEF 7.1310 0.011
## gender 20.2039 0.001
## HEF:gender 0.0855 0.772
# 10% kırpılmış
t2way(gen_att~HEF*gender,data=dataWBT_Kayseri,tr=.1)
## Call:
## t2way(formula = gen_att ~ HEF * gender, data = dataWBT_Kayseri,
## tr = 0.1)
##
## value p.value
## HEF 8.4235 0.005
## gender 33.1599 0.001
## HEF:gender 0.0361 0.850
# 5% kırpılmış
t2way(gen_att~HEF*gender,data=dataWBT_Kayseri,tr=.05)
## Call:
## t2way(formula = gen_att ~ HEF * gender, data = dataWBT_Kayseri,
## tr = 0.05)
##
## value p.value
## HEF 6.1688 0.015
## gender 29.8383 0.001
## HEF:gender 0.1642 0.6879.2.2.3 Örnek rapor: iki-yönlü bağlı olmayan gözlemler varyans analizi
Gösterim amaçlı seçtiğimiz dataWBT alt kümesi ile (Kayseri şehri) tamamlanan geleneksel ANOVA ve dirençli ANOVA aynı sonuçları vermiştir. Varsayımların ihlalleri büyük çapta olmadığı için bu sonuçlar şaşırtıcı değildir. Bu gibi geleneksel ve dirençli yöntemlerin aynı karara götürdüğü durumlarda, geleneksel yöntemlerin raporlanması tercih edilebilir.
Tablo 4 Kayseri ilinde yaşayan katılımcılara ait TCA puanlarını cisiyet ve yüksek öğretim faktörlerine göre raporlamıştır. 2x2 varyans analizi sonuçları raporlanmıştır. F testleri alfa=0.05 ile tamamlanmıştır. Cinsiyet etkisi istatistiksel olarak anlamlı bulunmuştur \(F(1,248)=45.39, p<.001\). Yüksek öğretim etkisi anlamlı bulunmuştur, \(F(1,248)=6.24, p=.013\). İki faktör arasında etkileşimin mevcut olduğuna dair kanıt bulunamamıştır,\(F(1,248)=0.25, p=.617\). ezANOVA (Lawrence (2016)) fonksiyonu cinsiyet faktörü için 0.15, yüksek öğretim faktörü için 0.02 genelleştirilmiş eta kare (\(\hat\eta^2_G\)) değeri hesaplamıştır. Tablo 5 ANOVA sonuçlarını bildirir.
9.2.2.4 Takviye çözümlemeler (Follow-ups): iki-yönlü bağlı olmayan gözlemler varyans analizi
To be added.
9.2.2.4.1 İkili kıyaslamalar: iki-yönlü bağlı olmayan gözlemler varyans analizi
To be added.
9.2.2.4.2 Karmaşık kıyaslamalar: iki-yönlü bağlı olmayan gözlemler varyans analizi
To be added.
9.2.2.5 Kayıp veri teknikleri: iki-yönlü bağlı olmayan gözlemler varyans analizi
To be added
9.2.2.6 İstatiksel güç hesapları: iki-yönlü bağlı olmayan gözlemler varyans analizi
To be added
9.3 Bağlı gözlemler varyans analizi
Aynı katılımcıya ait puanlar birden fazla faktör alt sınıfında yer alıyorsa veya aynı katılımcı belirli zaman aralıkları ile tekrar gözlemleniyorsa (repeated measures) bağlı gözlemler varyans çözümlemesi kullanılabilir. Blokların kullanıldığı tasarılarda da kullanılabilir. Bağlı olmayan gözlemler varyans analizi ile karşılaştırıldığında , bu yöntemin varyansın artmasına sebep olabilecek katılımcı farklılıklarını ortadan kaldırabilir. Geride bırakılan bu birey kaynaklı varyans fazlalığı genellikle hatayı azalttığından, istatistiksel gücün artmasını sağlar. Bir diğer ifade ile, örneklem büyüklüğü sabit tutulduğunda, bu yöntem ile farklılıkları tespit edebilme olasılığı daha yüksektir. Bununla beraber bağlı gözlemler her zaman uygun değildir. Örneğin 3 farklı öğretim metodunun karşılaştırılması için aynı birey birden fazla programa müdahil olduğunda, programların etkisi birbirine karışabileceğinden bağlı gözlemler kullanmak uygun değildir.
9.3.1 Tek-yönlü bağlı gözlemler varyans analizi
9.4 Eklemesiz (non-additive) model için eşitlik;
\[\begin{equation} Y_{ij}=\mu + \eta_i + \alpha_j + (\eta \alpha)_{ij} + \epsilon_{ij} \tag{9.1} \end{equation}\]i bireyleri, i=1,…,n; j faktöre ait alt sınıfları, j=1,…,P temsil eder. Y puanları; \(\mu\) genel ortalamayı; \(\eta_i\) bireye ait ortalamanın genel ortalamadan farkını; \(\alpha_j\) j alt sınıfının genel ortalamadan farkını; \((\eta \alpha)_ij\) etkileşimi; ve \(\epsilon_{ij}\) hata terimini temsil eder. \((\eta \alpha)_ij\) ve \(\epsilon_{ij}\) aynı alt indise sahip olduğundan etkileri birbirine karışır. Genellikle ilgi \(\alpha_j\) üzerinedir ve \(H_0: \mu_1 = \mu_2 = \cdots = \mu_P\) boş hipotezi test edilir. Alternatif hipotez, en az bir aritmetik ortalamanın farklı olduğunu belirtir. Tek-yönlü bağlı gözlemler varyans analizi tablosu;
| SV | df | F |
|---|---|---|
| Subjects (S) | \(n-1\) | |
| Waves (A) | \(P-1\) | \(\frac{MS_A}{MS_{SA}}\) |
| SA | \((n-1)(P-1)\) | |
| Total | \(nP-1\) |
Not: Eklemesizlik Eşitlik (9.1) içerisinde yer alan \((\eta \alpha)_ij\) parametresinin 0 olmaması durumudur. Bu gerçekçi bir durumdur, çünkü bu parametrenin sıfır olması faktöre ait alt sınıfın bütün bireyleri eşit şekilde etkilemesi demektir. Tekrarlanan ölçümlerde bireylerin zaman içerisinde tamamen aynı puansal değişimi göstermesi anlamına gelir.
Tablo 9.1 bir deneye ait verileri gösterir. Bu deneyde bireylerin tükettiği alkol dozu artırılmış ve reaksiyon zamanları ölçülmüştür.
| id | Alkolyok | ikioz | dortoz | altioz |
|---|---|---|---|---|
| 1 | 1 | 2 | 5 | 7 |
| 2 | 2 | 3 | 5 | 8 |
| 3 | 2 | 3 | 6 | 8 |
| 4 | 2 | 3 | 6 | 9 |
| 5 | 3 | 4 | 6 | 9 |
| 6 | 3 | 4 | 7 | 10 |
| 7 | 3 | 4 | 7 | 10 |
| 8 | 6 | 5 | 8 | 11 |
Alt sınıflara ait ortalama, standart sapma ve bireye ait ortalama aşağıda verilmiştir. Bireye ait ortalama dört alt sınıfın ortalamasıdır.
# kozmetik virgülden sonraki basamak sayısı
options(digits = 2)
#bireylerin ortalaması
apply(owadata,1, mean)
## [1] 3.2 4.0 4.4 4.8 5.4 6.0 6.2 7.6
#alt sınıfların ortalaması
apply(owadata[,-1],2, mean)
## Alkolyok ikioz dortoz altioz
## 2.8 3.5 6.2 9.0
#alt sınıfların standart sapması
apply(owadata[,-1],2,sd)
## Alkolyok ikioz dortoz altioz
## 1.49 0.93 1.04 1.31Her katılımcının reaksiyon zamanları 4 farklı doz sonrasında da ölçüldüğünden, alkol oranı bağlı gözlem faktörüdür. Her doz alt sınıf çifti için korelasyon hesaplanabilir. Tablo 9.2 ile verilen bu korelasyonlar oldukça yüksektir. Her alt sınıf çifti için kovaryans da hesaplanabilir;
\[Cov_{pp^`}=S_pS_{p^`}r_{pp^`}\] \(p\) ve \(p'\) alkol faktörüne ait iki farklı alt sınıfı temsil eder. İlk iki alt sınıf için korelasyon \(r_{02}=0.93\) kovaryans ise \(Cov_{02}=1.5*0.9*0.93=1.26\) dir.
| Alkolyok | ikioz | dortoz | altioz | |
|---|---|---|---|---|
| Alkolyok | 1.00 | 0.93 | 0.88 | 0.88 |
| ikioz | 0.93 | 1.00 | 0.89 | 0.94 |
| dortoz | 0.88 | 0.89 | 1.00 | 0.95 |
| altioz | 0.88 | 0.94 | 0.95 | 1.00 |
P = bağlı-gözlemler faktörü alt sınıf sayısı, örneğimizde P=4 ;
\(\bar C\) = ortalama kovaryans; örneğimizde \(\bar C\) = 1.26.
F istatistiği
\[F_W=\frac{MS_A}{MS_{SA}}=\frac{MS_A}{MS_{S/A}- \bar C}\] \(MS_A\) ve \(MS_{S/A}\) bağlı olmayan faktör analizinde olduğu gibi hesaplanır. W harfi F test istatistiğinin bağlı gözlemler (within) için hesaplandığını gösterir. Kritik değer \(F_{\alpha,P-1,(P-1)(n-1)}\) ile hesaplanır.
Bağlı olmayan gözlemler için \(F_B=MS_A/MS_{S/A}\) iken bağlı gözlemlerde hesaplanan \(F_W\) korelasyonları dikkate alır.Korelasyon sıfır değil ise aynı veriye uygulandığında \(F_W \geq F_B\) olduğu görülür.
9.4.0.1 Varsayımlar: Tek-yönlü bağlı gözlemler varyans analizi
Küresellik (Sphericity) Kovaryans örüntüsü hakkında bir varsayımdır. Küresellik sağlanırsa her bir tekrarlanan ölçüm çifti farkı için hesaplanan varyans aynıdır.
Örnek kovaryans matrisi;
| \(Y_1\) | \(Y_2\) | \(Y_3\) | |
|---|---|---|---|
| \(Y_1\) | 10 | 7.5 | 10 |
| \(Y_2\) | 7.5 | 15 | 12.5 |
| \(Y_3\) | 10 | 12.5 | 20 |
Küresellik mevcut;
| \(Y_p-Y_{p'}\) | \(\sigma^2_p + \sigma^2_{p'} - 2\sigma_{pp'}\) |
|---|---|
| \(Y_1-Y_2\) | 10+15-2(7.5)=10 |
| \(Y_1-Y_3\) | 10+20-2(10)=10 |
| \(Y_2-Y_3\) | 15+20-2(12.5)=10 |
Box epsilon değeri — küreselliğin ne kadar zedelendiğini ölçer
\[\frac{1}{P-1}\leq \epsilon \leq 1\]
\(\epsilon\) parametresinin tahminlerinden iki tanesi Greenhouse-Geisser (\(\hat \epsilon\)) ve Huynh-Feldtdir (\(\tilde{\epsilon}\)) . \(\tilde{\epsilon}\) 1’den büyük olabilir; bu durumda \(\tilde{\epsilon}\) 1’e eşitlenir.
Küresellik varsayımı ile kritik değer \(F_{alpha,(P-1),(n-1)(P-1)}\).
Küresellik varsayımı ihlal edildi ise yaklaşık kritik değer \(F_{alpha,\epsilon (P-1),\epsilon (n-1)(P-1)}\).
hataların normal dağılımı Eşitlik (9.1) içerisinde \(\epsilon_{ij}\) ile temsil edilen hataların ortalaması sıfır olan bir normal dağılımdan geldiği varsayılır.
\(\eta_i\) normal dağılımı Eşitlik (9.1) içerisinde \(\eta_i\) ile temsil edilen değerlerin ortalaması sıfır olan bir normal dağılımdan geldiği varsayılır.
Listelenen bu varsayımlar, tekrarlanan ölçümlerin çokdeğişkenli normal dağılımdan (multivariate normal distribution) geldiği anlamındadır.
9.4.0.1.1 Eklemesizlik ve Küresellik arasındaki ilişki
Varasyımlar \(\eta_{i}\) ve \(\epsilon_{ij}\) üzerinden tanımlanabilse dahi daha basit bir varsayım tanımı verilerin çokdeğişkenli normal dağılımdan gelmesi ve küreselliği sağlaması olarak da yapılabilir. Eğer çokdeğişkenli normal dağılım varsayımı gerçekci ise ve varyanslar ve kovaryanslar eşit ise (bileşik simetri, compound symmetry) hesaplanacak F testi geceçerlidir.
Eğer eklemelilik (additivity) ve eş varyanslılık mevcut ise bileşik simetri sağlanmış olur. Fakat bileşik simetri küresellik varsayımına nazaran gerçekleşmesi daha zor bir varsayımdır. Verilerin çokdeğişkenli norma varsayımdan geldiği durumlarda küresellik varsayımının ihlal edilmemesi F testinin geçerli olması için yeterlidir. Dolayısı ile küresellik varsayımını kontrol etmek eklemelilik varsayımını kontrol etmekten daha önemlidir. Bununla birlikte, küresellik varsayımının ihlal edilmesi durumunda kritik değer düzeltme prosedürleri mevcut olduğu için eklemelilik varsayımını kontrol etmek gereksizdir.
9.4.0.2 R betiği: Tek-yönlü bağlı gözlemler varyans analizi
Gösterim amaçlı Daunic et al. (2012) tarafından toplanan verilerden bir alt küme seçilmiştir. Seçilen sınıfta 17 öğrenci mevcuttur. Bağımlı değişken problem çözme bilgisidir. Öğrencilerin 1 sene arayla problem çözme bilgisi ölçülmüştür. Yüksek puanlar bilginin arttığını gösterir.
Basamak 1 Veriyi hazırla
# datayı gir
PSdata=data.frame(id=factor(1:17),
wave1=c(20,19,13,10,16,12,16,11,11,14,13,17,16,12,12,16,16),
wave2=c(28,27,18,17,29,18,26,21,15,26,28,23,29,18,26,21,22),
wave3=c(21,24,14,8,23,15,21,15,12,21,23,17,26,18,14,18,19))Betimsel analizleri raporla
# kozmetik, basamak sayısını belirle
options(digits = 3)
#veriyi uzun formata çevir
#head(PSdata)
library(tidyr)
data_long = gather(PSdata, wave, PrbSol, wave1:wave3, factor_key=TRUE)
#betimsel analizler
library(doBy)
library(moments)
desc1W=as.matrix(summaryBy(PrbSol~wave, data = data_long,
FUN = function(x) { c(n = sum(!is.na(x)),
mean = mean(x,na.rm=T), sdv = sd(x,na.rm=T),
skw=moments::skewness(x,na.rm=T),
krt=moments::kurtosis(x,na.rm=T)) } ))
# Tablo 6
desc1W
## wave PrbSol.n PrbSol.mean PrbSol.sdv PrbSol.skw PrbSol.krt
## 1 "wave1" "17" "14.4" "2.91" " 0.311" "2.10"
## 2 "wave2" "17" "23.1" "4.67" "-0.224" "1.64"
## 3 "wave3" "17" "18.2" "4.77" "-0.315" "2.45"
#write.csv(desc1W,file="onewayW_ANOVA_desc.csv")
#write.csv2(desc1W,file="onewayW_ANOVA_desc.csv")Kovaryans matrisi
# Tablo 7
cov(PSdata[,-1])
## wave1 wave2 wave3
## wave1 8.49 8.85 9.87
## wave2 8.85 21.81 18.49
## wave3 9.87 18.49 22.78Basamak 2 Varsayım kontrolü
ggplot(data_long, aes(x=wave, y=PrbSol))+
geom_boxplot()+
labs(x = "Wave",y="Problem çözme bilgisi")
Figure 9.5: Problem çözme bilgisi
Küresellik varsayımını test etmek için ezANOVA tarafından verilen Mauchy testi kullanılmıştır.
require(ggplot2)
ggplot(data_long, aes(x=wave, y=PrbSol, group=id))+
geom_line() + labs(x = "Wave",y="Problem çözme bilgisi")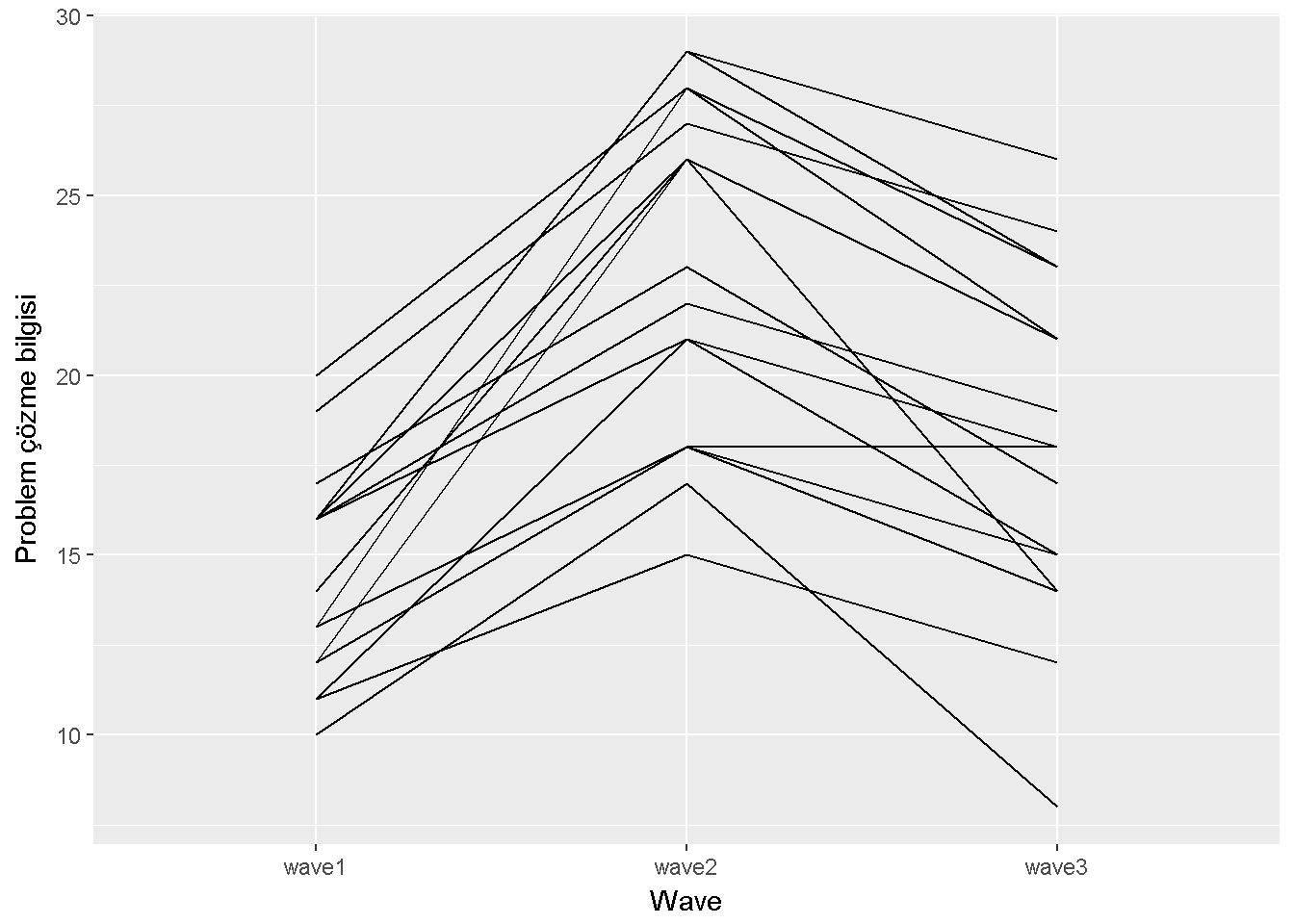
Figure 9.6: Problem çözme bilgisi çizgi grafigi
Bu grafik, \(\eta \beta_{ij}\)’nin sıfır olmayacağı şeklinde yorumlanabilir. asbio paketinde (Aho (2016)) yer alan tukey.add.test fonksiyonu \(H_0\) : asıl etkiler ve bloklar eklemeli ilerler boş hipotezini test etmek için kullanılabilir. Fakat daha önce beirtildiği gibi bu varsayımın ihlali, küresellik varsayımı ihlal edilmediği veya düzeltmesi yapıldığı sürece, öenmsizdir.
library(asbio)
with(data_long,tukey.add.test(PrbSol,wave,id))
##
## Tukey's one df test for additivity
## F = 5.943 Denom df = 31 p-value = 0.021
# eğer eklemelilik mevcut ise rassal bloklar tasarısı kullanılabilir
#additive=with(data_long,lm(PrbSol~id+wave))
#anova(additive)Tukey eklemelilik testi boş hipotezin terkedilebileceğini dolayısıyla eklemesiz modelin daha uygun olduğunu göstermiştir.
Basamak 3: Varyans analizi (küresellik ve hataların normal dağılımı varsayımı kontrolleri ile birlikte).
library(ez)
#birinci yol ezANOVA fonksiyonu
alternative1 = ezANOVA(
data = data_long,
wid=id, dv = PrbSol, within = wave,
detailed = T,return_aov=T)
alternative1
## $ANOVA
## Effect DFn DFd SSn SSd F p p<.05 ges
## 1 (Intercept) 1 16 17510 680 412.0 7.62e-13 * 0.954
## 2 wave 2 32 647 169 61.2 1.16e-11 * 0.433
##
## $`Mauchly's Test for Sphericity`
## Effect W p p<.05
## 2 wave 0.918 0.526
##
## $`Sphericity Corrections`
## Effect GGe p[GG] p[GG]<.05 HFe p[HF] p[HF]<.05
## 2 wave 0.924 6.17e-11 * 1.04 1.16e-11 *
##
## $aov
##
## Call:
## aov(formula = formula(aov_formula), data = data)
##
## Grand Mean: 18.5
##
## Stratum 1: id
##
## Terms:
## Residuals
## Sum of Squares 680
## Deg. of Freedom 16
##
## Residual standard error: 6.52
##
## Stratum 2: id:wave
##
## Terms:
## wave Residuals
## Sum of Squares 647 169
## Deg. of Freedom 2 32
##
## Residual standard error: 2.3
## Estimated effects may be unbalancedPrbSolres=sort(alternative1$aov$id$residuals)
qqnorm(PrbSolres);qqline(PrbSolres)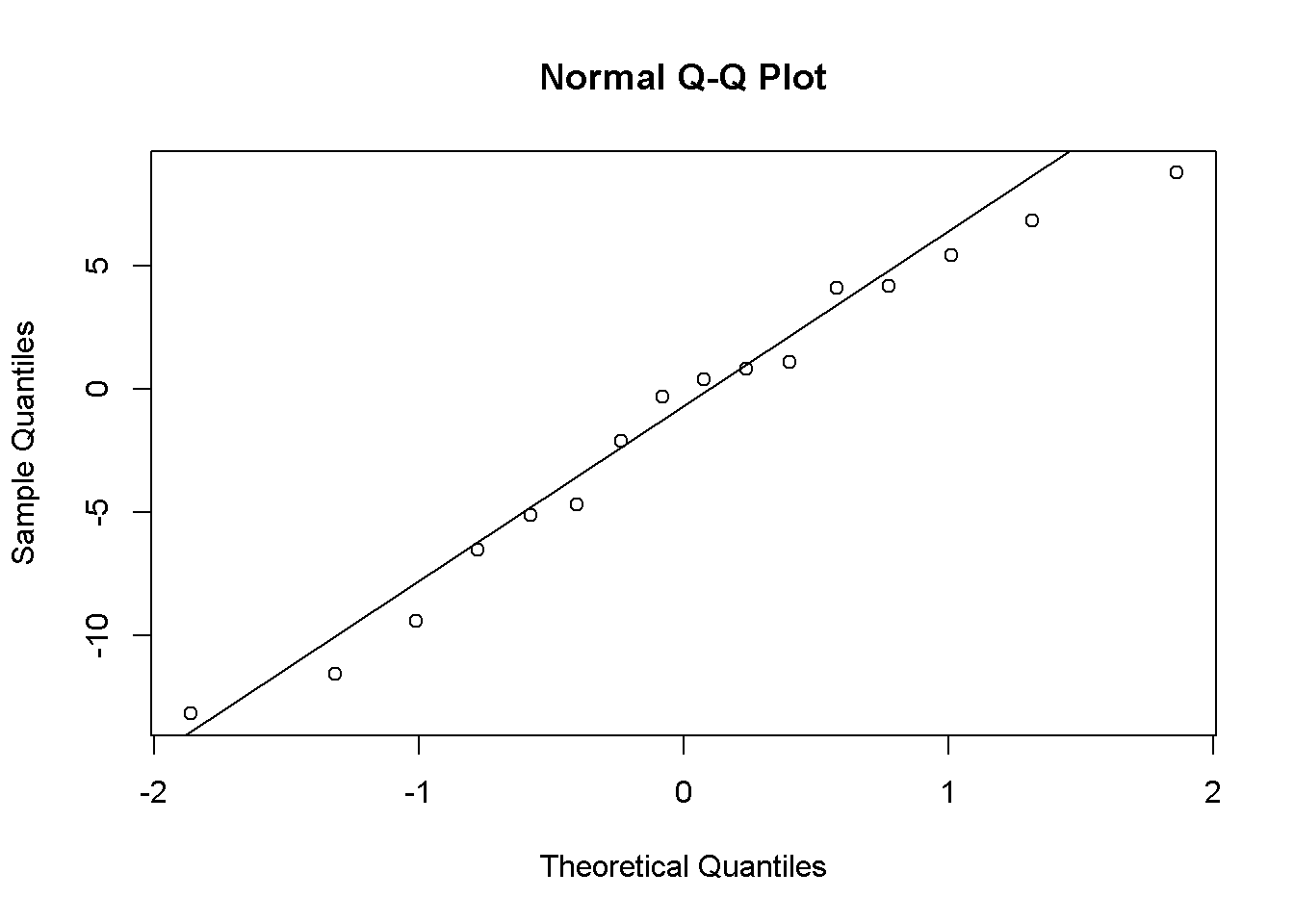
Figure 9.7: Problem çözme bilgisi hata terimleri
Hataların dağılımı normal sayılabilir.
# ikinci yol aov fonksiyonu
summary(aov(PrbSol ~ wave + Error(id/wave), data=data_long))
##
## Error: id
## Df Sum Sq Mean Sq F value Pr(>F)
## Residuals 16 680 42.5
##
## Error: id:wave
## Df Sum Sq Mean Sq F value Pr(>F)
## wave 2 647 324 61.2 1.2e-11 ***
## Residuals 32 169 5
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 19.4.0.3 Dirençli tahminleme yöntemi: tek-yönlü bağlı gözlemler varyans analizi
Wilcox (2012) tarafından bir araya toplanan dirençli prosedürlerden bir tanesi Mair and Wilcox (2016) paketi ile kullanılabilecek rmanova fonksiyonu ile tamamlanabilir. Kırpılmış ortalamalar için farklı-varyanslı(heteroscedastic) ve tek yönlü tekrarlanan ölçümler ANOVA yöntemini kullanan bu fonksiyonun detayları için inceleyiniz ;?rmanova
library(WRS2)
#rmanova
# 20% kırpılmış
with(data_long,rmanova(PrbSol,wave,id,tr=.20))
## Call:
## rmanova(y = PrbSol, groups = wave, blocks = id, tr = 0.2)
##
## Test statistic: 34.9
## Degrees of Freedom 1: 1.9
## Degrees of Freedom 2: 19
## p-value: 09.4.0.4 Example writeup tek-yönlü bağlı gözlemler varyans analizi
Her bir ölçme durumu için betimleyici istatistikler Tablo 6 ile verilmiştir. Kovaryans matrisi tablo 7 ile verilmiştir. Tek-yönlü bağlı gözlemler varyans analizi raporlanmıştır. F testi alfa=0.05 ile tamamlanmıştır. Varsayım ihlali tespit edilmemiştir ve ölçme durumları arasında anlamlı bir fark bulunmuştur. \(F(2,32)=61.2, p<.001\), genelleştirilmiş eta kare değeri (\(\hat\eta^2_G\)) 0.43 olarak hesaplanmıştır.
9.4.0.5 Takviye çözümlemeler: Tek-yönlü bağlı gözlemler varyans analizi
Eklenecek
9.4.0.6 Kayıp veri teknikleri: Tek-yönlü bağlı gözlemler varyans analizi
Eklenecek
9.4.0.7 İstatistiksel güç: Tek-yönlü bağlı gözlemler varyans analizi
Eklenecek
9.5 Karma tasarı (Mixed design)
Eklenecek
References
Myers, Jerome L., A. Well, Robert F. Lorch, and Ebooks Corporation. 2013. Research Design and Statistical Analysis. 3rd ed. New York: Routledge.
Lawrence, Michael A. 2016. Ez: Easy Analysis and Visualization of Factorial Experiments. https://CRAN.R-project.org/package=ez.
Bakeman, Roger. 2005. “Recommended Effect Size Statistics for Repeated Measures Designs.” Behavior Research Methods 37 (3): 379–84. doi:10.3758/BF03192707.
Olejnik, Stephen, and James Algina. 2003. “Generalized Eta and Omega Squared Statistics: Measures of Effect Size for Some Common Research Designs.” Psychological Methods 8 (4): 434–47.
Wilcox, Rand R. 2012. Introduction to Robust Estimation and Hypothesis Testing. 3rd;3; US: Academic Press.
R Core Team. 2016b. R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing. https://www.R-project.org/.
Holm, Sture. 1979. “A Simple Sequentially Rejective Multiple Test Procedure.” Scandinavian Journal of Statistics 6 (2): 65–70.
Mair, Patrick, and Rand Wilcox. 2016. WRS2: A Collection of Robust Statistical Methods. https://CRAN.R-project.org/package=WRS2.
Daunic, Ann P., Stephen W. Smith, Cynthia W. Garvan, Brian R. Barber, Mallory K. Becker, Christine D. Peters, Gregory G. Taylor, Christopher L. Van Loan, Wei Li, and Arlene H. Naranjo. 2012. “Reducing Developmental Risk for Emotional/Behavioral Problems: A Randomized Controlled Trial Examining the Tools for Getting Along Curriculum.” Journal of School Psychology 50 (2): 149–66.
Aho, Ken. 2016. Asbio: A Collection of Statistical Tools for Biologists. https://CRAN.R-project.org/package=asbio.
Bu katılımcı analizlerden çıkarılsa da sonuçlar değişmiyor↩