10 Korelasyon
Değişkenlerin birbiri ile olan ilişkilerini açıklamak çoğu araştırmacının ilgisini çekmiştir. İki değişkene ait çarpımlar toplamı (sum of cross products) \(S_{XY}=\sum(X-\bar X)(Y- \bar Y)\) iki değişken arasındaki ilişki hakkında sınırlı olsa da bilgi verebilir. Örneğin Şekil 10.1 X ve Y değişkeni arasındaki ilişkiyi gösterir ve çarpımlar toplamı sıfırdır.
## x y deviationX deviationY crossPRODUCT
## 1 1.00 0.00 0.93 0.00 0.00
## 2 0.90 0.43 0.83 0.43 0.36
## 3 0.62 0.78 0.56 0.78 0.44
## 4 0.22 0.97 0.16 0.97 0.15
## 5 -0.22 0.97 -0.29 0.97 -0.28
## 6 -0.62 0.78 -0.69 0.78 -0.54
## 7 -0.90 0.43 -0.97 0.43 -0.42
## 8 -1.00 0.00 -1.07 0.00 0.00
## 9 -0.90 -0.43 -0.97 -0.43 0.42
## 10 -0.62 -0.78 -0.69 -0.78 0.54
## 11 -0.22 -0.97 -0.29 -0.97 0.28
## 12 0.22 -0.97 0.16 -0.97 -0.15
## 13 0.62 -0.78 0.56 -0.78 -0.44
## 14 0.90 -0.43 0.83 -0.43 -0.36
## 15 1.00 0.00 0.93 0.00 0.00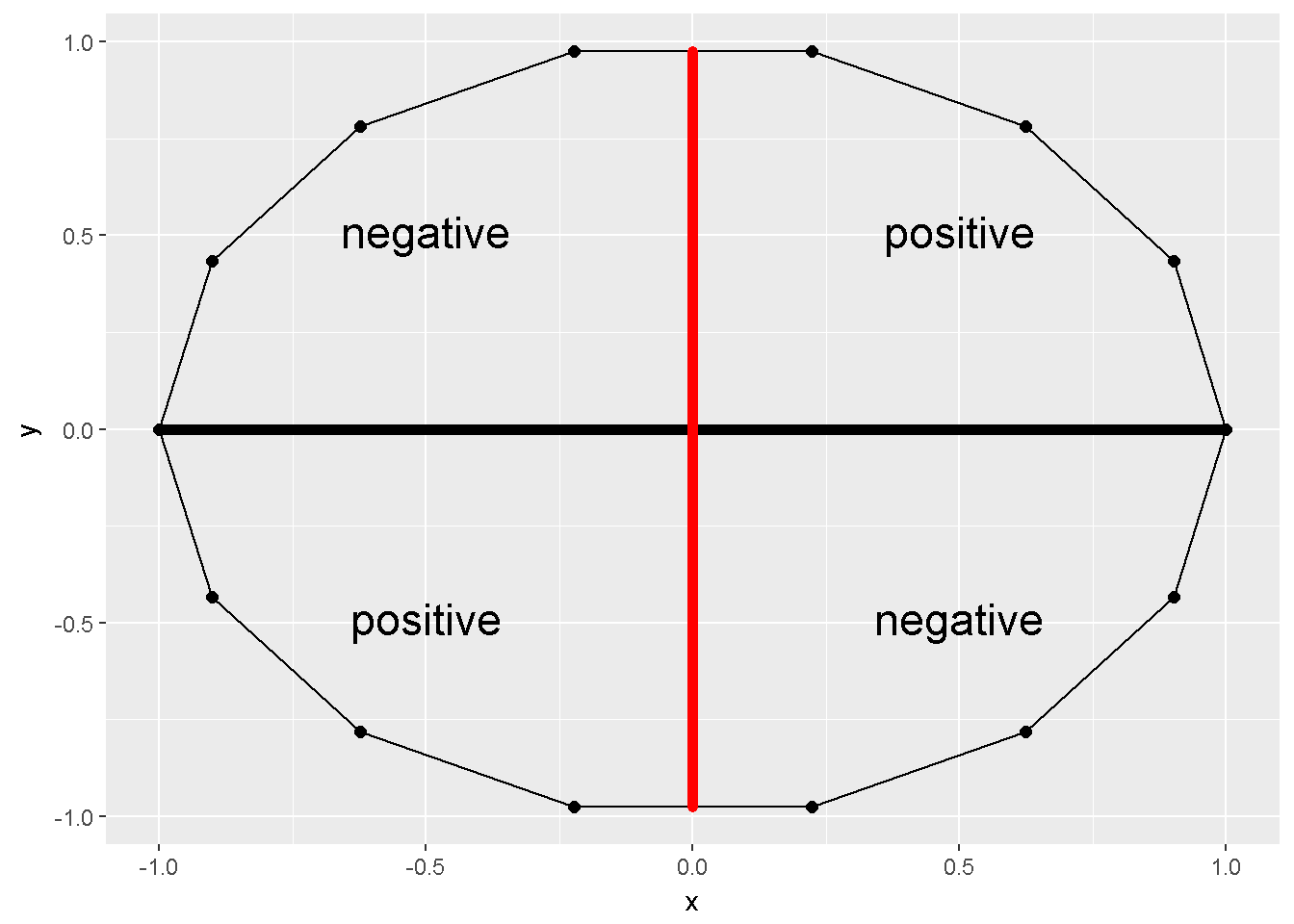
Figure 10.1: Çarpimlar toplami=0
İki değişken arasındaki kovaryans ise \(Cov_{XY}=S_{XY}/n-1\) ile hesaplanabilir. Fakat kovaryans ölçülen değişkenlerin skalasına bağımlıdır. Bir diğer ifade ile, değişkenlerin sayısal değerleri arttıkça kovaryans artar. Bu durum kovaryans yorumunu zorlaştırır. Bir korelasyon katsayısı ise genellikle -1 ve 1 arasındadır ve sınırları olduğu için yorumlaması daha kolaydır.
10.1 Pearson korelasyon katsayısı
Pearson 1986 yılında bir korelasyon katsayısı hesaplama yöntemi tanıtmıştır. Bu katsayı -1 ile +1 arasında değişir ve \(Cov_{XY}/S_X S_Y\) ile hesaplanabilir. Bu katsayı iki değişken arasındaki doğrusal ilişkiyi ölçer. Şekil 10.1 aralarındaki korelasyonun sıfır olduğu iki değişken ile çizilmiştir. Aslında şekil içerisindeki X ve Y bir biri ile ilişkisiz değillerdir çünkü şekil kabaca bir çemberdir. X ve Y beraber bir çember oluşturabilecek ilişkiye sahip oldukları halde , ilişki doğrusal olmadığından, aralarındaki korelasyon sıfırdır. Şekil 10.2 aralarında ilişki olan değişkenlere örnekler gösterir,(A) kusursuz pozitif korelasyon, +1, (B) 0.7 pozitif korelasyon, (C) 0 korelasyon, (D) -0.4 korelasyon ve (E) kusursuz negatif korelasyon,-1.
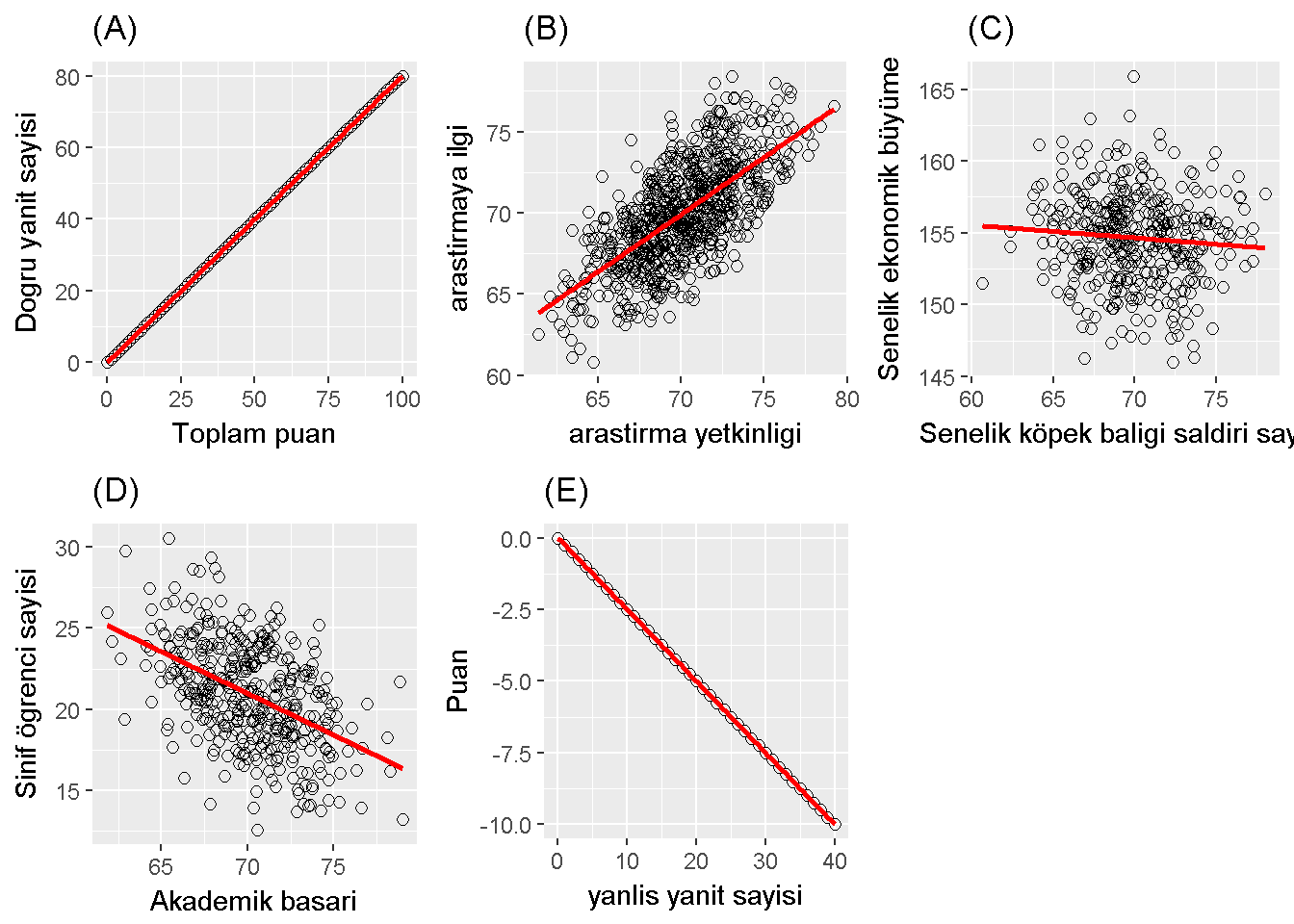
Figure 10.2: Correlation examples
10.1.1 Pearson korelasyon katsayısının evren bazında yorumu
Örneklemden gelen bilgi (\(r\)) , evren (\(\rho\)) düzeyinde çıkarım yapmak zere kullanılabilir.
z transformasyonu . İkili normallik (bivariate normality) varsayımı ve en az 10 örneklem ile z transformasyonu kullanılarak evrene ait parametre hakkında yorum yapılabilir (Myers et al. (2013)). Transformasyon formülü \[z_r = \frac{1}{2}ln \left( \frac{1+r}{1-r} \right)\]
Standart hata \[\sigma_r = \frac{1}{\sqrt{n-3}}\] Güven aralığı \(z_r \pm z_{\alpha / 2} \sigma_r\). Korelasyon katsayısı yorumunu kolaylaştırması amacı ile ters transformasyon \(r=\frac{e^{2z_r}-1}{e^{2z_r}+1}\).
\(H_0:\rho=0\) boş hipotezi normal bir dağılımın uygun olduğu varsayımı ile sınanabilir; \[z=\frac{z_r - z_{\rho_{null}}}{\frac{1}{\sqrt{n-3}}}\]
t dağılımı da \(H_0:\rho=0\) boş hipotezini test etmek için kullanılabilir.
\[t=r\sqrt{\frac{n-2}{1-r^2}}\]
Bu istatistik \(n-2\) serbestlik derecesine sahip t dağılımını takip eder.
10.1.2 R betiği: Pearson korelasyon katsayısı
Gösterim amaçlı dataWBT (2.3) içerisinde yer alan Bayburt ilçesi seçilmiştir. TCA puanları ile kişi başı senelik gelir arasındaki korelasyon incelenmiştir.
# CSV yükle
urlfile='https://raw.githubusercontent.com/burakaydin/materyaller/gh-pages/ARPASS/dataWBT.csv'
dataWBT=read.csv(urlfile)
#URL sil
rm(urlfile)
#Bayburt ilini seç
# sıralı silme uygula (listwise deletion)
dataWBT_Bayburt=dataWBT[dataWBT$city=="BAYBURT",]
#hist(dataWBT_Bayburt$income_per_member)İkili normal dağılım @ref(fig:testbivarnorm zerinden incelenebilir. rgl (Adler and Murdoch (2017)) paketi ile oluşturulan bu grafik interaktiftir, fare ile inceleyiniz.
## wgl
## 1Figure 10.3: Bayburt TCA ve Gelir
İkili normallik varsayımı gerçekci görünmüyor. Karşılaştırmanız amacı ile 10.4 korelasyonun 0.7 olduğu bir ikili normal dağılımı gösterir. Varsayım ihlalinin sonuçları etkileyebileceğini göz ardı ederek, gösterim amaçlı, eldeki veri ile \(H_0: \rho=0\) boş hipotezi \(H_1: \rho \neq0\) alternatif hipotezine karşı test edilmiştir.Saçılım grafiği Şekil 10.5 ile verilmiştir.

Figure 10.4: Ikili normal dagilim
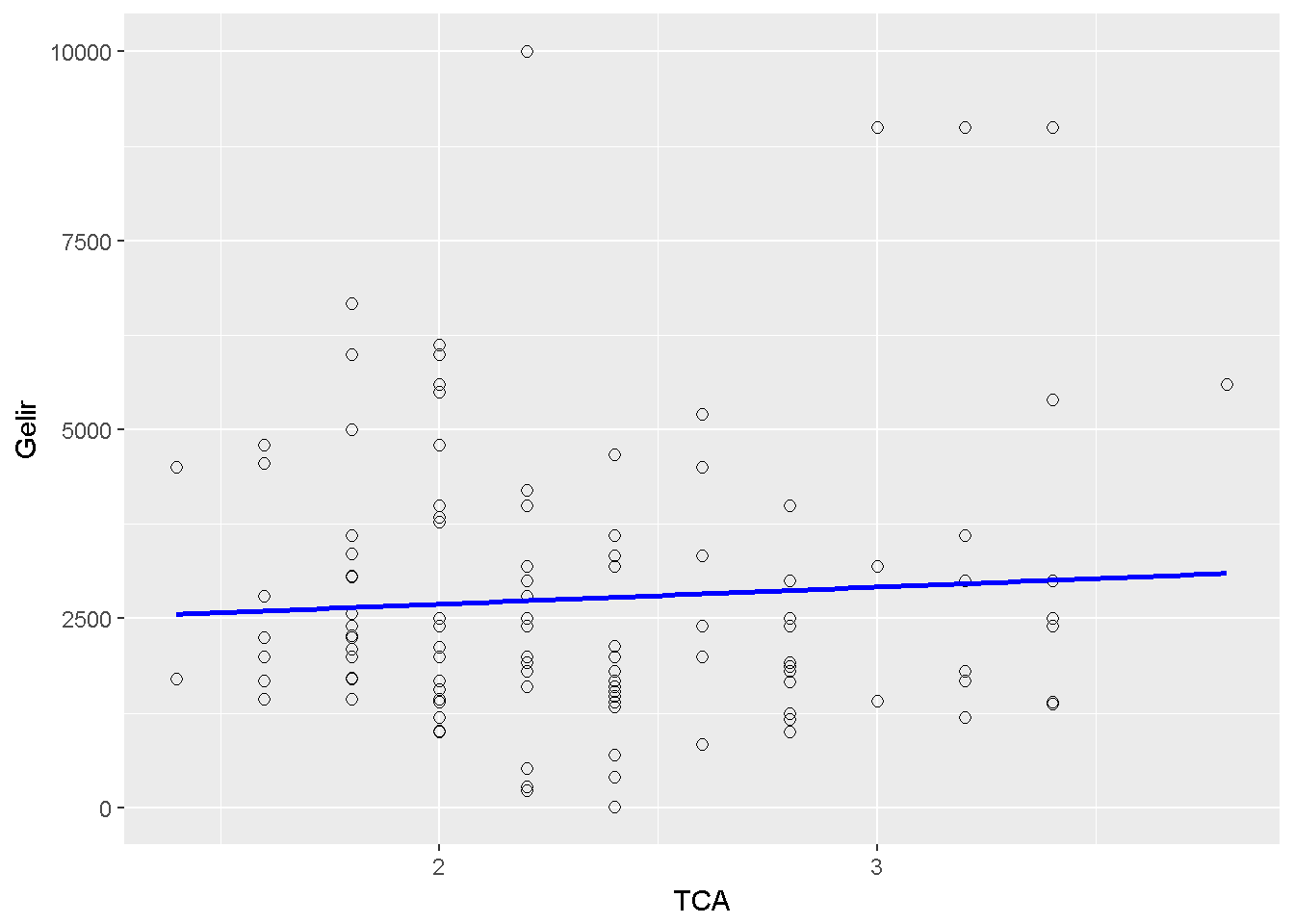
Figure 10.5: Bayburt TCA ve gelir
Bu iki değişken arasındaki korelasyon stats paketinde (R Core Team (2016b)) yer alan cor fonksiyonu ile hesaplanabilir. Aynı paket içerisinde yer alan cor.test fonksiyonu t testi sonuçlarını ve z transformasyonu ile hesaplanmış güven aralığı hesaplarını rapor eder.
#?cor komutu ile use = "complete.obs" argümanının ikili silme kullandığını görebilirsiniz
with(dataWBT_Bayburt,cor(gen_att,income_per_member,
use = "complete.obs",method="pearson"))
## [1] 0.0664
with(dataWBT_Bayburt,cor.test(gen_att,income_per_member,
alternative = "two.sided",
method="pearson",
conf.level = 0.95,
na.action="na.omit"))
##
## Pearson's product-moment correlation
##
## data: gen_att and income_per_member
## t = 0.8, df = 100, p-value = 0.4
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
## -0.102 0.232
## sample estimates:
## cor
## 0.0664Eğer kendiniz hesaplamak isterseniz, \(H_0: \rho=0\) ve \(H_0: \rho \neq 0\);
sample_r=0.06641641
r0=0 #boş hipotez
sample_n=137 # örneklem sayısı
zr=(0.5)*log((1+sample_r)/(1-sample_r)) # z transformasyonu
z0=(0.5)*log((1+r0)/(1-r0)) # z transformasyonu
sigmar=1/(sqrt(sample_n-3))
#z istatistiği
(zr-z0)/sigmar
## [1] 0.77
ll=zr-(qnorm(0.975)*sigmar) # alt limit
ul=zr+(qnorm(0.975)*sigmar) # üst limit
(exp(2*ll)-1)/(exp(2*ll)+1) #ters transform
## [1] -0.102
(exp(2*ul)-1)/(exp(2*ul)+1) #ters transform
## [1] 0.232
t=sample_r*(sqrt((sample_n-2)/(1-sample_r^2)))
qt(c(.025, .975), df=(sample_n-2))
## [1] -1.98 1.98
p.value = 2*pt(-abs(t), df=sample_n-2)
p.value
## [1] 0.441Yüzdeli bootstrap yönetimi varsayım ihlallerine dirençli bir yöntem olabilir (Myers et al. (2013)).
#Normallik varsayımı olmadan bootstrap ile %95 güven aralığı hesabı
set.seed(31012017)
B=5000 # bootstraps tekrarı
alpha=0.05 # alfa
#TCA ve gelir
originaldata=dataWBT_Bayburt2
# id ekle
originaldata$id=1:nrow(originaldata)
output=c()
for (i in 1:B){
#sample rows
bs_rows=sample(originaldata$id,replace=T,size=nrow(originaldata))
bs_sample=originaldata[bs_rows,]
output[i]=cor(bs_sample$gen_att,bs_sample$income_per_member)
}
output=sort(output)
## Yönsüz
# alt limit
output[as.integer(B*alpha/2)]
## [1] -0.138
# d yıldız üst
output[B-as.integer(B*alpha/2)+1]
## [1] 0.252Yüzdeli bootstrap dışında alternatif dirençli yöntemler mevcuttur. Wilcox (2012) dirençli korelasyon katsayısı hesaplama yöntemlerini bir araya toplamıştır. WRS2 paketi pbcor ve wincor fonksiyonları incelenebilir.
# WRS2 paketi
library(WRS2)
pbcor(dataWBT_Bayburt2$gen_att,dataWBT_Bayburt2$income_per_member,beta=.2)
## Call:
## pbcor(x = dataWBT_Bayburt2$gen_att, y = dataWBT_Bayburt2$income_per_member,
## beta = 0.2)
##
## Robust correlation coefficient: -0.0351
## Test statistic: -0.407
## p-value: 0.684
wincor(dataWBT_Bayburt2$gen_att,dataWBT_Bayburt2$income_per_member,tr=.2)
## Call:
## wincor(x = dataWBT_Bayburt2$gen_att, y = dataWBT_Bayburt2$income_per_member,
## tr = 0.2)
##
## Robust correlation coefficient: -0.0197
## Test statistic: -0.229
## p-value: 0.82Rapor örneği: Bayburt ilinde yaşayan katılımcılar göz önünde bulundurularak, TCA puanları ile gelir düzeyi değişkenleri arasında korelasyon olmadığı boş hioptezi test edilmiştir. Pearson korelasyon katsayısı \(r=.066 (p=.44)\) ve bu katsayı için %95 güvern aralığı [-.10,.23] olarak hesaplanmıştır.İki değişken arasında korelasyonun sıfır olduğunu ileri süre boş hipotez terkedilmemiştir. Aynı çıkarıma 5000 tekrarlı boostrap yöntemi ile de ulaşılmıştır (%95 güven aralığı [-.138 to .252 ]).
Not: Farklı işaret Pearson katsayısı istatistiksel olarak sıfırdan farklı değildirfakat işareti pozitiftir (.066). WRS paketinde yer alan fonksiyonlar da korelasyonun sıfırdan farklı olmadığı sonucuna ulaşmıştır. Fakat hesaplanan korelasyon negatiftir. Gelir değişkenine ait dağılımın çarpık olduğu ikili normallik dağılım grafiğinde de göze çarpmaktadır. World Bank araştırma takımı bu değişkenin çarpık dağılım göstermesi sebebi ile değişkeni trabnsform ederek analiz etmişlerdir ( Hirshleifer et al. (2016)). Benzer transformasyonu kullanırsak;
Figure 10.6: Transform edilmis Gelir
with(dataWBT_Bayburt2,cor.test(gen_att,incomeTC,
alternative = "two.sided",
method="pearson",
conf.level = 0.95,
na.action="na.omit"))
##
## Pearson's product-moment correlation
##
## data: gen_att and incomeTC
## t = -0.009, df = 100, p-value = 1
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
## -0.169 0.167
## sample estimates:
## cor
## -0.00081Transformasyon sonucunda gelir değişkeni daha normal bir dağılım göstermiştir ve Pearson korelasyon katsaysının işareti negatiftir.
10.2 Spearman rho ve Kendall tau
Verilerin sıralı veri olması durumunda veya sürekli değişkenlerde aykırı değerlerin etkisi azaltılmak istenildiğinde Spearman rho veya Kendall tau kullanılabilir. Burada bahsedilen aykırı değerlerin etkisinin azaltılması durumu Pearson korelasyona kıyasla geçerlidir. Aykırı değerlere karşı rho ve tauya nazaran daha iyi koruma sağlayan dirençli yöntemler mevcuttur, Wilcox (2012).
10.2.1 R betiği: Spearman’s rho ve Kendall’s tau
Pearson korelasyon katsayısı hesaplama örneğinde kullanılan TCA puanları ve gelir ilişkisi için Spearman rho hesaplaması;
with(dataWBT_Bayburt,cor.test(gen_att,income_per_member,
alternative = "two.sided",
method="spearman",
conf.level = 0.95,
na.action="na.omit",
exact=FALSE))
##
## Spearman's rank correlation rho
##
## data: gen_att and income_per_member
## S = 5e+05, p-value = 0.6
## alternative hypothesis: true rho is not equal to 0
## sample estimates:
## rho
## -0.0508Sıralama verisinde eş-sıra (ties) durumu var ise cor.test fonksiyonu Spearman rho hesaplanışında düzeltme yapar fakat p değeri hesaplamaz. Eğer exact=FALSE argümanı kullanılırsa t dağılımı üzerinden p değeri hesaplanabilir. Field, Miles, and Field (2012) eş-sıralılık durumunun çok olması durumunda Kendall tau hesaplanmasını önerir.
#use ?cor to see use="complete.obs" is doing casewise deletion
with(dataWBT_Bayburt,cor.test(gen_att,income_per_member,
alternative = "two.sided",
method="kendall",
conf.level = 0.95,
na.action="na.omit",
exact=FALSE))
##
## Kendall's rank correlation tau
##
## data: gen_att and income_per_member
## z = -0.6, p-value = 0.5
## alternative hypothesis: true tau is not equal to 0
## sample estimates:
## tau
## -0.0373exact=FALSE argümanı method=“kendall” ile kullanılınca normal dağılım üzerinden p değeri hesaplar.
Gelir değişkeninde bulunan aykırı değerlerin etkisini azaltmak üzere Spearman ve Kendall korelasyon katsayıları hesaplanmıştır. Spearman rho değeri \(r_S=-.051 (p=.56)\) ve Kendall tau değeri \(\tau = -.037,p=.54\) olarak bulunmuştur.
10.3 R betiği: Çift Serili ve Nokta-Çift Serili Korelasyonlar
Çift serili korelasyon bir sürekli değişken ve örtük bir sürekli değişkeni yansıtan ikili değişken (dichotomous) arasındaki korelasyonu hesaplamak için kullanılabilir. Örneğin öğrencilerin bir soruya verdiği doğru veya yanlış yanıt değişkeni ile toplam puanlar arasındaki ilişki çift serili korelasyon ile hesaplanabilir.
Gösterim amaçlı veri setinde yer alan birinci TCA sorusunu ikili veri olarak kodlayalım10. Bu ikili değişken ile 2.,3.,4.,5. ve 6. soruların ortalaması olan TCA puanları arasındaki ilişki psych paketinde (Revelle (2016)) yer alan biserial fonksiyonu ile hesaplanabilir.
dataWBT_Bayburt$binitem1=ifelse(dataWBT_Bayburt$item1==4,1,0)
require(psych)
with(dataWBT_Bayburt,biserial(gen_att,binitem1))
## [,1]
## [1,] 0.317Nokta çift serili korelasyon ise sürekli bir değişken ve ikili bir değişken arasındaki ilişkiyi ölçmek için kullanılabilir. cor.test fonksiyonu ve method=“pearson” argumanı ile nokta çift serili korelasyon hesaplanabilir. TCA puanları ve cinsiyet arasındaki nokta-çift serili korelasyon;
dataWBT_Kayseri=dataWBT[dataWBT$city=="KAYSERI",]
dataWBT_Kayseri$genderNUM=ifelse(dataWBT_Kayseri$gender=="Female",1,0)
with(dataWBT_Kayseri,cor.test(gen_att,genderNUM,
alternative = "two.sided",
method="pearson",
conf.level = 0.95,
na.action="na.omit"))
##
## Pearson's product-moment correlation
##
## data: gen_att and genderNUM
## t = -7, df = 200, p-value = 2e-10
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
## -0.487 -0.277
## sample estimates:
## cor
## -0.38710.4 R betiği: Phi korelasyon katsayısı
Değişkenler ikili ise aralarındaki ilişki phi(\(\phi\)) korelasyon katsayısı ile ölçülebilir. Gösterim amaçlı cinsiyet ve maaş durumu ilişkisi incelenmiştir. Maaş durumu katılımcının son 12 ay boyunca maaş alıp almadığını gösterir. psych paketinde yer alan phi fonksiyonu 2x2 frekans tablosu üzerinden hesaplama yapabilir.
dataWBT_Kayseri=dataWBT[dataWBT$city=="KAYSERI",]
table(dataWBT_Kayseri$gender,dataWBT_Kayseri$wage01)
##
## No Yes
## Female 52 97
## Male 49 54
## Unknown 0 0
genderWAGE=matrix(c(52,49,97,54),ncol=2)
library(psych)
phi(genderWAGE)
## [1] -0.1310.5 Tetrakorik ve polikorik korelasyon katsayısı
Aralarında korelasyon belirlenmesi istenen değişkenlerin doğasının sürekli ve normal dağılımlı olduğu hâlde iki kategorili (dikatom) olarak gözlenmiş olması durumunda, bir diğer ifade ile, dikatom değişkenlerin örtük sürekli değişkenleri yansıtıyor olması durumunda, tetrakorik (rt) korelasyon katsayısı kullanılır. Bu noktada araştırmacı, karşılaştığı dikatom değişkenlerin doğası gereği sürekli olup olmadığına karar vermesi ve kararını savunabilmesi gerekir. Örneğin öğrencilerin doğru-yanlış sorularına verdiği yanıtlar (0: yanlış, 1: doğru) sürekli bir değişkenin yansıması olarak düşünülebilir. Diğer bir örnek ankete katılan bireylerin yaşlarının 30 yaş altı ve 30 yaş üstü olarak toplanmış olmasıdır. Gösterim amaçlı, veri setinde yer alan üçüncü ve altıncı TCA sorularını ikili veri olarak kodlayarak ve psych paketinde yaralan tetrachoric fonksiyonunu kullanılarak tetrakorik korelasyon katsayısı hesaplanabilir. Hesaplanan korelasyon 0.07’dir.
# 3. ve 6. sorular dikatom yapılsın
# Dünya Bankası araştırma grubu tarafından kullanılan yöntem,
# eğer yanıt 1 (strongly disagree) veya 2 (disagree) ise 1, değilse 0.
dataWBT_Kayseri$Bitem3=ifelse(dataWBT_Kayseri$item3==1|dataWBT_Kayseri$item3==2,1,0)
dataWBT_Kayseri$Bitem6=ifelse(dataWBT_Kayseri$item6==1|dataWBT_Kayseri$item6==2,1,0)
require(psych)
tetrachoric(as.matrix(dataWBT_Kayseri[,c("Bitem3","Bitem6")]))
## Call: tetrachoric(x = as.matrix(dataWBT_Kayseri[, c("Bitem3", "Bitem6")]))
## tetrachoric correlation
## Bitm3 Bitm6
## Bitem3 1.00
## Bitem6 0.07 1.00
##
## with tau of
## Bitem3 Bitem6
## -0.23 0.54Polikorik korelasyon katsayısı eldeki değişkenlerin sıralı (ordinal) kategorik olduğu durumlarda hesaplanır. Tetrakorik korelasyonda olduğu gibi, polikorik korelasyon hesaplanırken de kategorik değişkenlerin sürekli bir değişeni yansıttığı varsayımı yapılır. Bu iki korelasyon katsayısı örtük sürekli korelasyonlar (latent continuous correlation) olarak tek bir terim altında düşünülebilir (Uebersax (2015)). Tetrakorik ve polikorik korelasyonların hesaplanmasında kullanılan yöntemler kapalı ve açık form olarak düşünülebilir. Kapalı form nispeten daha basittir ve formüllerle basitçe ifade edilebilir. Fakat kapalı formlar genellikle yaklaşık değerler hesaplar. Açık form yöntemlerden kasıt iteratif prosedürlerdir ve oldukça karmaşık olabilirler, fakat kapalı formlara kıyasla daha doğru sonuçlar vermesi beklenir. Kategorik değişkenler için yürütülen faktör analizlerinde bu iki tür korelasyon birçok yazılım tarafından kullanılmaktadır. Tetrakorik veya polikorik korelasyon hesaplayacak olan araştırmacıların kullandığı yöntemi ve yazılımı açık olarak ifade etmesi doğru bir yaklaşım olacaktır, çünkü farklı yazılımlar ve farklı yöntemler kullanıldığında sonuçlar arasında farklılık görülebilir. Sonuçların birbirinden neden farklı olabileceğini daha detaylı araştırmak isteyen okuyucular Olsson (1979) tarafından kaleme alınan makaleyi inceleyebilirler. Bu noktada okuyucular psych paketinde yer alan polychoric fonksiyonunun argümanlarını dikkatlice incelemek isteyebilirler. Gösterim amaçlı veri setinde yer alan üçüncü ve altıncı TCA sorular için polikorik korelasyon hesaplanmış ve 0.16 bulunmuştur.
require(psych)
polychoric(as.matrix(dataWBT_Kayseri[,c("item3","item6")]))
## Call: polychoric(x = as.matrix(dataWBT_Kayseri[, c("item3", "item6")]))
## Polychoric correlations
## item3 item6
## item3 1.00
## item6 0.16 1.00
##
## with tau of
## 1 2 3
## item3 -0.72 0.23 1.30
## item6 -1.37 -0.54 0.8210.6 Korelasyon katsayısı hakkında dikkat edilmesi gerekenler
Sebep-Sonuç Bir korelasyon katsayısı sebep-sonuç belirtmez. Sebep-sonuç ilişkisi kurulmak istense dahi dört farklı senaryo mevcuttur, (a) X Y’yi etkiler, (b) Y X’i etkiler, (c) X ve Y bir veya daha fazla ortak sebebin sonucudur, (d) X ve Y farklı sebeplerle ortaya çıkmıştır fakat bu farklı sebepler ilişkilidir.
Büyüklük Bir korelasyon katsayısının büyük veya küçük oluşu konuya göre değişir. Birbirine benzemesi üzerine tasarlanmış iki matematik sınavından sonra hesaplanan korelasyon 0.6 ise bu küçük bir korelasyon olarak düşünülebilir çünkü paralel formlar korelasyonunun en az .70 olması beklenir. Fakat ALES puanları ile yüksek lisans not ortalaması arasında hesaplanacak bir 0.6 korelasyon oldukça büyüktür çünkü alan yazında bu değer genellikle .1 ve .3 arasındadır.
Aykırı değerler Veri setinde yer alan aykırı değerler korelasyon katsayılarını etkiler.
Güvenirlik X veya Y ölçme hatası (measurement error) içeriyorsa hesaplanan korelasyon aşağı yönde etkilenir. Düzeltme yapmak için \[r_{T_x T_y}=\frac{r_{xy}}{\sqrt(r_{xx}r_{yy})}\] kullanılabilir, \(r_{xx}\) ve \(r_{yy}\) X ve Y için güvenirlik katsayılarıdır.
• Bu düzeltme ne zaman kullanılmaz: Gerçek hayatta yeri olacak bir karar verilecekse bu düzeltme yapılmamalıdır. Kararlar gözlemlenen veriler üzerine verilmelidir.
• Bu düzeltme ne zaman kullanılır: Teorilerin geliştirilmesi aşamasında düzeltme kullanılabilir.
Varyans Korelasyon katsayısı değişkenlerin varyansından etkilenir. Varyansın yapay olarak küçültülmesi korelasyonun da küçülmesine sebep olur. Varyansın yapay olarak küçülmesine örnekler;
• Sürekli verilerin kategorize edilmesi
• Ranj sınırlılığı
• Taban ve Tavan etkisi (Floor and Ceiling Effects)
References
Myers, Jerome L., A. Well, Robert F. Lorch, and Ebooks Corporation. 2013. Research Design and Statistical Analysis. 3rd ed. New York: Routledge.
Adler, Daniel, and Duncan Murdoch. 2017. Rgl: 3D Visualization Using Opengl. https://CRAN.R-project.org/package=rgl.
R Core Team. 2016b. R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing. https://www.R-project.org/.
Wilcox, Rand R. 2012. Introduction to Robust Estimation and Hypothesis Testing. 3rd;3; US: Academic Press.
Hirshleifer, Sarojini, David McKenzie, Rita Almeida, and Cristobal Ridao-Cano. 2016. “The Impact of Vocational Training for the Unemployed: Experimental Evidence from Turkey.” The Economic Journal 126 (597): 2115–46.
Field, Andy P., Jeremy Miles, and Zoë Field. 2012. Discovering Statistics Using R. Thousand Oaks, Calif;London; Sage.
Revelle, William. 2016. Psych: Procedures for Psychological, Psychometric, and Personality Research. https://CRAN.R-project.org/package=psych.
Uebersax, John S. 2015. “Introduction to the Tetrachoric and Polychoric Correlation Coefficients.” Obtenido de Http://Www. John-Uebersax. Com/Stat/Tetra. Htm.[Links].
Olsson, Ulf. 1979. “Maximum Likelihood Estimation of the Polychoric Correlation Coefficient.” Psychometrika 44 (4). Springer: 443–60.
World Bank araştırma takımı bu soruyu ikili değişken olarak yeniden kodlayarak analiz etmiştir↩