8 İki Ortalamanın Karşılaştırılması, t-testi
Bölüm 7.3.1 örnekleme dağılım (sampling distribution) konusunun ana hatlarını tek bir aritmetik ortalama üzerinden ele almıştır. Eğer iki farklı aritmetik ortalama kıyaslanmak isteniyorsa t testi kullanılabilir, bu prosedür aritmetik ortalamaların örnekleme dağılımı üzerine inşaa edilmiştir.
\(\bar{Y_1}-\bar{Y_2}\) \((\mu_{\bar{Y_1}-\bar{Y_2}})\) sonucunun örnekleme dağılım ortalaması daima \(\mu_1 - \mu_2\) ’dir. Fakat örnekleme dağılım standart sapması \((\sigma_{\bar{Y_1}-\bar{Y_2}})\) araştırmanın tasarısına göre değişir.
Örnek Bir cerrahın yaraların iyileşmesi konusunda araştırma yaptığını düşünelim. Cerrahın kapanan bir yaradan sonra gerilme direncini araştırdığını, yara bandı ve dikiş atma tedavisinin arasında bir fark olup olmadığını araştırdığını varsayalım. Bu çalışmada tek bir faktör vardır, yara kapatma yöntemi ve bu faktöre ait iki alt sınıf vardır, yara bandı ve dikiş. Bu araştırmayı iki farklı şekilde tasarlamak mümkündür.
Bağlı gözlemler (within-subjects) 10 tavşanın her birinin sırtına (omurganın sağına ve soluna) 2 kesik oluşturulur. 2 kesikten bir tanesi yeni geliştirilen bir yara bandı ile diğeri dikiş ile kapatılır, hangi kapatma yönteminin hangi yarayı kapatacağı rassal (random) seçilmelidir. Bu tasarı bağlı-gözlemler olarak isimlendirilmiştir çünkü faktöre ait iki alt sınıf aynı tavşan üzerinde gözlemlenmiştir.
Bağlı olmayan gözlemler (between-subjects) 20 tavşan rassal olarak 2 gruba ayrılır, birinci grupta yer alan tavşanların yaraları bant ile, ikinci grupta yer alan tavşanların yaraları ise dikiş ile kapatılır. Yaralar omurganın sağ veya sol tarafında rassal olarak açılmalıdır. Bu tasarı bağlı olmayan gözlemler olarak isimlendirilmiştir çünkü faktöre ait alt sınıflar farklı tavşanlar üzerinde gözlemlenmiştir ve bu tavşanların herhangi bir şekilde eşlenmiş değillerdir. Örneğin aynı anneden gelen iki tavşan rassal olarak gruplara atansa idi gözlemler bağlı olurdu.
Her iki yara kapatma yönteminden sonra yapılacak gerilme direnci ölçümlerinin evren bazında bir ortalaması ve standart sapması olduğu aşikardır.
Konuyu açıklama amaçlı, yara bandı yönteminden sonra yapılan gerilme direnci ölçümlerine ait ortalamanın ve standart sapmanın bağlı gözlem veya bağlı olmayan gözlem tasarılarında aynı olduğunu düşünelim.
| Parametres | Bant | Dikiş |
|---|---|---|
| Ortalama | \(\mu_B\) | \(\mu_D\) |
| Standart Sapma | \(\sigma_B\) | \(\sigma_D\) |
| Örneklem | \(n_B\) | \(n_D\) |
Buradan itibaren \(\mu_B\) yerine \(\mu_1\), \(\mu_D\) yerine \(\mu_2\), \(\sigma_B\) yerine \(\sigma_1\),\(\sigma_D\) yerine \(\sigma_2\) kullanılmıştır.
| Örnekleme dağılım parametresi | Bağlı olmayan gözlem | Bağlı gözlem |
|---|---|---|
| Ortalama (\(\mu_{\bar{Y_1}-\bar{Y_2}}\)) | \(\mu_1-\mu_2\) | \(\mu_1-\mu_2\) |
| Standart sapma (\(\sigma_{\bar{Y_1}-\bar{Y_2}}\)) | \(\sqrt{\frac{\sigma_1^2+\sigma_2^2}{n}}\) | \(\sqrt{\frac{\sigma_1^2+\sigma_2^2-2\sigma_1 \sigma_2 \rho_{12}}{n}}\) |
\(\rho_{12}\) bağlı gözlemlerde, bant ve dikiş sonrası yapılan ölçümlerin arasındakı korelasyondur.
Standart sapmadaki değişiklik \(\rho_{12}\)’den kaynaklanır. Eğer bu korelasyon 0 ise iki tasarının da örneklem dağılımına ait standart sapma aynıdır.
Bir araştırma tasarısında hedeflerden biri standart hatayı mümkün olduğunca küçük tutmaktır. Standart hatanın küçük olması elde edilen test istatistiğinin tahmin edilen parametreye yakın olduğu anlamına gelir.
Veri çözümleme sürecinde hata varyansı (error variance) hesaplamak için bir formül seçilir. Yanlış formülün kullanılması büyük bir hatadır.
Uygulamada, standart hatanın hesaplanışı tasarının bağlı mı bağsız mı olduğuna göre değişir. Tasarının yanlış sınıflandırılması, çözümleme sürecinde büyük bir hatadır.
8.1 Bağımsız gruplar t-test (The Independent Groups t-test)
Uşak ilinde yaşayan katılımcıların Toplumsal Cinsiyet Algısı (TCA) puanları yüksek öğretim durumuna göre karşılaştırılmıltır (2.3). Her grup için yoğunluk grafikleri;
# csv yükle
urlfile='https://raw.githubusercontent.com/burakaydin/materyaller/gh-pages/ARPASS/dataWBT.csv'
dataWBT=read.csv(urlfile)
#URL sil
rm(urlfile)
dataWBT_USAK=dataWBT[dataWBT$city=="USAK",]
# factor ve droplevels fonksiyonları bölüm 5.2.4 ile verilmiştir.
# yeni oluşturulan HEF (Higher Education Factor)
# katılımcı lise veya altı diplomaya sahipse 0, non-college
# katılımcı lise üstü diplomaya sahip ise 1, college
dataWBT_USAK$HEF=droplevels(factor(dataWBT_USAK$higher_ed,
levels = c(0,1),
labels = c("non-college", "college")))
require(ggplot2)
plotdata=na.omit(dataWBT_USAK[,c("gen_att","HEF")])
ggplot(plotdata, aes(x = gen_att)) +
geom_histogram(aes(y = ..density..),col="black",binwidth = 0.2,alpha=0.7) +
geom_density(size=2) +
theme_bw()+labs(x = "Uşak ilinde Yüksek Öğretim Durumuna göre TCA puanları")+ facet_wrap(~ HEF)+
theme(axis.text=element_text(size=15),
axis.title=element_text(size=14,face="bold"))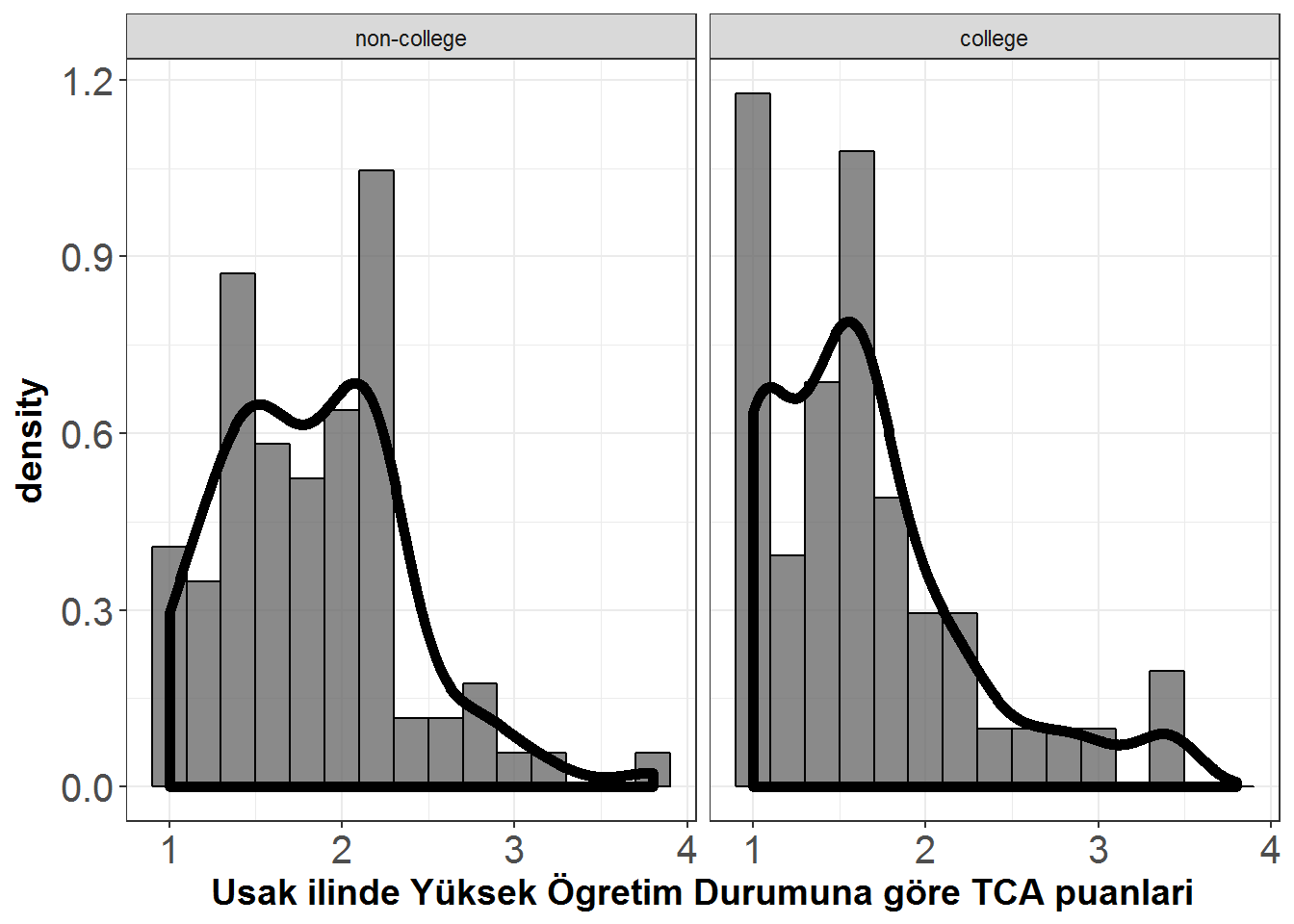
Figure 8.1: Yüksek Ögretim Durumuna göre TCA puanlari
8.1.1 R betiği: Bağımsız gruplar t testi
Takip edilen basamaklar;
- Betimsel istatistikler
- Test istatistiğinin hesabı
\[t=\frac{\bar{Y_1}-\bar{Y_2}}{S_p \sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}\]
\[ S_p = \sqrt{\frac{(n_1-1)S_1^2 + (n_2-1)S_2^2 }{n_1+n_2-2}} \] 3. Kritik değerin hesabı \(\pm t_{\alpha/2,n_1+n_2-2}\) \[H_0:\mu_1-\mu_2=0\] \[H_1:\mu_1-\mu_2 \neq0\]
library(psych)
descIDT=with(dataWBT_USAK,describeBy(gen_att, HEF,mat=T,digits = 2))
descIDT
## item group1 vars n mean sd median trimmed mad min max range
## X11 1 non-college 1 86 1.83 0.54 1.8 1.80 0.59 1 3.8 2.8
## X12 2 college 1 51 1.64 0.61 1.6 1.54 0.59 1 3.4 2.4
## skew kurtosis se
## X11 0.72 0.90 0.06
## X12 1.19 1.09 0.09
# rapor etmek için
#write.csv(descIDT,file="independent_t_test_desc.csv")
#türkçe excel için
# #write.csv2(descIDT,file="independent_t_test_desc.csv")
# ss
sp=sqrt((85*.543^2 + 50*.608^2)/(86+51-2))
# t-istatistik
tstatistic=(1.832-1.635)/(sp*sqrt(1/86+1/51))
# alfa=0.05 kritik değer
qt(.975,df=135)
## [1] 1.9776921.963 kritik değer \(t_{.975,135}=1.978\)’den küçük olduğu için, \(H_0\) kabul edilir.
\(H_1:\mu_1-\mu_2 > 0\) alternatif hipotezi kurulsa idi, kritik değer \(t_{.95,135}=1.66\), 1.963’ten küçük olduğu için \(H_0\) terkedilirdi.
\(H_1:\mu_1-\mu_2 < 0\) alternatif hipotezi kurulsa idi, 1.963 kritik değer olan \(t_{.05,135}=-1.66\)’ ten küçük olmadığı için \(H_0\) kabul edilirdi (Burada alternatif hipotez ile örneklem arası farklılık zıt yönde).
Daha kullanışlı bir R betiği;
# dataWBT HEF faktörünü içermez, yukarıda HEF faktörü oluşturulmuştur.
t.test(gen_att~HEF,data=dataWBT_USAK,var.equal=T,
alternative="two.sided",
conf.level=0.95)
##
## Two Sample t-test
##
## data: gen_att by HEF
## t = 1.9587, df = 135, p-value = 0.05221
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## -0.001903268 0.394880924
## sample estimates:
## mean in group non-college mean in group college
## 1.831783 1.635294
# büyüktür
t.test(gen_att~HEF,data=dataWBT_USAK,var.equal=T,
alternative="greater",
conf.level=0.95)
##
## Two Sample t-test
##
## data: gen_att by HEF
## t = 1.9587, df = 135, p-value = 0.0261
## alternative hypothesis: true difference in means is greater than 0
## 95 percent confidence interval:
## 0.03034529 Inf
## sample estimates:
## mean in group non-college mean in group college
## 1.831783 1.635294
# küçüktür
t.test(gen_att~HEF,data=dataWBT_USAK,var.equal=T,
alternative="less",
conf.level=0.95)
##
## Two Sample t-test
##
## data: gen_att by HEF
## t = 1.9587, df = 135, p-value = 0.9739
## alternative hypothesis: true difference in means is less than 0
## 95 percent confidence interval:
## -Inf 0.3626324
## sample estimates:
## mean in group non-college mean in group college
## 1.831783 1.6352948.1.1.1 Yönsüz alternatif için rapor örneği
Uşak ilinde yaşayan katılımcılardan yüksek öğretim diplomasına sahip olan 51 kişi için TCA puanları ortalaması 1.64, standart sapması 0.61, puanlara ait dağılım çarpıklık değeri 1.19 ve basıklık değeri 1.09 olarak bulunmuştur. Aynı ilde yüksek öğretim diploması olmayan 86 katılımcının ise TCA puanları ortalaması 1.83, standart sapması 0.54, puanlara ait dağılımın çarpıklığı 0.72 ve basıklığı 0.90 olarak hesaplanmıştır.Bağımsız gruplar t-testi sonuçları, Uşak ilinde yaşayan katılımcıların Toplumsal Cinsiyet Algısı puanlarının yüksek öğretim durumuna göre değişeceği tezini desteklememiştir, t(135)=1.96, p=0.052. Puanlar arasındaki fark için %95 güven aralığı [-0.002,0.395] olarak hesaplanmıştır.7
8.1.1.2 Yönlü alternatif için rapor örneği
Uşak ilinde yaşayan katılımcılardan yüksek öğretim diplomasına sahip olan 51 kişi için TCA puanları ortalaması 1.64, standart sapması 0.61, puanlara ait dağılım çarpıklık değeri 1.19 ve basıklık değeri 1.09 olarak bulunmuştur. Aynı ilde yüksek öğretim diploması olmayan 86 katılımcının ise TCA puanları ortalaması 1.83, standart sapması 0.54, puanlara ait dağılımın çarpıklığı 0.72 ve basıklığı 0.90 olarak hesaplanmıştır. Bağımsız gruplar t testi sonuçları, yüksek öğretim diploması olmayanların TCA puanları yüksek öğretimlere nazaran daha yüksektir tezini desteklemiştir, t(135)=1.96, p=0.026. Puanlar arasındaki fark için %95 güven aralığı [0.030,\(\infty\)] olarak hesaplanmıştır.
8.1.2 Varsayımlar: Bağımsız gruplar t testi
Geleneksel t-testi sonuçlarının geçerliği 3 varsayımın ihlal edilmemesi ile mümkündür.
Yanıtların bağımsızlığı (independence). Her gruba ait puanların dağılımı birbirinden bağımsız olmalıdır. Yanıtların bağımsızlığını tehdit eden durumlardan biri aynı grup içeresinde yer alan bireylerin birbirlerinin yanıtlarını etkilemesidir (Yantların bağımsızlığı 9.2.1.4 bölümünde daha detaylı ele alınmıştır).
Normallik. Her gruba ait puanlar normal bir dağılımdan çekilmiştir. Myers et al. (2013) grupların örneklem sayısı (n) eşit olduğunda ve toplam örneklemin 40 veya daha fazla olduğu durumlarda t test istatistiğinin normallik varsayımı ihlallerine dirençli olduğunu belirtmiştir. Fakat bu direnç normal dağılımdan büyük çaplı sapmalar (extreme) için geçerli değildir. Bu kitabın yazarları normallik testlerinin bu varsayımı kontrol etmek için kullanılmasına sıcak bakmamaktadır. Görsel bir değerlendirmeden sonra özellikle küçük örneklemlerde, normallik varsayımının ihlal edildiği kaygısı varsa araştırmacılar dirençli tahminleme yöntemlerini kullanmalıdırlar.
Eş varyanslılık. Varyans homojenliği olarak da bilinen bu varsayım, iki grupta yer alan puanların evren bazında eşit varyanslı dağılımlardan çekildiğini kabul eder. Myers et al. (2013) grup örneklem sayılarının eşit ve en az 5 olduğu durumlarda varyans eşitliği sağlanamasa dahi 1. tip hata oranlarının önemli ölçüde değişmeyeceğini belirtmiştir. Fakat bu direnç büyük çaplı heterojenlikler için geçerli değildir, örnğin \(s_1^2/s_2^2>100\). Field, Miles, and Field (2012) Levene testi gibi eşvaryanslılık testlerinin örneklem sayılarının eşit olmadığı ve küçük örneklemlerde sağlıklı sonuçlar vermediğini belirtmiştir, halbuki bu testlere en çok ihtiyaç durumlar küçük örneklem ve eşit olmayan örneklem sayısı durumlarıdır. Eş varyanslılık testleri ile ilgili bir diğer kaygı, bu test sonucunda varyansların eşit sayılabileceği kararı verilmiş olsa da varyanslar arası farklılığın t test istatistiğini etkileyebileceğidir. t.test fonksiyonu , aksi istenmediği sürece, varyans eşitliği varsayımı yapmaz ve Welch t testini hesaplar.
Varsayımlar hakkındaki bu kısa tanıtımın ele almadığı durumlar vardır. Örneğin hem normalliğin hem eş varyanslılığın ihlal edildiği durumlar tartışılmamıştır. Ayrıca direnç konusu tartışmaya açıktır. Önreğin n1=n2=10 örneklem sayısı ve eş olmayan varyans durumu için 100000 tekrarla yaptığımız bir simülasyon, alfa=.01 ve yönsüz bir t testi için 1. tip hata oranını .018 bulmuştur. Bu oranın kabul edilebilir olup olmadığı tartışmaya açıktır.
Sonuç olarak, eğer yanıtların bağımsızlığı kabul ediliyorsa, örneklem sayısı eşitse ve her grupta en az 20 ise bağımsız gruplar t istatistiğinin büyük ölçüde dirençli olduğu kabulu makul bir kabuldur. Diğer durumlarda varsayım ihlalleri tespit edildi ise araştırmacılar alternatif çözümleme yöntemlerini kullanabilirler.
8.1.3 Welch t test
Normalliğin ciddi ölçüde zedelenmediği ve örneklem sayılarının her grup için en az 20 olduğu durumlarda Welch testi geçerli sonuçlar üretir. Bu test varyans eşdeğerli varsayımı yapmaz.
t.test(gen_att~HEF,data=dataWBT_USAK,var.equal=F,
alternative="two.sided",
conf.level=0.95)
##
## Welch Two Sample t-test
##
## data: gen_att by HEF
## t = 1.9028, df = 95.885, p-value = 0.06006
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## -0.008484626 0.401462282
## sample estimates:
## mean in group non-college mean in group college
## 1.831783 1.6352948.1.3.1 Raporlama örneği: Welch t testi
Uşak ilinde yaşayan katılımcılardan yüksek öğretim diplomasına sahip olan 51 kişi için TCA puanları ortalaması 1.64, standart sapması 0.61, puanlara ait dağılım çarpıklık değeri 1.19 ve basıklık değeri 1.09 olarak bulunmuştur. Aynı ilde yüksek öğretim diploması olmayan 86 katılımcının ise TCA puanları ortalaması 1.83, standart sapması 0.54, puanlara ait dağılımın çarpıklığı 0.72 ve basıklığı 0.90 olarak hesaplanmıştır.Bağımsız gruplar Welch t-testi sonuçları, Uşak ilinde yaşayan katılımcıların Toplumsal Cinsiyet Algısı puanlarının yüksek öğretim durumuna göre değişeceği tezini desteklememiştir, t(95.89)=1.9, p=0.06. Puanlar arasındaki fark için %95 güven aralığı [-0.082,0.402] olarak hesaplanmıştır.
Eğer normallik varsayımı ciddi ölçüde süpheli ise ve özellikle iki grup farklı şekillerde dağılım gösteriyor ise yüzdeli bootstrap prosedürü (percentile bootstrap) kullanılabilir (Wilcox (2012),page 171).
#bootstrap ile %95 güven aralığı (normallik varsayımı yok)
set.seed(04012017)
B=5000 # bootstrap tekrar sayısı
alpha=0.05 # alfa
# grupları tanımla
GroupCollege=na.omit(dataWBT_USAK[dataWBT_USAK$HEF=="college","gen_att"])
GroupNONcollege=na.omit(dataWBT_USAK[dataWBT_USAK$HEF=="non-college","gen_att"])
output=c()
for (i in 1:B){
x1=mean(sample(GroupCollege,replace=T,size=length(GroupCollege)))
x2=mean(sample(GroupNONcollege,replace=T,size=length(GroupNONcollege)))
output[i]=x2-x1
}
output=sort(output)
## yönsüz
# D yıldız alt
output[as.integer(B*alpha/2)+1]
## [1] -0.01338349
# D yıldız üst
output[B-as.integer(B*alpha/2)]
## [1] 0.3899111
##Yönlü x2>x1
# D yıldız alt
output[as.integer(B*alpha)+1]
## [1] 0.02202462
#hatalı yön x2<x1
# D yıldız üst
output[as.integer(B*(1-alpha))]
## [1] 0.35756958.1.3.2 Yüzdeli bootstrap yöntemi için raporlama örneği
Uşak ilinde yaşayan katılımcılardan yüksek öğretim diplomasına sahip olan 51 kişi için TCA puanları ortalaması 1.64, standart sapması 0.61, puanlara ait dağılım çarpıklık değeri 1.19 ve basıklık değeri 1.09 olarak bulunmuştur. Aynı ilde yüksek öğretim diploması olmayan 86 katılımcının ise TCA puanları ortalaması 1.83, standart sapması 0.54, puanlara ait dağılımın çarpıklığı 0.72 ve basıklığı 0.90 olarak hesaplanmıştır.Puanlar arasındaki fark için %95 bootstrap güven aralığı [-0.013,0.390] olarak hesaplanmıştır. Güven aralığı 0 değerini içerdiği için puanlar arasındaki farkın istatistiksel olarak anlamlı olduğu savunulamaz.
Yönlü test Alternatif hipotez, yüksek öğretim mezunu olmayan katılımcıların puanlarının yüksek olacağını belirtmiş ise; Puanlar arasındaki fark için %95 bootstrap güven aralığı [0.022,\(\infty\)] olarak hesaplanmıştır. Eldeki veri yüksek öğretim mezunu olmayanların puanlarının daha yüksek olacığı tezini desteyecek kanıt sunmuştur, \(H_0:\mu_{non-college} = \mu_{college}\) in favor of \(H_1:\mu_{non-college}-\mu_{college} > 0\).
Yönlü test Alternatif hipotez, yüksek öğretim mezunu olmayan katılımcıların puanlarının düşük olacağını belirtmiş ise; Puanlar arasındaki fark için %95 bootstrap güven aralığı [\(-\infty\),0.358] olarak hesaplanmıştır. Eldeki veri yüksek öğretim mezunu olmayanların puanlarının daha düşük olacağı tezini desteklememektedir. \(H_0:\mu_{non-college} = \mu_{college}\) ve \(H_1:\mu_{non-college}-\mu_{college} < 0\).
Yönlü ve yönsüz alternatif testler farklı kriterler kullanır. Yönlü testlerde yönün nasıl belirlendiği savunulmalıdır. Kullanılan örnekte yönsüz alternatif kullanıldığında Welch t testi p değeri 0.06 bulunmuştur. Bu sonuç marjinal anlamlılık olarak yorumlanabilir. Ülkemizde TCA puanları ve yüksek öğretim ilişkisi hakkında alanyazın sınırlı olduğu için yönlü bir alternatif savunulması zordur.
8.1.4 Etki büyüklüğü: Bağımsız gruplar t testi için
Bir t testi istatistiği ortalamaların birbirinden farklı olup olmadığı hakkında karar vermeye yardımcı olsa da, bu farklılığın büyüklüğünü yorumlamak için etki büyüklüğü hesaplamaları geliştirilmiştir. Bağımsız gruplar t testi için Cohen etki büyüklüğü , ortalamarın farkını bileşik standart sapmaya (pooled) bölünmesi ile hesaplanır. \[EB=\frac{t}{\sqrt{\frac{n_1n_2}{n_1+n_2}}}\]
Cohen (1962) etki büyüklüğü sınıflaması
| Etki büyüklüğü | Tanım |
|---|---|
| .2 | Küçük |
| .5 | Orta |
| .8 | Büyük |
## normallik ve eş varyanslılık varsayımı yapıldığında
## (dirençli yöntem benzer sonuç verdiğiiçin varsayımların kabulü makuldür.)
n1=51
n2=86
tval=1.96
EB=tval/sqrt((n1*n2)/(n1+n2))
EB
## [1] 0.3464033
#veya effsize paketi ile
t.test(gen_att~HEF,data=dataWBT_USAK,var.equal=F,
alternative="two.sided",
conf.level=0.95)
##
## Welch Two Sample t-test
##
## data: gen_att by HEF
## t = 1.9028, df = 95.885, p-value = 0.06006
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## -0.008484626 0.401462282
## sample estimates:
## mean in group non-college mean in group college
## 1.831783 1.635294
library(effsize)
cohen.d(gen_att~HEF,data=dataWBT_USAK, paired=F, conf.level=0.95,noncentral=F)
##
## Cohen's d
##
## d estimate: 0.346177 (small)
## 95 percent confidence interval:
## inf sup
## -0.005791781 0.698145741
# noncentral=T argümanını araştırabilirsiniz.effsize paketi (Torchiano 2016) etki büyüklüğünü 0.35 ve ilgili %95 güven aralığını [-0.008, 0.701] olarak hesaplamıştır.
8.1.5 Extra: Pratikte anlamlılık ve istatistiksel anlamlılık
Bir çalışma sonucunda elde edilen sonuçların istatistiksel olarak anlamlı olmadığı fakat prtaikte anlamlı olduğu öne sürülebilir. Bu sakıncalı bşr durumdur ve sadece küçük örneklemlerde görülür. Küçük bir örneklem ile yapılan çalışmadan sonra pratikte anlamlılıktan bahsetmek tezat oluşturur.
Bir çalısma sonucunda elde edilen sonuçların istatistiksel olarak anlamlı olduğu fakat pratikte anlamlı olmadığı öne sürülebilir. Bu doğru olabilir. 400 kişi ile tamamlanan bir çalışmada istatistiksel anlamlı farklılık .05 etki büyüklüğüne sahip olabilir. Eğer .05 etki büyüklüğü çalışmanın yapıldığı alanda küçük adlediliyorsa istatististiksel anlamlılık pratikte anlamlılığı desteklemez.
8.1.6 Kayıp veriler ile bağımsız gruplar t testi
Eklenecek
8.1.7 Destekleyici grafikler
Eklenecek
8.1.8 İstatisksel güç
İstatistiksel güç konusunun ana hatlarına bölüm 7.3.8’de değinilmiştir.
#power.t.test
power.t.test(delta=.35, sd=.6,sig.level=0.05, power=0.95,
type="two.sample", alternative="two.sided")
##
## Two-sample t test power calculation
##
## n = 77.35093
## delta = 0.35
## sd = 0.6
## sig.level = 0.05
## power = 0.95
## alternative = two.sided
##
## NOTE: n is number in *each* groupBu örnekte belirlenmiş değerler ortalamalar farkı 0.35, standart sapma 0.6, alfa 0.05, yönsüz test ve hedeflenen güç 0.95 seçildiğinde gereken örneklem sayısı her grup için 78’dir. Diğer bir ifade ile, 156 katılımcı ile belirlenen değerlere (ortalamalar farkı 0.35, standart sapma 0.6, alfa 0.05, yönsüz test) ulaşılması durumunda \(H_0:\mu_1-\mu_2=0\) boş hipotezinin terkedilme olasılığı %95’tir.
8.2 Bağlı gruplar t-testi (Within-subjects t-test)
20 tavşan ile gerçekleştirilen deneyde, yara bandı ve dikiş yöntemlerinin yara kapandıktan 10 gün sonra ölçülen germe mukavemeti değerleri üzerinde etkisi araştırılmıştır.
gerMUK=data.frame(tavid=1:20,
bant=c(6.59,9.84 ,3.97,5.74,4.47,4.79,6.76,7.61,6.47,5.77,
7.36,10.45,4.98,5.85,5.65,5.88,7.77,8.84,7.68,6.89),
dikis=c(4.52,5.87,4.60,7.87,3.51,2.77,2.34,5.16,5.77,5.13,
5.55,6.99,5.78,7.41,4.51,3.96,3.56,6.22,6.72,5.17))
# Grafik verisi
library(tidyr)
plotdata=gather(gerMUK, metot, mukavemet, bant:dikis, factor_key=TRUE)
require(ggplot2)
ggplot(plotdata, aes(x = mukavemet)) +
geom_histogram(aes(y = ..density..),col="black",alpha=0.7) +
geom_density(size=2) +
theme_bw()+labs(x = "mukavemet")+ facet_wrap(~ metot)+
theme(axis.text=element_text(size=15),
axis.title=element_text(size=14,face="bold"))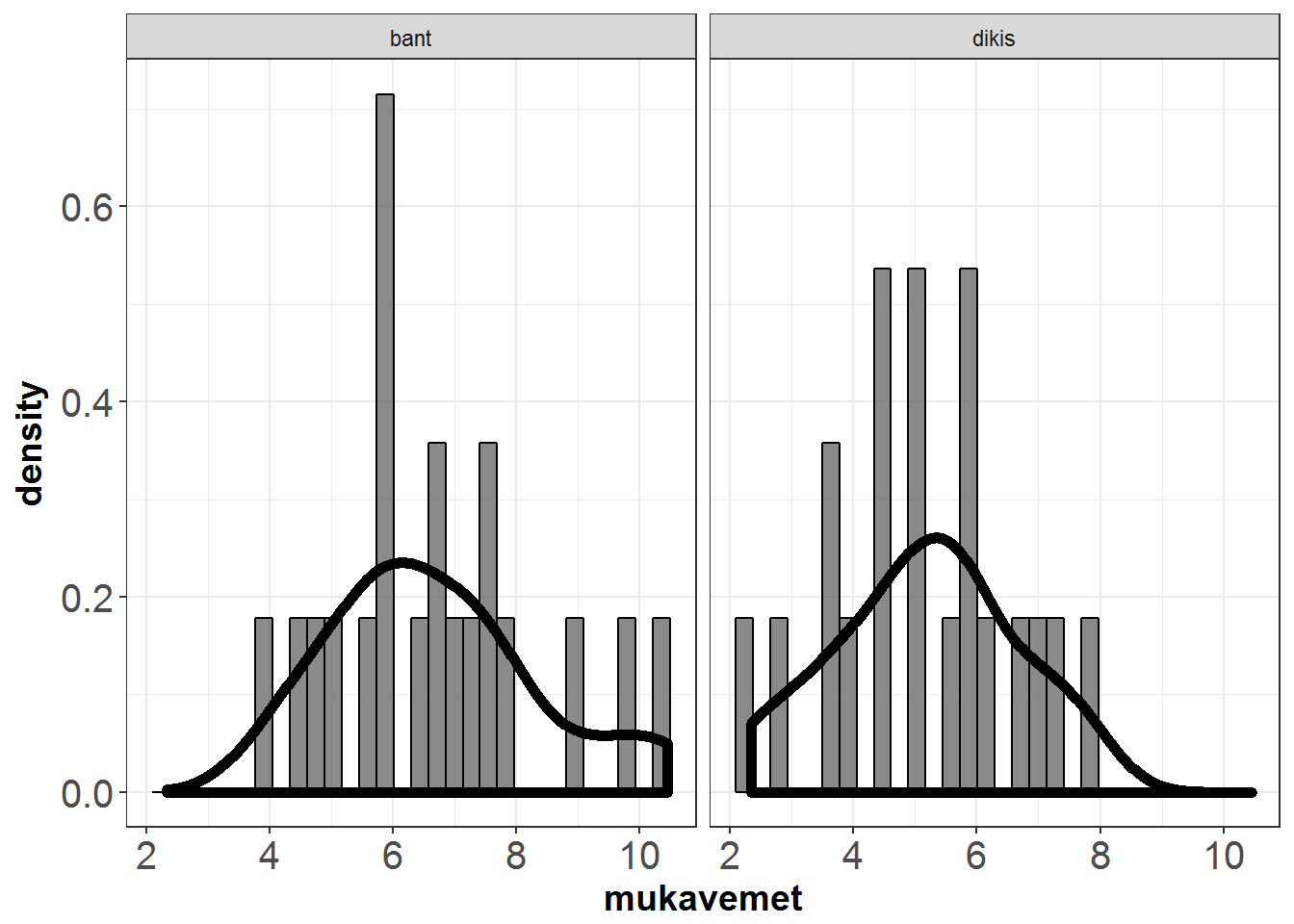
Figure 8.2: Bagli gruplar örnegi
8.2.1 Bağlı gruplar için t testi
Takip edilen basamaklar;
- Betimsel istatistikler
- Test istatistiğinin hesabı
\[t=\frac{\bar{Y_1}-\bar{Y_2}}{\sqrt{\frac{S_1^2+S_2^2-2S_1 S_2 r_{12}}{n}}}\]
3.Kritik değerin hesabı \(\pm t_{\alpha/2,n-1}\), \[H_0:\mu_1-\mu_2=0\] \[H_1:\mu_1-\mu_2 \neq0\]
library(psych)
descDT=with(gerMUK,describe(cbind(bant,dikis)))
descDT
## vars n mean sd median trimmed mad min max range skew
## bant 1 20 6.67 1.71 6.53 6.54 1.45 3.97 10.45 6.48 0.55
## dikis 2 20 5.17 1.49 5.17 5.19 1.30 2.34 7.87 5.53 -0.08
## kurtosis se
## bant -0.45 0.38
## dikis -0.87 0.33
corDT=with(gerMUK,cor(bant,dikis,use="complete.obs"))
corDT
## [1] 0.3536491
# tahmin edilen standart hata (tsh)
tsh=sqrt(((1.71^2+1.49^2)-(2*1.71*1.49*corDT))/(20))
# t-istatistik
tstatistic=(6.67-5.17)/tsh
# alfa=0.05 kritik değer
qt(.975,df=19)
## [1] 2.093024Hesaplanan 3.67, kritik değerden (\(t_{.975,19}=2.09\)) büyük olduğu için boş hipotez terkedilebilir.
Daha kolay bir R satırı;
library(psych)
with(gerMUK, t.test(bant,dikis,paired=T,
alternative="two.sided",
conf.level=0.95))
##
## Paired t-test
##
## data: bant and dikis
## t = 3.6678, df = 19, p-value = 0.001636
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## 0.6429426 2.3520574
## sample estimates:
## mean of the differences
## 1.49758.2.1.1 Raporlama örneği:
Bağlı gruplar t testi hesaplarına dayanarak, gerilim mukavemetinin bant tedavisi (ort=6.67,SS=1.71,çarpıklık=0.55,basıklık=-0.45) ve dikiş tedavisi (ort=5.17,SS=1.49,çarpıklık=-0.08,basıklık=-0.87) arasında farklılık gösterdiği sonucuna varılmıştır, t(19)=3.67, p=0.002 ,r=0.35. Aritmetik ortalamaların farkı için 95% güven aralığı [0.64,2.35] olarak hesaplanmıştır.
8.2.2 Varsayımlar: bağlı gruplar için t testi
Puanların farkı (\(Y_{1i} - Y_{2i}\)) normal bir dağılımdan çekilmiş olmalıdır. Puanların farkları her birey için bağımsız olmalıdır. Bağlı gruplar t testi , örneklem küçük değil ise, normallik varsayımı ihlallerine karşı genellikle dirençlidir.
8.2.3 Dirençli tahminleme yöntemi: bağlı gruplar için t testi
Eğer dağılım normallikten büyük ölçüde ayrılıyor ise, yüzdeli bootstrap prosedürü kullanılabilir (Wilcox (2012),page 201).
#bootstrap ile %95 güven aralığı (normallik varsayımı yok)
set.seed(04012017)
B=5000 # bootstrap tekrar sayısı
alpha=0.05 # alfa
gerMUK=data.frame(ratid=1:20,
bant=c(6.59,9.84 ,3.97,5.74,4.47,4.79,6.76,7.61,6.47,5.77,
7.36,10.45,4.98,5.85,5.65,5.88,7.77,8.84,7.68,6.89),
dikis=c(4.52,5.87,4.60,7.87,3.51,2.77,2.34,5.16,5.77,5.13,
5.55,6.99,5.78,7.41,4.51,3.96,3.56,6.22,6.72,5.17))
output=c()
for (i in 1:B){
#satırları örnekle
bs_rows=sample(gerMUK$ratid,replace=T,size=nrow(gerMUK))
bs_sample=gerMUK[bs_rows,]
mean1=mean(bs_sample$bant)
mean2=mean(bs_sample$dikis)
output[i]=mean1-mean2
}
output=sort(output)
## yönsüz
# d yıldız alt
output[as.integer(B*alpha/2)+1]
## [1] 0.6865
# d yıldız üst
output[B-as.integer(B*alpha/2)]
## [1] 2.2415
##Yönlü x2>x1
# d yıldız alt
output[as.integer(B*alpha)+1]
## [1] 0.837
#yanlış yön x2<x1
# d yıldız üst
output[as.integer(B*(1-alpha))]
## [1] 2.14458.2.3.1 Yönsüz yüzdeli bootstrap için örnek rapor:
Yaraların tedavisinden 10 gün sonra gerilim mukavemeti ölçümleri yapılmıştır. Yara bandı ile (ort=6.67,SS=1.71,çarpıklık=0.55,basıklık=-0.45) dikiş tedavisi (ort=5.17,SS=1.49,çarpıklık=-0.08,basıklık=-0.87) ölçümleri arasındaki fark için 5000 tekrarlı bootstrap prosedürü %95 güven aralığı [0.667,2.2555] olarak hesaplanmıştır. Yeni geliştirilen yara bandı sonrası gerilim mukavemetinin daha yüksek olduğu ve bu farklılığın istatistiksel olarak anlamlı olduğu sonucuna varılmısştır.
8.2.4 Etki büyüklüğü: bağlı gruplar t testi
En basit etki büyüklüğü hesaplama yöntemlerinden biri;8
\[ES=\frac{t}{\sqrt{n}}\]
## dirençli prosedürler farklı sonuç vermediği için
## normallik ve varyans eşitliği varsayımları yapılmıştır.
n=20
tval=3.6678
EB=tval/sqrt(n)
EB
## [1] 0.820145
library(effsize)
cohen.d(gerMUK$bant,gerMUK$dikis,
paired=T, conf.level=0.95,noncentral=F)
##
## Cohen's d
##
## d estimate: 0.820134 (large)
## 95 percent confidence interval:
## inf sup
## 0.1535955 1.4866725effsize paketi (Torchiano 2016) etki büyüklüğünü 0.820 ve ilgili %95 güven aralığını [0.135, 1.505] olarak hesaplamıştır.
8.2.5 Kayıp veriler ile bağlı gruplar t testi
Eklenecek
8.2.6 Destekleyici grafikler
Eklenecek
8.2.7 İstatistiksel güç: bağlı gruplar t testi
#power.t.test
power.t.test(delta=.35, sd=.6,sig.level=0.05, power=0.95,
type="paired", alternative="two.sided")
##
## Paired t test power calculation
##
## n = 40.16447
## delta = 0.35
## sd = 0.6
## sig.level = 0.05
## power = 0.95
## alternative = two.sided
##
## NOTE: n is number of *pairs*, sd is std.dev. of *differences* within pairsBu örnekte belirlenmiş değerler ortalamalar farkı 0.35, standart sapma 0.6, alfa 0.05, yönsüz test ve hedeflenen güç 0.95 seçildiğinde gereken örneklem sayısı 41’dir. Diğer bir ifade ile, 41 katılımcı ile belirlenen değerlere (ortalamalar farkı 0.35, standart sapma 0.6, alfa 0.05, yönsüz test) ulaşılması durumunda \(H_0:\mu_1-\mu_2=0\) boş hipotezinin terkedilme olasılığı %95’tir.
8.3 Yaygın Tasarılar
Sosyal bilimlerde iki ortalamayı kıyaslamak üzere kurulan tasarılardan yaygın olanları özetlenmiştir.
8.3.1 Grupların ilişkili olduğu durumlar
Ortalamaların hesaplandığı puanların farklı gruplar altında ilişkili olup olmadğı önemlidir.
8.3.1.1 Tekrarlanan ölçümler
Aynı katılımcı içiin aynı değişkenin birden fazla ölçülmesi durumu.
- Bireylerin kendi kontrol grubunu oluşturması:
Semantik hafızanın aktivasyon hızını ölçmek üzere 100 üniversite öğrencisi ile araştırma yapılmıştır. Her öğrenci çiftler halinde verilen kelimeleri okumuştur. Okudukları ilk kelime ya bir silah (örneğin mermi, hançer) ya da silah olmayan bir kelimedir. Okudukları ikinci kelime mutlaka agresif bir kelimedir (örneğin yarala, imha et). Her bir öğrenci 192 çift kelimeyi bilgisayarda görüp sesli olarak okumuştur. Bilgisayar ilk kelimeyi 1.25 saniye ekranda tutmuş, .5 saniye siyah ekran göstermiş ve ikinci kelimeyi ekranda göstermiş, her ikinci kelimeden önce reaksiyon zamanını ölçmüştür. Her bireyin reaksiyon zamanı ortalamaları alınmış ve analiz edilmiştir.
| İlk kelime | ||
|---|---|---|
| Öğrenci | Silah | Silah Değil |
| 1 | ||
| 2 | ||
| … | ||
| 100 |
Her öğrencinin kendi okuma hızı olduğundan, Silah ve Silah olmayan kelimeleri okumak için gereken reaksiyon zamanları birbiri ile ilişkilidir.
- Boylamsal tasarılar: 6. sınıf öğrencilerinin matematik başarısı dönem başında ve dönem sonunda ölçülmüştür. Amaç puanların değişip değişmediğini görmektir.
| Zaman | ||
|---|---|---|
| Öğrenci | Dönem başı | Dönem sonu |
| 1 | ||
| 2 | ||
| … | ||
| 48 |
Ölçümler aynı öğrenciler ile tekrarlandığı için puanlar ilişkilidir.
8.3.1.2 Blok tasarıları
Katılımcıların blok olarak ikili eşleştirilmesidir. Her çiftin (blok içindeki) benzer davranması beklenir.
- Rassal blok tasarı: Okuma hızını artırmak için bir program geliştirilmiştir, etkililiğini araştırmak üzere, 30 ikinci sınıf öğrencisi bir okuma testini cevaplamış, ve puanlarına göre çiftler oluşturmuştur.
| Çift | Okuma testi puan sırası |
|---|---|
| 1 | 1,2 |
| 2 | 3,4 |
| … | … |
| 15 | 29,30 |
Görüldüğü gibi en hızlı okuyan 2 öğrenci ilk çifti, en yavas okuyan iki öğrenci son çifti oluşturmuştur.Çiftlerden her biri rassal olarak yeni program grubuna veya kontrol grubuna atanmıştır. As shown, the students with the two highest scores were in the first pair, the students with the
Yeni program son bulduktan sonra öğrencilerin okuma hızları ölçülmüştür
| Çift | Yeni Program | Kontrol |
| 1 | ||
| 2 | ||
| … | ||
| … | ||
| 15 |
- Rassal olmayan blok tasarı: Şiddete maruz kalmış grup çocuğun, şiddet görmemiş daha kalabalık bir gruptan çocuklar ile genel kaygı düzeyi üzerinden eşleştiğini düşünelim. Sonrasında stres anında gösterdikleri endişe durumlarını ölçelim
| Çift | Şiddete maruz kalan | Kontrol |
| 1 | ||
| 2 | ||
| … | ||
| 20 |
- Kalıtsal tasarılar (Familial): 25 anne ve erişkin kızlarının politik görüşleri alınmıştır.
| Çift | ||
|---|---|---|
| Anne | Kız | |
| 1 | ||
| 2 | ||
| … | ||
| 25 |
- Dyadik tasaıları: Afrikalı-Amerikalı ve Avrupalı-Amerikalı çocuklardan oluşturulan çiftler işbirliği gerektiren küçük oyunlar oyamışlardır. Her bir çocuk eşinin işbirlikçiliğini puanlamıştır.
| Etnisite | ||
|---|---|---|
| Çift | Afrikalı-Amerikalı | Avrupalı-Amerikalı |
| 1 | ||
| 2 | ||
| … | ||
| 25 |
8.3.2 Bağlı olmayan grup tasarılarına örnekler
- Tamamen rassal tasarı
İki farklı manyetik ağrı kesici makinesinin performansı karşılaştırılacaktır. 50 hasta rassal olarak, 25-25, iki makineye alınmış, tedaviden sonra ağrı düzeylerini rapor etmişlerdir.
| Makine | |
|---|---|
| 1 | 2 |
| . | |
| . | |
| . |
- Rassal olmayan tasarı: Sekizinci sınıf öğrencilerinden 50 kız ve 50 erkek seçilmiş 2 basamaklı toplama işlemi yapma hızları ölçülmüştür.
References
Myers, Jerome L., A. Well, Robert F. Lorch, and Ebooks Corporation. 2013. Research Design and Statistical Analysis. 3rd ed. New York: Routledge.
Field, Andy P., Jeremy Miles, and Zoë Field. 2012. Discovering Statistics Using R. Thousand Oaks, Calif;London; Sage.
Wilcox, Rand R. 2012. Introduction to Robust Estimation and Hypothesis Testing. 3rd;3; US: Academic Press.
Cohen, Jacob. 1962. “The Statistical Power of Abnormal-Social Psychological Research: A Review.” The Journal of Abnormal and Social Psychology 65 (3): 145–53.
Torchiano, Marco. 2016. Effsize: Efficient Effect Size Computation. https://CRAN.R-project.org/package=effsize.
Çözümlemeler R programlama dili kullanılarak tamamlanmıştır, betimsel istatistikler psych paketi(Revelle 2016), t test istatistiği ise stats paketi (R Core Team 2016b) ile hesaplanmıştır.↩
Lakens (2013) Eşitlik 7, fakat bu değer korelasyon 1’e yaklaştıkça sonsuza yaklaşır. Lakens (2013) Eşitlik 10 daha uygun bir tercih olabilir.\(\frac{mean difference}{(SD_1+SD_2)/2}\)↩