7 Betimleyici İstatistikler ve Hipotez Testi
Betimleyici istatistikler örneklemi tanımlamayı amaçlar. Bu bölüm içeriside daha önce tanıtılan dataWBT (2.3) kullanılarak (a) betimleyici istatistikler hesaplanmış (b) basit grafikler çizilmiş ve (c) hipotez testi açıklanmıştır.
Bu bölümde yer alan R kodlarını kullanmak isteyen araştırmacıların bir önceki bölümü inceledikleri varsayılmıştır. Bu bölümde yer alan basamakların atlanmadan takip edildiği varsayımı da yapılmıltır. dataWBT çalışma alanınıza çağırmak için;
# CSV yükle
urldosya='https://raw.githubusercontent.com/burakaydin/materyaller/gh-pages/ARPASS/dataWBT.csv'
dataWBT=read.csv(urldosya)
#remove URL
rm(urldosya)7.1 Betimleyici İstatistikler
Bu alt bölümde ortalama, ortanca, varyans, standart sapma, çarpıklık ve basıklık hesaplanmıştır. Örneklerde toplumsal cinsiyet algısı (gen_att) değişkeni kullanılmıştır.
7.1.1 Ortalama
Eşitlik (7.1) ’de verildiği gibi, ortalama, bir değişkeni oluşturan değerlerin toplamının toplam değer sayısına bölünmesi ile hesaplanır.
\[\begin{equation} \bar{Y} = \frac{1}{n} \sum\limits_{i=1}^n {Y_i} \tag{7.1} \end{equation}\]# gen_att değişkeninin ortalamasını hesapla
mean(dataWBT$gen_att,na.rm = T)
## [1] 1.940576
# birden fazla değişkenin ortalamasını hesapla
# ?colMeans
colMeans(dataWBT[,c("gen_att","item1")],na.rm = T)
## gen_att item1
## 1.940576 3.4510147.1.2 Ortanca
Büyükten küçüğe veya küçükten büyüğe dizilmiş bir değişkenin orta noktasına ortanca denir. Eğer değişkenin eleman sayısı (n) tek sayı ise \(({(n+1)/2}).\) sırada yer alan, eğer çift sayı ise \((n/2).\) ve \(((n+1)/2).\) değerin ortalaması ortancayı verir.
# Ortanca hesapla
median(dataWBT$gen_att,na.rm = T)
## [1] 27.1.3 Varyans
Varyans değişkenin ne kadar yayıldığını anlamada çok kullanılan bir ölçüdür. Eşitlik (7.2) ile hesaplanır.
\[\begin{equation} s_Y^2 = \frac{1}{{n - 1}}\sum\limits_{i = 1}^n {\left( {Y_i - \bar Y} \right)^2 } \tag{7.2} \end{equation}\]#varyans hesapla
var(dataWBT$gen_att,na.rm = T)
## [1] 0.36384087.1.4 Standart Sapma
Varyansın kareköküdür ve Eşitlik (7.3) ile hesaplanır.
\[\begin{equation} s_Y = \sqrt {\frac{1}{{n - 1}}\sum\limits_{i = 1}^n {\left( {Y_i - \bar Y} \right)^2 } } \tag{7.3} \end{equation}\]#SS hesapla
sd(dataWBT$gen_att,na.rm = T)
## [1] 0.60319227.1.5 Çarpıklık (Skewness)
Çarpıklık değeri dağılımın şekli hakkında bilgi verir. Tamamen simetrik olan bir dağılımın çarpıklık değeri 0’dır.
Dağılımın sol kuyruğu sağ kuyruğuna nazaran uzun olduğunda çarpıklık değerinin sıfırdan küçük çıkması tipiktir. Bu tür dağılımlar sola çarpık veya negatif çarpık olarak isimlendirilir. Bu tür dağılımlarda medyan ortalamadan yüksektir
Dağılımın sağ kuyruğu sol kuyruğuna nazaran uzun olduğunda çarpıklık değerinin sıfırdan büyük hesaplanması tipiktir. Bu tür dağılımlar sağa çarpık veya pozitif çarpık olarak isimlendirilir. Bu tür dağılımlarda medyan ortalamadan küçüktür.
Örneklem için çarpıklık formülü2
\[\begin{equation} \sqrt{n}\frac{\sum_{i}^{n}\left ( X_{i}-\bar{X} \right )^{3}} {\left (\sum_{i}^{n} \left ( X_{i}-\bar{X} \right )^{2} \right )^{3/2}} \tag{7.4} \end{equation}\]Örneklem için çarpıklık değeri moments (Komsta and Novomestky 2015) paketinde yer alan skewness fonksiyonu ile hesaplanabilir.
#çarpıklık hesapla
library(moments)
skewness(dataWBT$gen_att,na.rm = T)
## [1] 0.377095NOT: Çarpıklık ve basıklık değerleri için standart hata ve sonrasında z-puanı hesaplanabilir.
Hesaplanan bu z-puanı seçilen bir kritik değer ile (ör. 1.96) kıyaslanarak
çarpıklık veya basıklığın istatistiksel olarak anlamlı olup olmadığı sınanabilir.
Benzer şekilde normallik testleri de (ör. Shapiro-Wilk) yapılabilir. Fakat bu testler
örneklem büyüklüğüne hassasstır. Bir diğer deyişle örneklem büyüdükçe çok küçük farklılıklar
istatistiksel olarak anlamlı bulunabilir.
Çarpıklık,basıklık veya normallik testlerinin varsayım ihlallerini tespit etmek
üzere kullanılışı nispeten eskimiş yöntemlerdir. Bu testleri kullanmak yerine normallik
grafik üzerinden incelenip, dirençli tahminleyicilerin (robust estimators) veya
Monte Carlo simulasyon tekniklerinin çıktıları incelenebilir.7.1.5.1 Çarpıklık örnekleri
Normal bir dağılım ve çarpıklık istatistiği;
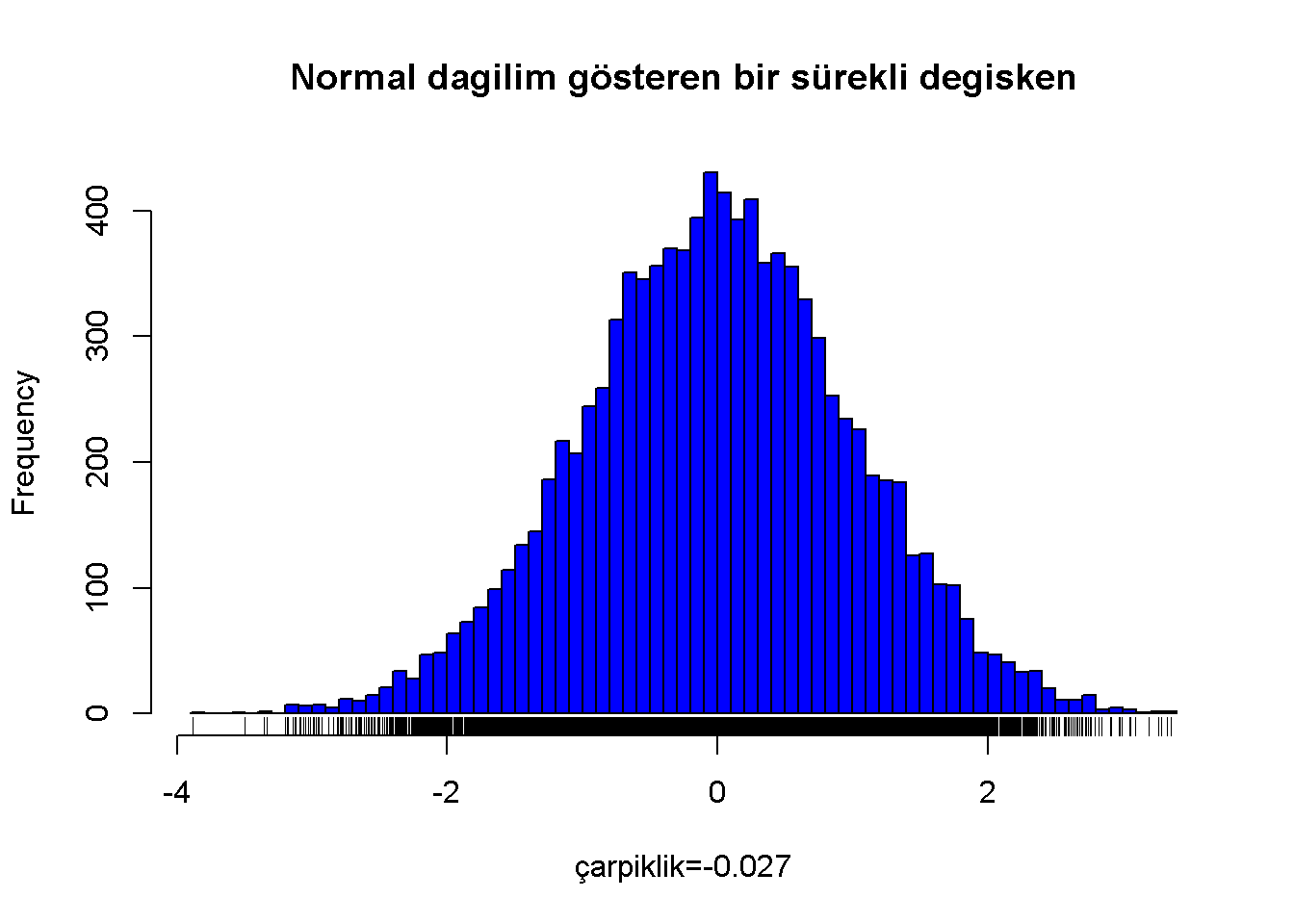
Figure 7.1: Normal dagilim gösteren bir sürekli degisken
Sola çarpık sürekli değişken;
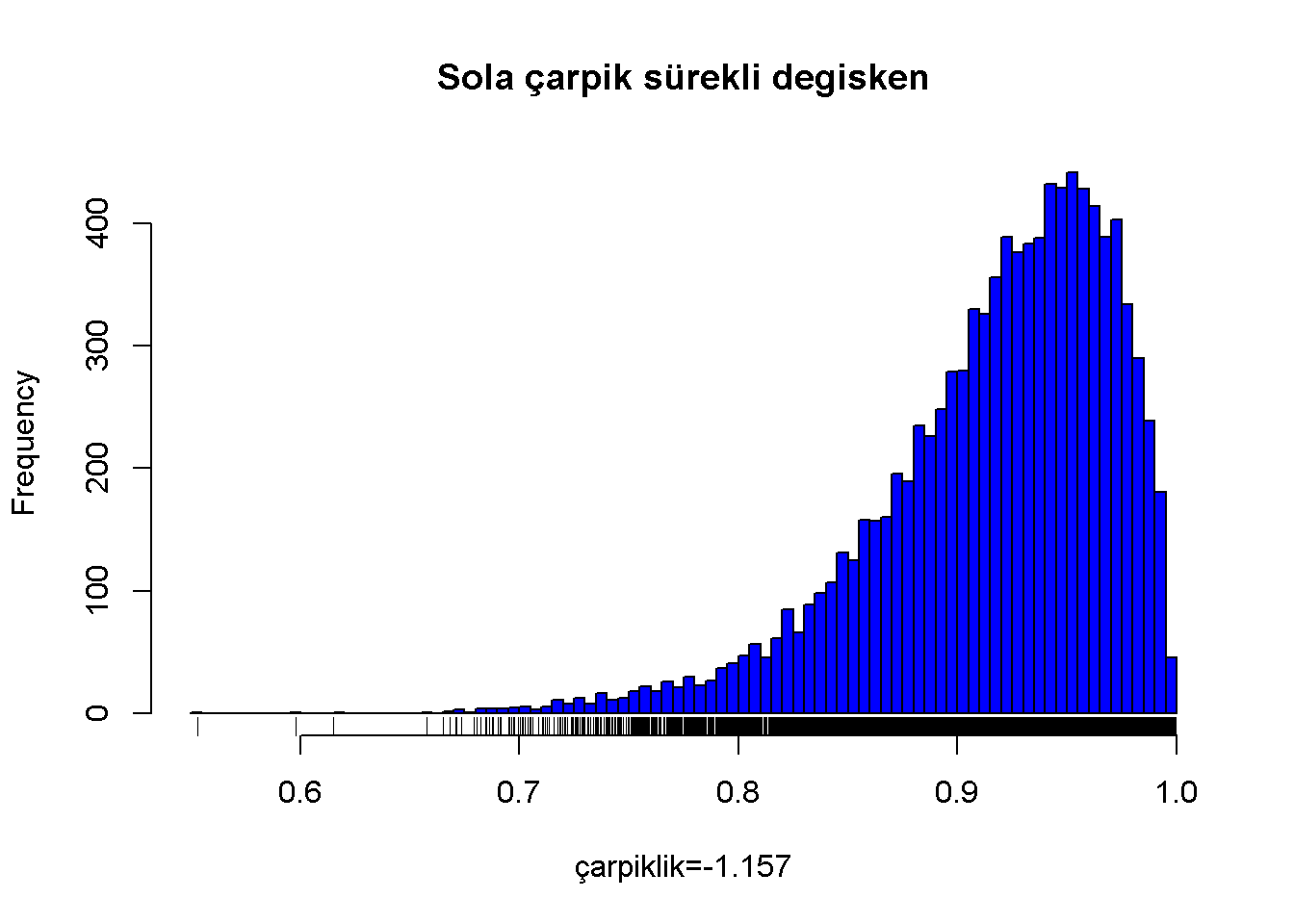
Figure 7.2: Sola çarpik sürekli degisken
Sağa çarpık sürekli değişken;
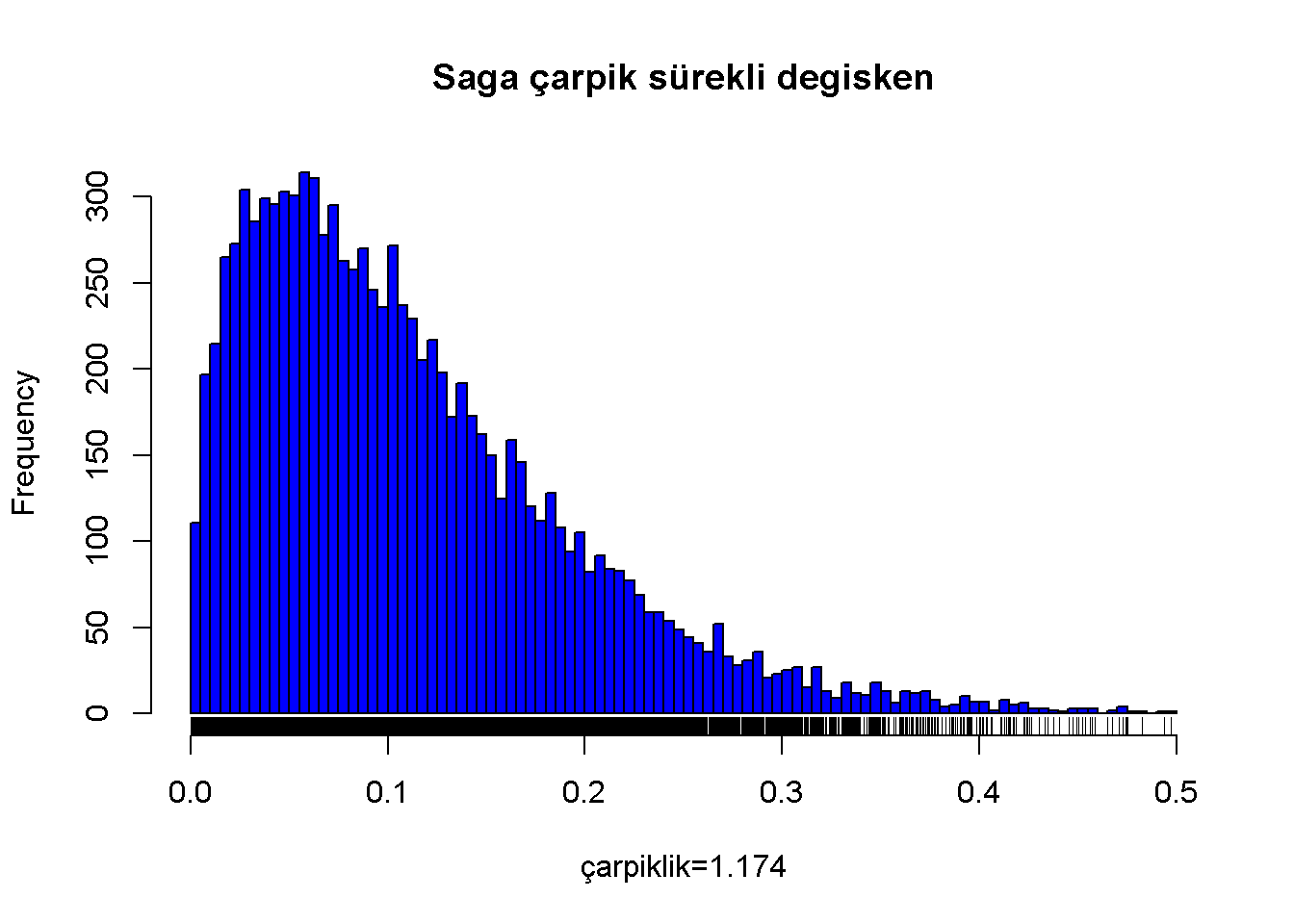
Figure 7.3: Saga çarpik sürekli degisken
7.1.6 Basıklık (Kurtosis)
Basıklık değeri dağılımın şekli hakkında bilgi verir. Normal bir dağılımın Pearson basıklık değeri 3’tür. Eşitlik (7.5) basıklık değerinin hesaplanışını gösterir.
\[\begin{equation} n\frac{\sum_{i}^{n}(X_i-\bar{X})^4}{(\sum_{i}^{n}(X_i-\bar{X})^2)^2} \tag{7.5} \end{equation}\]Eşitlik (7.5) sıfırdan küçük değerler vermez. 0 ile 3 arasında yer alan değerler genellikle düz dağılımlarda hesaplanır, örneğin tekdüzey dağılımlar. Uzun kuyruklu dağılımlarda 3’ten büyük değerler görülebilir. Alanyazında yorumu kolaylaştırmak için Eşitlik (7.5) ’ten 3 çıkarıldığı durumlar mevcuttur.
Örneklem için Pearson basıklık değeri moments (Komsta and Novomestky 2015) paketinde yer alan kurtosis fonksiyonu ile hesaplanabilir.
#basıklık hesapla
library(moments)
kurtosis(dataWBT$gen_att,na.rm = T)
## [1] 2.9039057.1.6.1 Basıklık Örnekleri
Normal bir dağılım ve basıklık ölçüsü
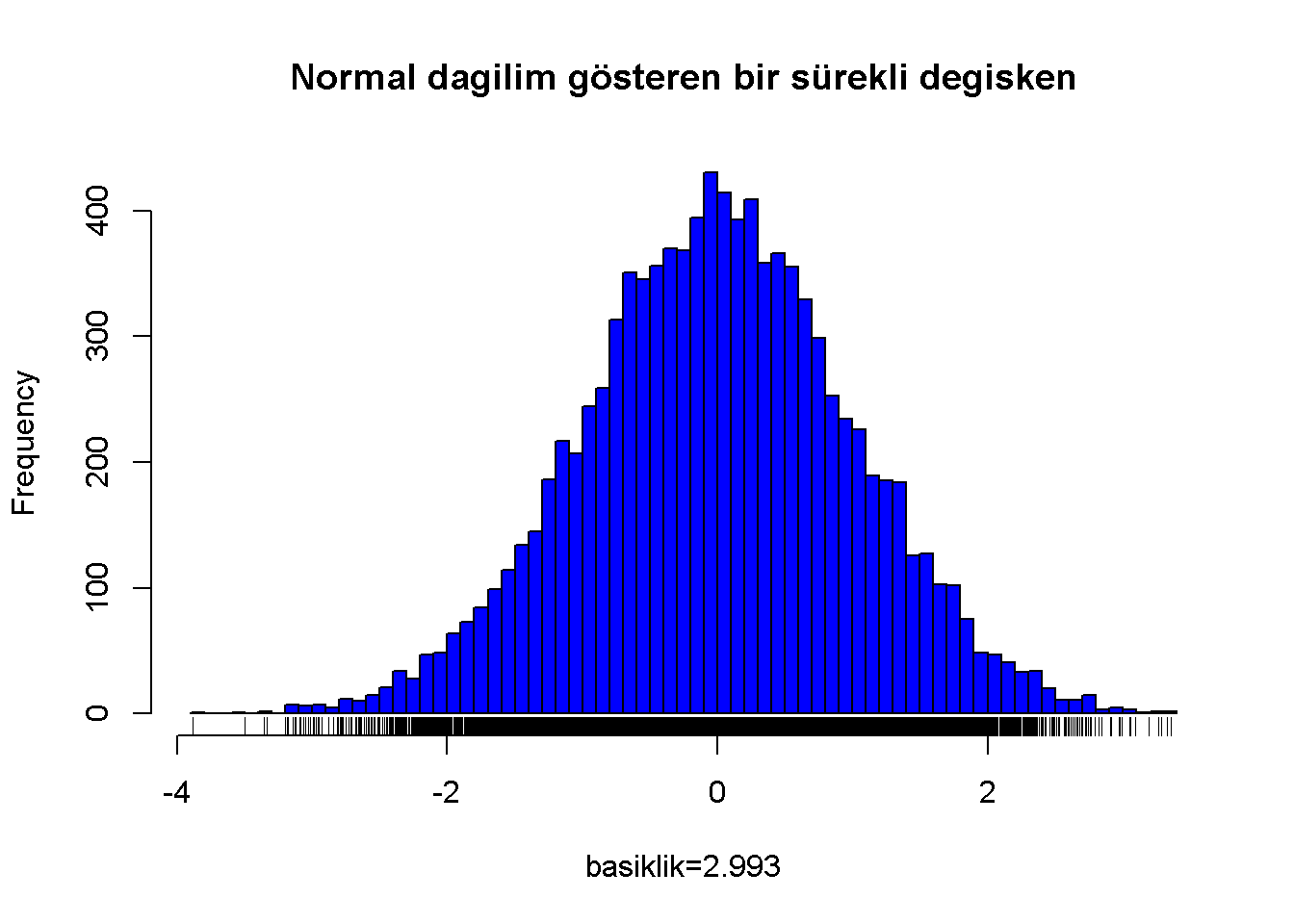
Figure 7.4: Normal dagilim gösteren bir sürekli degisken
Tekdüzey bir dağılım ve basıklık değeri
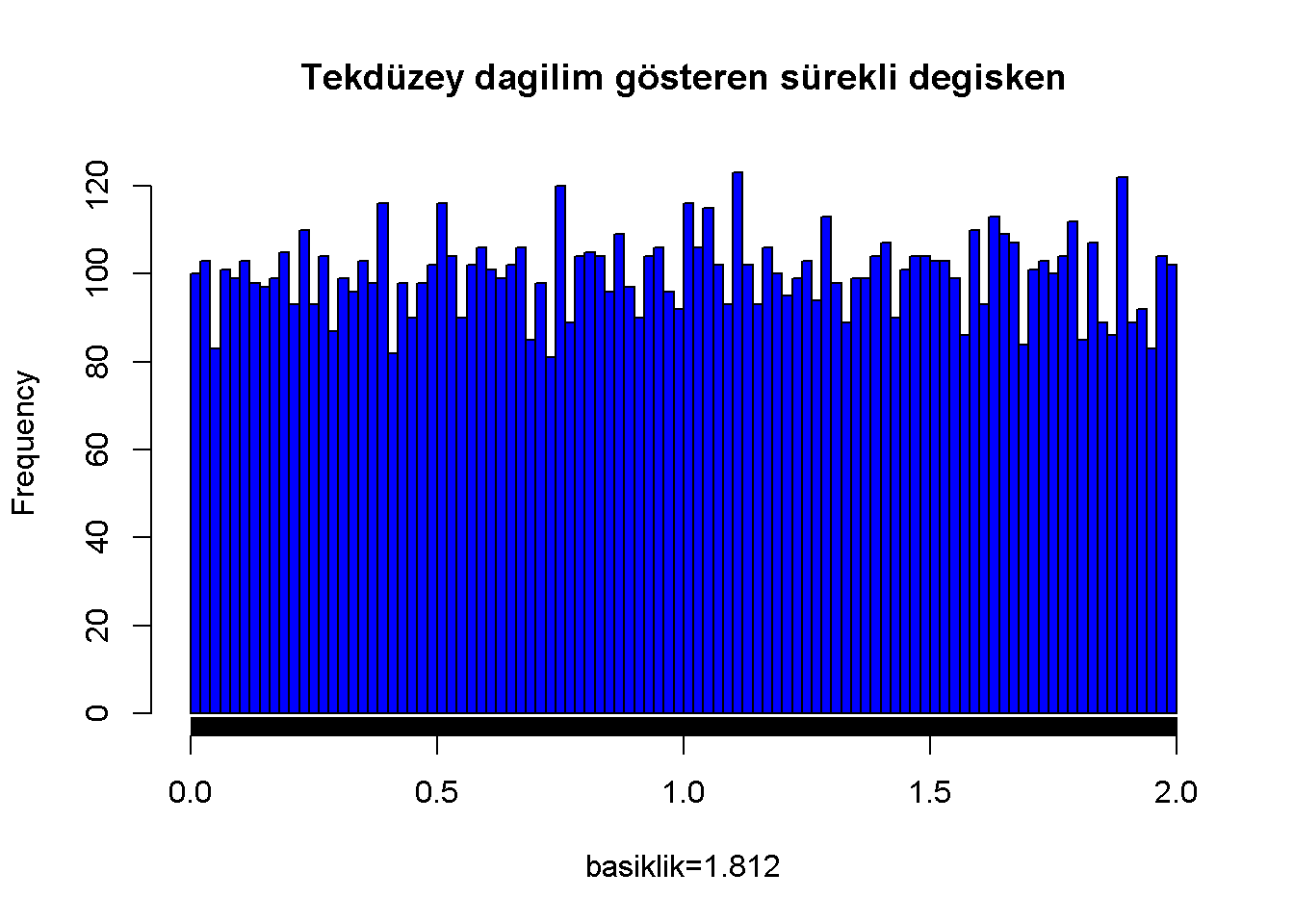
Figure 7.5: Tekdüzey dagilim gösteren sürekli degisken
Beta dağılımı gösteren bir sürekli değişken
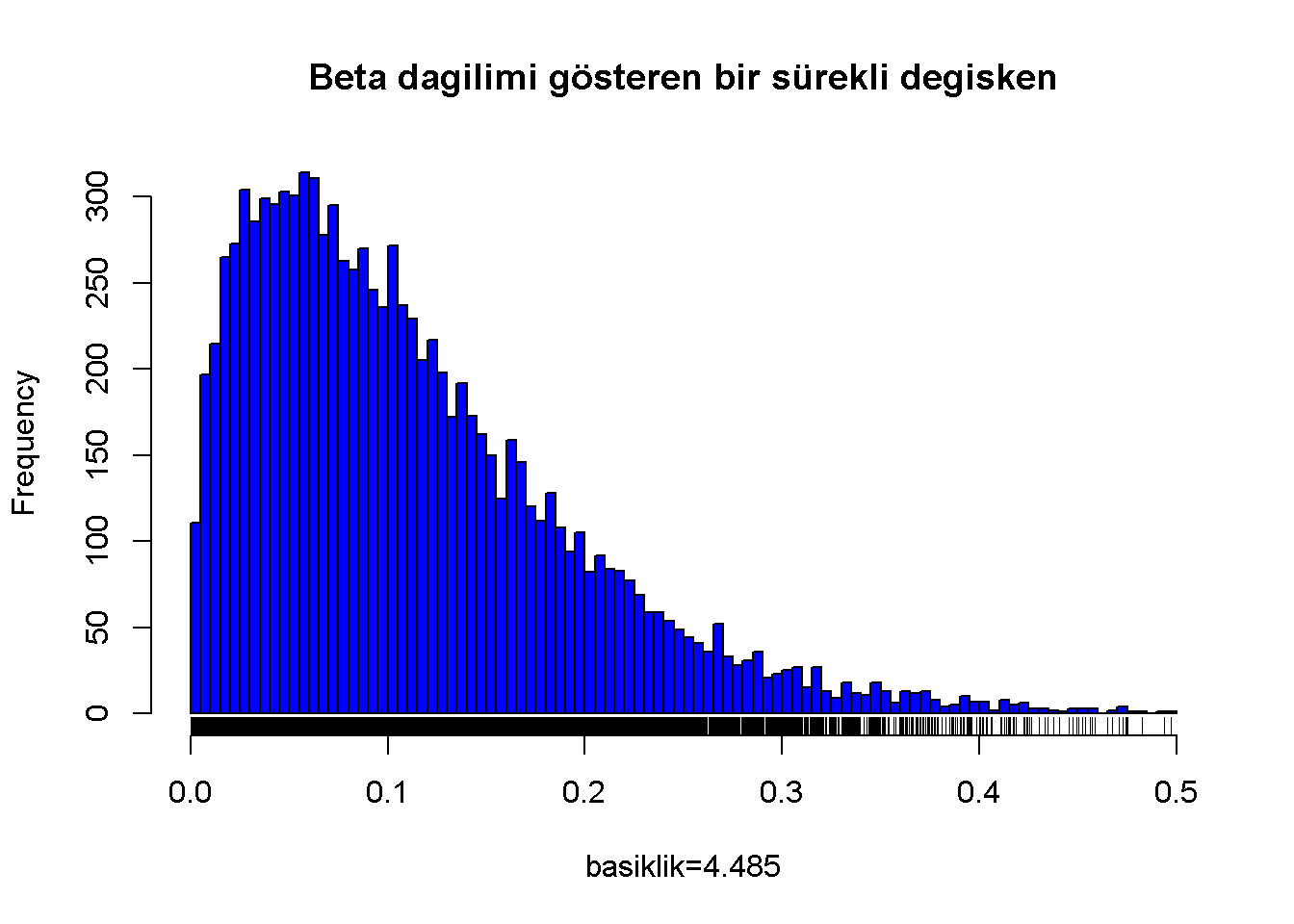
Figure 7.6: Beta dagilimi gösteren bir sürekli degisken
7.1.7 Betimleyici İstatisklerin Raporlanması
psych (Revelle 2016), doBy (Højsgaard and Halekoh 2016) ve apaStyle (de Vreeze 2016) paketleri betimsel analizleri rapor etmede yardımcı olabilir.
# psych paketi describe fonksiyonu sırasıyla;
# n: gözlem sayısı (kayıp veriler hariç)
# ortalama, ss, ortanca, budanmış ortalama (trim=0.05 5% budanmış)
# ortanca mutlak dağılımı (median absolute deviation),
# minimum, maksimum, ranj
# çarpıklık ve basıklık-3 (type=2 popülasyon basıklık ve çarpıklık)
# standart hata
library(psych)
desc1=describe(dataWBT[,c("gen_att","age")],trim = 0.05,type=3)
desc1
## vars n mean sd median trimmed mad min max range skew
## gen_att 1 5302 1.94 0.60 2 1.92 0.59 1 4 3 0.38
## age 2 5308 27.08 7.21 25 26.62 5.93 15 60 45 0.96
## kurtosis se
## gen_att -0.10 0.01
## age 0.63 0.10
# kaydet
write.csv(desc1,file="pscyhbetimsel.csv")
#doBy
# program değişkenine göre betimleyici istatistikler
library(doBy)
library(moments)
desc2=as.matrix(summaryBy(gen_att+age~treatment, data = dataWBT,
FUN = function(x) { c(n = sum(!is.na(x)), nmis=sum(is.na(x)),
m = mean(x,na.rm=T), s = sd(x,na.rm=T),
skw=moments::skewness(x,na.rm=T),
krt=moments::kurtosis(x,na.rm=T)) } ))
#yuvarlama
round(desc2,2)
## treatment gen_att.n gen_att.nmis gen_att.m gen_att.s gen_att.skw
## 1 1 2736 265 1.93 0.6 0.38
## 2 2 2566 335 1.95 0.6 0.38
## gen_att.krt age.n age.nmis age.m age.s age.skw age.krt
## 1 2.90 2739 262 26.89 7.17 0.99 3.69
## 2 2.91 2569 332 27.28 7.24 0.93 3.57
write.csv(round(desc2,2),file="doBydesc.csv")
#apaStyle
# APA formatında tablo
library(apaStyle)
apa.descriptives(data = dataWBT[,c("gen_att","age")],
variables = c("Gender Attitude","Age"), report = c("M", "SD"),
title = "APAtableGenderAge", filename = "APAtableGenderAge.docx",
note = NULL, position = "lower", merge = FALSE,
landscape = FALSE, save = TRUE)
##
## Word document succesfully generated in: C:/Users/Burak/Desktop/github/SARP
#apaStyle paketi hata veriyorsa;
#https://www.r-statistics.com/2012/08/how-to-load-the-rjava-package-after-the-error-java_home-cannot-be-determined-from-the-registry/
#Sys.setenv(JAVA_HOME='C:\\Program Files\\Java\\jre1.8.0_111')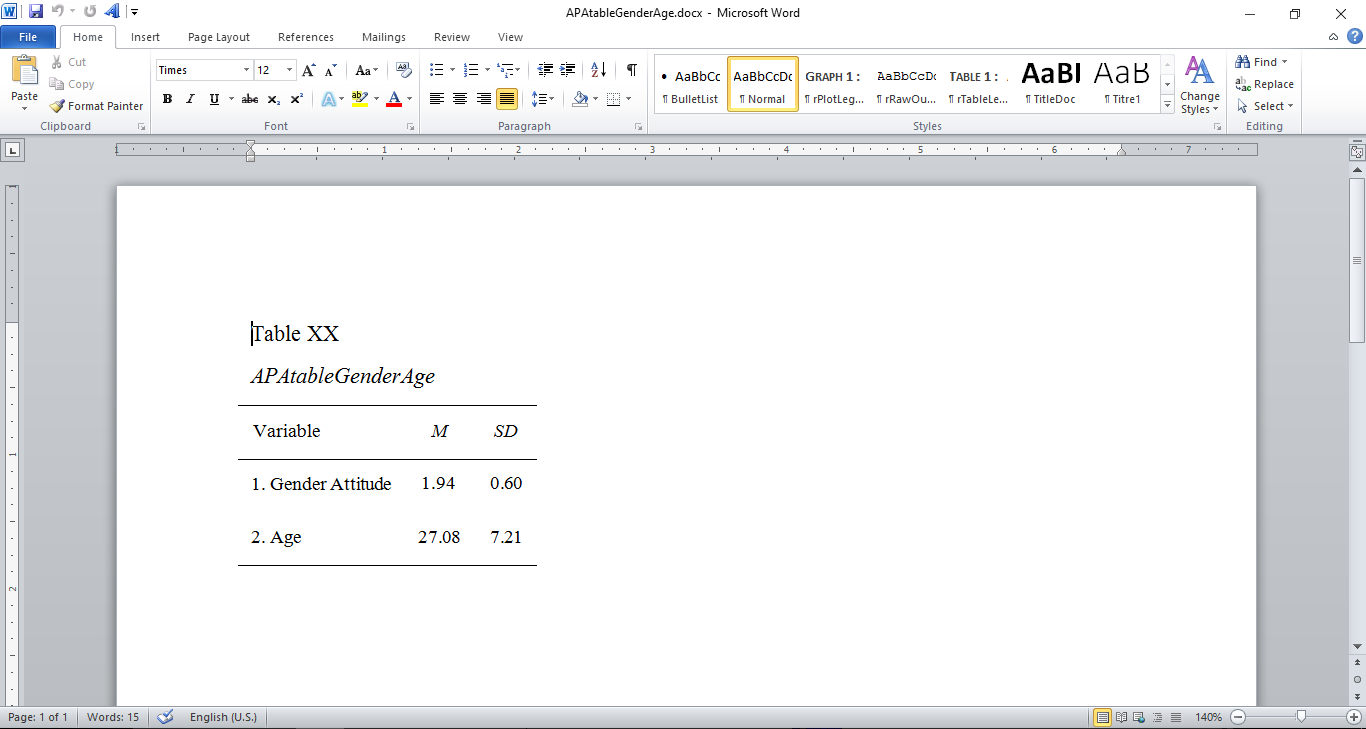
Figure 7.7: APA Tablo.docx
7.1.7.1 Betimsel İstatistik Rapor Örneği
Toplumsal cinsiyet algısı puanları 5302 katılımcı için 1 ve 4 arasında değişmiştir, ortanca 2, ortalama 1.94 ve standart sapma 0.6 olarak hesaplanmıştır. Puanların dağılımı örneklem bazında 0.38 çarpıklık ve -0.1 basıklık değerine sahiptir.
7.2 Basit Grafikler
R programı ile basit olmayan grafikler çizilebilir. Popüler olan grafik oluşturma yöntemlerinden dört tanesi, base(R Core Team 2016b), lattice(Sarkar 2016), ggplot2(Wickham and Chang 2016) ve plotrixtir(Lemon et al. 2016). Bu materyal ggplot2 kullanmıştır. Bir ggplot fonksiyonunda argüman sayısı oldukça fazladır, bu sayede kullanıcılar grafiğin her noktasında değişiklik yapabilirler.
7.2.1 Histogram
Dikdörtgenlerden oluşan histogram grafikleri değişken içerisinde yer alan değerlerin frekanslarına göre oluşturulur.
7.2.1.1 Tek değişken için histogram
Dağılım hakkında bilgi sahibi olmak için kullanışlıdır.
library(ggplot2)
ggplot(dataWBT, aes(x = gen_att)) +
geom_histogram(binwidth = 0.2)+ theme_bw()+labs(x = "Toplumsal Cinsiyet Algısı ")+
theme(axis.text=element_text(size=15),
axis.title=element_text(size=14,face="bold"))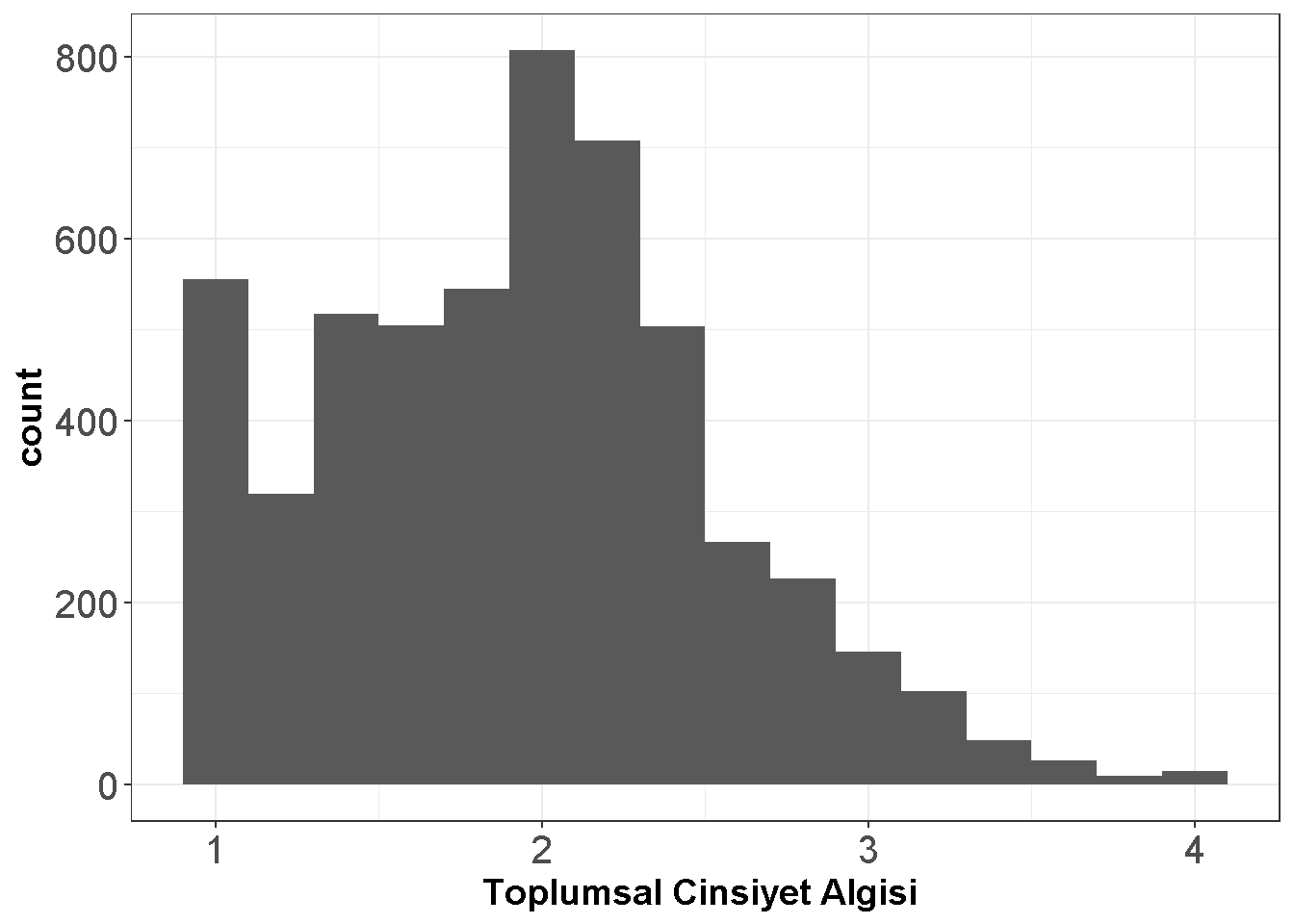
Figure 7.8: Toplumsal Cinsiyet Algisi Puan Dagilimi
7.2.1.2 Tek değişken tek faktör histogram
Gruplara dayalı farklılıkları görmek için kullanışlı
dataWBT$HEF=droplevels(factor(dataWBT$higher_ed,
levels = c(0,1),
labels = c("Lise ve altı", "Üniversite")))
ggplot(dataWBT, aes(x = gen_att, fill=HEF,drop=T)) +
geom_histogram(breaks=seq(1, 4, by =0.2),alpha=.5,col="black")+
theme_bw()+labs(x = "Toplumsal Cinsiyet Algısı",fill='Yüksek Öğretim Durumu')+
theme(axis.text=element_text(size=15),
axis.title=element_text(size=14,face="bold"))
dataWBT2=na.omit(dataWBT[,c("gen_att","HEF")])
ggplot(dataWBT2, aes(x = gen_att)) +
geom_histogram(breaks=seq(1, 4, by =0.2),alpha=.5,col="black")+
theme_bw()+labs(x = "Toplumsal Cinsiyet Algısı")+ facet_wrap(~ HEF)+
theme(axis.text=element_text(size=15),
axis.title=element_text(size=14,face="bold"))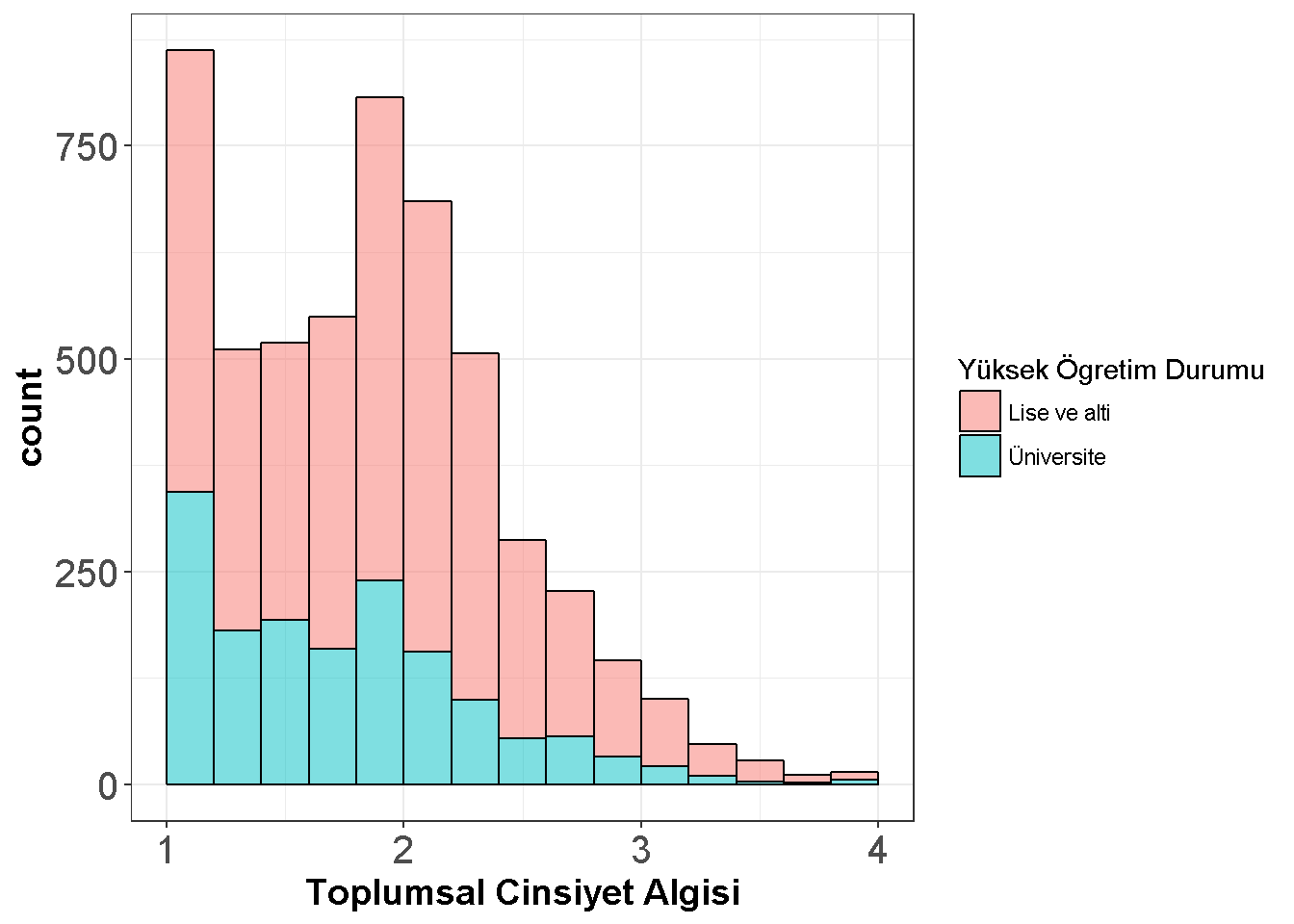
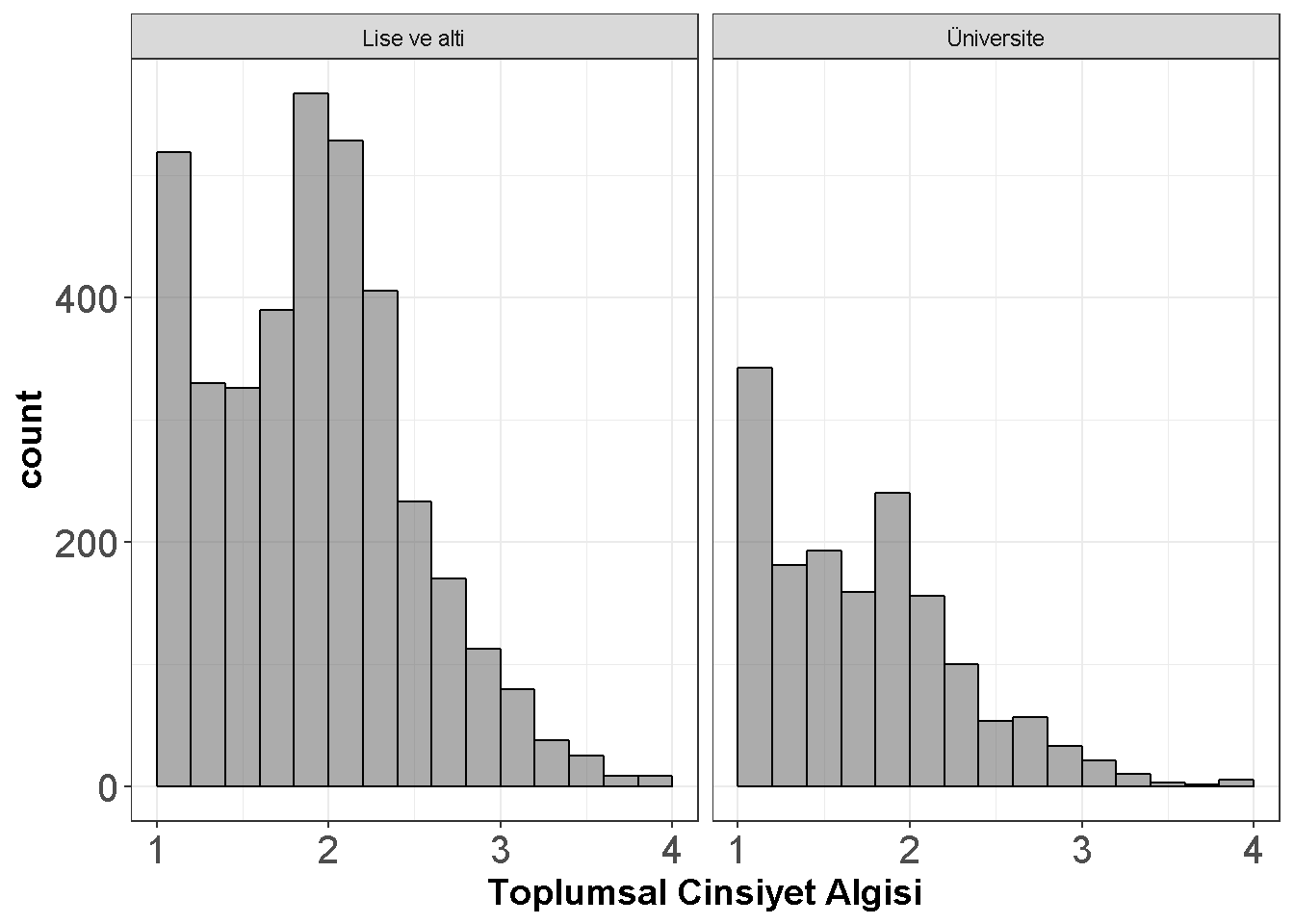
Figure 7.9: Egitime Göre Toplumsal Cinsiyet Algisi
library(ggplot2)
ggplot(dataWBT, aes(x = gen_att)) +
geom_histogram(binwidth = 0.2)+ theme_bw()+
facet_wrap(~city, ncol = 8)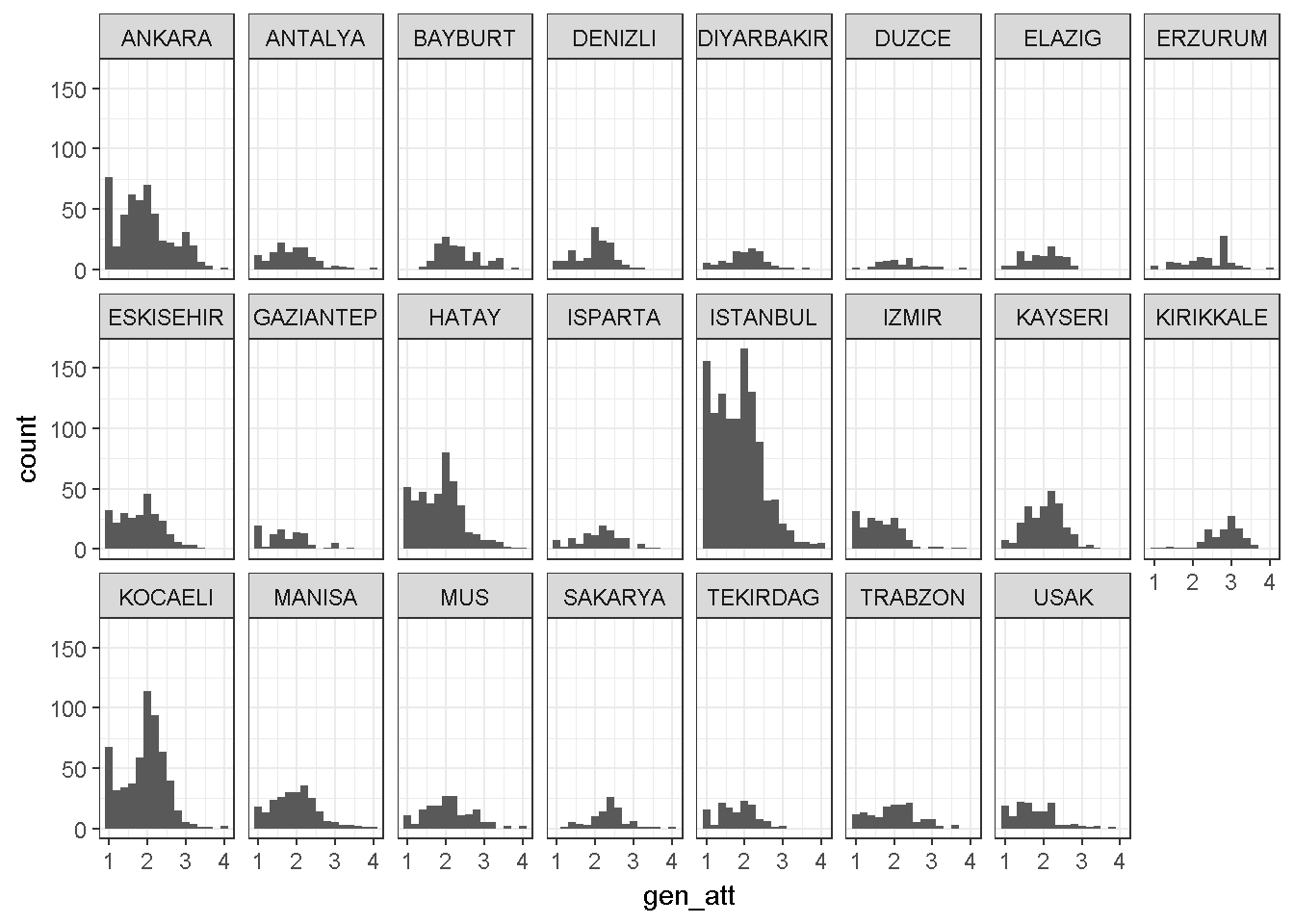
7.2.1.3 Tek değişken iki faktör histogram
Useful for two way interactions
dataWBT2=na.omit(dataWBT[,c("gen_att","HEF","gender")])
ggplot(dataWBT2, aes(x = gen_att,fill=gender)) +labs(fill='Gender')+
geom_histogram(binwidth = 0.2,alpha=.5)+ theme_bw()+
facet_grid(~HEF)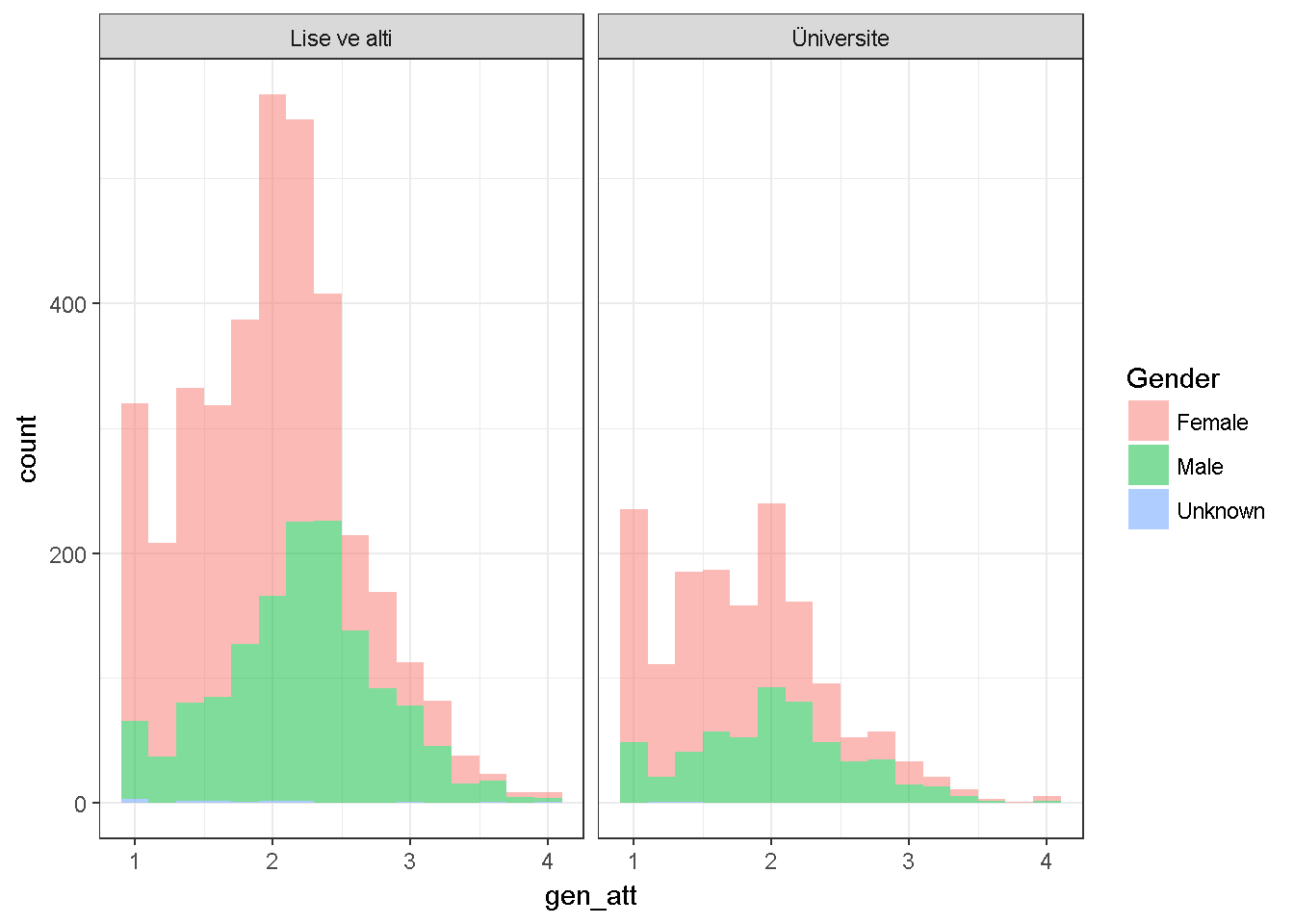
7.2.1.4 Tek değişken üç faktör histogram
Etkileşim (interaction) açıklamada kullanışlı
dataWBT$Condition=droplevels(factor(dataWBT$treatment,
levels = c(1,2),
labels = c("treatment", "control")))
dataWBT2=na.omit(dataWBT[,c("gen_att","HEF","gender","Condition")])
ggplot(dataWBT2, aes(x = gen_att,fill=gender)) +labs(fill='Gender')+
geom_histogram(binwidth = 0.2,alpha=.5)+ theme_bw()+
facet_grid(~HEF+Condition)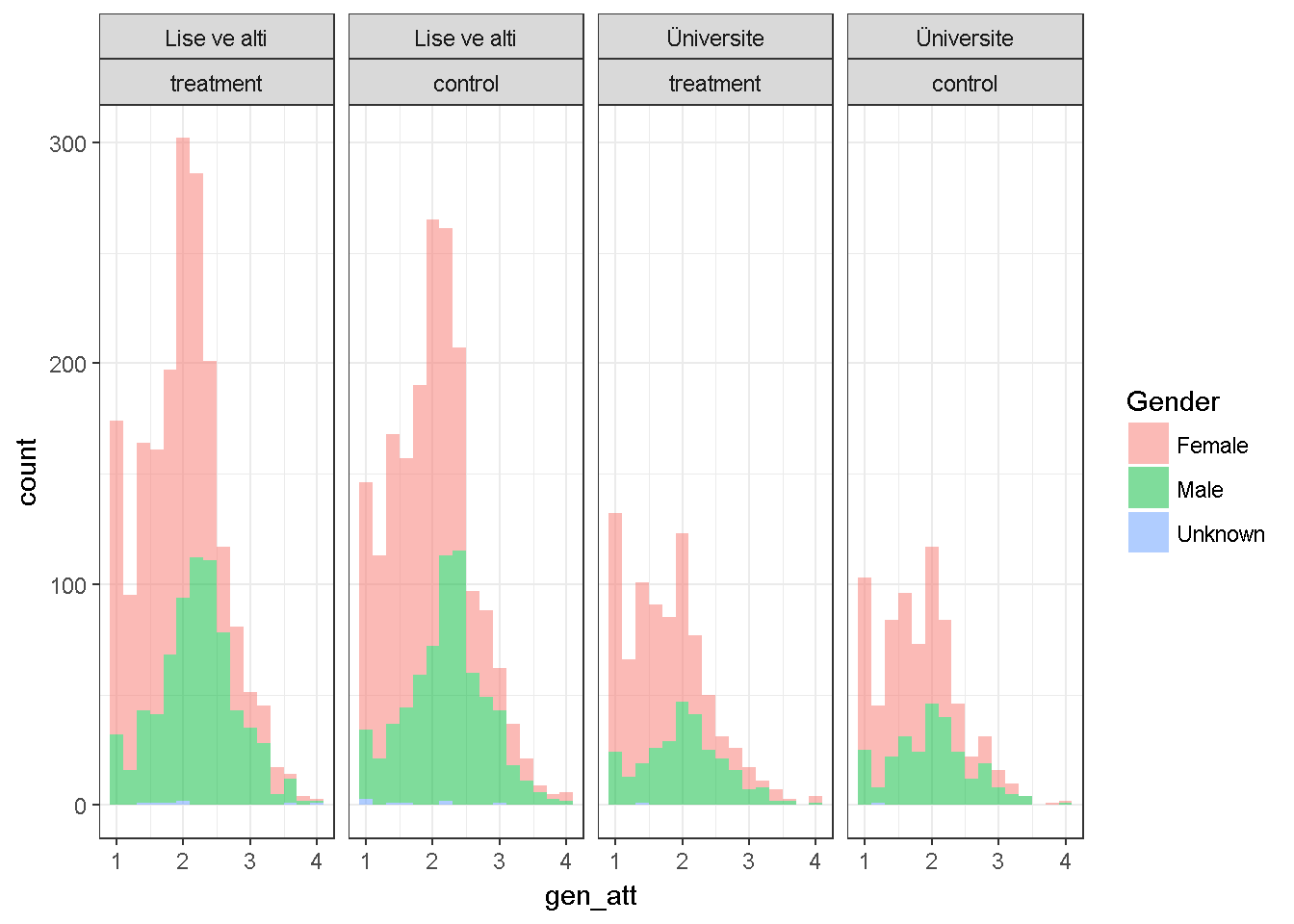
7.3 Hipotez Testi Tanıtım
Cambridge sözlüğü evren (popülasyon) tanımı olarak “aynı ülke, aynı alan veya aynı yerde yaşayan insan veya canlı grubu” cümlesini kullanır. Sosyal bilimlerde evren genellikle “belli bir gruba ait bütün insanlar” olarak belirlenir. Örneğin sekiz yaşındaki tüm öğrenciler, belli bir ülkede bulunan sekiz yaşındaki tüm öğrenciler, 8 yaşında disleksi teşhisi konulan öğrenciler.
Sosyal bilimciler araştırma soruları doğrultusunda ilgili evreni tanımlar. Evrende yer alan bireylerin (unit) gözlenlenebilen karakteristik özellikleri değişkenleri oluşturur. Diğer bir ifade ile değişkene ait popülasyon tanımlanabilir. Bölüm 5.2.3 ’de değişken türleri açıklanmıştır. Evren değişkene ait bütün değerleri kapsar, bu değerlere ait bir ranj ve görülme olasılığı (probability of occurence) vardır. Yoğunluk (probability, sürekli değişken için) ve çoğunluk (mass, sürekli olmayan değişken için) fonksiyonları görülme olasılıklarını formüle etmek için kullanışlıdır. Dağılım hakkında yapılacak geçerli bir varsayım ile örneklemden evrene genellemeler yapılabilir.
Seçkisiz seçilen bir örneklem ile ulaşılan değişken evrende sahip olduğu bütün değerleri içermeyebilir. Fakat, özellikle gözlem sayısı küçük değil ise, seçkisiz seçme işleminde sistematik bir yanlılık görülmeyeceği düşünüldüğünde, örneklemin evrene benzer özellikler göstermesi beklenir.Bu bilgi kullanılarak evrene ait bir parametre örneklemden yola çıkarak tahmin edilebilir. Bu işlem genellikle bir model sayesinde olur. Modelin veriye gösterdiği uyum araştırmacı tarafından değerlendirilir. Hipotez testleri kullanılan bir model sonrasında araştırma soruları ile ilgili karara varma sürecidir.
7.3.1 Örnekleme Dağılım (Sampling Distribution)
Seçkisiz bir örneklem için hesaplanmış bir istatistik aslında bir değişkendir ve belli bir dağılıma sahiptir. Örnekleme dağılım konusununu açıklamak için en çok kullanılan istatistik aritmetik ortalamadır. Merkezi limit teoremine göre basit seçkisiz örneklem kullanıldığında3 değişkenin evrende gösterdiği dağılımdan bağımsız olarak, o değişkene ait örneklem ortalamalarının dağılımı yaklaşık olarak normaldir. Örneklem büyüdükçe ;
\[\begin{equation} \bar X_n \sim N(\mu, \frac{\sigma^2}{n}). \tag{7.6} \end{equation}\]Eğer evren bazında dağılım normal ise (7.6) küçük örneklemler için de doğrudur. Ortalamanın örnekleme dağılımına ait standart sapma ortalamanın standart hatası olarak isimlendirilir ve istatistiksel çıkarımlarda kullanılır. Eşitlik (7.6) içinde yer alan \(\mu\) ve \(\sigma^2\) bilinmezdir. Fakat bu eşitlik örnekleme ait ortalamanın evrene ait ortalamayı ne derecede kestirebileceğini anlamada önemlidir. Örneğin bir araştırmacının basit seçkisiz yöntemle 10 kişilik bir örneklem seçtiğini düşünelim. Araştırmacının bilemeceği parametrelerin ise \(\mu=100\) ve \(\sigma=15\) olduğunu düşünelim. Bu durumda örnekleme dağılım için standart sapma \((15⁄\sqrt{10})=4.74\) olarak bulunur. %95 olasılıkla araştımacının 10 kişilik örneklem ile ulaşacağı aritmetik ortalama 90.7 ve 109.3 arasında olacaktır. Bu oldukça geniş bir aralıktır. Fakat araştırmacı 10 kişi yerine 100 kişiyi aynı örneklem ile seçseydi ulaşacağı örneklem ortalaması %95 olasılıkla 97.1 ve 102.9 olacaktır.
Bu noktada önem taşıyan konu, örneklemden gelen bilgilerle evrene ait parametrelerin hangi tahminleme yöntemleri (estimator) ile yansız, tutarlı ve keskin (unbiased, consistent and efficient) olarak kestirebileceğidir. Örneğin \(\mu\), Eşitlik (7.1) ile, \(\sigma^2\) ise Eşitlik (7.2) ile yansız olarak kestirilebilir.
7.3.1.1 Yansız tahminleme ve örnneklem seçimi
Eklenecek
7.3.2 Güven Aralıkları (The Confidence Intervals (CI))
Dağılım hakkında yapılacak bir varsayım, örneklemden gelen bilgi ve uygun bir tahminleyici (estimator to produce a point estimate) kullanılarak güven aralıkları oluşturulabilir. Bir güven aralığı evren parametresinin muhtemelen hangi aralıkta olduğunu gösterir. Fakat bu evren parametresinin bu aralıkta kesinlikle yer aldığı anlamına gelmez. Örnekleme ait aritmetik ortalamadan yola çıkarak evren parametresi için güven aralığı hesaplamak oldukça basittir.Değişkene ait dağılımın normal olduğu varsayıldığında, ortalamanın örnekleme dağılımı da normaldir ve örnekleme ait ortalama yansız bir tahmindir. Normal dağılım bilindik özellikleri vardır, yoğunluk fonksiyonu değerlerin %95’inin ortalamadan 1.96 standart sapma aşağıda ve yukarıda olduğunu gösterir. Normal dağılımın bu özelliği grafik 7.10 ile gösterilmiştir. Mavi ile işaretlenen bölgeden bir gözlem yapma olasılığı %5tir. Benzer şekilde, mavi veya sarı ile işaretlenen bölgeden gözlem yapma olasılığı da %10’dur. Gri bölge (\(\pm 1\)) yoğunluğun yaklaşık olarak %68’ini kapsar.Bu bilgi kullanışlıdır. Örneklem için hesaplanan ortalama ve varyans \(\mu\) için güven aralığı hesaplamada kullanılabilir.
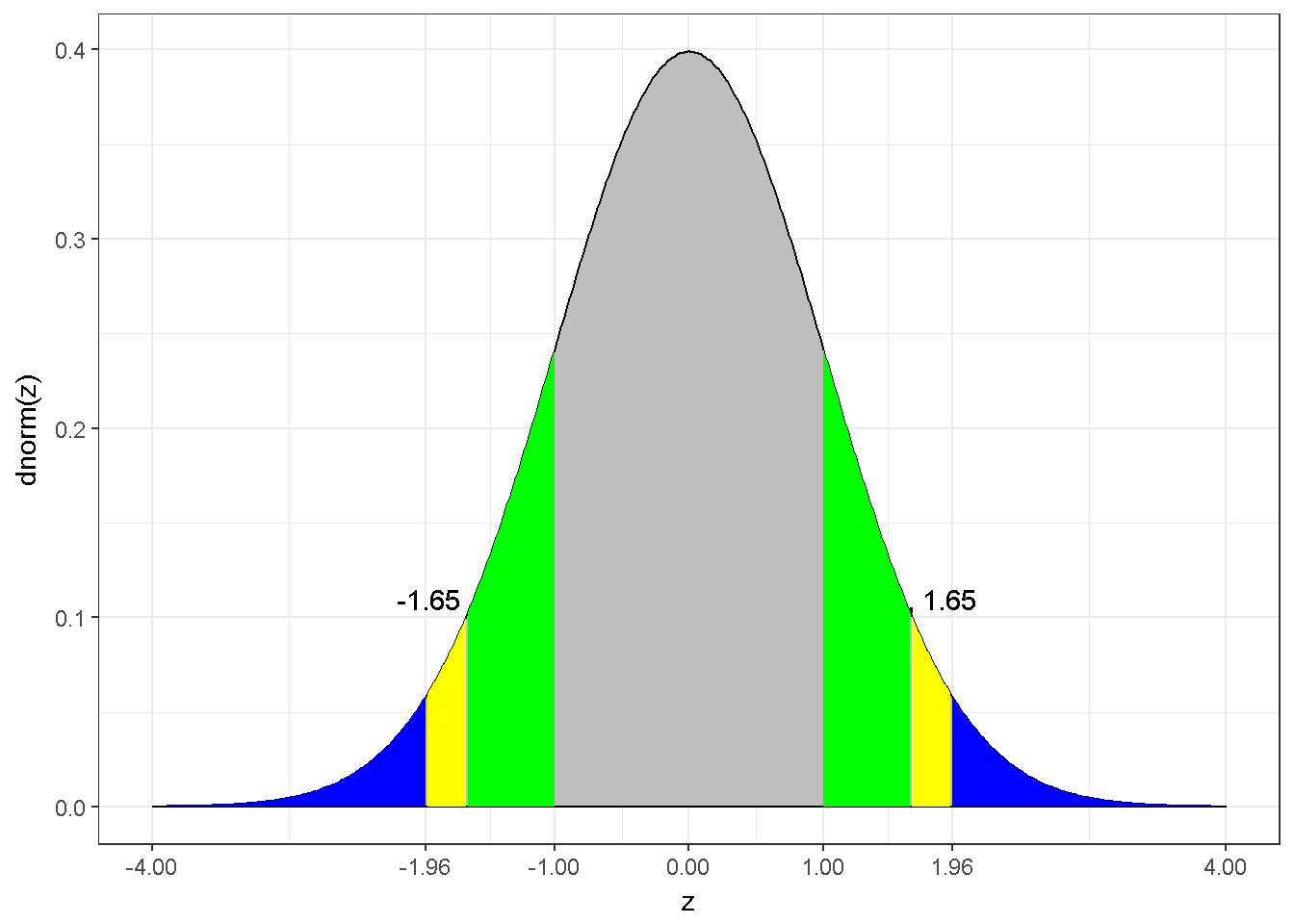
Figure 7.10: The z distribution
7.3.2.1 Güven Aralığı Örneği
Toplumsal Cinsiyet Algısına ait ortalama ve güven aralığı hesaplamaları
# gözlem sayısı, n
GA_n=sum(!is.na(dataWBT$gen_att))
#ortalama
GA_m=mean(dataWBT$gen_att,na.rm = T)
#ss
GA_s=sd(dataWBT$gen_att,na.rm = T)
#95% güven aralığı
alt=GA_m - 1.96 * (GA_s/sqrt(GA_n))
alt
## [1] 1.924339
ust=GA_m + 1.96 * (GA_s/sqrt(GA_n))
ust
## [1] 1.956812
#veya
GA_m +c(-1,1)*1.96 * (GA_s/sqrt(GA_n))
## [1] 1.924339 1.956812
#1.96 için qnorm(0.975)7.3.2.2 Ortalama için güven aralığı raporlama
5302 katılımcı için Toplumsal Cinsiyet Algısı puanlarına ait ortalama 1.94 (%95 GA [1.92-1.96]), standart sapma 0.60 bulunmuştur.
7.3.3 Boş Hipotez
Hipotez testinin amacı evren hakkında öne sürülen iki hipotezden hangisinin örneklem tarafından desteklendiğine karar vermektir. Bir hipotez testi beş basamaktan oluşur;
Boş hipotezin4 belirlenmesi (örneğin \(\mu=0\))
Alternatif hipotezin belirlenmesi. (örneğin \(\mu \neq 0\))
Test istatistiğinin seçilmesi
Test istatistiği ve belirlenen kritik değeri karşılaştırarak karar verilmesi. Eğer hesaplanan test istatistiği kritik değerden daha yüksekse boş hipotezin ret edilmesi (kritik değer alternatif hipoteze göre değişir).
Sonucun açıklanması. Araştırma sorusuna yanıt vermek üzere kararın ifade edilmesi.
Boş hipotez (\(H_0\)) ve alternatif hipotez (\(H_1\)) araştırma sorusunu cevaplamak üzere belirlenir. İstatistiksel kanıtlar boş hipotezini kabul veya terketmek için kullanılır. Boş hipotezi kabul etmek veya terketmek bir karardır, teorik istatistik açısından bu karara yönelik oluşabilecek durumlar şunlardır;
| Gerçekte Durum | Karar | Sonuç |
|---|---|---|
| \(H_0\) | Kabul \(H_0\) | Doğru Karar |
| \(H_0\) | Red \(H_0\) | Yanlış Karar (Tip I hata,\(\alpha\)) |
| \(H_1\) | Red \(H_0\) | Doğru Karar |
| \(H_1\) | Kabul \(H_0\) | Yanlış Karar (Tip II hata, \(\beta\)) |
Tip-I hata: Gerçekte doğru olduğu halde boş hipotezin terkedilmesi durumudur. Alfa , \(\alpha\), boş hipotezin gerçekte doğru olduğu halde red edilme olasılığıdır. Hipotez testi sürecinde önemli olan noktalardan biri \(\alpha\)’nın yeterince küçük olması gerektiğidir. Sosyal bilimlerde sıklıkla \(\alpha=.05\) kullanılır.
Tip-II hata: Gerçekte yanlış olan bir boş hipotezin terkedilememisidir. Beta, \(\beta\), gerçekte yanlış olan bir boş hipotezi kabul etme olasılığıdır.
7.3.4 z-puanı ve z-testi
z-puanı için genel formül; \[z_X=\frac{X-\bar{X}}{s_X}\]
Hesaplanan bu z değişkeni 0 ortalamaya ve 1 standart sapmaya sahiptir. Eğer X normal dağılım gösteriyorsa z de normal dağılım gösterir.
# z puanı hesapla
GA_m=mean(dataWBT$gen_att,na.rm = T)
GA_s=sd(dataWBT$gen_att,na.rm = T)
z_GA=(dataWBT$gen_att-GA_m)/GA_s
#veya
z_GA=scale(dataWBT$gen_att, center=T, scale=T)
# scale fonksiyonu ile birden fazla değisken için z hesaplanabilir.
# center=T her X puanından ortalamayı çıkarır
# scale=T farkı standart sapmaya böler
# scale(dataWBT$gen_att, center=3, scale=2)her değerden 3 çıkarıp 2'ye böler.Ortalama için z-istatistiği hesaplamak kolaydır;
\[ z=\frac{\bar{X}-\mu_{hipotez}}{Standart Hata} = \frac{\bar{X}-\mu_{hipotez}}{\sigma_X/\sqrt{n}}\] Hesaplanan bu z istatistiği bir z dağılımı kullanılarak yorumlanabilir (Figür 7.10);
Eğer alternatif hipotez, gözlemlenen ortalamanın, hipotez değerinden küçük olacağını belirtiyorsa, hesaplanan z istatistiği \(z_{alpha}\) veya \(-z_{(1-alpha)}\) ile kıyaslanır. Eğer hesaplanan z , \(z_{alpha}\)’ya eşit veya küçük ise boş hipotez terkedilir.
Eğer alternatif hipotez, gözlemlenen ortalamanın, hipotez değerinden farklı olacağını belirtiyorsa, hesaplanan z istatistiğinin mutlak değeri \(z_{1-(alpha/2)}\) ile kıyaslanır. Eğer mutlak z , \(z_{1-(alpha/2)}\)’ya eşit veya büyük ise boş hipotez terkedilir.
Eğer alternatif hipotez, gözlemlenen ortalamanın, hipotez değerinden büyük olacağını belirtiyorsa, hesaplanan z istatistiği \(z_{1-alpha}\) ile kıyaslanır. Eğer hesaplanan z , \(z_{1-(alpha)}\)’ya eşit veya büyük ise boş hipotez terkedilir.
Burada dikkat edilmesi gereken nokta a ve c senaryolarında (yönlü alternatif) kullanılan kritik değerin b senaryosunda (yönsüz alternatif) kullanılan kritik değerden farklı oluşudur. Araştırmacılar alternatif hipotezlerinin yönlü veya yönsüz oluşunu savunabilmelidir.
7.3.4.1 z testi örnek-1 (yönsüz)
Boş hipotez \(H_0: \mu_{Cinsiyet Algisi} = 2\) ve alternatif hipotez \(H_1: \mu_{Cinsiyet Algisi} \neq 2\) ve \(\alpha=0.05\);
# n
GA_n=sum(!is.na(dataWBT$gen_att))
#ortalama
GA_m=mean(dataWBT$gen_att,na.rm = T)
#ss
GA_s=sd(dataWBT$gen_att,na.rm = T)
# boş hipotez
mu_hyp=2
# z istatistiği
(GA_m-mu_hyp)/(GA_s/sqrt(GA_n))
## [1] -7.17343
#alpha=0.05 ve yönsüz alternatif için kritik değer
qnorm(1-(0.05/2))
## [1] 1.9599645302 katılımcıya ait Toplumsal Cinsiyet Algısı puanları için ortalama 1.94 ve standart sampma 0.6 olarak hesaplanmıştır. Tek örneklem için hesaplanan z testi, gözlemlenen ortalamanın, hipotez ile öne sürülen 2’den 7.17 standart hata daha düşük olduğunu göstermiştir. Kritik değer olarak 1.96 (\(z_{1-(0.05/2)}\)) seçildiğinde ve gözlemlenen ortalama ve hipotez ile öne sürülen ortalama arasındaki farkın istatistiksel olarak anlamlı olduğu kararı verilmiştir.
7.3.4.2 z testi örnek-2 (yönlü)
Bu örnekte Toplumsal Cinsiyet Algısı değişkeninin evren bazında ortalaması 1.9 ve standart sapması 0.75 olarak varsayılmıştır. Eğer evren bazında standart sapma biliniyorsa istatistik hesaplarken kullanılmalıdır. \(H_0: \mu_{Cinsiyet Algisi} = 1.9\) ve \(H_1: \mu_{Cinsiyet Algisi} > 1.9\) ve \(\alpha=0.01\);
# boş hipotez
mu_hyp=1.9
# z istatistik
(GA_m-mu_hyp)/(0.75/sqrt(GA_n))
## [1] 3.939368
#yönlü alternatif ve alfa=.01
qnorm(1-(0.01))
## [1] 2.326348Kritik değer olarak 2.33 kullanıldığında (\(z_{0.99}\)) gözlemlenen ortalamanın hipotez ile öne sürülen ortalamadan büyük olduğu ve bu farkın istatistiksel olarak anlamlı olduğu kararına varılmıştır \(z=3.94\).
7.3.5 Tek örneklem t-testi
Evrene ait dağılım normal olsa dahi küçük örneklemler için z dağılımı yerine t dağılımı kullanmak daha geçerlidir. bu t dağılımının serbestlik derecesi n-1’dir.
7.3.5.1 t test örnek-1 (yönsüz)
Örnek için Düzce ilinde yaşadığını belirten katılımcılara ait Toplumsal Cinsiyet Algısı puanları kullanılmıştır.
\(H_0: \mu_{Cinsiyet Algisi} = 1.94\) ve alternatif \(H_1: \mu_{Cinsiyet Algisi} \neq 1.94\) ve \(\alpha=0.05\);
dataWBT_DUZCE=dataWBT[dataWBT$city=="DUZCE",]
#betimleyici
describe(dataWBT_DUZCE[,"gen_att"],type=3)
## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 47 2.18 0.55 2 2.14 0.59 1 3.8 2.8 0.56 0.28 0.08
#t test
t.test(dataWBT_DUZCE$gen_att,
alternative="two.sided",
mu=1.94,
conf.level = 0.95)
##
## One Sample t-test
##
## data: dataWBT_DUZCE$gen_att
## t = 2.9391, df = 46, p-value = 0.005133
## alternative hypothesis: true mean is not equal to 1.94
## 95 percent confidence interval:
## 2.014224 2.336840
## sample estimates:
## mean of x
## 2.175532
#kritik değer
qt(.975,df=46)
## [1] 2.012896Düzce ilinde yaşayan katılımcıların Cinsiyet Algısı puanları 1 ve 3.8 arasında değişmiştir, ortanca 2, ortalama 2.18, standart sapma 0.55, örnekleme ait dağılımın çarpıklığı 0.56 ve basıklığı 0.28 olarak hesaplanmıştır. Düzce şehrinde yaşayan katılımcılara ait Toplumsal Cinsiyet Algısı ortalaması, hipotez ile öne sürülen 1.94 değerinden farklıdır ve bu farklılık istatistiksel olarak anlamlıdır, t(46)=2.94 ve \(t_{.975,46}=2.01\)
7.3.5.2 t test örnek-2
\(H_0: \mu_{Cinsiyet Algisi} = 1.94\) ve alternatif \(H_1: \mu_{Cinsiyet Algisi} \leq 1.94\) ve \(\alpha=0.05\);
#t test
t.test(dataWBT_DUZCE$gen_att,
alternative="less",
mu=1.94,
conf.level = 0.95)
##
## One Sample t-test
##
## data: dataWBT_DUZCE$gen_att
## t = 2.9391, df = 46, p-value = 0.9974
## alternative hypothesis: true mean is less than 1.94
## 95 percent confidence interval:
## -Inf 2.310055
## sample estimates:
## mean of x
## 2.175532
#kritik değer
qt(.05,df=46)
## [1] -1.67866Test istatistiği t(46)=2.94 ve kritik değer \(t_{.05,46}=-1.68\) kullanılarak örneklemin, evrene ait ortalamanın 1.94’ten küçük olduğu hipotezini destekleyecek kanıtı içermediği kararı verilmiştir.
7.3.6 p-değeri
Tek örneklem ile t testi için kullanılan t.test fonksiyonu bir p değeri rapor etmiştir. Bu p değeri hesabı, boş hipotezin ve dağılım için yapılan varsayımın doğru olduğu kabulü üzerine yapılır. Bu p-değerinin amacı araştıracıyı hesaplanan istatistiğin sıradan olup olmadığı yönünde bilgilendirmektir. Uzun yıllardır araştırmacılar hesapladıkları bu p-değerini daha önceden belirledikleri bir alfa kriteri ile kıyaslayıp, buldukları sonuçların istatistiksel olarak anlamlı olup olmadığına karar vermişlerdir.
7.3.7 p değeri örnek-1
Bir z-dağılımın geçerli olduğu ve z değerinin 1.80 hesaplandığı durum için grafik;
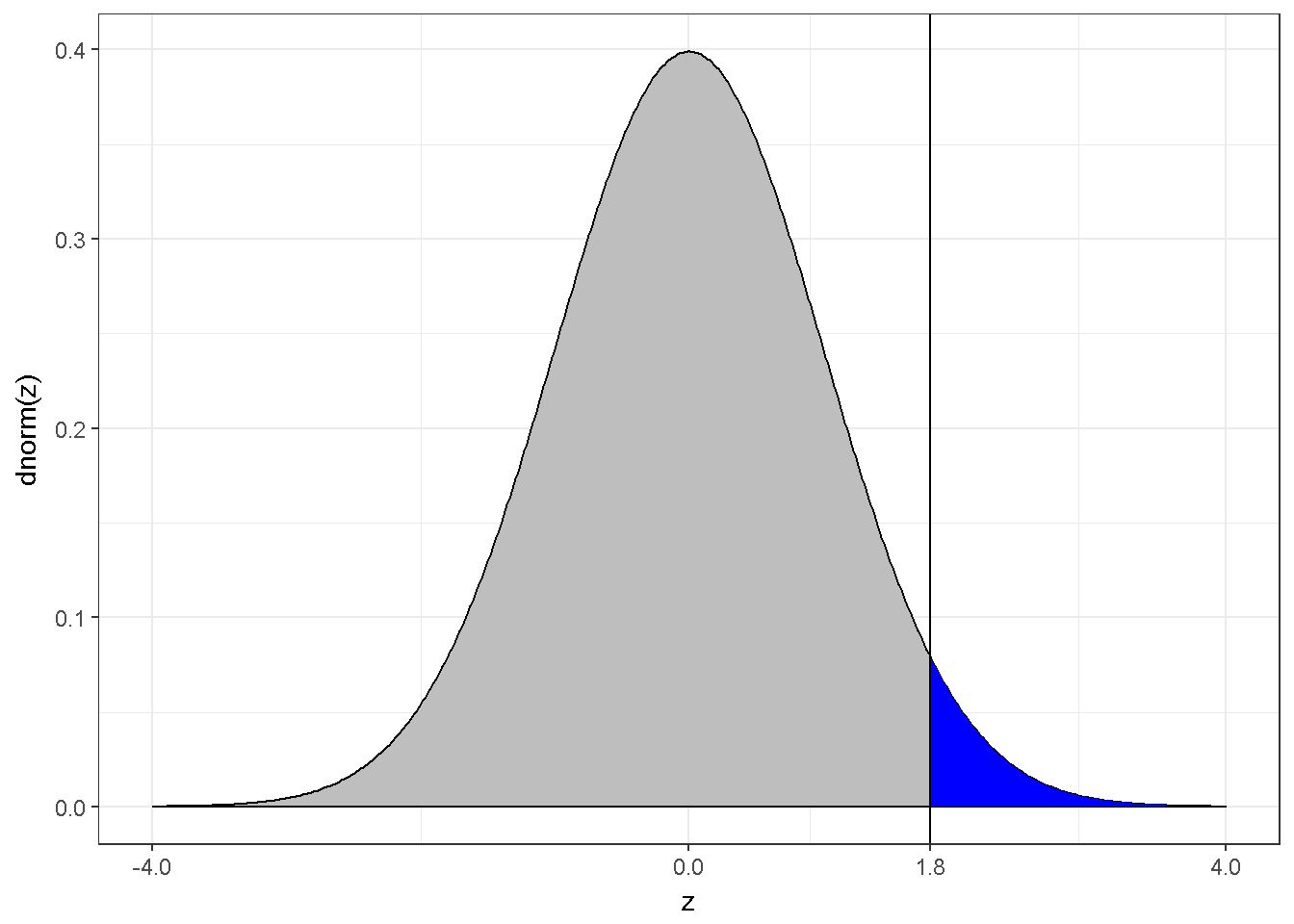
Figure 7.11: z dagilimi ve z=1.8
Mavi alan yoğunluğun %3.6’sını gösterir, p=0.0359
1-pnorm(1.8)## [1] 0.03593032Bu p değeri yönlü bir alternatif hipotez için hesaplanmıştır. Yönsüz alternatif için geçerli değildir. Yönsüz alternatif için ;
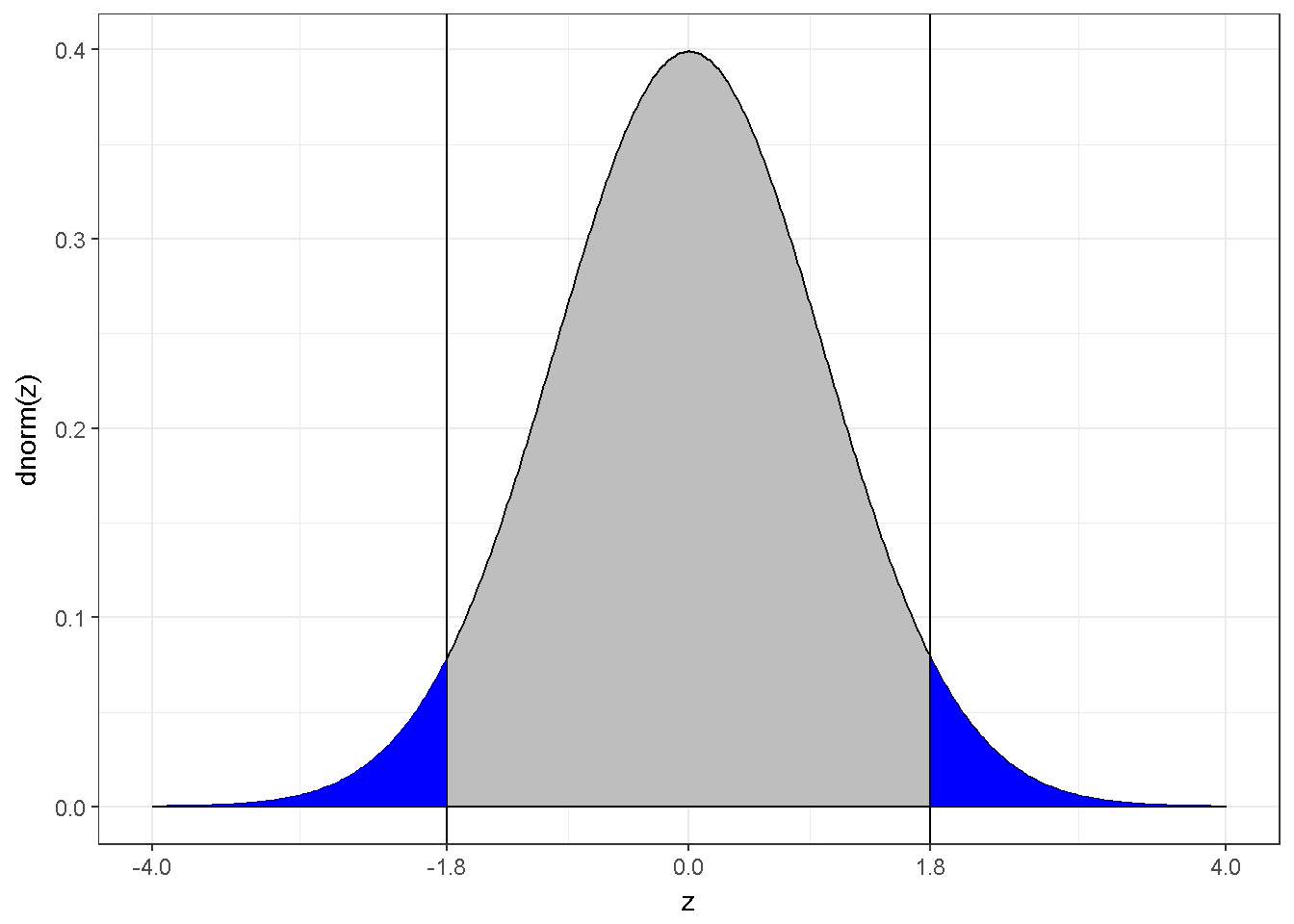
Figure 7.12: z dagilimi ve |z|)=1.8
Mavi alan yoğunluğun %7.2’sini gösterir, p=0.0719;
2*(1-pnorm(1.8))## [1] 0.071860647.3.8 İstatiksel Güç
İstatistiksel güç, gerçekte yanlış olan bir boş hipotezi terketme olasılığıdır ve \((1-\beta) 'ya\) eşittir. Bu olasılık istatistiksel sınamalar yapıldıktan önce (a-priori) veya sonra (post-hoc) hesaplanabilir, fakat sınama sonrasında yapılan güç analizi genellikle işlevsizdir. Sınama yapılmadan önce, daha doğrusu veriler toplanmadan önce yapılacak bir güç hesabı ile çalışma tasarısı gözden geçirebilir, yeniden düzenlenebilir ve örneklem sayısı belirlenebilir. Amerika’da bir çok proje başvurusu istatistiksel güç analizlerini mecbur tutar.
İstatisksel gücü açıklamak için R ile çizilen grafik ve kod5;
x <- seq(-4, 8, 0.02)
zdat <- data.frame(x = x, y1 = dnorm(x, 0, 1), y2 = dnorm(x, 2.5, 1))
ggplot(zdat, aes(x = x)) +
geom_line(aes(y = y1), size=2) +
geom_line(aes(y = y2), color='red',size=2) +
geom_vline(xintercept = c(0,2.5), color="black", linetype = "longdash")+
geom_vline(xintercept = qnorm(1 - 0.05))+
scale_x_continuous(breaks = c(-4,0,1.65,2.5,4))+
annotate("text", label="beta" , x=1.1, y=0.05, parse=T, fontface =2, size=6)+
annotate("text", label="alpha", x=2 , y=0.02, parse=T, fontface =2, size=6)+
annotate("text", label="1-~beta", x=3.3, y=0.1, parse=T, fontface =2,size=6)+
geom_area(aes(y=y1, x = ifelse(x > qnorm(.95), x, NA)), fill = 'blue' , alpha=0.25) +
geom_area(aes(y=y2, x = ifelse(x > qnorm(.95), x, NA)), fill = 'green' , alpha=0.25) +
geom_area(aes(y=y2, x = ifelse(x < qnorm(.95), x, NA)), fill = 'yellow', alpha=0.25) +
xlab("z") + ylab("dnorm(z)") + theme_bw()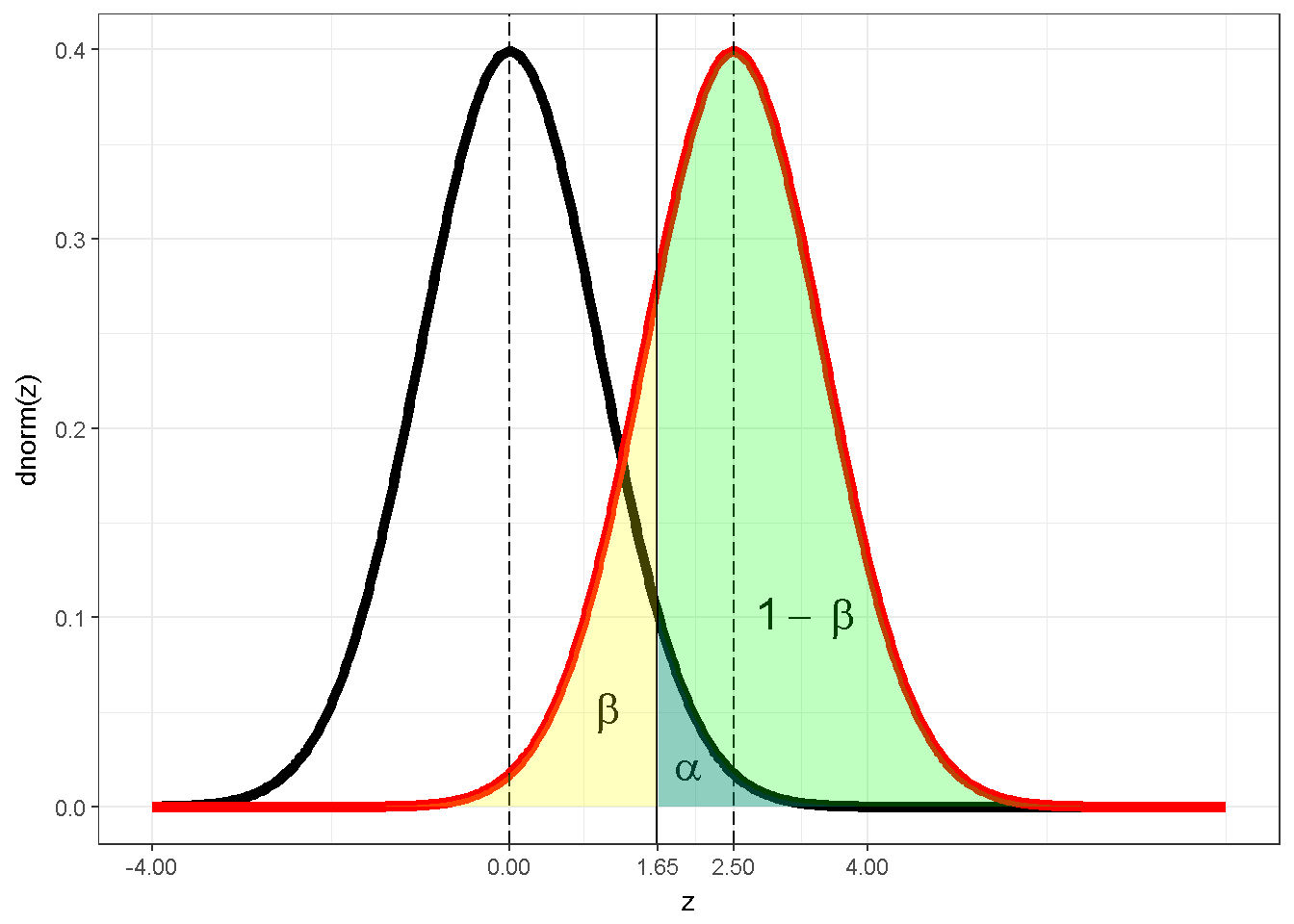
Figure 7.13: z dagilimi ile istatistiksel güç
\(H_0:\mu=0\) boş hipotezini doğru kabul eden bir z dağılımı siyah çizgiler ile gösterilmiştir, bu dağılımın ortalaması sıfırdır ve kesik çizgiler ile gösterilmiştir. Kırmızı çizgiler ile gösterilen dağılım (a) boş hipotezin yanlış olduğu ve (b) evrene ait ortalama ve standard sapma ile hesaplanan z-istatistiğinin \(((\mu-\mu_{hypothesis} )⁄(\sigma⁄\sqrt{n})=2.5)\) olduğu varsayımı ile çizilmiştir. Bu görsel yönlü bir alternatif hipotez ve alfa=0.05, dolayısıyla kritik değer \(z_{0.95}=1.65\) için geçerlidir. Mavi alan \(\alpha\)’yı, sarı alan \(\beta\)’yı ve yeşil alan istatistiksel gücü yansıtır. Bu görselde istatistiksel güç .804’tür.
1-pnorm(qnorm(0.95),mean=2.5)## [1] 0.8037649Figüre6 7.13 , istatistiksel güç hesaplamak için iki farklı dağılımın, bir alfa değerinin ve bir test istatistiğinin olması gerektiğini gösterir. Bu bilinenler ile istatistiksel güç hesaplanabilir. Burda önemli olan detay bir test istatistiğinin kendi bileşenleri olduğudur, genellikle bu bileşenler bir bölünen ve bir bölendir. z testi için bölünen , hipotez ile öne sürülen değer ile gözlemlenen değer arasındaki fark, bölen ise ortalamanın standart hatasıdır (\(\sigma/\sqrt(n)\)). Eğer istatistiksel güç sabit tutulursa (örneğin .8) eşitlik seçilen bir bilinmeyene göre çözülebilir. Genellikle de seçilen bilinmeyen örneklem sayısıdır, n.
İstatistiksel güç ilerleyen bölümlerde tekrar değinilmiştir. Test istatistikleri, parametre kestirimleri, standart hatalar, dağılımsal varsayımlar tasarlanan araştırmaya göre değişecektir. Tek örneklem için t testi düşünüldüğünde power.t.test fonksiyonu işeyarardır.
#power.t.test
power.t.test(delta=.1, sd=.6,sig.level=0.05, power=0.9,
type="one.sample", alternative="one.sided")
##
## One-sample t test power calculation
##
## n = 309.6563
## delta = 0.1
## sd = 0.6
## sig.level = 0.05
## power = 0.9
## alternative = one.sidedBu örnek, belirlenmiş bir ortalama fark 0.1, standart sapma 0.6, alfa 0.05, yönlü alternatif ve istenilen güç 0.9 için örneklemin 310 olması gerektiğini gösterir. Bir diğer ifade ile, araştırmacı 310 kişiden gelen bir veride, ortalama fark 0.1 , standart sapme 0.6 tespıt eder ve alfa 0.05 ile yönlü bir test kullanırsa boş hipotezi (\(H_0:\mu=0\)) terketme olasılığı 0.90’dır.
7.3.9 z ve t dağılımları geçerli değil ise
Bilinenlerden (örneklem) bilinmeyenlere (evren) genelleme varsayımların yapılmasını gerektirir. Bir test istatistiğine ait örnekleme dağılımın, belli bir örneklem sayısında, belirli bir varsayımın ihlal edilmesi ile büyük ölçüde değişmemesi durumu direnç (robustness) olarak isimlendirilir (Verzani (2014)). Burda dikkat edilmesi gereken, bir test istatitiğinin bir varsayım ihlaline dirençli iken başka bir varsayım ihlaline dirençsiz olabileceğidir. Ayrıca, bir varsayım ihlaline dirençli olan bir test istatistiği, ikinci bir varsayım ihlalinin de yaşanması durumunda direncini yitirebilir. Bir test istatistiği dirençli olduğu için kullanılması şart değildir çünkü aynı şartlar altında daha iyi çalışan bir başka test istatistiği olabilir.
z istatistiği, örneklem 30’dan büyük ise normallik varsayımının ihlallerine karşı dirençlidir(Field, Miles, and Field (2012), page 198). Örnekleme dağılımın z dağılımına yakınlığını etkileyen bir faktör diğer faktörde örneklemin nasıl bir dağılım gösterdiğidir. Ayrıca, evrene ait dağılımın normal olduğu varsayımı ile küçük örneklemler için t dağılımı geçerlidir.
Tek örneklem ile aritmetik ortalama için yapılacak dirençli istatistikler detaylı olarak Wilcox (2012) tarafından verilmiştir. Verilen R kodu bootstrap-t metodu içim %95 güven aralığı hesaplar (Wilcox (2012), page 117).
#ikinci tür bootstrap t metodu
# Düzce katılımcılarını seç
dataWBT_DUZCE=na.omit(dataWBT[dataWBT$city=="DUZCE",c("id","gen_att")])
# normallik varsayımı ve t test kullanarak
# evren ortalamasının 1.94 olup olmadığını sına
t.test(dataWBT_DUZCE$gen_att,mu=1.94,conf.level = 0.95)
##
## One Sample t-test
##
## data: dataWBT_DUZCE$gen_att
## t = 2.9391, df = 46, p-value = 0.005133
## alternative hypothesis: true mean is not equal to 1.94
## 95 percent confidence interval:
## 2.014224 2.336840
## sample estimates:
## mean of x
## 2.175532
# bootstrap ile 95% GA (normallik varsayımı yok)
set.seed(04012017)
B=5000 # bootstrap sayısı
alpha=0.05 # alfa
#x değişken
# xBAR gözlemlenen ortalama
tstar=function(x,xBAR) sqrt(length(x))*abs(mean(x)-xBAR)/sd(x)
output=c()
for (i in 1:B){
output[i]=tstar(sample(dataWBT_DUZCE$gen_att,
replace=T,
size=length(dataWBT_DUZCE$gen_att)),
xBAR=mean(dataWBT_DUZCE$gen_att))
}
output=sort(output)
Tc=output[as.integer(B*(1-alpha))]
#bootstrap GA
mean(dataWBT_DUZCE$gen_att)+c(-1,1)*(Tc*sd(dataWBT_DUZCE$gen_att)/sqrt(length(dataWBT_DUZCE$gen_att)))
## [1] 2.011540 2.3395247.3.9.1 Raporlama
Düzce ilinden 47 katılımcının verdiği yanıtlar ile hesaplanan Toplumsal Cinsiyet Algısı puanları 1 ve 3.8 arasında değişmiş, ortancası 2, ortalaması 2.18, standart sapması 0.55 bulunmuştur. Puanların dağılımına ait çarpıklık değeri 0.56, basıklık değeri 0.28 olarak hesaplanmıştır. Kritik değer olarak 2.01 (\(t_{.975,46}\)) kullanıldığında, tek örneklem t testi anlamlı bir farklılığa işaret etmiştir,t(46)=2.94, bu şehirdeki katılımcıların puanları hipotez ile öne sürülen 1.94 değerinden farklıdır. Normallik varsayımı yapıldığında %95 güven aralığı [2.01,2.34] olarak bulunmuştur. Normallik varsayımı yapılmadığıda 5000 tekrarlı bootstrap metodu ile hesaplanan güven aralığı [2.01,2.34] olarak bulunmuştur.
References
Komsta, Lukasz, and Frederick Novomestky. 2015. Moments: Moments, Cumulants, Skewness, Kurtosis and Related Tests. https://CRAN.R-project.org/package=moments.
Revelle, William. 2016. Psych: Procedures for Psychological, Psychometric, and Personality Research. https://CRAN.R-project.org/package=psych.
Højsgaard, Søren, and Ulrich Halekoh. 2016. DoBy: Groupwise Statistics, Lsmeans, Linear Contrasts, Utilities. https://CRAN.R-project.org/package=doBy.
de Vreeze, Jort. 2016. ApaStyle: Generate Apa Tables for Ms Word. https://CRAN.R-project.org/package=apaStyle.
R Core Team. 2016b. R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing. https://www.R-project.org/.
Sarkar, Deepayan. 2016. Lattice: Trellis Graphics for R. https://CRAN.R-project.org/package=lattice.
Wickham, Hadley, and Winston Chang. 2016. Ggplot2: Create Elegant Data Visualisations Using the Grammar of Graphics. https://CRAN.R-project.org/package=ggplot2.
Lemon, Jim, Ben Bolker, Sander Oom, Eduardo Klein, Barry Rowlingson, Hadley Wickham, Anupam Tyagi, et al. 2016. Plotrix: Various Plotting Functions. https://CRAN.R-project.org/package=plotrix.
Verzani, John. 2014. Using R for Introductory Statistics. Second. Boca Raton: CRC Press Taylor; Francis Group.
Field, Andy P., Jeremy Miles, and Zoë Field. 2012. Discovering Statistics Using R. Thousand Oaks, Calif;London; Sage.
Wilcox, Rand R. 2012. Introduction to Robust Estimation and Hypothesis Testing. 3rd;3; US: Academic Press.
Bu formül popülasyon için yanlı (biased) bir tahminleyicidir. R yanlı olmayan çarpıklık ve basıklık istatistikleri hesaplayabilir, describe fonksiyonu type argümanı incelenebilir.↩
evrende yer alan her üyenin eşit seçilme olasılığı olduğunda ve seçilen bir üyenin diğer bir üyenin seçilme olasılığını etkilemediği durumlarda↩
yokluk veya sıfır hipotezi olarak da bilinir↩
partially based on http://multithreaded.stitchfix.com/blog/2015/05/26/significant-sample/↩
accurate only for post hoc power↩