Chapter 5 Standardization and the normal distribution

5.1 Data standardization (z-score)

Sometimes tools of mathematical statistics, machine learning, or data analysis require the standardization of quantitative data. Standardizing a set of numbers involves transforming the data using the following formula:

\[ z = \frac{x - \text{mean}}{\text{standard deviation}}\]

This produces standardized values, or “z-scores.”

5.2 Normal distribution

The normal distribution is a mathematical tool useful for modeling many sets of quantitative data. The distribution of many natural and social phenomena is approximately normal — for example, human height, newborn weight, or other biological characteristics, deviations of temperature from the long-term average, or measurement errors. The distribution of the sample mean in repeated sampling also approaches the normal distribution as the sample size increases. For data that follow or approximate the normal distribution, the histogram takes on a characteristic bell shape (hence the term “bell curve”).

5.3 Empirical Rule

For a normal or approximately normal distribution3:

  • about 68% of values lie within one standard deviation from the mean,

  • about 95% of values lie within two standard deviations from the mean,

  • about 99.7% of values (almost all) lie within three standard deviations from the mean.

The empirical rule works quite well for many datasets but not for all of them.

In particular, in many real datasets, the standard deviation can be roughly estimated based on the 95% rule. This is why the standard deviation is often interpreted through the lens of the empirical rule.

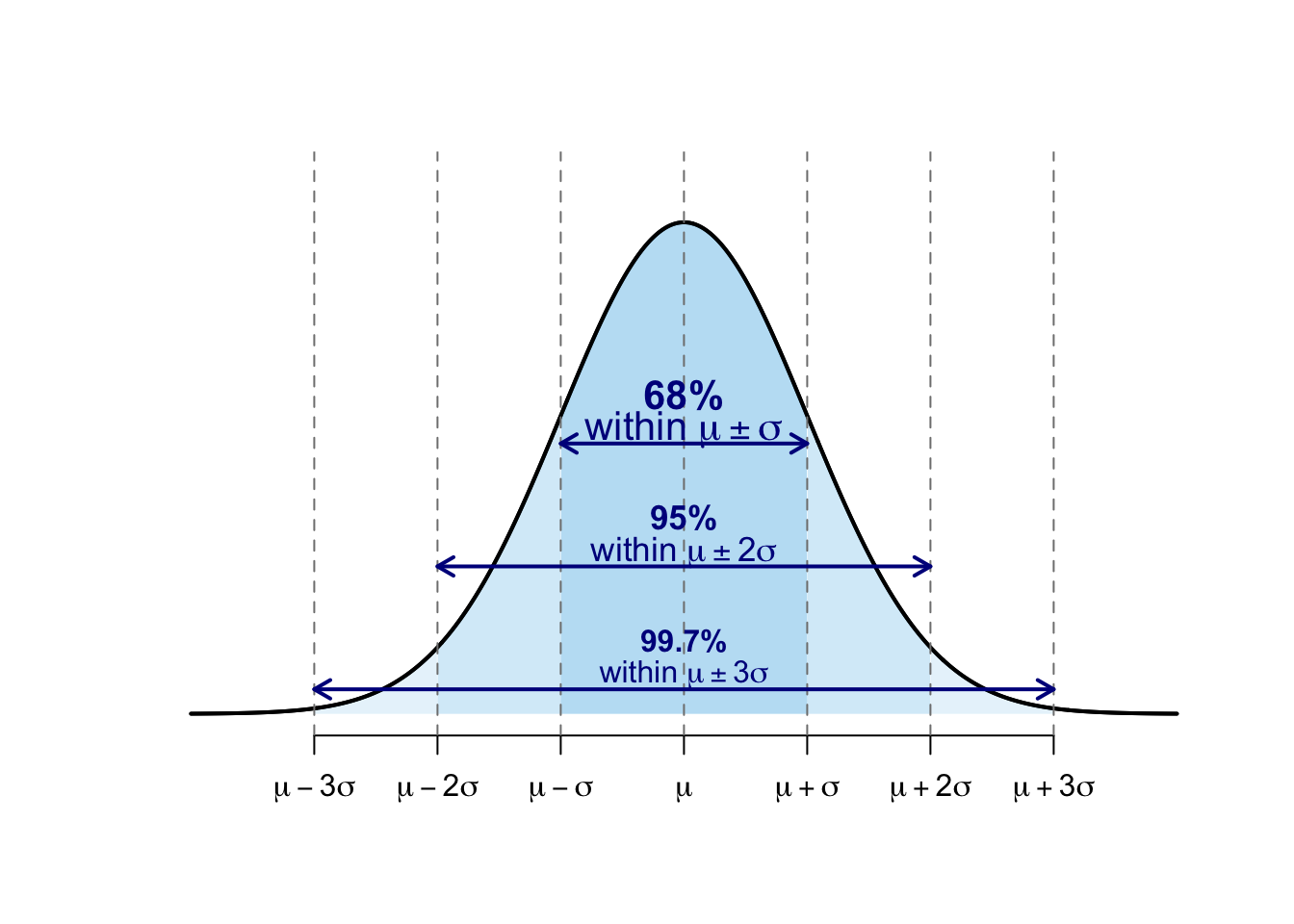
Empirical rule for normal distributions – illustration.

Figure 5.1: Empirical rule for normal distributions – illustration.

5.4 Chebyshev’s Inequality

The empirical rule works well for bell-shaped data, but not all datasets look like that. Chebyshev’s inequality is more general — it applies to any dataset, no matter its shape. According to Chebyshev’s rule:

  • at least 75% of values are within two standard deviations from the mean,

  • at least 89% within three,

  • at least 94% within four.

Chebyshev’s rule gives minimum values, not exact ones. It’s useful when data are skewed or irregular.

Table 5.1: Empirical Rule vs. Chebyshev’s Rule
Distance from the mean Empirical rule (normal) Chebyshev’s rule (any shape)
1 SD ~68% —
2 SD ~95% ≥75%
3 SD ~99.7% ≥89%
4 SD ~100% ≥94%

  1. For a normal distribution, these values, rounded to two decimal places, are: 68.27%, 95.45%, and 99.73%.↩︎