1 Objetivos de la actividad

El cliente quiere un modelo para predecir la distancia de tiro de la catapulta. Además, quiere que el tiro caiga en un radio de 7 centímetros alrededor del objetivo.

Elige 3 variables para utilizar como variables experimentales. Estos factores deberían ser fácilmente ajustables y tener una influencia alta en la distancia de tiro de la catapulta.
Decide los niveles de las tres variables experimentales. Utiliza 2 niveles por cada variable en el experimento. Los niveles deberían estar suficientemente espaciados para que el efecto del factor sea máximo. Asegúrate de que dichos niveles no están demasiado separados o de que se estén induciendo efectos secundarios. Idealmente los dos niveles deberían representar los extremos del rango de operaciones normales para esa variable.
Confecciona todas las combinaciones posibles en una hoja de cálculo y construye la matriz (de diseño). Replícala 4 veces para registrar la información que obtendrás al repetir 4 veces cada tiro. Aleatoriza los 4 tiros de cada combinación para asegurar la independencia de las observaciones.
Analiza los datos y ajusta modelos predictivos para la distancia de tiro. Confirma el modelo con los datos observados.
Fijándote en la tabla de predicciones y resultados elige una distancia predicha para la que no tengas datos y calcula un intervalo de confianza para la predicción. Marca también los límites de especificación. Después ajusta la catapulta con las condiciones especificadas por el modelo y realiza varios tiros para confirmar la predicción y el error. Anota los resultados.
Calcula el índice de capacidad del proceso y el valor ZBench. Establece un coste por defecto y evalúa el coste total por millón de oportunidades. Extrae conclusiones.

2 Experimento

Utilizamos la catapulta virtual en Sigmazone. Fijamos las siguientes condiciones de experimentación: FA: Firing angle = 90 BP: Bungee Position = 200 Experimentamos variando las siguientes variables: PE: Pin Elevation = 150 y 200 CE: Cup Elevation = 230 y 300 RA: Release Angle = 120 y 150

Repetimos cada una de las \(2^3=8\) combinaciones resultantes 4 veces, con el fin de tener replicaciones suficientes con las que estimar la varibilidad.

Leemos los datos y los visualizamos:

datos<-read.csv2("./datos/datos_catapulta.csv",sep=",",header=TRUE)
#datos=read.csv2("https://raw.githubusercontent.com/umh1479/MejoraProcesos/master/data-exercices/datos_catapulta.csv",sep=",",header=TRUE)
str(datos)

## 'data.frame':    32 obs. of  7 variables:
##  $ fa       : int  90 90 90 90 90 90 90 90 90 90 ...
##  $ bp       : int  200 200 200 200 200 200 200 200 200 200 ...
##  $ pe       : int  150 150 150 150 200 200 200 200 150 150 ...
##  $ ce       : int  230 230 230 230 230 230 230 230 300 300 ...
##  $ ra       : int  120 120 120 120 120 120 120 120 120 120 ...
##  $ tiro     : chr  "t1" "t2" "t3" "t4" ...
##  $ distancia: num  92 90 94 95.5 110.5 ...

datos$PE=factor(datos$pe)
datos$CE=factor(datos$ce)
datos$RA=factor(datos$ra)

ggplot(datos,aes(x=RA,y=distancia))+
  geom_point(aes(fill=CE,color=CE),position=posn.j)+
  facet_grid(vars(PE))+
  labs(caption="Fig1: Datos registrados de tiros con la catapulta virtual.")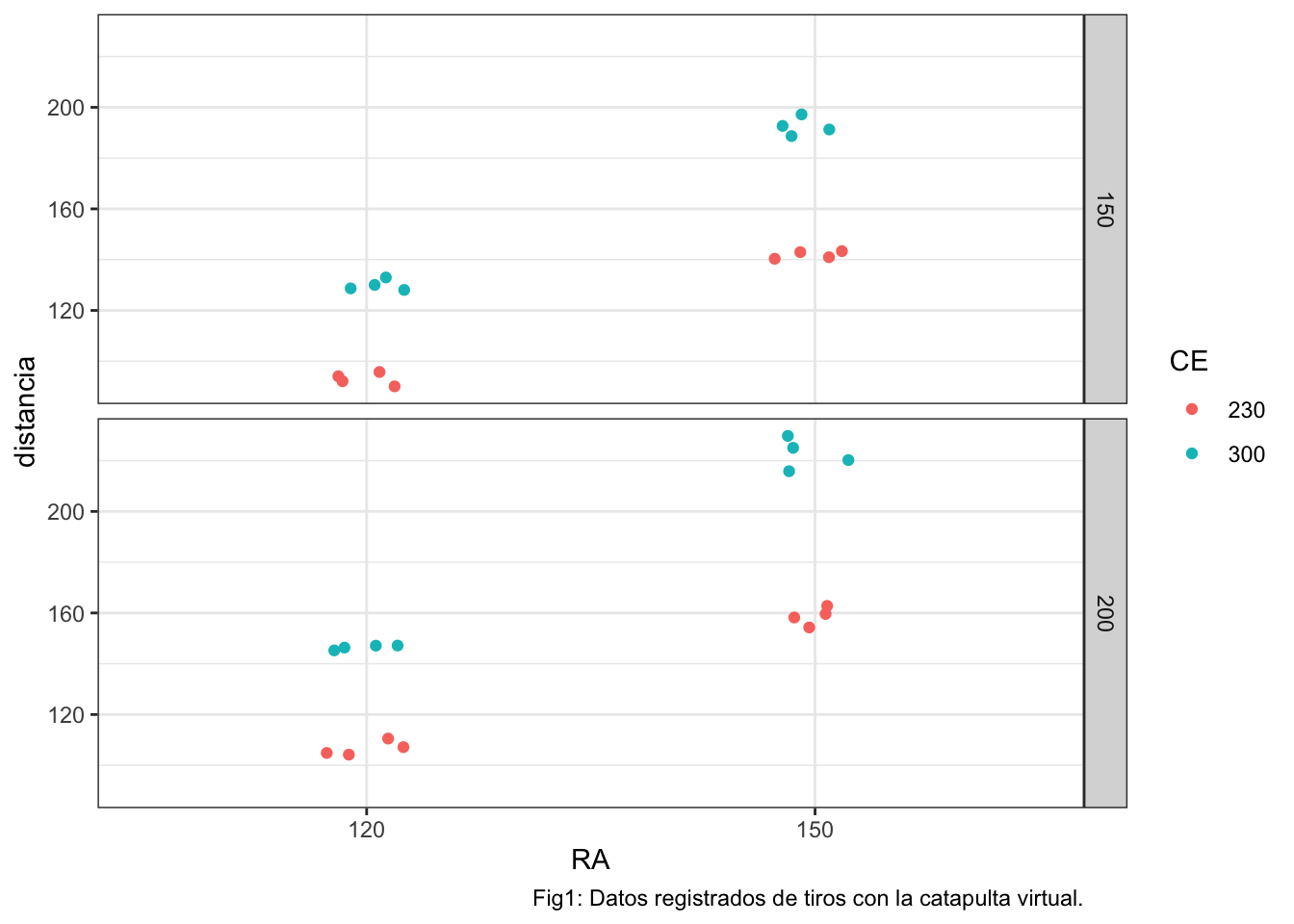

A la vista del gráfico, tenemos unas primeras conclusiones sobre el comportamiento de la catapulta respecto a la distancia de alcance: - El ángulo de lanzamiento (RL) afecta de modo directo: a mayor ángulo, mayor alcance. - La elevación de la cazuela de la bola (CE) afecta de modo directo: a mayor elevación, mayor alcance. - La altura del pin de agarre en el brazo fijo (PE) afecta de modo directo: a mayor elevación, mayor alcance.

Ajustamos ahora el modelo lineal para predecir el alcance en función de las variables controladas:

fit<-lm(distancia ~ PE*CE*RA,data=datos)
anova(fit)

## Analysis of Variance Table
## 
## Response: distancia
##           Df  Sum Sq Mean Sq  F value    Pr(>F)
## PE         1  2974.1  2974.1  285.731 7.837e-15
## CE         1 18360.1 18360.1 1763.890 < 2.2e-16
## RA         1 28770.0 28770.0 2763.994 < 2.2e-16
## PE:CE      1   126.0   126.0   12.106 0.0019389
## PE:RA      1   146.6   146.6   14.087 0.0009804
## CE:RA      1   726.8   726.8   69.821 1.448e-08
## PE:CE:RA   1    59.1    59.1    5.681 0.0254109
## Residuals 24   249.8    10.4

Puesto que todos los efectos resultan significativos, dejamos el modelo así. Con el modelo ajustado, procedemos con la predicción, que es la herramienta de valor en el DOE. Reproducimos las combinaciones de los diferentes niveles de las variables (factores) explicativos -causas- para predecir la respuesta (alcance de la catapulta). Pedimos así mismo, el error estándar y el intervalo de predicción para nuevos tiros. Visualizamos estas predicciones.

newdata<-expand.grid(PE=factor(levels(datos$PE)),
                     CE=factor(levels(datos$CE)),
                     RA=factor(levels(datos$RA)))
pred.fit<-predict(fit,newdata,se.fit=TRUE, interval="prediction")  
prediccion<-cbind(newdata,pred=pred.fit$fit,sd=pred.fit$se.fit,df=pred.fit$df)

ggplot(prediccion,aes(x=RA,y=pred.fit,group=CE))+
geom_point(aes(fill=CE,color=CE),position=posn.jd)+
  geom_errorbar(aes(ymin = pred.lwr, ymax = pred.upr,color=CE),position=posn.jd)+
  facet_grid(cols=vars(PE))+
  ylab("Alcance")+ggtitle("Predicción del alcance por PE")+
  labs(caption="Fig2: Ajuste ANOVA.")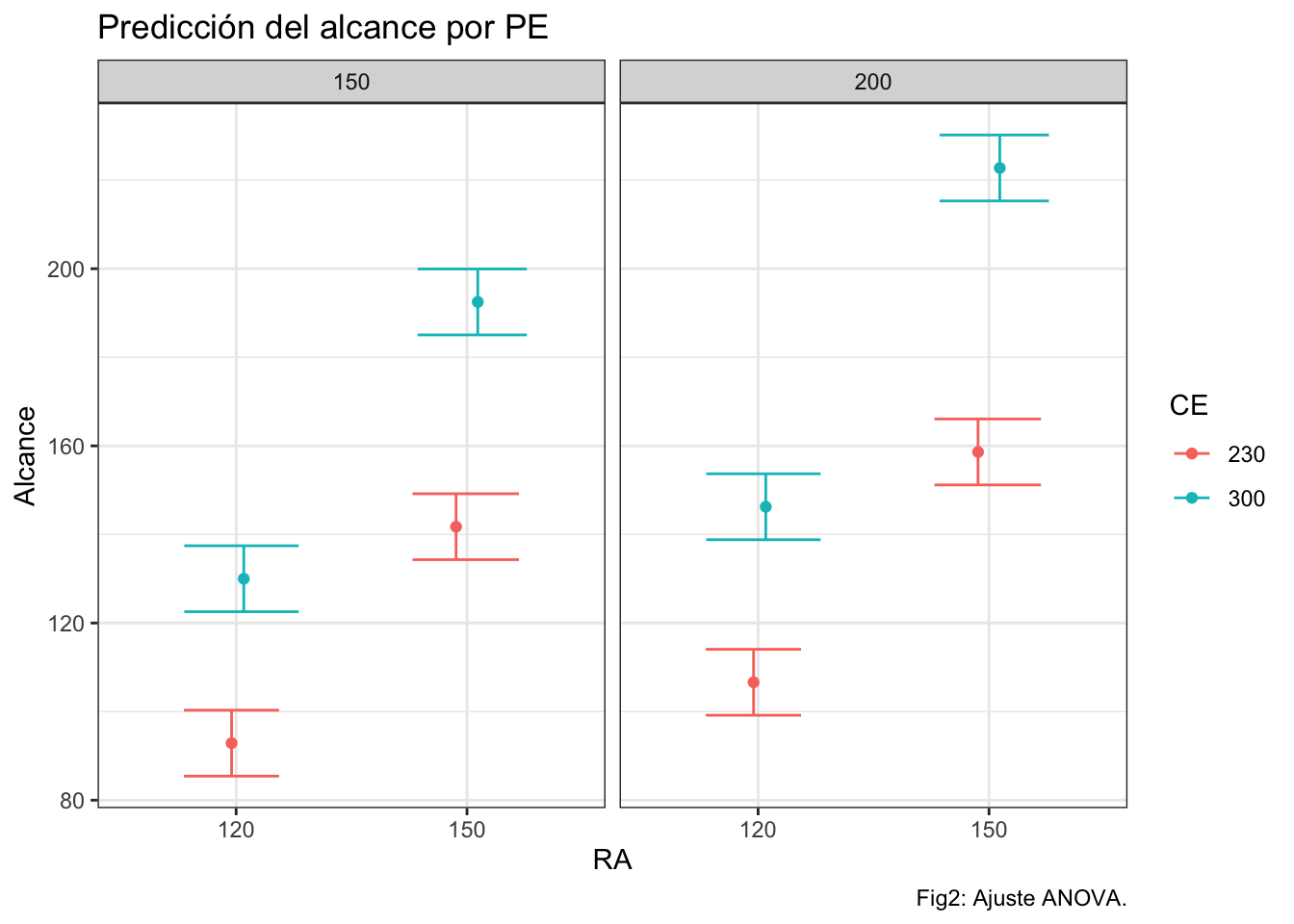

Calculamos ahora el rango de especificación a partir de la acotación impuesta por el cliente respecto de la precisión a conseguir en el tiro (7cm alrededor del objetivo). Visualizamos a continuación la relación entre el intervalo de predicción y este rango de especificación. Vemos en este gráfico que el rango de especificación está incluido dentro del intervalo de predicción, por lo que se espera una deficiente capacidad del proceso (entendida desde el nivel sigma).

espec<-7
prediccion$min.espec<-prediccion$pred.fit-espec
prediccion$max.espec<-prediccion$pred.fit+espec

ggplot(prediccion,aes(x=RA,y=pred.fit,group=CE))+
geom_point(aes(fill=CE,color=CE),position=posn.jd)+
  geom_errorbar(aes(ymin = pred.lwr, ymax = pred.upr,color=CE),position=posn.jd)+
  facet_grid(cols=vars(PE))+
  ylab("Alcance")+ggtitle("Predicción del alcance por PE")+
  geom_linerange(aes(ymin=min.espec,ymax=max.espec),position=position_dodge(width=0.1),size=2)+
  labs(caption="Fig3: Ajuste ANOVA e intervalo de especificación.")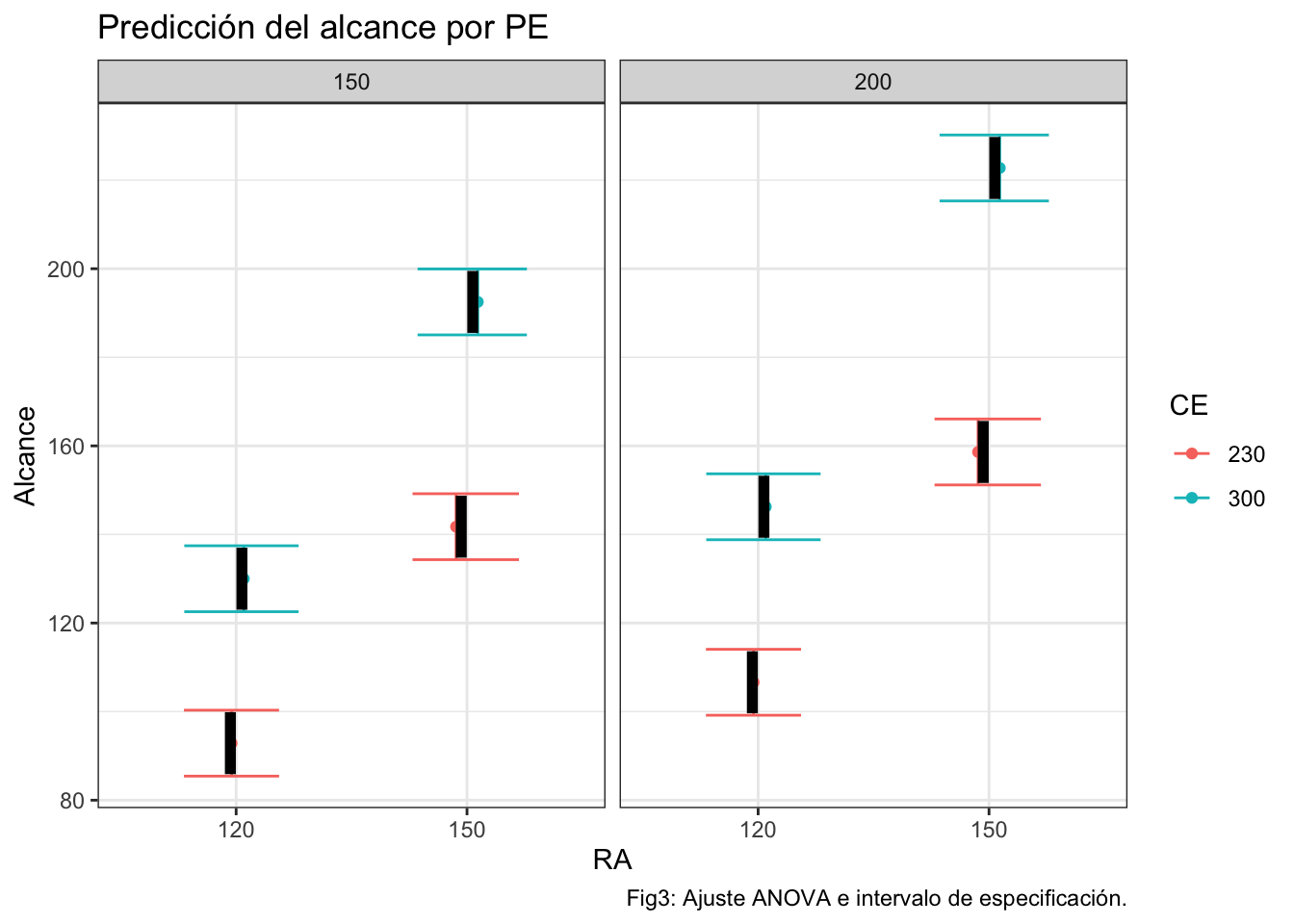

Pintamos las líneas de predicción. Vemos en este gráfico, que para conseguir un alcance de 120 podríamos utilizar tanto la configuración de PE=150 como de PE=200, siempre con CE=230, y encontrar -aproximadamente- la calibración RA de la catapulta.

ggplot(prediccion,aes(x=RA,y=pred.fit,group=CE))+
geom_point(aes(fill=CE,color=CE),position=posn.jd)+
  geom_errorbar(aes(ymin = pred.lwr, ymax = pred.upr,color=CE),position=posn.jd)+
  facet_grid(cols=vars(PE))+
  ylab("Alcance")+ggtitle("Predicción del alcance por PE")+
  geom_line(position=position_dodge(width=0.1))+
  geom_hline(yintercept=120,linetype=3)+
  geom_vline(xintercept=c(1.24,1.53),linetype=3)+
  labs(caption="Fig4: Ajuste ANOVA y líneas de interpolación.")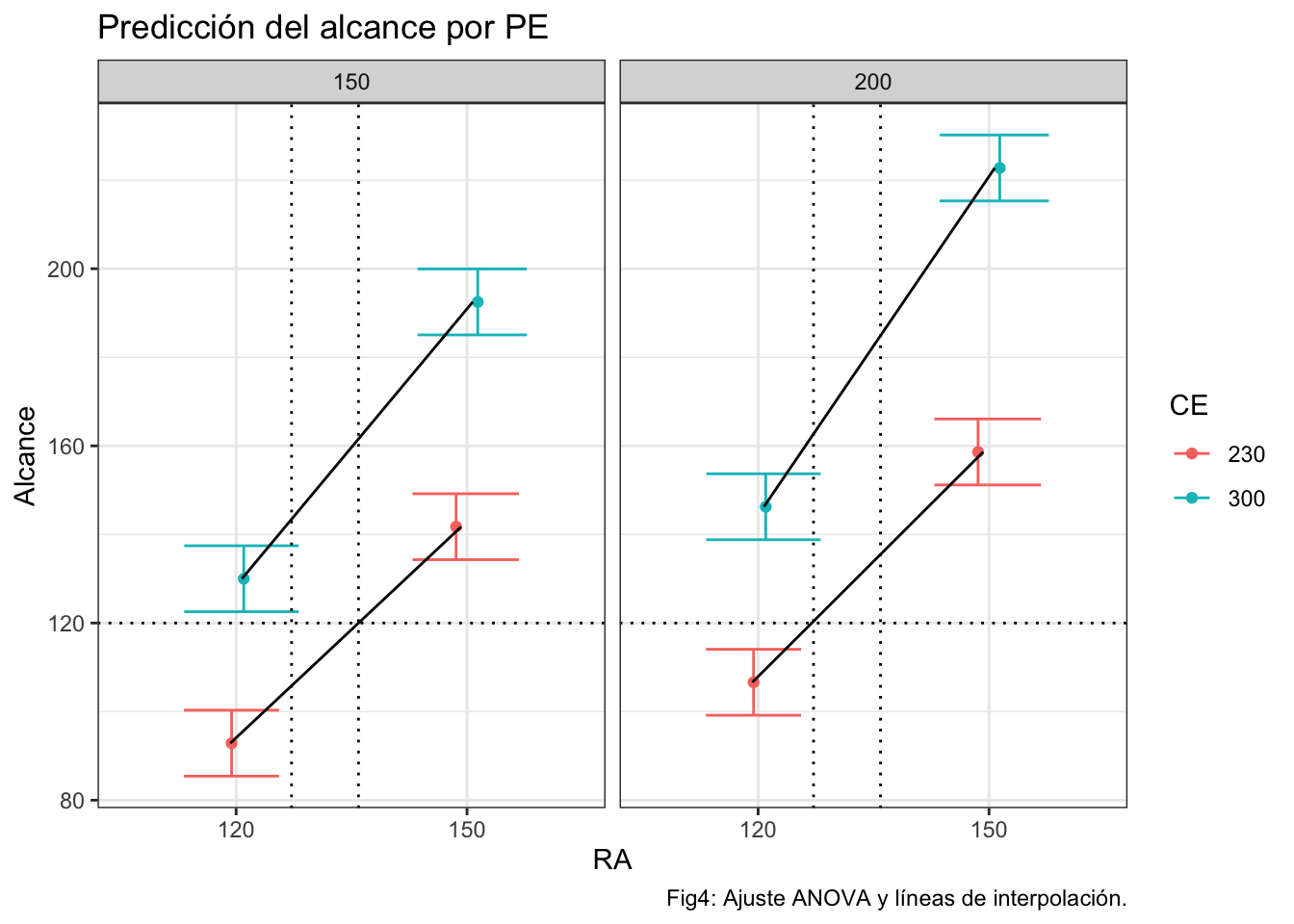

“A ojo” podemos encontrar los valores -aproximados- para RA (siempre con CE=230), que serían:

v1<-120+0.24*(150-120);v1 # en PE=200

## [1] 127.2

v2<-120+0.53*(150-120);v2  # en PE=150

## [1] 135.9

Para una predicción numérica, habríamos de haber empleado una recta de regresión, con las variables explicativas operando en continuo y prescindiendo por tanto, de interacciones:

ggplot(datos, aes(x = RA, y = distancia,group=CE)) +
 geom_point(aes(fill=CE,color=CE),position=posn.jd)+  
  geom_smooth(method="lm")+
  facet_grid(cols=vars(PE))+
  ggtitle("Regresión lineal múltiple")+
    geom_hline(yintercept=120,linetype=3)+
  geom_vline(xintercept=c(1.24,1.53),linetype=3)+
  labs(caption="Fig5: Interpolación con mínimos cuadrados.")

## `geom_smooth()` using formula 'y ~ x'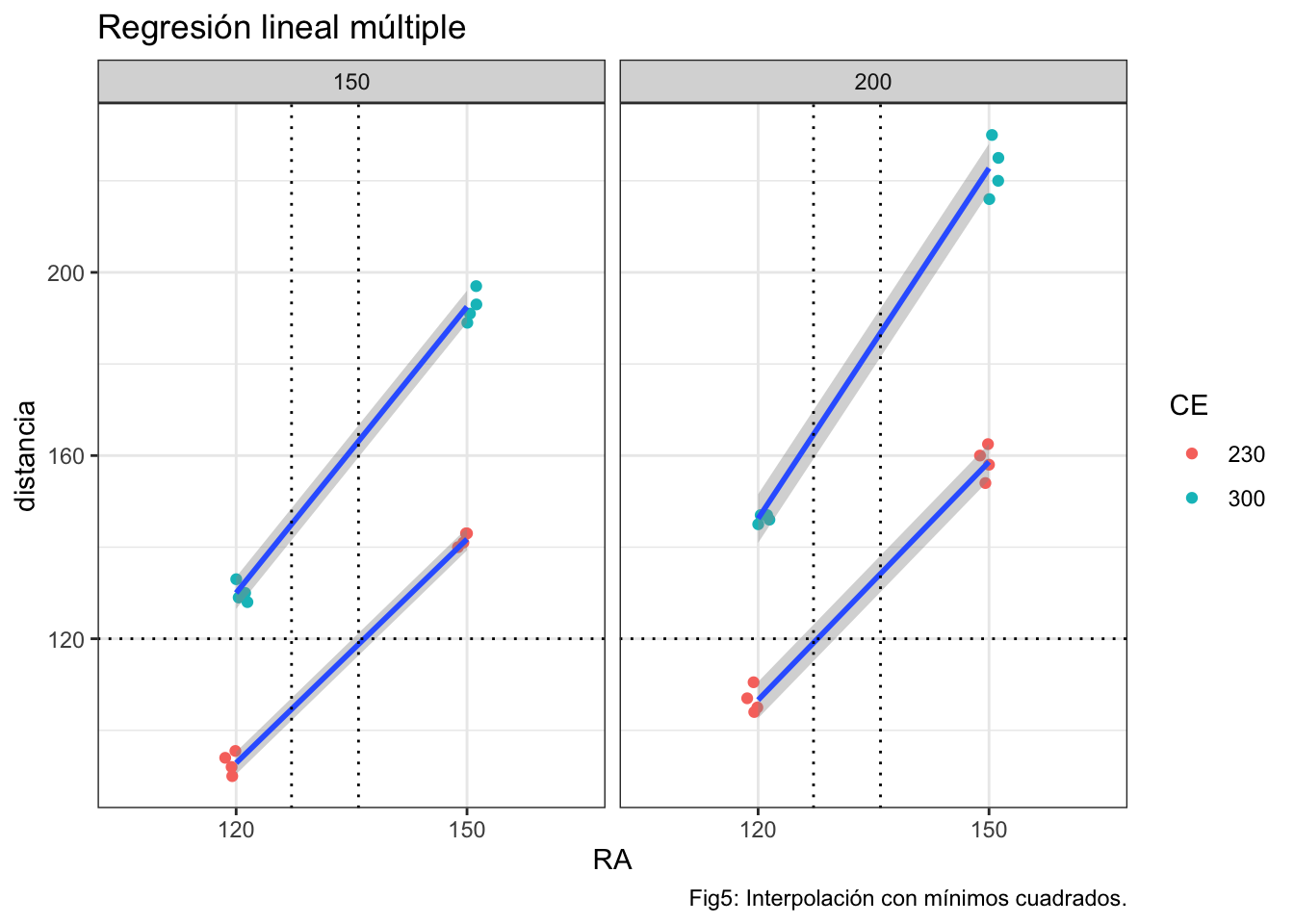

rectas que conseguiríamos con el siguiente ajuste (que difiere del anterior en tanto y cuanto ‘ra’ se introduce como variable numérica, y en consecuencia no es posible incluir la interacción triple:

fitr<-lm(distancia ~ ra*PE*CE,data=datos)
anova(fitr)

## Analysis of Variance Table
## 
## Response: distancia
##           Df  Sum Sq Mean Sq  F value    Pr(>F)
## ra         1 28770.0 28770.0 2763.994 < 2.2e-16
## PE         1  2974.1  2974.1  285.731 7.837e-15
## CE         1 18360.1 18360.1 1763.890 < 2.2e-16
## ra:PE      1   146.6   146.6   14.087 0.0009804
## ra:CE      1   726.8   726.8   69.821 1.448e-08
## PE:CE      1   126.0   126.0   12.106 0.0019389
## ra:PE:CE   1    59.1    59.1    5.681 0.0254109
## Residuals 24   249.8    10.4

Una aproximación a la predicción numérica con error incorporado se podría obtener a través de la predicción con el modelo de regresión (una predicción exacta de ‘ra’ habría que obtenerla con modelos PLS):

newdata<-expand.grid(PE=factor(levels(datos$PE)),
                     CE=factor(levels(datos$CE)),
                     ra=seq(120,150,by=1))
pred.fitr<-round(predict(fitr,newdata,interval = "prediction"),2)
prediccionr<-cbind(newdata,pred=pred.fitr)
datatable(prediccionr,filter="top",colnames=c("PE","CE","ra","Alcance.pred", "IP.inf","IP.sup"),
          caption="Tabla1: Predicción del alcance en función de la configuración PE, CE, RA.")

ggplot(prediccionr,aes(x=ra,y=pred.fit,group=CE))+
  geom_line(aes(color=CE))+
  geom_line(aes(x=ra,y=pred.upr,color=CE),linetype=2)+
  geom_line(aes(x=ra,y=pred.lwr,color=CE),linetype=2)+
  facet_grid(cols=vars(PE))+
  ylab("Alcance")+ggtitle("Predicción del alcance por PE")+
   geom_hline(yintercept=120.49)+
  geom_vline(xintercept=c(128,137))+
  labs(caption="Fig6: Ajuste con ANCOVA y predicción.")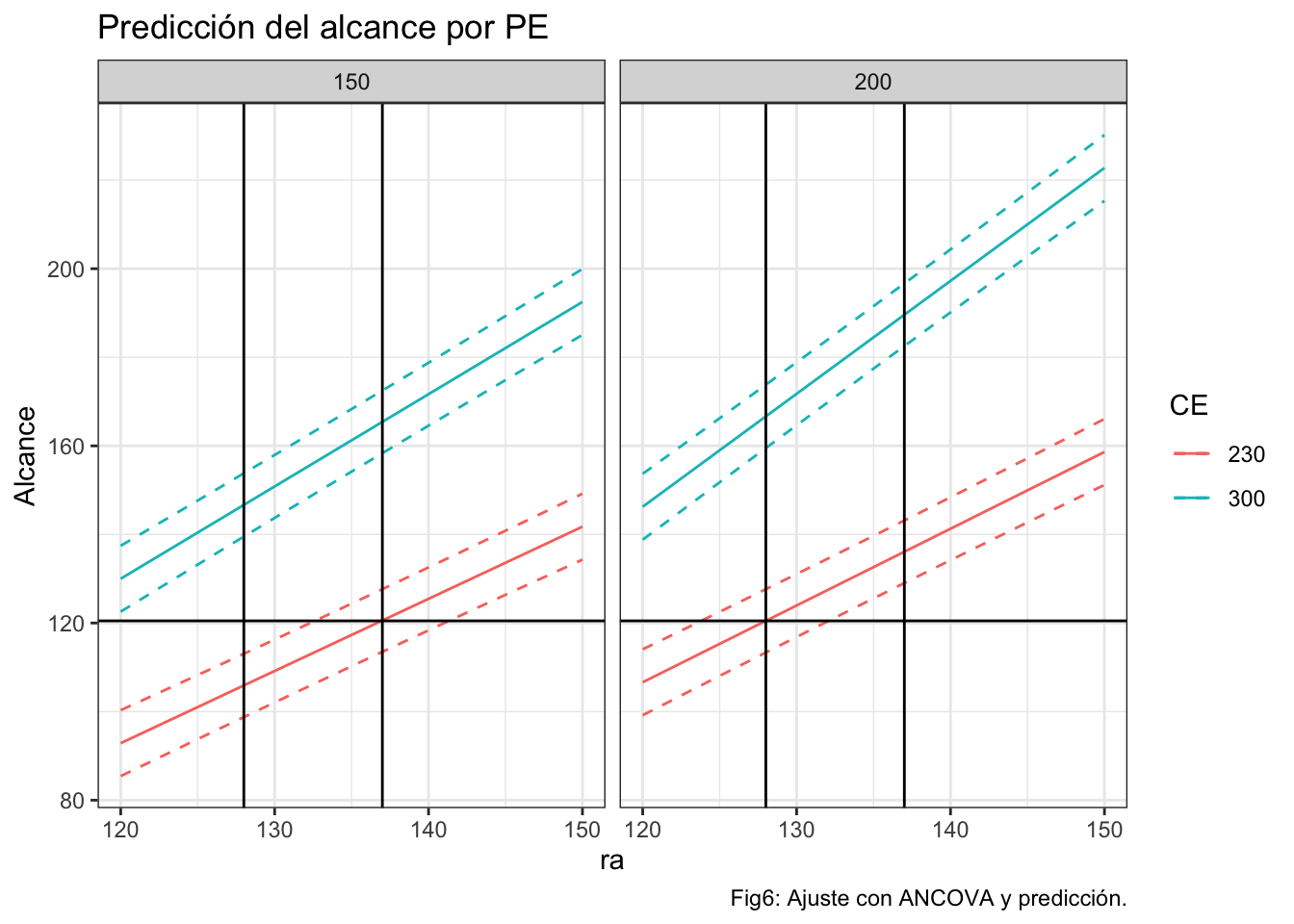

Verificamos a continuación la capacidad del proceso para conseguir un alcance aproximado de 120, la configuración de la catapulta PE=2OO, CE=230 y ra=128 (FA=90,BP=200). Lanzamos 20 tiros y registramos el alcance.

datosc<-read.csv2("./datos/datos_capacidad.csv",header=TRUE,sep=",")
#datosc=read.csv2("https://raw.githubusercontent.com/umh1479/MejoraProcesos/master/data-exercices/datos_capacidad.csv",sep=",",header=TRUE)

#library(qcc)
cap <- qcc.groups(datosc$distancia,1:length(datosc$distancia))
q <- qcc(cap, type="xbar.one", nsigmas=3, plot=FALSE)

target= 120.49
lsl=target-7;usl=target+7
process.capability(q, spec.limits=c(lsl,usl),target=target)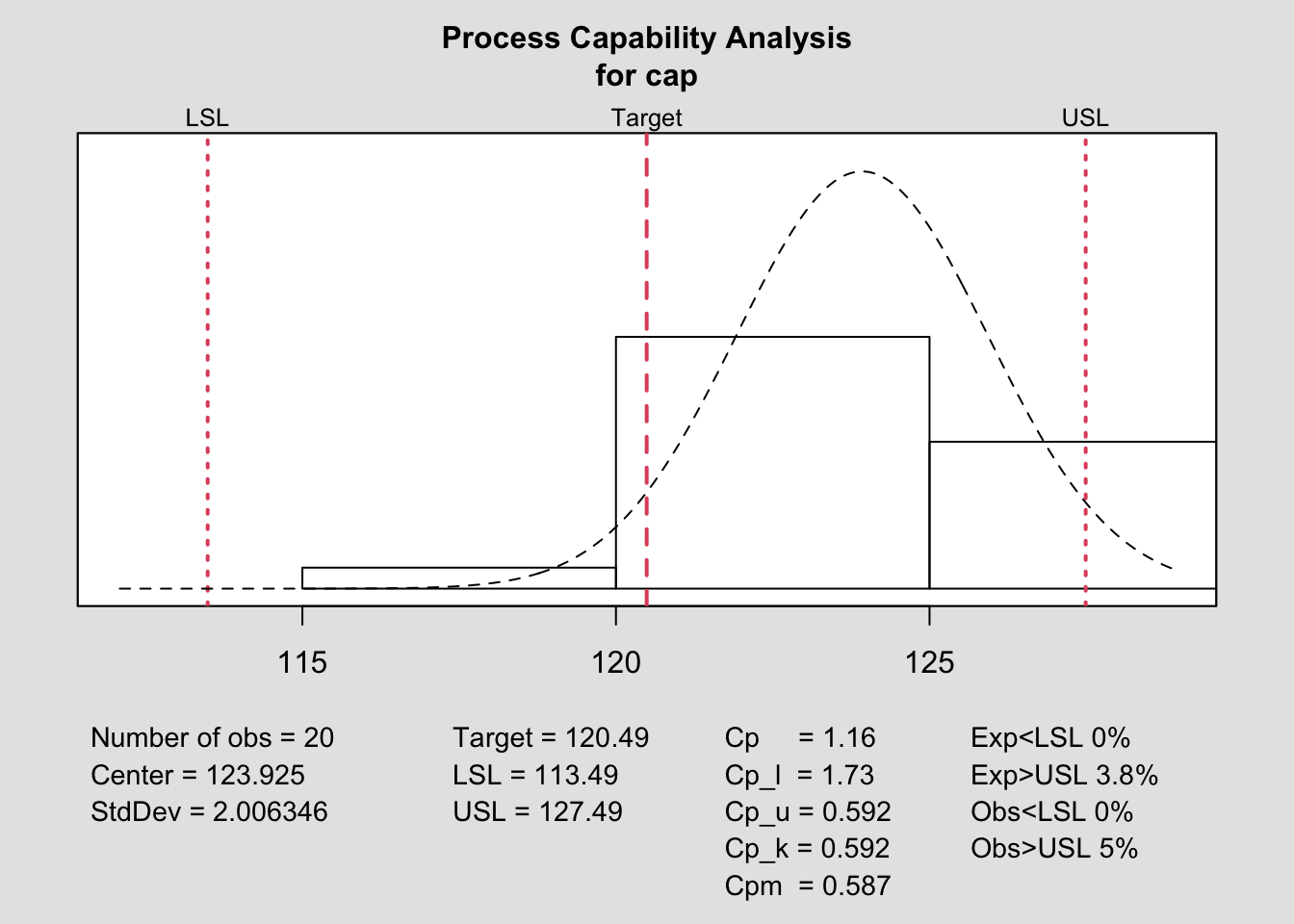

## 
## Process Capability Analysis
## 
## Call:
## process.capability(object = q, spec.limits = c(lsl, usl), target = target)
## 
## Number of obs = 20           Target = 120.5
##        Center = 123.9           LSL = 113.5
##        StdDev = 2.006           USL = 127.5
## 
## Capability indices:
## 
##        Value    2.5%   97.5%
## Cp    1.1630  0.7962  1.5292
## Cp_l  1.7337  1.2551  2.2122
## Cp_u  0.5923  0.3923  0.7923
## Cp_k  0.5923  0.3540  0.8306
## Cpm   0.5866  0.3501  0.8233
## 
## Exp<LSL 0%    Obs<LSL 0%
## Exp>USL 3.8%  Obs>USL 5%

La capacidad del proceso para cumplir las especificaciones del cliente, cuantificada por el índice Cpk=0.592 resulta muy pobre. Utilizar este valor está justificado porque el proceso se descentra respecto del target, con un valor medio en las observaciones relativamente superior a la predicción (cabe pensar en algún desajuste en la toma de datos) y ampliando así la cola derecha.

cap.fun=function(datos,lsl,usl){
  xbar=mean(datos)
  s=sd(datos)
  zu=(usl-xbar)/s
  zl=(lsl-xbar)/s
  pdfe=pnorm(zl)+1-pnorm(zu)
zbench=qnorm(pdfe)
zscore=min(c(zu,-zl))
Pp=(usl-lsl)/(6*s)
Ppk=min(c(zu/3,-zl/3 ))
return(data.frame(zl=zl,zu=zu,pdfe=pdfe,zbench=zbench,zscore=zscore,Pp=Pp,Ppk=Ppk))}

cap.fun(datosc$distancia,lsl,usl)

##          zl       zu       pdfe    zbench   zscore      Pp      Ppk
## 1 -4.626967 1.580751 0.05696934 -1.580735 1.580751 1.03462 0.526917

El z-bench es el valor en un proceso normal estándar, que acumula a su izquierda la probabilidad estimada del proceso de rebasar los límites de especificación. Para entender su significado, hay que referirlo a una escala de 1+1.5, dado que 1 es la desviación típica de una normal estándar Y 1.5 es la corrección por variabilidad a largo plazo que asumen los teóricos. Cuanto más próximo a cero (en valor absoluto), mayor es el problema de capacidad del proceso para cumplir con las especificaciones, pues con alta probabilidad se rebasan los límites de especificación. Si el proceso está centrado, un valor z-bench de 4.5 (en valor absoluto) estaría indicando que el proceso funciona a un nivel sigma próximo a 6, puesto que estaría confinado a 6 desviaciones típicas a cada lado de la media (con la corrección por varianza a largo plazo). Para más información ver el soporte de Minitab.

En nuestro caso, el z-bench (en valor absoluto) resulta de 1.58, que hablaría de un nivel sigma próximo a 3 (1.6+1.5).

coste<-5
dpo<-(sum(datosc$distancia>usl)+sum(datosc$distancia<lsl))/length(datosc$distancia)
dpmo<-dpo*1000000
coste.total<-coste*dpmo

El índice ‘DPMO’ se puede obtener a partir del ‘dpo’, y resulta de 5^{4}, lo que se corresponde según la tabla de conversión dpmo-sigma a un nivel sigma aproximadamente de 3.1, conclusión similar a la obtenida con el valor z-bench (ver la tabla de conversión. Asumiendo un coste por defecto de ‘5’ unidades, tendríamos un coste por millón de oportunidades de 2.5^{5} unidades monetarias.

DOE con catapulta

1 Objetivos de la actividad

2 Experimento