Diseños Factoriales

1 Introducción

El DISEÑO DE EXPERIMENTOS (Design of Experiments DOE), se utiliza para descubrir relaciones de causa-efecto, esto es, para identificar qué factores/variables condicionan realmente una o varias respuestas de interés, y con ello poder controlar la respuesta, configurando dichos factores en los niveles que producen resultados óptimos desde el punto de vista de la mejora de un proceso.

2 Objetivos

Partimos del problema de diseñar un experimento en el que contamos con ciertos factores cuyo efecto deseamos investigar sobre una variable respuesta objetivo.

Vamos a proponer realizar un diseño de experimentos bajo dos supuestos, ambos desde el punto de vista de optimizar los recursos disponibles y por consiguiente de minimizar el número de datos a conseguir o pruebas a realizar:

• A. Queremos identificar todos los efectos principales e interacciones existentes. Tenemos suficiente presupuesto para probar y testar todas las posibilidades de combinación entre los factores disponibles.
• B. Queremos identificar los efectos principales y asumimos que algunas de las interacciones son despreciables. Tenemos recursos limitados para probar y testar todas las posibilidades de combinación entre los factores disponibles, bien por ser alto su número o el número de niveles en cada uno.

Para el primero de los supuestos introduciremos el diseño factorial completo. Para el segundo, con alguna más limitación de muestreo, el diseño factorial fraccional.

3 Diseño factorial Completo

Se observan todas las combinaciones posibles de todos los niveles de los factores considerados, con el fin de identificar todos los efectos principales y posibles interacciones existentes de cualquier orden.

Para obtener en R la matriz de diseño básica en un diseño factorial completo, introducimos como argumentos los factores a utilizar y sus niveles en el comando:

expand.grid()

Por ejemplo, supongamos 3 factores f1, f2 y f3, con 3, 2 y 2 niveles respectivamente. Conseguimos la matriz de diseño, para un diseño factorial completo, con:

expand.grid(f1=c("a", "b","c"),f2=c(-1,1),f3=c(0,1))

##    f1 f2 f3
## 1   a -1  0
## 2   b -1  0
## 3   c -1  0
## 4   a  1  0
## 5   b  1  0
## 6   c  1  0
## 7   a -1  1
## 8   b -1  1
## 9   c -1  1
## 10  a  1  1
## 11  b  1  1
## 12  c  1  1

3.1 Diseño \(2^2\)

Consideramos dos factores, A y B, con dos niveles/categorías cada uno de ellos. Los efectos a estimar son:

• \(\mu\) la media global
  
• 2 efectos principales: \(\alpha\) para el factorA y \(\beta\) para el factorB
  
• 1 efecto de interacción \(\alpha\beta\) para la interacción AB.

Los grados de libertad que consume el modelo son por lo tanto 4, lo que requerirá un mínimo de 4 observaciones en total para tener estimaciones de todos los efectos.

El modelo lineal que representa cómo ambos factores y su interacción explican una respuesta \(y\) viene dado por: \[y=\mu+\alpha A + \beta B + (\alpha\beta) AB + \epsilon\] donde \(\epsilon\) representa un error aleatorio que se distribuye \(N(0,\sigma^2)\).

El hecho de tener dos niveles para cada factornos da un total de \(2^2=4\) combinaciones posibles y distintas entre los diferentes niveles de los factores. Representando los dos niveles de los factores A y B con signos “+/-”, es muy fácil construir el término de interacción AB a partir del producto de los signos en los factores A y B. Asimismo, la matriz de diseño definida en las tres primeras columnas nos permite obtener fácilmente la predicción media para cada una de las combinaciones existentes, utilizando la expresión del modelo anterior:

A	B	AB	Estimación
+	+	+	\(\hat{\mu}+\hat{\alpha}+\hat{\beta}+ \hat{\alpha\beta}\)
+	-	-	\(\hat{\mu}+\hat{\alpha}-\hat{\beta}- \hat{\alpha\beta}\)
-	+	-	\(\hat{\mu}-\hat{\alpha}+\hat{\beta}- \hat{\alpha\beta}\)
-	-	+	\(\hat{\mu}-\hat{\alpha}-\hat{\beta}+ \hat{\alpha\beta}\)

Consideremos obtener dos observaciones de una variable respuesta \(Y\) por cada una de las combinaciones posibles en la tabla anterior, de manera que podamos estimar el error. Calculamos a continuación los promedios resultantes para cada combinación, mostrados en las filas 1-4 de la tabla.

A	B	AB	obs1	obs2	promedio
1	1	1	89	89.5	89.25
1	-1	-1	126.5	127.5	127
-1	1	-1	118	117.5	117.8
-1	-1	1	173	171.8	172.4

A continuación consideramos el cálculo del efecto positivo/negativo en cada uno de los factores A, B e interacción AB, utilizando todos los datos en cada uno de dichos niveles (positivo/negativo):

	A	B	AB
mu+	108.1	103.5	130.8
mu-	145.1	149.7	122.4
Delta	-36.94	-46.19	8.438
Delta/2	-18.47	-23.09	4.219

La fila \(mu_+\) contiene, para cada factor (A, B y la interacción AB), el promedio de los promedios en la tabla anterior que van asociados a los niveles ‘+1’. Por ejemplo, \[mu_+^A=108.1=(89.25+127)/2\]

La fila Delta contiene el incremento o cambio \(\Delta\) que sufre la variable respuesta cuando varía el factor correspondiente de su nivel “-” a su nivel “+”, \(\Delta=\mu_+-\mu_-\).

Por último, la fila Delta/2 muestra el valor de la pendiente en la recta que une los dos puntos observados (eje X=factory eje Y=respuesta), calculada como el incremento en el eje Y, \(\Delta\), dividido por el incremento en el eje X, que tiene un valor de 2 por la codificación elegida (“+”=1; “-”=-1). Se entiende claramente a partir del gráfico a continuación, cómo se calcula la pendiente de la recta: \[pendiente=(\mu_+-\mu_-)/2=\Delta/2\]

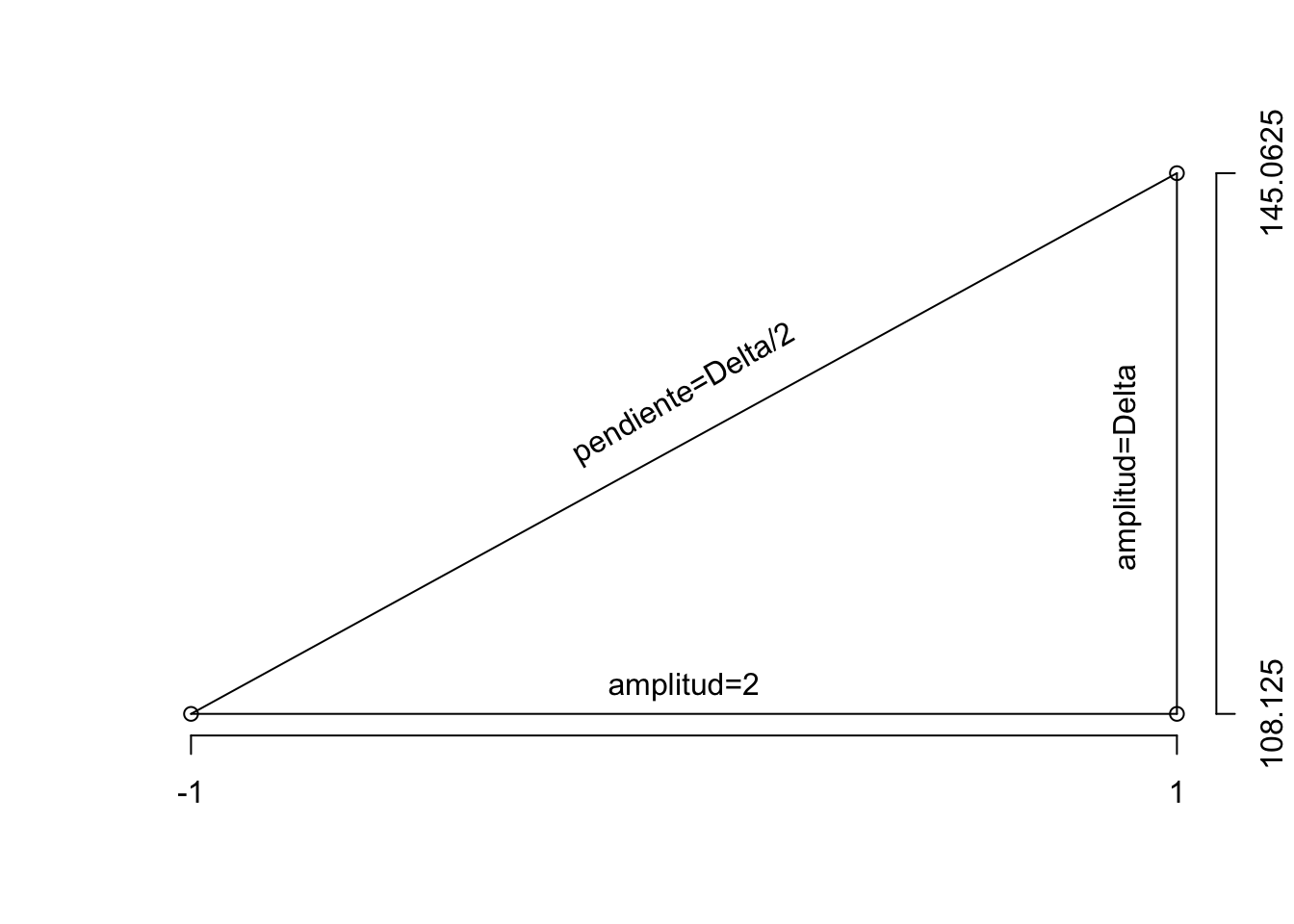
Así el modelo resultante estima: \[\hat{\alpha}=\Delta_{\alpha}/2\]

\[\hat{\beta}=\Delta_{\beta}/2\]

\[\hat{\alpha\beta}=\Delta_{\alpha\beta}/2\]

de manera que el modelo de ajuste-predicción viene dado por:

\[\hat{y}=\hat{\mu}+\hat{\alpha} A + \hat{\beta} B + \hat{\alpha\beta} AB\] y a partir de él podremos evaluar fácilmente la predicción en cualquiera de los puntos de muestreo (+/-), así como en cualquiera de los niveles referenciados “entre” los niveles de muestreo.

A	B	estimacion
1	1	89.25
1	-1	127
-1	1	117.8
-1	-1	172.4

Finalmente, si queremos predecir la respuesta en el nivel intermedio entre los dos considerados, bastará con utilizar \(A=0\) y \(B=0\), de donde la predicción de la respuesta resultará: \[\hat{y}(0)=\hat{\mu}=126.6\]

En R estos cálculos los hacemos directamente a través del ajuste del modelo lineal.

Construimos la matriz de datos

A=factor(c(1,1,1,1,-1,-1,-1,-1))
B=factor(c(1,1,-1,-1,1,1,-1,-1))
obs=rep(c(1,2),4)
datos=data.frame(A,B,obs,y);datos

##    A  B obs      y
## 1  1  1   1  89.00
## 2  1  1   2  89.50
## 3  1 -1   1 126.50
## 4  1 -1   2 127.50
## 5 -1  1   1 118.00
## 6 -1  1   2 117.50
## 7 -1 -1   1 173.00
## 8 -1 -1   2 171.75

Ajustamos el modelo lineal para estimar y con los factores A y B y la interacción AB,

fit=lm(y~A*B,data=datos)
summary(fit)

## 
## Call:
## lm.default(formula = y ~ A * B, data = datos)
## 
## Residuals:
##      1      2      3      4      5      6      7      8 
## -0.250  0.250 -0.500  0.500  0.250 -0.250  0.625 -0.625 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)
## (Intercept) 172.3750     0.4375  394.00 2.49e-10
## A1          -45.3750     0.6187  -73.34 2.07e-07
## B1          -54.6250     0.6187  -88.29 9.87e-08
## A1:B1        16.8750     0.8750   19.29 4.26e-05
## 
## Residual standard error: 0.6187 on 4 degrees of freedom
## Multiple R-squared:  0.9998, Adjusted R-squared:  0.9996 
## F-statistic:  6215 on 3 and 4 DF,  p-value: 8.625e-08

Y predecimos con el modelo las medias sobre la matriz de diseño base, para cada una de las combinaciones de niveles de factores posibles:

newdata=expand.grid(A=factor(c(-1,1)),B=factor(c(-1,1)))
cbind(newdata,pred=predict(fit,newdata))

##    A  B    pred
## 1 -1 -1 172.375
## 2  1 -1 127.000
## 3 -1  1 117.750
## 4  1  1  89.250

Obtenemos, como era de esperar, las mismas predicciones media que en la tabla que ajustamos manualmente arriba, para cada una de las combinaciones posibles de los factores A y B.

3.2 Diseño factorial Completo \(2^4\)

En un modelo con cuatro factores, A, B, C y D, cada uno de ellos con 2 niveles, los efectos a estimar son:

• \(\mu\) la media global
  
• 4 efectos principales: \(\alpha\) para el factorA, \(\beta\) para el factor B, \(\delta\) para el factor C y \(\gamma\) para el factor D
• 6 efectos para las interacciones de orden 2, AB, AC, AD, BC, BD, CD
• 4 efectos para las interacciones de orden 3, ABC, ABD, BCD, ACD
• 1 efecto para la interacción de orden 4, ABCD

Tendremos en consecuencia \(2^4=16\) combinaciones posibles entre todos los niveles de todos los factores, para estimar los 16 parámetros del modelo lineal \[y=\mu+\alpha+\beta+\delta+\gamma+\alpha\beta+\alpha\delta+\alpha\gamma+\beta\delta+\beta\gamma+\delta\gamma+\alpha\beta\delta+\alpha\beta\gamma+ \alpha\delta\gamma+\beta\delta\gamma+\alpha\beta\delta\gamma + \epsilon\]

La matriz de diseño viene dada por

m=expand.grid(A=factor(c(-1,1)),B=factor(c(-1,1)),
              C=factor(c(-1,1)),D=factor(c(-1,1)))
m

##     A  B  C  D
## 1  -1 -1 -1 -1
## 2   1 -1 -1 -1
## 3  -1  1 -1 -1
## 4   1  1 -1 -1
## 5  -1 -1  1 -1
## 6   1 -1  1 -1
## 7  -1  1  1 -1
## 8   1  1  1 -1
## 9  -1 -1 -1  1
## 10  1 -1 -1  1
## 11 -1  1 -1  1
## 12  1  1 -1  1
## 13 -1 -1  1  1
## 14  1 -1  1  1
## 15 -1  1  1  1
## 16  1  1  1  1

Una vez tenemos la matriz de diseño base, basta con utilizar las diferentes configuraciones que nos marca, para proceder con la toma de observaciones bajo cada una de las 16 especificaciones. Si consideramos 2 repeticiones de cada combinación/configuración, requeriremos 32 datos. Si consideramos 3 repeticiones, requeriremos 48 datos.

Una vez observados los datos, la estimación se realiza de igual modo que en el modelo \(2^2\) anterior, a partir del ajuste de un modelo lineal y su predicción.

fit=lm(y~A*B*C*D,data=datos)
m.pred=cbind(m,pred=predict(fit,m))

4 Diseño Factorial Fraccional

Consideremos el ejemplo presentado en el apartado anterior con un diseño \(2^4\). Si no podemos llevar a cabo el muestreo factorial completo con al menos 32 observaciones (para el error), y además presumimos que las interacciones de orden superior son despreciables y nos interesan básicamente los efectos principales, podemos reducir el diseño factorial completo a un diseño factorial fraccional.

4.1 Diseño Fraccional Mitad

Con este diseño reducimos a la mitad el número de datos necesarios en el diseño factorial completo.

Consideremos el caso general de un diseño \(2^k\), que convertimos a un diseño fracional mitad \(2^{k-1}_IV\).

1. Construimos el diseño base factorial completo para \(k-1\) factores, con \(2^{k-1}\) pruebas.

En R creamos una matriz numérica -las columnas no son factores- para poderla operar y así calcular el resto de interacciones a través de productos.

m=expand.grid(A=c(-1,1),B=c(-1,1),C=c(-1,1))
m

##    A  B  C
## 1 -1 -1 -1
## 2  1 -1 -1
## 3 -1  1 -1
## 4  1  1 -1
## 5 -1 -1  1
## 6  1 -1  1
## 7 -1  1  1
## 8  1  1  1

2. A continuación determinamos los niveles a observar para el factor k-ésimo (no incluido en el diseño base), a partir de la interacción de los otros \(k-1\) factores, esto es, con el producto de las columnas del diseño base.

m$D=m$A*m$B*m$C
m

##    A  B  C  D
## 1 -1 -1 -1 -1
## 2  1 -1 -1  1
## 3 -1  1 -1  1
## 4  1  1 -1 -1
## 5 -1 -1  1  1
## 6  1 -1  1 -1
## 7 -1  1  1 -1
## 8  1  1  1  1

Y completamos el resto de columnas de interacciones, con los productos pertinentes.

##    A  B  C  D AB AC AD BC BD CD ABC ABD ACD BCD ABCD
## 1 -1 -1 -1 -1  1  1  1  1  1  1  -1  -1  -1  -1    1
## 2  1 -1 -1  1 -1 -1  1  1 -1 -1   1  -1  -1   1    1
## 3 -1  1 -1  1 -1  1 -1 -1  1 -1   1  -1   1  -1    1
## 4  1  1 -1 -1  1 -1 -1 -1 -1  1  -1  -1   1   1    1
## 5 -1 -1  1  1  1 -1 -1 -1 -1  1   1   1  -1  -1    1
## 6  1 -1  1 -1 -1  1 -1 -1  1 -1  -1   1  -1   1    1
## 7 -1  1  1 -1 -1 -1  1  1 -1 -1  -1   1   1  -1    1
## 8  1  1  1  1  1  1  1  1  1  1   1   1   1   1    1

3. Identificamos claramente que hay columnas repetidas cuyos efectos se estarán confundiendo en la estimación. En concreto, los efectos confundidos por pares, –se estima su suma, y no cada uno de ellos independientemente–, se muestran a continuación por columnas:

fun.id=function(M){
  v=list()
  for(i in 1:(dim(M)[2])){
  v[[i]]=names(which(apply(M,2,FUN =identical,x=M[,i])==TRUE))
  } 
  return(v)
  }

knitr::kable(unique(fun.id(m.full)),format="html")

x A BCD

x B ACD

x C ABD

x D ABC

x AB CD

x AC BD

x AD BC

x ABCD

Esto implica, por ejemplo, que la estimación que se obtenga para el tamaño del efecto A en realidad será una estimación del efecto A+BCD. Si BCD es despreciable, realmente estaremos estimando el efecto A.

Surge así un nuevo concepto que es de la RESOLUCIÓN de un diseño fraccional. La resolución \(XX\), que se escribe como un subíndice en números romanos en la notación de un diseño fraccional, \(2^{k-p}_{R}\), describe el grado de confusión en la estimación de efectos en el diseño. Así tendremos:

• resolución III. Los efectos principales se confunden con interacciones de orden 2 y mayores, pero no con otros factores principales;
• resolución IV. Los efectos principales se confunden con interacciones de O3 y mayores, pero no con otros factores principales o interacciones O2. Los efectos principales están libres de las interacciones O2;
• resolución V. Los efectos principales se confunden con interacciones de O4 y mayores, pero no con otros factores principales o interacciones O2/O3. Las interacciones O2 no se confunden entre sí, pero sí con interacciones O3 o mayores. Las interacciones O2 están libres entre sí.

Notacionalmente, un diseño factorial fraccional \(2^{k-p}_{R}\) es aquel en que se reduce un diseño factorial completo \(2^k\) a la \(2^p\) parte, siendo:

• 2 es el número de niveles para cada factor,
• k es el número de factores,
• k-p es el número de factores necesarios para generar el diseño básico,
• p es el número de factores asignados a interacciones del diseño base
• R es la resolución del diseño.

4.2 Diseño Fraccional Factorial General

Se pueden consultar las tablas de todos los diseños fraccionales más frecuentes, con información sobre la matriz de diseño y los efectos confundidos, en Summary tables of useful fractional factorial designs.

En Rse pueden crear diseños factoriales fraccionales directamente con la librería FrF2. Por ejemplo, si queremos crear un diseño fraccional para \(k=3\) factores que en lugar de tener las 8 combinaciones de un diseño factorial completo, tenga sólo 4, basta con cargar esta librería

library(FrF2)

y ejecutar la función FrF2:

FrF2(4,3)

##    A  B  C
## 1 -1 -1  1
## 2  1 -1 -1
## 3  1  1  1
## 4 -1  1 -1
## class=design, type= FrF2

Podemos incluso, simular una respuesta a partir de una matriz de diseño base, y generar así un banco de datos a analizar:

##     A  B  C  D  E  F  G           y
## 1  -1 -1 -1  1 -1  1  1 -0.46668374
## 2   1  1  1 -1  1 -1 -1 -1.16268681
## 3  -1  1  1  1 -1 -1 -1  0.16109453
## 4  -1  1 -1 -1  1  1 -1  0.04483678
## 5   1 -1 -1 -1  1  1  1 -0.04533662
## 6   1  1 -1 -1 -1 -1  1 -0.89002287
## 7   1 -1  1  1 -1 -1  1  0.56676364
## 8  -1 -1 -1 -1 -1 -1 -1  0.85059671
## 9   1 -1 -1  1  1 -1 -1 -0.78572666
## 10  1 -1  1 -1 -1  1 -1  0.16657330
## 11 -1  1  1 -1 -1  1  1  0.22651715
## 12 -1 -1  1 -1  1 -1  1 -1.16231147
## 13  1  1 -1  1 -1  1 -1 -1.10217685
## 14 -1  1 -1  1  1 -1  1  1.91307095
## 15 -1 -1  1  1  1  1 -1  0.75893713
## 16  1  1  1  1  1  1  1  0.20107991
## class=design, type= FrF2

Cuando ajustamos modelos lineales con pocos datos para estimar todos los efectos implicados, como ocurre en los diseños fraccionales, podemos tener problemas a la hora de testar del modo habitual la significatividad de los efectos, e identificar en consecuencia cuáles de los factores en el diseño explican de algún modo la respuesta.

En estos casos se procede y concluye fundamentalmente a través de análisis gráficos del ajuste, y de tests de normalidad. La base de este modo de proceder viene justificada por las hipótesis de normalidad de los datos y en consecuencia de los estimadores de los efectos (obtenidos de minimizar el error cuadrático medio y maximizar verosimilitud). Todos ellos además, comparten la misma varianza, por la hipótesis de homogeneidad de varianzas en los datos. En consecuencia, cuando topamos con un factor no activo, esto es, que no influye en la respuesta, la estimación del efecto estará en torno a cero, pues su parámetro, el tamaño del efecto, sigue una distribución \(N(0,\sigma_{eff}^2)\). Cuando el factor es activo, el tamaño del efecto tomará un valor distanciado de cero.

Si ordenamos los tamaños de los efectos estimados, y los representamos confrontándolos con los cuantiles de una distribución normal (normal plot), aquellos que queden más distanciados del cero estarán identificando a los factores activos para explicar la respuesta. Los factores no activos quedarán alineados en torno a una recta que pasa por el punto \((0,0.5)\) (ver Daniel, 1976). Si en su lugar utilizamos un gráfico normal-mitad (half-normal plot, ver Daniel, 1959), representando los valores absolutos de los efectos versus la distribución del valor absoluto de una variable normal estándar, los factores no activos se alinearán a lo largo de una recta que pasa por el origen. Los factores activos quedarían pues, alejados de dicha recta.

Por otro lado, Lenth (1989) propuso un método para estimar el error estándar de los efectos, y a través de él testar la significatividad de un efecto vía un estimador \(ME\) basado en una Student-t. En R podemos realizar fácilmente los gráficos normal y normal-mitad de Daniel, así como testar la significatividad de los efectos con el test de Lenth, a partir del ajuste de un modelo lineal.

Utilizamos para ello el banco de datos speedo en la librería faraway, con 15 factores binivel y 16 observaciones en un diseño fraccional $2^{16-8}. Ajustamos un modelo sólo con efectos principales, dada la imposibilidad de estimar efecto alguno adicional.

library(faraway)

data(speedo);speedo

##    h d l b j f n a i e m c k g o      y
## 1  - - + - + + - - + + - + - - + 0.4850
## 2  + - - - - + + - - + + + + - - 0.5750
## 3  - + - - + - + - + - + + - + - 0.0875
## 4  + + + - - - - - - - - + + + + 0.1750
## 5  - - + + - - + - + + - - + + - 0.1950
## 6  + - - + + - - - - + + - - + + 0.1450
## 7  - + - + - + - - + - + - + - + 0.2250
## 8  + + + + + + + - - - - - - - - 0.1750
## 9  - - + - + + - + - - + - + + - 0.1250
## 10 + - - - - + + + + - - - - + + 0.1200
## 11 - + - - + - + + - + - - + - + 0.4550
## 12 + + + - - - - + + + + - - - - 0.5350
## 13 - - + + - - + + - - + + - - + 0.1700
## 14 + - - + + - - + + - - + + - - 0.2750
## 15 - + - + - + - + - + - + - + - 0.3425
## 16 + + + + + + + + + + + + + + + 0.5825

fit=lm(y~.,data=speedo)

Para visualizar los efectos principales, MEPlotproporciona un gráfico que representa las estimaciones de los dos extremos para cada factor, con el fin de identificar visualmente cuándo se produce un efecto relevante al variar de nivel en un factor.

MEPlot(fit)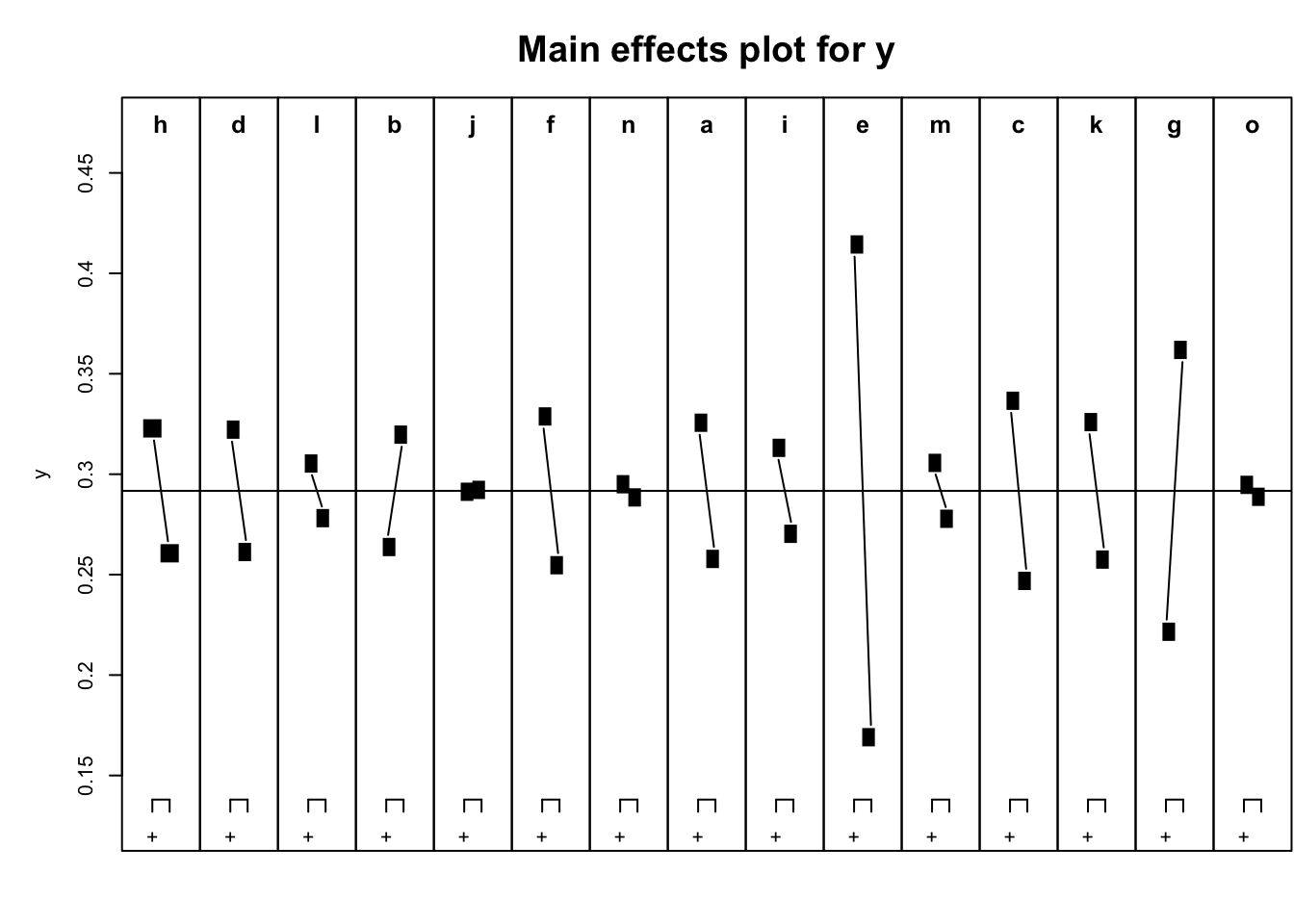

Y por último, los gráficos normal y normal-mitad de Daniel, que nos permiten especificar la significatividad para identificar distanciamientos significativos del cero basados en el estadístico de Lenth.

par(mfrow=c(1,2))
DanielPlot(fit,autolab=TRUE,alpha=0.05)
DanielPlot(fit,autolab=TRUE,half=TRUE,alpha=0.05)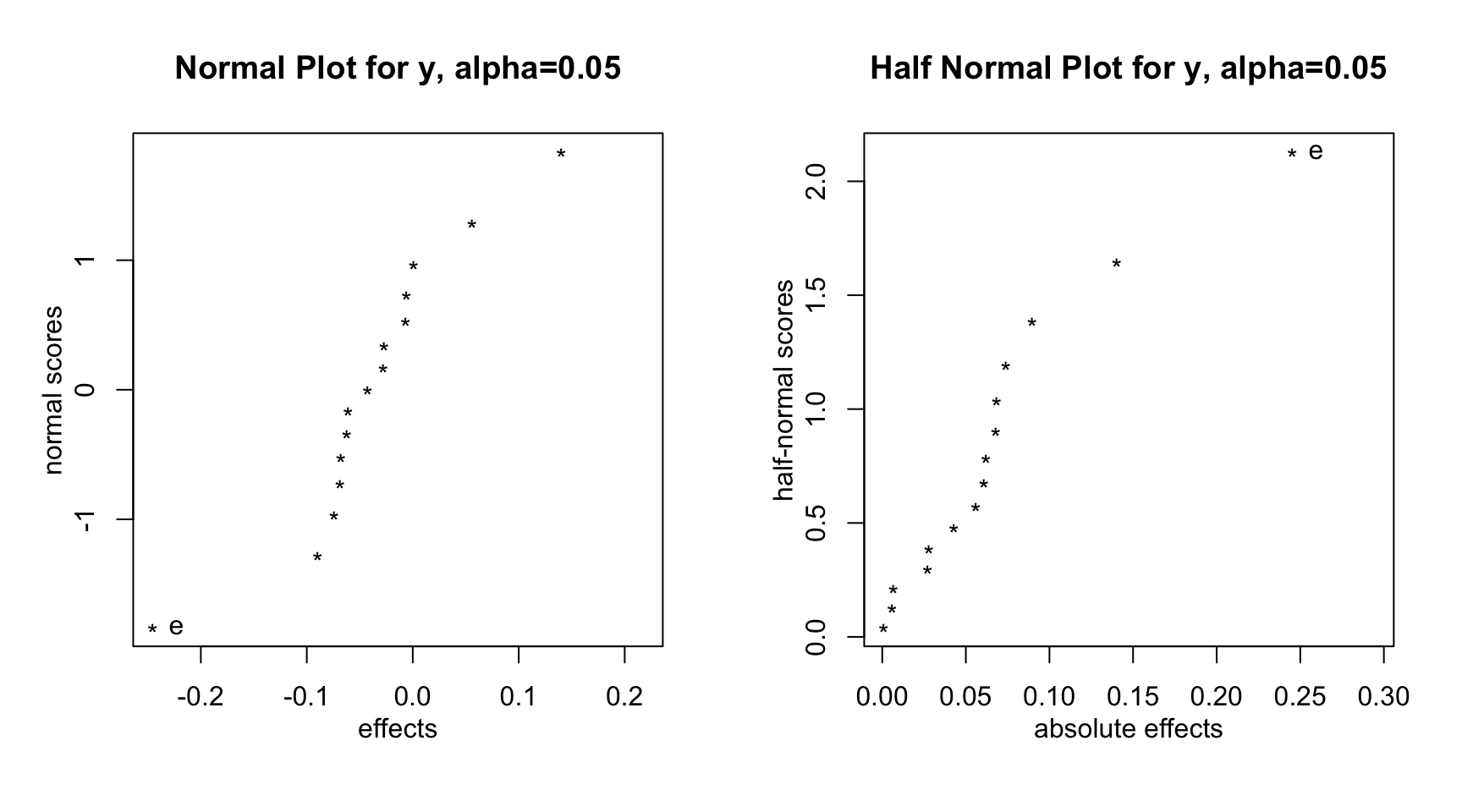

En el caso en que hubiéramos podido estimar interacciones, el comando aliasesnos da información sobre los efectos que se confunden, y el comando IAPlotnos permite confrontar los efectos principales entre sí para identificar interacciones activas. Y EL

aliases(fit)
IAPlot(fit)

5 Referencias

• Half-Normal probability plot, in Engineering Statistics Handbook (http://www.itl.nist.gov/div898/handbook/pri/section5/pri598.htm).

• Daniel, C. (1959). Use of half-normal plots in interpreting factorial two-level experiments, Technometrics 1(4), 311-341.

• Daniel, C. (1976). Applications of statistics to industrial experimentation, NY: Wiley.

• Lenth, R. V. (1989). Quick and easy analysis of unreplicated factorials. Technometrics 31(4), 469-473.