Problemas delivery (costes)
library(robustbase)
library(gridExtra)
library(tidyverse)
library(sjPlot)
library(skimr)1 El problema
Un CEO de una empresa de máquinas expendedoras (inspirada en el ejemplo de Montgomery & Peck, 1982, sobre tiempos de entrega) está en una situación complicada. Los beneficios de la empresa se vienen resintiendo últimamente en sus beneficios.
- La empresa está teniendo problemas de solvencia para asumir los costes de inversión.
- Han surgido otras empresas competidoras que ya han capturado parte de su mercado.
- La empresa ha perdido un sello de calidad, indispensable para competir en el mercado y ante una competencia cada día más severa.
- Ha estado fabricando piezas que han fallado a sus clientes, lo que está ocasionándole costes de fabricación y también costes a sus clientes. Si esto no se corrige, perderá a sus mejores clientes.
- Trabajan a un ritmo de producción continua push.
- En ciertos periodos han de alquilar naves extra para acumular el stock.
- Suelen tener problemas con la distribución.
- Para recuperar capacidad y sello de calidad, deberían garantizar abastecimientos rápidos a los compradores, tanto en producción como en distribución.
- Los costes de reparto son variables en función del volumen del pedido y de la distancia de entrega. Todo el transporte lo alquilan.
- Necesariamente ha de reducir sus costes en un 5%, con el fin de generar un retorno superior en el capital invertido y poder asumir las reducciones de precios que está demandando el mercado.
En definitiva, la empresa necesita mejorar la calidad y los tiempos de distribución en un corto periodo de tiempo. Veremos que Lean Seis Sigma proporciona una estrategia eficaz para conseguir estos objetivos.
2 Datos
Disponemos de los datos de venta de los últimos 3 meses, con los que investigar posibles carencias:
- Número de pedidos
- Volumen de cada pedido
- Tiempos de entrega desde el pedido
- Distancia de entrega.
3 Producción
La empresa trabaja a un ritmo constante de producción construyendo máquinas expendedoras. El tiempo neto de producción de una máquina, eliminando todas las demoras en el proceso es de \(x_1=3\) días.
4 Stock
Hasta el momento el alquiler de una nave extra es de \(x_2=3000€/mes\).
5 Reparto
Disponemos de una recopilación de datos relativos al tiempo de entrega de compras de máquinas expendedoras, junto con el número de productos de stock solicitados y la distancia entre el proveedor y el comprador. (Fte: (Montgomery & Peck, 1982) Vincentarelbundock.github.io).
El coste por kilómetro \(x_4\) es aproximadamente de 250€ en recorridos inferiores a 300km y de 350€ en recorridos superiores, para camiones ligeros o livianos (hasta 3.5 toneladas) y de 400€/kmy 500€/km respectivamente, para camiones de entre 3.5 y 5.5 toneladas.
6 Costes y beneficios
Los precios de venta de cada máquina \(x_5\) se establecen en función del volumen del pedido: 500€ en pedidos inferiores a 4 máquinas, 450€ si los pedidos están entre 4 y 8 máquinas, 400€ para pedidos entre 9 y 20 máquinas y pedidos superiores a 20 aplican un precio de 350€ a cada máquina.
1. Cuál es la situación actual de la empresa.
Hacemos un descriptivo del volumen de negocio, volumen de pedidos, distancia de compradores, tiempos de entrega, y una evaluación de costes/beneficios.
data(delivery, package="robustbase")
summary(delivery)## n.prod distance delTime
## Min. : 2.00 Min. : 36.0 Min. : 8.00
## 1st Qu.: 4.00 1st Qu.: 150.0 1st Qu.:13.75
## Median : 7.00 Median : 330.0 Median :18.11
## Mean : 8.76 Mean : 409.3 Mean :22.38
## 3rd Qu.:10.00 3rd Qu.: 605.0 3rd Qu.:21.50
## Max. :30.00 Max. :1460.0 Max. :79.24# con skim conseguimos unos descriptivos más completos
skim(delivery)| Name | delivery |
| Number of rows | 25 |
| Number of columns | 3 |
| _______________________ | |
| Column type frequency: | |
| numeric | 3 |
| ________________________ | |
| Group variables | None |
Variable type: numeric
| skim_variable | n_missing | complete_rate | mean | sd | p0 | p25 | p50 | p75 | p100 | hist |
|---|---|---|---|---|---|---|---|---|---|---|
| n.prod | 0 | 1 | 8.76 | 6.88 | 2 | 4.00 | 7.00 | 10.0 | 30.00 | ▇▃▁▁▁ |
| distance | 0 | 1 | 409.28 | 325.19 | 36 | 150.00 | 330.00 | 605.0 | 1460.00 | ▇▅▃▁▁ |
| delTime | 0 | 1 | 22.38 | 15.52 | 8 | 13.75 | 18.11 | 21.5 | 79.24 | ▇▁▁▁▁ |
En datos con tanta dispersión, los percentiles suelen dar información más útil sobre los estándares o pedidos más comunes. Sería razonable utilizar las medianas para identificar cual es el tamaño estándar de los pedidos, y cuál la distancia más habitual al comprador.
¿Cómo predecirías el tiempo de entrega en función del volumen de compra y la distancia al proveedor? Tras visualizar los datos (con la variable delTime -tiempo de entrega- como respuesta), parece razonable ajustar un modelo lineal en el que ambas variables distance y n.prod entran en el modelo como covariables.
data(delivery, package="robustbase")
ggplot(delivery,aes(n.prod))+
geom_bar()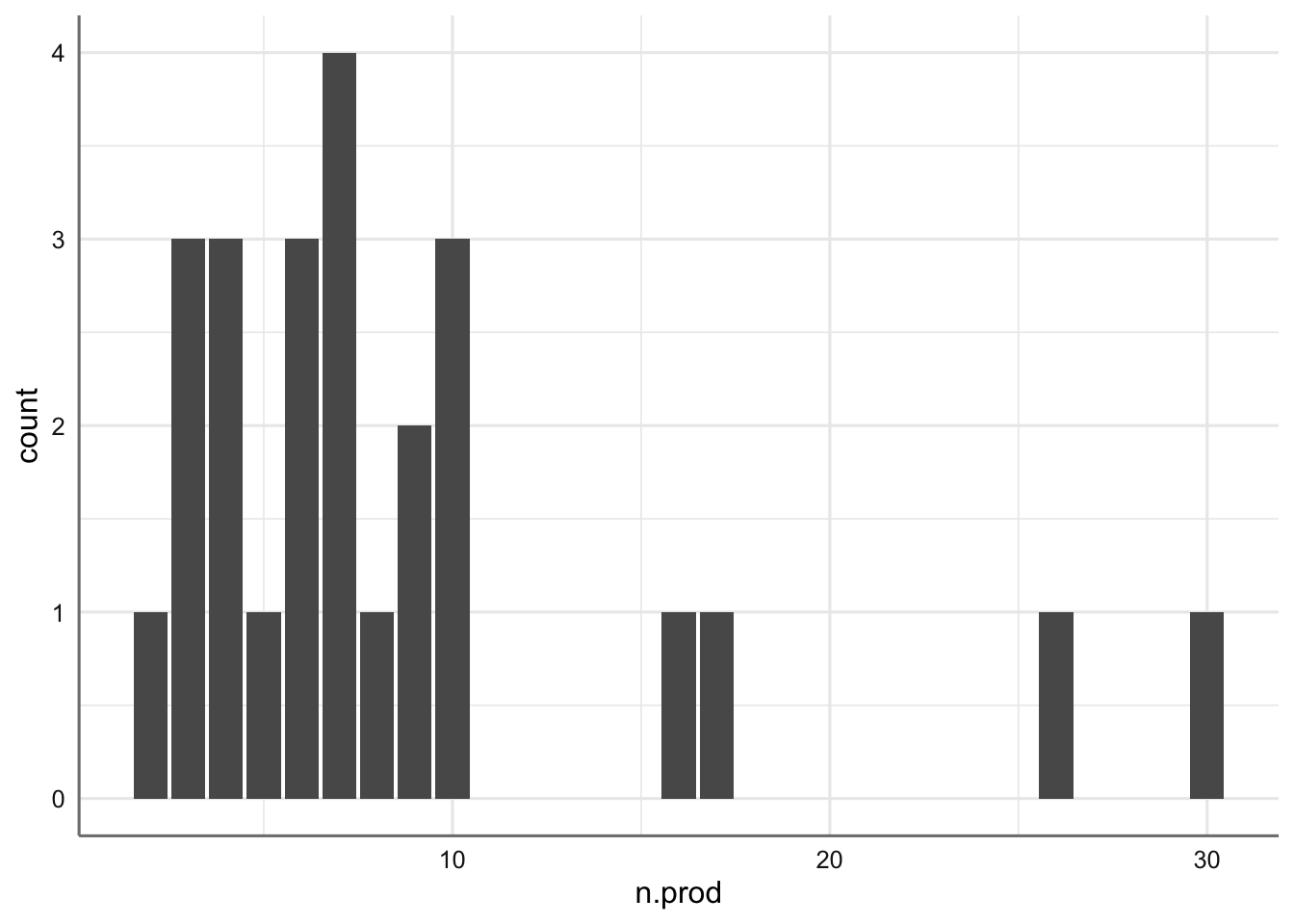
median(delivery$n.prod)## [1] 7g1=ggplot(delivery,aes(x=distance,y=delTime))+
geom_point(aes(size=n.prod))+
labs(x="Distancia",y="Tiempo de entrega",size="Volumen \n de compra")
g2=ggplot(delivery,aes(x=n.prod,y=delTime))+
geom_point(aes(size=distance))+
labs(x="Volumen de compra",y="Tiempo de entrega",size="Distancia")
grid.arrange(g1,g2,ncol=2)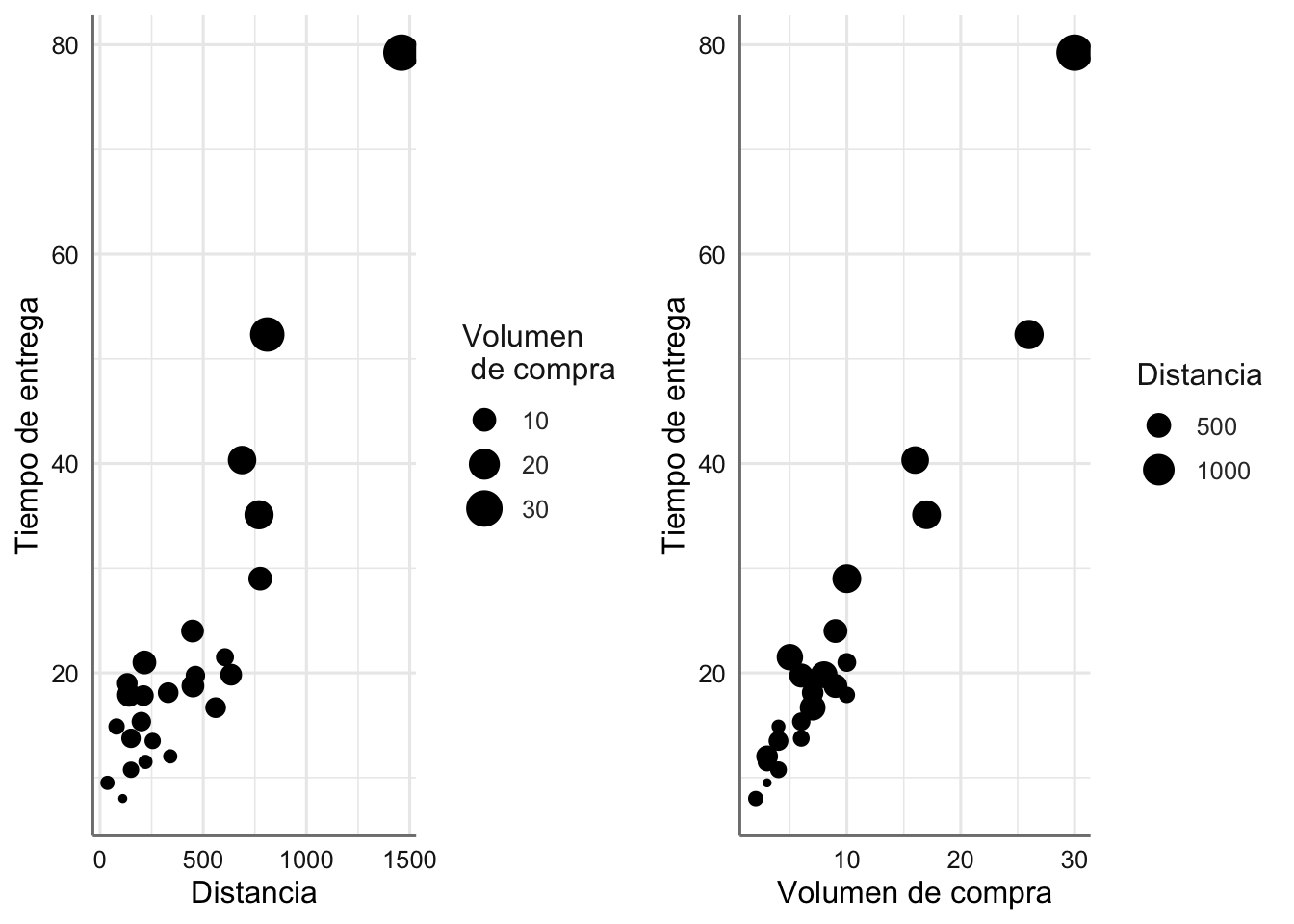
tab_model(lm.deli <- lm(delTime ~ ., data = delivery))| delTime | |||
|---|---|---|---|
| Predictors | Estimates | CI | p |
| (Intercept) | 2.34 | 0.07 – 4.62 | 0.044 |
| n.prod | 1.62 | 1.26 – 1.97 | <0.001 |
| distance | 0.01 | 0.01 – 0.02 | 0.001 |
| Observations | 25 | ||
| R2 / R2 adjusted | 0.960 / 0.956 | ||
plot_model(lm.deli,"pred",terms=c("distance","n.prod [1,5,10,15,20,25,30]"),ci.lvl = NA)+
labs(x="Distancia",y="Tiempo de entrega",title="Predicciones del tiempo de entrega", color="Stock")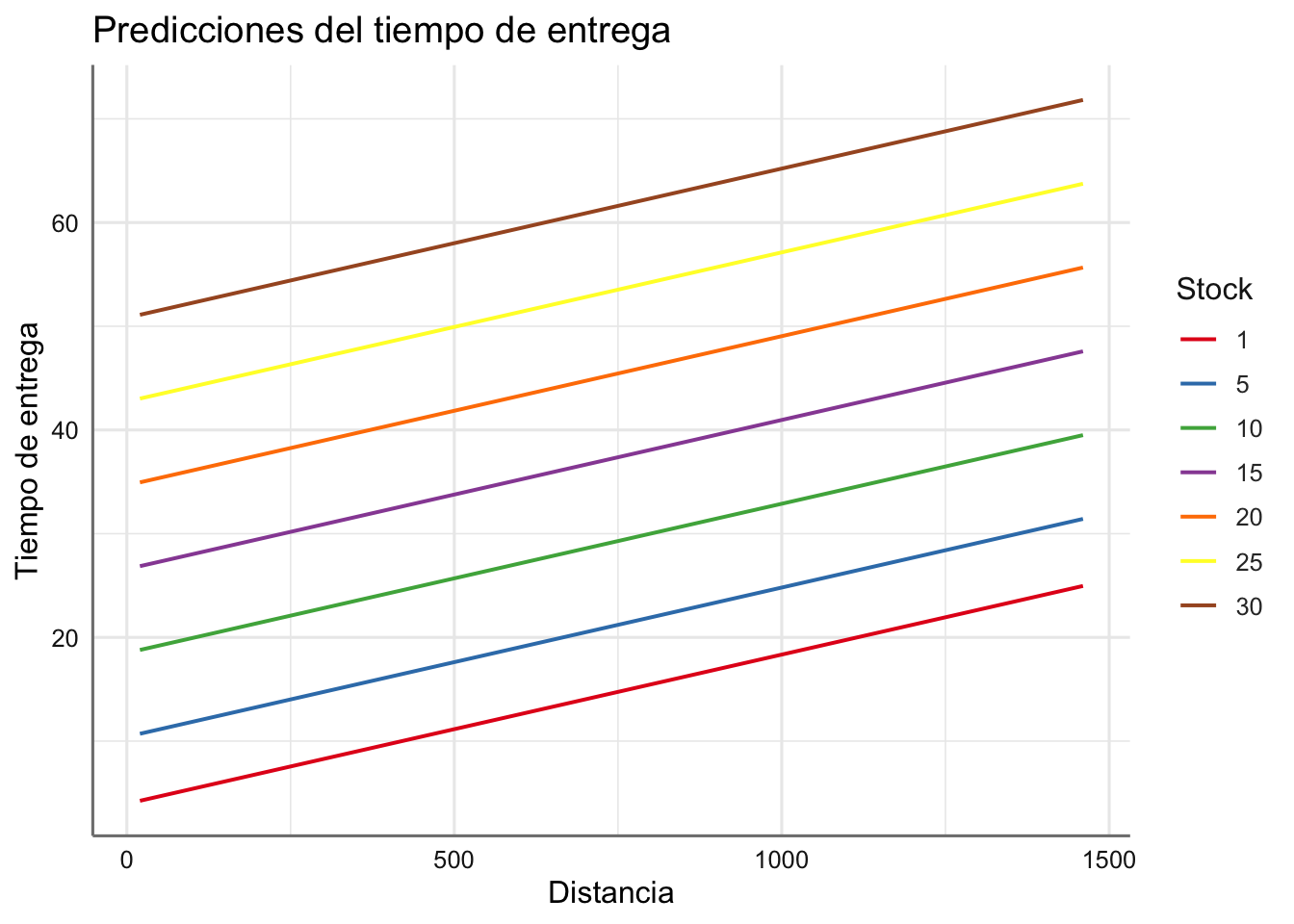
Teniendo en cuenta el volumen estándar de los pedidos, ¿cuál sería la predicción y el rango de variación factible (a un nivel de confianza del 99.9997% \(\approx 6\sigma\))? ¿Cómo explicas a la empresa el significado de ese intervalo de predicción en términos estadísticos y en términos de “calidad” (nivel sigma)?
Obtenemos las predicciones para n.prod=7, en el rango de variación de la covariable distance, junto con un intervalo de confianza al nivel 99.9997%. Un intervalo de confianza establece unos límites tales que podemos garantizar al nivel dado, que el intervalo va a capturar el verdadero valor a predecir. En términos de calidad, implicaría que por cada millón de repartos, sólo nos equivocaríamos con los márgenes de entrega (rebasándolos) en 3.4 ocasiones.
plot_model(lm.deli,"pred",terms=c("distance","n.prod [7]"),ci.lvl = 0.99997)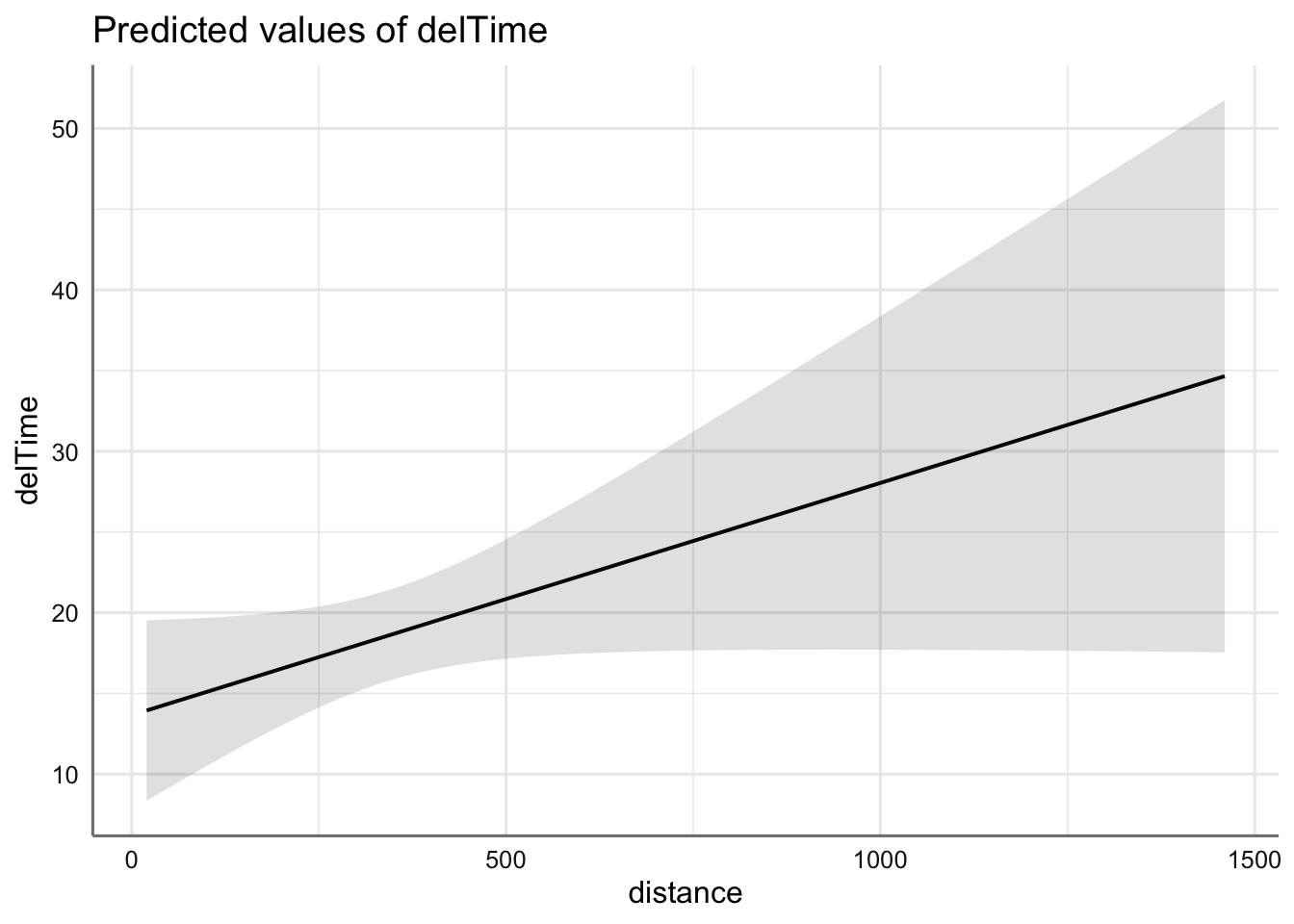
pred=plot_model(lm.deli,"pred",terms=c("distance [520,522,523,524,526,530]","n.prod [5]"),ci.lvl = 0.99997)
cbind(pred$data,rango=pred$data[,5]-pred$data[,4])## x predicted std.error conf.low conf.high group group_col rango
## 1 520 17.90088 1.191827 12.92683 22.87493 5 5 9.948102
## 2 522 17.92965 1.197469 12.93205 22.92724 5 5 9.995196
## 3 523 17.94403 1.200297 12.93463 22.95343 5 5 10.018796
## 4 524 17.95842 1.203128 12.93720 22.97963 5 5 10.042432
## 5 526 17.98719 1.208804 12.94228 23.03209 5 5 10.089807
## 6 530 18.04473 1.220205 12.95224 23.13721 5 5 10.184968