Capacidad
library(SixSigma)
library(pander) # para tablas en Rmarkdown
library(qcc)
library(tidyverse)1 Datos
Vamos a utilizar los tiempos de espera en cola de los clientes (estudiantes) que han solicitado el reconocimiento de créditos transversales en algún momento a lo largo del curso 2015-16.
Leemos en primer lugar los datos y seleccionamos las variables ‘tpo.espera.min’, de los tiempos de espera en cola expresados en minutos, y ‘mes’, referido al mes en el que se ha presentado la solicitud. Excluimos los registros con datos faltantes y con tiempos de espera negativos.
# utilizamos un banco de datos de tiempos de espera en cola del curso 2016-17
load("./datos/cegeca16.RData")
# Seleccionamos exclusivamente los tiempos de espera y el mes
datos=tiemposespera %>%
dplyr::select(tpo.espera.min,mes)%>%
mutate(mes=factor(mes,levels=c("sept.","oct.","nov.","dic." , "ene." , "feb.","mar.","abr." ,"may.", "jun.", "jul.")))%>%
filter(tpo.espera.min != is.na(tpo.espera.min)) %>%
filter(tpo.espera.min>=0)
dim(datos)## [1] 3750 22 Descripción
Para los tiempos de espera en cola calculamos una descriptiva global y otra por meses:
resumen=datos %>%
summarise(media=mean(tpo.espera.min),min=min(tpo.espera.min),max=max(tpo.espera.min),total=n())
pander(resumen)| media | min | max | total |
|---|---|---|---|
| 27.83 | 1 | 155 | 3750 |
resumen.mes=datos %>%
group_by(mes)%>%
summarise(media=mean(tpo.espera.min),min=min(tpo.espera.min),max=max(tpo.espera.min),total=n())
pander(resumen.mes)| mes | media | min | max | total |
|---|---|---|---|---|
| sept. | 66.65 | 1 | 155 | 955 |
| oct. | 27.32 | 1 | 95 | 497 |
| nov. | 10.11 | 1 | 43 | 400 |
| dic. | 5.311 | 1 | 23 | 161 |
| ene. | 8.662 | 1 | 35 | 222 |
| feb. | 6.589 | 1 | 30 | 236 |
| mar. | 6.293 | 1 | 28 | 157 |
| abr. | 4.636 | 1 | 32 | 99 |
| may. | 5.439 | 1 | 105 | 114 |
| jun. | 12.29 | 1 | 121 | 300 |
| jul. | 21.37 | 1 | 75 | 609 |
# Y los visualizamos gráficamente:
ggplot(datos,aes(mes,tpo.espera.min))+geom_boxplot(aes(colour=as.factor(mes)))+
theme(legend.position = "none")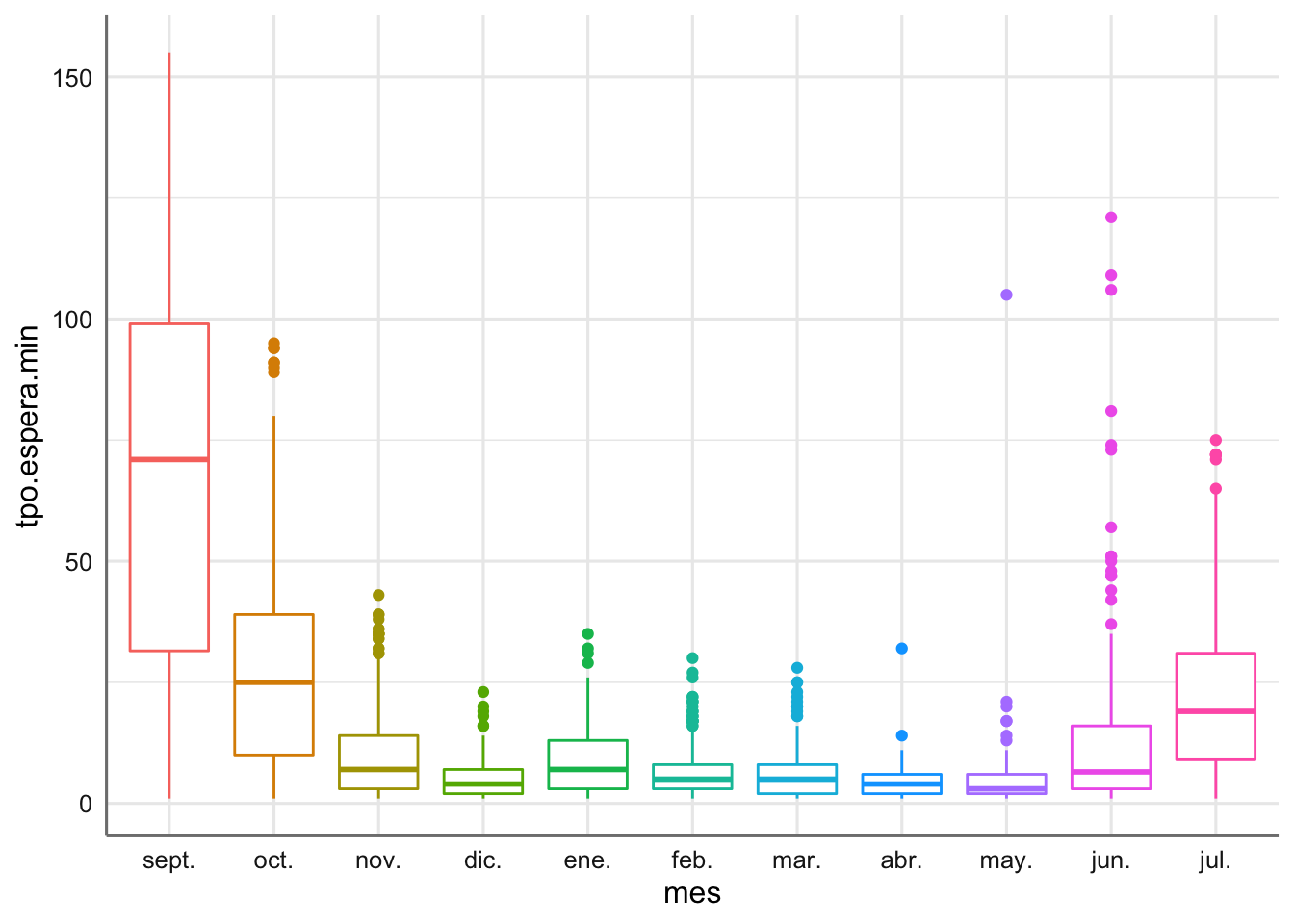
Se aprecia claramente que los meses de junio a noviembre tienen un comportamiento especialmente diferente al resto de meses, con unos tiempos de espera claramente altos en comparación con el periodo de diciembre a mayo. Estudiemos este comportamiento respecto a rendimiento/capacidad del sistema.
3 Rendimiento
Con los límites de especificación (lsl=0,usl=60), calculamos el rendimiento (YIELD) y todas las medidas relacionadas para cuantificar capacidad en términos del número de defectos. Globalmente tenemos:
usl=60
lsl=0
defectos=sum(datos$tpo.espera.min>usl)+sum(datos$tpo.espera.min<lsl)
opp=length(datos$tpo.espera.min)
pander(ss.ca.yield(defects = defectos, rework = 0, opportunities = opp))| Yield | FTY | RTY | DPU | DPMO |
|---|---|---|---|---|
| 0.8443 | 0.8443 | 0.8443 | 584 | 155733 |
Creamos además una función que nos calcula los índices de capacidad básicos:
cap.fun=function(datos,lsl,usl){
xbar=mean(datos)
s=sd(datos)
zu=(usl-xbar)/s
zl=(lsl-xbar)/s
pdfe=pnorm(zl)+1-pnorm(zu)
zbench=qnorm(pdfe)
zscore=min(c(zu,-zl))
Pp=(usl-lsl)/(6*s)
Ppk=min(c(zu/3,-zl/3 ))
return(data.frame(zl=zl,zu=zu,pdfe=pdfe,zbench=zbench,zscore=zscore,Pp=Pp,Ppk=Ppk))}Y calculamos dichos índices de capacidad de modo global con todos los datos, utilizando como límites de especificación lsl=0 y usl=60 minutos (si bien el límite inferior no es un obstáculo y no debería intervenir en las especificaciones):
lsl=0;usl=60
cap.global=cap.fun(datos$tpo.espera.min,lsl,usl)
pander(cap.global)| zl | zu | pdfe | zbench | zscore | Pp | Ppk |
|---|---|---|---|---|---|---|
| -0.8488 | 0.981 | 0.3613 | -0.3551 | 0.8488 | 0.305 | 0.2829 |
y de modo específico cada mes:
pormes=tapply(datos$tpo.espera.min,INDEX=as.factor(datos$mes),FUN=cap.fun,lsl=lsl,usl=usl)
pander(pormes)sept.:
zl zu pdfe zbench zscore Pp Ppk -1.73 -0.1725 0.6103 0.2801 -0.1725 0.2596 -0.0575 oct.:
zl zu pdfe zbench zscore Pp Ppk -1.341 1.604 0.1443 -1.061 1.341 0.4909 0.4471 nov.:
zl zu pdfe zbench zscore Pp Ppk -1.131 5.582 0.1289 -1.131 1.131 1.119 0.3771 dic.:
zl zu pdfe zbench zscore Pp Ppk -1.238 12.75 0.1078 -1.238 1.238 2.332 0.4128 ene.:
zl zu pdfe zbench zscore Pp Ppk -1.271 7.535 0.1018 -1.271 1.271 1.468 0.4238 feb.:
zl zu pdfe zbench zscore Pp Ppk -1.19 9.646 0.117 -1.19 1.19 1.806 0.3967 mar.:
zl zu pdfe zbench zscore Pp Ppk -1.111 9.478 0.1334 -1.111 1.111 1.765 0.3702 abr.:
zl zu pdfe zbench zscore Pp Ppk -1.121 13.38 0.1312 -1.121 1.121 2.417 0.3736 may.:
zl zu pdfe zbench zscore Pp Ppk -0.5329 5.347 0.297 -0.5329 0.5329 0.9799 0.1776 jun.:
zl zu pdfe zbench zscore Pp Ppk -0.7622 2.959 0.2245 -0.7571 0.7622 0.6202 0.2541 jul.:
zl zu pdfe zbench zscore Pp Ppk -1.384 2.502 0.08933 -1.345 1.384 0.6477 0.4614
Como resultado del análisis de rendimiento, observamos que en global tenemos un rendimiento muy bajo, sin embargo el rendimiento del sistema mejora especialmente entre los meses de noviembre a mayo.
4 Capacidad
Utilizando la librería ‘qcc’ realizamos el análisis de capacidad con todos los datos disponibles, considerando como submuestras los meses del curso, un objetivo o target de 30 minutos de espera en la cola, y un límite superior de especificación de 60 minutos:
cap <- qcc.groups(datos$tpo.espera.min, datos$mes)
q <- qcc(cap, type="xbar", nsigmas=3, plot=TRUE)
plot(q)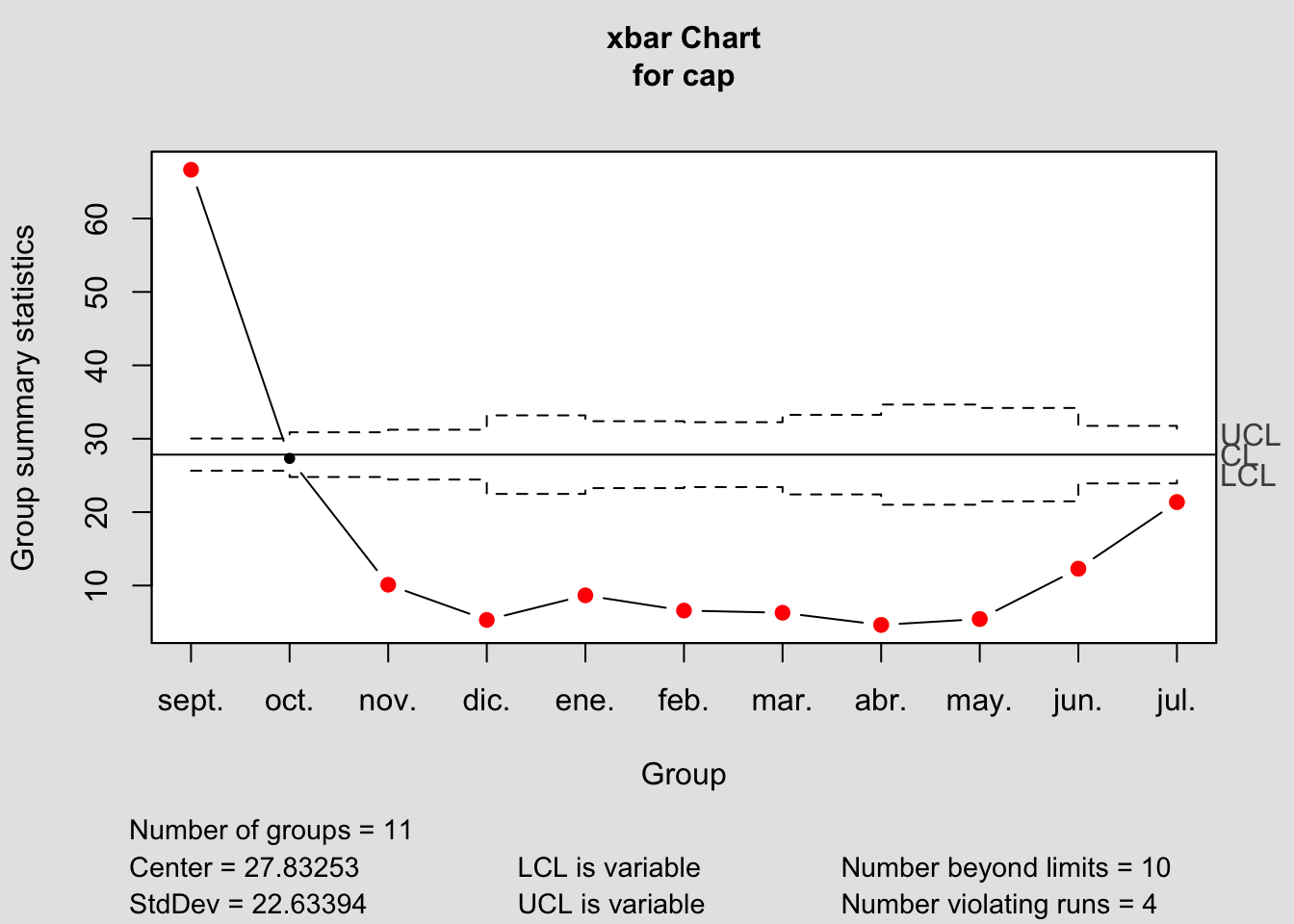
lsl=0;usl=60
target=30
process.capability(q, spec.limits=c(NA,usl),target=target)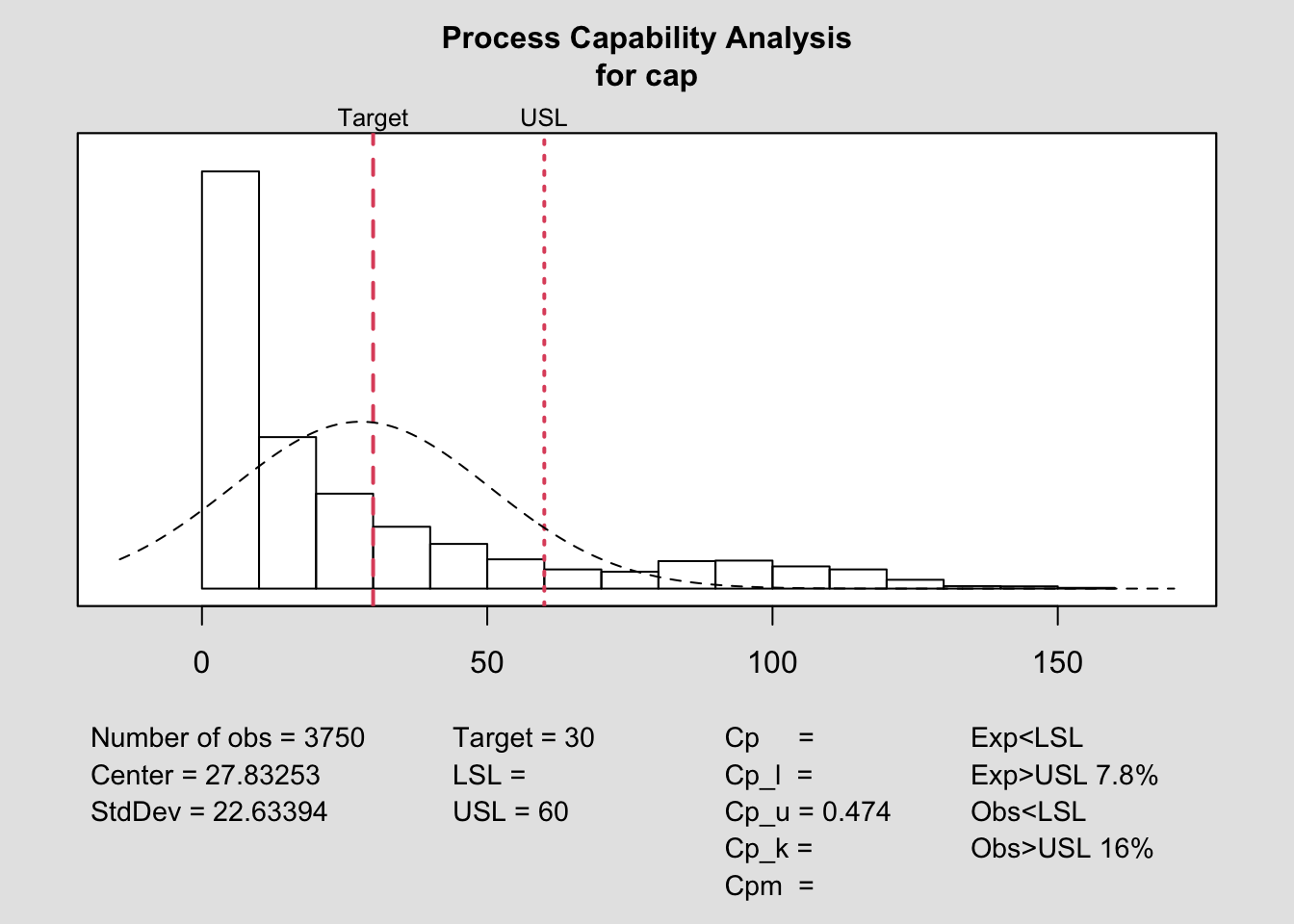
##
## Process Capability Analysis
##
## Call:
## process.capability(object = q, spec.limits = c(NA, usl), target = target)
##
## Number of obs = 3750 Target = 30
## Center = 27.83 LSL =
## StdDev = 22.63 USL = 60
##
## Capability indices:
##
## Value 2.5% 97.5%
## Cp
## Cp_l
## Cp_u 0.4737 0.461 0.4864
## Cp_k
## Cpm
##
## Exp<LSL Obs<LSL Exp>USL 7.8% Obs>USL 16%Al tener un proceso asimétrico, es razonable utilizar los índices \(C_{pk}\), que resulta de 0.474
Separamos en particular el mes de septiembre y repetimos el análisis de capacidad con idénticos objetivos y límites de especificación, pero diferenciando muestras por días (fecha); esta vez consideramos lsl=0 para que el programa nos facilite otros índices de capacidad por la izquierda:
datos.sep=tiemposespera%>%
dplyr::select(fecha,mes,tpo.espera.min)%>%
filter(mes=="sept.")%>%
mutate(fecha=factor(fecha,levels=as.character(unique(fecha[mes=="sept."]))))
cap <- qcc.groups(datos.sep$tpo.espera.min, datos.sep$fecha)
q <- qcc(cap, type="xbar", nsigmas=3, plot=TRUE)
plot(q)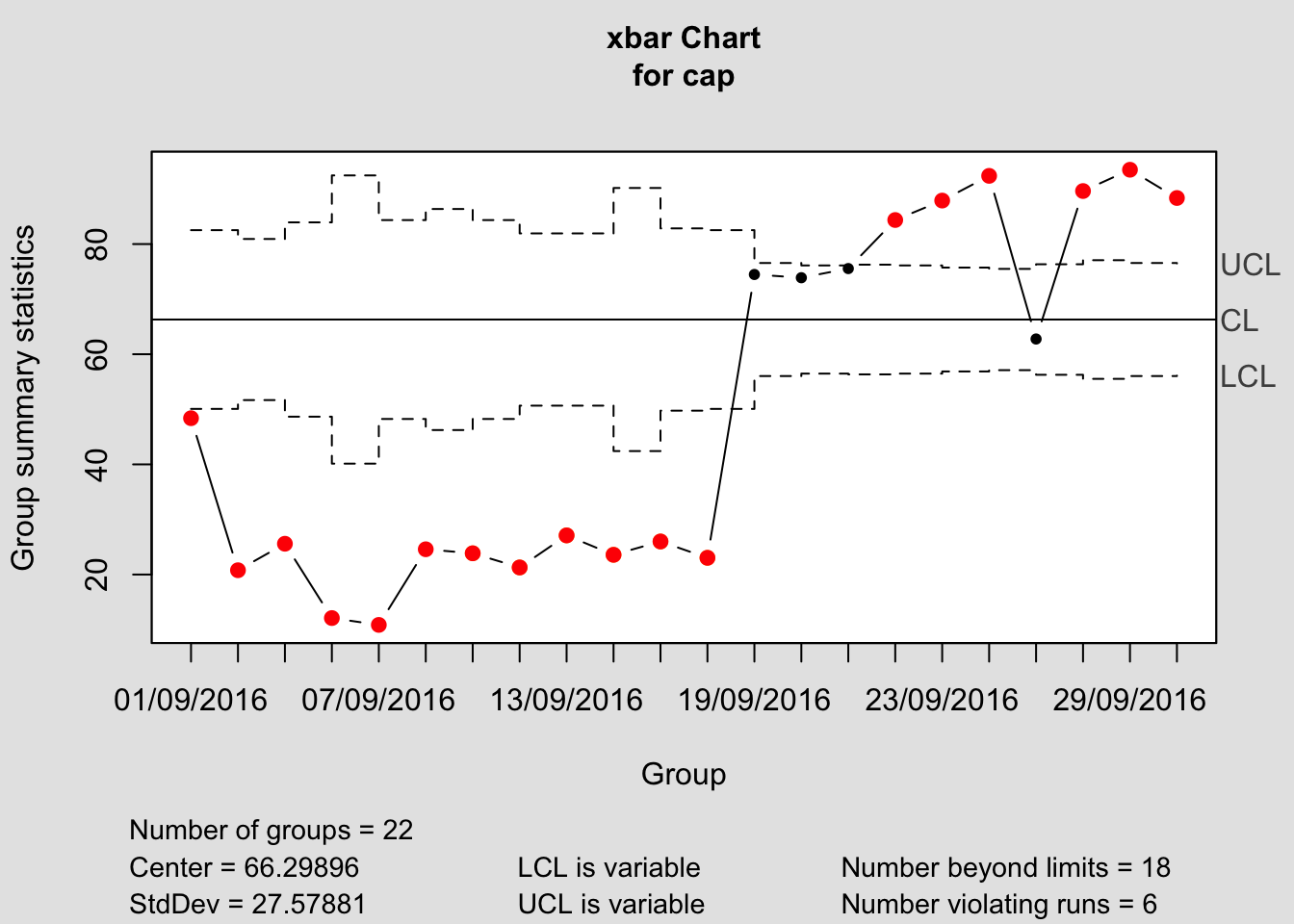
lsl=0;usl=60
target=30
process.capability(q, spec.limits=c(0,usl),target=target)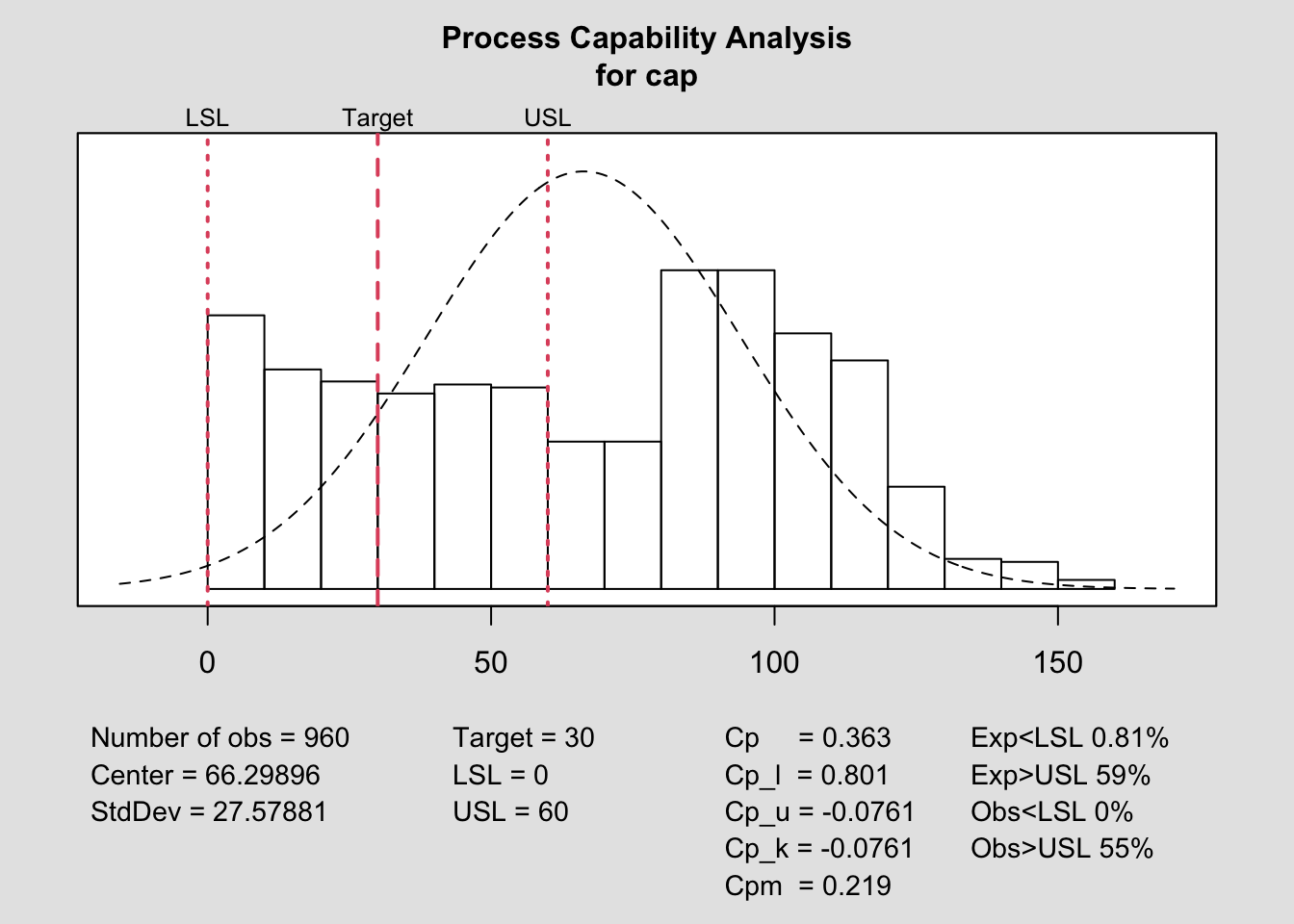
##
## Process Capability Analysis
##
## Call:
## process.capability(object = q, spec.limits = c(0, usl), target = target)
##
## Number of obs = 960 Target = 30
## Center = 66.3 LSL = 0
## StdDev = 27.58 USL = 60
##
## Capability indices:
##
## Value 2.5% 97.5%
## Cp 0.36260 0.34637 0.37882
## Cp_l 0.80133 0.76641 0.83624
## Cp_u -0.07613 -0.05821 -0.09406
## Cp_k -0.07613 -0.05477 -0.09749
## Cpm 0.21936 0.20682 0.23189
##
## Exp<LSL 0.81% Obs<LSL 0%
## Exp>USL 59% Obs>USL 55%El índice de capacidad referente es \(C_p\) (el proceso es simétrico respecto límites de especificación), que toma un valor claramente deficitario por debajo de 1, con lo cual el sistema es definitivamente incapaz de cumplir las especificaciones del cliente durante el mes de septiembre.
Quitamos ahora los meses críticos, de junio a noviembre (ambos incluidos):
datos.p=datos %>%
filter(mes %in% c( "dic.","ene.", "feb.", "mar.", "abr.", "may.")) %>%
mutate(mes=factor(mes,levels=unique(mes)))
cap <- qcc.groups(datos.p$tpo.espera.min, datos.p$mes)
q <- qcc(cap, type="xbar", nsigmas=3, plot=TRUE)
plot(q)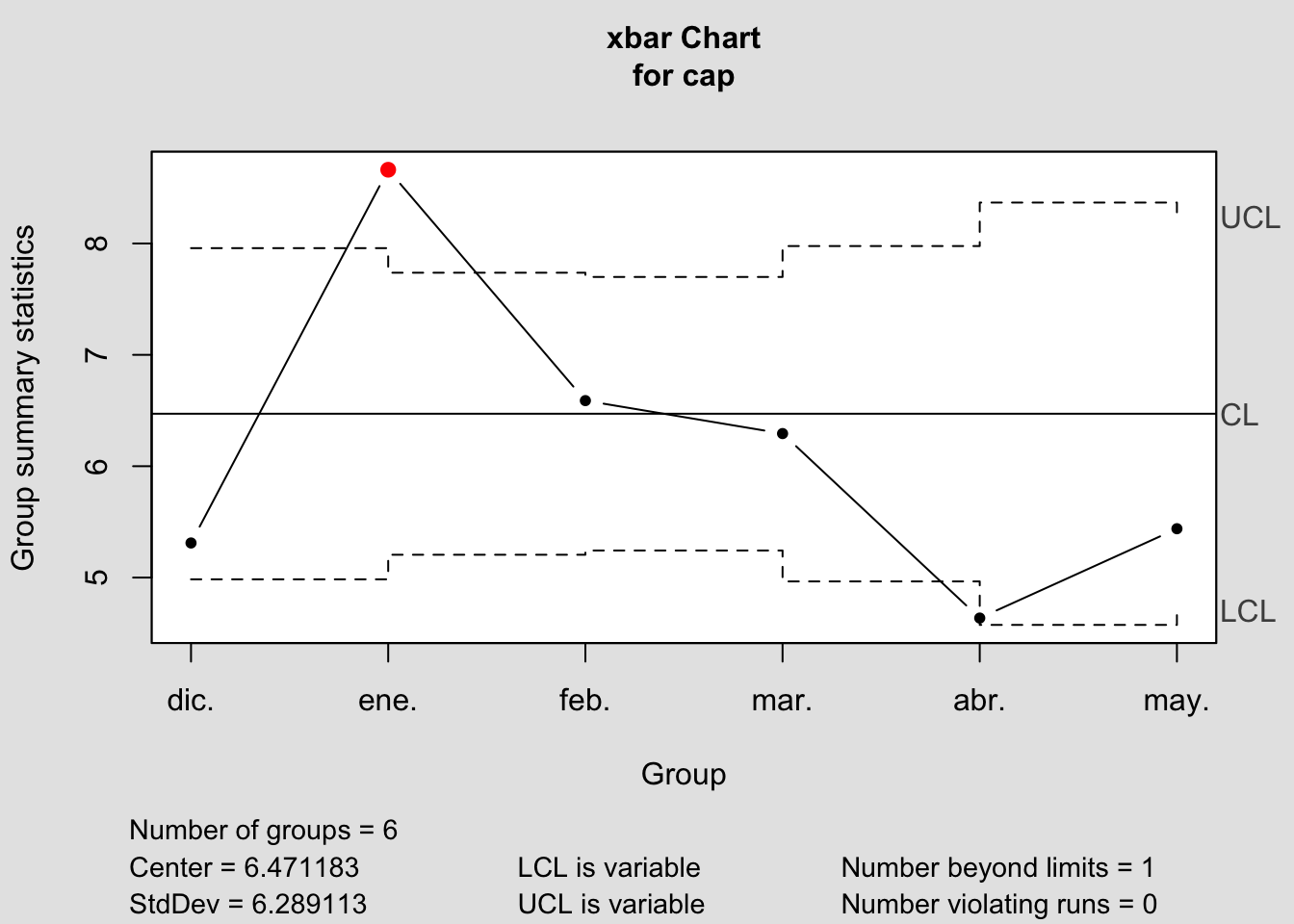
lsl=0;usl=60
target=30
process.capability(q, spec.limits=c(lsl,usl),target=target)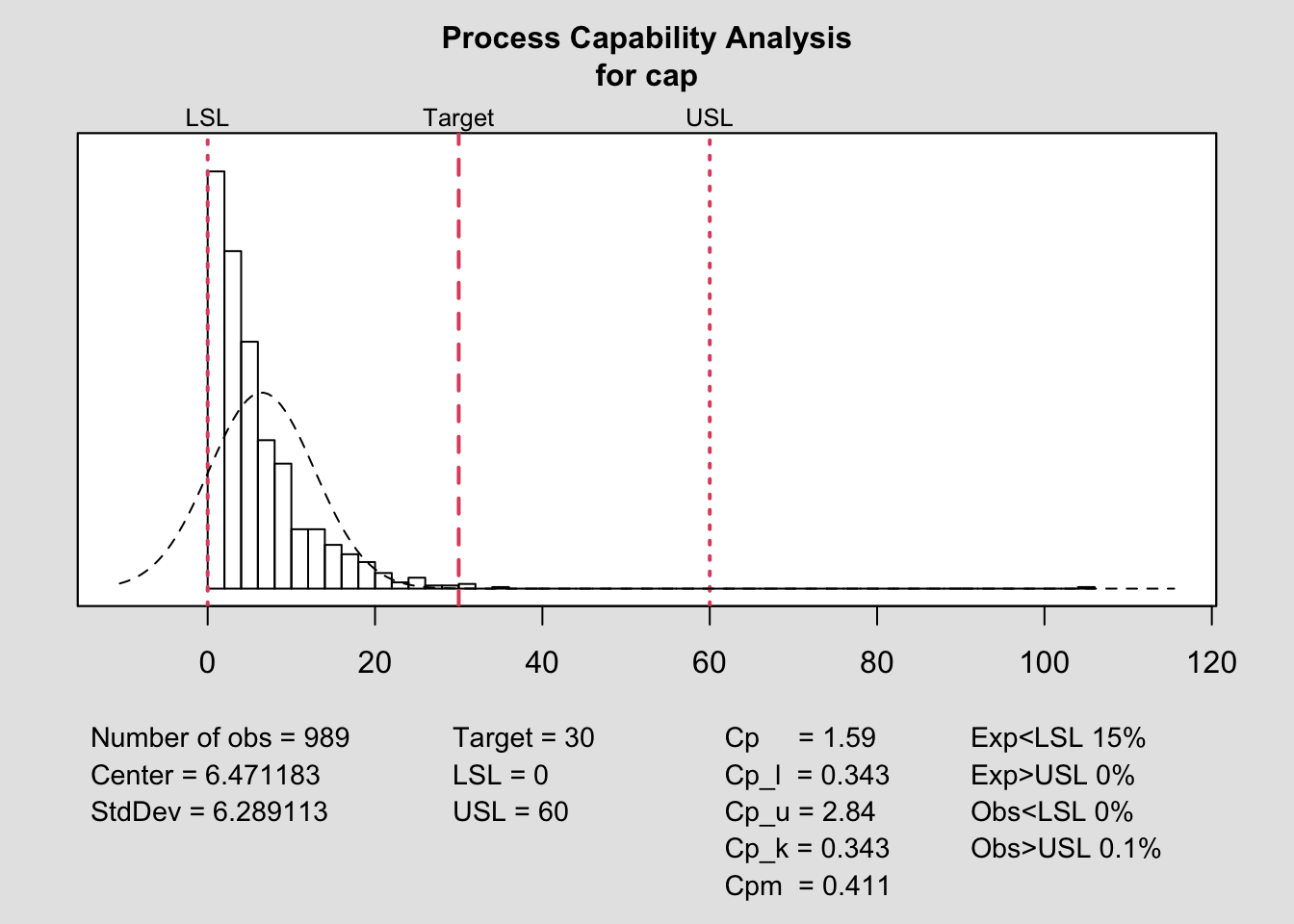
##
## Process Capability Analysis
##
## Call:
## process.capability(object = q, spec.limits = c(lsl, usl), target = target)
##
## Number of obs = 989 Target = 30
## Center = 6.471 LSL = 0
## StdDev = 6.289 USL = 60
##
## Capability indices:
##
## Value 2.5% 97.5%
## Cp 1.5900 1.5199 1.6601
## Cp_l 0.3430 0.3214 0.3645
## Cp_u 2.8371 2.7307 2.9435
## Cp_k 0.3430 0.3173 0.3687
## Cpm 0.4106 0.3854 0.4357
##
## Exp<LSL 15% Obs<LSL 0%
## Exp>USL 0% Obs>USL 0.1%Reconocemos el índice \(C_{pu}\) como el referente para interpretar el análisis de capacidad, dada la asimetría del proceso respecto de los límites de especificación. El proceso es claramente capaz, con un índice de 2.84, durante los meses de diciembre a mayo.
Un análisis de capacidad a largo plazo y también a corto plazo durante una franja de tiempo determinada y más reducida, lo podríamos realizar directamente con la librería SixSigma:
lsl=0
usl=60
target=30
levels(datos$mes)## [1] "sept." "oct." "nov." "dic." "ene." "feb." "mar." "abr." "may."
## [10] "jun." "jul."ss.study.ca(xST=datos[datos$mes %in% c("dic.", "ene." , "feb." ,"mar." , "abr." , "may." ),1],
xLT=datos[,1],USL=usl,Target=target,
f.main="Análisis de capacidad a corto y largo plazo",
f.sub="Corto plazo: diciembre-mayo")## Warning in ss.study.ca(xST = datos[datos$mes %in% c("dic.", "ene.", "feb.", :
## Normality test/s failed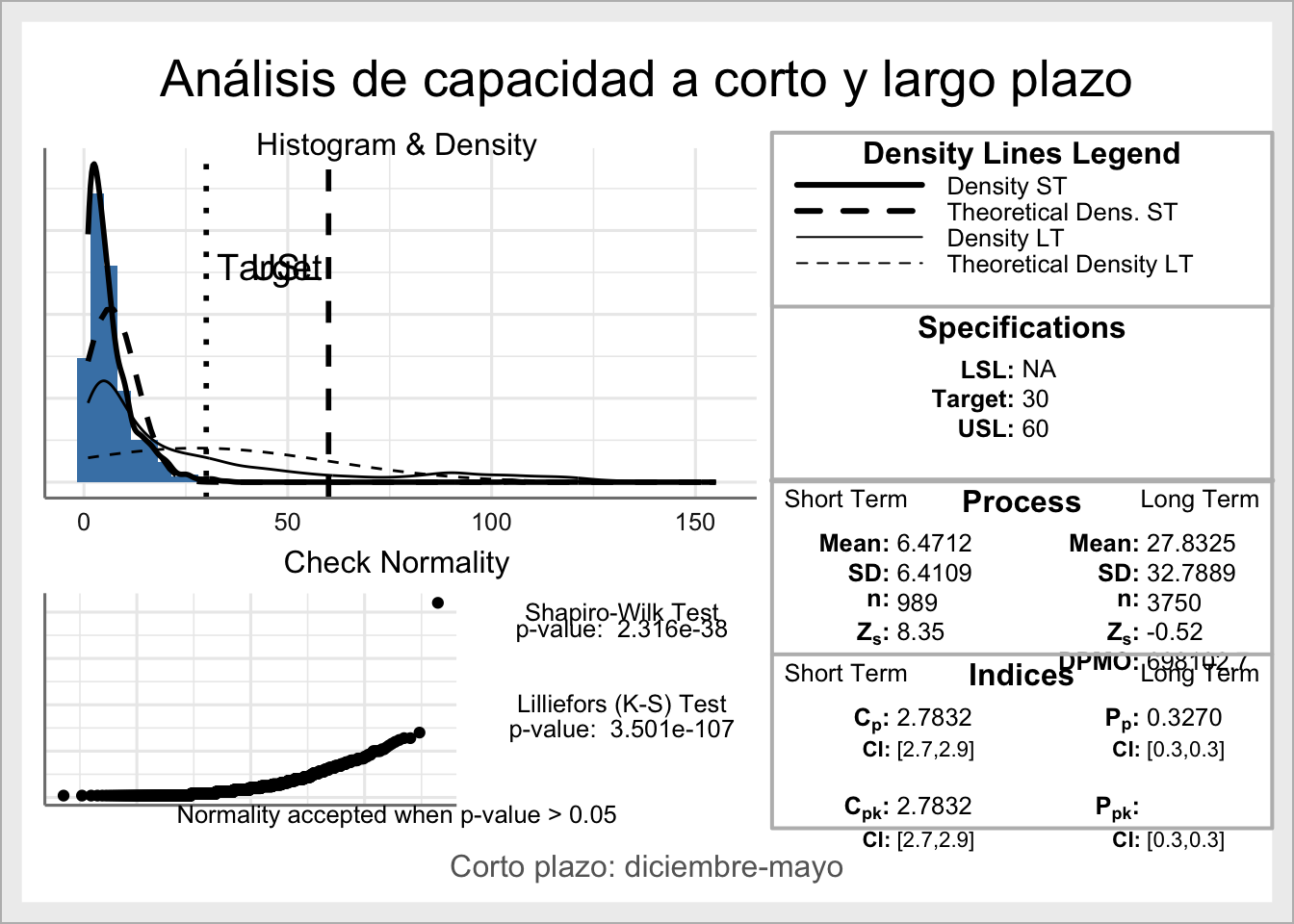
Donde comprobamos la buena capacidad del sistema para cumplir con las especificaciones de los clientes durante los meses de diciembre a mayo \(C_{pk}=2.78\), mientras que el sistema a largo plazo considerando todo el curso académico, es incapaz de cumplir, como indica el índice de capacidad \(P_{pk}=0.327\). Es posible pues, que el sistema funcione eficientemente (buena capacidad potencial), pero hay que estabilizar el proceso y corregir (reducir) la alta variabilidad durante los meses críticos de junio a noviembre.