Problemas delivery (base)
1 El problema
Disponemos de una recopilación de datos (Montgomery & Peck, 1982) relativos al tiempo de entrega (delTime) de máquinas expendedoras (desde que se gestiona la compra), junto con lo que vamos a entender como el número de productos demandados (n.prod) y la distancia entre el proveedor y el comprador (distance).
data(delivery, package="robustbase")
#load("/datos/delivery.RData")2 Expectativas
Ponte en el lugar del cliente que solicita un pedido a la empresa: ¿cuáles serían tus expectativas de calidad relativas a los tiempos de entrega?
Espero un tiempo máximo de entrega de una semana desde que realizo un pedido inferior a 5 máquinas. Si fuera superior, estaría dispuesta a esperar hasta 15 días.
NOTA Es importante conocer la opinión del cliente vinculada a su perfil como cliente: qué tipo de pedidos hace, dónde se ubica, …, con el fin de poder incluso segmentar a la población de clientes en diferentes perfiles con necesidades diversas.
3 Problemas
Es posible que la empresa tenga problemas para cumplir con los intereses de sus clientes. Investiga esta cuestión desde un punto de vista meramente descriptivo,a través de las cuestiones a continuación, y expresa tus conclusiones exclusivamente respondiendo a la pregunta ¿qué problemas parece tener la empresa para cumplir con las expectativas de sus clientes?
- ¿Cuál suele ser el número de máquinas demandadas en cada pedido?
- ¿A qué distancia están los compradores?
- ¿Cuántos días suele tardar en llegar un pedido?
- ¿Qué relación existe entre los tiempos de entrega y el volumen de los pedidos?
- ¿Qué relación existe entre los tiempos de entrega de los pedidos y la distancia al proveedor?
- ¿Qué relación existe entre el volumen de los pedidos y la distancia al proveedor?
Solicitamos un descriptivo rápido:
skim(delivery)| Name | delivery |
| Number of rows | 25 |
| Number of columns | 3 |
| _______________________ | |
| Column type frequency: | |
| numeric | 3 |
| ________________________ | |
| Group variables | None |
Variable type: numeric
| skim_variable | n_missing | complete_rate | mean | sd | p0 | p25 | p50 | p75 | p100 | hist |
|---|---|---|---|---|---|---|---|---|---|---|
| n.prod | 0 | 1 | 8.76 | 6.88 | 2 | 4.00 | 7.00 | 10.0 | 30.00 | ▇▃▁▁▁ |
| distance | 0 | 1 | 409.28 | 325.19 | 36 | 150.00 | 330.00 | 605.0 | 1460.00 | ▇▅▃▁▁ |
| delTime | 0 | 1 | 22.38 | 15.52 | 8 | 13.75 | 18.11 | 21.5 | 79.24 | ▇▁▁▁▁ |
En base al descriptivo:
- El plazo mínimo de entrega de los pedidos es de 8 días, y en la cuarta parte de los pedidos tardan más de 3 semanas en ser entregados. Hay pedidos que han llegado a tardar un mes en llegar al comprador.
- El estándar en el número de máquinas solicitadas en cada pedido está en torno a las 7; un 25% de los clientes piden a lo sumo 4 y otra cuarta parte compran 10 o más máquinas en cada pedido.
- Respecto a las ventas, la distancia media a los compradores está entre 300 y 400km, si bien una cuarta parte de los compradores están a más de 600km y otra cuarta parte en un radio inferior a 150km de la fábrica.
Nos interesa además, conocer algo sobre cómo se distribuye la variable de interés, esto es, delTime, para lo que graficamos los datos con un histograma (cuidado cuando hay otras variables clasificadoras). Dada la asimetría que presenta (y los beneficios de la “normalidad”), intentamos simetrizar con alguna transformación, que no proporciona mejoras relevantes.
g1=ggplot(delivery,aes(delTime))+
geom_histogram(fill="thistle",color="tomato",bins=10)
g2=ggplot(delivery,aes(log(delTime)))+
geom_histogram(fill="thistle",color="tomato",bins=10)
grid.arrange(g1,g2,ncol=2)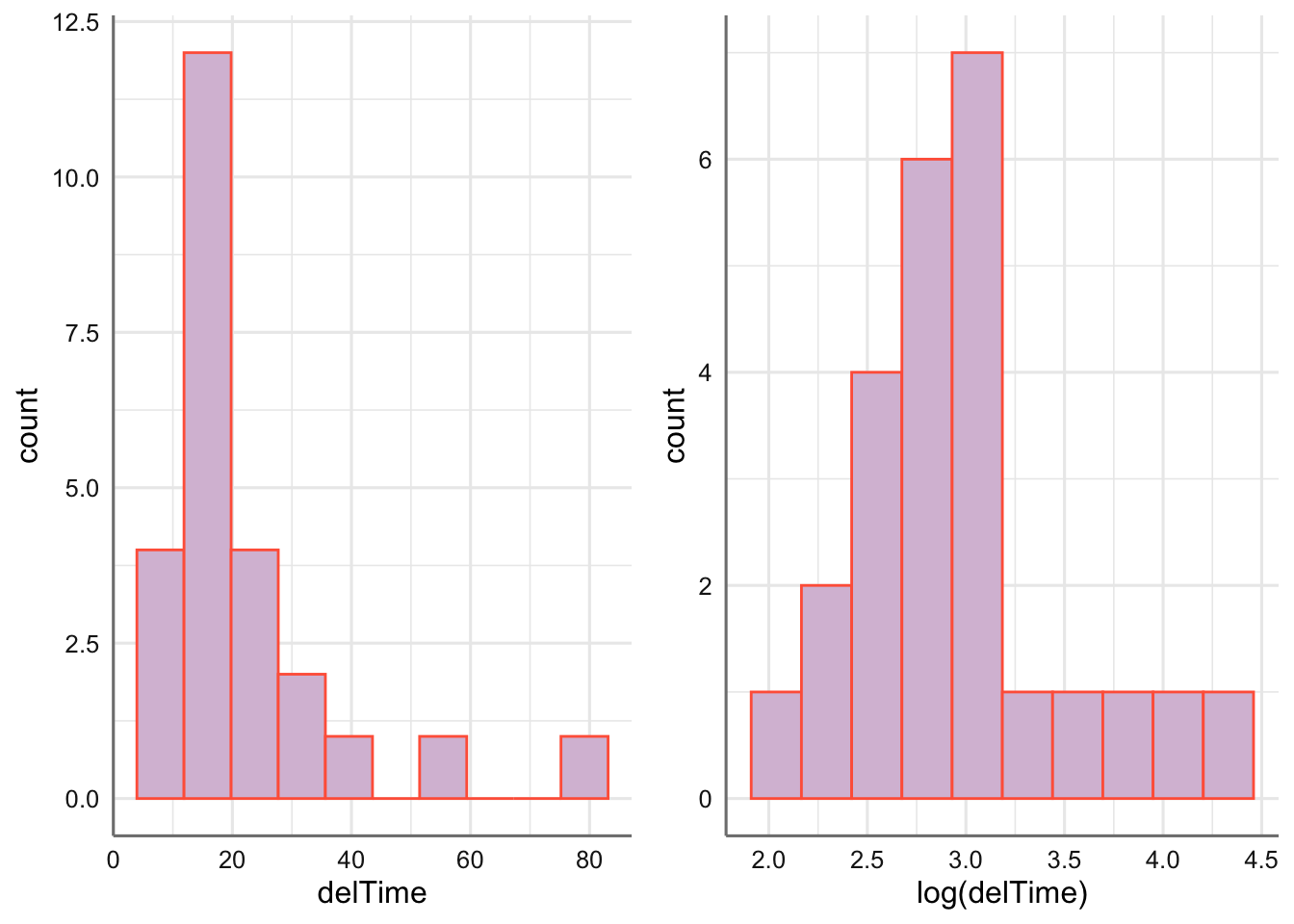
Para investigar relaciones entre el tiempo de entrega, el volumen de compra y la distancia al proveedor, graficamos con diagramas de dispersión y probamos varias transformaciones en un intento de linealizar relaciones no lineales (si bien no aportan mejoras relevantes).
g1=ggplot(delivery,aes(x=distance,y=delTime))+
geom_point(aes(color=n.prod))+geom_smooth()+
scale_color_continuous(type="viridis")
g2=ggplot(delivery,aes(x=n.prod,y=delTime))+
geom_point()+geom_smooth()
g3=ggplot(delivery,aes(x=distance,y=log(delTime)))+
geom_point(aes(color=n.prod))+geom_smooth()+
scale_color_continuous(type="viridis")
g4=ggplot(delivery,aes(x=log(distance),y=log(delTime)))+
geom_point(aes(color=n.prod))+geom_smooth()+
scale_color_continuous(type="viridis")
grid.arrange(g1,g2,g3,g4,ncol=2)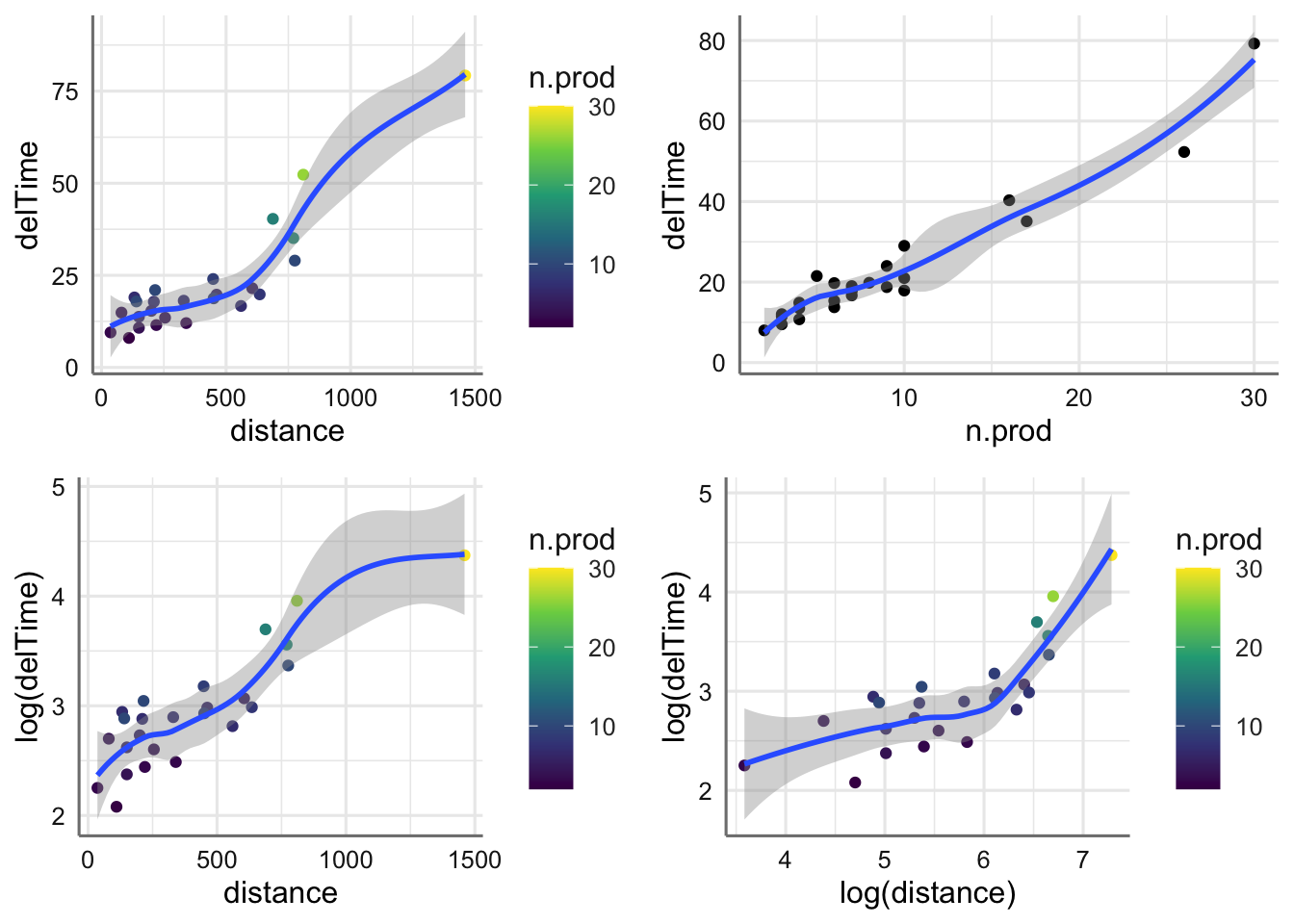
# Inspeccionamos los valores de los datos más extremos, de modo manual
library(plotly)
ggplotly(g1)Conclusión: Si el objetivo es garantizar la entrega en una semana, habría de hacer cambios severos: ninguno de los pedidos en el histórico ha sido entregado en menos de 8 días. Por otro lado, se aprecian ciertos valores muy extremos, que corresponden a pedidos de gran volumen (10 o más máquinas) y a largas distancias. Excluyendo esos valores, la distancia al comprador influye de modo lineal y positivo en el tiempo de entrega: a mayor distancia, mayor tiempo de entrega, pero nunca rebasando -en el histórico- los 25 días. Para ese otro tipo de pedidos “extremos”, el comportamiento difiere del resto, y los problemas con los tiempos de entrega son considerablemente más graves, y llegan a prácticamente 80 días. Por otro lado, la relación entre el volumen de los pedidos y el tiempo de entrega es claramente lineal.
Dado que después de transformar no se aprecia una ganancia relevante en cuanto a simetrización de los datos o linealización de la tendencia, continuaremos el análisis con las variables originales, sin transformar.
4 Tiempos
La empresa quiere mejorar su servicio a los clientes. En concreto, quiere dar a sus clientes una estimación/rango de estimación “fiable” con el número de días que tardará en recibir su pedido. Investiga este objetivo a través de las cuestiones a continuación y expresa tus conclusiones exclusivamente respondiendo a la pregunta ¿cómo vas a estimar el tiempo de entrega en el próximo pedido que reciba la empresa?
- ¿Qué información del cliente podrías aprovechar para afinar la estimación del tiempo de entrega de su pedido?
- ¿En qué tipo de ventas la empresa tiene más información para proporcionar una estimación fiable del tiempo de entrega?
4.1 Modelo 1
Si consideramos todos los datos, y a la vista de los descriptivos, para capturar el comportamiento más extraño de los valores extremos, podríamos probar cierto efecto polinómico (de grado 2-3) entre distance y delTime. La relación lineal entre volumen del pedido y tiempo de reparto entraría también en el modelo. Partimos de un modelo con esta premisa y procedemos con una selección de modelos, que en el caso polinómico resolvemos con Anova, excluyendo los términos de mayor grado hacia abajo, pero manteniendo todos los grados menores al mayor en el modelo.
fit1=lm(delTime~n.prod+distance+I(distance^2)+I(distance^3),data=delivery)
anova(fit1)## Analysis of Variance Table
##
## Response: delTime
## Df Sum Sq Mean Sq F value Pr(>F)
## n.prod 1 5382.4 5382.4 896.3155 < 2.2e-16 ***
## distance 1 168.4 168.4 28.0435 3.497e-05 ***
## I(distance^2) 1 113.0 113.0 18.8098 0.00032 ***
## I(distance^3) 1 0.7 0.7 0.1128 0.74051
## Residuals 20 120.1 6.0
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1# prescindimos del grado 3, que no es significativo
fit1=lm(delTime~n.prod+distance+I(distance^2),data=delivery)
summary(fit1)##
## Call:
## lm(formula = delTime ~ n.prod + distance + I(distance^2), data = delivery)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.7481 -1.3012 0.1413 1.0925 4.9065
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 6.343e+00 1.211e+00 5.238 3.43e-05 ***
## n.prod 1.416e+00 1.335e-01 10.610 6.81e-10 ***
## distance -7.979e-04 4.336e-03 -0.184 0.855781
## I(distance^2) 1.473e-05 3.324e-06 4.432 0.000231 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 2.398 on 21 degrees of freedom
## Multiple R-squared: 0.9791, Adjusted R-squared: 0.9761
## F-statistic: 328.3 on 3 and 21 DF, p-value: < 2.2e-16# y hacemos la validación del modelo
par(mfrow=c(2,2))
plot(fit1)## Warning in sqrt(crit * p * (1 - hh)/hh): Se han producido NaNs
## Warning in sqrt(crit * p * (1 - hh)/hh): Se han producido NaNs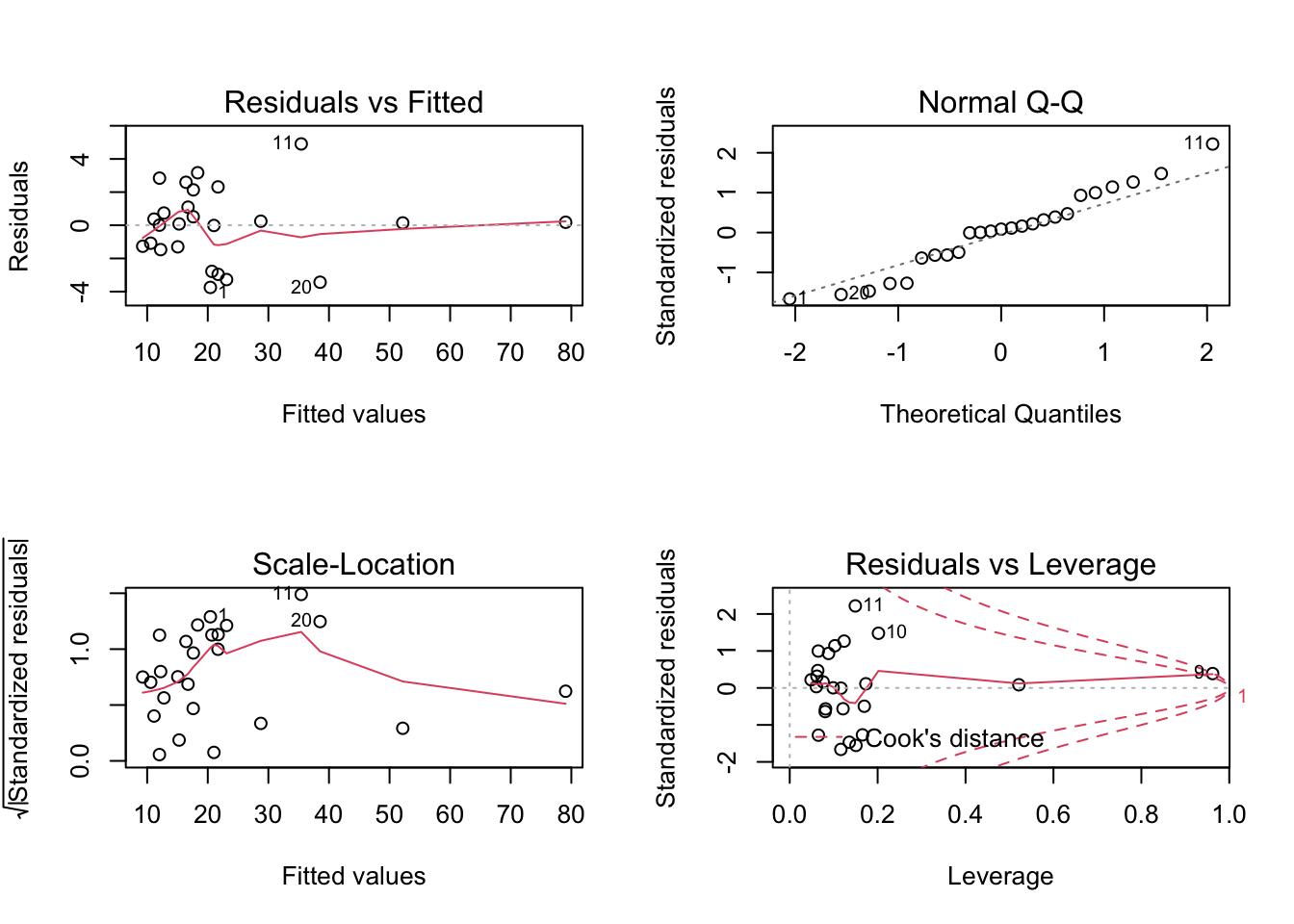
bptest(fit1) # test Breusch-Pagan para heterocedasticidad##
## studentized Breusch-Pagan test
##
## data: fit1
## BP = 5.2593, df = 3, p-value = 0.1538shapiro.test(resid(fit1)) # test Shapiro-Wilk para normalidad##
## Shapiro-Wilk normality test
##
## data: resid(fit1)
## W = 0.96526, p-value = 0.5288Optamos por un modelo cuadrático: \[ \hat{delTime}= \theta+ \alpha \cdot n.prod + \beta_1 \cdot distance + \beta_2 \cdot distance^2\]
El ajuste es razonablemente bueno (bondad del ajuste significativa (p-valor del estadístico F), errores pequeños (residual standard error) y valor del \(R^2\). La validación no muestra datos inquietantes y los tests de homocedasticidad y normalidad dan buenos resultados (no rechazamos igualdad de varianza y no rechazamos normalidad, al no tener p-valores significativos).
La predicción (media) es bastante precisa y más o menos certera para las distancias más cortas y pedidos menos voluminosos, y menos precisa y desacertada para distancias más largas y pedidos más voluminosos, como se aprecia en los intervalos de predicción a continuación.
g1=plot_model(fit1,"pred", terms="distance",
ci.lvl = 0.95,
show.data = TRUE,
axis.title = c("Distancia","Tiempo de entrega"),
title = "")
g2=plot_model(fit1,"pred", terms="n.prod",
ci.lvl = 0.95,
show.data = TRUE,
axis.title = c("Volumen del pedido","Tiempo de entrega"),
title = "")
grid.arrange(g1,g2,ncol=2)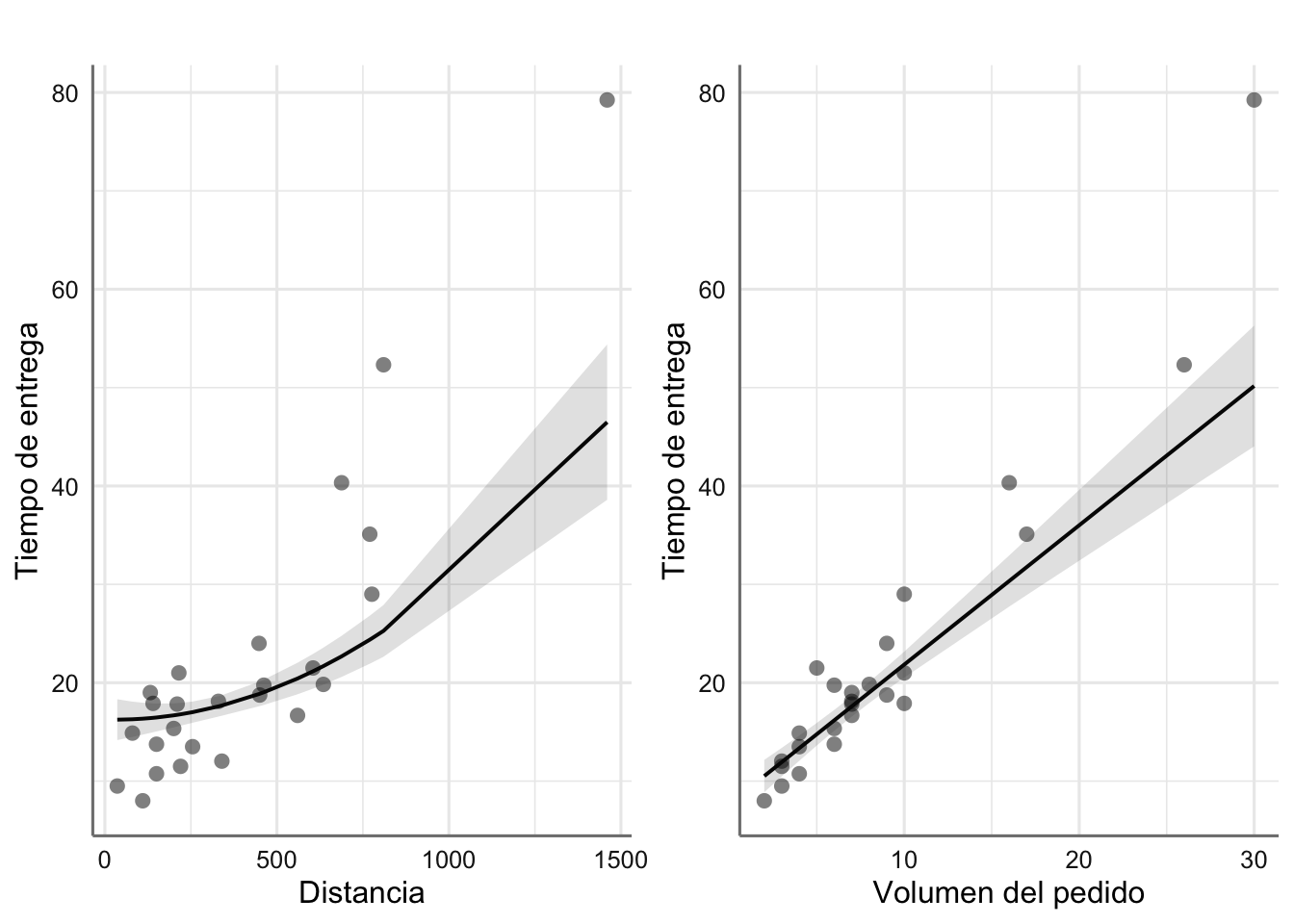
Conclusión: ¿cómo vas a estimar el tiempo de entrega en el próximo pedido que reciba la empresa?. En base a las relaciones que hemos detectado en los datos disponibles relativas a cómo influye el volumen de un pedido o la distancia al comprador sobre el tiempo de entrega, optamos por modelizar estadísticamente estas variables y aprovechar así al máximo toda la información existente para un pedido (volumen y distancia), para predecir en base a dicho modelo, el tiempo de entrega. Optamos por un modelo sencillo en el que el volumen de pedidos predice el tiempo de entrega de un modo lineal y la distancia al comprador de un modo cuadrático. Con todo, dado el comportamiento más extraño de los pedidos más extremos, a más distancia (más de 630km) y con pedidos más voluminosos (al menos 10 máquinas), las predicciones de los tiempos de entrega en esas situaciones son algo pobres.
5 Atendiendo un pedido
Si la empresa recibiera hoy un pedido de 5 máquinas expendedoras, utilizando el guión de preguntas/tareas a continuación, expresa tus conclusiones respondiendo exclusivamente a la pregunta ¿cuánto tiempo tardaría en llegar el pedido de 5 máquinas?
- Utiliza un nivel de confianza del 99.9997% (6). ¿Cómo explicas al cliente y a la empresa el significado de ese intervalo de predicción, en términos de “calidad”?
- ¿Puedes garantizar a todos los clientes, independientemente de dónde vivan, el mismo rango de variación en los días de entrega de su pedido? ¿Por qué?
- ¿Consigues alguna predicción en la que el rango de variación que das al cliente sobre el tiempo que tardará en recibir el pedido, no supere los 5 días? ¿Y los 10 días?
5.1 Predicción Modelo 1
g=plot_model(fit1,"pred", terms = c("distance ", "n.prod [5]"),
ci.lvl = 0.999997, # nivel de significatividad
show.data = TRUE,
axis.title = c("Distancia","Tiempo de entrega"),
title = "",
show.legend =FALSE)
attributes(g)## $names
## [1] "data" "layers" "scales" "mapping" "theme"
## [6] "coordinates" "facet" "plot_env" "labels" "guides"
##
## $class
## [1] "gg" "ggplot"g$data## # Predicted values of delTime
##
## distance | Predicted | group_col | 99.9997% CI
## -------------------------------------------------
## 36 | 13.41 | 5 | [ 8.80, 18.03]
## 132 | 13.57 | 5 | [10.26, 16.89]
## 200 | 13.85 | 5 | [11.11, 16.60]
## 220 | 13.96 | 5 | [11.31, 16.61]
## 330 | 14.76 | 5 | [12.03, 17.49]
## 450 | 16.05 | 5 | [12.47, 19.62]
## 605 | 18.33 | 5 | [13.30, 23.36]
## 1460 | 43.66 | 5 | [23.81, 63.50]g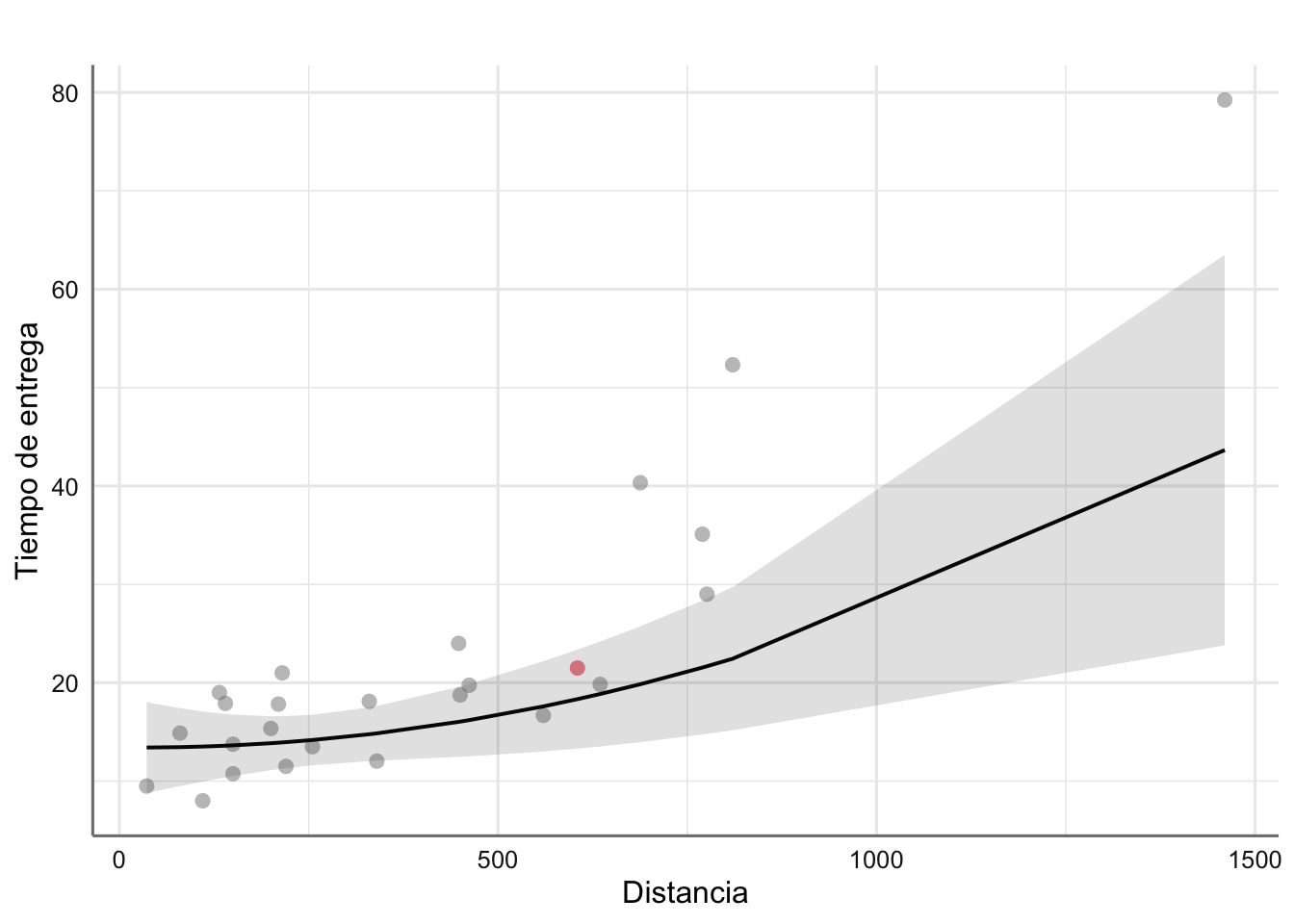
Conclusión: ¿cuánto tiempo tardaría en llegar el pedido de 5 máquinas? Cuando el pedido es de 5 máquinas, según el modelo ajustado con todos los datos, los tiempos de entrega estimados, si bien dependen de la distancia al comprador, varían entre 13 y 16 días para distancias inferiores a 500km. Para distancias mayores (hasta 1500km aprox.), el tiempo de entrega varía entre 18 y 43 días. Para cada estimación, se proporciona un rango de variación plausible en el tiempo de entrega
El rango de estimación proporcionado, al nivel de confianza 99.9997%, implica que esas son las garantías de que los extremos de variación proporcionados capturen el valor real del tiempo de entrega. En términos de calidad estaríamos hablando de que la empresa garantiza con ese nivel que el tiempo de entrega no va a ser menor al extremo inferior ni mayor que el extremo superior proporcionado. Por ejemplo, para un cliente que pide 5 máquinas y está a 200 km. del proveedor, el tiempo estimado de entrega es de 14 días; no se espera conseguir la entrega antes de 11 días, pero tampoco rebasará los 17 días; las garantías de cumplir con estos plazos serán del 99.9997%.
Pues bien, el rango de variación es de unos 5 días (+/-2 en torno a la estimación) para distancias entre 100 y 300km (aprox.); sin embargo, pero que es mayor (hay mayor incertidumbre) en distancias muy cortas y máslargas (en torno a +/-5 días cuando la distancia al comprador es inferior a 100km y cuando es superior a 500km aprox.); en distancias muy grandes (1400km) el rango de incertidumbre está en torno a +/-20 días en torno a la estimación proporcionada. Esta incertidumbre en distancias muy pequeñas y muy grandes es debida a las carencias de información acumulada de pedidos con estas características.
5.2 Modelo 2
Puesto que contamos con mucha más información (datos) relativa a pedidos de menos de 10 máquinas, y dado que la relación en este grupo de datos era bastante más lineal entre distance y delTime, es de esperar que si ajustamos un modelo sólo con estos datos, los resultados (predicciones) resulten más precisas y acertadas.
library(plotly)
g=delivery %>%
mutate(n.prod.c=cut(n.prod,c(0,10,31),right=FALSE)) %>%
ggplot(aes(x=distance,y=delTime))+
geom_point(aes(color=n.prod.c))+
geom_smooth(method="lm",se=FALSE)+
facet_grid(cols=vars(n.prod.c))+
theme(legend.position="none")
ggplotly(g)## `geom_smooth()` using formula 'y ~ x'Además, si tenemos claro que el objetivo es predecir tiempos de entrega para pedidos estándar en torno a 5 máquinas, podemos plantear un modelo en el que prescindamos directamente de los pedidos más voluminosos con 10 o más máquinas, que son pocos y añade mucha variabilidad (y por consiguiente dificultades en la modelización).
peq=which(delivery$n.prod<10)
fit2=lm(delTime~n.prod+distance,data=delivery[peq,])
anova(fit2)## Analysis of Variance Table
##
## Response: delTime
## Df Sum Sq Mean Sq F value Pr(>F)
## n.prod 1 233.080 233.080 48.2726 4.67e-06 ***
## distance 1 24.512 24.512 5.0767 0.03965 *
## Residuals 15 72.426 4.828
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1summary(fit2)##
## Call:
## lm(formula = delTime ~ n.prod + distance, data = delivery[peq,
## ])
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.0970 -1.5508 -0.2845 1.7422 4.0872
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 6.005520 1.476114 4.068 0.001009 **
## n.prod 1.354485 0.297338 4.555 0.000379 ***
## distance 0.007661 0.003400 2.253 0.039647 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 2.197 on 15 degrees of freedom
## Multiple R-squared: 0.7805, Adjusted R-squared: 0.7513
## F-statistic: 26.67 on 2 and 15 DF, p-value: 1.149e-05g=plot_model(fit2,"pred", terms=c("distance","n.prod [5]"),
ci.lvl = 0.95,
show.data = TRUE,
axis.title = c("Distancia","Tiempo de entrega"),
title = "")+
theme(legend.position = "none")
g$data## # Predicted values of delTime
##
## distance | Predicted | group_col | 95% CI
## -------------------------------------------------
## 36 | 13.05 | 5 | [11.16, 14.94]
## 110 | 13.62 | 5 | [12.12, 15.13]
## 150 | 13.93 | 5 | [12.60, 15.25]
## 210 | 14.39 | 5 | [13.26, 15.51]
## 255 | 14.73 | 5 | [13.68, 15.79]
## 340 | 15.38 | 5 | [14.24, 16.53]
## 450 | 16.23 | 5 | [14.64, 17.81]
## 635 | 17.64 | 5 | [15.00, 20.28]g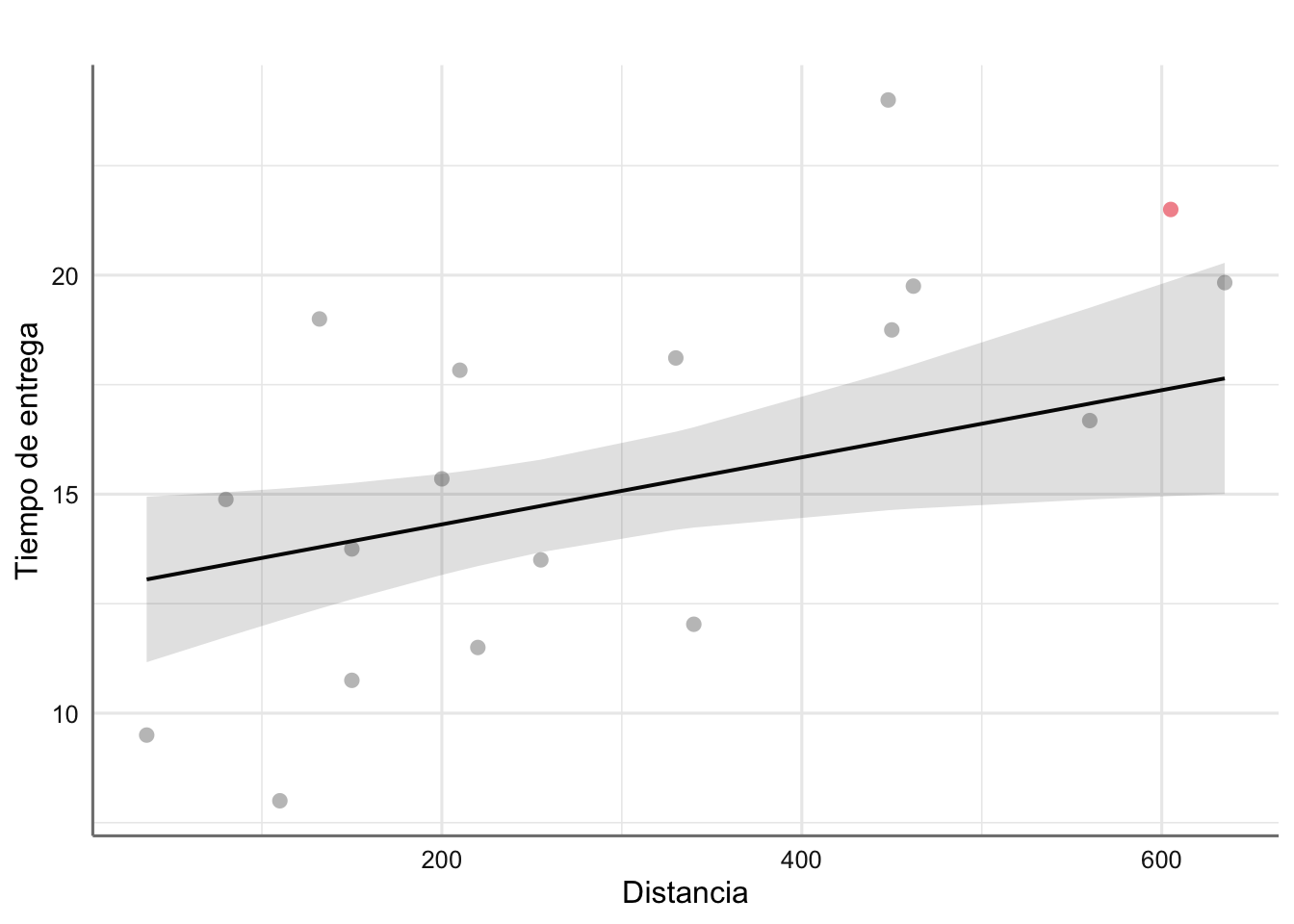
Según el modelo 2, ajustado con datos de pedidos por debajo de 10 máquinas (y por tanto en el rango en que se encuentra el pedido a predecir), la estimación del tiempo de entrega sigue dependiendo de la distancia al comprador, pero la precisión es considerablemente mayor: el tiempo de entrega varía entre 13 y 16 días para distancias inferiores a 450km, y el rango de incertidumbre entre 2 días arriba/abajo (para distancias más cortas <100), y en torno a 1.5 días para el resto de distancias.
Si bien las estimaciones son similares a las obtenidas con el modelo 1, la confianza en dichas estimaciones es considerablemente mayor, de ahí la mejor capacidad predictiva de este modelo.
5.3 Modelo 3
Podemos probar aún otra modelización alternativa. Volvemos al descriptivo y podríamos marcar tres zonas de comportamiento para la relación distance-delTime; esto nos llevaría a categorizar la variable distance en tres niveles y modelizar cada zona por separado en base a la información disponible
g1=ggplot(delivery,aes(x=distance,y=delTime))+
geom_point()+
geom_smooth()+
geom_vline(xintercept=c(300,650),color="red",linetype="dashed")
delivery$distcat=cut(delivery$distance,
breaks=c(0,300,650,max(delivery$distance)),right = TRUE)
ggplotly(g1)## `geom_smooth()` using method = 'loess' and formula 'y ~ x'g2=ggplot(delivery,aes(x=distance,y=delTime))+
geom_point()+
geom_smooth(method="lm")+
facet_wrap(vars(distcat),as.table=FALSE)
g2## `geom_smooth()` using formula 'y ~ x'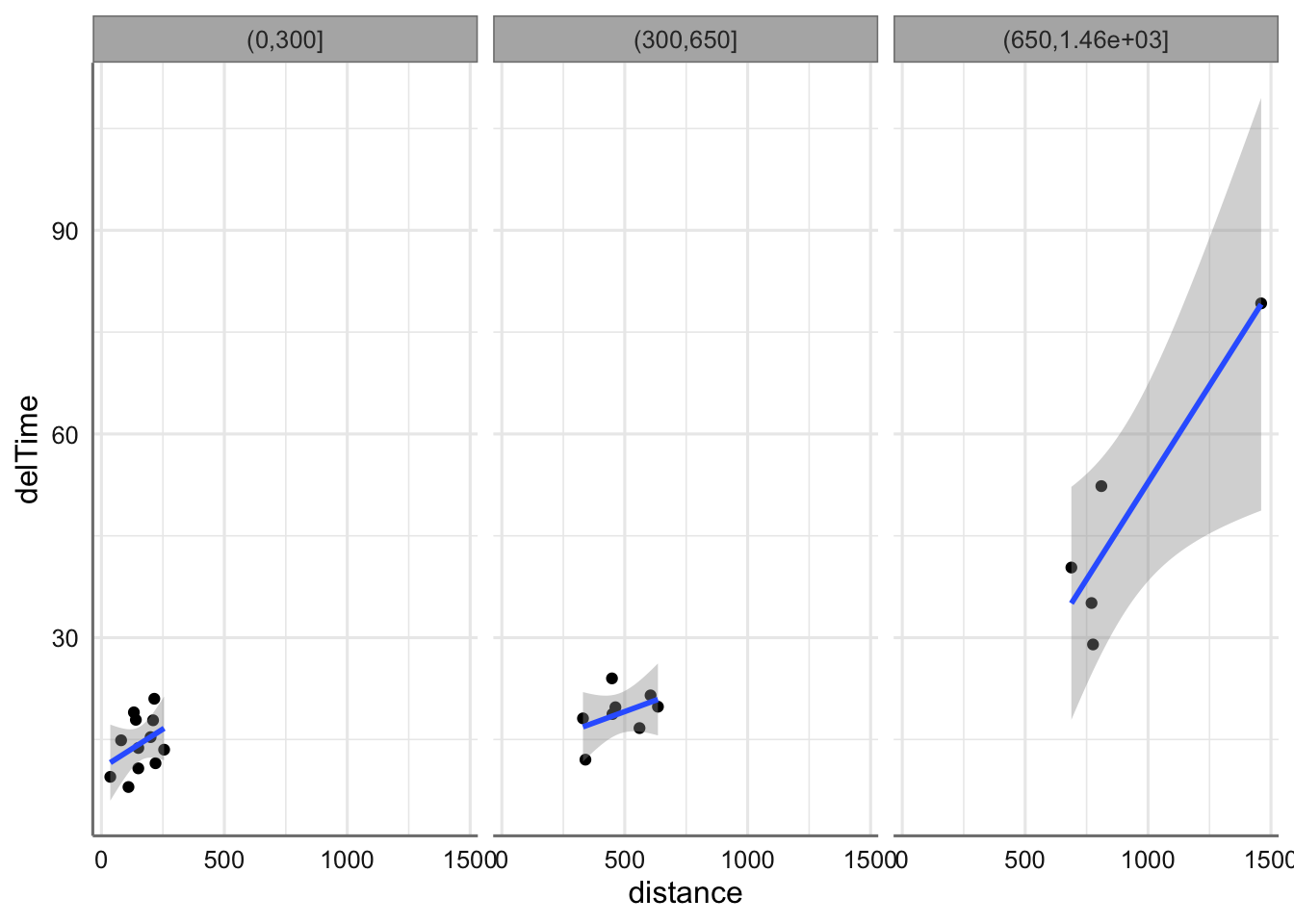
Surgen pues, tres zonas en las que podríamos obtener predicciones quizás más precisas con modelos muy simples: rectas de hecho. Nos interesa entonces el concepto de spline
Los splines de regresión son curvas definidas a trozos mediante polinomios, es decir, dividimos el rango de X en trozos y sobre cada trozo ajustamos un modelo polinómico con la única restricción que las funciones obtenidas en cada trozo deben unirse formando una curva suave. (Ampliar info en Morales, 2020).
library(splines)
knots=c(300,650)
ggplot(delivery,aes(x=distance,y=delTime))+
geom_point()+
geom_smooth(method = lm, formula = y ~ bs(x, knots=knots,degree=1))+
geom_vline(xintercept=c(300,650),color="red",linetype="dashed")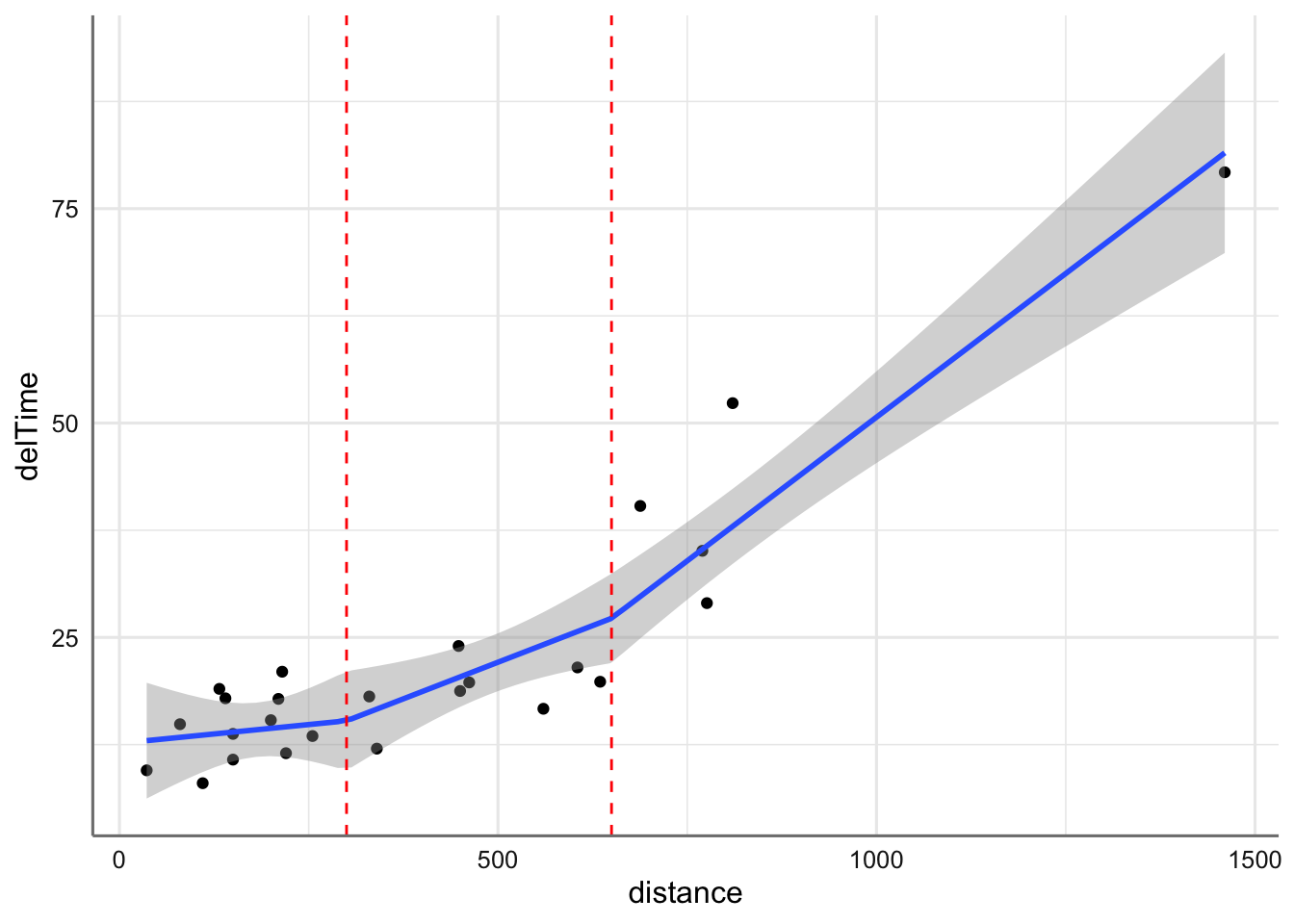
Cuando sólo nos preocupa predecir con esa variable, utilizamos los splines:
library(splines)
fit3 <- lm (delTime ~ bs(distance, knots = knots,degree=1), data = delivery)
summary(fit3)##
## Call:
## lm(formula = delTime ~ bs(distance, knots = knots, degree = 1),
## data = delivery)
##
## Residuals:
## Min 1Q Median 3Q Max
## -7.475 -3.461 -1.058 3.344 14.369
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 12.961 3.246 3.993 0.00066
## bs(distance, knots = knots, degree = 1)1 2.314 5.204 0.445 0.66113
## bs(distance, knots = knots, degree = 1)2 14.267 3.852 3.703 0.00132
## bs(distance, knots = knots, degree = 1)3 68.549 6.552 10.462 8.74e-10
##
## (Intercept) ***
## bs(distance, knots = knots, degree = 1)1
## bs(distance, knots = knots, degree = 1)2 **
## bs(distance, knots = knots, degree = 1)3 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 5.753 on 21 degrees of freedom
## Multiple R-squared: 0.8799, Adjusted R-squared: 0.8627
## F-statistic: 51.26 on 3 and 21 DF, p-value: 7.757e-10plot_model(fit3,"pred", terms = "distance",
ci.lvl = 0.95,
show.data = TRUE,
axis.title = c("Distancia","Tiempo de entrega"),
title = "Predicción con SPLINES")## Warning: Some model terms could not be found in model data. You probably need to load the
## data into the environment.
## Warning: Some model terms could not be found in model data. You probably need to load the
## data into the environment.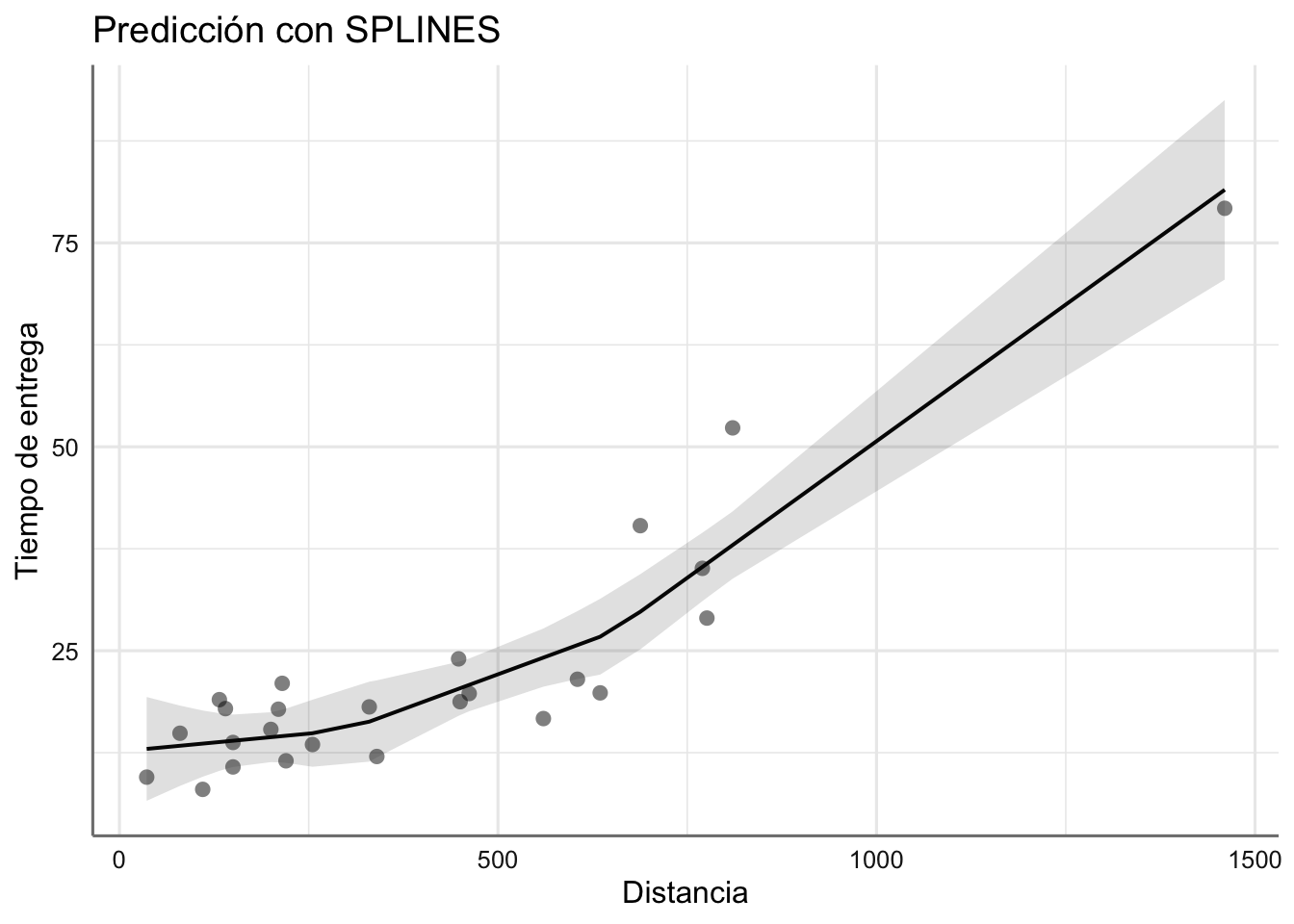
Al incorporar como predictor n.prod, obviamente repetimos el efecto de siempre, y conseguimos mejores predicciones (más precisas y certeras) en la zona en la que disponemos de más datos.
library(splines)
fit3 <- lm (delTime ~ bs(distance, knots = knots,degree=1) +n.prod, data = delivery)
g=plot_model(fit3,"pred", terms = c("distance","n.prod [5]"),
ci.lvl = 0.95,
show.data = TRUE,
axis.title = c("Distancia","Tiempo de entrega"),
title = "Predicción con SPLINES y nprod=5",
show.legend = FALSE)## Warning: Some model terms could not be found in model data. You probably need to load the
## data into the environment.
## Warning: Some model terms could not be found in model data. You probably need to load the
## data into the environment.g$data## # Predicted values of delTime
##
## distance | Predicted | group_col | 95% CI
## -------------------------------------------------
## 36 | 12.89 | 5 | [10.12, 15.66]
## 132 | 13.54 | 5 | [12.00, 15.08]
## 200 | 14.01 | 5 | [12.68, 15.34]
## 220 | 14.15 | 5 | [12.70, 15.60]
## 330 | 15.02 | 5 | [12.87, 17.17]
## 450 | 16.31 | 5 | [14.64, 17.97]
## 605 | 17.97 | 5 | [15.57, 20.38]
## 1460 | 44.38 | 5 | [35.37, 53.40]
##
## Adjusted for:
## * delTime = 22.38La predicción del tiempo de entrega con el Modelo 3 para pedidos de 5 máquinas sigue variando entre 13 y 16 días cuando la distancia es inferior a 450km, los rangos de incertidumbre respecto a cuánto podría oscilar dicha entrega es de 2.77 días para distancias inferiores a 40km, en torno a 1.5 días para distancias entre 130 y 450. En distancias en torno a 600km el tiempo de entrega se va a 18 días (5 arriba-5 abajo) y para distancias muy grandes en torno a 1400km, el tiempo de entrega es de 44 días, con una incertidumbre de 9 días arriba/abajo.
6 Problemas
Concluye, en base a todo el análisis que has realizado, respondiendo la pregunta: ¿cuáles son los problemas más relevantes que has detectado y que afectan a la satisfacción de los clientes y en consecuencia a la imagen y fiabilidad de la empresa?
Los problemas básicos detectados son:
- Los tiempos de entrega son algo largos respecto de lo esperado, y especialmente críticos cuando el comprador está a más de 500-600km de distancia.
- En distancias moderadas, se consigue una precisión razonable en torno a 1-2 días de demora/adelanto respecto de la fecha estimada de entrega.
- La empresa tiene muy pocos pedidos a distancias grandes, y eso impide obtener estimaciones precisas para ese tipo de pedidos.
- Cuando el número de pedidos es grande (>10) y la distancia también, los tiempos de entrega han sido excesivamente largos; además ha habido mucha variabilidad en los pedidos entregados, de modo que es poco fiable dar una estimación. Quizá haya habido problemas de stock.
Sería preciso acortar tiempos de entrega en todos los pedidos y revisar la política de stocks.