Análisis amonio
0.1 Descripción
Resumimos los datos, agrupando por ubicación y por operador.
load("./datos/datosamonio.RData")
rlim=function(x,u){
# función que calcula el porcentaje de puntos en un vector por encima del valor u
round(sum(x>u)/length(x)*100,2)}
r=datos %>%
group_by(operador,ubicacion) %>%
summarize(m=round(mean(amonio),2),s=round(sd(amonio),2),
p95=round(quantile(amonio,0.95),2),pup25=rlim(amonio,25))
datatable(r,
caption="Tabla 1. Sumario por medias (m), desviaciones típicas (s), percentil 95 (p95) y proporción de mediciones por encima de 25 (pup25).",
rownames =FALSE,filter="none")A la hora de tratar los datos, añadimos un identificador de “días”, asumiendo que los dos operadores han medido ambos en la misma ubicación durante 15 días consecutivos. En este caso tendremos medidas repetidas y comparables para poder testar la eficiencia de los dos operadores.
# Muestreo doble durante 15 días
dia=rep(1:15,4)
datos$dia=dia
ggplot(datos,aes(x=dia,y=amonio))+geom_line(aes(color=operador))+
geom_point(aes(color=operador))+
facet_wrap(~ubicacion)+
geom_hline(yintercept=25, linetype="dashed")+
ggtitle("",subtitle="Figura 1. Mediciones por día, operador y ubicación.")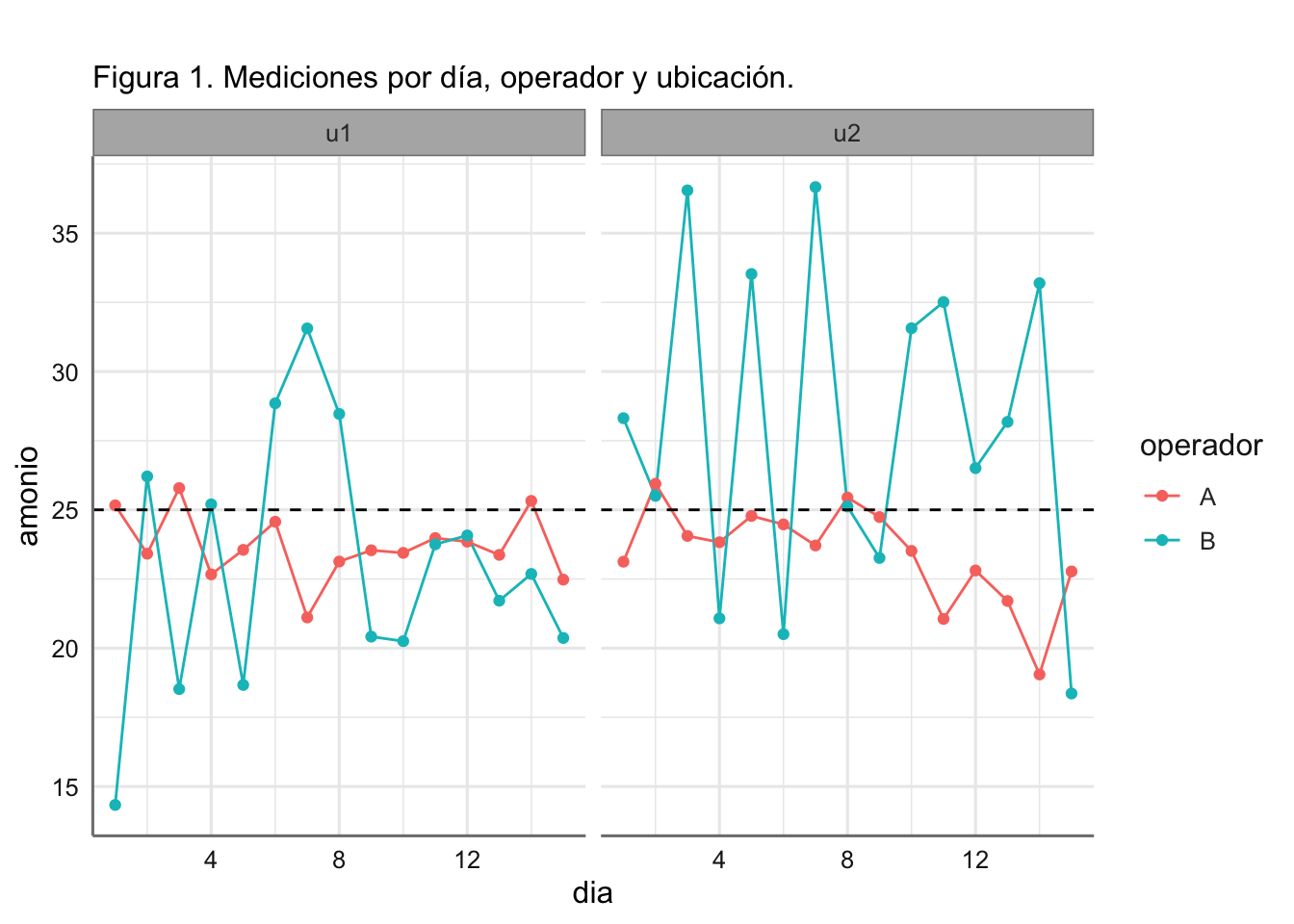
ggplot(datos,aes(x=ubicacion,y=amonio))+
geom_boxplot(aes(color=operador))+
geom_hline(yintercept=25, linetype="dashed")+
ggtitle("",subtitle="Figura 2. Mediciones por operador y ubicación.")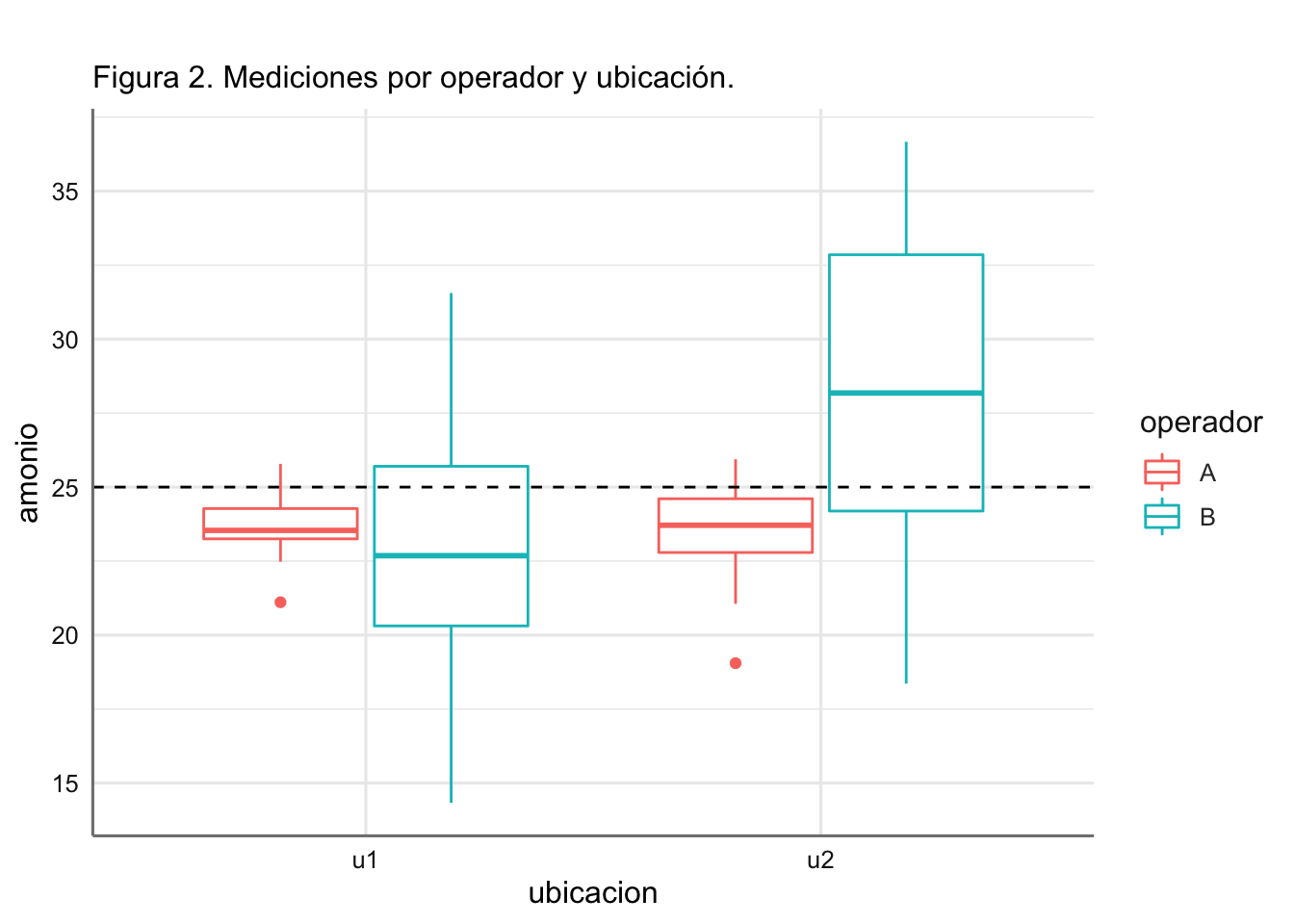
0.2 Inferencia
1 Cuestión 1. Investiga si la empresa consigue su propósito de calidad en cada una de las ubicaciones.
La política actual de la empresa es asegurarse a un 95% de confianza que el contenido medio de amonio queda por debajo de 25 en todas las muestras que se realizan en un mes, puesto que reducirlo más les supone gastos energéticos que no les compensa asumir.
Testamos a continuación cuándo se dan las condiciones que la empresa asume como “garantía de calidad”. El test que se plantea (a un nivel de confianza del 95%) es: \[H_0: \mu \geq 25 \, vs \, H_1:\mu < 25 \] Resolvemos esta cuestión a través de un test Student-t.
t.test(datos$amonio,alternative="less",mu=25)##
## One Sample t-test
##
## data: datos$amonio
## t = -0.83563, df = 59, p-value = 0.2034
## alternative hypothesis: true mean is less than 25
## 95 percent confidence interval:
## -Inf 25.46171
## sample estimates:
## mean of x
## 24.5382Si no consideramos las ubicaciones y utilizamos todos los datos, obtenemos que no podemos rechazar \(H_0\), lo que significa que no podemos aceptar que efectivamente la empresa consiga medias por debajo de 25 con un nivel de garantías del 95%.
Si distinguimos por ubicaciones, podemos asegurar (con confianza 95%) que en la ubicación u1 sí que se están cumpliendo los requisitos de calidad, mientras que no podemos concluir de modo similar para la ubicación u2. Esto nos llevaría a hablar de diferencias en la dilución de tóxicos entre una y otra ubicación.
t.test(datos$amonio[datos$ubicacion=="u1"],alternative="less",mu=25)##
## One Sample t-test
##
## data: datos$amonio[datos$ubicacion == "u1"]
## t = -2.7474, df = 29, p-value = 0.005109
## alternative hypothesis: true mean is less than 25
## 95 percent confidence interval:
## -Inf 24.36979
## sample estimates:
## mean of x
## 23.34832t.test(datos$amonio[datos$ubicacion=="u2"],alternative="less",mu=25)##
## One Sample t-test
##
## data: datos$amonio[datos$ubicacion == "u2"]
## t = 0.82249, df = 29, p-value = 0.7912
## alternative hypothesis: true mean is less than 25
## 95 percent confidence interval:
## -Inf 27.2322
## sample estimates:
## mean of x
## 25.728092 Cuestión 2. Investiga la precisión al medir de cada operario.
Ya apreciamos en la Tabla 1 y en las Figuras 1 y 2, las diferencias de precisión en las mediciones de los dos operadores en ambas ubicaciones: el operador A es mucho más preciso (sd máxima de 1.78 para u2) que el operador B (sd mínima de 4.56 para u1). La estabilidad en la medición (precisión) nos reporta un mayor nivel de garantías sobre la coherencia al medir y por lo tanto sobre la calidad de las mediciones.
Si la empresa ha de marcar unos protocolos en la medición, entendemos que optaría por utilizar los protocolos/procedimientos de medición que utiliza el operador A. Para este operador, comprobemos si las mediciones cumplen con el sistema de calidad de la empresa.
# sin diferenciar por ubicación
t.test(datos$amonio[datos$operador=="A"],alternative="less",mu=25)##
## One Sample t-test
##
## data: datos$amonio[datos$operador == "A"]
## t = -5.3261, df = 29, p-value = 5.125e-06
## alternative hypothesis: true mean is less than 25
## 95 percent confidence interval:
## -Inf 24.01004
## sample estimates:
## mean of x
## 23.54627# diferenciando por ubicación
t.test(datos$amonio[(datos$operador=="A")&(datos$ubicacion=="u1")],alternative="less",mu=25)##
## One Sample t-test
##
## data: datos$amonio[(datos$operador == "A") & (datos$ubicacion == "u1")]
## t = -4.2522, df = 14, p-value = 0.0004023
## alternative hypothesis: true mean is less than 25
## 95 percent confidence interval:
## -Inf 24.23378
## sample estimates:
## mean of x
## 23.69199t.test(datos$amonio[(datos$operador=="A")&(datos$ubicacion=="u2")],alternative="less",mu=25)##
## One Sample t-test
##
## data: datos$amonio[(datos$operador == "A") & (datos$ubicacion == "u2")]
## t = -3.4821, df = 14, p-value = 0.001832
## alternative hypothesis: true mean is less than 25
## 95 percent confidence interval:
## -Inf 24.20957
## sample estimates:
## mean of x
## 23.40054Verificamos así que con los protocolos de medición del operador A, la empresa satisface sus requisitos de calidad, asegurando a un 95% de confianza, que los niveles medios de amonio son inferiores a 25ppm, en cualesquiera de las ubicaciones consideradas.
De hecho, dado que las conclusiones son similares en las dos ubicaciones, testemos si existen diferencias significativas en lo que resta con 30 observaciones “similares”, en lugar de con dos grupos de 15 distintos.
datos.sel=datos[datos$operador=="A",]
t.test(amonio~ubicacion,data=datos.sel,alternative="two.sided")##
## Welch Two Sample t-test
##
## data: amonio by ubicacion
## t = 0.52721, df = 24.454, p-value = 0.6028
## alternative hypothesis: true difference in means between group u1 and group u2 is not equal to 0
## 95 percent confidence interval:
## -0.8483859 1.4312939
## sample estimates:
## mean in group u1 mean in group u2
## 23.69199 23.40054No se evidencian pues, diferencias significativas en los niveles de amonio entre las 2 ubicaciones para el operador A.
3 Cuestión 3. Investiga qué posibilidades tiene la empresa de ser multada, manteniendo esta política de calidad.
El gobierno monitorea diariamente determinados puntos del río a varias distancias del volcado de residuos. Si en 5 muestras consecutivas en el tiempo en una misma ubicación se aprecia un contenido de amonio superior a 25, la empresa es multada.
Estudiemos a continuación si, en el caso de que la empresa establezca los protocolos de medición que utiliza el operador A, esta se librará de la multa.
# Control del comportamiento a largo plazo en el caso de medir como el operador A
#library(qicharts)
# Graficamos los datos sin diferenciar por
qic(datos.sel$amonio, chart = 'i',target=25)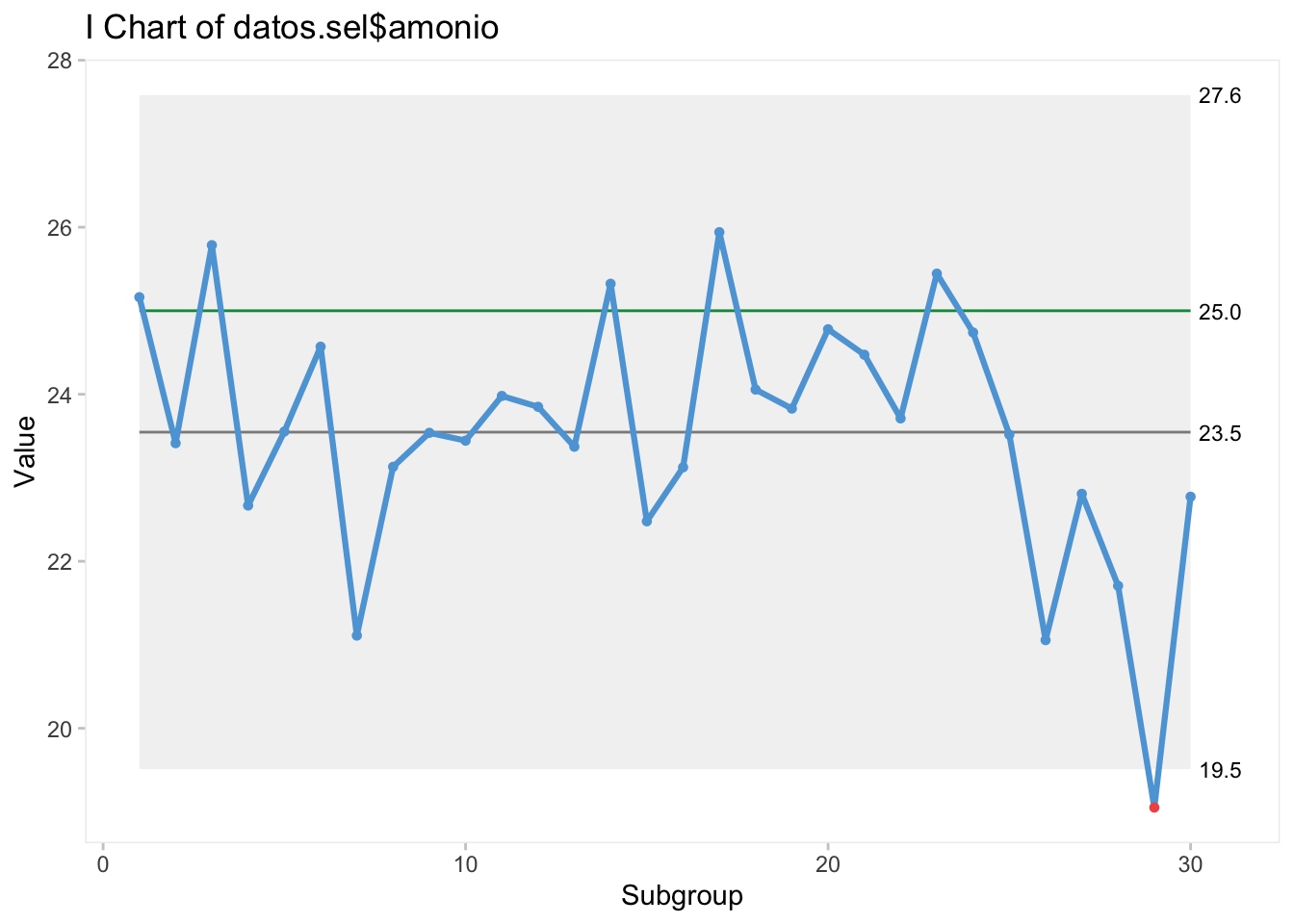
En principio, no podríamos concluir que las mediciones van a quedar siempre por debajo de 25ppm y en ningún caso se darán 5 muestras consecutivas por encima de 25. El nivel superior de confianza visible en el gráfico de control de calidad es de 28ppm.