1 Investigación

Investiga sobre los orígenes de la metodología SixSigma: quién, dónde, por qué, cómo y para qué desarrolló esta metodología.Resume a continuación la información que hayas encontrado y cita las fuentes.

La metodología Six Sigma fue desarrollada en la década de los 80 en Motorola por dos de sus ingenieros, Bill Smith y Mikel Harry. Escribieron un informe en el que proponían un sistema de gestión de la calidad basado en que a menor número de defectos en cada etapa de la producción, mejores eran los resultados. Consiguieron un ahorro de 2.2 billones de dólares en 4 años y 16 billones en 15 años. Incorporaron la estadística como herramienta básica en la reducción de la varianza y del número de defectos. Six Sigma comenzó a adquirir relevancia en General Electric, donde Jack Welch la implantó en 1995 con el objetivo de eliminar el gran número de defectos detectados. Durante los 5 primeros años tras implantarlo, la empresa ahorró 12 billones de dólares.

Fuentes:

2 Creatividad

**Una empresa de pvc vierte aguas residuales en un río. El gobierno monitorea periódicamente determinados puntos del río a cierta distancia del volcado de residuos. Si en el 5% de muestras consecutivas se aprecia un contenido de amonio superior a 30ppm, la empresa es multada. Por otro lado, la política actual de la empresa es conseguir un contenido medio de amonio de 25ppm, puesto que reducirlo más les supone gastos energéticos que no les compensa asumir frente al hecho de pagar una multa.

Trabajando como estadístico para la empresa, ¿cómo podrías conseguir demostrar si la empresa lo está haciendo bien y conseguirá evitar la multa? Propón qué información le pedirías recabar a la empresa para comprobarlo.**

Para conseguir demostrar si la empresa lo está haciendo bien o no en la cuestión de la generación de residuos y el respeto al medio ambiente, es preciso recabar información útil y analizarla. La propuesta de recogida de información consistiría en realizar muestreos periódicos en la parte del río monitoreada por el gobierno, midiendo el nivel de amonio en el río. Sería interesante asimismo, medir dentro de la empresa cualquier condicionante o circunstancia vinculada al proceso de producción y de generación de residuos, y que pueden estar influyendo en la producción de residuos con un mayor o menor contenido de amonio: volumen de producción, factores medioambientales en el proceso de producción (temperatura, humedad,…), materiales base o materias primas (procedencia, calidad, características,…), ajustes y calibraciones de la maquinaria, aparatos de medición, operarios que miden, …

3 Resolución de problemas

Dispones de una muestra de datos relativa al nivel de amonio medido en varias tomas en las aguas residuales que vierte la empresa, junto con información sobre la temperatura media en el proceso de generación del residuo y el registro de qué operador ha realizado la medición.

1. Investiga si la temperatura tiene alguna relación con el contenido en amonio de los vertidos. Comenta tus conclusiones.

Investigamos en primer lugar la relación entre las mediciones de amonio y la temperatura, a través de un gráfico de dispersión (dado el carácter continuo de ambas variables).

load("./datos/datosi.RData" )
library(ggplot2)
p1=qplot(temperatura,amoniaco,data=datosi);p1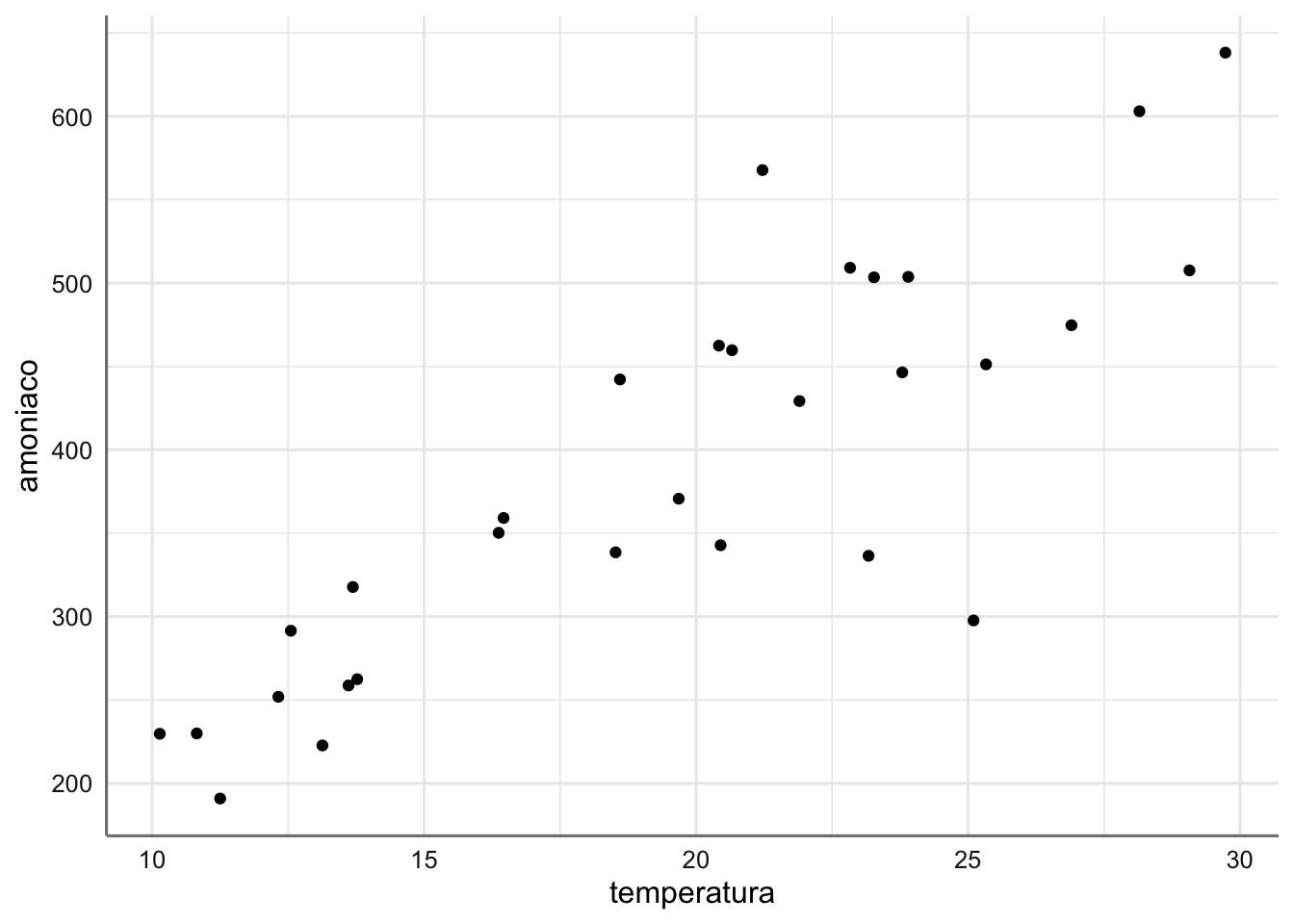

Observamos que a mayor temperatura, mayor es el contenido de amonio en las muestras, y además la relación entre ambas variables es de tipo lineal (se acomoda a una recta). Se aprecia bastante variabilidad en torno a lo que sería una recta de ajuste en torno a los valores centrales observados para la temperatura.

Para corroborar estadísticamente dicha relación lineal podemos utilizar el test de correlación lineal de Pearson, que resulta significativo a favor de reconocer la alta relación lineal entre temperatura y amonio:

cor.test(datosi$amoniaco,datosi$temperatura,method="pearson")
## 
##  Pearson's product-moment correlation
## 
## data:  datosi$amoniaco and datosi$temperatura
## t = 8.4548, df = 28, p-value = 3.408e-09
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  0.7016898 0.9253480
## sample estimates:
##       cor 
## 0.8476703

e igualmente podemos testarlo tras ajustar un modelo de regresión lineal y verificar la significatividad del coeficiente de la regresión para la variable temperatura, o lo que es lo mismo, de la variable explicativa temperatura en la tabla de ANOVA:

fit1=lm(amoniaco ~temperatura,data=datosi)
summary(fit1)
## 
## Call:
## lm(formula = amoniaco ~ temperatura, data = datosi)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -188.962  -37.448   -1.973   46.545  149.966 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   41.176     42.764   0.963    0.344    
## temperatura   17.748      2.099   8.455 3.41e-09 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 65.48 on 28 degrees of freedom
## Multiple R-squared:  0.7185, Adjusted R-squared:  0.7085 
## F-statistic: 71.48 on 1 and 28 DF,  p-value: 3.408e-09
anova(fit1)
## Analysis of Variance Table
## 
## Response: amoniaco
##             Df Sum Sq Mean Sq F value    Pr(>F)    
## temperatura  1 306465  306465  71.483 3.408e-09 ***
## Residuals   28 120043    4287                      
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Visualizamos a continuación la recta de regresión ajustada con la que podremos predecir el nivel de amonio en función de la temperatura observada.

beta=coef(fit1)
p1+geom_abline(slope=beta[2],intercept=beta[1],color="red")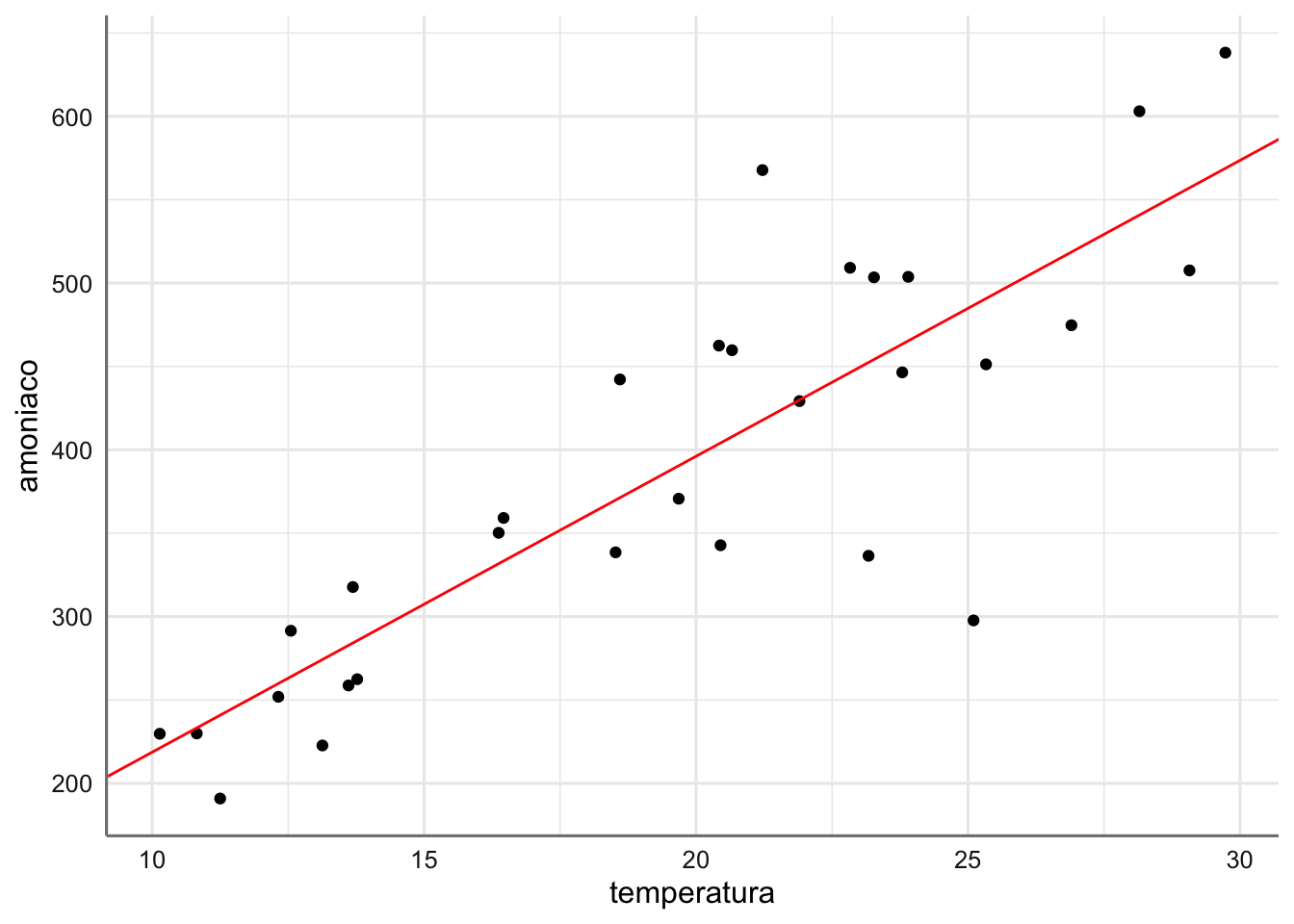

2. Investiga si hay diferencias entre los operadores en la toma de datos. Comenta tus conclusiones.

Investigamos seguidamente la relación entre el nivel de amonio y el hecho de que la medición la realice uno u otro operador. Calculamos en primer lugar medias y desviaciones típicas en cada grupo, con el fin de concluir sobre si existe o no diferencia y conocer su magnitud y visualizamos los datos con gráficos de cajas:

library(dplyr)
knitr::kable(summarise(group_by(datosi,operador),mean(amoniaco),sd(amoniaco)))
operador mean(amoniaco) sd(amoniaco)
A 410.9821 122.6991
B 365.6550 119.6208 
qplot(operador, amoniaco,data=datosi)+geom_boxplot()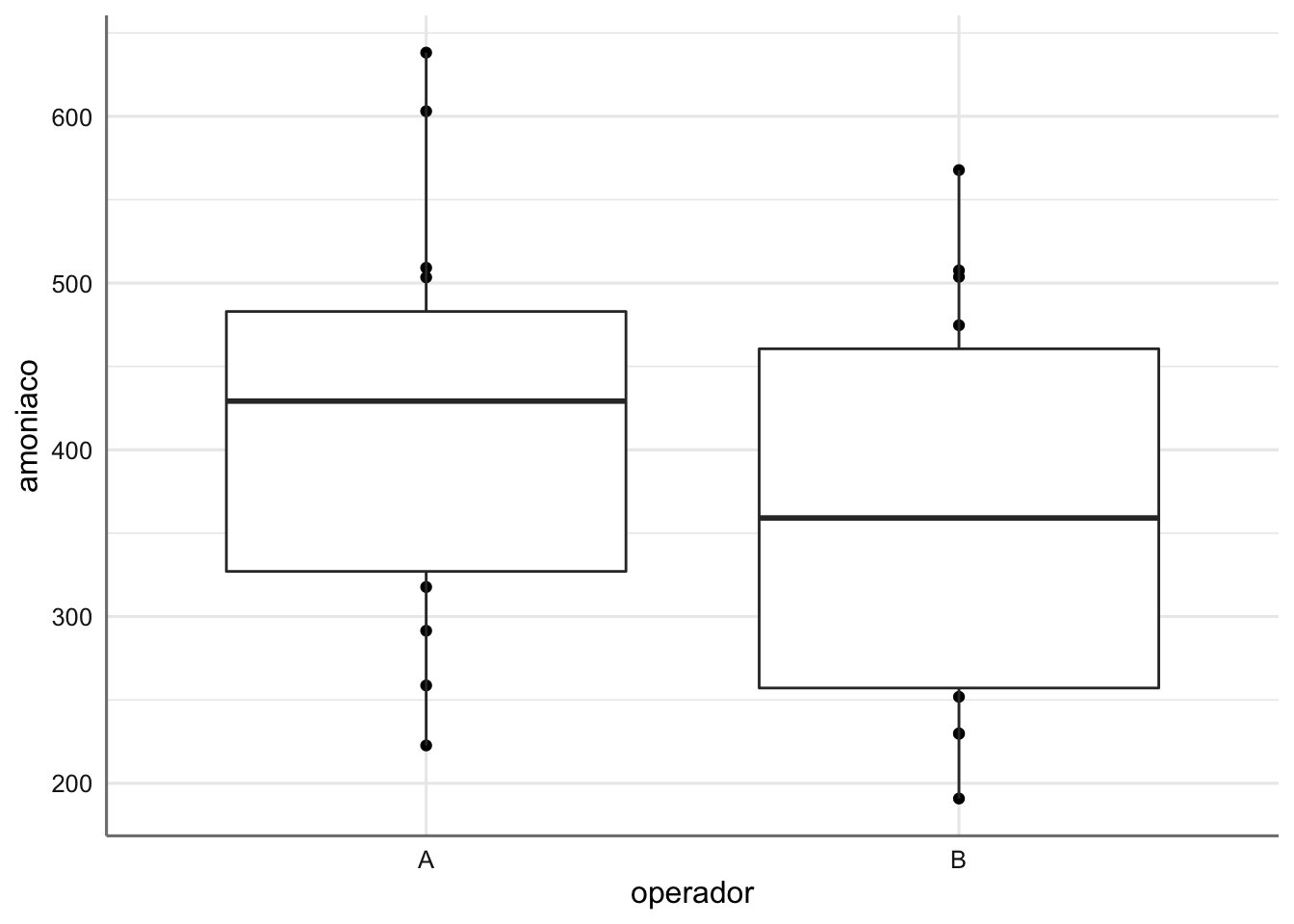

Si bien se aprecian ciertas diferencias en medias (y medianas), la variabilidad de las observaciones de uno y otro operador es muy alta y a priori no parece que las diferencias vayan a resultar significativas. Para testar estadísticamente si existen diferencias hemos de utilizar un test t-Student, o equivalentemente (al existir únicamente dos categorías en la variable ‘operador’) un análisis de ANOVA (tras ajustar un modelo lineal):

t.test(datosi$amoniaco~datosi$operador,alternative="two.sided")
## 
##  Welch Two Sample t-test
## 
## data:  datosi$amoniaco by datosi$operador
## t = 1.0245, df = 27.982, p-value = 0.3144
## alternative hypothesis: true difference in means between group A and group B is not equal to 0
## 95 percent confidence interval:
##  -45.30717 135.96137
## sample estimates:
## mean in group A mean in group B 
##        410.9821        365.6550
aov(amoniaco~operador,data=datosi)
## Call:
##    aov(formula = amoniaco ~ operador, data = datosi)
## 
## Terms:
##                 operador Residuals
## Sum of Squares   15409.1  411099.0
## Deg. of Freedom        1        28
## 
## Residual standard error: 121.1697
## Estimated effects may be unbalanced

El pvalor resultante no nos permite efectivamente, concluir a favor de la desigualdad entre las mediciones que realiza uno y otro operador (no podemos rechazar la igualdad de medias entre las mediciones que realizan los dos operadores).

3. Busca una respuesta integral y coméntala. El tratamiento integral de ambas cuestiones pasaría por buscar y ajustar un modelo razonable con las dos variables proporcionadas. Puesto que se trata de una variable continua (temperatura) y una categórica (operador) que podrían actuar como predictores de la variable continua amonio, y dada la relación lineal observada con temperatura, optamos por un modelo lineal de ajuste que involucre a todas las variables explicativas.

Cabría que existiera interacción entre operador y temperatura, hecho que comprobamos en primer lugar. Que existiera interacción significaría que habríamos de ajustar dos rectas de regresión diferentes (amonio vs temperatura) para las observaciones de uno y otro operador:

p1+geom_point(aes(colour=operador))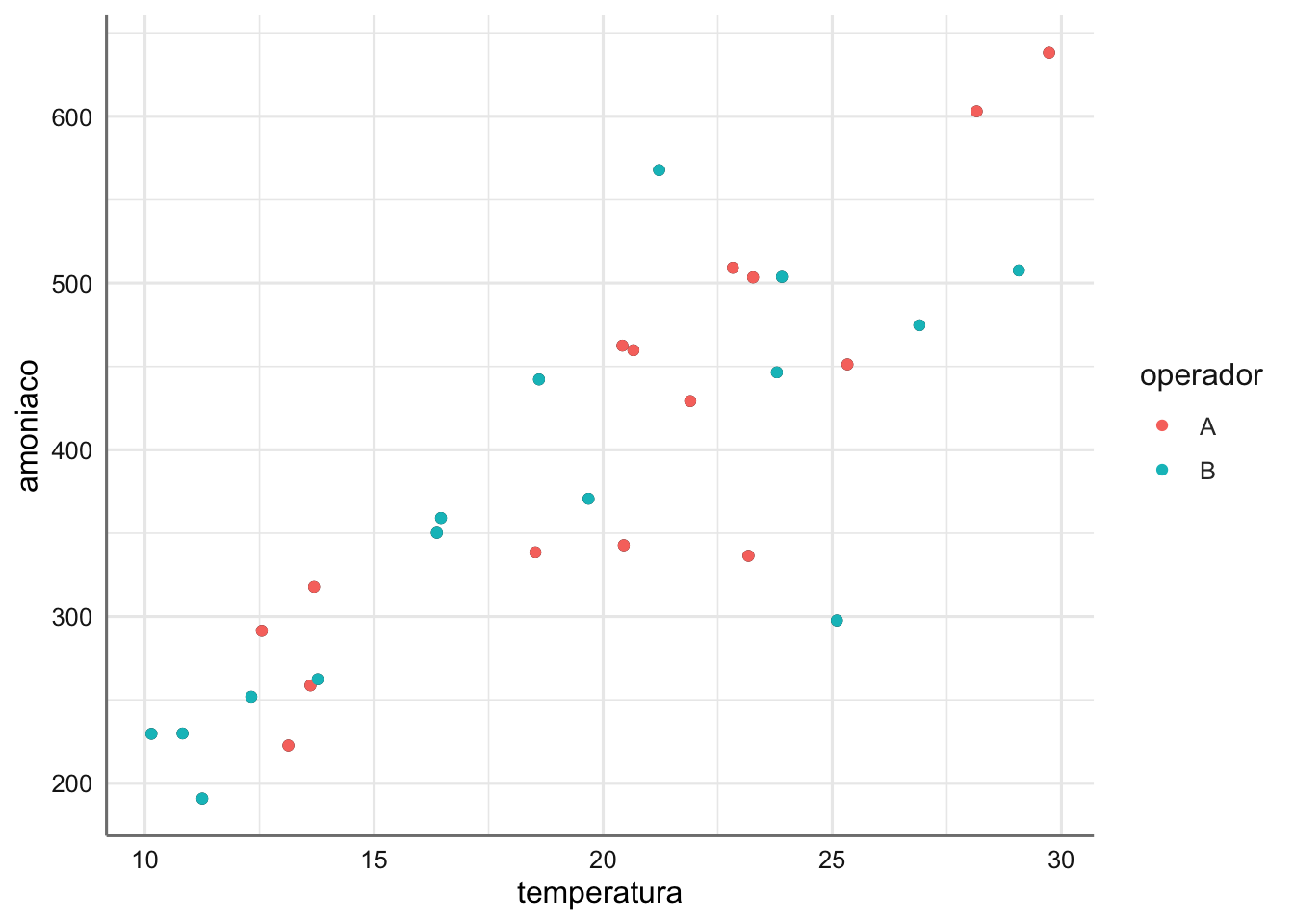

anova(lm(amoniaco~temperatura*operador,data=datosi))
## Analysis of Variance Table
## 
## Response: amoniaco
##                      Df Sum Sq Mean Sq F value    Pr(>F)    
## temperatura           1 306465  306465 70.3202 7.234e-09 ***
## operador              1   1142    1142  0.2621    0.6130    
## temperatura:operador  1   5589    5589  1.2824    0.2678    
## Residuals            26 113312    4358                      
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Puesto que el efecto de interacción no es significativo, lo excluimos del modelo.

anova(lm(amoniaco~temperatura+operador,data=datosi))
## Analysis of Variance Table
## 
## Response: amoniaco
##             Df Sum Sq Mean Sq F value    Pr(>F)    
## temperatura  1 306465  306465 69.5923 5.949e-09 ***
## operador     1   1142    1142  0.2594    0.6147    
## Residuals   27 118900    4404                      
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Tampoco operador resulta significativo, por lo que el mejor modelo de ajuste es el que nos proporcionaba ‘fit1’, incluso cabría mejorarlo excluyendo el término de interceptación:

fit2=lm(amoniaco~-1+temperatura,data=datosi)
summary(fit2)
## 
## Call:
## lm(formula = amoniaco ~ -1 + temperatura, data = datosi)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -196.50  -29.50   13.09   47.46  149.96 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## temperatura  19.6882     0.5861   33.59   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 65.39 on 29 degrees of freedom
## Multiple R-squared:  0.9749, Adjusted R-squared:  0.9741 
## F-statistic:  1129 on 1 and 29 DF,  p-value: < 2.2e-16

sobre el que abordaríamos la validación del modelo, esto es, verificar sobre los residuos las hipótesis del modelo lineal:

  • normalidad
  • homocedasticidad
  • independencia
  • valores influyentes y outliers

Para realizar la validación, referirse a http://www.statmethods.net/stats/rdiagnostics.html.