Fiabilidad y Gage R&R
1 Análisis Gage R&R para datos continuos.
El análisis Gage R&R no es útil para evaluar un producto o proceso, sino para evaluar la habilidad de medir el producto o proceso de una forma precisa y consistente. Un análisis Gage R&R nos permite investigar:
- si la variabilidad del sistema de medida es pequeña comparada con la variabilidad del proceso
- cuánta de la variabilidad en el sistema de medida está causada por diferencias entre los operadores
- si el sistema de medida es capaz de discriminar entre diferentes elementos (parts).
Gage R&R calcula la variación total (VT) a partir de tres fuentes:
- Parts o elementos que son medidos.
- Appraisers u operarios
- Equipment (gage) o equipación de medida.

Descomposición de la variabilidad total: diferencias entre elementos y variabilidad asociada al sistema de medida (Gage R&R).
Gage R&R utiliza la variación total para determinar cuánta de esta variación es atribuible a los aparatos (repetitividad: habilidad de un operador de repetir consistentemente la misma medida del mismo elemento,, utilizando la misma equipación bajo las mismas condiciones) y a los operarios (capacidad de una equipación de medida, utilizada por varios operadores, de reproducir consistentemente la misma medición del mismo elemento bajo las mismas condiciones).
En un análisis Gage consideraremos siempre un factor operario (appraisal) con \(n_o\) niveles, que representa a quien hace la medición (o el aparato de registro), un factor elemento (part) con \(n_p\) niveles, que representa a cada uno de los elementos distintos que se miden, y asumiremos un diseño cross en el que cada operario mide todos los elementos, y cada uno de ellos un número \(n_{run}\) de veces.
La varianza total se puede descomponer por lo tanto según:
\[\sigma^2=\sigma^2_{error}+\sigma^2_{part}+\sigma^2_{operador}+\sigma^2_{operador:part}\] donde \(\sigma^2_{error}\) estará representando el error inherente a la medición, no explicable por variaciones entre los operarios/aparatos que miden, y por lo tanto identifica la consistencia en la medición de un mismo elemento por un mismo operario, esto es, el error de repetitividad, \[\sigma^2_{repetitividad}=\sigma^2_{error}=MSE\], siendo \(MSE\) el cuadrado medio de los residuos.
Cuando la interacción no es significativa, calculamos \(\sigma^2_{operador}\) a partir del cuadrado medio del operador, \(MSO\) y del cuadrado medio del error, \(MSE\), y considerando el número total de mediciones que ha realizado cada operador, que es el producto del número de elementos (parts), \(n_p\) y del número de veces que ha medido cada elemento, \(n_{run}\): \[\sigma^2_{operador}=\frac{MSO-MSE}{n_p \times n_{run}}\] La variabilidad atribuíble a las diferencias entre los elementos (Parts) proviene del cuadrado medio \(MSP\), y se calcula considerando en el denominador el número de mediciones que se han realizado de cada elemento, esto es, el número de operadores \(n_o\) por el número de repeticiones de cada elemento por el mismo operador, \(n_{run}\): \[\sigma^2_{part}=\frac{MSP-MSE}{n_o \times n_{run}}.\]
Cuando hay interacción, la variabilidad atribuíble a reproducibilidad se obtiene de la del operador y la de su interacción con los elementos (considerando posibles variaciones en el comportamiento del operador al medir distintos elementos): \[\sigma^2_{reproducibilidad}=\sigma^2_{operador}+\sigma^2_{operador:part}\]
La variabilidad Gage se calcula con las componentes de repetitividad y reproducibilidad: \[\sigma^2_{Gage}=\sigma^2_{repetitividad}+\sigma^2_{reproducibilidad}\]
Una vez calculada la descomposición de la varianza del proceso, el sistema de medida lo evaluaremos en términos de:
- El %Contribution de la varianza (% de contribución), que es el porcentaje de la variación del proceso que proviene de cada una de las fuentes posibles. Se calcula como la varianza de cada componente (Gage R&R, Repetitividad, Reproducibilidad y Elemento -Part-to-Part) dividida por la varianza total y multiplicada por 100. Cuanto mayor sea %Contribution(Gage), mayores serán los problemas manifiestos sobre el sistema de medida.
%Contribución (Gage)=Varianza.Gage /Var.total x 100%- La variación del estudio o Study Variation se calcula a partir de la desviación típica (raíz cuadrada de la varianza), multiplicada por el sigma asumido (habitualmente 6). El %Study Variation (% de variación del estudio), calculado como el porcentaje de error asumido por cada una de las fuentes sobre el error total. El error se calcula como la raíz cuadrada de la varianza. La variación del estudio que nos interesará para concluir sobre el sistema de medida corresponde a la parte Gage: Reproducibilidad y Repetitividad:
%Study Variation (Gage)=se.Gage/se.total x 100%Típicamente, la variación del proceso (Study Variation) se define como \(6s\), siendo \(s\) la desviación estándar, estimación de \(\sigma\). Cuando los datos se distribuyen Normal, aproximadamente el \(99.73\%\) de los datos caen dentro de 6 desviaciones estándar (a \(\pm 3\) desviaciones estándar de la media), y aproximadamente el \(99\%\) de los datos caen entre \(5.15\) desviaciones estándar (a \(\pm 2.575\) desviaciones estándar de la media). Fte: Minitab https://goo.gl/WLNaMo
If the Total Gage R&R contribution in the %Study Var column (% Tolerance, %Process) is:
Less than 10% - the measurement system is acceptable. Between 10% and 30% - the measurement system is acceptable depending on the application, the cost of the measuring device, cost of repair, or other factors. Greater than 30% - the measurement system is unacceptable and should be improved.
If you are looking at the %Contribution column, the corresponding standards are:
- Less than 1% - the measurement system is acceptable.
- Between 1% and 9% - the measurement system is acceptable depending on the application, the cost of the measuring device, cost of repair, or other factors.
- Greater than 9% - the measurement system is unacceptable and should be improved.
Fte: Minitab tutorial https://goo.gl/RgfCJv
- El %Tolerance (% de porcentaje de tolerancia), calculado como el porcentaje del rango de tolerancia del proceso (distancia entre los límites de especificación) que es consumido por el error de cada una de las fuentes. Para su cálculo hay que especificar la tolerancia.
%Tolerancia (Gage)=se.Gage/Rango TOLERANCIA x 100%.Which metric to use Use %Tolerance or %StudyVar to evaluate the measuring system, depending on the measuring system. • If the measurement system is used for process improvement (reducing part-to-part variation), %StudyVar is a better estimate of measurement precision. • If the measurement system evaluates parts relative to specifications, %Tolerance is a more appropriate metric. Fte: Minitab https://goo.gl/WLNaMo
- Un análisis Gage también devuelve el número de categorías distintas, que representa el número de grupos de elementos que la herramienta de medida puede distinguir a partir de los datos. Cuanto mayor sea este número, mayor es la posibilidad de que la herramienta de medida pueda discernir entre un elemento y otro.
Según el Automobile Industry Action Group (AIAG):
- Cuando el número de categorías es menor a 2, el sistema de medida no tiene valor para controlar el proceso porque una parte no se puede distinguir de otras.
- Cuando el número de categorías es 2, los datos sólo se pueden dividir en dos grupos diferenciables: alto y bajo.
- Cuando el número de categorías es 3, los datos se pueden dividir en tres grupos diferenciables: alto, medio y bajo.
- 5 o más categorías da indicios de un sistema de medida aceptable. Fte: Minitab https://goo.gl/vuSVDG
También los gráficos ayudan a visualizar problemas en el sistema de medida.
- El gráfico R (R Chart) representa el rango (diferencia entre el valor máximo y el mínimo observados) medio de las mediciones conseguidas por cada operador/herramienta para cada elemento considerado. Superpone además una línea central con el rango medio observado en todas las mediciones, y unos límites obtenidos a partir de las constantes de Shewart \(d_2\) y \(d_3\) (ver Appendix Springer). Da información sobre la consistencia en las medidas de cada operador/herramienta en cada elemento (en términos de rangos).
\[lim_{sup}=Rmedio \cdot ( 1+d_3/d_2); lim_{inf}=Rmedio \cdot( 1-d_3/d_2)\]
Si el gráfico R Chart por operador es tal que todos los puntos caen dentro del intervalo delimitado por los límites anteriores, significa que el operador mide consistentemente todos los elementos, esto es, que no hay problemas de repetitividad. Si hay puntos fuera, significa que para algunos elementos las mediciones de un mismo operador son muy dispares (hay mayor variabilidad) y por lo tanto manifiesta problemas de repetitividad.
- El gráfico xbar (Xbar Chart) por operador representa los valores medios medidos por cada operador para cada uno de los elementos. De nuevo superpone una línea central con el promedio de todas las mediciones (xbar), y unos límites obtenidos a partir de la constante de Shewart y el rango medio observado. Da idea de la variación que ocasiona cada operador/herramienta cuando mide diferentes elementos. \[lim_{sup}=\bar{x} +3 \cdot Rmedio/(d_2 \sqrt{n}); lim_{inf}=\bar{x} -3 \cdot Rmedio/(d_2 \sqrt{n})\]
Nos permitirá detectar problemas de reproducibilidad (promedios muy diferentes para diferentes operadores).
##Ejemplo1: PILAS
Ejemplo 5.1 (voltaje en pilas, de Cano et al 2013) proporciona un ejemplo desarrollado para el cálculo del estudio Gage R&R completo. Un fabricante de baterías hace varios tipos de baterías/pilas para uso doméstico. El BB de la compañía quiere empezar un proyecto Seis Sigma para mejorar la línea de producción de las pilas de voltaje 1.5. Ha relacionado la CTQ identificada en la fase I (Definir) mediante la variable output “voltaje”. Ahora el sistema de medida ha de ser evaluado antes de comenzar otros análisis. Hay 2 voltímetros disponibles y 3 pilas diferentes son seleccionadas al azar al final de la línea de producción. Se mide el voltaje de cada pila con cada voltímetro 3 veces. Los datos son los siguientes:
voltmeter = factor(rep(1:2, each = 9))
battery = factor(rep(rep(1:3, each = 3), 2))
run = factor(rep(1:3, 6))
voltage = c(1.4727, 1.4206, 1.4754, 1.5083, 1.5739, 1.4341, 1.5517, 1.5483, 1.4614,
1.3337,1.6078, 1.4767, 1.4066, 1.5951, 1.8419,1.7087, 1.8259, 1.5444)
batteries = data.frame(voltmeter, battery,run, voltage)
ggplot(batteries,aes(voltmeter,voltage))+geom_boxplot(aes(colour=battery))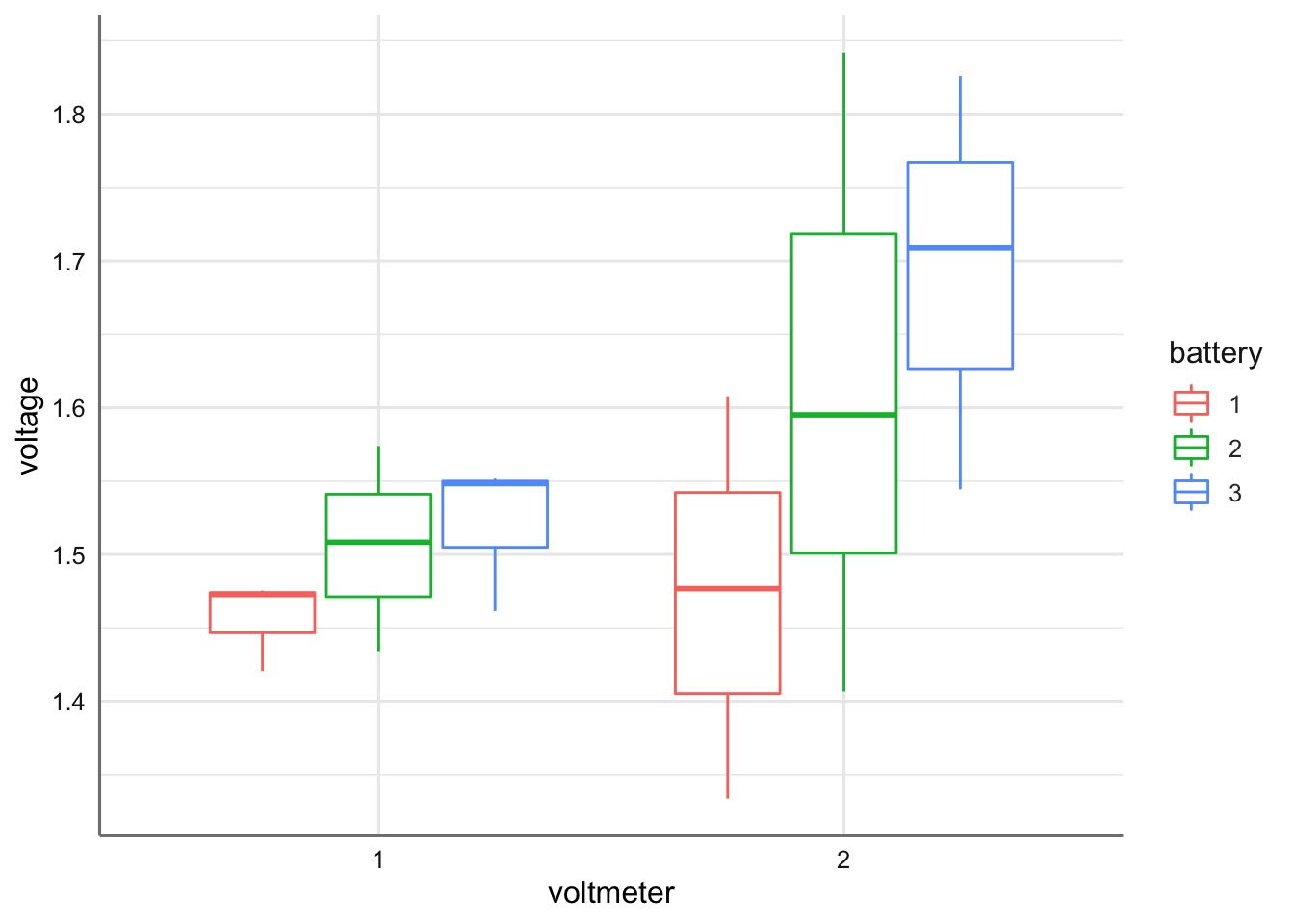
Pregunta 1: ¿Qué aprecias en el gráfico? Pregunta 2. Interpreta los resultados del análisis Gage. ¿Hay problemas con el sistema de medida? Justifícalo. ¿Se corresponde con lo que apreciaste en el gráfico inicial? Pregunta 3. Identifica la relación entre la tabla de Anova y la tabla Gage de descomposición de la varianza.
El objetivo en un proyecto de mejora es poder discriminar entre las pilas (parts). El voltímetro hace el papel de operador/aparato que realiza la medida (appraisal).
Utilizamos la función de la librería SixSigma que proporciona el análisis Gage R&R íntegro, incluida la tabla de ANOVA y la descomposición Gage de la varianza:
#ss.rr(var, part, appr, data, main, sub)
my.rr <- ss.rr(var = voltage, part = battery,
appr = voltmeter,
data = batteries,
main = "Six Sigma Gage R&R Measure",
sub = "Batteries Project MSA")## Complete model (with interaction):
##
## Df Sum Sq Mean Sq F value Pr(>F)
## battery 2 0.06308 0.03154 3.415 0.227
## voltmeter 1 0.04444 0.04444 4.812 0.160
## battery:voltmeter 2 0.01847 0.00924 0.584 0.573
## Repeatability 12 0.18982 0.01582
## Total 17 0.31582
##
## alpha for removing interaction: 0.05
##
##
## Reduced model (without interaction):
##
## Df Sum Sq Mean Sq F value Pr(>F)
## battery 2 0.06308 0.03154 2.120 0.157
## voltmeter 1 0.04444 0.04444 2.987 0.106
## Repeatability 14 0.20829 0.01488
## Total 17 0.31582
##
## Gage R&R
##
## VarComp %Contrib
## Total Gage R&R 0.018162959 86.74
## Repeatability 0.014878111 71.05
## Reproducibility 0.003284848 15.69
## voltmeter 0.003284848 15.69
## Part-To-Part 0.002777127 13.26
## Total Variation 0.020940086 100.00
##
## StdDev StudyVar %StudyVar
## Total Gage R&R 0.13477002 0.8086201 93.13
## Repeatability 0.12197586 0.7318552 84.29
## Reproducibility 0.05731359 0.3438816 39.61
## voltmeter 0.05731359 0.3438816 39.61
## Part-To-Part 0.05269846 0.3161907 36.42
## Total Variation 0.14470690 0.8682414 100.00
##
## Number of Distinct Categories = 1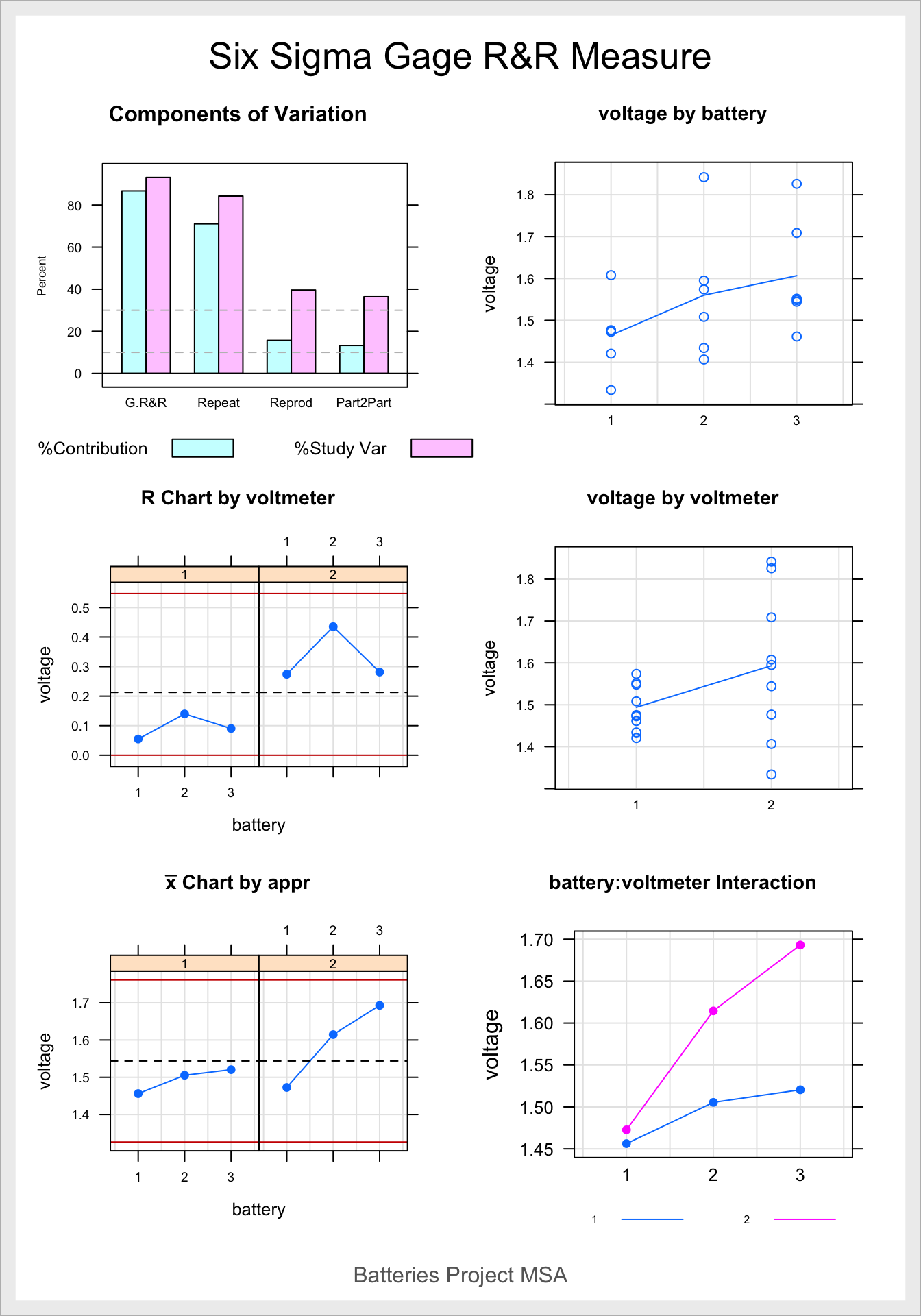
1.0.1 Conclusiones del análisis Gage para el Ejemplo1
A la vista de los resultados del análisis Gage R&R, la componente de la varianza asociada al sistema de medida constituye un 84,15% de la variabilidad total. El sistema de medida adolece de un problema claro. La variabilidad asociada a las diferencias entre las pilas que se miden sólo representa un 15,85% de la variabilidad total. La interacción entre voltímetro y pilas es despreciable.
El número de categorías distintas es 1, de modo que el sistema de medida no es aceptable.
Observando el gráfico resultante, la interpretación es la siguiente:
- Var By Part: muestra las mediciones obtenidas para los diferentes elementos considerados, y traza una línea entre los promedios para cada elemento, que muestra las tendencias en cuanto a mediciones. Permite apreciar diferencias entre elementos a través de las mediciones que se han realizado de cada uno de ellos. Las mediciones del voltímetro 2 son mucho más variables que las realizadas con el voltímetro 1. Hay diferencias claras entre los voltímetros.
- Var By Appraiser: muestra las mediciones obtenidas para los diferentes elementos considerados, y traza una línea entre los promedios para cada elemento, que muestra las tendencias en cuanto a mediciones. Permite apreciar diferencias entre operarios/herramientas con las mediciones que ha realizado cada uno de ellos. Las mediciones del voltímetro 2 son mucho más variables que las del voltímetro 1, y en promedio algo superiores. Hay diferencias claras entre los voltímetros, y las deficiencias (variabilidad) se manifiestan en el voltímetro 2.
- Part x Appraiser Interaction: muestra el promedio de las mediciones de cada uno de los elementos que ha realizado cada operario/herramienta, y traza líneas de tendencia para cada operario/herramienta. Permite apreciar diferencias entre operarios a la hora de medir los distintos elementos. El voltímetro 2 mide de forma diferente (en promedio) cada una de las tres pilas, mientras que el voltímetro 1 es más estable en sus mediciones de las tres pilas. Sin embargo, la tendencia en las mediciones es similar para los dos voltímetros (no se cruzan las líneas o cambian de dirección, lo que daría idea de interacción latente). La interacción es irrelevante.
- Components of Variation: representa el %Contribution (contribución a la varianza total) y %StudyVar (contribución a la desviación típica) asociadas al sistema de medida. La variabilidad asociada al sistema de medida es claramente muy superior a la asociada a las diferencias entre los elementos, lo que manifiesta la debilidad del sistema de medida. Gráficamente se aprecia muy bien el problema más grave detectado: repetitividad.
- R Chart by Appraiser: Claramente el voltímetro 2 ha generado mucha más variabilidad al medir cualquiera de las tres pilas que el voltímetro 2. El rango medio y el intervalo de control queda en la zona central de los gráficos generados por los dos voltímetros, cuyas mediciones quedan en extremos opuestos. Se aprecia el problema de repetitividad provocado por el voltímetro 2.
- xbar Chart by appraiser: es similar al gráfico Part*appraiser Interaction. El voltímetro 1 es más estable en sus mediciones de las tres pilas que el voltímetro 2, que provoca una media global superior a la obtenida en todas las mediciones del primer voltímetro. Hay diferencias claras a la hora de medir entre los dos voltímetros, y muchas diferencias en las mediciones de las tres pilas por el voltímetro 2. Se aprecia el problema de reproducibilidad ocasionado por las diferencias entre las mediciones de las pilas por diferentes voltímetros.
1.1 Ejemplo 2. GLOBOS
Disponemos de 120 mediciones del perímetro de un total de 8 globos distintos (identificados por su color) por 5 medidores (persona). Cada uno de ellos ha realizado n=3 mediciones de cada globo.
load("./datos/globos.RData")
#library(SixSigma)
my.rr <- ss.rr(var = perimetro, part = color, appr = persona,data = glob,
main = "Six Sigma Gage R&R Measure", sub = "Globos")## Complete model (with interaction):
##
## Df Sum Sq Mean Sq F value Pr(>F)
## color 7 13191 1884.4 460.002 < 2e-16
## persona 4 2 0.4 0.109 0.978
## color:persona 28 115 4.1 4.868 1.34e-08
## Repeatability 80 67 0.8
## Total 119 13375
##
## alpha for removing interaction: 0.05
##
## Gage R&R
##
## VarComp %Contrib
## Total Gage R&R 1.9264787 1.51
## Repeatability 0.8414687 0.66
## Reproducibility 1.0850100 0.85
## persona 0.0000000 0.00
## color:persona 1.0850100 0.85
## Part-To-Part 125.3533112 98.49
## Total Variation 127.2797899 100.00
##
## StdDev StudyVar %StudyVar
## Total Gage R&R 1.387976 8.327859 12.30
## Repeatability 0.917316 5.503896 8.13
## Reproducibility 1.041638 6.249829 9.23
## persona 0.000000 0.000000 0.00
## color:persona 1.041638 6.249829 9.23
## Part-To-Part 11.196129 67.176776 99.24
## Total Variation 11.281835 67.691007 100.00
##
## Number of Distinct Categories = 11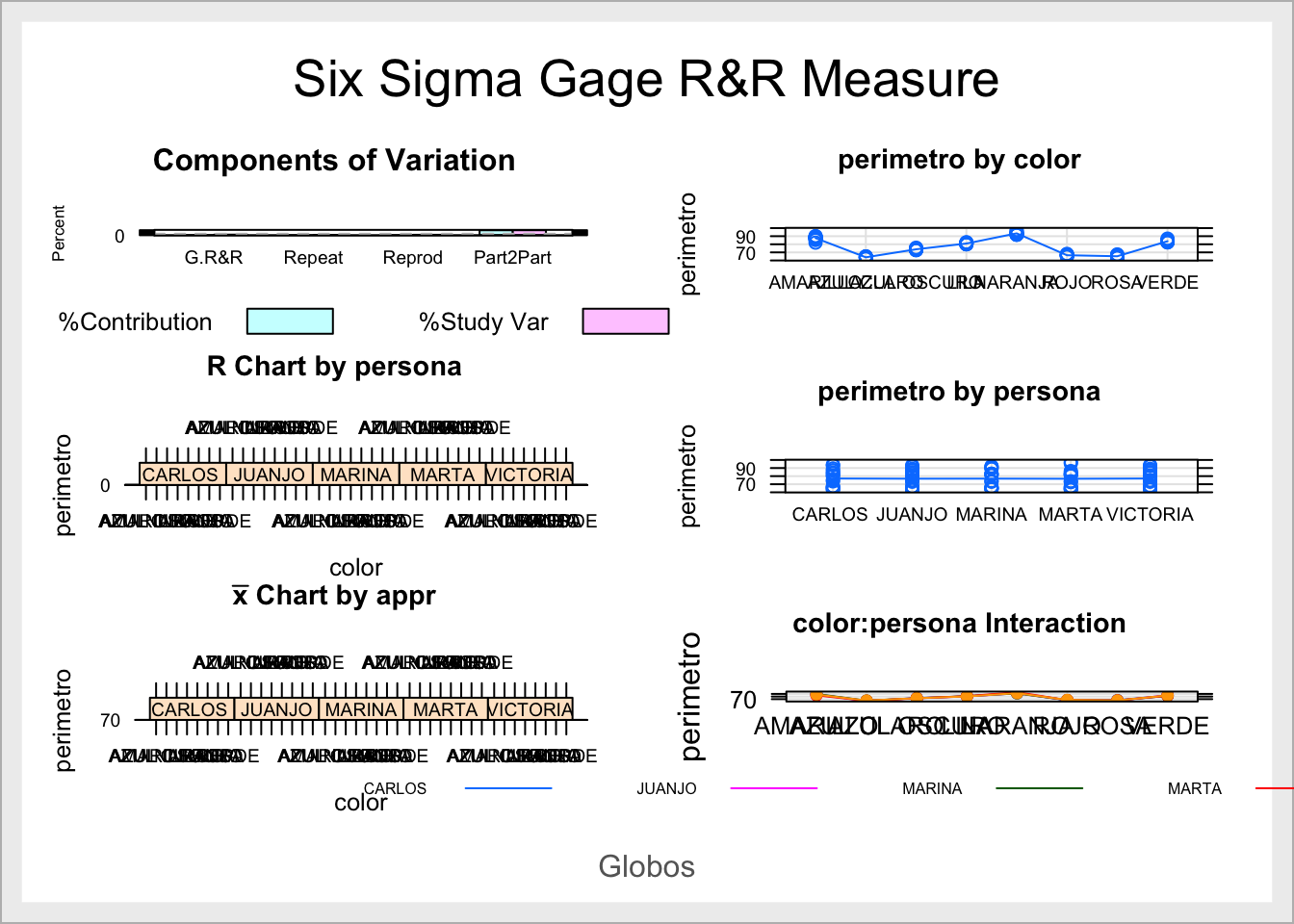
¿Qué conclusiones extraes del análisis Gage para el Ejemplo2?
2 Análisis Gage R&R para datos cualitativos
Cuando las variables son de tipo cualitativo, con datos que no se miden sino que se cuentan , también se pueden cometer errores de recuento. Veamos a continuación cómo validar un sistema de medida para este tipo de datos. Un ejemplo sencillo de sistemas de medida con datos categóricos es la revisión de un conjunto de piezas y su clasificación como defectuosas o no defectuosas.
En este tipo de sistemas hemos de preocuparnos, además de por la repetitividad (suponer que el observador va a ver lo mismo en dos o más observaciones distintas) y la reproducibilidad (suponer que dos observadores van a ver lo mismo cuando realizan la misma observación), por la exactitud. La exactitud está ligada a la decisión que toma un observador cuando discrimina un defecto: puede ver un defecto que no existe, o no ver un defecto que existe.
Un mismo observador puede ser consistente en sus observaciones de un mismo elemento (repetitividad ok), pero dar una clasificación (defecto/no defecto) incorrecta. El sistema será repetible pero no exacto. Asimismo, varios observadores pueden ser consistentes en sus observaciones, pero éstas no ser correctas porque no han discriminado correctamente el defecto; el sistema sería reproducible pero no exacto.
El análisis del sistema de medida con datos categóricos tiene en cuenta ambos conceptos:
- el de desviación, para juzgar si la decisión adoptada es correcta, y
- el de dispersión, para comprobar si adoptan la misma decisión de dos observaciones diferentes, provengan del mismo observador o de observadores distintos.

Exactitud en la medición de variables cualitativas. Identificación de defectos.
La exactitud de una inspección se mide a través de los defectos identificados correctamente, esto es, con el cociente entre: + los defectos reales que fueron identificados como tales tras una revisión de la primera inspección sobre los defectos declarados allí: los rechazados por el observador (a) menos los que han sido rechazados sin tener defectos (c), + los defectos totales, esto es, todos los detectados en una segunda inspección o revisión: los identificados entre los clasificados como defectos en la primera inspección, más los que no se identificaron como defectos en dicha primera inspección (a-c) y pasaron inadvertidos (b).
\[Exactitud = \frac{defectos \cdot reales \cdot identificados \cdot (a-c)}{defectos \cdot totales \cdot (a-c+b)}\]
Al pretender testar también la repetitividad y la reproducibilidad, será necesario también comparar las decisiones de un mismo inspector en diferentes observaciones, y las de diferentes observadores en varias mediciones. Con todo ello podremos evaluar de modo completo, E+ R&R, el método de recogida de información o sistema de medida.
El método para realizar estudios E+R&R con variables categóricas es sencillo. Básicamente se trata de realizar diferentes observaciones y revisiones de un conjunto de elementos y clasificarlos en la categoría que corresponda:
- Trata datos binarios (bien/mal) o una cantidad limitada de atributos.
- Compara los elementos observados con respecto a un “patrón” para aceptar/rechazar o asociar a una categoría y así poder reconocer la exactitud del método y de los observadores.
- Focaliza también la eficacia para diferenciar entre categorías.
- Se realiza con al menos 2 observadores, 2 observaciones cada uno, de unos 20 elementos representativos del objetivo a evaluar, con el fin de poder concluir sobre repetitividad y reproducibilidad.
Para evaluar el sistema introducimos los datos: observador1 (defecto/no-defecto), observador2 (d/nd), inspección (d/nd), observación (1/2).
2.1 Ejemplo 4. LACASITOS
Se considera una muestra de 20 Lacasitos que son evaluados cuidadosamente por un inspector para reconocer los defectuosos de los no defectuosos. A continuación dos miembros de cada equipo, que desconocen la clasificación correcta, realizan su comprobación en dos momentos diferentes, para evaluar repetitividad y reproducibilidad.
load("./datos/lacasitos.RData")
# part= identificador del lacasito (de 1 a 20)
# patt=patrón o clasificación correcta (1=ok, 0=defectuoso)
# appr=observador/inspector (1 y 2)
# rev=revisión que realiza cada observador (1 y 2)
# result=clasificación del observador (1=ok, 0=defectuoso)
# Y cargamos una función propia para resolver el análisis de un sistema de medida binario
source("./datos/gagerr-binario.R")
gage.rr.binary(part,appr,patt,rev,result,lacasitos)## $Repetitivity
## inspected matched.rev Repetitivity Repet.IC95.1 Repet.IC95.2
## Inspector1 20 10 50 % 29.93 % 70.07 %
## Inspector2 20 19 95 % 73.06 % 99.74 %
##
## $Repetitivity.Exact
## inspected matched.patt Repetitivity.Exact Repet.Exact.IC95.1
## Inspector1 20 8 40 % 19.98 %
## Inspector2 20 11 55 % 32.05 %
## Repet.Exact.IC95.2
## Inspector1 63.59 %
## Inspector2 76.17 %
##
## $Reproducibility
## inspected matched.rev Reproducibility Reprod.IC95.l Reprod.IC95.u
## Results 40 29 72.5 % 55.86 % 84.86 %
##
## $Reproducibility.Exact
## inspected matched.patt Reproducibility.Exact Reprod.Exact.IC95.l
## Results 40 22 55 % 38.66 %
## Reprod.Exact.IC95.u
## Results 70.4 %Las conclusiones son las siguientes:
Repetitividad El inspector1 es menos consistente en sus dos inspecciones (sólo coinciden un 50% de las inspecciones en las dos revisiones que realiza), mientras que el inspector2 resulta bastante consistente con un 95% de coincidencias entre ambas revisiones. Los intervalos de confianza mantienen la misma conclusión.
Repetitividad y Exactitud El inspector1 además de inconsistente es poco fiable a la hora de identificar lacasitos defectuosos, sólo con un 40% de detecciones correctas. El inspector2 aunque consistente, es poco preciso y sólo identifica correctamente -siendo consistente en su juicio las dos ocasiones que revisa- un 55% de los lacasitos.
Reproducibilidad De las 40 inspecciones realizadas por cada uno de los 2 inspectores, ambos han coincidido en un 72,5% de los lacasitos, si bien el intervalo de confianza queda entre 56% y 85%, lo que da poca fiabilidad a la reproducibilidad de las inspecciones.
Reproducibilidad y Exactitud El porcentaje baja al 55% cuando exigimos a la par coincidencia en los juicios de los inspectores e identificación correcta de los defectuosos. Hay problemas de reproducibilidad, aunque no tan severos como los de repetitividad para el inspector2, y de exactitud.
2.2 Referencias
Cómo interpretar el resultado de un análisis Gage R&R. Tutorial de Minitab http://blog.minitab.com/blog/quality-data-analysis-and-statistics/how-to-interpret-gage-output-part-2
How are the variance components calculated. In Minitab https://goo.gl/wBPSts
Tutorial de la librería qualityTools https://cran.r-project.org/web/packages/qualityTools/vignettes/qualityTools.pdf