Chapter 2 随机数生成

2.1 有限总体抽样

在R中，对有限总体抽样直接采用sample()函数即可。例如：

# toss some coins
sample(0:1, size = 10, replace = TRUE)

##  [1] 1 1 1 1 1 0 1 1 0 1

# choose some lottery numbers
sample(1:100, size = 6, replace = FALSE)

## [1]  4 31  3 88 54 57

# with weights (multinomial distribution)
sample(1:3, size = 20, replace = TRUE, prob = c(.2, .3, .5))

##  [1] 3 3 3 3 3 1 2 1 2 2 1 3 1 2 3 2 2 3 2 2

2.2 特殊分布抽样

对于概率论及数理统计中的常见分布，R中都有对应的函数生成相应分布的随机数。例如：

# uniform(0, 1)
runif(10, 0, 1)

##  [1] 0.8848778 0.7227399 0.5069511 0.5985456 0.6815278 0.6113222 0.3246392 0.9903550 0.5526703
## [10] 0.8790690

# norm(1, 4)
rnorm(10, 1, 2)  # the second parameter is std

##  [1] -0.4703085 -2.6019040  3.2626811  2.3249242  0.4006870 -1.1652514 -1.9347774  0.1366040  1.9639211
## [10]  2.3443152

对于其他分布，只需要在分布的缩写前加上r即可，例如rpois、rf、rexp等等。

2.3 逆变换法

根据概率论中的知识可知，如果随机变量 $X$ 具有分布函数 $F(x)$，那么 $U=F(X)\sim U(0,1)$。因此如果 $F_X^{-1}(U)$ 与 $X$ 同分布，所以逆变换法的步骤如下：

• 生成均匀随机变量 $U\sim U(0,1)$；
• 计算并返回 $X\sim F_X^{-1}(U)$ 即得相应分布随机变量。

例如：对 $$X\sim F(x)=\left\{\begin{array}{ll} 0, & x\leq0,\\ x^3, & 0<x\leq1,\\ 1, & x>1, \end{array}\right.$$ 只需利用如下代码就可以生成服从相应分布的随机数。

n <- 1000   # sample size
u <- runif(n)
x <- u^{1/3}   # inverse of F

为了更加直观，下图给出了随机数直方图和概率密度函数的对比。

hist(x, prob = TRUE, main = expression(f(x)==3*x^2))
y <- seq(0, 1, .01)
lines(y, 3*y^2)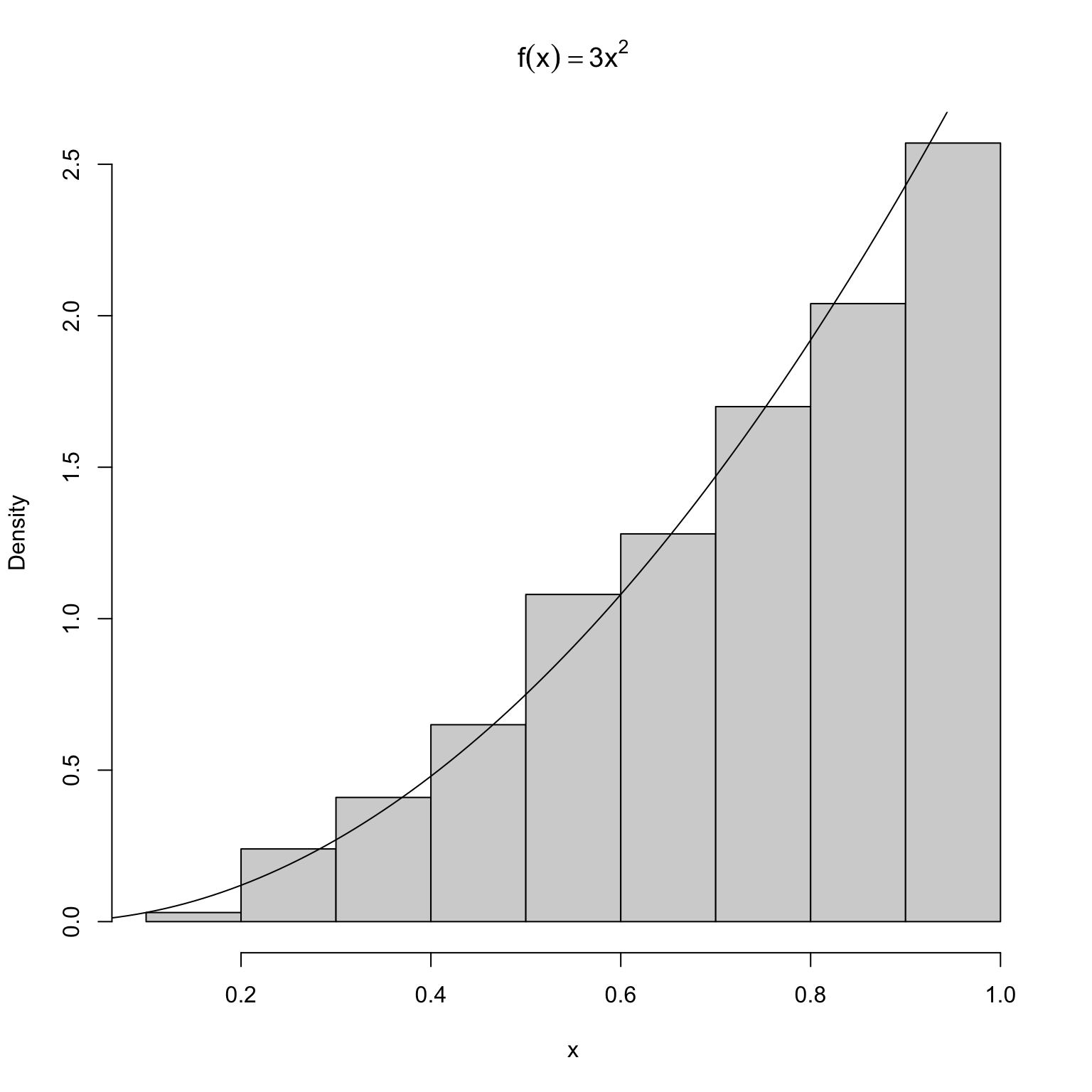

上述方法适用于分布函数具有显式表达并且其逆便于计算的情形，而我们知道，对于离散型随机变量而言，这样的反函数通常采用广义反函数，即 $$F^{-1}(u)=\inf\{x:F(x)\geq u\}.$$

基于此，对离散型随机变量的逆变换算法如下：

• 生成均匀随机变量 $U\sim U(0,1)$；
• 如果 $F_X(x_{i-1})<U\leq F_X(x_i)$，则返回 $X=x_i$。

在实际问题中，我们通常先对概率进行累加，而随机数落在何区域，就取其右端点作为随机数的值。

例1. 对 $$X\sim\left(\begin{array}{cccc} 1 & 2 & 4 & 10\\ 0.1 & 0.2 & 0.3 & 0.4 \end{array}\right)$$ 产生随机数服从该分布。

x <- c(1, 2, 4, 10)
p <- 1:4/10
cp <- cumsum(p)   # similar to calculating c.d.f.
n <- 1000   # sample size
u <- runif(n)
r <- x[findInterval(u, cp)+1]

下面这段代码是检验对应生成的随机数频率与概率是否一致。

ct <- as.vector(table(r))
ct/sum(ct)/p

## [1] 0.880 1.150 0.960 0.985

输出结果中的4个值基本接近于1。

例2. 使用逆变换法产生几何分布随机数。由于几何分布的分布函数 $F_X(x)=1-q^{x+1}$, $x=0,1,2,\dots$. 因此对每个随机数都要计算 $$1-q^x<u\leq 1-q^{x+1}.$$ 即 $x+1=\lceil\log(1-u)/\log q\rceil$，其中 $\lceil t\rceil$ 表示不小于 $t$ 的最小整数。

n <- 1000
p <- 0.4
u <- runif(n)
x <- ceiling(log(u) / log(1-p)) - 1
y <- rgeom(n, p)

counts <- table(c(rep(0, n), rep(1, n)), c(x, y))
barplot(counts, main = 'Geometry distribution',
        xlab = 'x', ylab = 'count', col = c('darkblue', 'red'),
        legend = c('InvTrans', 'rgeom'), beside = TRUE)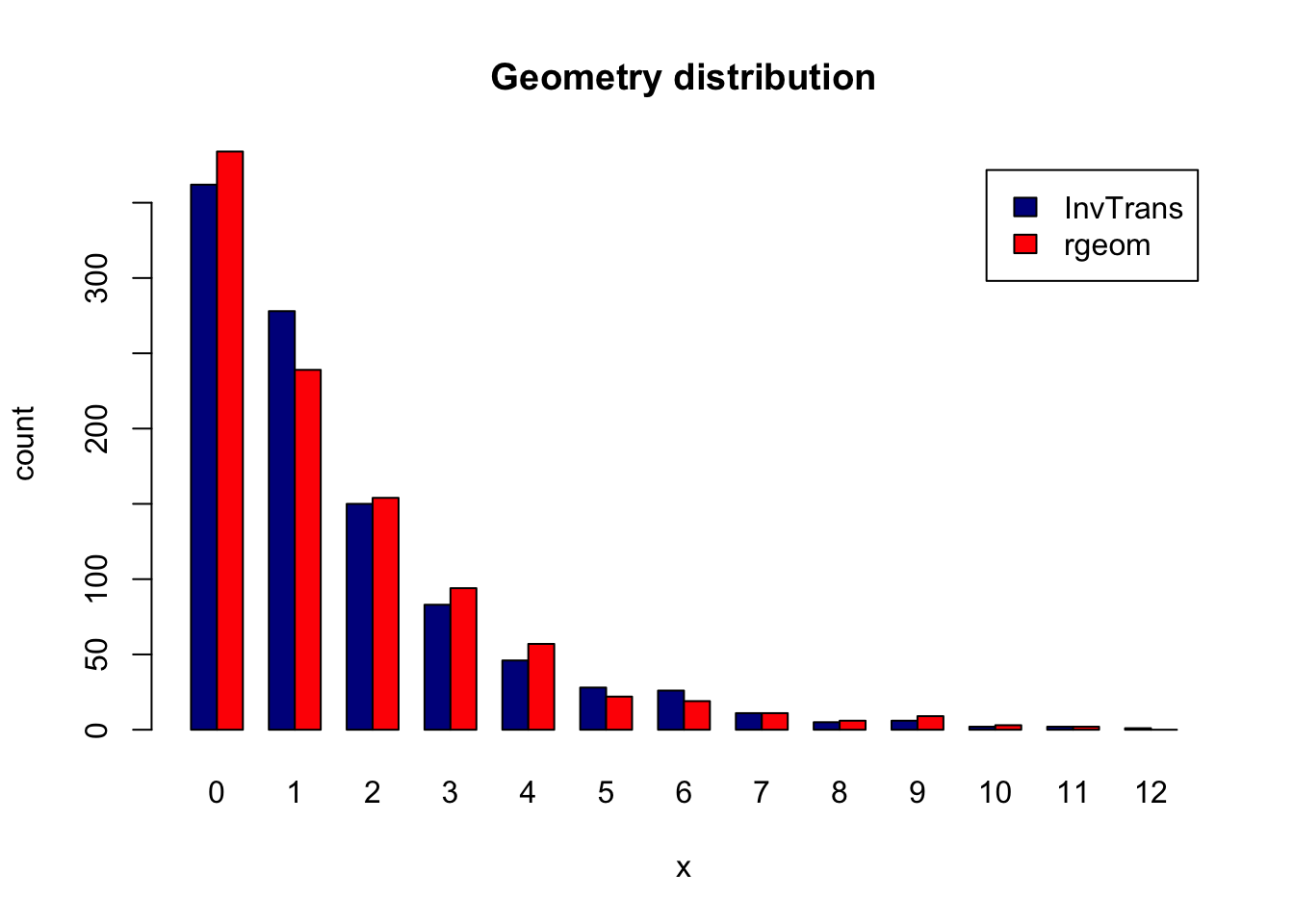

通过逆变换法得到的几何分布随机数与标准rgeom生成的基本一致。

在某些问题中，求解 $F(x-1)<u\leq F(x)$十分复杂，比如对Poisson分布，实际中利用如下递推关系产生和存储分布函数从而得到不等式的解： $$f(x+1)=\dfrac{\lambda f(x)}{x+1};\quad F(x+1)=F(x)+f(x+1).$$

例3. 使用逆变换法产生如下对数分布随机数： $$f(x)=\mathbb P(X=x)=\dfrac{a\cdot\theta^x}{x},\quad x=1,2,\dots,$$ 其中 $0<\theta<1$ 以及 $a=(-\log(1-\theta))^{-1}$。它所满足的递推关系为 $$f(x+1)=\dfrac{\theta^x}{x+1}f(x),\quad x=1,2,\dots.$$ 理论上可以通过这个递推关系求 $f(x)$ 的值，但对很大的 $x$ 值这种方法的精度不够。实际中往往直接计算 $f(x)$ 的值再存储 $F(x)$ 的值。

rlogarithmic <- function(n, theta) {
  u <- runif(n)
  N <- ceiling(-16 / log10(theta))
  k <- 1:N
  a <- - 1 / log(1 - theta)
  fk <- exp(log(a) + k * log(theta) - log(k))
  Fk <- cumsum(fk)
  x <- integer(n)
  for (i in 1:n) {
    x[i] <- as.integer(sum(u[i] > Fk))
    while (x[i] == N) {
      logf <- log(a) + (N + 1) * log(theta) - log(N + 1)
      fk <- c(fk, exp(logf))
      Fk <- c(Fk, Fk[N] + fk[N + 1])
      N <- N + 1
      x[i] <- as.integer(sum(u[i] > Fk))
    }
  }
  return(x + 1)
}

n <- 1000
theta <- 0.5
x <- rlogarithmic(n, theta)
k <- sort(unique(x))
p <- - 1 / log(1 - theta) * theta^k / k
se <- sqrt(p * (1 - p) / n)

下面的结果表明样本的频率分布符合理论分布：

round(rbind(table(x)/n, p, se), 3)

##        1     2     3     4     5     6     7     8     9    11
##    0.718 0.173 0.068 0.025 0.004 0.005 0.002 0.002 0.002 0.001
## p  0.721 0.180 0.060 0.023 0.009 0.004 0.002 0.001 0.000 0.000
## se 0.014 0.012 0.008 0.005 0.003 0.002 0.001 0.001 0.001 0.000

2.4 接受-拒绝法

接受-拒绝法的基本思想是用一个易于生成随机数的分布作为建议分布来近似实现目标密度函数的抽样。具体来说，分为以下几步：

• 选择简单函数 $g(x)$，满足 $f(x)\leq cg(x),~\forall x$；
• 根据 $g(x)$ 生成“建议随机数” $y$；
• 生成均匀分布随机数 $u\sim U(0,1)$；
• 如果 $u<\dfrac{f(y)}{cg(y)}$，则接受 $y$，并记 $x=y$，否则丢弃 $y$；
• 重复第2～4步直至样本量满足要求。

从理论上可以证明这样生成的随机数服从 $f(x)$ 对应的分布。事实上， $$\begin{align*} \mathbb P(X\leq x) &= \mathbb P\left(Y\leq x\mid U\leq\dfrac{f(Y)}{cg(Y)}\right)\\ &= \dfrac{\mathbb P\left(U\leq\dfrac{f(Y)}{cg(Y)},Y\leq x\right)}{\mathbb P\left(U\leq\dfrac{f(Y)}{cg(Y)}\right)}\\ &= \dfrac{\displaystyle\int_{-\infty}^x\mathbb P\left(U\leq\dfrac{f(Y)}{cg(Y)}\mid Y=y\right)g(y)\text{d}y}{\displaystyle\int_{-\infty}^{+\infty}\mathbb P\left(U\leq\dfrac{f(Y)}{cg(Y)}\mid Y=y\right)g(y)\text{d}y}\\ &= \dfrac{\displaystyle\int_{-\infty}^x\dfrac{f(y)}{cg(y)}g(y)\text{d}y}{\displaystyle\int_{-\infty}^{+\infty}\dfrac{f(y)}{cg(y)}g(y)\text{d}y}=F(x). \end{align*}$$

在实际问题中，对于常数 $c$ 的选取是一个智慧，因为接受概率 $$\displaystyle\mathbb P(\text{接受})=\mathbb E[\mathbb P(\text{接受}\mid Y)]=\mathbb E\left[\dfrac{f(Y)}{cg(Y)}\right]=\dfrac{1}{c}<1.$$

如果 $c$ 越接近于 $1$，那么接受概率就越大，算法效率就越高。当然，最朴实的想法就是用均匀分布对之进行分布建议。例如：对 $X\sim\text{Beta}(2,2)$ 产生随机数服从该分布，其密度函数为 $$f(x)=6x(1-x)\pmb 1_{\{0<x<1\}};$$ 可取均匀分布 $U(0,1)$ 作为建议分布，此时 $c=6$，代码如下。

n <- 1000
k <- 0
x <- numeric(n)   # 首先生成一个n维的容器
while (k < n) {
    y <- runif(1)   # 生成建议分布随机数
    u <- runif(1)   # 这个随机数用于判断是否接受上面这个随机数
    if (y * (1 - y) > u) {
        # 符合接受准则
        k <- k + 1
        x[k] <- y
    }
}

我们可以用Q-Q图对产生的随机数服从的分布进行检验。

r <- rbeta(1000, 2, 2)
qqplot(x, r)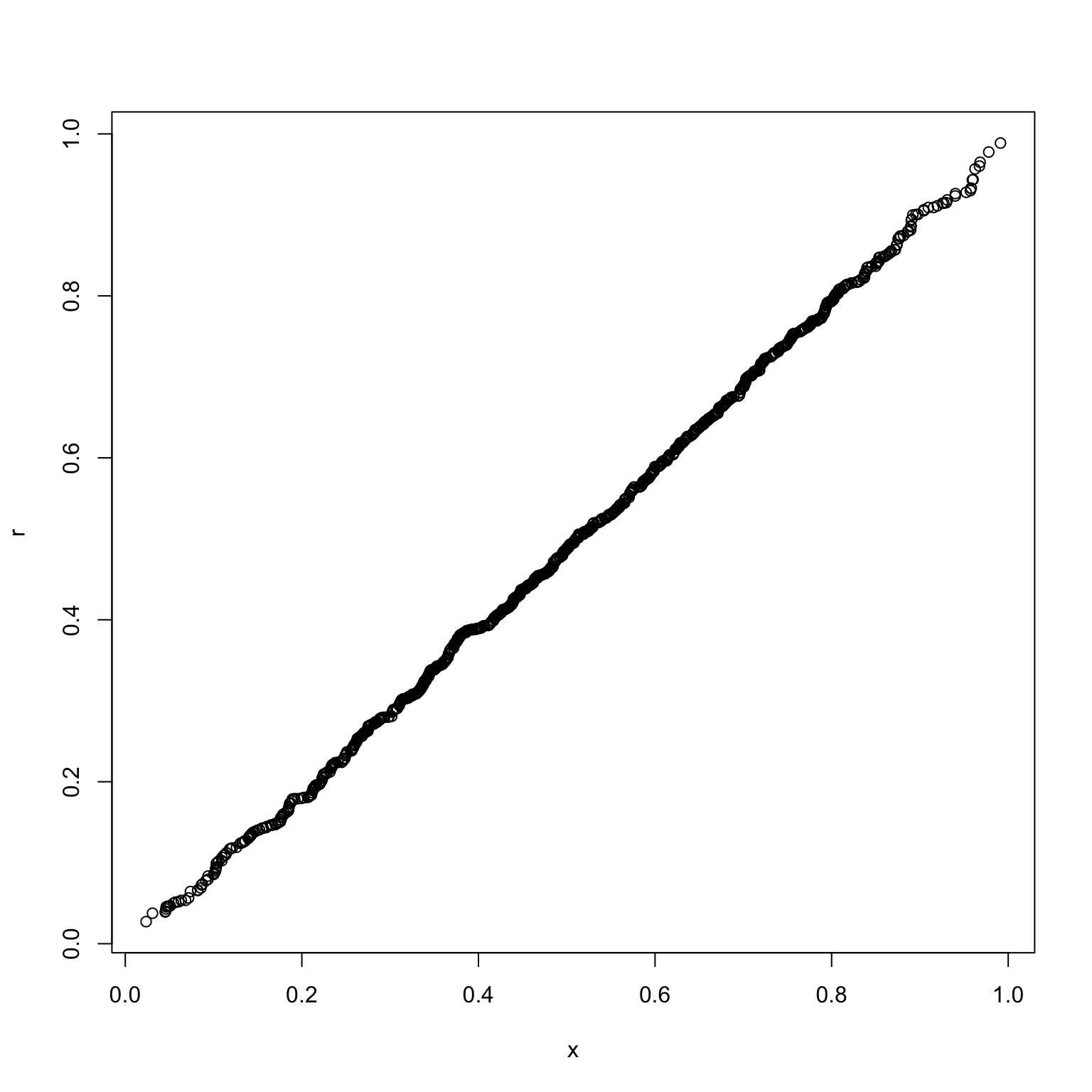

2.5 随机变量的变换

根据Box-Muller变换，我们可以根据均匀随机变量得到正态变量，具体公式如下 $$\left\{\begin{array}{l} Z_1=\sqrt{-2\log U}\cos(2\pi V),\\ Z_2=\sqrt{-2\log U}\sin(2\pi V), \end{array}\right.$$ 其中 $U,V\sim U(0,1)$。这样得到的 $Z_1,Z_2$ 是独立的标准正态变量。

n <- 10000
u <- runif(n)
v <- runif(n)
z1 <- sqrt(-2*log(u))*cos(2*pi*v)
z2 <- sqrt(-2*log(u))*sin(2*pi*v)
par(mfrow = c(1,2))
hist(z1, prob = TRUE, main = 'normal')
hist(z2, prob = TRUE, main = 'normal')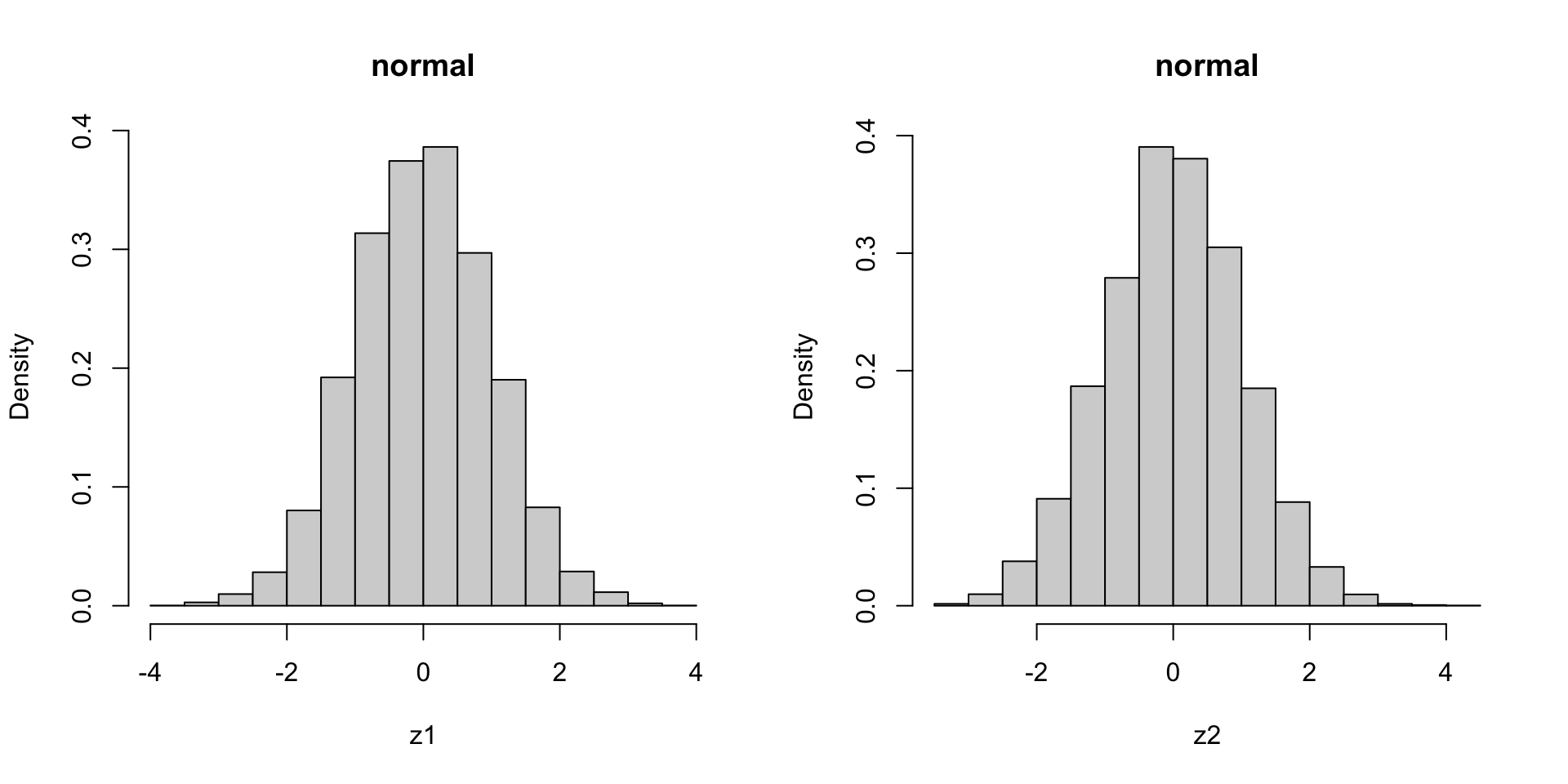

cor(z1, z2)

## [1] -0.007795011

代码得到的二者的相关系数接近于0，也就意味着两个正态随机变量相互独立。

有了标准正态变量之后，统计中的三大分布就有了落脚点，因为他们都是从标准正态分布中导出的。不过在实际运用中，我们更多还是采用R自带的随机数生成函数来得到相应分布的随机数。

例如，我们使用随机变量的和产生 $\chi^2$ 分布随机数，注意到 $\nu$ 个标准正态随机变量的平方和就是 $\chi^2(\nu)$ 分布随机变量。

n <- 1000
nu <- 2
X <- matrix(rnorm(n * nu), n, nu)^2
y <- apply(X, 1, sum)

我们可以用P-P图对产生的随机数服从的分布进行检验。

ry <- rchisq(n, nu)
qqplot(y, ry)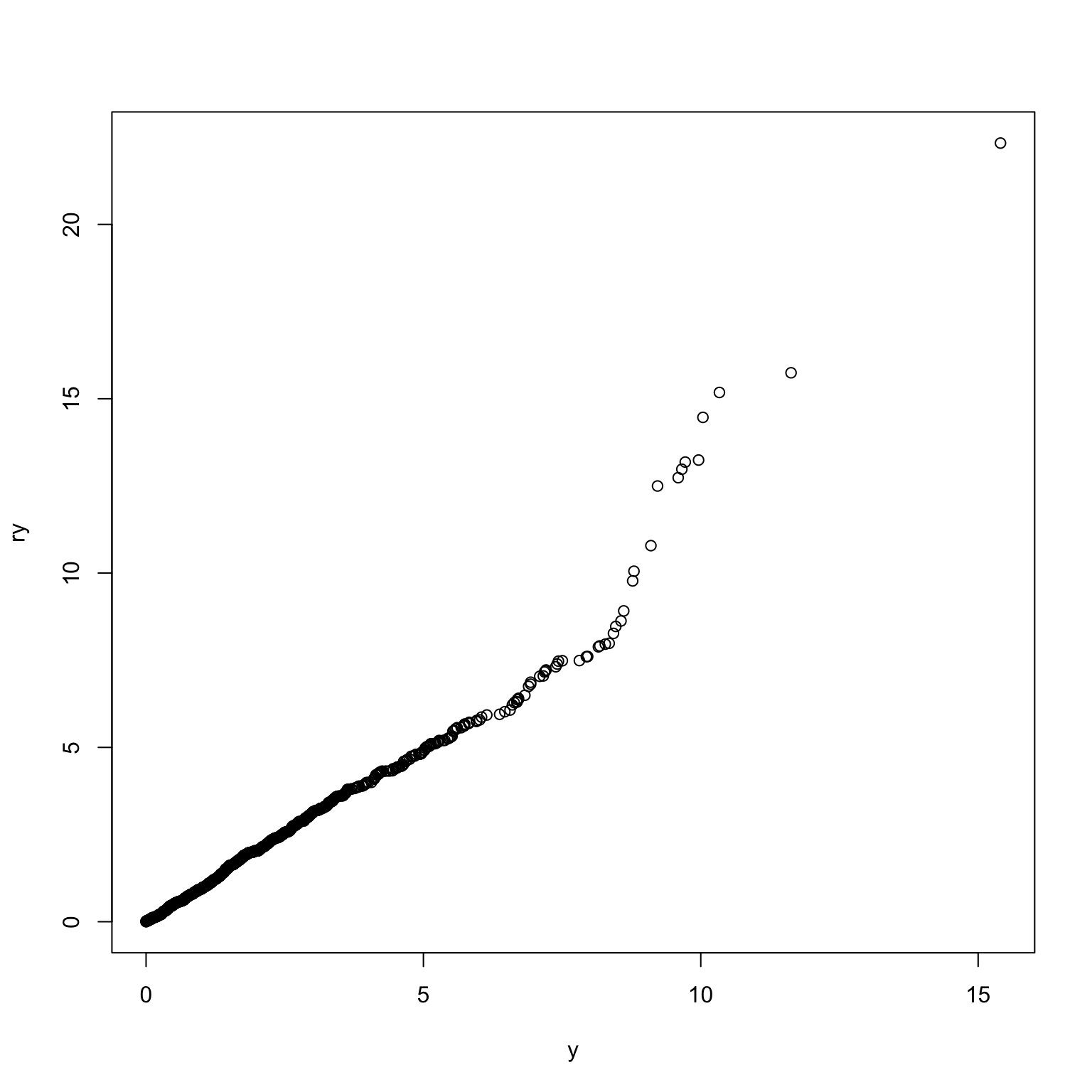

2.6 混合模型

设 $X_1\sim F_1(x)$，$X_2\sim F_2(x)$，现希望生成混合模型 $Y\sim 0.5F_1(x)+0.5F_2(x)$ 的随机数，一般情况下，显然不能使用上述方法进行模拟生成，需要考虑混合生成。例如：考虑两个卡方分布的混合模型。

n <- 10000
x1 <- rchisq(n, 5)
x2 <- rchisq(n, 10)
r <- sample(c(0, 1), replace = TRUE)
y <- r*x1 + (1-r)*x2
hist(y, prob = TRUE, main = 'mixture of chisq')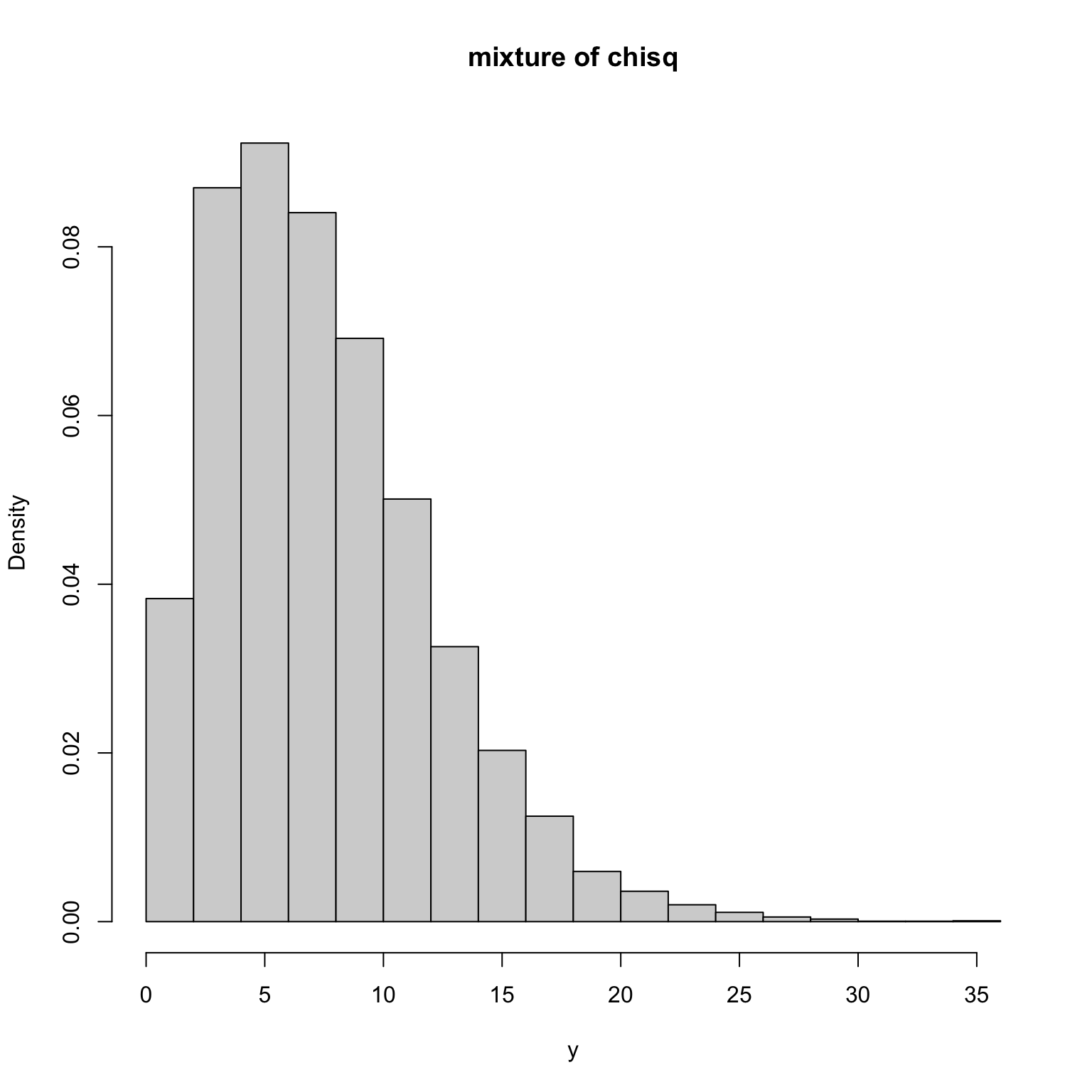

如果二者的混合比例不是相等的，则可以在生成两点分布时指定对应的成功概率。

2.7 贝叶斯模型

在贝叶斯统计推断中，参数具有一先验分布，而已知参数条件下，总体具有分布，通常我们需要生成总体的样本，则需要求出总体的边际分布，但这在大部分情况下不容易计算，因此考虑贝叶斯模型（实际上是贝叶斯统计推断中的分层先验模型）来生成随机数。

例如：设 $X\mid\Lambda\sim\text{Poisson}(\Lambda)$，而 $\Lambda\sim\text{Gamma}(r,\beta)$，可以通过如下代码生成 $X$ 的边际分布随机数。

n <- 10000
r <- 4
beta <- 3
lambda <- rgamma(n, r, beta)
x <- rpois(n, lambda)

当然，对于这个例子来说，$X$ 的边际分布是参数为 $r$ 和 $p=\dfrac{\beta}{1+\beta}$ 的负二项分布。事实上， $$\begin{align*} f(x) &= \displaystyle\int_0^{+\infty}f(x\mid\lambda)\pi(\lambda)\text{d}\lambda\\ &= \displaystyle\int_0^{+\infty}\frac{\lambda^x}{x!}\text{e}^{-\lambda}\cdot\frac{\beta^r}{\Gamma(r)}\lambda^{r-1}\text{e}^{-\beta\lambda}\text{d}\lambda\\ &= \displaystyle\dfrac{\beta^r}{x!\Gamma(r)}\int_0^{+\infty}\lambda^{x+r-1}\text{e}^{-\lambda(\beta+1)}\text{d}\lambda\\ &= \displaystyle\dfrac{\beta^r}{x!\Gamma(r)}\dfrac{\Gamma(x+r)}{(\beta+1)^{x+r}}=\binom{x+r-1}{r-1}p^r(1-p)^x,\quad x=0,1,\dots. \end{align*}$$

因此我们直接从负二项分布中进行采样，看看两种算法的效果差异。

y <- rnbinom(n, r, beta/(1+beta))
counts <- table(c(rep(0, n), rep(1, n)), c(x, y))
barplot(counts, main = 'Negative binomial distribution',
        xlab = 'x', ylab = 'count', col = c('darkblue', 'red'),
        legend = c('Bayes', 'rbinom'), beside = TRUE)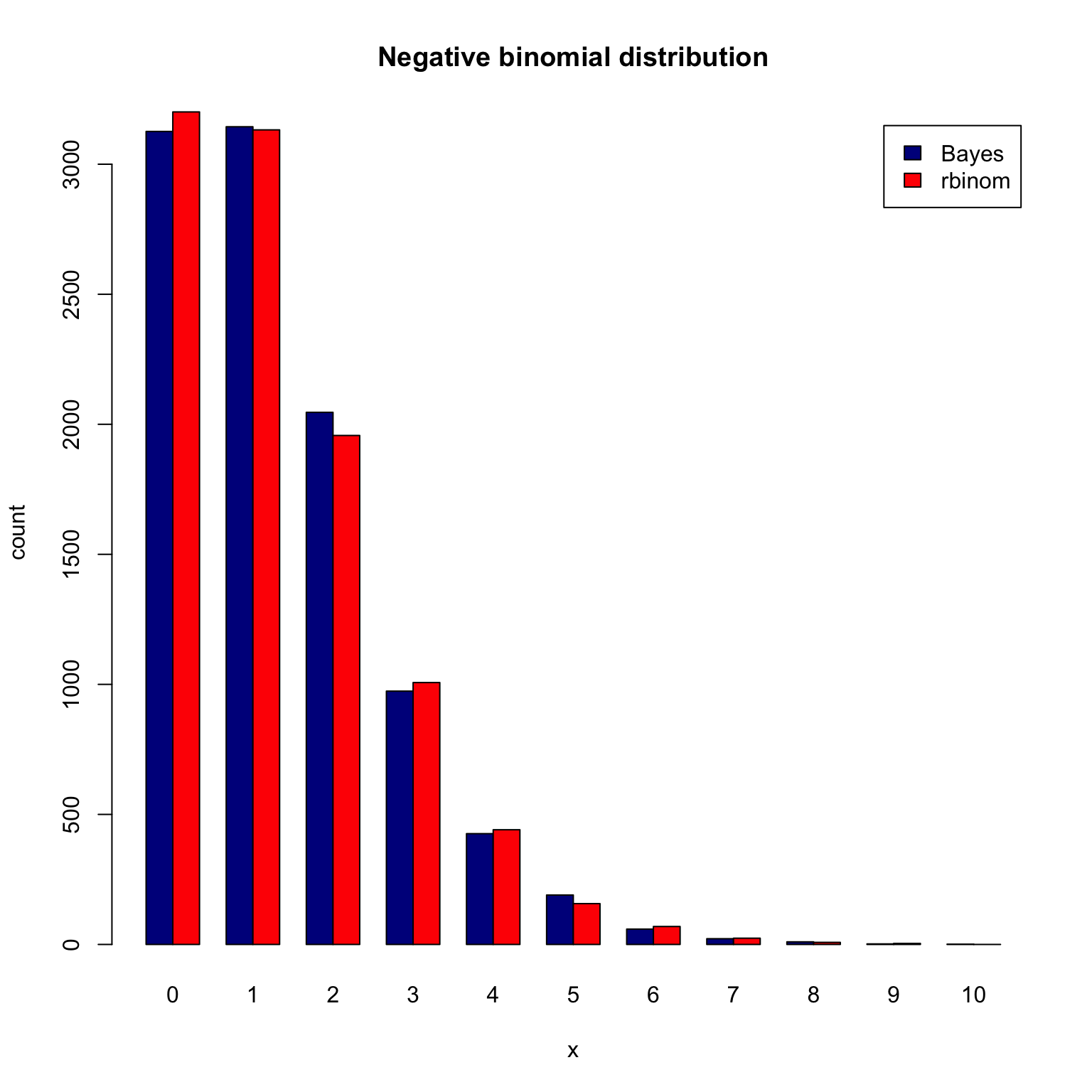

2.8 多元正态分布的随机数生成

2.8.1 多元正态分布随机数

对于协方差矩阵为单位矩阵的多元正态随机向量的随机数生成是容易的，但是如果要求不同分量之间的协方差（或相关系数）各异，则需要利用协方差矩阵的特征值分解来实现。具体算法如下：

• 计算协方差矩阵 $\pmb\Sigma$ 的特征值和特征向量，作特征分解 $\pmb\Sigma=\pmb V\pmb\Lambda\pmb V^{\textsf{T}}$；
• 计算变换矩阵 $\pmb C=\pmb V\pmb\Lambda^{1/2}\pmb V^{\textsf{T}}$；
• 生成标准正态随机向量 $\pmb Z$；
• 生成一般正态随机向量 $\pmb Y=\pmb\mu+\pmb C\pmb Z$。

由此得到的 $\pmb Y$ 服从多元正态分布 $MVN(\pmb\mu,\pmb\Sigma)$。

rmvn.eigen <- function(n, mu, Sigma) {
  d <- length(mu)
  ev <- eigen(Sigma, symmetric = TRUE)
  lambda <- ev$values
  V <- ev$vectors
  C <- V %*% diag(sqrt(lambda)) %*% t(V)
  Z <- matrix(rnorm(n*d), nrow = n, ncol = d)
  Y <- Z %*% C + matrix(mu, n, d, byrow = TRUE)
  return(Y)
}

mu <- c(0, 1)
Sigma <- matrix(c(1, .8, .8, 2), nrow = 2, ncol = 2)
X <- rmvn.eigen(5000, mu, Sigma)
cov(X)

##           [,1]      [,2]
## [1,] 1.0010328 0.8278887
## [2,] 0.8278887 2.0270493

由样本计算得到的协方差矩阵估计为 $\hat{\pmb\Sigma}=\left(\begin{array}{cc} 1.0010328 & 0.8278887\\ 0.8278887 & 2.0270493 \end{array}\right)$，这与真实参数基本一致，随机向量的分布图如下。

plot(X, main = 'Multivariate Normal', xlab = 'x', ylab = 'y', pch = 20)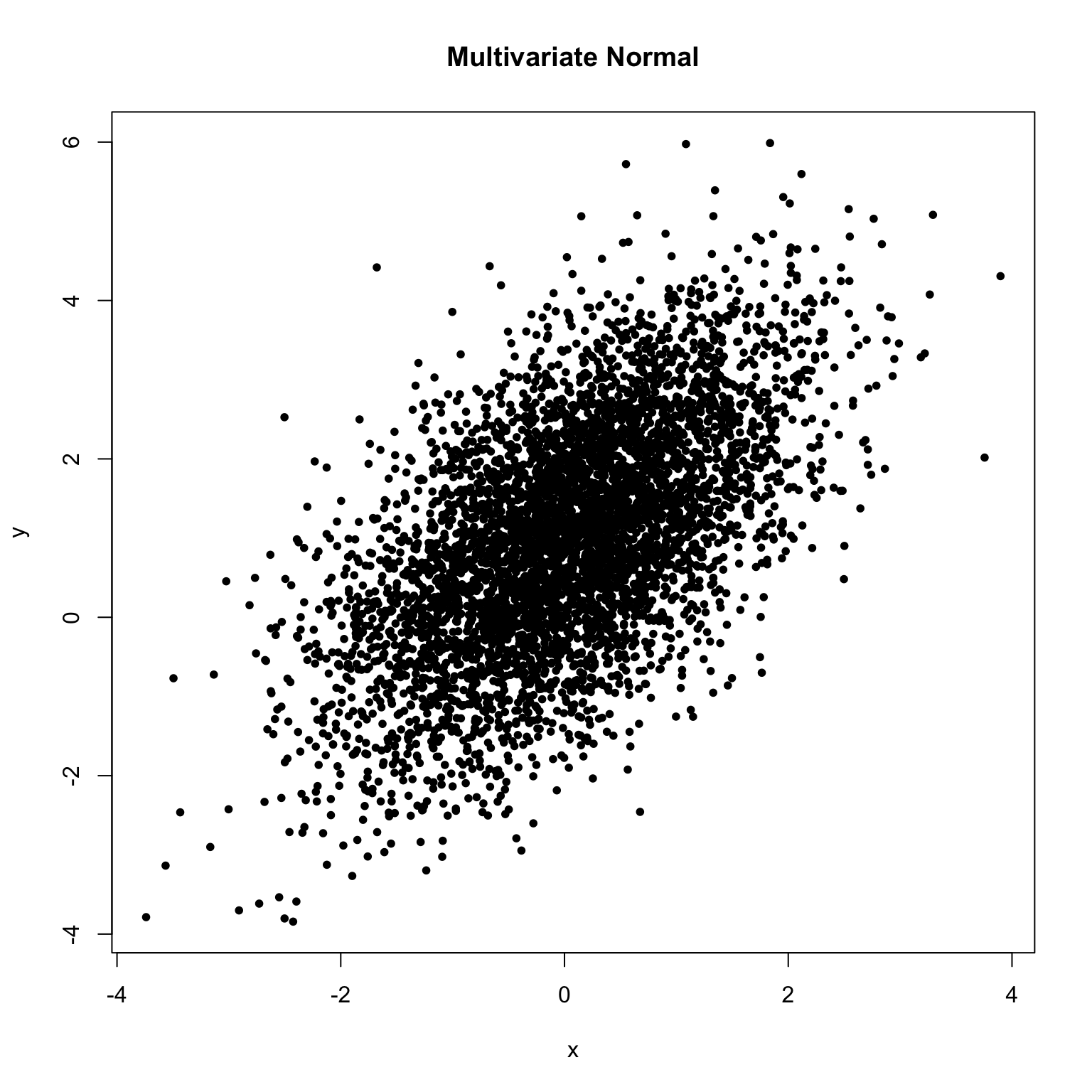

2.8.2 多元正态分布的混合

下面考虑多元正态分布的混合： $$pN_d(\pmb\mu_1,\pmb\Sigma_1)+(1-p)N_d(\pmb\mu_2,\pmb\Sigma_2).$$

library(MASS)
loc.mix <- function(n, p, mu1, mu2, Sigma) {
  n1 <- rbinom(1, size = n, prob = p)
  n2 <- n - n1
  x1 <- mvrnorm(n1, mu = mu1, Sigma)
  x2 <- mvrnorm(n2, mu = mu2, Sigma)
  X <- rbind(x1, x2)
  return(X[sample(1:n), ])
}

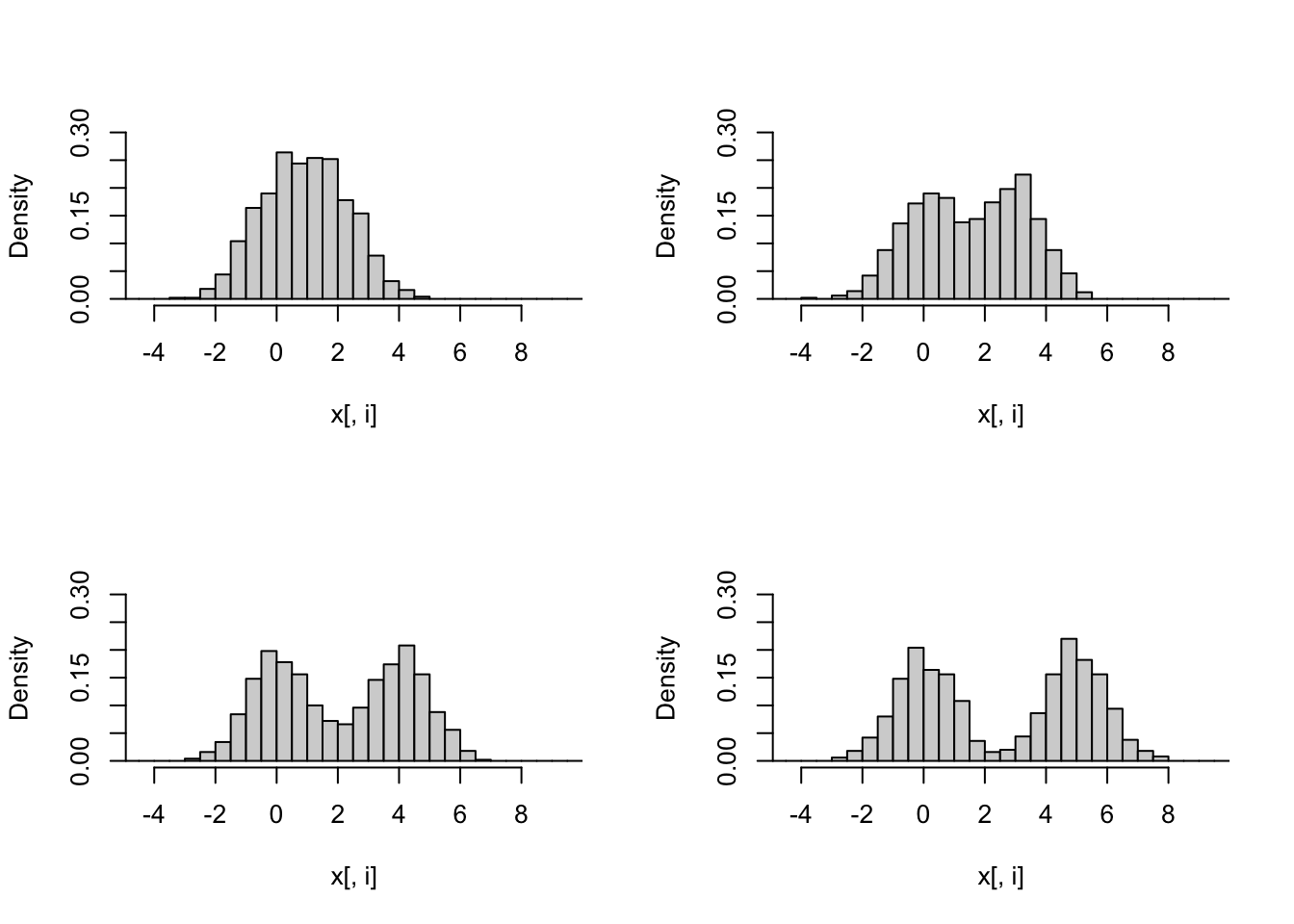
x <- loc.mix(1000, 0.5, rep(0, 4), 2:5, Sigma = diag(4))
r <- range(x) * 1.2
par(mfrow = c(2, 2))
for (i in 1:4) {
  hist(x[, i], xlim = r, ylim = c(0, 0.3), freq = FALSE,
       main = "", breaks = seq(-5, 10, 0.5))
}

2.8.3 Wishart分布

设 $\pmb X$ 是来自多元正态分布 $N_d(\pmb 0,\pmb\Sigma)$ 的 $n\times d$ 维数据矩阵，则 $\pmb W=\pmb X^\textsf{T}\pmb X$ 服从Wishart分布 $W_d(\pmb\Sigma,n)$，于是从Wishart分布中产生随机数可通过如下方式：

• 从 $N_d(\pmb 0,\pmb\Sigma)$ 中产生 $\pmb X$；
• 计算$\pmb W=\pmb X^\textsf{T}\pmb X$。

这种方法必须产生 $nd$ 个随机数来决定 $\dfrac{d(d+1)}{2}$ 个元素值，比较低效。一种效率更高的方法是基于Bartlett分解：令 $\pmb T=(\pmb T_{ij})_{d\times d}$ 为下三角矩阵，其元素满足：

1. $\pmb T_{ij}$ i.i.d. $\sim N(0,1)$, $i>j$；
2. $\pmb T_{ii}\sim\sqrt{\chi^2(n-i+1)}$, $i=1,\dots,d$。

则矩阵 $A=\pmb T\pmb T^\textsf{T}$ 服从 $W_d(\pmb I_d,n)$。因此产生 $W_d(\pmb\Sigma,n)$ 可以通过 $\pmb\Sigma$ 的Choleski分解 $\pmb\Sigma=\pmb L\pmb L^\textsf{T}$，则 $\pmb L\pmb A\pmb L^\textsf{T}\sim W_d(\pmb\Sigma,n)$。

rWish <- function(Sigma, n) {
  d <- nrow(Sigma)
  L <- chol(Sigma)
  T <- matrix(0, d, d)
  for (j in 1:d) {
    for (i in 1:d) { T[i, j] <- rnorm(1) }
    T[j, j] <- sqrt(rchisq(1, n - i + 1))
  }
  A = T %*% t(T)
  return(L %*% A %*% t(L))
}

rWish(diag(3), 5)

##             [,1]        [,2]        [,3]
## [1,]  1.15737726  0.01319342 -0.02769096
## [2,]  0.01319342  2.26241733 -2.81267965
## [3,] -0.02769096 -2.81267965  3.50889766

2.8.4 $d$ 维球面上的均匀分布

在 $d$ 维球面（即集合 $\{x\in\mathbb R^d:\|x\|^2=1\}$）上均匀分布的随机向量有相同的可能方向，产生此随机数可以基于如下性质：若 $X_1,\dots,X_d$ i.i.d. $N(0,1)$，则

$(U_1,\dots,U_d)$ 服从 $\mathbb R^d$ 中单位球面上的均匀分布，

其中 $U_j=\dfrac{X_j}{\|x\|}$, $j=1,\dots,d$。

runif.sphere <- function(n, d) {
  M <- matrix(rnorm(n * d), nrow = n, ncol = d)
  L <- apply(M, 1, function(x) {sqrt(sum(x*x))})
  D <- diag(1 / L)
  U <- D %*% M
  return(U)
}

X <- runif.sphere(200, 2)
par(pty = 's')
plot(X, xlab = bquote(x[1]), ylab = bquote(x[2]))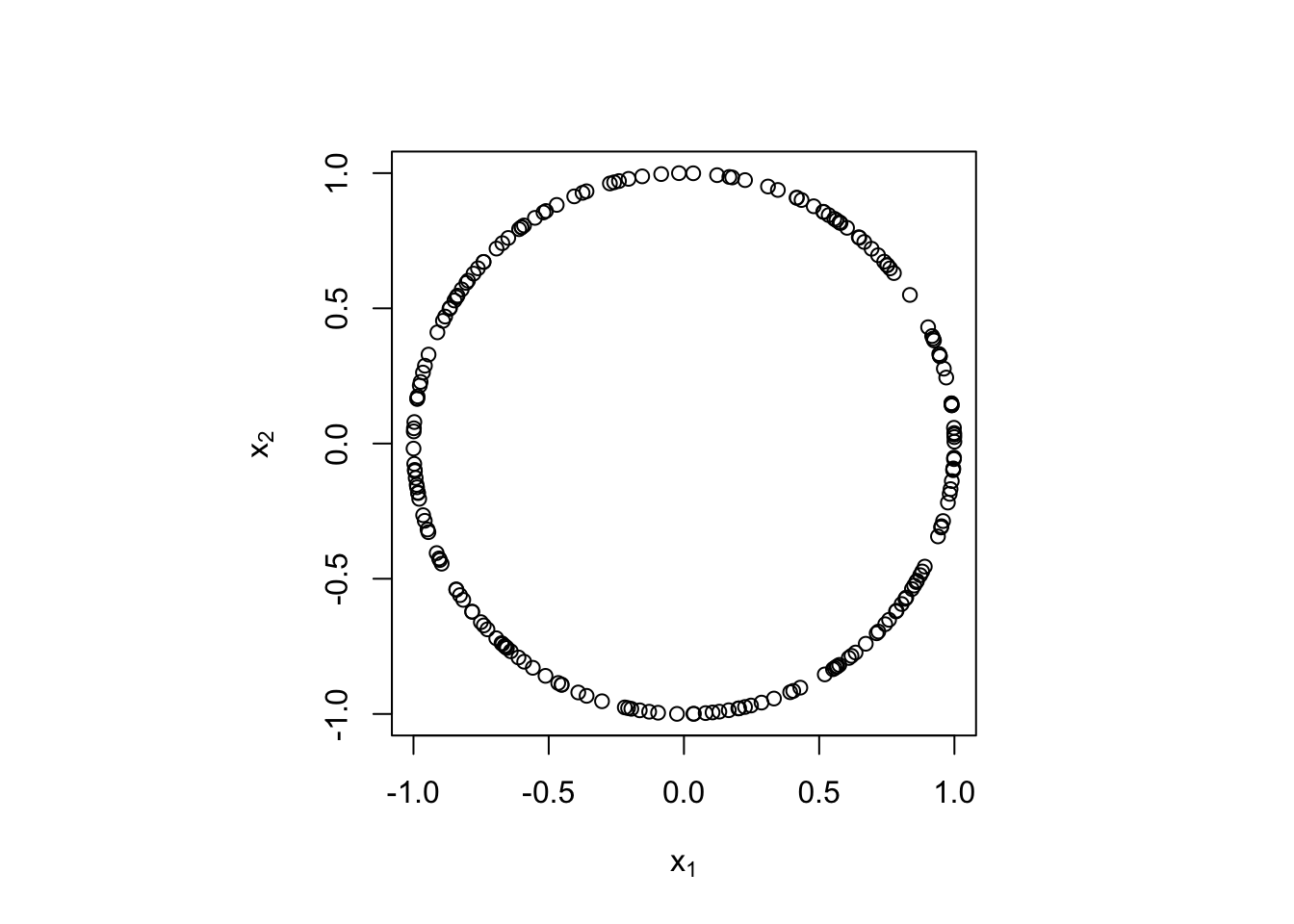

2.9 随机过程

2.9.1 齐次Poisson过程

对齐次Poisson过程，我们知道事件的到达时间间隔 $T_1,T_2,\dots$ 是i.i.d.的参数为速率 $\lambda$ 的指数分布随机变量，则第 $n$ 个事件的到达时刻为 $S_n=T_1+\cdots+T_n$，序列 $\{T_n\}_{n=1}^{\infty}$ 或 $\{S_n\}_{n=1}^{\infty}$ 可以表示过程的一个路径。当然也可以利用 $$(S_1,\dots,S_n\mid N(t)=n)\overset{d}{=}U_1,\dots,U_n,\quad U_i\sim U(0,t)$$ 这一性质来得到过程的一个路径。

为表示计数值，注意到 $N(t)$ 的等价表述为 $$N(t)=\min\{k:S_k>t\}-1.$$ 因此可以直接模拟齐次Poisson过程的状态。

lambda <- 2
t0 <- 3
Tn <- rexp(100, lambda)
Sn <- cumsum(Tn)
n <- min(which(Sn > t0))

n-1

## [1] 8

round(Sn[1:n], 4)

## [1] 0.0854 0.4220 0.4959 0.6602 0.9074 1.1398 1.5385 2.9762 3.5503

使用同分布的性质得到路径的方法如下。

lambda <- 2
t0 <- 3
upper <- 100
pp <- numeric(10000)
for (i in 1:10000) {
  N <- rpois(1, lambda * upper)
  Un <- runif(N, 0, upper)
  Sn <- sort(Un)
  n <- min(which(Sn > t0))
  pp[i] <- n - 1
}
c(mean(pp), var(pp))

## [1] 6.005100 5.978472

这个结果与理论 $\mathbb E(N(t))=\lambda t$ 和 $\text{Var}(N(t))=\lambda t$ 是一致的。

2.9.2 非齐次Poisson过程

考虑强度函数 $\lambda(t)$ 有界的非齐次Poisson过程，记 $\lambda(t)\leq\lambda_0<\infty$。考虑从强度为 $\lambda_0$ 的齐次Poisson过程中抽样，在时刻 $t$ 发生的事件以概率 $\lambda(t)/\lambda_0$ 被接受，则最终得到的计数过程就是强度为 $\lambda(t)$ 的非齐次Poisson过程。

例如 $\lambda(t)=3\cos^2(t)\leq3=\lambda_0$，因此第 $j$ 个到达时刻 $S_j$ 当 $U_j\leq\cos^2(S_j)$ 时被接受。

lambda <- 3
upper <- 100
N <- rpois(1, lambda * upper)
Tn <- rexp(N, lambda)
Sn <- cumsum(Tn)
Un <- runif(N)
keep <- (Un <= cos(Sn)^2)
res <- Sn[keep]

过程在时间 $[0,t)$ 内的样本轨道就可以如下计算。

round(res[which(res < 4)], 4)

## [1] 0.2236 0.4474 0.5056 2.3284 3.9053

2.9.3 更新过程

一般地，如果一个计数过程 $\{N(t),t\geq0\}$ 的到达时间间隔 $T_1,T_2,\dots$ 是i.i.d.的，则称之为更新过程。

例如，假设到达时间间隔服从参数为 $p$ 的几何分布，因此 $S_j=T_1+\cdots+T_j$ 服从参数为 $(j,p)$ 的负二项分布，考虑更新过程的计算如下。

t0 <- 5
Tn <- rgeom(100, prob = 0.2)
Sn <- cumsum(Tn)
min(which(Sn > t0)) - 1

## [1] 2

Nt0 <- replicate(1000, expr = {
  Sn <- cumsum(rgeom(100, prob = 0.2))
  min(which(Sn > t0)) - 1
})
table(Nt0) / 1000

## Nt0
##     0     1     2     3     4     5     6     7     8    10 
## 0.273 0.336 0.195 0.115 0.048 0.016 0.011 0.004 0.001 0.001

其均值函数 $\mathbb E[N(t)]$ 可通过如下估计。

t0 <- seq(0.1, 30, 0.1)
mt <- numeric(length(t0))
for (i in 1:length(t0)) {
  mt[i] <- mean(replicate(100, expr = {
    Sn <- cumsum(rgeom(100, prob = 0.2))
    min(which(Sn > t0[i])) - 1
  }))
}
plot(t0, mt, type = "l", xlab = "t", ylab = "mean")
abline(0, 0.25)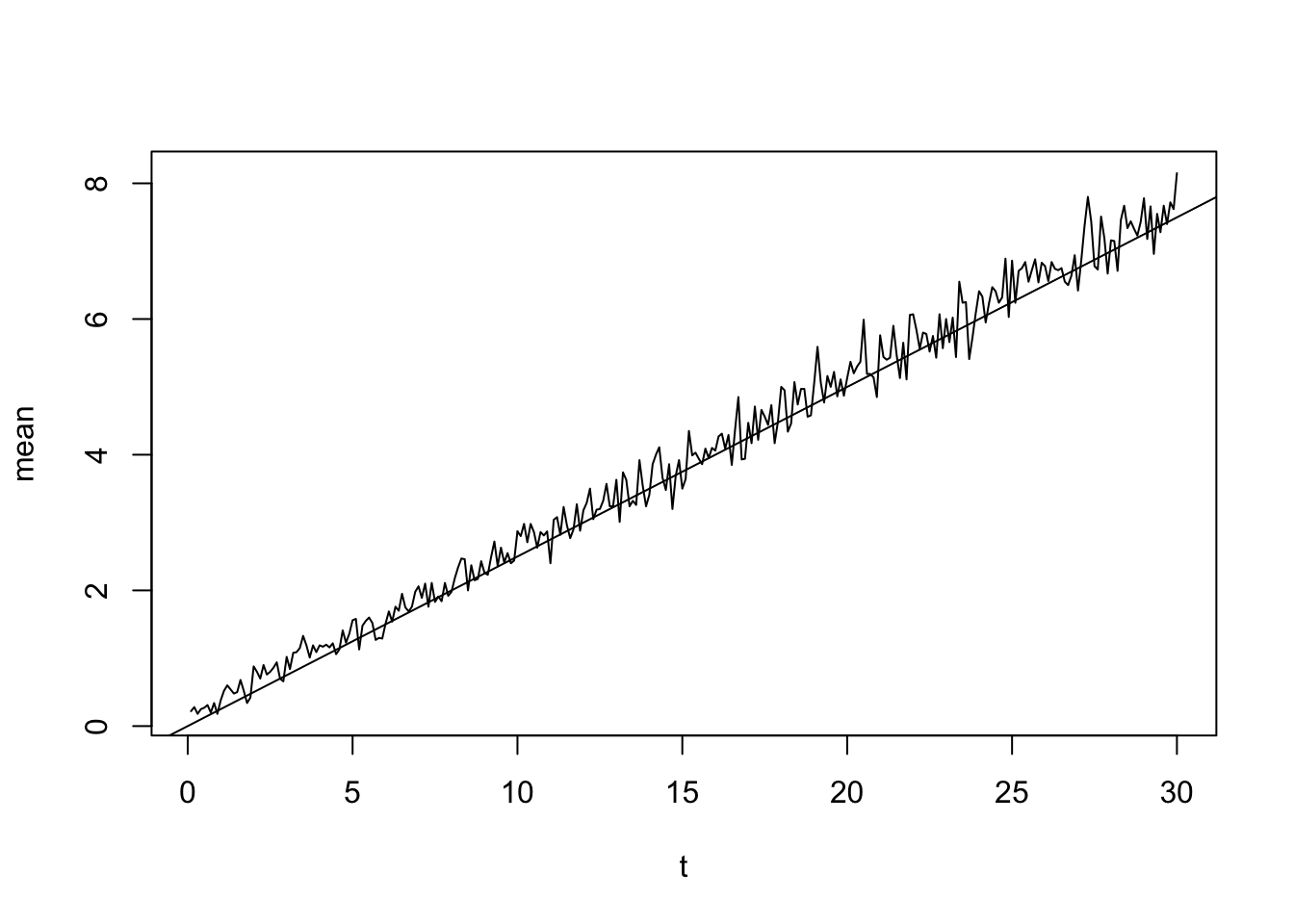

注：在这个例子中 $p=0.2$，则对于齐次Poisson过程而言，平均到达时间间隔为 $0.8/0.2=4$，因此均值函数为 $t/4$。

2.9.4 对称的随机游走

设 $X_1,X_2,\dots$ 是一列i.i.d.的 $B(1,0.5)$ 随机变量，令 $\displaystyle S_n=\sum_{i=1}^nX_i$，以及 $S_0=0$，则过程 $\{S_n;n\geq0\}$ 称为对称的随机游走。从定义中就可以很容易地得到对称随机游走的模拟实现。

n <- 500
incr <- sample(c(-1, 1), size = n, replace = TRUE)
S <- as.integer(c(0, cumsum(incr)))
plot(0:n, S, type = "l", main = "", xlab = "i")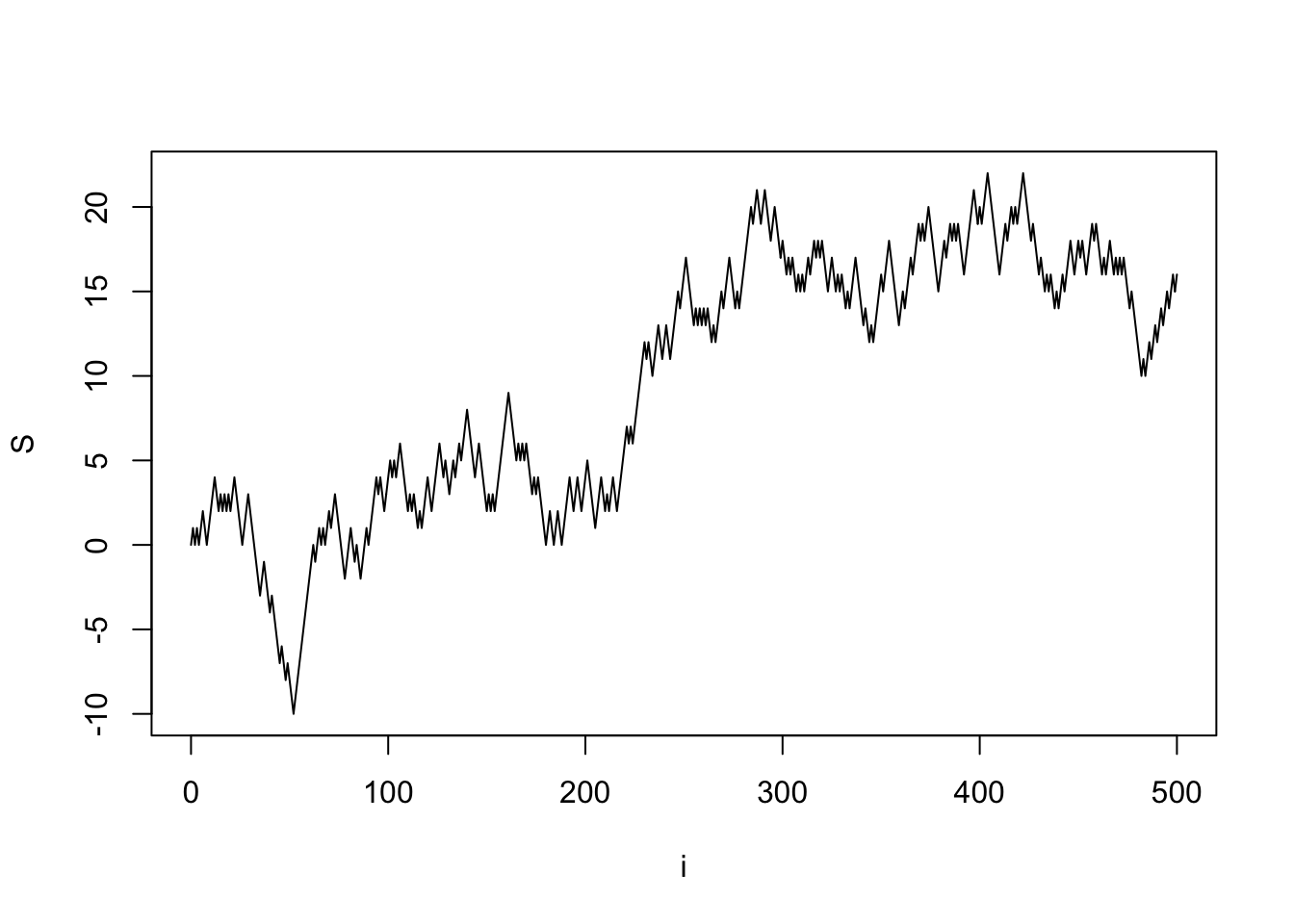

如果需要的是过程 $S_n$ 在时间 $n$ 时刻的状态，而不是历史值，对比较大的 $n$，上述方式效率不是很高。可以考虑过程的Markov性，假设 $S_0=0$ 为过程的初始状态，令 $T$ 为过程首次返回到0的时刻，则我们只需要产生等待时间 $T$，直到总时间首次超过 $n$，然后从 $n$ 时刻之前的最近一次返回到0的时刻开始产生增量 $X_i$ 再相加即可。

根据随机过程的相关知识，可求得 $T$ 的分布为 $$p_{2n}=\mathbb P(T=2n)=\text{C}_{2n-2}^{n-1}\dfrac{1}{n\cdot2^{2n-1}}=\dfrac{\Gamma(2n-1)}{n\cdot2^{2n-1}\Gamma^2(n)},~n\geq1;\quad p_{2n+1}=0,~\forall n\geq0.$$ 给出如下算法：令 $W_j$ 为第 $j$ 次返回初始位置需要的等待时间，

• 设置 $W_1=0$
• 对满足 $W_j\leq n$ 的 $j=1,2,\dots$,
  • 从时间的分布中产生 $T_j$, 直至首次返回到0.
  • 令 $W_j=T_1+\cdots+T_j$.
• 令 $t_0=W_j-T_j$, 设置 $s_1=0$.
• 产生从 $t_0+1$ 到时刻 $n$ 的增量. 对 $i=1,2,\dots,n-t_0$,
  • 产生随机增量 $x_i\sim \mathbb P(X=\pm1)=0.5$.
  • 设置 $s_i=x_1+\cdots+x_i$.
  • 若 $s_i=0$, 设置计数器为 $i=1$.
• 返回 $s_i$.

注意到 $p_{2n}=\dfrac{1}{2n}\mathbb P(X=n-1)$, $X\sim B(2n-2,0.5)$, 因此可以直接计算

n <- 1:10000
p2n <- exp(lgamma(2 * n - 1) - log(n) - (2 * n - 1) * log(2) - 2 * lgamma(n))

也可以使用二项分布来计算

P2n <- 0.5 / n * dbinom(n - 1, size = 2 * n - 2, prob = 0.5)

pP2n <- cumsum(P2n)
u <- runif(1)
Tj <- 2 * (1 + sum(u > pP2n))
n <- 200
sumT <- 0
while (sumT <= n) {
  u <- runif(1)
  Tj <- 2 * (1 + sum(u > pP2n))
  sumT <- sumT + Tj
}
sumT - Tj

## [1] 156

然后从这个值开始（$S_{156}=0$）产生对称随机游走随机数即可。（注意：期间到达0的时刻应当被舍去。）

start <- sumT - Tj
sumincr <- 0
while (start < n) {
  incr <- sample(c(-1, 1), size = 1)
  sumincr <- sumincr + incr
  if (sumincr == 0) { sumincr <- sumincr - incr }
  else { start <- start + 1 }
}
sumincr

## [1] -4