Chapter 5 Bootstrap,Jackknife和Permutation
5.1 Bootstrap
5.1.1 Bootstrap估计
Bootstrap是一类非参数蒙特卡洛方法,它主要通过重采样来估计总体的分布,对总体分布没有做假设,这也是非参数的重要特点。一般地,Bootstrapping方法的模式图如下:\[\begin{array}{l} F\rightarrow\pmb X\leftrightarrow F_n\rightarrow\hat{\theta}\quad(\text{real data}),\\ F_n\rightarrow\pmb X^\star\leftrightarrow F_n^\star\rightarrow\hat{\theta}_n^\star\quad(\text{resampling data}). \end{array}\]
因此,算法的流程如下:
- 给定原始样本 \(x_1,\dots,x_n\) 和参数 \(\theta\) 的估计量 \(\hat{\theta}\).
- 对第 \(b(b=1,\dots,B)\) 次Bootstrap:
- 通过对观测样本 \(\{x_1,\dots,x_n\}\) 有放回抽样得到样本 \(\pmb x_{(b)}^\star=\{x_{b1}^\star,\dots,x_{bn}^\star\}\);
- 利用这个样本计算 \(\theta\) 的估计值 \(\hat{\theta}_{(b)}^\star\).
- \(F_{\hat{\theta}}(\cdot)\) 的Bootstrap估计就是 \(\hat{\theta}_{(1)}^\star,\dots,\hat{\theta}_{(B)}^\star\) 的经验分布函数。
这一过程是具有理论保障的。事实上,在一定的正则条件下,当 \(n\rightarrow\infty\) 时,\[\sup_x\left\vert\mathbb P\big(\sqrt{n}(\hat{\theta}^\star-\hat{\theta}-\mathbb E(\hat{\theta}-\theta_0))\leq x\mid\pmb X\big)-\mathbb P\big(\sqrt{n}(\hat{\theta}-\theta_0-\mathbb E(\hat{\theta}-\theta_0))\leq x\big)\right\vert\overset{P}{\rightarrow}0.\]
5.1.2 Bootstrap估计偏差与标准误差
估计的偏差\[\mathbb E(\hat{\theta})-\theta_0\approx\mathbb E(\hat{\theta}^\star-\hat{\theta}\mid\pmb X)=\mathbb E(\hat{\theta}^\star\mid\pmb X)-\hat{\theta}\]可以用 \(\overline{\theta}^\star-\hat{\theta}\) 来估计,其中\[\overline{\theta}^\star=\frac{1}{B}\sum_{b=1}^B\hat{\theta}_{(b)}^\star\] 是 \(\hat{\theta}^\star\) 的样本均值。而 \(\hat{\theta}\) 的标准误差可以用 \(\hat{\theta}^\star\) 的样本标准误差来估计:\[\sqrt{\frac{1}{B-1}\sum_{b=1}^B(\hat{\theta}_{(b)}^\star-\overline{\theta}^\star)^2}.\]
考虑有限样本\[x=\{2,2,1,1,5,4,4,3,1,2\}.\] 感兴趣参数为均值,利用如下代码可以实现Bootstrap估计。
x <- c(2, 2, 1, 1, 5, 4, 4, 3, 1, 2)
theta <- mean(x)
B <- 10000
thetastar <- numeric(B)
for (b in 1:B) {
xstar <- sample(x, replace = TRUE)
thetastar[b] <- mean(xstar)
}
round(c(bias = mean(thetastar) - theta,
se.boot = sd(thetastar),
se.sample = sd(x) / sqrt(length(x))), 4) bias se.boot se.sample
-0.0027 0.4266 0.4534 可以看到估计的偏差很低,而且Bootstrap标准误差与实际标准误差十分接近。
hist(thetastar)
abline(v = theta, col = 'red', lwd = 2)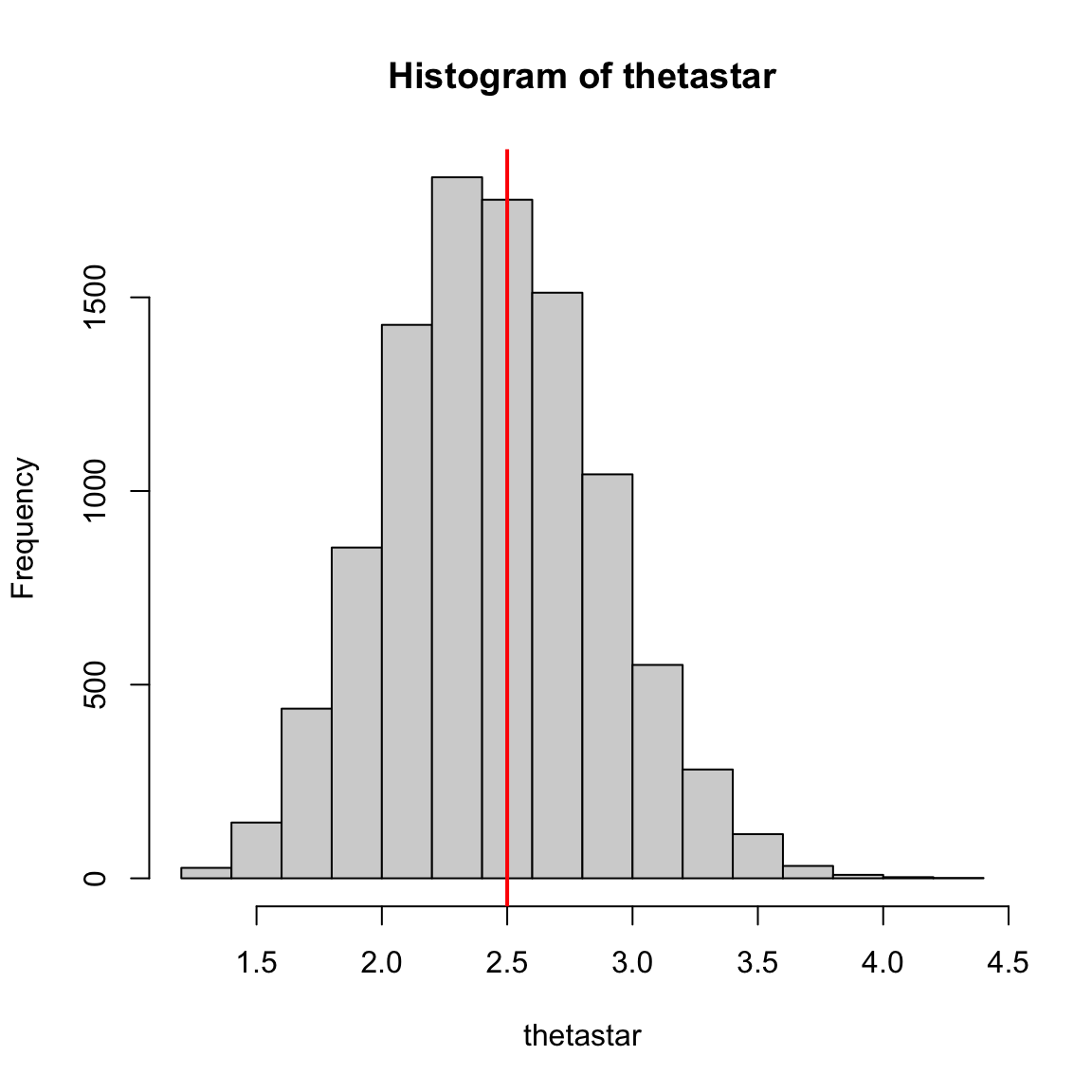
此外,利用boot包里的boot函数也可以实现Bootstrap。注意boot函数中的参数statistic是一个函数,用于返回感兴趣的统计量的值,它必须至少有两个参数,其中第一个是数据,第二个表示Bootstrap抽样中的指标向量、频率或权重等。
library(boot)
library(MASS)
b.cor <- function(x, i) { cor(x[i,1], x[i,2]) }
# zero mean the corvariance matrix
set.seed(12345)
n <- 100
x <- mvrnorm(n, rep(0, 2), matrix(c(1, 0.8, 0.8, 1), 2))
obj <- boot(data = x, statistic = b.cor, R = 1000)
round(c(original = obj$t0,
bias = mean(obj$t) - obj$t0,
se.boot = sd(obj$t)), 4)## original bias se.boot
## 0.8338 -0.0022 0.0304对协方差的原始估计不准是因为产生的样本只有100个,但是Bootstrap的效率很高,估计的偏差很低。
又如,假设 \(x=(x_1,\dots,x_{10})\sim N(\mu,\sigma^2)\),利用如下代码可以求 \(\sigma^2\) 的估计量 \(\hat{\sigma}^2=\dfrac{1}{n}\sum\limits_{i=1}^n(x_i-\overline{x})^2\) 的Bootstrap偏差。
n <- 10
x <- rnorm(n, mean = 0, sd = 10)
sigma2.hat <- (n - 1) * var(x) / n
# Bootstrap
B <- 1000
sigma2.b <- numeric(B)
for (b in 1:B) {
i <- sample(1:n, size = n, replace = TRUE)
sigma2.b[b] <- (n - 1) * var(x[i]) / n
}
bias <- mean(sigma2.b) - sigma2.hat
bias## [1] -4.730601可以看到 \(\hat{\sigma}^2\) 低估了参数 \(\sigma^2\)。
5.1.3 Bootstrap置信区间
一般而言,标准Bootstrap置信区间是最简单的方法,但有时候它往往并不是最优的。根据中心极限定理可知置信水平为 \(1-\alpha\) 的近似置信区间为\[(\hat{\theta}-z_{\alpha/2}\hat{\text{se}}(\hat{\theta}),\hat{\theta}+z_{\alpha/2}\hat{\text{se}}(\hat{\theta})),\] 其中 \(z_{\alpha/2}\) 是标准正态分布的上 \(\alpha/2\) 分位数。
学生化Bootstrap置信区间是对上述方法的修正,它对应置信水平为 \(1-\alpha\) 的近似置信区间为\[(\hat{\theta}-t_{\alpha/2}\hat{\text{se}}(\hat{\theta}),\hat{\theta}+t_{\alpha/2}\hat{\text{se}}(\hat{\theta})),\]
其中 \(t_{\alpha/2}\) 是 \((\hat{\theta}^{(b)}-\hat{\theta})/\hat{\text{se}}(\hat{\theta}^{(b)})\) 的上 \(\alpha/2\) 分位数,注意 \(\hat{\text{se}}(\hat{\theta}^{(b)})\) 涉及到二次重采样。
基本Bootstrap置信区间通过对重采样样本减去观察到的统计量来得到转换后的分布,利用此得到置信区间。具体来说,注意到 \(\hat{\theta}^\star-\hat{\theta}\mid\pmb X\) 和 \(\hat{\theta}-\theta\) 具有相同的极限分布,因此置信水平为 \(1-\alpha\) 的置信区间为\[(\hat{\theta}-F^{-1}(1-\alpha/2),\hat{\theta}-F^{-1}(\alpha/2)),\] 其中 \(F^{-1}(x)\) 可以用 \(\hat{\theta}^\star-\hat{\theta}\) 的 \(x\) 分位数 \(\hat{\theta}_{x}^\star-\hat{\theta}\) 来估计,因此最终置信水平为 \(1-\alpha\) 的近似置信区间为\[(2\hat{\theta}-\hat{\theta}_{1-\alpha/2}^\star,2\hat{\theta}-\hat{\theta}_{\alpha/2}^\star).\]
分位数Bootstrap置信区间直接利用重采样样本的经验分布作为建议分布,将其分位数作为 \(\hat{\theta}\) 的分位数估计,得到置信水平为 \(1-\alpha\) 的近似置信区间 \[(\hat{\theta}_{\alpha/2}^\star,\hat{\theta}_{1-\alpha/2}^\star).\]
偏差修正和加速(BCa)置信区间 \((\hat{\theta}_{\alpha_1}^\star,\hat{\theta}_{\alpha_2}^\star)\) 对上述分位数进行了修正:\[\alpha_1=\Phi\left(\hat{z}_0+\frac{\hat{z}_0-z_{\alpha/2}}{1-\hat{a}(\hat{z}_0-z_{\alpha/2})}\right),\quad\alpha_2=\Phi\left(\hat{z}_0+\frac{\hat{z}_0+z_{\alpha/2}}{1-\hat{a}(\hat{z}_0+z_{\alpha/2})}\right),\] 其中 \(\displaystyle\hat{z}_0=\Phi^{-1}\left(\dfrac{1}{B}\sum_{b=1}^BI(\hat{\theta}_{(b)}^\star<\hat{\theta})\right)\) 是偏差修正项,\(\hat{a}=\dfrac{\sum\limits_{i=1}^n(\overline{\theta}_{(\cdot)}^\star-\theta_{(i)})^3}{6\left(\sum\limits_{i=1}^n(\overline{\theta}_{(\cdot)}^\star-\theta_{(i)})^2\right)^{3/2}}\) 是偏度(加速项)。
BCa置信区间具有良好的性质:
- 不变性,即若 \(\theta\) 的置信区间为 \((\hat{\theta}_{\alpha_1}^\star,\hat{\theta}_{\alpha_2}^\star)\),\(g(\cdot)\) 为一一变换函数,则 \(g(\theta)\) 的置信区间为 \((g(\hat{\theta}_{\alpha_1}^\star),g(\hat{\theta}_{\alpha_2}^\star))\);
- 二阶精确性,即误差以 \(1/n\) 的速度趋于0.
上述置信区间都可以用boot::boot.ci得到对应的结果。
library(boot)
set.seed(12345)
mu <- 1; b <- 1; n <- 10; m <- 100
boot.median <- function(x, i) { median(x[i]) }
ci.norm <- ci.basic <- ci.perc <- ci.bca <- matrix(NA, m, 2)
for (i in 1:m) {
U <- runif(n, -0.5, 0.5)
R <- mu - b * sign(U) * log(1 - 2 * abs(U))
de <- boot(data = R, statistic = boot.median, R = 500)
ci <- boot.ci(de, type = c("norm", "basic", "perc", "bca"))
ci.norm[i,] <- ci$norm[2:3]
ci.basic[i,] <- ci$basic[4:5]
ci.perc[i,] <- ci$perc[4:5]
ci.bca[i,] <- ci$bca[4:5]
}
cat("norm =", mean(ci.norm[, 1] <= mu & ci.norm[, 2] >= mu),
"basic =", mean(ci.basic[, 1] <= mu & ci.basic[, 2] >= mu),
"perc =", mean(ci.perc[, 1] <= mu & ci.perc[, 2] >= mu),
"bca =", mean(ci.bca[, 1] <= mu & ci.bca[, 2] >= mu))norm = 0.95 basic = 0.9 perc = 0.93 bca = 0.92可以看到只有正态置信区间的覆盖概率都高于95%,其余都低于95%。
5.2 Jackknife
5.2.1 Jackknife估计
Jackknife类似于交叉验证方法中的“留一(leave-one-out)交叉验证”。令 \(x=(x_1,\dots,x_n)\) 为观测到的样本,定义第 \(i\) 个Jackknife样本为丢掉第 \(i\) 个样本后的剩余样本,即\[x_{(i)}=(x_1,\dots,x_{i-1},x_{i+1},\dots,x_n).\] 若 \(\hat{\theta}=T_n(x)\),则第 \(i\) 个Jackknife重复为 \(\hat{\theta}_{(i)}=T_{n-1}(x_{(i)})\),\(i=1,\dots,n\)。
5.2.2 Jackknife估计偏差与标准误差
对偏差 \(\mathbb E(\hat{\theta})-\theta_0\) 的无偏估计为\[(n-1)(\overline{\hat{\theta}}_{(\cdot)}-\hat{\theta}),\] 其中 \(\overline{\hat{\theta}}_{(\cdot)}=\dfrac{1}{n}\sum\limits_{i=1}^n\hat{\theta}_{(i)}\)。
下面以 \(\theta\) 为总体方差为例来说明为什么偏差的Jackknife估计中系数是 \(n-1\)。注意到方差的plug-in估计\[\hat{\theta}=\dfrac{1}{n}\sum_{i=1}^n(x_i-\overline{x})^2\] 是 \(\sigma^2\) 的无偏估计,其偏差为\[\text{bias}(\hat{\theta})=\mathbb E(\hat{\theta})-\sigma^2=-\dfrac{\sigma^2}{n}.\] 由于每个Jackknife估计是基于样本量为 \(n-1\) 的样本构造的,因此Jackknife重复 \(\hat{\theta}_{(i)}\) 的估计偏差为 \(-\dfrac{\sigma^2}{n-1}=\dfrac{n}{n-1}\text{bias}(\hat{\theta})\),从而\[\mathbb E[\hat{\theta}_{(i)}-\hat{\theta}]=\text{bias}(\hat{\theta}_{(i)})-\text{bias}(\hat{\theta})=\dfrac{\text{bias}(\hat{\theta})}{n-1}.\] 所以在Jackknife偏差估计中的系数为 \(n-1\)。
对标准差 \(\text{se}(\hat{\theta})\) 的无偏估计为\[\widehat{\text{se}}(\hat{\theta})=\sqrt{\dfrac{n-1}{n}\sum_{i=1}^n(\hat{\theta}_{(i)}-\overline{\hat{\theta}}_{(\cdot)})^2}.\]
下面以 \(\theta\) 为总体均值为例来说明为什么标准差的Jackknife估计中系数是 \(\dfrac{n-1}{n}\)。注意到样本均值 \(\hat{\theta}=\overline{x}\) 的方差估计为\[\widehat{\text{Var}}(\hat{\theta})=\dfrac{\hat{\sigma}^2}{n}=\dfrac{1}{n(n-1)}\sum_{i=1}^n(x_i-\overline{x})^2.\] 注意到 \(\hat{\theta}_{(i)}=\dfrac{n\overline{x}-x_i}{n-1}\),于是 \[\overline{\hat{\theta}}_{(\cdot)}=\dfrac{1}{n}\sum\limits_{i=1}^n\hat{\theta}_{(i)}=\hat{\theta},\quad\hat{\theta}_{(i)}-\overline{\hat{\theta}}_{(\cdot)}=\dfrac{\overline{x}-x_i}{n-1},\] 所以在Jackknife标准差估计中的系数为 \(\dfrac{n-1}{n}\)。
例如,在之前那个估计多元正态随机变量相关系数的例子中,考虑使用Jackknife估计如下。
library(MASS)
set.seed(12345)
n <- 100
x <- mvrnorm(n, rep(0, 2), matrix(c(1, 0.8, 0.8, 1), 2))
theta.hat <- b.cor(x, 1:n)
theta.jack <- numeric(n)
for (i in 1:n) {
theta.jack[i] <- b.cor(x,(1:n)[-i])
}
theta.jack.mean <- mean(theta.jack)
bias.jack <- (n - 1) * (theta.jack.mean - theta.hat)
se.jack <- sqrt((n - 1) * mean((theta.jack - theta.jack.mean)^2))
round(c(original = theta.hat, bias.jack = bias.jack, se.jack = se.jack, se.boot = sd(obj$t)), 4)## original bias.jack se.jack se.boot
## 0.8338 -0.0012 0.0297 0.0304可以看到Jackknife估计比Bootstrap估计要稍好一些。
5.2.3 Jackknife失效情形
如果估计量 \(\hat{\theta}\) 不够平滑,Jackknife方法可能就会失效。中位数就是一个不平滑统计量的例子。
n <- 100; m <- 100
M <- numeric(n)
var.jack <- var.boot <- est <- numeric(m)
b.median <- function(x, i) { median(x[i]) }
for (k in 1:m) {
x <- rnorm(n)
est[k] <- median(x)
for (i in 1:n) { M[i] <- median(x[-i]) }
M.mean <- mean(M)
var.jack[k] <- (n - 1) * mean((M - M.mean)^2)
var.boot[k] <- var(boot(x, b.median, R = 500)$t)
}
round(c(v.emp = var(est), v.boot = mean(var.boot), v.jack = mean(var.jack)), 4)## v.emp v.boot v.jack
## 0.0154 0.0162 0.0243可以看到Jackknife估计和Bootstrap估计和经验估计相差甚远,这显然是失效了。
5.3 Jackknife-after Bootstrap
前面介绍了使用一个估计量的偏差和标准差的Bootstrap估计,这些估计本身又是统计量,这些估计量的方差就可以用Jackknife方法来估计。
注意到 \(\hat{\text{se}}(\hat{\theta})\) 是 \(B\) 次 \(\hat{\theta}\) 的Bootstrap重复统计量的样本标准差,如果我们丢掉第 \(i\) 个样本,则Jackknife算法就是对每个 \(i\),从剩下的 \(n-1\) 个样本值中再抽样 \(B\) 次,来计算 \(\hat{\text{se}}(\hat{\theta}_{(i)})\),即一个Jackknife重复。最终得到\[\hat{\text{se}}(\hat{\text{se}}_B(\hat{\theta}))=\sqrt{\dfrac{n-1}{n}\sum_{i=1}^n(\hat{\text{se}}_{B(i)}(\hat{\theta})-\overline{\hat{\text{se}}}_{B(\cdot)}(\hat{\theta}))^2},\] 其中 \(\overline{\hat{\text{se}}}_{B(\cdot)}(\hat{\theta})=\dfrac{1}{n}\sum\limits_{i=1}^n\hat{\text{se}}_{B(i)}(\hat{\theta})\)。
不过,这样做效率比较低,我们有方法可以避免重复Bootstrap。
记 \(x_i^*=(x_1^*,\dots,x_n^*)\) 为一次Bootstrap抽样,\(x_1^*,\dots,x_B^*\) 表示样本大小为 \(B\) 的Bootstrap样本。令 \(J(i)\) 为Bootstrap样本中不含 \(x_i\) 的那些样本指标,\(B(i)\) 为不含 \(x_i\) 的Bootstrap样本个数,因此我们可以使用丢掉 \(B-B(i)\) 个含有 \(x_i\) 的样本后其余的样本来计算一个Jackknife重复,故标准差估计量的Jackknife估计为\[\hat{\text{se}}_{jack}(\hat{\text{se}}_B(\hat{\theta}))=\sqrt{\dfrac{n-1}{n}\sum_{i=1}^n(\hat{\text{se}}_{B(i)}-\overline{\hat{\text{se}}}_{B(\cdot)})^2},\] 其中 \(\displaystyle\hat{\text{se}}_{B(i)}=\sqrt{\dfrac{1}{B(i)}\sum_{j\in J(i)}[\hat{\theta}_{(j)}-\overline{\hat{\theta}}_{(J(i))}]^2}\), \(\displaystyle\overline{\hat{\theta}}_{(J(i))}=\dfrac{1}{B(i)}\sum_{j\in J(i)}\hat{\theta}_{(j)}\)。
还是以之前那个估计多元正态随机变量相关系数的例子为例。
library(MASS)
set.seed(12345)
n <- 100
x <- mvrnorm(n, rep(0, 2), matrix(c(1, 0.8, 0.8, 1), 2))
B <- 1000
theta.boot <- numeric(B)
# set up storage for the sampled indices
indices <- matrix(0, nrow = B, ncol = n)
# jackknife-after-bootstrap step 1: run the bootstrap
for (b in 1:B) {
i <- sample(1:n, size = n, replace = TRUE)
theta.boot[b] <- b.cor(x, i)
# save the indices for the jackknife
indices[b, ] <- i
}
# jackknife-after-bootstrap to est. se(se)
se.jack <- numeric(n)
for (i in 1:n) {
# in i-th replicate omit all samples with x[i]
keep <- (1:B)[apply(indices, 1, function(k) { !any(k == i) })]
se.jack[i] <- sd(theta.boot[keep])
}
se.jack.mean <- mean(se.jack)
se.se.boot <- sqrt((n - 1) * mean((se.jack - se.jack.mean)^2))
round(c(se.boot = sd(theta.boot), se.se.boot = se.se.boot), 4)## se.boot se.se.boot
## 0.0314 0.01025.4 Jackknife的应用:交叉验证
交叉验证(Cross Validation)是一种分割数据方法,可以用来验证参数估计的稳健性、分类算法的准确度、模型的合理性(惩罚项调节参数 \(\lambda\) 的选取)等等。Jackknife可以被视作是交叉验证的一种特例,其主要用于估计偏差和估计量的标准差。
最简单的交叉验证方法是所谓的hold out方法,其基本思想是:将数据随机分成训练集和验证集,然后仅使用训练集对样本进行建模,再通过验证集来对模型进行评估。但这种方法依赖于数据的分隔方式,结果容易出现波动性。
\(k\)-折交叉验证是对hold out方法的改进,其基本思想是:将数据分成 \(k\) 个子集,然后重复hold out方法 \(k\) 次,每次第 \(i\) 个子集被作为验证集,而其他 \(k-1\) 个子集被作为训练集进行建模,最后计算 \(k\) 次的平均误差。
前面所介绍的Jackknife(Leave-one-out)实际上就是 \(n\)-折交叉验证,计算的时间复杂度较高。
下面的例子是交叉验证在模型选择中的应用。包DAAG里的ironslag数据描述了两种方法(chemical和magnetic)测量含铁量的53次结果。散点图显示chemical和magnetic变量是正相关的,但是这种关系可能不是线性的——多项式模型、指数模型、对数模型可能更好地拟合数据。
基于此,我们候选的模型有
- 线性模型: \(Y=\beta_0+\beta_1X+\varepsilon\);
- 多项式模型: \(Y=\beta_0+\beta_1X+\beta_2X^2+\varepsilon\);
- 指数模型: \(\ln Y=\beta_0+\beta_1X+\varepsilon\);
- 对数模型: \(\ln Y=\beta_0+\beta_1\ln X+\varepsilon\)。
par(mfrow = c(2, 2))
attach(DAAG::ironslag)
a <- seq(10, 40, 0.1)
L1 <- lm(magnetic ~ chemical)
plot(chemical, magnetic, main = "Linear", pch = 16)
yhat1 <- L1$coef[1] + L1$coef[2] * a
lines(a, yhat1, lwd = 2)
L2 <- lm(magnetic ~ chemical + I(chemical^2))
plot(chemical, magnetic, main = "Quadratic", pch = 16)
yhat2 <- L2$coef[1] + L2$coef[2] * a + L2$coef[3] * a^2
lines(a, yhat2, lwd = 2)
L3 <- lm(log(magnetic) ~ chemical)
plot(chemical, magnetic, main = "Exponential", pch = 16)
yhat3 <- exp(L3$coef[1] + L3$coef[2] * a)
lines(a, yhat3, lwd = 2)
L4 <- lm(log(magnetic) ~ log(chemical))
plot(log(chemical), log(magnetic), main = "Log-Log", pch = 16)
logyhat4 <- L4$coef[1] + L4$coef[2] * log(a)
lines(log(a), logyhat4, lwd = 2)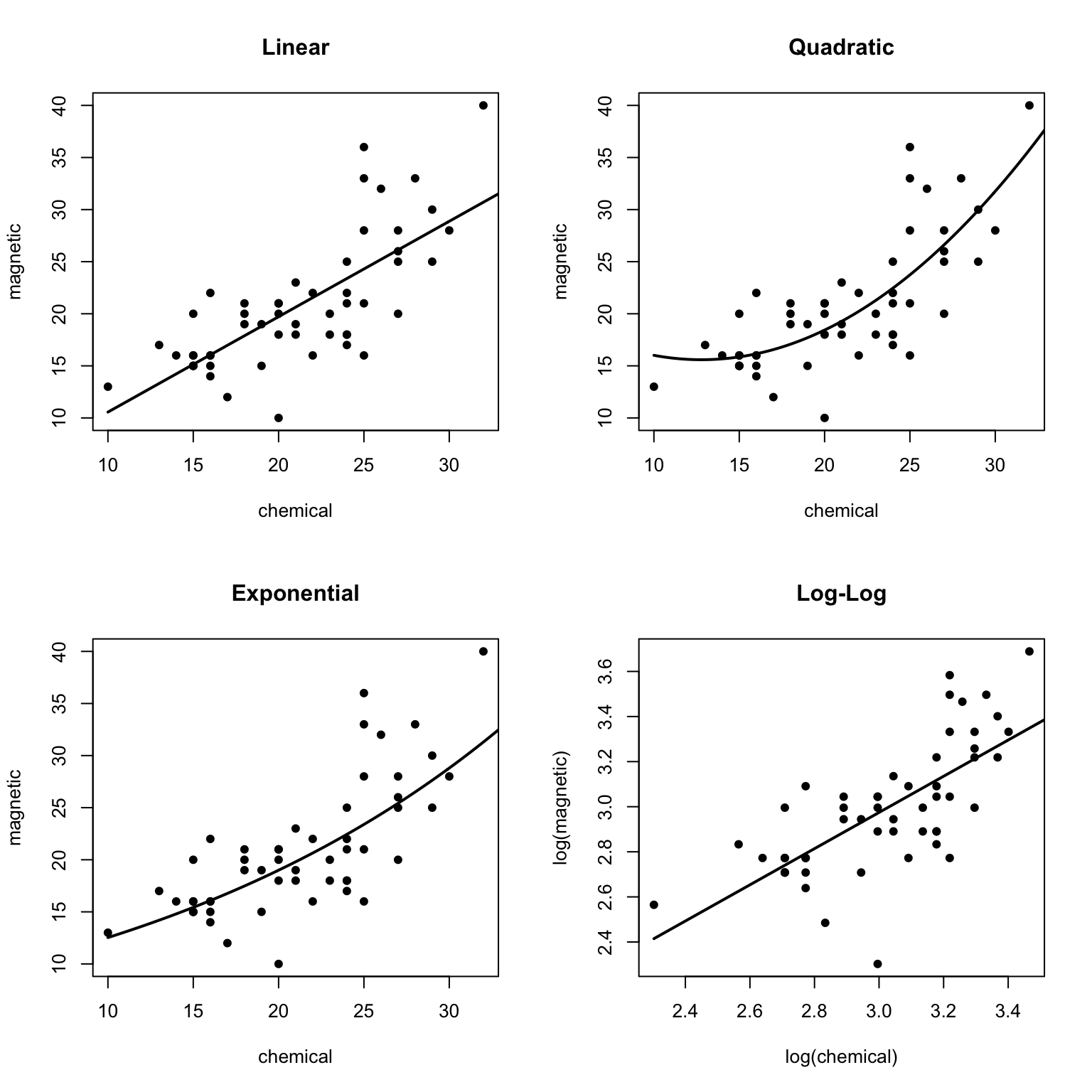
然后使用交叉验证方法对每个模型的预测误差进行估计。
- 对 \(k=1,\dots,n\),令 \((x_k,y_k)\) 为验证样本,使用其余样本对模型参数进行估计,然后计算预测误差。
- 使用其余的样本 \((x_i,y_i)~(i=1,\dots,k-1,k+1,\dots,n)\) 对模型进行拟合;
- 计算预测值: \(\hat{y}_k=\hat{\beta}_0+\hat{\beta}_1x_k\);
- 计算预测误差: \(e_k=y_k-\hat{y}_k\)。
- 计算均方误差 \(\sigma_e^2=\dfrac{1}{n}\sum\limits_{i=1}^ne_k^2\)。
n <- length(magnetic)
e1 <- e2 <- e3 <- e4 <- numeric(n)
for (k in 1:n) {
y <- magnetic[-k]
x <- chemical[-k]
J1 <- lm(y ~ x)
yhat1 <- J1$coef[1] + J1$coef[2] * chemical[k]
e1[k] <- magnetic[k] - yhat1
J2 <- lm(y ~ x + I(x^2))
yhat2 <- J2$coef[1] + J2$coef[2] * chemical[k] + J2$coef[3] * chemical[k]^2
e2[k] <- magnetic[k] - yhat2
J3 <- lm(log(y) ~ x)
yhat3 <- exp(J3$coef[1] + J3$coef[2] * chemical[k])
e3[k] <- magnetic[k] - yhat3
J4 <- lm(log(y) ~ log(x))
yhat4 <- exp(J4$coef[1] + J4$coef[2] * log(chemical[k]))
e4[k] <- magnetic[k] - yhat4
}
c(Linear = mean(e1^2), Quad = mean(e2^2), Exp = mean(e3^2), LogLog = mean(e4^2))## Linear Quad Exp LogLog
## 19.55644 17.85248 18.44188 20.45424结果表明使用二次多项式回归的预测误差更小,因此考虑选择模型L2。
par(mfrow = c(2, 2))
plot(L2)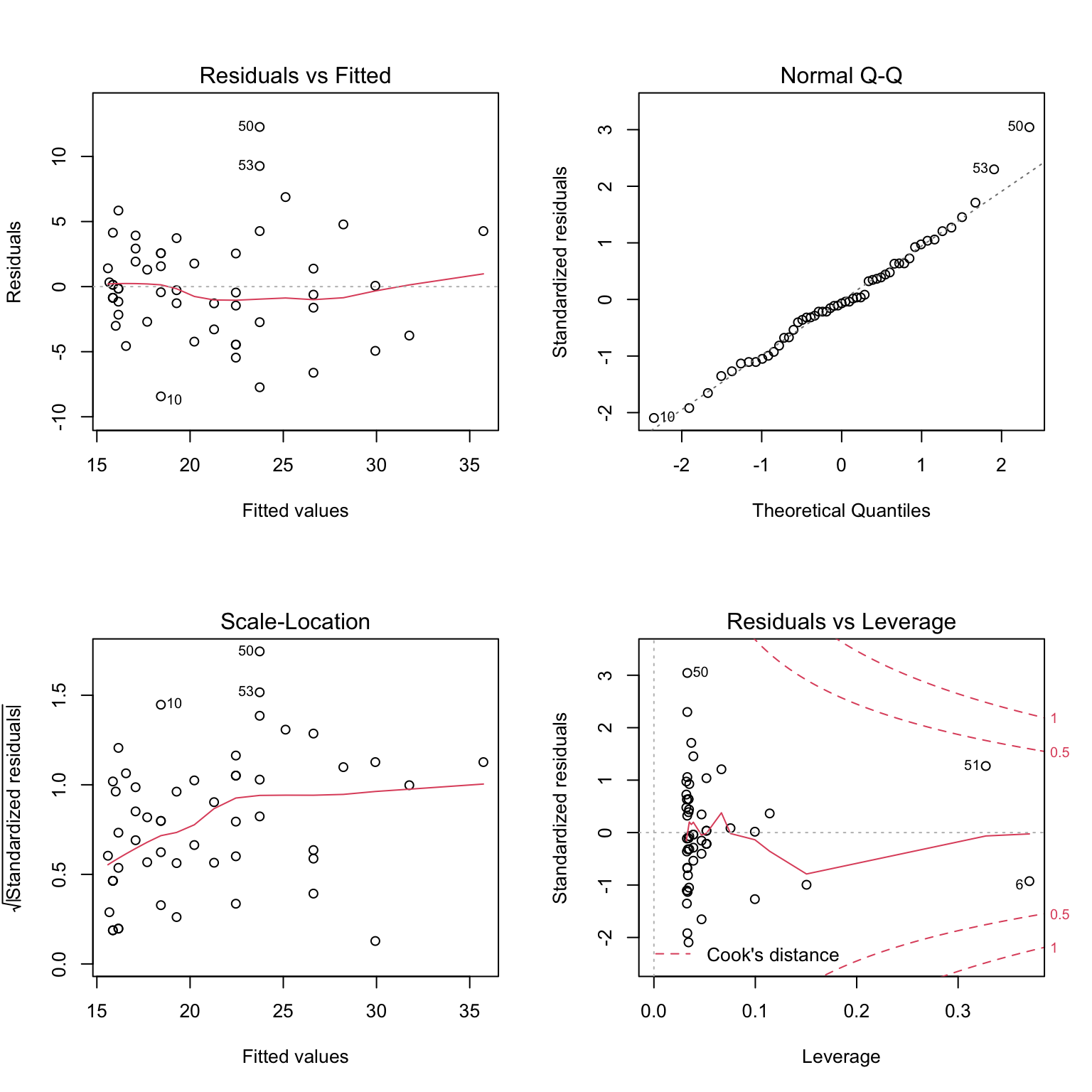
5.5 Permutation
置换(Permutation)检验同样基于重采样,它是不放回抽样,往往用于非参数假设检验问题。
同分布检验:\(H_0:F=G\leftrightarrow H_a:F\neq G\).
多
独立检验:\(H_0:F_{X,Y}=F_XF_Y\leftrightarrow H_a:F_{X,Y}\neq F_XF_Y\).
关联分析:对GLM问题\[g\{\mathbb E(Y\mid X,Z)\}=\alpha+\beta^\textsf{T}X+\gamma^\textsf{T}Z,\]
在给定 \(Z\) 条件下的独立性检验:\(H_0:\beta=0\leftrightarrow H_a:\beta\neq0\).
5.5.1 置换分布
设样本 \(\pmb X=(X_1,\dots,X_n)\) 和 \(\pmb Y=(Y_1,\dots,Y_m)\) 分别来自分布 \(F_X\) 和 \(F_Y\)。令\[\pmb Z=(Z_1,\dots,Z_N)=(X_1,\dots,X_n,Y_1,\dots,Y_m)\] 为合样本(其中 \(N=n+m\)),而 \(\pmb Z^*=(\pmb X^*,\pmb Y^*)\) 为 \(\pmb Z\) 的一个置换(注意这里 \(\pmb X^*\) 并不一定是 \(\pmb X\) 的一个置换)。
设检验统计量为 \(T=T(\pmb X,\pmb Y)\),则置换检验统计量为 \(T^*=T(\pmb X^*,\pmb Y^*)\)。如果 \(T\) 与样本 \(\pmb X\) 和 \(\pmb Y\) 的顺序无关,那么它有 \(\binom{N}{n}\) 个可能取值 \(T_1^*,\dots,T_{\binom{N}{n}}^*\)。一个直观的想法是,在原假设 \(H_0:F_X=F_Y\) 下,每个置换的概率应当等可能的是 \(1/\binom{N}{n}\),从而 \(T^*\) 的分布函数为\[F_{T^*}(t)=\binom{N}{n}^{-1}\sum_{j=1}^{\binom{N}{n}}I(T_j^*\leq t).\] 这个c.d.f.可以近似为 \(T\) 的零分布。于是检验的p值为\[\mathbb P_{H_0}(|T^*|\geq|T|\mid\text{data})=\binom{N}{n}^{-1}\sum_{j=1}^{\binom{N}{n}}I(|T_j^*|\geq|T|).\]
当 \(N\) 比较小时,所有置换的可能种数也很少,可以直接按上述方法计算,但是当 \(N\) 很大时,我们需要做近似,即从中不放回抽样地选取一部分样本进而计算。
- 计算原检验统计量的值 \(T=T(\pmb X,\pmb Y)\);
- 对第 \(b(b=1,\dots,B)\) 次重复:
- 生成一次置换样本 \(\pmb Z_b^*=(\pmb X_b^*,\pmb Y_b^*)\);
- 计算检验统计量的值 \(T_b^*=T(\pmb X_b^*,\pmb Y_b^*)\).
- 如果检验统计量的值越大就越倾向于备择假设,则p值约为 \[\hat{p}=\dfrac{1+\sharp\{T_b^*\geq T\}}{1+B}=\dfrac{1+\sum\limits_{b=1}^BI(T_b^*\geq T)}{1+B}.\] 对其他两种备择假设的形式计算类似.
- 当 \(\hat{p}\leq\alpha\) 时就在检验水平为 \(\alpha\) 上拒绝原假设 \(H_0\).
例如,对两样本 \(t\) 检验,可以采用如下代码实现置换检验。
attach(chickwts)
x <- sort(as.vector(weight[feed == "soybean"]))
y <- sort(as.vector(weight[feed == "linseed"]))
detach(chickwts)
cat(' x:', x, '\n', 'y:', y)## x: 158 171 193 199 230 243 248 248 250 267 271 316 327 329
## y: 141 148 169 181 203 213 229 244 257 260 271 309R <- 999
z <- c(x, y)
K <- 1:length(z)
n <- length(x)
reps <- numeric(R)
t0 <- t.test(x, y)$statistic
for (i in 1:R) {
k <- sample(K, size = n, replace = FALSE)
x1 <- z[k]
y1 <- z[-k]
reps[i] <- t.test(x1, y1)$statistic
}
p <- mean(abs(c(t0, reps)) >= abs(t0))
round(c(p, t.test(x, y)$p.value), 3)## [1] 0.199 0.198如果关心的问题是多重检验问题,则需要考虑进行p值修正,为了计算效率的提升,考虑如下方法:
- 对一个较大的 \(B\) 做一次多重检验问题;
- 剔除那些p值较大的假设,对剩下的假设再设定偏大的 \(B\) 做多重检验问题;
- 重复上述步骤直到p值的精度达到问题要求;
- 采用p值修正方法(如Bonferroni或FDR等)对p值进行调整。
5.5.2 同分布检验
设样本 \(\pmb X=(X_1,\dots,X_n)\) 和 \(\pmb Y=(Y_1,\dots,Y_m)\) 分别来自分布 \(F\) 和 \(G\),要检验的问题是\[H_0:F=G\leftrightarrow H_a:F\neq G.\] 记合样本为 \(\pmb Z=(Z_1,\dots,Z_N)=(X_1,\dots,X_n,Y_1,\dots,Y_m)\),\(F\) 和 \(G\) 的经验分布函数分别为 \(F_n\) 和 \(G_m\)。
考虑单变量的两样本检验,利用K-S统计量\[D=\sup_{1\leq i\leq N}|F_n(z_i)-G_m(z_i)|\]作为检验统计量,它的值越大就越支持备择假设 \(H_a:F\neq G\),表明两个分布之间的差距越大。
同样对于之前这个例题,我们使用基于K-S统计量的置换检验如下。
options(warn = -1)
D <- numeric(R)
D0 <- ks.test(x, y, exact = FALSE)$statistic
for (i in 1:R) {
k <- sample(K, size = n, replace = FALSE)
x1 <- z[k]
y1 <- z[-k]
D[i] <- ks.test(x1, y1, exact = FALSE)$statistic
}
mean(c(D0, D) >= D0)## [1] 0.434从结果中可以看到,我们没有充分的理由认为两样本来自的总体分布有差异。
除了利用K-S统计量,也可以使用Cramer-von Mises统计量\[W_2=\dfrac{mn}{(m+n)^2}\left[\sum_{i=1}^n(F_n(x_i)-G_m(x_i))^2+\sum_{j=1}^m(F_n(y_j)-G_m(y_j))^2\right]\] 作为检验统计量,它刻画了两个分布之间的融合平方距离,值越大就越支持备择假设 \(H_a:F\neq G\),表明两个分布之间的差距越大。
同样对于之前这个例题,我们使用基于 \(W_2\) 的置换检验如下(标准包nortest::cvm.test用于检验正态性,因此我们要重写函数)。
cvm.test <- function(x, y, R = 999) {
n <- length(x)
m <- length(y)
z <- c(x, y)
N <- length(z)
# 以下标代替数值求样本点处的e.c.d.f.值
Fn <- Gm <- numeric(N)
for (i in 1:N) {
Fn[i] <- mean(z[i] <= x)
Gm[i] <- mean(z[i] <= y)
}
cvm0 <- (m * n) / N * sum((Fn - Gm)^2)
cvm <- numeric(R)
for (i in 1:R) {
k <- sample(1:N, size = n, replace = FALSE)
x1 <- z[k]
y1 <- z[-k]
z1 <- c(x1, y1)
for (j in 1:N) {
Fn[j] <- mean(z1[j] <= x1)
Gm[j] <- mean(z1[j] <= y1)
}
cvm[i] <- (m * n) / N * sum((Fn - Gm)^2)
}
p <- mean(c(cvm0, cvm) >= cvm0)
return(c(statistic = cvm0, p.value = p))
}
cvm.test(x, y)## statistic p.value
## 4.228022 0.404000下面考虑多元变量的两样本检验问题,此时样本 \(X_1,\dots,X_n,Y_1,\dots,Y_m\in\mathbb R^d\),则合样本为\[\pmb Z_{N\times d}=\left[\begin{array}{cccc} x_{11} & x_{12} & \cdots & x_{1d}\\ \vdots & \vdots & \ddots & \vdots\\ x_{n1} & x_{n2} & \cdots & x_{nd}\\ y_{11} & y_{12} & \cdots & y_{1d}\\ \vdots & \vdots & \ddots & \vdots\\ y_{m1} & y_{m2} & \cdots & y_{md} \end{array}\right].\]关心的假设检验问题仍然是 \(H_0:F=G\leftrightarrow H_a:F\neq G\)。
考虑最近邻(NN)检验,它基于合样本中的 \(r\) 阶最近邻。记 \(\text{NN}_r(Z_i)\) 为距离 \(Z_i\) 最近的第 \(r\) 个最近邻样本,\(l_i(r)=1\) 表示 \(Z_i\) 和 \(\text{NN}_r(Z_i)\) 来自同一个样本,否则其值为0。由此,考虑检验统计量\[T_{N,J}=\dfrac{1}{NJ}\sum_{i=1}^N\sum_{r=1}^Jl_i(r),\] 它的值越大就越支持备择假设 \(H_a:F\neq G\),表明两个分布之间的差距越大。
代码中需要用到RANN包中的nn2函数,它用于找到样本的最近邻居,首先给出它的用法示例。
library(RANN) # for locating nearest neighbors
test_data = data.frame(rnorm(10))
nn2(data = test_data, k = 3)## $nn.idx
## [,1] [,2] [,3]
## [1,] 1 10 7
## [2,] 2 7 10
## [3,] 3 8 6
## [4,] 4 9 5
## [5,] 5 2 7
## [6,] 6 8 1
## [7,] 7 2 10
## [8,] 8 6 3
## [9,] 9 4 5
## [10,] 10 1 7
##
## $nn.dists
## [,1] [,2] [,3]
## [1,] 0 0.01662495 0.07947581
## [2,] 0 0.00758830 0.07043916
## [3,] 0 0.20531098 0.33589143
## [4,] 0 0.08858641 0.72165808
## [5,] 0 0.60321477 0.61080307
## [6,] 0 0.13058045 0.30020783
## [7,] 0 0.00758830 0.06285086
## [8,] 0 0.13058045 0.20531098
## [9,] 0 0.08858641 0.63307167
## [10,] 0 0.01662495 0.06285086结果中$nn.idx给出了最近邻的下标,当然第一列就是它本身,在我们的算法中要将第一列去除,$nn.dists给出了最近的距离,对我们算法而言没有帮助。
library(boot)
Tn <- function(z, ix, sizes, J) {
n <- sizes[1]
m <- sizes[2]
N <- n + m
if (is.vector(z)) { z <- data.frame(z) }
z <- z[ix, ]
NN <- nn2(data = z, k = J + 1)
block1 <- NN$nn.idx[1:n, -1]
block2 <- NN$nn.idx[(n+1):N, -1]
i1 <- sum(block1 <= n)
i2 <- sum(block2 > n)
return ((i1 + i2) / (N * J))
}
attach(chickwts)
x <- as.vector(weight[feed == "sunflower"])
y <- as.vector(weight[feed == "linseed"])
detach(chickwts)
z <- c(x, y)
set.seed(12345)
boot.obj <- boot(data = z, statistic = Tn, R = 9999,
sim = "permutation", sizes = c(length(x), length(y)), J = 3)
ts <- c(boot.obj$t0, boot.obj$t)
p <- mean(ts >= ts[1])
c(statistic = ts[1], p.value = p)## statistic p.value
## 0.8055556 0.0003000可以看到检验的p值只有 \(3\times10^{-4}\),故拒绝原假设,认为 \(F\neq G\)。
hist(ts, freq = FALSE, main = "", xlab = "replicates of NN statistic (J = 3)")
abline(v = ts[1], col = "red", lwd = 2)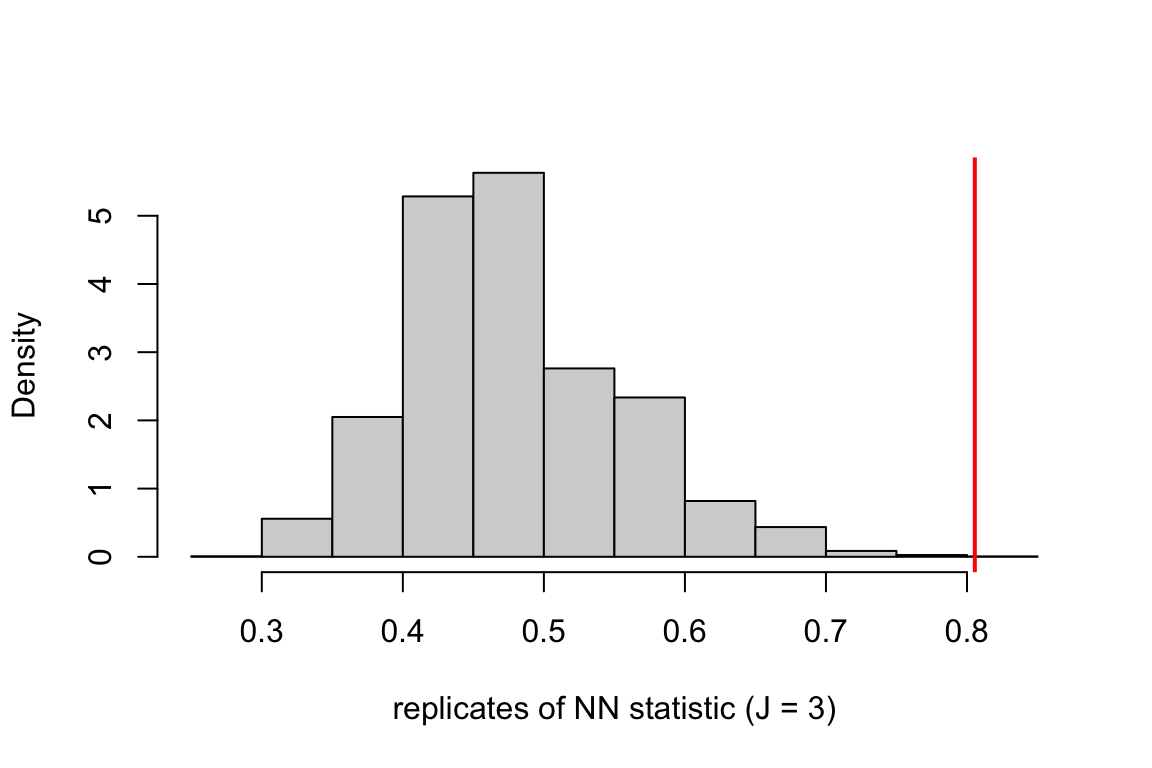
考虑能量(Energy)检验,提出检验统计量为能量距离\[e(\pmb X,\pmb Y)=\dfrac{nm}{n+m}\left(\dfrac{2}{nm}\sum_{i=1}^n\sum_{j=1}^m\|X_i-Y_j\|-\dfrac{1}{n^2}\sum_{i=1}^n\sum_{j=1}^n\|X_i-X_j\|-\dfrac{1}{m^2}\sum_{i=1}^m\sum_{j=1}^m\|Y_i-Y_j\|\right).\] 原假设下它的期望为零,因此过大的 \(e(\pmb X,\pmb Y)\) 将更倾向于备择假设 \(H_a:F\neq G\),认为两个分布之间的差距越大。
library(energy)
boot.obs <- eqdist.etest(z, sizes = c(length(x), length(y)), R = 9999)
boot.obs$p.value## [1] 1e-04检验的p值为 \(1\times10^{-4}\),故拒绝原假设,认为 \(F\neq G\)。
考虑球统计量检验(Wang et al., 2018)。
library(Ball)
bd.test(x, y, num.permutation = 9999)$p.value## bd.constant.pvalue
## 2e-04检验的p值为 \(2\times10^{-4}\),故拒绝原假设,认为 \(F\neq G\)。
下面对这三种检验进行功效的比较。
n <- m <- 50; N <- n + m; Nc <- c(n, m); R <- 999
reps <- 100; J <- 3; p <- 2; mu <- 0.3
eqdist.nn <- function(z, sizes, J) {
boot.obj <- boot(data = z, statistic = Tn, R = R,
sim = "permutation", sizes = sizes, J = J)
ts <- c(boot.obj$t0, boot.obj$t)
p <- mean(ts >= ts[1])
return(list(statistic = ts[1], p.value = p))
}
p.value <- matrix(nrow = reps, ncol = 3)
for (i in 1:reps) {
x <- matrix(rnorm(n * p, 0, 1.5), ncol = p)
y <- cbind(rnorm(m), rnorm(m, mean = mu))
z <- rbind(x, y)
p.value[i, 1] <- eqdist.nn(z, Nc, J)$p.value
p.value[i, 2] <- eqdist.etest(z, sizes = Nc, R = R)$p.value
p.value[i, 3] <- bd.test(x, y, R)$p.value
}
alpha <- 0.1
colMeans(p.value < alpha)## [1] 0.53 0.79 0.95可以看到,球统计量检验在非位置参数族的同分布检验问题中,有良好的功效。
5.6 Permutation的应用:距离相关系数
对随机向量 \(X\in\mathbb R^p\) 和 \(Y\in\mathbb R^q\),关心对假设检验问题为\[H_0:F_{XY}=F_XF_Y\leftrightarrow H_a:F_{XY}\neq F_XF_Y.\] 考虑一个距离相关系数度量 \(R(X,Y)\),它应当满足:
- \(0\leq R(X,Y)\leq1,\forall X,Y\);
- \(R(X,Y)=0\),当 \(X\) 和 \(Y\) 相互独立;
当 \(R(X,Y)\) 的值越大时,我们越倾向于备择假设 \(F_{XY}\neq F_XF_Y\),即 \(X\) 和 \(Y\) 不独立。
定义变量内部成对距离 \(a_{kl}=\|X_k-X_l\|\),\(b_{kl}=\|Y_k-Y_l\|\),和经验距离协方差\[V_n^2(\pmb X,\pmb Y)=\dfrac{1}{n^2}\sum_{k=1}^n\sum_{l=1}^nA_{kl}B_{kl},\] 其中 \(A_{kl}=a_{kl}-\overline{a}_{k\cdot}-\overline{a}_{\cdot l}+\overline{a}_{\cdot\cdot}\),\(B_{kl}=b_{kl}-\overline{b}_{k\cdot}-\overline{b}_{\cdot l}+\overline{b}_{\cdot\cdot}\) 是中心化的距离。
进一步定义经验距离相关系数为\[R_n^2(\pmb X,\pmb Y)=\left\{\begin{array}{ll} \dfrac{V_n^2(\pmb X,\pmb Y)}{\sqrt{V_n^2(\pmb X)V_n^2(\pmb Y)}}, & \text{若}~V_n^2(\pmb X)V_n^2(\pmb Y)>0,\\ 0, & \text{若}~V_n^2(\pmb X)V_n^2(\pmb Y)=0. \end{array}\right.\]
\(R_n^2(\pmb X,\pmb Y)\) 的极限零分布是具有二次形式的中心化正态随机变量,但系数与 \(\pmb X\) 和 \(\pmb Y\) 有关,但是我们可以构建置换检验。
dCov <- function(x, y) {
x <- as.matrix(x); y <- as.matrix(y)
n <- nrow(x); m <- nrow(y)
kl <- function(x) {
d <- as.matrix(dist(x))
m1 <- rowMeans(d); m2 <- colMeans(d); M <- mean(d)
a <- sweep(d, 1, m1)
b <- sweep(a, 2, m2)
return (b + M)
}
A <- kl(x); B <- kl(y)
return (sqrt(mean(A * B)))
}
z <- as.matrix(iris[1:50, 1:4])
x <- z[, 1:2]
y <- z[, 3:4]
dCov(x, y)## [1] 0.06436159# a wrap-up of dCov for permutation test
ndCov2 <- function(z, ix, dims) {
p <- dims[1]; q <- dims[2]; d <- p + q
x <- z[, 1:p]; y <- z[ix, -(1:p)]
return(nrow(z) * dCov(x, y)^2)
}
boot.obj <- boot(data = z, statistic = ndCov2, R = 999,
sim = "permutation", dims = c(2, 2))
tb <- c(boot.obj$t0, boot.obj$t)
p.cor <- mean(tb >= tb[1])
p.cor## [1] 0.077因此在水平 \(\alpha=0.10\) 下原假设被拒绝,认为 \(X\) 与 \(Y\) 不独立。
hist(tb, nclass = "scott", xlab = "", main = "", freq = FALSE)
abline(v = tb[1], col = "red", lwd = 2)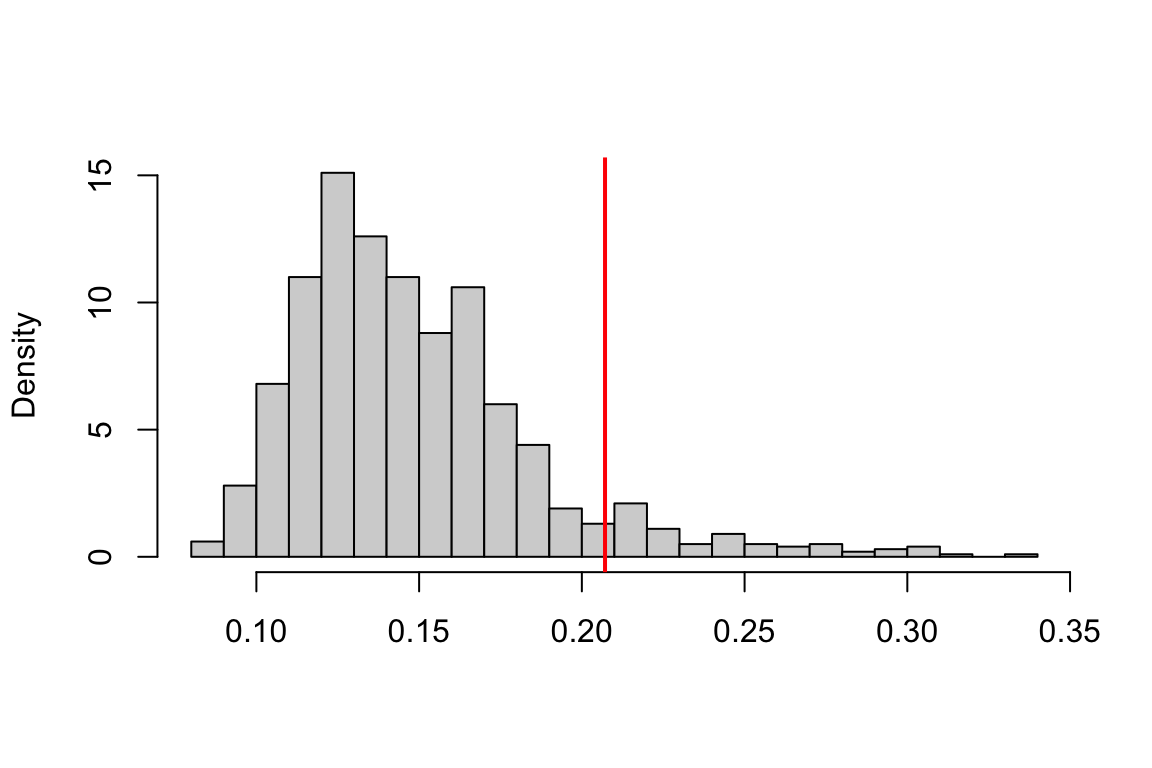
考虑Ball包中的多元随机向量独立性检验结果如下。
p.ball <- bcov.test(x, y, 999)$p.value
p.ball## bcov.constant.pvalue
## 0.211