Chapter 6 MCMC方法

6.1 介绍

前面介绍蒙特卡洛方法估计积分\[\int_Ag(t)\text{d}t,\] 是把此积分表示成一个对某个概率密度 \(f(t)\) 下的期望，从而积分估计问题转化成从目标概率密度 \(f(t)\) 中产生随机样本。

在MCMC方法中，首先建立一个Markov链，使得 \(f(t)\) 为其平稳分布，则可以运行此Markov链充分长时间直至收敛到平稳分布，那么从目标分布 \(f(t)\) 中产生随机样本，就是从达到平稳状态的Markov链中产生其样本路径。

一个好的链应该具有快速混合性质——从任意位置出发很快达到平稳分布。

6.1.1 贝叶斯推断中的积分问题

从贝叶斯的观点来看，模型中的观测变量和参数都是随机变量。因此，样本 \(\pmb x=(x_1,\dots,x_n)\) 和参数 \(\theta\) 的联合分布可以表示为\[f_{\pmb x,\theta}(\pmb x,\theta)=f_{\pmb x|\theta}(x_1,\dots,x_n)\pi(\theta).\] 从而根据Bayes定理，可以通过样本 \(\pmb x\) 的信息对 \(\theta\) 的分布进行更新：\[f_{\theta|\pmb x}(\theta\mid\pmb x)=\dfrac{f_{\pmb x|\theta}(\pmb x)\pi(\theta)}{\int_\Theta f_{\pmb x|\theta}(\pmb x)\pi(\theta)\text{d}\theta}.\] 则在后验分布下，\(g(\theta)\) 的期望为\[\mathbb E[g(\theta\mid\pmb x)]=\int_\Theta g(\theta)f_{\theta|\pmb x}(\theta\mid\pmb x)\text{d}\theta=\dfrac{\int_\Theta g(\theta)f_{\pmb x|\theta}(\pmb x)\pi(\theta)\text{d}\theta}{\int_\Theta f_{\pmb x|\theta}(\pmb x)\pi(\theta)\text{d}\theta}.\] 在许多情况下，得到直接积分的结果是十分困难的，需要通过数值计算。

6.1.2 MCMC积分

积分 \(\displaystyle\mathbb E[g(\theta\mid\pmb x)]=\int_\Theta g(\theta)f_{\theta|\pmb x}(\theta\mid\pmb x)\text{d}\theta\) 的蒙特卡洛估计为样本均值\[\overline{g}=\dfrac{1}{m}\sum_{i=1}^m g(\theta_i),\] 其中 \(\theta_i\) 是从分布 \(f_{\theta|\pmb x}(\theta\mid\pmb x)\) 中抽取的样本。当 \(\theta_1,\dots,\theta_m\) 独立时，则可以根据大数律知当样本量 \(m\) 趋于无穷时，\(\overline{g}\) 收敛到 \(\mathbb E[g(\theta\mid\pmb x)]\)。

MCMC方法的理论依据在于下述的极限定理：

定理1. 设 \(\{X_t,t\geq0\}\) 为一不可约、非周期的状态空间为 \(\Omega\) 的Markov链，\(\pi\) 为平稳分布，\(\pi_0\) 为初始分布，则\[\pi_t\rightarrow\pi,\quad t\rightarrow\infty.\]

这一定理揭示了当Markov链运行充分长时间后，链的状态分布即平稳分布，且与初始分布无关。

定理2. 若 \(X_1,X_2,\dots\) 为一遍历的平稳分布为 \(\pi\) 的Markov链值，则 \(X_n\) 依分布收敛到分布为 \(\pi\) 的随机变量 \(X\)，且对任意函数 \(f\)，当 \(\mathbb E_\pi|f(X)|\) 存在时，且 \(n\rightarrow\infty\) 时，则\[\overline{f}_n=\dfrac{1}{n}\sum_{t=1}^nf(X_t)\rightarrow\mathbb E_\pi f(X),\quad\text{a.s.}\]

下面计算遍历均值 \(\overline{f}_n\) 的方差。记 \(f^t=f(X_t)\)，\(\gamma_k=\text{Cov}(f^t,f^{t+k})\)，则 \(f^t\) 的方差为 \(\sigma^2=\gamma_0\)，\(k\) 步相关系数 \(\rho_k=\gamma_k/\sigma^2\)。从而 \[\begin{align*} \tau_n^2&=n\text{Var}_\pi(\overline{f}_n)=n\text{Var}_\pi\left(\dfrac{1}{n}\sum_{t=1}^nf^t\right)\\ &=\dfrac{1}{n}\sum_{t=1}^n\text{Var}_\pi(f^t)+\dfrac{2}{n}\sum_{k=1}^{n-t}\text{Cov}(f^t,f^{t+k})=\sigma^2\left[1+2\sum_{k=1}^{n-1}\dfrac{n-k}{n}\rho_k\right]. \end{align*}\]

可以证明\[\tau_n^2\rightarrow\tau^2=\sigma^2\left[1+2\sum_{k=1}^{\infty}\rho_k\right].\] 因此遍历均值 \(\overline{f}_n\) 的方差为\[\text{Var}_\pi(\overline{f}_n)=\dfrac{\sigma^2}{n}\left[1+2\sum_{k=1}^{n-1}\dfrac{n-k}{n}\rho_k\right].\]

定理3. 若一个链是一致的几何遍历（转移概率以速度 \(\lambda^t,0<\lambda<1\) 收敛）的，以及 \(f\) 相对于平稳分布 \(\pi\) 是平方可积的，则有\[\sqrt{n}\cdot\dfrac{\overline{f}_n-\mathbb E_\pi f(X)}{\tau}\rightarrow N(0,1),\quad n\rightarrow\infty.\]

这个定理对构造平稳分布 \(\pi\) 的参数的置信区间提供了理论依据。

综合上述定理：

不可约+非周期+正常返 \(\Rightarrow\) 唯一的平稳分布；
LLN：Markov链的实值函数的遍历均值以概率1收敛到极限分布下的均值；
CLT：遍历均值作合适的变化依分布收敛到标准正态分布。

因此，我们可以建立一个以 \(\pi\) 为平稳分布的Markov链，则在运行此链足够长时间后，该Markov链就会达到平稳状态，此时Markov链的值相当于从分布 \(\pi\) 中抽取样本。

MCMC算法的优点在于适用于广泛且困难的问题，此外问题维数的增加通常不会降低其收敛速度或使其更复杂。下面介绍两种重要的MCMC算法。

6.2 Metropolis-Hastings算法

M-H算法是一类常用的构造Markov链的方法。MCMC抽样方法的核心问题是确定满足要求（不可约、非周期、正常返且平稳分布为目标抽样分布）的一个马尔可夫链，因此确定从当前值转移到下一个值的规则十分重要。M-H抽样方法通过如下方式产生Markov链 \(\{X_0,X_1,X_2,\dots\}\)：

构造合适的提议分布 \(g(\cdot\mid X_t)\).
从某个分布 \(g\) 中产生 \(X_0\).
重复（直到Markov链达到平稳状态）
- 从 \(g(\cdot\mid X_t)\) 中产生 \(Y\).
- 从 \(U(0,1)\) 中产生 \(U\).
- 计算接受概率\[\alpha(X_t,Y)=\min\left\{1,\dfrac{f(Y)g(X_t\mid Y)}{f(X_t)g(Y\mid X_t)}\right\}.\]
- 如果 \(U\leq\alpha(X_t,Y)\) 则接受 \(Y\) 并令 \(X_{t+1}=Y\)，否则 \(X_{t+1}=X_t\).
- 增加 \(t\)，返回到循环内的第一步。

上述过程是有理论保证的。事实上，记 \(q_{ij}=g(x_{t+1}=j\mid x_t=i)\)，首先由M-H抽样方法产生的序列 \(\{x_0,x_1,\dots\}\) 为一马尔可夫链，其转移概率为\[p_{ij}=q_{ij}\alpha(i,j)+\delta_i(j)(1-r(i)),\] 其中 \(r(i)=\sum_jq_{ij}\alpha(i,j)\)，\(\alpha_{i,j}=\min\{1,f_jq_{ji}/f_iq_{ij}\}\)，\(\delta_i(j)=1\) 当且仅当 \(i=j\)。所以\[f_ip_{ij}=f_iq_{ij}\min\left\{1,\dfrac{f_jq_{ji}}{f_iq_{ij}}\right\}=f_jq_{ji}\min\left\{1,\dfrac{f_iq_{ij}}{f_jq_{ji}}\right\}=f_jp_{ji},\quad i\neq j.\] 而 \(i=j\) 时，\(f_i\delta_i(j)(1-r(i))=f_j\delta_j(i)(1-r(j))\)，因此细致平稳方程满足，\(f\) 即该链的平稳分布。进一步可以验证该链是不可约、正常返、非周期的。此外，如果状态空间是连续的，证明类似，只需将转移概率修改为转移核即可。

注意，提议分布 \(g\) 的选择要使得产生的马尔可夫链满足不可约、正常返、非周期且具有平稳分布 \(f\) 等正则化条件外，还应满足：

提议分布的支撑集包含目标分布的支撑集；
容易从提议分布中抽样，常取为已知的分布，如正态分布或 \(t\) 分布等；
提议分布应使接受概率容易计算；
提议分布的尾部要比目标分布的尾部厚。

此外，Robert和Casella（1999）指出，接受概率并非越大越好，因为这可能导致较慢的收敛性；Gelman等（1996）建议当参数维数为1时，接受概率应略小于0.5，当参数维数大于5时，接受概率应降至0.25左右。

例如，使用M-H抽样方法从瑞利（Rayleigh）分布中抽样，其密度函数为\[f(x)=\dfrac{x}{\sigma^2}\text{e}^{-\frac{x^2}{2\sigma^2}},\quad x\geq0,\sigma>0.\] 瑞利分布通常被用来建模具有快速衰减的生存时间，因为风险率 \(f(x)/S(x)=x/\sigma^2\) 是线性增长的。

使用M-H抽样方法如下：

令 \(g(\cdot\mid X)\) 为 \(\chi^2(X)\)；
从 \(\chi^2(1)\) 中产生 \(X_1\)；
对 \(i=2,\dots,N\)，重复：
- 从 \(\chi^2(X_{i-1})\) 中产生 \(Y\)；
- 产生 \(U\sim U(0,1)\)；
- 计算\[r(X_{i-1},Y)=\dfrac{f(Y)g(X_{i-1}\mid Y)}{f(X_{i-1})g(Y\mid X_{i-1})},\]
- 若 \(U\leq r(X_{i-1},Y)\)，则接受 \(Y\)，令 \(X_i=Y\)；否则令 \(X_i=X_{i-1}\)。
- 增加 \(i\)，返回到循环内的第一步。

f <- function(x, sigma) {
  if (any(x < 0)) return(0)
  return(x / sigma^2 * exp(-x^2 / (2 * sigma^2)))
}

m <- 10000
sigma <- 4
x <- numeric(m)
x[1] <- rchisq(1, 1)
k <- 0
u <- runif(m)
for (i in 2:m) {
  y <- rchisq(1, x[i-1])
  r <- f(y, sigma) * dchisq(x[i-1], y) / f(x[i-1], sigma) / dchisq(y, x[i-1])
  if (u[i] <= r) { x[i] <- y }
  else { x[i] <- x[i-1]; k <- k + 1 }
}
print(k / m)

## [1] 0.4016

可以看到约有40.16%的候选点被拒绝了，可见算法效率不是特别高。

index <- 5000:5500
plot(index, x[index], type = "l", main = "", ylab = "x")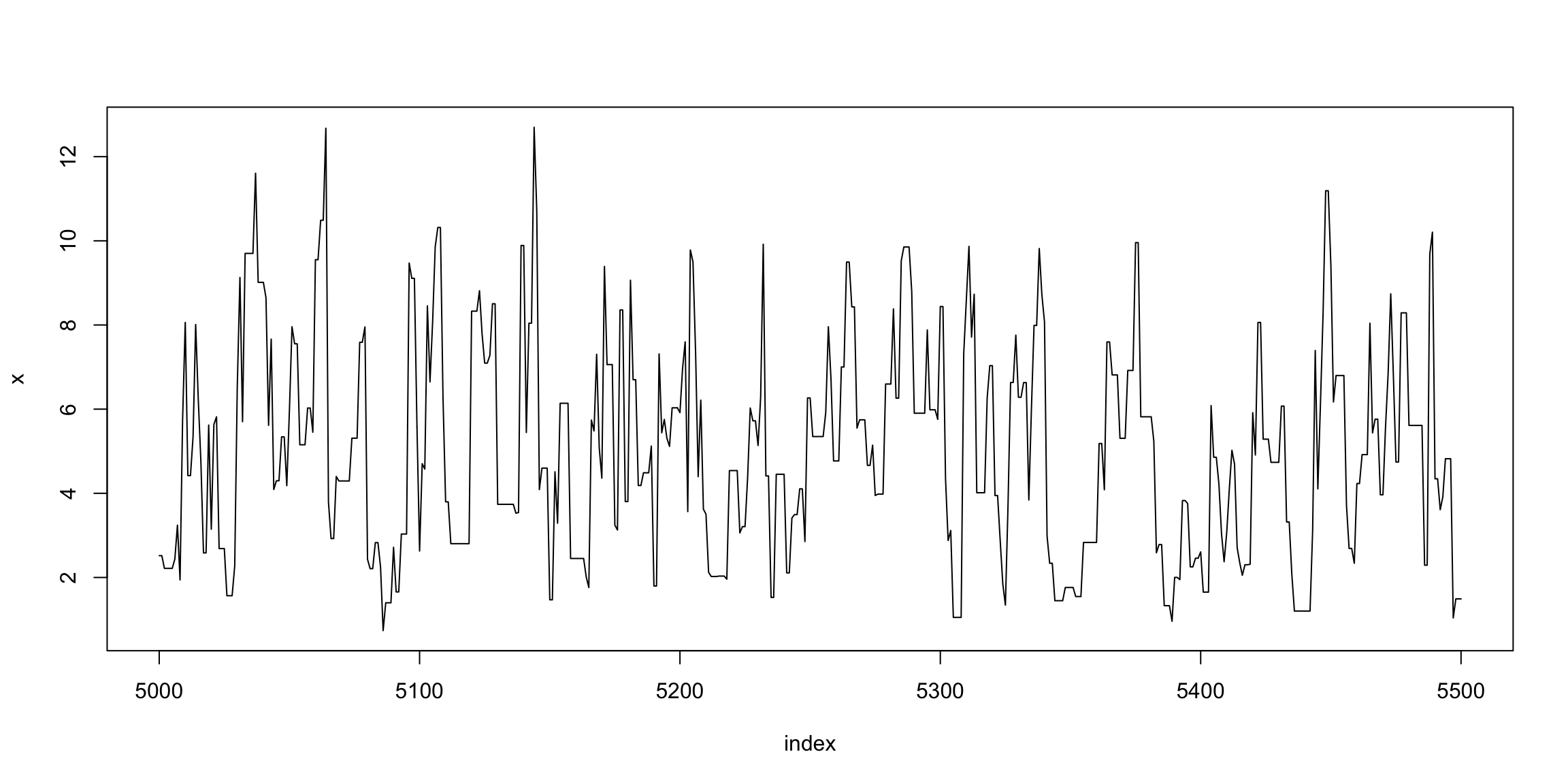

b <- 2000 # burnin period
y <- x[(b+1):m]
a <- ppoints(100)
QR <- sigma * sqrt(-2 * log(1 - a))
Q <- quantile(x, a)

par(mfrow = c(1,2))
hist(y, breaks = "scott", xlab = "sample", freq = FALSE)
lines(QR, f(QR, sigma))
qqplot(QR, Q, xlab = "Rayleigh Quantiles", ylab = "Sample Quantiles")
abline(0, 1, col = 2, lwd = 2)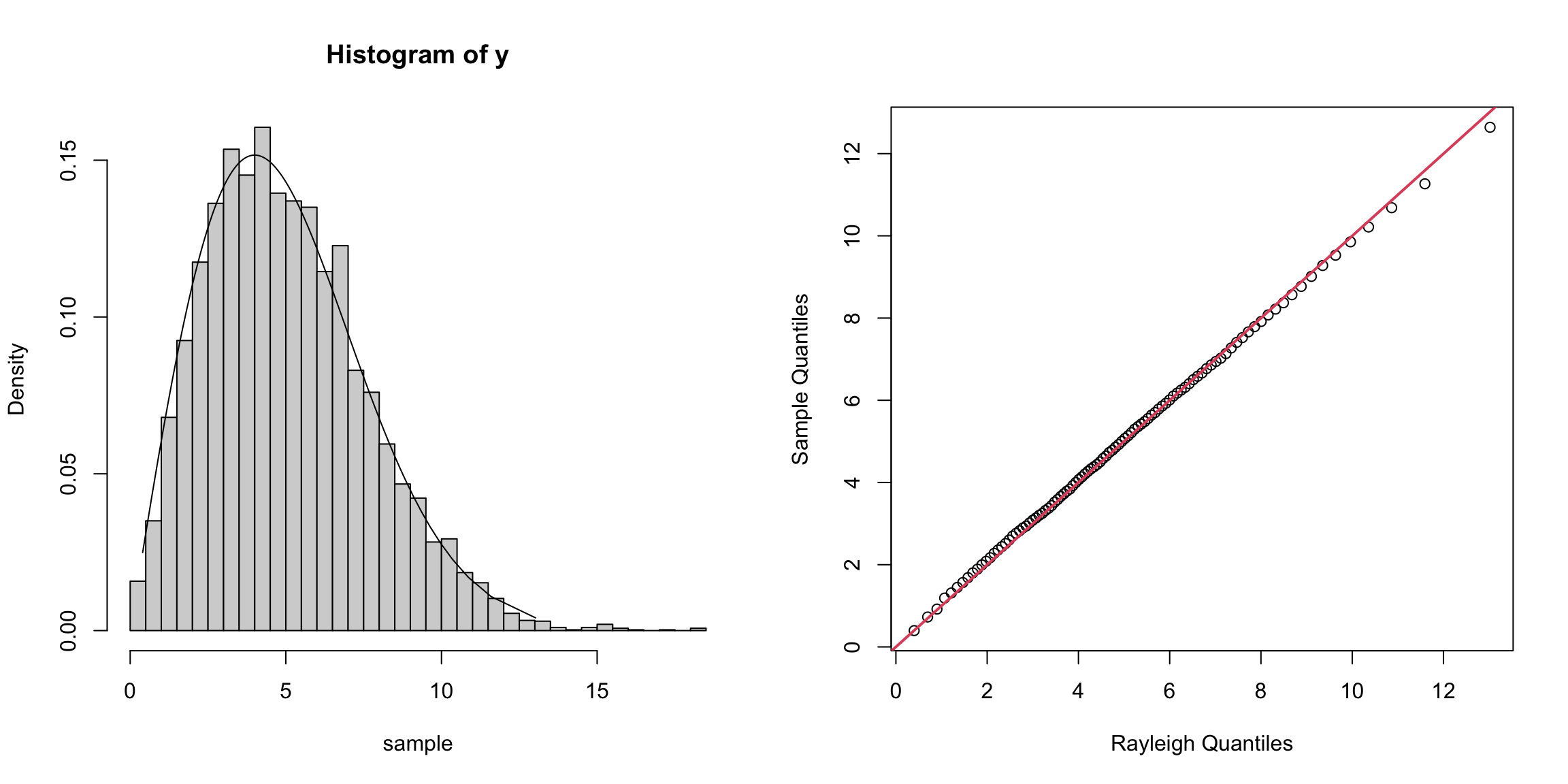

从分布拟合的角度看，预烧期2000之后的样本基本已经达到平稳分布，拟合效果较好。

根据提议分布 \(g\) 的不同选择，M-H抽样方法衍生出了几个不同的变种。

6.2.1 Metropolis抽样方法

在Metropolis抽样方法中，提议分布是对称的，即 \(g(\cdot\mid X_n)\) 满足 \(g(X\mid Y)=g(Y\mid X)\)，因此接受概率为\[\alpha(X_t,Y)=\min\left\{1,\dfrac{f(Y)}{f(X_t)}\right\}.\]

6.2.2 随机游动Metropolis抽样方法

随机游动Metropolis抽样方法是Metropolis方法的一个应用例子。假设候选点 \(Y\) 从一个对称的提议分布 \(g(Y\mid X_t)=g(\vert X_t-Y\vert)\) 中产生，则在每一次迭代中，从 \(g(\cdot)\) 中产生一个随机增量 \(Z\)，然后 \(Y=X_t+Z\)。比如增量 \(Z\) 可以从正态分布中产生，此时 \(Y\mid X_t\sim N(X_t,\sigma^2)\)，\(\sigma^2>0\)。

例如，使用提议分布 \(N(X_t,\sigma^2)\) 和随机游动Metropolis算法产生自由度为 \(\nu\) 的 \(t\) 分布随机数，并对不同方差 \(\sigma^2\) 重复此过程。记 \(f(x)\) 为 \(t_\nu\) 的密度函数，则接受概率为\[\alpha(X_t,Y)=\min\left\{1,\dfrac{f(Y)}{f(X_t)}\right\}.\]

rw.Metropolis <- function(n, sigma, x0, N) {
  x <- numeric(N)
  x[1] <- x0
  u <- runif(N)
  k <- 0
  for (i in 2:N) {
    y <- rnorm(1, x[i-1], sigma)
    if (u[i] <= dt(y, n) / dt(x[i-1], n)) { x[i] <- y }
    else { x[i] <- x[i-1]; k <- k + 1 }
  }
  return(list(x = x, k = k))
}

n <- 4
N <- 2000
sigma <- c(0.05, 0.5, 2, 16)
x0 <- 25
rw1 <- rw.Metropolis(n, sigma[1], x0, N)
rw2 <- rw.Metropolis(n, sigma[2], x0, N)
rw3 <- rw.Metropolis(n, sigma[3], x0, N)
rw4 <- rw.Metropolis(n, sigma[4], x0, N)
print(c(rw1$k, rw2$k, rw3$k, rw4$k) / N)

## [1] 0.0035 0.0945 0.4605 0.8985

可以看到只有第三个链的拒绝率在区间 \([0.15,0.5]\) 内。

par(mfrow = c(2, 2))
refline <- qt(c(0.025, 0.975), n)
rw <- cbind(rw1$x, rw2$x, rw3$x,  rw4$x)
for (j in 1:4) {
  plot(rw[,j], type = "l", xlab = bquote(sigma == .(round(sigma[j],3))),
       ylab = "X", ylim=range(rw[,j]))
  abline(h = refline)
}

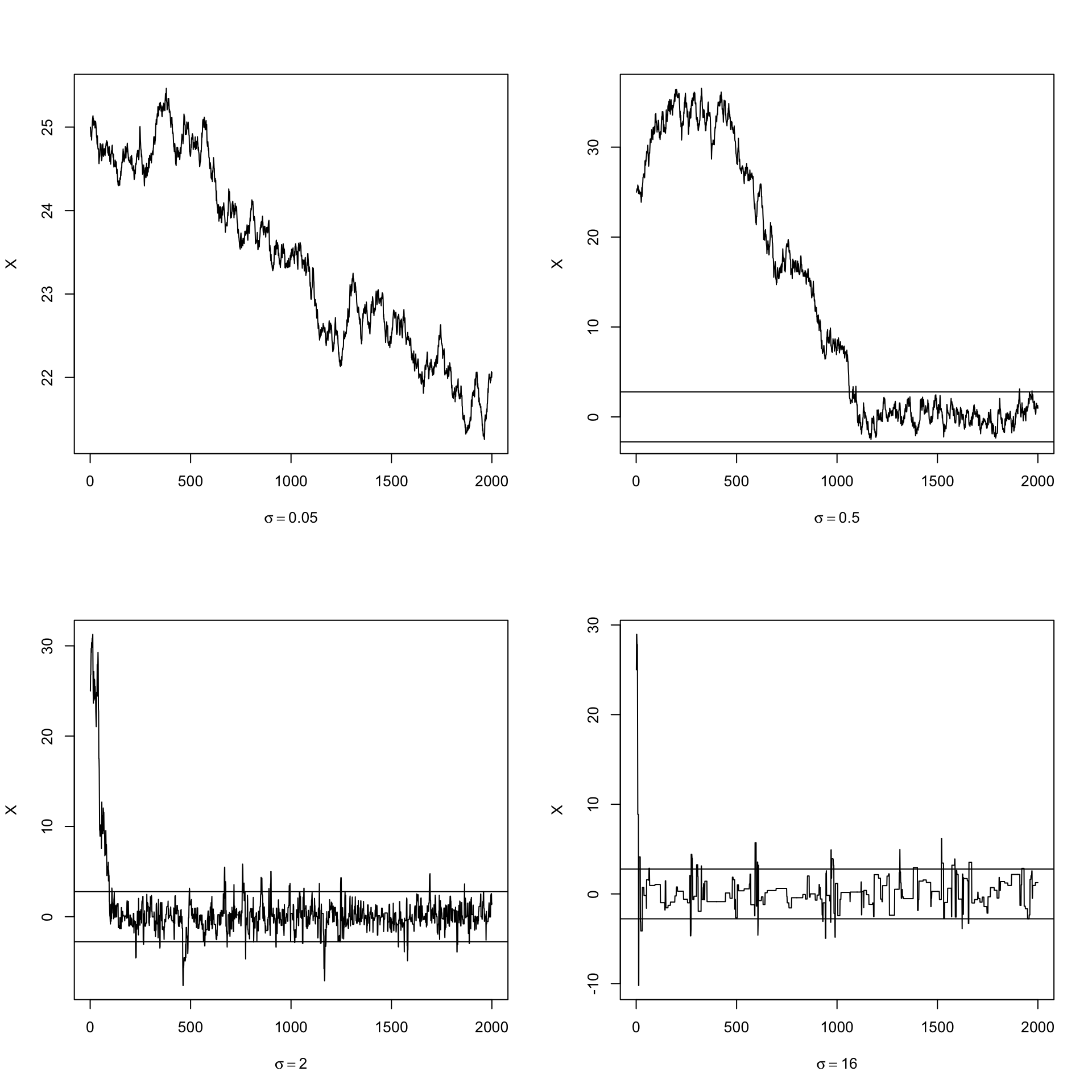
par(mfrow = c(1,1))

可以看到，当 \(\sigma=0.05\) 时增量太小，几乎每个候选点都被接受了，链在迭代2000次后还没有收敛；当 \(\sigma=0.5\) 时，链的收敛较慢；当 \(\sigma=2\) 时，链的收敛很快；当 \(\sigma=16\) 时，接受的概率太小，链虽然收敛了，但是效率很低。

a <- c(0.05, seq(0.1, 0.9, 0.1), 0.95)
Q <- qt(a, n)
mc <- rw[501:N,]
Qrw <- apply(mc, 2, function(x) quantile(x, a))
QQ <- data.frame(round(cbind(Q, Qrw), 3))
names(QQ) <- c('True', 'sigma=0.05', 'sigma=0.5', 'sigma=2', 'sigma=16')
knitr::kable(QQ)

	True	sigma=0.05	sigma=0.5	sigma=2	sigma=16
5%	-2.132	21.639	-1.404	-2.144	-2.376
10%	-1.533	21.848	-0.945	-1.521	-1.370
20%	-0.941	22.132	-0.399	-0.860	-0.694
30%	-0.569	22.420	0.128	-0.535	-0.482
40%	-0.271	22.587	0.596	-0.267	-0.065
50%	0.000	22.790	1.160	0.005	0.272
60%	0.271	23.207	2.157	0.232	0.494
70%	0.569	23.510	8.362	0.535	0.923
80%	0.941	23.766	16.147	0.959	1.378
90%	1.533	24.073	20.063	1.650	2.168
95%	2.132	24.718	26.414	2.377	2.936

可以看到第三个链的分位数和真实分布的分位数也是十分接近的。

6.2.3 独立抽样方法

独立抽样是M-H抽样方法的另一个特殊情形，其中的提议分布不依赖于链的前一步状态值，因此 \(g(Y\mid X_t)=g(Y)\)，此时接受概率为\[\alpha(X_t,Y)=\min\left\{1,\dfrac{f(Y)g(X_t)}{f(X_t)g(Y)}\right\}.\]

例如，假设从一个正态混合分布 \(pN(\mu_1,\sigma_1^2)+(1-p)N(\mu_2,\sigma_2^2)\) 中观测到一个样本 \(\pmb z=(z_1,\dots,z_n)\)，利用独立抽样方法求 \(p\) 的估计。在 \(p\) 无先验信息可以利用时，考虑先验分布 \(\pi(p)\) 为 \(U(0,1)\)，则 \(p\) 的后验分布为\[\pi(p\mid\pmb z)\propto\prod_{j=1}^n[pf_1(z_j\mid p)+(1-p)f_2(z_j\mid p)].\]

其中 \(f_1,f_2\) 分别为两个正态的密度。考虑提议分布为贝塔分布 \(Be(a,b)\)，其密度函数为 \(g(y)\propto y^{a-1}(1-y)^{b-1}\)，接受概率为\[\alpha(X_t,Y)=\min\left\{1,\dfrac{\pi(Y\mid\pmb z)g(X_t)}{\pi(X_t\mid\pmb z)g(Y)}\right\}.\]

set.seed(12345)
m <- 10000
xt <- numeric(m)
a <- 1
b <- 1
p <- 0.2
n <- 100
mu <- c(0, 5)
sigma <- c(1, 1)
i <- sample(1:2, size = n, replace = TRUE, prob = c(p, 1-p))
x <- rnorm(n, mu[i], sigma[i])

u <- runif(m)
y <- rbeta(m, a, b)
xt[1] <- 0.5
for (i in 2:m) {
  fy <- y[i] * dnorm(x, mu[1], sigma[1]) + (1 - y[i]) * dnorm(x, mu[2], sigma[2])
  fx <- xt[i-1] * dnorm(x, mu[1], sigma[1]) + (1 - xt[i-1]) * dnorm(x, mu[2], sigma[2])
  r <- prod(fy / fx) * dbeta(xt[i-1], a, b) / dbeta(y[i], a, b)
  if (u[i] <= r) { xt[i] <- y[i] }
  else { xt[i] <- xt[i-1] }
}

par(mfrow = c(1, 2))
plot(xt, type = "l", ylab = "p")
abline(h = p, v = 101, lty = 3)
hist(xt[-(1:1000)], main = "", xlab = "p", prob = TRUE)
z <- seq(min(xt), max(xt), length = 100)
lines(z, dnorm(z, mean(xt), sd(xt)))
abline(v = mean(xt), col = 2, lwd = 2)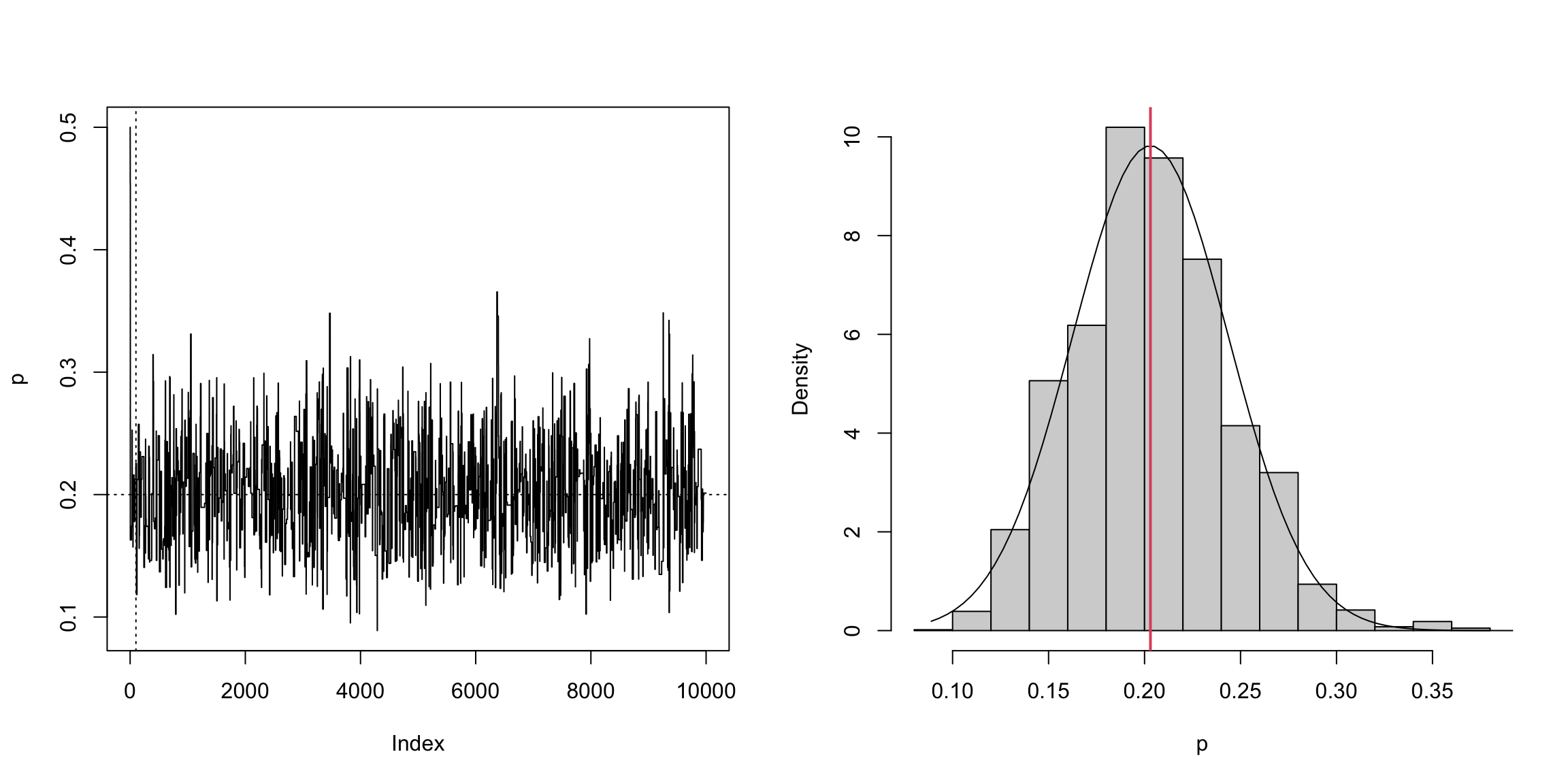

可以看到 \(p\) 的后验期望接近0.2（真值）。

6.3 Gibbs算法

Gibbs抽样方法特别适合于目标分布是多元的场合，其最令人感兴趣的方面是为了产生不可约、非周期、并以高维空间的目标分布作为其平稳分布的马尔可夫链，只需要从一些一元分布（全条件分布）中进行抽样就可以了。即将从多元目标分布中抽样转化为从一元目标分布抽样，这是Gibbs抽样的重要性所在。

令 \(\pmb X=(X_1,\dots,X_p)\in\mathbb R^p\) 为随机变量，其联合分布 \(f(\pmb x)\) 为目标分布。记 \[\pmb X_{-i}=(X_1,\dots,X_{i-1},X_{i+1},\dots,X_p)\in\mathbb R^{p-1},\] 并记 \(X_i\mid\pmb X_{-i}\) 的满（全）条件密度为 \(f(x_i\mid\pmb x_{-i})\) \((i=1,\dots,p)\)。Gibbs抽样方法是从这 \(p\) 个条件分布中产生候选点，以解决直接从 \(f\) 中进行抽样的困难。Gibbs抽样从一个初始值 \(\pmb x^{(0)}=(x_1^{(0)},\dots,x_p^{(0)})\) 出发，按下述过程迭代更新分量： \[\begin{align*} x_1^{(t)}&\sim f(x_1\mid x_2^{(t-1)},x_3^{(t-1)},\dots,x_p^{(t-1)}),\\ x_2^{(t)}&\sim f(x_2\mid x_1^{(t)},x_3^{(t-1)},\dots,x_p^{(t-1)}),\\ &\vdots\\ x_i^{(t)}&\sim f(x_i\mid x_1^{(t)},\dots,x_{i-1}^{(t)},x_{i+1}^{(t-1)},\dots,x_p^{(t-1)}),\\ &\vdots\\ x_p^{(t)}&\sim f(x_p\mid x_1^{(t)},\dots,x_{p-1}^{(t)}). \end{align*}\]

有时候对所有分量完成一次更新比较复杂，可以采用随机化的方式，每次仅更新一个分量（随机选择），而其它分量保持不变。注意，这里无需计算每一个候选点的接受概率 \(\alpha\)，全部接受。

例如，使用Gibbs抽样方法产生二元正态分布 \(N(\mu_1,\mu_2,\sigma_1^2,\sigma_2^2,\rho)\) 的随机数。注意到 \[\begin{align*} X_1\mid X_2=x_2&\sim N\left(\mu_1+\rho\dfrac{\sigma_1}{\sigma_2}(x_2-\mu_2),(1-\rho^2)\sigma_1^2\right),\\ X_2\mid X_1=x_1&\sim N\left(\mu_2+\rho\dfrac{\sigma_2}{\sigma_1}(x_1-\mu_1),(1-\rho^2)\sigma_2^2\right). \end{align*}\]

于是通过如下代码就可以实现目的。

m <- 10000
burnin <- 1000
X <- matrix(0, m, 2)
rho <- 0.8
mu <- c(0, 2)
sigma <- c(1, 0.5)
s <- sqrt(1 - rho^2) * sigma
X[1,] <- mu
for (i in 2:m) {
  x2 <- X[i-1, 2]
  m1 <- mu[1] + rho * (x2 - mu[2]) * sigma[1] / sigma[2]
  X[i,1] <- rnorm(1, m1, s[1])
  x1 <- X[i, 1]
  m2 <- mu[2] + rho * (x1 - mu[1]) * sigma[2] / sigma[1]
  X[i,2] <- rnorm(1, m2, s[2])
}
x <- X[-(1:burnin),]
plot(x[,1], x[,2], xlab = bquote(X[1]), ylab = bquote(X[2]),
     main = "", cex = 0.5, ylim = range(x[,2]))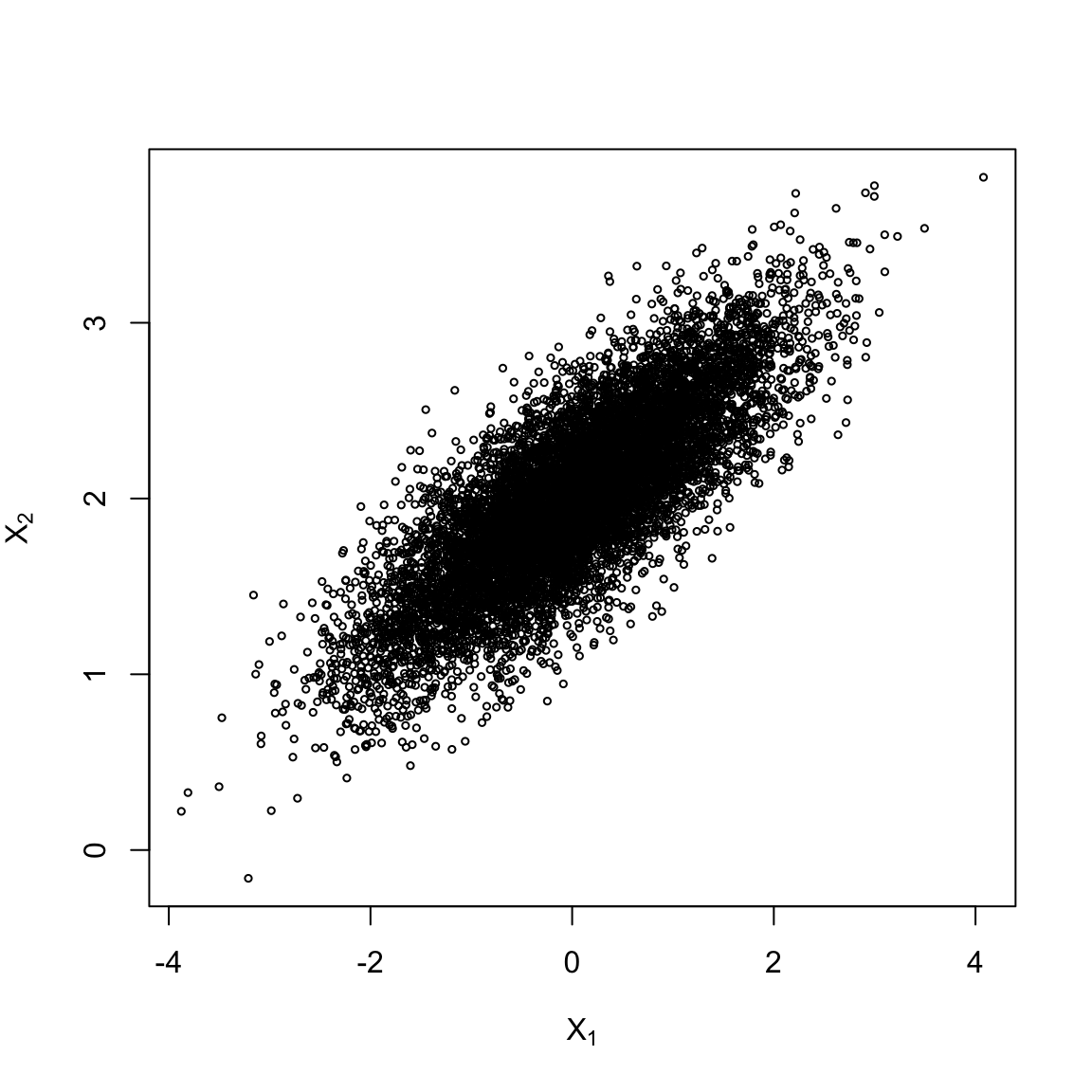

colMeans(x)

## [1] 0.004515394 2.005059651

cov(x)

##           [,1]     [,2]
## [1,] 0.9821537 0.396883
## [2,] 0.3968830 0.248386

cor(x)

##           [,1]      [,2]
## [1,] 1.0000000 0.8035431
## [2,] 0.8035431 1.0000000

可以看到，模拟的数值与真值十分接近。

6.4 收敛监视

较主观的监视收敛的方法有

监视蒙特卡洛误差：较小的MC误差表明在计算感兴趣的量时精度较高，即MC误差越小表明马尔可夫链的收敛性越好。
样本路径图：将马尔可夫链生成的值对迭代次数作图，如果所有的值都在一个区域里没有明显的周期性或趋势性，则认为收敛性已经达到。
累积均值图：将马尔可夫链的累积均值对迭代次数作图，如果累积均值在经过一些迭代后基本稳定，则认为收敛性已经达到。
自相关函数（ACF）图：将马尔可夫链生成样本的自相关函数对迭代次数作图，较低或较高的自相关性分别表明了收敛性的好与坏。

除此之外，下面介绍一种基于统计量的方法。

6.4.1 Gelman-Rubin方法

假设有 \(k\) 个链，每个链有 \(n\) 个样本，感兴趣的量记为 \(\phi\)，其在目标分布下有期望 \(\mu\) 和方差 \(\sigma^2\)。记 \(\phi_{jt}\) 表示到链 \(j\) 的第 \(t\) 个样本时 \(\phi\) 的值，那么在混合样本中，\(\mu\) 的一个无偏估计为 \(\hat{\mu}=\overline{\phi}_{\cdot\cdot}\)，而链之间的方差 \(B_n\) 和链内的方差 \(W_n\) 分别为\[B_n=\dfrac{n}{k-1}\sum_{j=1}^k(\overline{\phi}_{j\cdot}-\overline{\phi}_{\cdot\cdot})^2,\quad W_n=\dfrac{1}{k(n-1)}\sum_{j=1}^k\sum_{t=1}^n(\phi_{jt}-\overline{\phi}_{j\cdot})^2.\]

从而可以使用 \(B_n\) 和 \(W_n\) 的加权估计 \(\sigma^2\)：\[\hat{\sigma}^2=\dfrac{n-1}{n}W_n+\dfrac{1}{n}B_n.\]

如果初始值是从目标分布中抽取的，那么 \(\hat{\sigma}^2\) 是 \(\sigma^2\) 的无偏估计，但如果初始值过度分散，则会高估 \(\sigma^2\)。

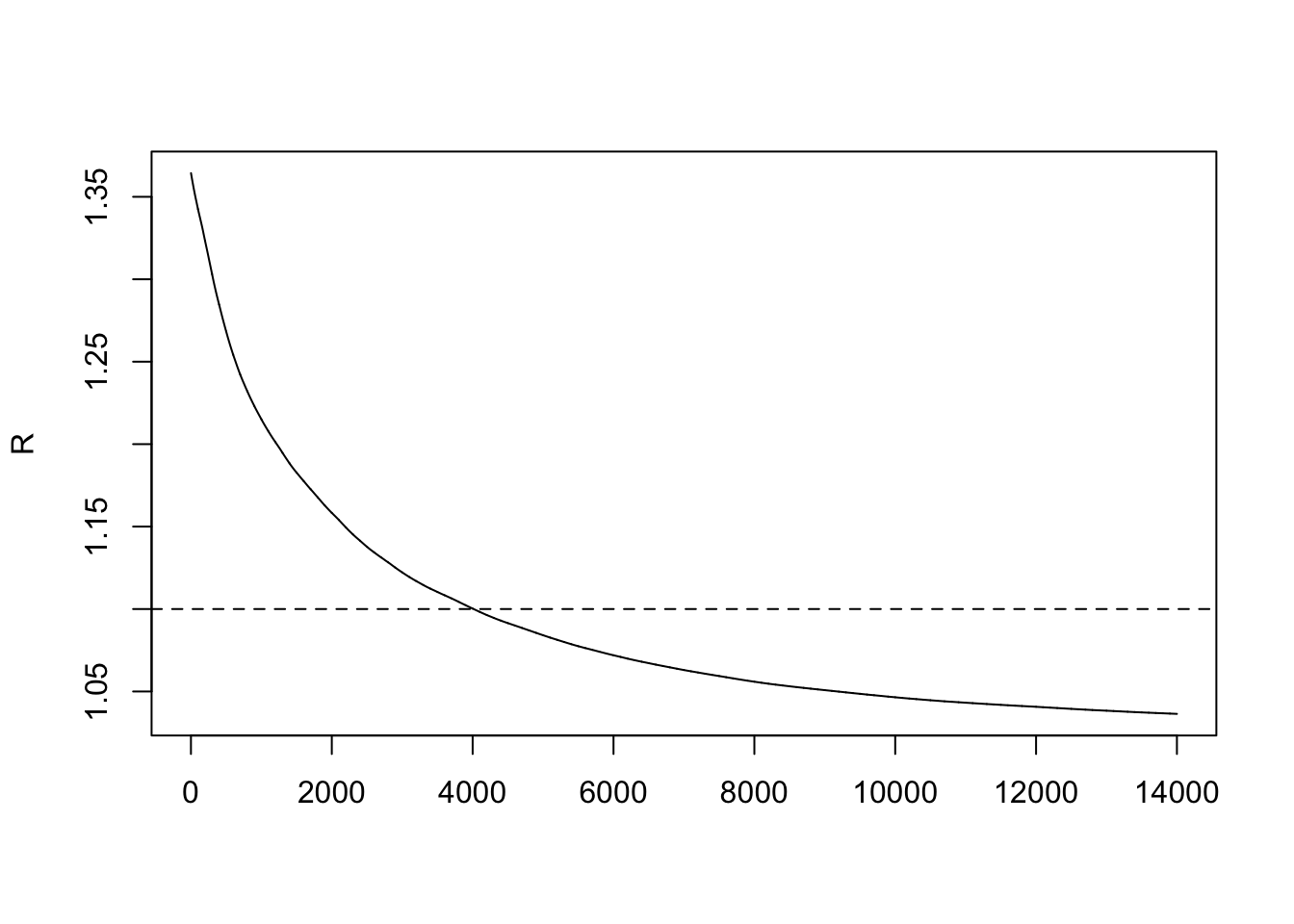
一个自然的想法就是令 \(R=\hat{\sigma}^2/\sigma^2\)，则称 \(\sqrt{R}\) 为尺度缩减因子，它的估计为\[\hat{R}=\dfrac{\hat{\sigma}^2}{W_n},\] 称 \(\sqrt{\hat{R}}\) 为潜在尺度缩减因子。当链达到收敛并且产生的数据很大时，\(\hat{R}\) 应该趋于1，一般而言，当 \(\hat{R}<1.1\) 或 \(1.2\) 时就认为已达到收敛。

例如，目标分布为 \(N(0,1)\)，提议分布为 \(N(X_t,\sigma^2)\)，\(\phi_{jt}\) 表示第 \(j\) 个链前 \(t\) 个样本的平均。

# 计算潜在尺度缩减因子
Gelman.Rubin <- function(phi) {
  phi <- as.matrix(phi)
  k <- nrow(phi); n <- ncol(phi)
  phi.means <- rowMeans(phi)
  B <- n * var(phi.means)
  phi.w <- apply(phi, 1, var)
  W <- mean(phi.w)
  v.hat <- W * (n - 1) / n + B / n
  r.hat <- v.hat / W
  return(r.hat)
}

# 采用M-H算法生成链
normal.chain <- function(sigma, N, X1) {
  x <- rep(0, N)
  x[1] <- X1
  u <- runif(N)
  for (i in 2:N) {
    xt <- x[i - 1]
    y <- rnorm(1, xt, sigma)
    r1 <- dnorm(y, 0, 1) * dnorm(xt, y, sigma)
    r2 <- dnorm(xt, 0, 1) * dnorm(y, xt, sigma)
    if (u[i] <= r1 / r2) { x[i] <- y} else { x[i] <- xt }
  }
  return(x)
}

set.seed(12345)
sigma <- 1
k <- 4 # numebr of chains
n <- 15000 # length of chains
b <- 1000 # burnin period
x0 <- c(-10, -5, 5, 10) # initial value
X <- matrix(nrow = k, ncol = n)
for (i in 1:k) {
  X[i, ] <- normal.chain(sigma, n, x0[i])
}

# 绘制累积均值(phi)图
phi <- t(apply(X, 1, cumsum))
for (i in 1:nrow(phi)) {
  phi[i,] <- phi[i,] / (1:ncol(phi))
}
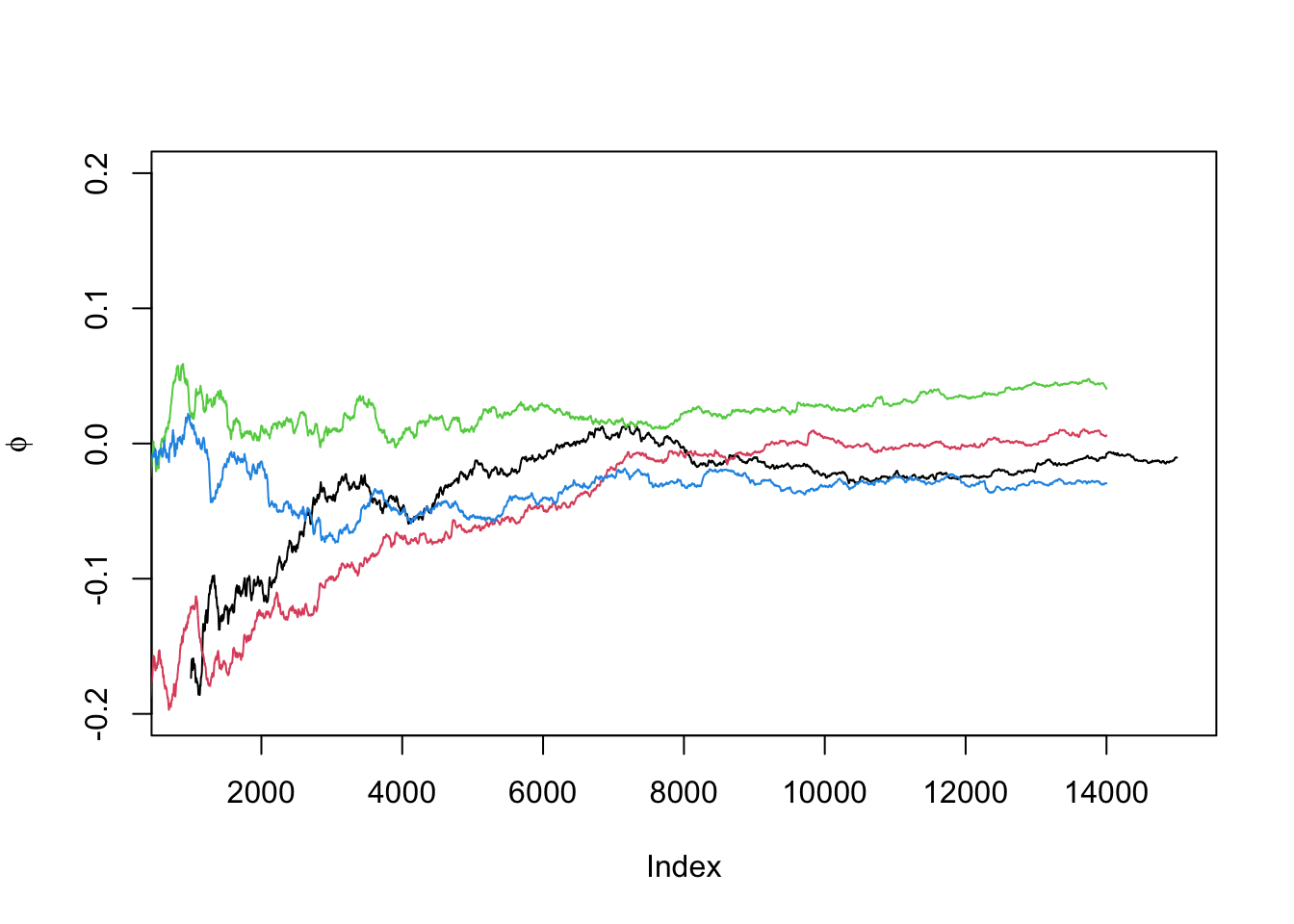
for (i in 1:k) {
  if (i == 1) {
    plot((b+1):n, phi[i, (b+1):n], ylim = c(-0.2, 0.2),
         type = "l", xlab = 'Index', ylab = bquote(phi))
  } else { lines(phi[i, (b+1):n], col = i) }
}

# 绘制潜在尺度缩减因子图
rhat <- rep(0, n)
for (j in (b+1):n) {
  rhat[j] <- Gelman.Rubin(phi[, 1:j])
}
plot(rhat[(b+1):n], type = "l", xlab = "", ylab = "R")
abline(h = 1.1, lty = 2)