Chapter 3 蒙特卡洛积分

3.1 Buffon投针问题

平面上画有很多平行线，其间距为 $a$。现向此平面投掷长为 $l$ $(l<a)$ 的针，则针的位置可以由两个数决定：针的中点与最接近的平行线之间的距离 $x$ 和针与平行线的夹角 $\varphi$，则样本空间为 $$\Omega=\left\{(\varphi,x)\mid 0\leq\varphi\leq\pi,0\leq x\leq\dfrac{a}{2}\right\}.$$ 所感兴趣的事件“针与平行线相交”对应的区域为 $$g=\left\{(\varphi,x)\mid x\leq\dfrac{l}{2}\sin\varphi\right\}.$$ 因此，针与任一平行线相交的概率为 $$P=\dfrac{\vert g\vert}{\vert\Omega\vert}=\dfrac{\displaystyle\int_0^\pi\dfrac{l}{2}\sin\varphi\text{d}\varphi}{\pi(a/2)}=\dfrac{2l}{a\pi}.$$

这一问题可以用来估计 $\pi$ 的近似值。方法是重复投针 $N$ 次，统计与平行线相交的次数 $n$，则根据频率与概率的关系可知，当 $N$ 足够大时， $$\dfrac{2l}{a\pi}=P\approx\dfrac{n}{N}~\Rightarrow~\pi\approx\dfrac{2lN}{an}.$$

对应的R代码如下：

a <- 2
l <- 1
N <- 100000
x <- runif(N, 0, a/2)
phi <- runif(N, 0, pi)
pihat <- 2*l/a/mean(l*sin(phi)/2>x)
pihat

## [1] 3.141394

可见结果与真实的圆周率的值十分接近。

设计一个随机试验，通过大量重复试验得到某种结果，以确定我们感兴趣的量，由此发展而成了著名的蒙特卡洛（Monte-Carlo）方法。

3.2 简易蒙特卡洛估计

现在我们感兴趣的问题是要计算定积分 $\displaystyle\int_a^b f(x)\text{d}x$. 可以有几种做法：

• 分析方法（微积分）：具有局限性；
• 数值积分：对一维情形较容易；
• 蒙特卡洛方法：具有普适应用。

蒙特卡洛方法的想法就是利用样本均值代替总体均值，即 $$\displaystyle \int_a^b f(x)\text{d}x=\int_a^b g(x)\dfrac{1}{b-a}\text{d}x=\mathbb E[g(X)]\approx\dfrac{1}{m}\sum_{i=1}^m g(X_i),$$ 其中 $X\sim U(a,b)$，$g(x)=(b-a)f(x)$，$X_1,\dots,X_m$ i.i.d. $\sim U(a,b)$，而 $m$ 是一个充分大的正整数。

例如，要计算 $$\displaystyle\theta=\int_2^4\text{e}^{-x}\text{d}x=2\mathbb E(\text{e}^{-X}),\quad X\sim U(2,4),$$ 可依赖如下MC代码实现：

m <- 100000
x <- runif(m, 2, 4)
thetahat <- mean(exp(-x))*2
thetahat

## [1] 0.1170082

而积分的真值为 $\text{e}^{-2}-\text{e}^{-4}=0.1170196$，可见十分接近。

再如，要计算 $$\displaystyle\theta=\int_0^x\text{e}^{-\frac{t^2}{2}}\text{d}t=\mathbb E_Y\big[x\text{e}^{-\frac{Y^2}{2}}\big],\quad Y\sim U(0,x),$$

可依赖如下MC代码实现：

m <- 100000
x <- 1
y <- runif(m, 0, x)
thetahat <- mean(x*exp(-y^2/2))
thetahat

## [1] 0.8555551

而积分的真值为 $\sqrt{2\pi}(\Phi(1)-0.5)=0.8556244$，可见十分接近。

3.2.1 理论性质

考虑蒙特卡洛积分估计的一般情形，即 $$\displaystyle\theta=\int_Af(x)\text{d}x=\int_Ag(x)h(x)\text{d}x=\mathbb E_X[g(X)],$$ 其中 $X$ 是在支撑 $A$ 上具有 p.d.f./p.m.f. $h(x)$ 的随机变量。蒙特卡洛积分估计为 $$\displaystyle\hat{\theta}=\dfrac{1}{m}\sum_{i=1}^mg(X_i),$$ 其中 $X_1,\dots,X_m$ i.i.d. $\sim h(x)$。

不难证明 $\hat{\theta}$ 是无偏估计、相合估计，而它的方差为 $\dfrac{1}{m}\text{Var}[g(X_1)]$，它的估计为 $$\displaystyle\hat{\sigma}_m^2=\dfrac{1}{m(m-1)}\sum_{i=1}^m(g(x_i)-\overline{g(x)})^2,$$ 其中 $\displaystyle\overline{g(x)}=\frac{1}{m}\sum_{i=1}^mg(x_i)$。进而可以给出 $\theta$ 的近似置信区间等。

例如，在上例中，可以进一步计算

thetas <- x*exp(-y^2/2)
se <- sd(thetas)/sqrt(m)
c(thetahat - 1.96*se, thetahat + 1.96*se)

## [1] 0.8548031 0.8563072

此即 $\theta$ 的水平为 95% 的近似置信区间。

3.3 方差缩减

为了提高蒙特卡洛估计的准确性，我们希望降低 $\hat{\theta}$ 的方差，当然我们可以通过增大样本量来实现这一功能，但一般地，我们还是希望能够减少 $\text{Var}[g(X_1)]$ 的值。

3.3.1 对偶变量

设 $U_1$ 和 $U_2$ 均为 $\theta$ 的无偏估计量，而且负相关，则 $(U_1+U_2)/2$ 也是 $\theta$ 的无偏估计量，且方差 $$\text{Var}\left(\dfrac{U_1+U_2}{2}\right)=\dfrac{\text{Var}(U_1)+\text{Var}(U_2)+\text{Cov}(U_1,U_2)}{4}<\dfrac{\text{Var}(U_1)+\text{Var}(U_2)}{4}.$$

不妨设 $\text{Var}(U_1)=\text{Var}(U_2)$，则如果分别用 $X_1,\dots,X_{m/2}$ (i.i.d.) 和 $Y_1,\dots,Y_{m/2}$ (i.i.d.) 来计算 $U_1$ 和 $U_2$ 的值，并且 $U_1$ 和 $U_2$ 是负相关的，那么 $(U_1+U_2)/2$ 的方差会小于用 $X_1,\dots,X_{m/2},X_{m/2+1},\dots,X_m$ (i.i.d.) 来计算的估计量的方差，这就实现了方差缩减的功能。

在实际应用中，如果要求生成的均匀随机变量来自 $U(a,b)$，我们常常考虑基于 $U$ 和 $a+b-U$ 来得到积分的（方差更小的）估计。

例如，在上面第二个例子中，我们可以考虑前 $m/2$ 部分由 $Y\sim U(0,x)$ 产生，而后 $m/2$ 部分由 $x-Y$ 产生（这里的 $Y$ 是刚刚产生的随机数），即 $$\displaystyle\hat{\theta}'=\dfrac{1}{m}\sum_{i=1}^{m/2}\big[x\text{e}^{-\frac{U_i^2}{2}}+x\text{e}^{-\frac{(x-U_i)^2}{2}}\big],\quad U_i\sim U(0,x).$$

参看下述代码：

MCtheta <- function(x, R = 1000, antithetic = TRUE) {
  u <- runif(R/2,0,x)
  if (!antithetic) v <- runif(R/2,0,x) else v <- x - u
  y <- c(u, v)
  thetahat <- mean(x*exp(-y^2/2))
  return(thetahat)
}
m <- 1000
MC1 <- MC2 <- numeric(m)
x <- 1
for (i in 1:m) {
  MC1[i] <- MCtheta(x, R = 1000, anti = FALSE)
  MC2[i] <- MCtheta(x, R = 1000)
}
c(sd(MC1), sd(MC2), sd(MC2)/sd(MC1))

## [1] 0.003814995 0.001128930 0.295919151

从最后一个值中可以看到，采用对偶变量法大大减少了估计量的方差。

3.3.2 控制变量

注意到如果 $g(X)$ 是 $\theta$ 的一个无偏估计量，那么 $$g(X)+c\big(f(X)-\mathbb E[f(X)]\big)$$ 也是 $\theta$ 的无偏估计量，这里 $c$ 是一个常数，而 $f(x)$ 是任意期望存在且有限的函数。

可以计算得到该估计量方差最小时对应的 $c^\star$ 为 $$\displaystyle c^\star=-\dfrac{\text{Cov}(g(X),f(X))}{\text{Var}(f(X))},$$ 对应的最小方差为 $$\text{Var}[g(X)][1-{\rm Corr}^2(g(X),f(X))].$$

由此可以实现方差缩减。但是需要注意以下几个问题：

• $\mathbb E[f(X)]$ 需要有显式表达，否则无偏估计量的形式无法得到；
• 当且仅当 $f(X)$ 和 $g(X)$ 相关时，这种方法才有效，而且强相关情况下，方差缩减的性能更佳。
• $c^\star$ 的值可以分析计算也可以数值计算。

例如，要计算 $\displaystyle\theta=\mathbb E(\text{e}^U)=\int_0^1\text{e}^u\text{d}u$，考虑控制函数 $f(U)=U$（$\text{e}^U$ 在 $U=0$ 处的一阶Taylor展开），于是 $$\displaystyle\mathbb E[f(U)]=0.5,\quad c^\star=-\frac{\text{Cov}(\text{e}^U,U)}{\text{Var}(U)}=6\text{e}-18.$$

不难计算得 $$\displaystyle\text{Var}[g(U)]\approx0.242,\quad\text{Var}[g(U)-c^\star(U-0.5)]\approx0.00394.$$

理论上看，方差得到了很大程度上的缩减。下面用代码验证之。

m <- 100000
cstar <- 6*exp(1)-18
U <- runif(m)
T1 <- exp(U)
T2 <- exp(U) + cstar*(U - 0.5)
c(mean(T1), mean(T2), exp(1)-1)

## [1] 1.716906 1.718269 1.718282

可以看到控制变量的方法得到的结果更接近真值。

c(var(T1), var(T2), (var(T1)-var(T2))/var(T1))

## [1] 0.241758782 0.003932706 0.983732933

而方差也是控制变量的结果更小，跟理论值一致，而方差也是缩减了98.37%之多。

cor(T1, U)

## [1] 0.9918333

可见 $f(U)$ 和 $g(U)$ 之间的相关性很强。

---

下面这个例子是 $c^\star$ 不容易分析计算而要采用数值计算的情况。

要计算 $\displaystyle\theta=\mathbb E\Big(\frac{\text{e}^{-U}}{1+U^2}\Big)=\int_0^1\frac{\text{e}^{-u}}{1+u^2}\text{d}u$，考虑控制函数 $f(U)=\dfrac{\text{e}^{-0.5}}{1+U^2}$，于是 $$\mathbb E[f(U)]=\text{e}^{-0.5}\pi/4,$$ 而 $c^\star$ 的值需要数值计算。参看如下代码：

f <- function(u) exp(-0.5)/(1+u^2)
g <- function(u) exp(-u)/(1+u^2)
u <- runif(10000)
cstar <- - cov(f(u), g(u)) / var(f(u))
m <- 100000
u <- runif(m)
T1 <- g(u)
T2 <- g(u) + cstar * (f(u) - exp(-0.5)*pi/4)
c(mean(T1), mean(T2))

## [1] 0.5243167 0.5246916

故积分的真值应约为0.524。

c(var(T1), var(T2), (var(T1)-var(T2))/var(T1))

## [1] 0.059914090 0.003098884 0.948277880

可见方差缩减了94.83%之多。

3.3.3 重要性采样

回到蒙特卡洛积分的一般情形，即 $$\displaystyle\theta=\int_Ag(x)\text{d}x=\int_A\frac{g(x)}{f(x)}f(x)\text{d}x=\mathbb E_X\Big[\frac{g(X)}{f(X)}\Big],$$ 其中 $X$ 是在支撑 $A$ 上具有 p.d.f./p.m.f. $f(x)$ 的随机变量。蒙特卡洛积分估计为 $$\displaystyle\hat{\theta}=\dfrac{1}{m}\sum_{i=1}^m\frac{g(X_i)}{f(X_i)},$$ 其中 $X_1,\dots,X_m$ i.i.d. $\sim f(x)$。

前面所讲述的方法都取了 $f(x)$ 为对应支撑上的均匀分布，也就是说将所有的都赋予相同的权重，但这有时候在计算时效率不是很高，这从前面两种方差缩减方法中也可以看出来。

重要性采样的思想是用一个十分接近 $g(x)$ 且容易采样的概率密度函数 $f(x)$ 来进行重要性采样，这种估计的方差 $$\displaystyle\text{Var}(\hat{\theta})=\frac{1}{m}\text{Var}\Big[\frac{g(X_1)}{f(X_1)}\Big]$$ 在 $g(\cdot)=cf(\cdot)$ 对某个常数 $c$ 成立时达到最小值0，这里的 $f(\cdot)$ 称为 $g(\cdot)$ 的重要性函数。

同样考虑上例中的积分 $\displaystyle\theta=\int_0^1\frac{\text{e}^{-x}}{1+x^2}\text{d}x$，考虑以下几个重要性函数：

$$\begin{align*} f_1(x) &= 1,\quad 0<x<1,\\ f_2(x) &= \text{e}^{-x},\quad 0<x<\infty,\\ f_3(x) &= \dfrac{1}{\pi(1+x^2)},\quad -\infty<x<\infty,\\ f_4(x) &= \dfrac{\text{e}^{-x}}{1-\text{e}^{-1}},\quad 0<x<1,\\ f_5(x) &= \dfrac{4}{\pi(1+x^2)},\quad 0<x<1. \end{align*}$$

记被积函数为 $g(x)=\dfrac{\text{e}^{-x}}{1+x^2},0<x<1$，先在同一坐标系中画出 0～1 范围内各自的函数图像比较。

x <- seq(0, 1, 0.01)
g <- exp(-x) / (1+x^2)
f1 <- replicate(length(x), 1)
f2 <- exp(-x)
f3 <- 1 / (1+x^2) / pi
f4 <- exp(-x) / (1 - exp(-1))
f5 <- 4 / (1+x^2) / pi

plot(x, g, type = 'l', xlab='x', ylab='', xlim=c(0,1), ylim=c(0,2), lwd=2)
lines(x, f1, col=2, lty=2, lwd=1.5)
lines(x, f2, col=7, lty=3, lwd=1.5)
lines(x, f3, col=3, lty=4, lwd=1.5)
lines(x, f4, col=4, lty=5, lwd=1.5)
lines(x, f5, col=5, lty=6, lwd=1.5)
legend("topright", c(expression(g(x)==e^{-x}/(1+x^2)),
                     expression(f[1](x)==1),
                     expression(f[2](x)==e^{-x}),
                     expression(f[3](x)==1/pi/(1+x^2)),
                     expression(f[4](x)==e^{-x}/(1-e^{-1})),
                     expression(f[5](x)==4/pi/(1+x^2))),
       col=c(1, 2, 7, 3, 4, 5), lty=c(1, 2, 3, 4, 5, 6), lwd=c(2, 1.5, 1.5, 1.5, 1.5, 1.5),
       x.intersp=0.5, y.intersp=1.2, inset = 0.02, bty = 'o', text.width=0.25)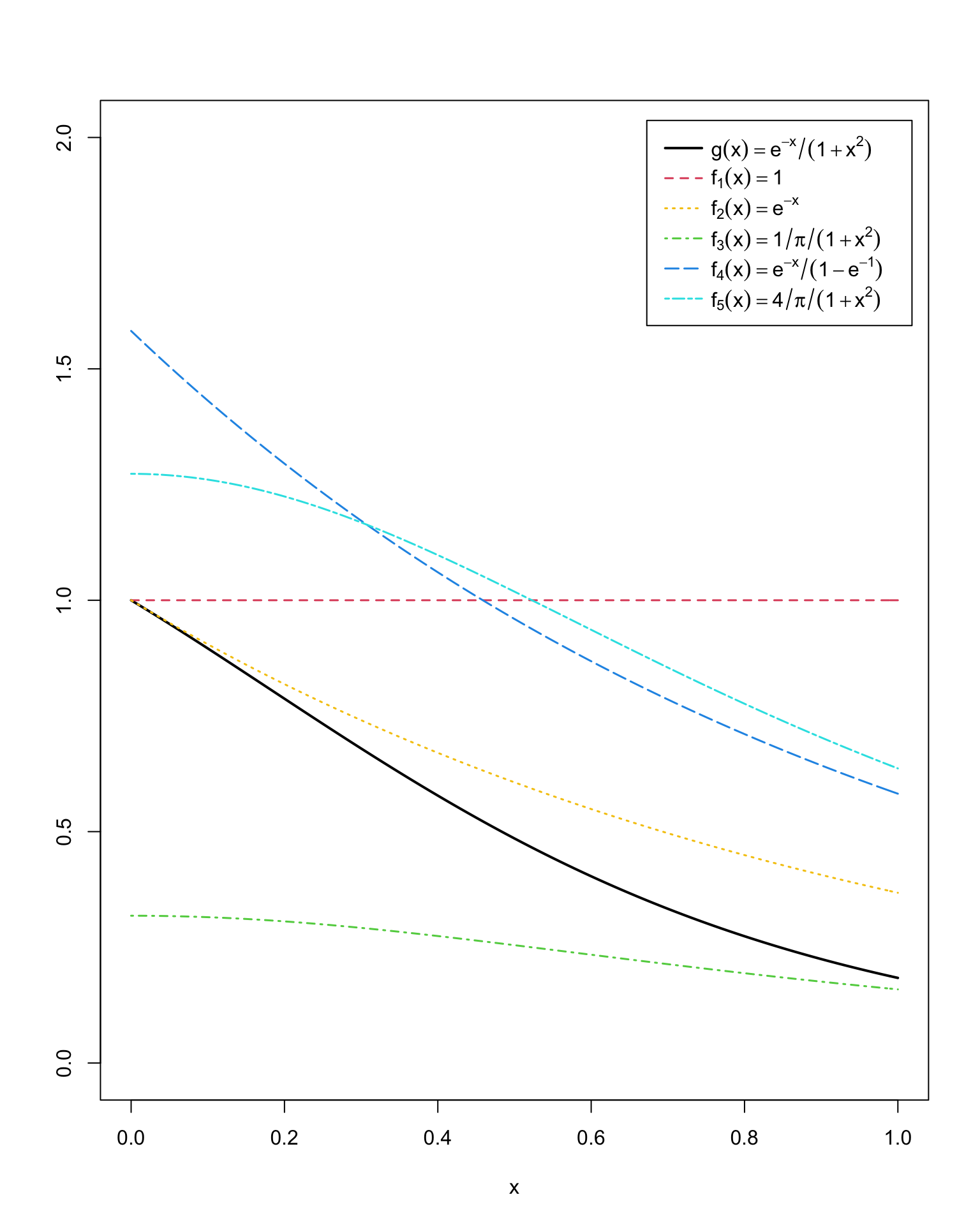

m <- 10000
thetahat <- se <- numeric(5)
g <- function(x) {exp(-x) / (1+x^2) * (x>0) * (x<1)}

x <- runif(m)  # f1
gf <- g(x)
thetahat[1] <- mean(gf)
se[1] <- sd(gf)

x <- rexp(m, 1) # f2
gf <- 1/(1+x^2) * (x<1)
thetahat[2] <- mean(gf)
se[2] <- sd(gf)

x <- rcauchy(m) # f3
x <- x * (x>0) * (x<1) # Note the range of x
gf <- pi * exp(-x) * (x>0) * (x<1)
thetahat[3] <- mean(gf)
se[3] <- sd(gf)

u <- runif(m) # f4
x <- - log(1 - u * (1 - exp(-1)))
gf <- (1 - exp(-1)) / (1 + x^2)
thetahat[4] <- mean(gf)
se[4] <- sd(gf)

u <- runif(m) # f5
x <- tan(pi * u / 4)
gf <- pi * exp(-x) / 4
thetahat[5] <- mean(gf)
se[5] <- sd(gf)

rbind(thetahat, se)

              [,1]      [,2]     [,3]       [,4]      [,5]
thetahat 0.5236325 0.5159951 0.523879 0.52507935 0.5277204
se       0.2448966 0.4204343 0.952761 0.09674458 0.1397128

可以看到，用与目标函数形式较一致的重要性函数所最终得到的结果更加精确，标准差也更小。

3.3.4 分层采样

考虑将 $M$ 个样本分层为 $k$ 层，每层样本数为 $m_i~(i=1,\dots,k)$，考虑分层估计量 $$\displaystyle\hat{\theta}^S=\sum_{i=1}^kw_i\hat{\theta}_i$$ 其中每一层的采用MC估计 $\hat{\theta}_i$，$w_i$ 是每一层的权重。不难证明 $\text{Var}(\hat{\theta}^S)\leq\text{Var}(\hat{\theta}^M)$，这里 $\hat{\theta}^M$ 是直接采用 $M$ 个样本做的简单MC估计。

---

命题. 记 $\displaystyle\hat{\theta}^M=\frac{1}{M}\sum_{i=1}^Mg(U_i)$ 为直接采用 $M$ 个样本做的简单MC估计，$\displaystyle\hat{\theta}^S=\frac{1}{k}\sum_{j=1}^k\hat{\theta}_j$ 为分层估计量（这里假设均匀分层，即 $m=M/k$），其中 $\displaystyle\hat{\theta}_j=\frac{1}{m}\sum_{i=1}^mg(U_{ji})$。于是 $$\displaystyle\text{Var}(\hat{\theta}^S)=\frac{1}{k^2}\sum_{j=1}^k\text{Var}(\hat{\theta}_j)=\frac{1}{k^2}\sum_{j=1}^k\frac{1}{m}\sigma_j^2=\frac{1}{Mk}\sum_{j=1}^k\sigma_j^2.$$

另外，设 $J$ 是随机选择的层，它服从概率为 $1/k$ 的离散均匀分布，于是

$$\begin{align*} \text{Var}(\hat{\theta}^M) &= \frac{\text{Var}(g(U))}{M}=\frac{1}{M}\big[\text{Var}(\mathbb E[g(U)\mid J])+\mathbb E[\text{Var}(g(U)\mid J)]\big]\\ &= \frac{1}{M}\big(\text{Var}(\theta_J)+\mathbb E(\sigma_J^2)\big)\\ &= \frac{1}{M}\left(\text{Var}(\theta_J)+\frac{1}{k}\sum_{j=1}^k\sigma_j^2\right)\\ &= \dfrac{1}{M}\text{Var}(\theta_J)+\text{Var}(\hat{\theta}^S)\geq\text{Var}(\hat{\theta}^S). \end{align*}$$

---

同样考虑上例中的积分 $\displaystyle\theta=\int_0^1\frac{\text{e}^{-x}}{1+x^2}\text{d}x$，注意到

$$\begin{align*} \displaystyle\int_0^1\frac{\text{e}^{-x}}{1+x^2}\text{d}x &= \displaystyle\sum_{i=1}^k\int_{(i-1)/k}^{i/k}\frac{\text{e}^{-x}}{1+x^2}\text{d}x\\ &= \displaystyle\frac{1}{k}\sum_{i=1}^k\int_{(i-1)/k}^{i/k}\frac{\text{e}^{-x}}{1+x^2}k\text{d}x\\ &= \displaystyle\dfrac{1}{k}\sum_{i=1}^k\mathbb E\left(\frac{\text{e}^{-X_i}}{1+X_i^2}\right),\quad X_i\sim U\left(\frac{i-1}{k},\frac{i}{k}\right). \end{align*}$$

因此，分层采样的代码实现如下：

M <- 10000
k <- 10
m <- M / k
N <- 100
T2 <- numeric(k)
est <- matrix(0, N, 2)
g <- function(x) {
  exp(-x)/(1+x^2) * (x>0) * (x<1)
}
for (i in 1:N) {
  est[i, 1] <- mean(g(runif(M)))
  for (j in 1:k) {
    T2[j] <- mean(g(runif(m, (j-1)/k, j/k)))
  }
  est[i, 2] <- mean(T2)
}
mu = apply(est, 2, mean)
se = apply(est, 2, sd)
rbind(mu, se)

          [,1]        [,2]
mu 0.524716298 0.524775325
se 0.002444945 0.000222032

可见分层采样的方差比简单MC方法的方差要小得多。