Chapter 4 统计推断中的蒙特卡洛方法

4.1 点估计问题

设 $\hat{\theta}(X_1,\dots,X_n)$ 是未知参数 $\theta$ 的估计量，关心以下问题：

• 这个估计的偏差（Bias）$\hat{\theta}-\theta$ 是多少？
• 这个估计的标准误差（SE）$\text{se}(\hat{\theta})$ 是多少？（对它而言，这个值越小越好）
• 这个估计的标准误差的估计（SEE）$\hat{\text{se}}(\hat{\theta})$ 是多少？（为进一步构建置信区间、做假设检验提供帮助）

一般地，我们考虑做 $m$ 次估计，来得到 $\hat{\theta}_1,\dots,\hat{\theta}_m$，基于此构建上述估计。具体算法如下：

• 设定随机种子、重复次数 $m$、样本量 $n$ 和参数真值 $\theta_0$；
• 对第 $j~(j=1,\dots,m)$ 次计算
  • 生成样本 $X_{j1},\dots,X_{jn}$；
  • 估计 $\theta$：$\hat{\theta}_j=\hat{\theta}(X_{j1},\dots,X_{jn})$ 及其标准误差 $\hat{\text{se}}_j=\hat{\text{se}}(\hat{\theta}_j)$；
• 计算相应的估计量：
  • 偏差 Bias $=\overline{\theta}-\theta_0$，其中 $\overline{\theta}=\dfrac{1}{m}\sum\limits_{j=1}^m\hat{\theta}_j$；
  • 标准误差 SE $=\sqrt{\dfrac{1}{m-1}\sum\limits_{j=1}^m(\hat{\theta}_j-\overline{\theta})^2}$；
  • 标准误差的估计 SEE $=\dfrac{1}{m}\sum\limits_{j=1}^m\hat{\text{se}}_j.$

一般情况下，即使方差估计是无偏的，但标准误差的估计不是标准误差的无偏估计，这是因为随机误差、试验设计、样本量等的影响。参考下面几个例子。

例1. (正态误差、随机预测) 对模型 $$Y_i=\alpha+\beta X_i+e,\quad e\sim N(0,1),~X_i\sim Exp(1).$$

考虑参数 $\beta$ 的最小二乘估计。

alpha <- 2; beta <- 1
m <- 1000; n <- 10; set.seed(1)
beta.hat <- beta.se <- numeric(m)
for (i in 1:m) {
  x <- rexp(n)
  y <- alpha + beta*x + rnorm(n)
  coef <- summary(lm(y~x))$coef
  beta.hat[i] <- coef[2,1]
  beta.se[i] <- coef[2,2]
}
c(mean(beta.hat), sd(beta.hat), mean(beta.se))

## [1] 1.0006017 0.4940051 0.4201906

c(var(beta.hat), mean(beta.se^2))

## [1] 0.2440410 0.2281339

例2. (非正态误差、随机预测) 对模型 $$Y_i=\alpha+\beta X_i+e,\quad e\sim ST(\alpha=8,\nu=2),~X_i\sim Exp(1).$$

考虑参数 $\beta$ 的最小二乘估计。

alpha <- 2; beta <- 1
m <- 1000; n <- 10; set.seed(1)
beta.hat <- beta.se <- numeric(m)
for (i in 1:m) {
  x <- rexp(n)
  y <- alpha + beta*x + sn::rst(n, alpha=8, nu=2)
  coef <- summary(lm(y~x))$coef
  beta.hat[i] <- coef[2,1]
  beta.se[i] <- coef[2,2]
}
c(mean(beta.hat), sd(beta.hat), mean(beta.se))

## [1] 1.0329123 1.1641705 0.7988274

c(var(beta.hat), mean(beta.se^2))

## [1] 1.355293 5.512689

例3. (正态误差、固定预测) 对模型$Y_i=\alpha+\beta X+e,\quad e\sim N(0,1),~X\sim Exp(1).$$

考虑参数 $\beta$ 的最小二乘估计。

alpha <- 2; beta <- 1
m <- 1000; n <- 10; set.seed(1)
beta.hat <- beta.se <- numeric(m)
x <- rexp(n)
for (i in 1:m) {
  y <- alpha + beta*x + rnorm(n)
  coef <- summary(lm(y~x))$coef
  beta.hat[i] <- coef[2,1]
  beta.se[i] <- coef[2,2]
}
c(mean(beta.hat), sd(beta.hat), mean(beta.se))

## [1] 0.9882903 0.4014756 0.3853365

c(var(beta.hat), mean(beta.se^2))

## [1] 0.1611826 0.1583228

例4. (非正态误差、固定预测) 对模型 $$Y_i=\alpha+\beta X+e,\quad e\sim ST(\alpha=8,\nu=2),~X\sim Exp(1).$$

考虑参数 $\beta$ 的最小二乘估计。

alpha <- 2; beta <- 1
m <- 1000; n <- 10; set.seed(1)
beta.hat <- beta.se <- numeric(m)
x <- rexp(n)
for (i in 1:m) {
  y <- alpha + beta*x + sn::rst(n, alpha=8, nu=2)
  coef <- summary(lm(y~x))$coef
  beta.hat[i] <- coef[2,1]
  beta.se[i] <- coef[2,2]
}
c(mean(beta.hat), sd(beta.hat), mean(beta.se))

## [1] 1.0056361 1.8029219 0.7475751

c(var(beta.hat), mean(beta.se^2))

## [1] 3.250527 5.934975

---

在估计量的评价准则中，还有一个十分常用的标准，那就是均方误差MSE： $$\text{MSE}=\mathbb E(\hat{\theta}-\theta)^2=\text{Var}(\hat{\theta})+(\mathbb E(\hat{\theta})-\theta)^2=\text{Variance}+\text{Bias}^2.$$

对它的估计可以采用 $\dfrac{1}{m}\sum\limits_{j=1}^m(\hat{\theta}_j-\theta)^2$。例如，在例4中，可以进一步计算MSE的估计如下：

mean((beta.hat-beta)^2)

## [1] 3.247309

这个值和它的方差3.2505273十分接近，因为在最小二乘估计中 $\hat{\beta}$ 是 $\beta$ 的无偏估计，那么MSE就是方差。

4.2 区间估计问题

在经典统计推断区间估计问题中，我们感兴趣的是重复试验下区间估计的覆盖概率（Coverage Probability）：如果 $\theta$ 的 $(1-\alpha)\%$ 置信区间为 $(\hat{\theta}_L,\hat{\theta}_U)$，那么覆盖概率定义为 $\mathbb P(\hat{\theta}_L<\theta<\hat{\theta}_U)$。（注意，在经典统计推断中，这里随机变量是 $\hat{\theta}_L$ 和 $\hat{\theta}_U$）

我们希望一个好的区间估计有接近于 $(1-\alpha)\%$ 的覆盖概率水平：

• 如果覆盖概率明显大于 $(1-\alpha)\%$，称这样的区间估计是保守的（conservative）；
• 如果覆盖概率明显小于 $(1-\alpha)\%$，称这样的区间估计是宽容的（liberal）。

对它的估计可以采用 $\dfrac{1}{m}\sum\limits_{j=1}^mI(\hat{\theta}_L^{(j)}\leq\theta\leq\hat{\theta}_U^{(j)})$，称之为经验覆盖概率。例如，在例4中，$\beta$ 的95%置信区间为 $$\left(\hat{\beta}-t_{0.975}(n-2)\hat{\sigma}_\beta,\hat{\beta}+t_{0.975}(n-2)\hat{\sigma}_\beta\right).$$

由下述代码可以计算它的经验覆盖概率。

mean((beta >= beta.hat - qt(0.975, n-2) * beta.se) *
       (beta <= beta.hat + qt(0.975, n-2) * beta.se))

## [1] 0.94

这个值比0.95小，可见这样的区间估计是宽容的，因为在模型设定有误时标准误差是会被低估的。

4.3 假设检验问题

考虑假设检验问题： $$H_0:\theta=\theta_0\longleftrightarrow H_a:\theta\neq\theta_0.$$

在水平 $\alpha$ 下拒绝假设 $H_0$ 如果：

• $T>\tau$ 对某个阈值 $\tau$ 成立；
• p值 $=\mathbb P_{H_0}(T>T^{(\text{o})}\mid\text{observed data})=\bar{F}(T^{(\text{o})})\leq\alpha$，这里 $\bar{F}$ 是 $T$ 在 $H_0$ 下的生存函数。

4.3.1 第一类错误率（Type I Error Rate）

假设检验中的第一类错误率定义为在 $H_0$ 下拒绝原假设（p值 $\leq\alpha$）的概率。由于p值的计算是在一个人为给定的原假设分布下进行，所以如果零假设分布正确并且分布连续，则第一类错误率可以在任何预先给定的水平下被控制： $$\mathbb P_{H_0}(\text{p值}\leq\alpha)=\alpha.$$

一个好的检验应到至少有一个接近于水平 $\alpha$ 的第一类错误率：

• 如果第一类错误率明显低于 $\alpha$，称这个检验是保守的（conservative），它扩大了假负率；
• 如果第一类错误率明显高于 $\alpha$，称这个检验是宽容的（liberal），它扩大了假正率。

在实际问题中，对它的估计可以采用 $\dfrac{1}{m}\sum\limits_{j=1}^mI(p_j\leq\alpha)$。

例如，在例4中，重新设定模型参数真值 $\beta=0$，考虑假设检验问题 $$H_0:\beta=0\longleftrightarrow H_a:\beta\neq0.$$

利用如下代码可以计算其第一类错误率。

alpha <- 2; beta <- 0
m <- 1000; n <- 10; set.seed(1)
beta.hat <- beta.se <- p.val1 <- numeric(m)
x <- rexp(n)
for (i in 1:m) {
  y <- alpha + beta*x + rt(n, 2)
  coef <- summary(lm(y~x))$coef
  beta.hat[i] <- coef[2,1]
  beta.se[i] <- coef[2,2]
  p.val1[i] <- coef[2,4]
}
p.val2 <- 2 * (1 - pt(abs(beta.hat/beta.se), n-2))
c(mean(p.val1 <= 0.05), mean(p.val2 <= 0.05))

## [1] 0.071 0.071

再例如，在例1中，重新设定模型参数真值 $\beta=0$，考虑假设检验问题 $$H_0:\beta=0\longleftrightarrow H_a:\beta\neq0.$$

利用如下代码可以计算其第一类错误率。

alpha <- 2; beta <- 0
m <- 1000; n <- 10; set.seed(5)
beta.hat <- beta.se <- p.val1 <- numeric(m)
for (i in 1:m) {
  x <- rexp(n)
  y <- alpha + beta*x + rnorm(n)
  coef <- summary(lm(y~x))$coef
  beta.hat[i] <- coef[2,1]
  beta.se[i] <- coef[2,2]
  p.val1[i] <- coef[2,4]
}
p.val2 <- 2 * (1 - pt(abs(beta.hat/beta.se), n-2))
c(mean(p.val1 <= 0.05), mean(p.val2 <= 0.05))

## [1] 0.053 0.053

思考： 如果在10000次蒙特卡洛试验中得到第一类错误率为0.053，可不可以说第一类错误率已经被控制在0.05？

• 建立第一类错误率的95%置信区间或检验假设 $H_0:$ 第一类错误率 $= 0.05$；
• 结果与二项分布有关。

binom.test(530, 10000, p = 0.05)

## 
##  Exact binomial test
## 
## data:  530 and 10000
## number of successes = 530, number of trials = 10000, p-value = 0.1686
## alternative hypothesis: true probability of success is not equal to 0.05
## 95 percent confidence interval:
##  0.04868974 0.05757286
## sample estimates:
## probability of success 
##                  0.053

可以看到p值为 $0.1686>0.05$，95%置信区间为 $[0.049,0.058]$，因此可以认为已被控制在0.05。

4.3.2 功效（Power）

假设检验中的功效定义为在 $H_a$ 下拒绝原假设（p值 $\leq\alpha$）的概率。

注意在讨论功效的问题时，首先要保证第一类错误率受水平 $\alpha$ 控制。一个好的检验应当在第一类错误率受水平 $\alpha$ 控制的情况下有尽可能高的功效。

至于实际问题中对它的估计与估计第一类错误率类似，只是生成数据的方式有所不同。例如，在例4中，考虑假设检验问题 $$H_0:\beta=0\longleftrightarrow H_a:\beta\neq0.$$

利用如下代码可以计算其 $\beta=1$ 时的功效。

alpha <- 2; beta <- 1
m <- 1000; n <- 10; set.seed(1)
beta.hat <- beta.se <- p.val1 <- numeric(m)
x <- rexp(n)
for (i in 1:m) {
  y <- alpha + beta*x + rt(n, 2)
  coef <- summary(lm(y~x))$coef
  beta.hat[i] <- coef[2,1]
  beta.se[i] <- coef[2,2]
  p.val1[i] <- coef[2,4]
}
p.val2 <- 2 * (1 - pt(abs(beta.hat/beta.se), n-2))
c(mean(p.val1 <= 0.05), mean(p.val2 <= 0.05))

## [1] 0.284 0.284

4.3.3 多重检验问题

考虑如下的混淆矩阵：

	$H_0$ 为真	$H_a$ 为真	总数
Positive (拒绝 $H_0$)	$V$ (FP)	$S$ (TP)	$R$
Negative (接受 $H_0$)	$U$ (TN)	$T$ (FN)	$m-R$
总数	$m_0$	$m-m_0$	$m$

考虑以下几个指标：

• 给定真假设条件
  • 假正率（FPR）：$V/m_0$，即第一类错误率；
  • 真正率（TPR）：$S/(m-m_0)$，即功效；
  • 假负率（FNR）：$T/(m-m_0)$；
  • 真负率（TNR）：$U/m_0$。
• 给定预测条件
  • 假查率（FDR）：$V/R$；
  • 真查率（TDR）：$S/R$。

检验的结果取决于检验统计量的阈值比如p值：

• 接受者操作特征（ROC）曲线：FPR vs TPR 曲线，通常用AUC(Area under the curve)指标；
• PR曲线：TDR(Precision) vs TPR(Recall) 曲线，通常用F1(P和R的调和平均)指标。

par(mfrow = c(1, 2))
library(ROCR)
data(ROCR.simple)
pred <- prediction(ROCR.simple$pred, ROCR.simple$labels)

# ROC curve
perf <- performance(pred, "tpr", "fpr")
plot(perf)
perf <- performance(pred, "auc")
auc <- perf@y.values[[1]]
text(0.5, 0.5, paste0("AUC = ", round(auc, 4)))

# PR curve
perf <- performance(pred, "prec", "rec")
plot(perf)
id <- which.max(abs(perf@x.values[[1]] + perf@y.values[[1]]))
P <- perf@x.values[[1]][id]
R <- perf@y.values[[1]][id]
F1 <- 2 / (1/P + 1/R)
text(0.8, 0.9, paste0("F1 = ", round(F1, 4)))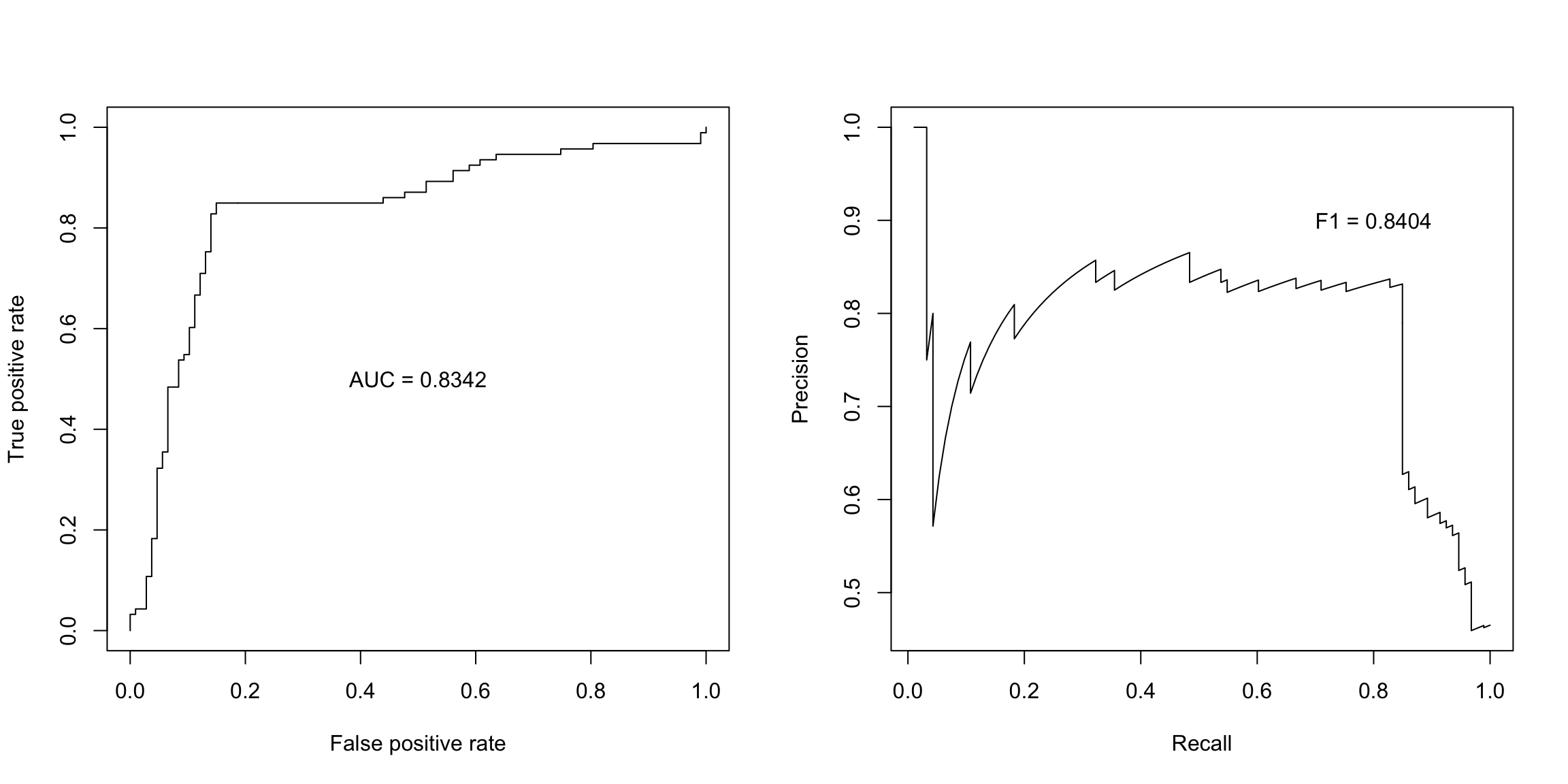

在多重检验下的p值调整：

• Family-wise error rate (FWER)：针对多个零假设 $H_{01},\dots,H_{0N}$, 有多个p值$p_1,\dots,p_N$，FWER定义为 $$\mathbb P(\text{拒绝任一原假设}\mid\text{所有}~N~\text{个原假设都成立}).$$ 如果$p_i<\alpha/N (i=1,\dots,N)$，则FWER可以在水平$\alpha$下被控制——称这种方法为Bonferroni修正.
• False discovery rate(FDR)：在被拒绝的假设下的期望错误发现的比例。通常做法是对p值进行排序而拒绝那些满足$p_{(k)}\leq k\alpha/N$的假设。这样FDR就被控制在水平$\alpha$下——称这种方法为FDR修正。

p <- sort(c(0.01, 0.01, 0.02, 0.05, 0.05, 0.5))
n <- length(p)
p.adj1 <- p/(1:n)*n
p.adj2 <- p.adjust(p, method = "fdr")
p.adj3 <- p.adjust(p, method = "bonferroni")
rbind(p.adj1, p.adj2, p.adj3)

       [,1] [,2] [,3]  [,4] [,5] [,6]
p.adj1 0.06 0.03 0.04 0.075 0.06  0.5
p.adj2 0.03 0.03 0.04 0.060 0.06  0.5
p.adj3 0.06 0.06 0.12 0.300 0.30  1.0

通常，FDR修正用于探索性研究（Exploring Research），而Bonferroni修正用于确认性研究（Confirmation Research）。