Chapter 7 R中的数值方法
7.1 介绍
7.1.1 恒等与约等
我们知道计算机中存储数据都是以二进制的形式,因此一个实数 \(x\) 通常可以由一串 \(\{0,1\}\) 序列唯一表示 \(a_ka_{k-1}\dots a_1a_0a_{-1}a_{-2}\dots\),满足 \[x=a_k\cdot2^k+a_{k-1}\cdot2^{k-1}+\cdots+a_1\cdot2+a_0+a_{-1}\cdot2^{-1}+a_{-2}\cdot2^{-2}+\cdots.\] 对一般的底 \(b\) 也可以有类似的表示,常用的有二进制、八进制、十进制和十六进制表示。
对于正整数而言,这种表示是有限长的;而对负整数,通常要引入反码、补码的概念。更特别地,对于实数(或者说浮点数)来说,这种存储就成为了一种近似存储,无法完全存储下来。
例如,下面这个例子表明在计算机中0.3 - 0.1并不真正意义上等于0.2,这是因为\[0.2=(0.00110011\dots)_2\]是二进制意义下的无限循环小数, 计算机不可能完全存储。
0.3 - 0.1## [1] 0.20.3 - 0.1 == 0.2## [1] FALSE(0.3 - 0.1) - 0.2## [1] -2.775558e-17因此,我们常常利用all.equal来得到比较合理的比较结果。
isTRUE(0.3 - 0.1 == 0.2)## [1] FALSEisTRUE(all.equal(0.3 - 0.1, 0.2))## [1] TRUE不过它也有它的不足之处,参看下例。这是因为all.equal的可容许限约为1.49e-08,而这里的1e-10显然超过了这一限。
isTRUE(all.equal(1e-10, 2e-10))## [1] TRUE除此之外,R中还有identical来确切比较两个数据容器是否一致,这与==的逐元素比较有差别,参看下例。
x <- 1:4; y <- 2
c(res1 = y == 2, res2 = identical(y, 2))## res1 res2
## TRUE TRUEc(res3 = x == y, res4 = identical(x, y))## res31 res32 res33 res34 res4
## FALSE TRUE FALSE FALSE FALSE尤其注意到res3输出了4个结果,因为x是1:4的integer容器。
identical(1:2, c(1,2))## [1] FALSEidentical(1, as.integer(1))## [1] FALSE此外,上述结果表明integer容器和numeric容器的区别。
7.1.2 似然比
在实际的统计问题中,我们经常需要计算似然比,而这也会涉及到近似或者计算量大的问题。对较大的 \(n\),\[\dfrac{n!}{(n-2)!}=n(n-1)\] 的结果计算较为简单,但是分子和分母的单独计算却给计算机带来了计算的负荷。因此,我们常常采用取对数的方式解决。
例如,为计算\[\dfrac{\Gamma(\frac{n-1}{2})}{\Gamma(\frac{1}{2})\Gamma(\frac{n-2}{2})},\]我们可以使用exp(lgamma())而不是gamma()来得到相应的结果。
n <- c(100, 400)
gamma((n-1)/2) / gamma(1/2) / gamma((n-2)/2)## [1] 3.939265 NaNexp(lgamma((n-1)/2) - lgamma(1/2) - lgamma((n-2)/2))## [1] 3.939265 7.953876可以看到当 \(n=400\) 时计算机已经承受不住这么大的计算了!
又如,考虑一个特殊的例子,即验证Taylor公式\[\ln\cos x=-\frac{x^2}{2}-\frac{x^4}{12}-\frac{x^6}{45}+o(x^6).\] 考虑\[\dfrac{\ln\cos x+\frac{x^2}{2}+\frac{x^4}{12}}{\frac{x^6}{45}}\]应当接近于\(-1\),于是有如下代码验证。
fun <- function(x) {
(log(cos(x)) + x^2 / 2 + x^4 / 12) / (x^6 / 45)
}
round(fun(c(0.5, 0.1, 0.01, 0.001, 0.0005)), 4)## [1] -1.0826 -1.0030 -1.0007 351.4172 123540.5607可以看到,当 \(x\) 很小时,由于分子分母都很小,导致结果计算有误。
7.2 方程求根问题
7.2.1 一元方程求根
假设 \(f:\mathbb R\rightarrow\mathbb R\) 为一连续函数,考虑求解方程 \(f(x)=0\) 的根。
- 二分法:不带有额外限制,但收敛速度较慢。
设 \(f\) 在 \([a,b]\) 上连续,且 \(f(a)f(b)<0\),则存在 \(x_0\in(a,b)\),使得 \(f(x_0)=0\)。根据这一事实就可以通过不断二分区间 \((a,b)\) 来得到方程在 \((a,b)\) 区间内的一个根。
f <- function(x) { x^5 - x - 1 }
a <- -5
b <- 5
it <- 0
eps <- 1e-6
r <- seq(a, b, length = 3)
y <- c(f(r[1]), f(r[2]), f(r[3]))
while (it < 1000 && abs(y[2]) > eps) {
it <- it + 1
if (y[1] * y[2] < 0) {
r[3] <- r[2]
y[3] <- y[2]
} else {
r[1] <- r[2]
y[1] <- y[2]
}
r[2] <- (r[1] + r[3]) / 2
y[2] <- f(r[2])
}
cbind(root = r[2], f.root = y[2], iter = it)## root f.root iter
## [1,] 1.167304 -4.843226e-07 23- Newton-Raphson方法:需要函数的一阶导数。
设 \(f\) 连续可微,且 \(f'(x)\neq0\),则Newton-Raphson方法提供了一种迭代求根的方式\[x_{n+1}=x_n-\dfrac{f(x_n)}{f'(x_n)}.\] 它的收敛速度比二分法要快,但是非常依赖于初值的选取。
f.diff <- function(x) { 5 * x^4 - 1 }
max.iters <- 100
x <- numeric(max.iters)
x[1] <- 2
for (i in 2:max.iters) {
x[i] <- x[i-1] - f(x[i-1]) / f.diff(x[i-1])
if (abs(x[i] - x[i-1]) < eps) { break }
}
cbind(root = x[i], f.root = f(x[i]), iter = i)## root f.root iter
## [1,] 1.167304 6.661338e-16 8- Brent算法:不使用函数的导数,主要通过逆插值的方式实现。
如果现有三个点为 \((a,f(a)), (b,f(b)), (c,f(c))\),其中 \(b\) 为当前最好的估计,则通过Lagrange多项式插值方法对方程进行根(其中 \(y=0\))的估计:\[x=\frac{[y-f(a)][y-f(b)]c}{[f(c)-f(a)][f(c)-f(b)]}+\frac{[y-f(b)][y-f(c)]a}{[f(a)-f(b)][f(a)-f(c)]}+\frac{[y-f(c)][y-f(a)]b}{[f(b)-f(c)][f(b)-f(a)]}.\]
在R中可以利用uniroot函数实现Brent算法求根。
res <- uniroot(f, c(-1, 2))
unlist(res)## root f.root iter init.it estim.prec
## 1.167301e+00 -2.826855e-05 9.000000e+00 NA 6.103516e-05在统计计算中,极大似然估计(得分函数求根)和估计方程(GEE)等都可以用到上述方案。
下面例子是通过方程求根来实现模拟实验中Logistic回归截距项确定的问题。考虑如下Logistic回归问题\[\mathbb P(D=1\mid X_1=x_1,X_2=x_2)=\dfrac{\exp(\alpha+\beta_1x_1+\beta_2x_2)}{1+\exp(\alpha+\beta_1x_1+\beta_2x_2)}.\] 在模拟实验中,一些重要参数会被提前指定:
- 参数(也称为对数OR值):\(\beta_1=1\),\(\beta_2=0.5\);
- 协变量分布:\(X_1\sim N(0,1)\),\(X_2\sim B(1,0.5)\);
- 先验概率 \(\mathbb P(D=1)=f_0\),其中 \(f_0\) 已知。
为了生成样本数据,我们就必须知道 \(\alpha\) 的值,也就是要求解方程\[f_0=\mathbb P(D=1)=\mathbb E[\mathbb P(D=1\mid X_1,X_2)].\] 事实上,我们可以将 \(f=\mathbb P(D=1)\) 看作 \(\alpha\) 的函数,通过样本数据估计 \(f(\alpha)\) 进而求根:
- 设定 \(f_0,\beta_1,\beta_2,N\)(足够大);
- 生成 \((x_{1i},x_{2i})\),\(i=1,\dots,N\);
- 构造函数 \[g(\alpha)=\dfrac{1}{N}\sum_{i=1}^N\dfrac{1}{1+\exp(-\alpha-\beta_1x_{1i}-\beta_2x_{2i})}-f_0;\]
- 利用
uniroot函数求 \(g(\alpha)=0\) 的根。
f0 <- 0.01
beta1 <- 1
beta2 <- 0.5
N <- 1e6
x1 <- rnorm(N)
x2 <- sample(0:1, N, replace = TRUE)
g <- function(alpha) {
p <- 1 / (1 + exp(-alpha - beta1 * x1 - beta2 * x2))
return(mean(p) - f0)
}
res <- uniroot(g, c(-10, 10))
unlist(res)## root f.root iter init.it estim.prec
## -5.360166e+00 -3.274244e-08 1.100000e+01 NA 6.103516e-05进一步也可以验证 \(f_0\) 的理论值与模拟值的差异是否很小。
alpha <- res$root
p <- 1 / (1 + exp(-alpha - beta1 * x1 - beta2 * x2))
d <- rbinom(N, 1, p)
mean(d)## [1] 0.009947.2.2 多元方程求根
设 \(f(\pmb x)=f(x_1,\dots,x_p)\) 是 \(\mathbb R^p\rightarrow\mathbb R\) 的连续函数,考虑求解方程 \(f(\pmb x)=0\)。
一般而言,前面所述的二分法与Newton-Raphson方法都可行。以Newton-Raphson方法为例,为求 \(f'(\pmb x)=0\) 的根,考虑 \(f(\pmb x^*)\) 的一阶逼近\[f(\pmb x^*)=f(\pmb x^{(t)})+(\pmb x^*-\pmb x^{(t)})^\textsf{T}f'(\pmb x^{(t)})+\frac{1}{2}(\pmb x^*-\pmb x^{(t)})^\textsf{T}f''(\pmb x^{(t)})(\pmb x^*-\pmb x^{(t)}).\] 令上式的梯度为0,可得迭代公式为\[\pmb x^{(t+1)}=\pmb x^{(t)}-[f''(\pmb x^{(t)})]^{-1}f'(\pmb x^{(t)}).\] 如果用一个矩阵 \(\pmb M^{(t)}\) 来近似Hessian矩阵,则得到Quasi-Newton方法\[\pmb x^{(t+1)}=\pmb x^{(t)}-[\pmb M^{(t)}]^{-1}f'(\pmb x^{(t)}).\] 而在得分函数求根问题中考虑的则是\(\pmb M^{(t)}=I(\pmb\theta^{(t)})\) 为Fisher信息阵。
除此之外,R中也提供了rootSolve::multiroot函数求解这一问题。
model <- function(x) {
f1 <- x[1] + x[2] + x[3]^2 - 12
f2 <- x[1]^2 - x[2] + x[3] - 2
f3 <- 2 * x[1] - x[2]^2 + x[3] - 1
return(c(f1 = f1, f2 = f2, f3 = f3))
}
solution <- rootSolve::multiroot(f = model, start = c(1, 1, 1))
rbind(root = solution$root)## [,1] [,2] [,3]
## root 1 2 3rbind(f.root = solution$f.root)## f1 f2 f3
## f.root 3.087877e-10 4.794444e-09 -8.678146e-097.3 数值积分
数值积分方法可以是自适应的或者非自适应的,其中非自适应的方法在整个积分区域内使用同一准则。
数值积分方法总是通过一个有限点集上函数值的加权和的形式来估计积分值\[\int_a^bf(x)\text{d}x\approx\sum_{i=0}^nf(x_i)w_i,\] 其中 \(\{x_i\}\) 是区间 \([a,b]\) 内的点列,\(w_i\) 是对应的权重。不同的点列和权重的选取会导致积分近似的不同精度,许多非自适应的方法都是通过建立插值函数来估计积分,常见的有:
- 矩阵法则:以常数函数做插值函数,得\[\int_a^bf(x)\text{d}x\approx(b-a)f\left(\frac{a+b}{2}\right).\]
- 梯形法则:以线性函数做插值函数,得\[\int_a^bf(x)\text{d}x\approx(b-a)\cdot\dfrac{f(a)+f(b)}{2}.\]
- 混合梯形法则:以分段线性函数做插值函数,得\[\int_a^bf(x)\text{d}x\approx\frac{h}{2}f(a)+h\sum_{i=1}^{n-1}f(x_i)+\frac{h}{2}f(b),\] 其中 \(a=x_0<x_1<\cdots<x_{n-1}=x_n=b\) 为 \([a,b]\) 的 \(n\) 等分点,\(h=(b-a)/n\)。
- Newton-Cotes公式:利用等分点列 \(\{x_i\}\) 构造 \(n\) 次多项式 \(L(x)\),得\[\int_a^bf(x)\approx\sum_{i=0}^nf(x_i)\int_a^bl_i(x)\text{d}x,\] 这里 \(l_i(x)\) 是基函数。
- Gauss型公式:考虑利用不等距划分点列 \(\{x_i\}\) 构造 \(n\) 次多项式来近似积分,得\[\int_a^bf(x)\text{d}x\approx\sum_{i=0}^nA_if(x_i),\] 其中 \(A_i\) 具有特定表达式,与基函数有关。
在R中我们可以借助integrate函数使用自适应方法来估计一元函数积分。例如,考虑\[\int_0^{+\infty}\dfrac{\text{d}y}{(\cosh y-\rho r)^{n-1}},\]
其中 \(-1<\rho<1\),\(-1<r<1\) 是常数,\(n\geq2\) 是整数。
f <- function(y, n, r, rho) { (cosh(y) - rho * r)^{1 - n} }
res <- integrate(f, lower = 0, upper = Inf, rel.tol = 1e-6,
n = 10, r = 0.5, rho = 0.2)
res## 1.053305 with absolute error < 5.1e-07下面的图显示了积分值随着参数 \(\rho\) 的变化而变化的情况。
ro <- seq(-.99, .99, .01)
v <- rep(0, length(ro))
for (i in 1:length(ro)) {
v[i] <- integrate(f, lower = 0, upper = Inf, rel.tol = 1e-6,
n = 10, r = 0.5, rho = ro[i])$value
}
plot(ro, v, type = "l", xlab = bquote(rho), ylab = "Integral Value (n=10, r=0.5)")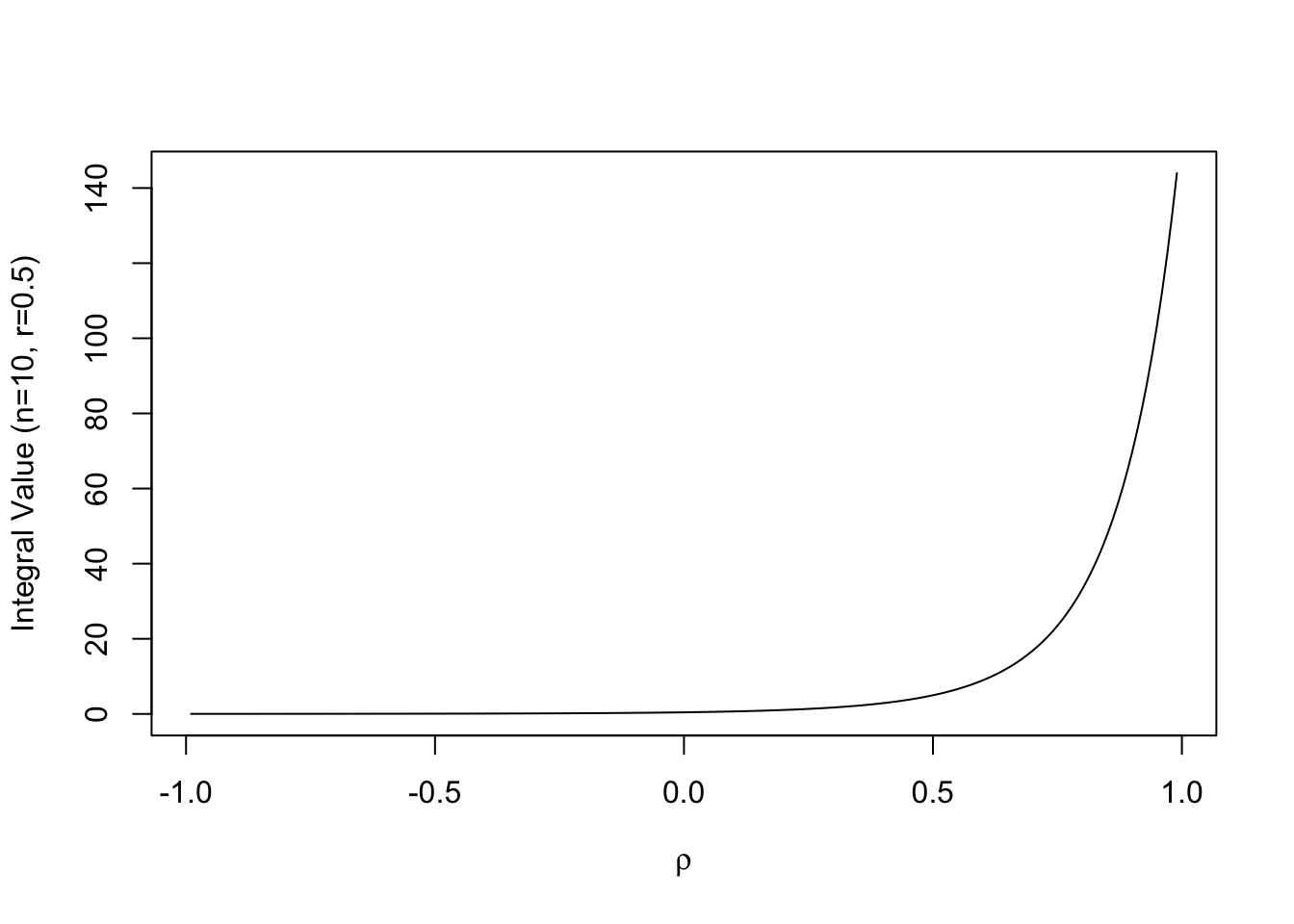
这个积分与统计中的样本相关系数 \(R\) 的分布有重要的联系。我们知道,样本相关系数\[R=\dfrac{\sum\limits_{i=1}^n(X_i-\overline{X})(Y_i-\overline{Y})}{\left[\sum\limits_{i=1}^n(X_i-\overline{X})^2\sum\limits_{i=1}^n(Y_i-\overline{Y})^2\right]^{1/2}}\] 是总体相关系数的估计。在样本 \((X_1,Y_1),\dots,(X_n,Y_n)\overset{\text{i.i.d.}}{\sim}N(\mu_1,\mu_2,\sigma_1^2,\sigma_2^2,\rho)\)的假设下,当 \(\rho=0\) 时,可以证明 \(R\) 的密度函数为\[f(r)=\dfrac{\Gamma(\frac{n-1}{2})}{\Gamma(\frac{1}{2})\Gamma(\frac{n-2}{2})}(1-r^2)^{\frac{n-4}{2}},\quad -1<r<1.\] 前面的正则化系数的计算已经在之前讨论过,因此计算并不复杂。但是当 \(0<|\rho|<1\) 时,\(R\) 的密度形式复杂,其中一种表示为\[f(r)=\dfrac{(n-2)(1-\rho^2)^{\frac{n-1}{2}}(1-r^2)^{\frac{n-4}{2}}}{\pi}\int_0^{+\infty}\frac{\text{d}w}{(\cosh w-\rho r)^{n-1}},\quad -1<r<1.\] 这就需要用到刚刚讨论的积分的近似。
dcorr <- function(r, n, rho = 0) {
# compute the density function of sample correlation
if (abs(r) > 1 || abs(rho) > 1) { return(0) }
if (n < 4) { return(NA) }
if (isTRUE(all.equal(rho, 0))) {
a <- exp(lgamma((n-1)/2) - lgamma(1/2) - lgamma((n-2)/2))
return (a * (1 - r^2)^((n - 4)/2))
}
# if rho not 0, need to integrate
f <- function(w, R, n, rho) { (cosh(w) - rho * R)^(1 - n) }
i <- integrate(f, lower = 0, upper = Inf, R = r, n = n, rho = rho)$value
c1 <- (n - 2) * (1 - rho^2)^((n - 1)/2)
c2 <- (1 - r^2)^((n - 4) / 2) / pi
return(c1 * c2 * i)
}
r <- as.matrix(seq(-1, 1, 0.01))
d1 <- apply(r, 1, dcorr, n = 10, rho = 0)
d2 <- apply(r, 1, dcorr, n = 10, rho = 0.5)
d3 <- apply(r, 1, dcorr, n = 10, rho = -0.5)
plot(r, d2, type = "l", lty = 2, lwd = 2, col = 2, ylab = "density")
lines(r, d1, lwd = 2)
lines(r, d3, lty = 4, lwd = 2, col = 3)
legend("top", inset = 0.02, c("rho = 0", "rho = 0.5", "rho = -0.5"),
lty = c(1,2,4), col = c(1, 2, 3), lwd = 2)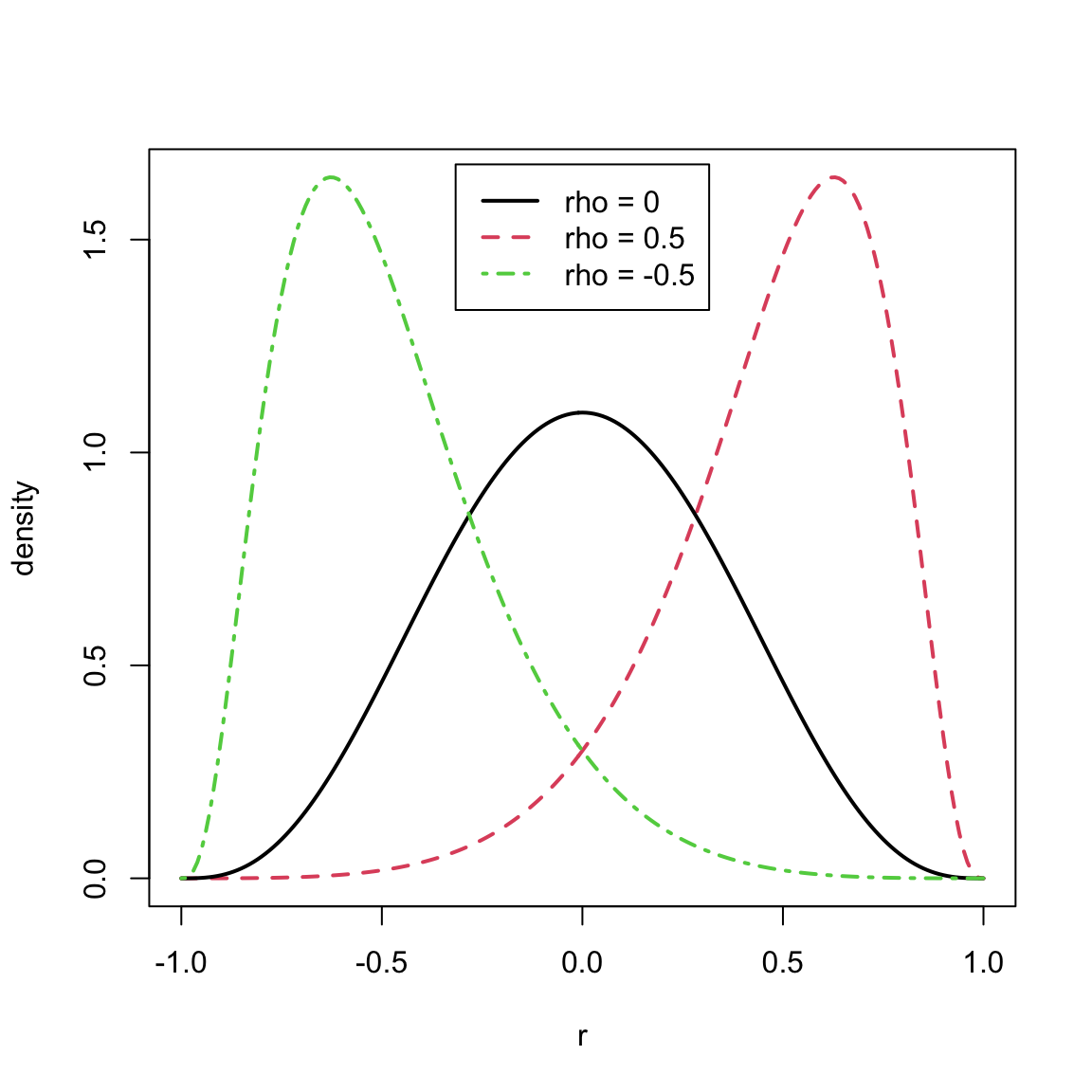
7.4 优化问题
7.4.1 极大似然估计
考虑样本 \(X_1,\dots,X_n\overset{\text{i.i.d.}}{\sim} f(x;\theta)\),则 \(\theta\) 的似然函数为\[L(\theta)=\prod_{i=1}^nf(x_i;\theta),\]
而对数似然函数为\[l(\theta)=\sum_{i=1}^n\ln f(x_i;\theta).\]
在R中可以使用stats4::mle函数来得到参数的极大似然估计及其协方差矩阵(即Fisher信息阵的逆),函数内部使用了optim函数对负对数似然函数进行了最小化。
例如,考虑指数分布总体 \(Exp(\theta)\),\(X_1,\dots,X_n\) 为i.i.d.样本,则 \(\theta\) 的对数似然函数为\[l(\theta)=n\ln\theta-\theta\sum_{i=1}^nx_i,\] 于是可以显式求得 \(\hat{\theta}_{\text{MLE}}=1/\overline{x}\)。下面代码是对这一结果的验证。
x <- c(0.04304550, 0.50263474)
ml <- function(theta = 1) {
-(length(x) * log(theta) - theta * sum(x))
}
fit <- stats4::mle(ml)
c(theta.mle = 1 / mean(x), hat = fit@coef, sd = sqrt(fit@vcov))## theta.mle hat.theta sd
## 3.665150 3.665150 2.5916527.4.2 一元函数优化
许多优化问题往往可以转化为函数求根问题,则可通过uniroot函数得到解决。此外,R中还提供了nlm函数使用Newton类型算法进行非线性优化;optimize函数使用黄金分割方法以及曲线插值等方法来最优化目标函数,其主要面向连续函数优化问题而设计。
例如,考虑最大化函数 \[f(x)=\frac{\ln(1+\ln(x))}{\ln(1+x)},\quad x>1.\] 可以用如下代码实现(首先画了其在 \((1,10)\) 区间内的图象)。
x <- seq(1, 10, 0.01)
y <- log(1 + log(x)) / log(1 + x)
plot(x, y, type = "l")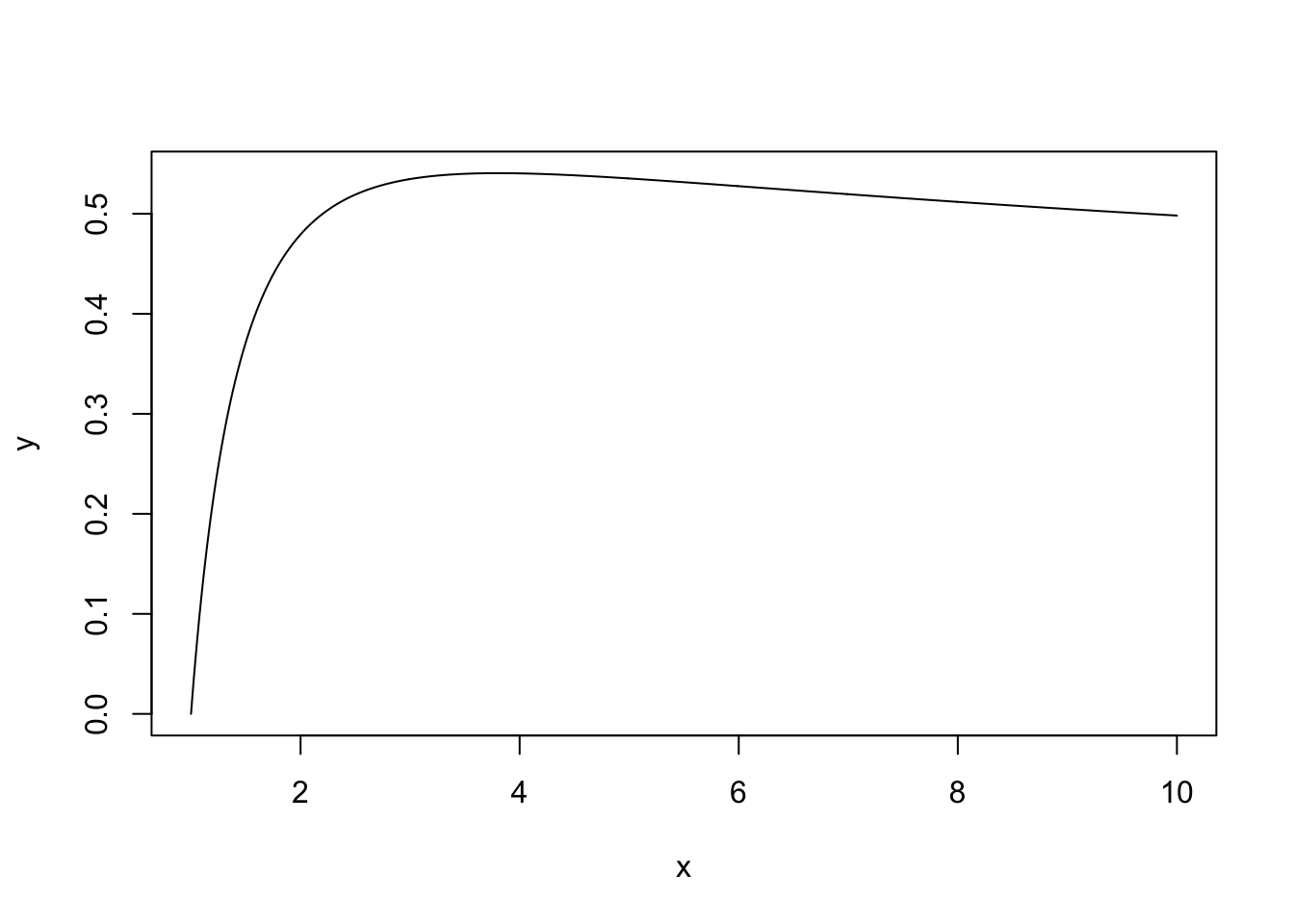
f <- function(x) { log(1 + log(x)) / log(1 + x) }
unlist(optimize(f, lower = 1, upper = 10, maximum = TRUE))## maximum objective
## 3.8039083 0.5406119而使用nlm函数时则需要实现将最大化问题转化为最小化问题。
g <- function(x) { -log(1 + log(x)) / log(1 + x) }
unlist(nlm(g, 2))## minimum estimate gradient code iterations
## -5.406119e-01 3.803912e+00 -6.207936e-08 1.000000e+00 9.000000e+00又如,考虑样本 \(X_1,\dots,X_n\overset{\text{i.i.d.}}{\sim}\Gamma(r,\lambda)\),要求 \(\theta=(r,\lambda)\) 的极大似然估计。容易得到 \(\theta\) 的对数似然函数为\[l(r,\lambda)=nr\ln\lambda-n\ln\Gamma(r)+(r-1)\sum_{i=1}^n\ln x_i-\lambda\sum_{i=1}^nx_i.\]
因此 \(\theta\) 的MLE满足对数似然方程
\[\begin{align*}
\dfrac{\partial}{\partial\lambda}l(r,\lambda)&=\frac{nr}{\lambda}-\sum_{i=1}^nx_i=0,\\
\dfrac{\partial}{\partial r}l(r,\lambda)&=n\ln\lambda-n\frac{\Gamma'(r)}{\Gamma(r)}+\sum_{i=1}^n\ln x_i=0.
\end{align*}\]
因此 \(\hat{\theta}=(\hat{r},\hat{\lambda})\) 可以通过求解方程 \[\ln\lambda+\frac{1}{n}\sum_{i=1}^n\ln x_i=\psi(\lambda\overline{x}),\quad\overline{x}=\frac{r}{\lambda}\]
得到,其中 \(\psi(t)=\dfrac{\text{d}\ln\Gamma(t)}{\text{d}t}=\dfrac{\Gamma'(t)}{\Gamma(t)}\)(在R中可用digamma实现)。
m <- 20000
est <- matrix(0, m, 2)
n <- 200
r <- 5
lambda <- 2
obj <- function(lambda, xbar, logx.bar) {
digamma(lambda * xbar) - logx.bar - log(lambda)
}
for (i in 1:m) {
x <- rgamma(n, r, lambda)
xbar <- mean(x)
logx.bar <- mean(log(x))
u <- uniroot(obj, lower = 0.001, upper = 1e5,
xbar = xbar, logx.bar = logx.bar)
lambda.hat <- u$root
r.hat <- xbar * lambda.hat
est[i,] <- c(r.hat, lambda.hat)
}
rbind(mean = colMeans(est), var = c(r = var(est[1,]), lambda = var(est[2,])))## r lambda
## mean 5.073964 2.032365
## var 5.268421 6.092699ML <- colMeans(est)
par(mfrow = c(1, 2))
hist(est[, 1], breaks = "scott", freq = FALSE, xlab = "r", main="")
abline(v = ML[1], col = 2, lwd = 2)
hist(est[, 2], breaks = "scott", freq = FALSE, xlab = bquote(lambda), main="")
abline(v = ML[2], col = 2, lwd = 2)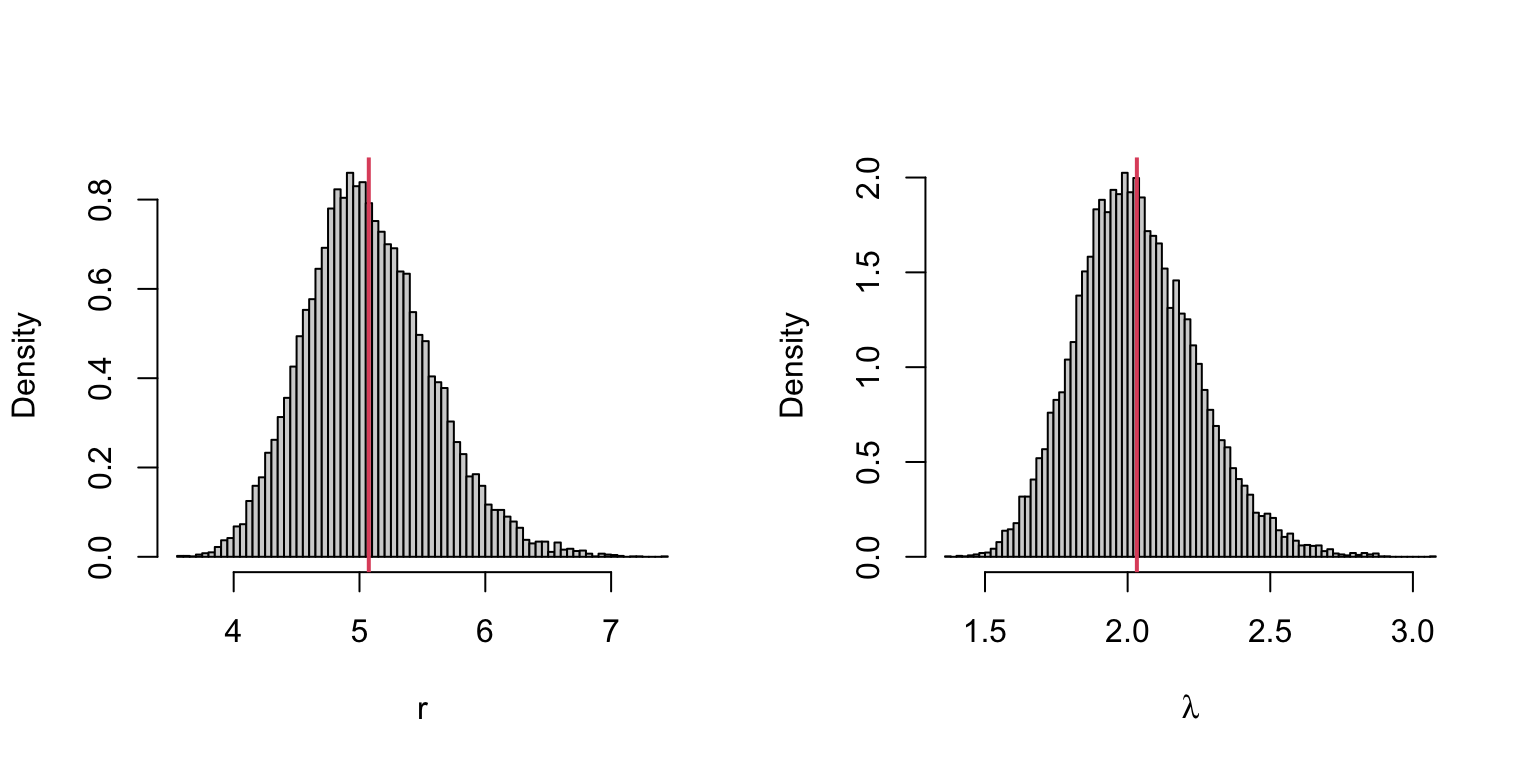
7.4.3 多元函数优化
在R中,对多元函数的优化往往使用optim函数实现优化,它的底层是使用了如Nelder-Mead单纯形方法(Nelder-Mead)、Qausi-Newton方法(BFGS)、共轭梯度算法(CG)、Box-constraint优化方法(L-BFGS-B)和模拟退火算法(SANN)等对目标函数进行优化。
例如,对伽马分布参数的极大似然估计问题中,现在我们可以直接考虑最大化联合对数似然函数。
mjl <- function(theta, sx, slogx, n) {
r <- theta[1]
lambda <- theta[2]
loglik <- n * r * log(lambda) - n * log(gamma(r)) + (r - 1) * slogx - lambda * sx
return(-loglik)
}
m <- 20000
est <- matrix(0, m, 2)
n <- 200
r <- 5
lambda <- 2
for (i in 1:m) {
x <- rgamma(n, r, lambda)
est[i,] <- optim(c(1, 1), mjl, sx = sum(x), slogx = sum(log(x)), n = n)$pa
}
rbind(mean = colMeans(est), var = c(r = var(est[1,]), lambda = var(est[2,])))## r lambda
## mean 5.075306 2.031837
## var 5.083545 5.494001对比二者的结果,点估计值差异不大,但是前者估计的方差更小一些。
除此之外,R中也提供了全局优化算法,用nloptr::nloptr函数实现凸优化问题
\[\begin{align*}
\min_{x\in\mathbb R^n} ~&~ f(x)\\
\text{s.t.} ~&~ g(x)\leq 0,\\
&~ h(x)=0,\\
&~ lb\leq x\leq ub.
\end{align*}\]
例如,考虑凸优化问题 \[\begin{align*} \min_{x_1,x_2} ~&~ \sqrt{x_2}\\ \text{s.t.} ~&~ (a_1x_1+b_1)^3\leq x_2,\\ &~ (a_2x_1+b_2)^3\leq x_2,\\ &~ x_2\geq 0. \end{align*}\] 这里 \(a_1=2,b_1=0,a_2=-1,b_2=1\)。
# object function
eval_f0 <- function(x, a, b) return(sqrt(x[2]))
# constraint function
eval_g0 <- function(x, a, b) return((a * x[1] + b)^3 - x[2])
# gradient of object function
eval_grad_f0 <- function(x, a, b) return(c(0, 0.5 / sqrt(x[2])))
# jacobian of constraint
eval_jac_g0 <- function(x, a, b) {
return(rbind(c(3 * a[1] * (a[1] * x[1] + b[1])^2, -1),
c(3 * a[2] * (a[2] * x[1] + b[2])^2, -1)))
}
options = list("algorithm" = "NLOPT_LD_MMA")
a <- c(2, -1)
b <- c(0, 1)
res <- nloptr::nloptr(x0 = c(1.234, 5.678),
eval_f = eval_f0, eval_grad_f = eval_grad_f0,
lb = c(-Inf, 0), ub = c(Inf, Inf),
eval_g_ineq = eval_g0, eval_jac_g_ineq = eval_jac_g0,
opts = options, a = a, b = b)
res##
## Call:
## nloptr::nloptr(x0 = c(1.234, 5.678), eval_f = eval_f0, eval_grad_f = eval_grad_f0,
## lb = c(-Inf, 0), ub = c(Inf, Inf), eval_g_ineq = eval_g0,
## eval_jac_g_ineq = eval_jac_g0, opts = options, a = a, b = b)
##
##
## Minimization using NLopt version 2.4.2
##
## NLopt solver status: 4 ( NLOPT_XTOL_REACHED: Optimization stopped because xtol_rel or xtol_abs (above)
## was reached. )
##
## Number of Iterations....: 11
## Termination conditions: relative x-tolerance = 1e-04 (DEFAULT)
## Number of inequality constraints: 2
## Number of equality constraints: 0
## Optimal value of objective function: 0.54433104762009
## Optimal value of controls: 0.3333333 0.29629637.4.4 线性规划
在R中,可以利用boot::simplex函数利用单纯形法求解线性规划问题
\[\begin{align*}
\min_{x\in\mathbb R^n} ~&~ a^\textsf{T}x\\
\text{s.t.} ~&~ A_1x\leq b_1,\\
&~ A_2x\geq b_2,\\
&~ A_3x=b_3,\\
&~ x\geq 0.
\end{align*}\]
例如,考虑线性规划问题 \[\begin{align*} \max_{x_1,x_2,x_3} ~&~ 2x_1+2x_2+3x_3\\ \text{s.t.} ~&~ -2x_1+x_2+x_3\leq 1,\\ &~ 4x_1-x_2+3x_3\leq 3,\\ &~ x_1\geq 0,x_2\geq 0,x_3\geq 0. \end{align*}\]
A1 <- rbind(c(-2, 1, 1), c(4, -1, 3))
b1 <- c(1, 3)
a <- c(2, 2, 3)
boot::simplex(a = a, A1 = A1, b1 = b1, maxi = TRUE)##
## Linear Programming Results
##
## Call : boot::simplex(a = a, A1 = A1, b1 = b1, maxi = TRUE)
##
## Maximization Problem with Objective Function Coefficients
## x1 x2 x3
## 2 2 3
##
##
## Optimal solution has the following values
## x1 x2 x3
## 2 5 0
## The optimal value of the objective function is 14.又如,考虑线性回归模型\[y_i=\beta^\textsf{T}x_i+e_i,\quad i=1,\dots,n.\]若要求最小化绝对偏差,即\[\min~\sum_{i=1}^n|x_i^\textsf{T}\beta-y_i|,\] 则问题可等价转化为线性规划问题 \[\begin{align*} \min_{a,\beta} ~&~ \sum_{i=1}^na_i\\ \text{s.t.} ~&~ a_i\geq x_i^\textsf{T}(\beta_1-\beta_2)-y_i,\\ &~ a_i\geq -x_i^\textsf{T}(\beta_1-\beta_2)+y_i,\\ &~ \beta_1\geq0,\beta_2\geq0. \end{align*}\]
注意到约束条件等价于\[\left(\begin{array}{ccc} X & -X & -I_n\\ -X & X & -I_n \end{array}\right)\left(\begin{array}{c} \beta_1\\ \beta_2\\ a \end{array}\right)\leq\left(\begin{array}{c} y\\ -y \end{array}\right),\] 于是有如下代码实现。
p <- 3
n <- 50
b <- c(-5, 1, -1)
X1 <- rnorm(n)
X2 <- sample(0:1, n, replace = TRUE)
X <- cbind(1, X1, X2)
y <- as.vector(X %*% b) + rnorm(n)
f.obj <- c(rep(0, 2*p), rep(1,n))
f.con <- cbind(rbind(X, -X), rbind(-X, X), rbind(-diag(n), -diag(n)))
f.rhs <- c(y, -y)
f.dir <- rep("<=", 2*n)
# simplex
A1 <- f.con[which(f.rhs >= 0),]
b1 <- f.rhs[which(f.rhs >= 0)]
A2 <- -f.con[which(f.rhs < 0),]
b2 <- -f.rhs[which(f.rhs < 0)]
res_simplex <- boot::simplex(a = f.obj, A1 = A1, b1 = b1, A2 = A2, b2 = b2)
beta1hat <- res_simplex$soln[1:p] - res_simplex$soln[(p+1):(2*p)]
# lp
res_lp <- lpSolve::lp("min", f.obj, f.con, f.dir, f.rhs)
beta2hat <- res_lp$solution[1:p] - res_lp$solution[(p+1):(2*p)]
# eq
res_quan <- quantreg::rq(y ~ X1 + X2, tau = 0.5)
beta3hat <- res_quan$coefficients
rbind(beta1hat, beta2hat, beta3hat)## x1 x2 x3
## beta1hat -5.65784 1.002679 -0.3640638
## beta2hat -5.65784 1.002679 -0.3640638
## beta3hat -5.65784 1.002679 -0.3640638可以看到三种方法得到的估计结果是一致的,而且与真实值也比较接近。
注:boot::simplex函数要求 \(b_1,b_2,b_3\) 的元素均非负。
7.5 E-M算法
7.5.1 E-M算法介绍
在现实问题中有许多缺失数据的情形或问题,如调查问卷数据、医疗健康记录数据、隐马尔可夫模型、混合模型、生存数据、因果推断等等。而处理缺失数据的方法也有许多:
- 丢弃有缺失数据的观测个体(会导致信息的损失);
- 填补或多重填补(通常用于调查问卷数据);
- E-M算法。
记可观测数据为 \(X\),缺失数据为 \(Z\),则完全数据为 \(Y=(X,Z)\),待估参数记为 \(\theta\)。现在我们有的是基于观测数据的似然函数 \(L(\theta\mid X)\),一般的填补方法是考虑将缺失的部分 \(Z\) 进行填补得到 \(\hat{Z}\),从而最大化合似然\[L(\theta;X,\hat{Z})\]得到 \(\theta\) 的估计。于是,原始的E-M算法的想法如下:
- E步:以 \(\mathbb E_{\theta_0}(Z\mid X)\) 填补 \(Z_0\);
- M步:最大化似然 \(L(\theta;X,Z_0)\) 得到 \(\theta_1\),
下一步以 \(\theta_1\) 代替 \(\theta_0\) 进行迭代,由此得到一列 \(\{\theta_i\}\),重复直至收敛。
在实际中,定义\[Q(\theta\mid\theta^{(t)})=\mathbb E[\ln L(\theta\mid X,Z)\mid X=x,\theta^{(t)}]\]为观测到 \(X=x\) 以及参数 \(\theta=\theta^{(t)}\) 的条件下完全数据的联合对数似然函数的期望,我们通常这么做:
- E步:计算 \(Q(\theta\mid\theta^{(t)})=\mathbb E[\ln L(\theta\mid X,Z)\mid X=x,\theta^{(t)}]\);
- M步:关于 \(\theta\) 最大化 \(Q(\theta\mid\theta^{(t)})\),并记 \(\theta^{(t+1)}\) 为最大值点;
- 返回E步,直至达到收敛准则。
可以证明,算法在每一步迭代时都增大了观测数据的对数似然量。
考虑一个进化和工业污染的例子,椒花蛾的色彩由某单个基因决定,该基因有三个可能的等位基因:\(C\)、\(I\) 和 \(T\),其中 \(C\) 对 \(I\) 是显性的,\(T\) 对 \(I\) 是隐性的,进而有3种表现型(深色 \(CC\), \(CI\), \(CT\)、浅色 \(TT\)、中间色 \(II\), \(IT\))。假设Hardy-Weinberg平衡律成立,记各个等位基因在种群中的频率为 \(p_C\), \(p_I\), \(p_T\) \((p_C+p_I+p_T=1)\),则基因型 \(CC\), \(CI\), \(CT\), \(II\), \(IT\), \(TT\) 的频率分别为 \(p_C^2\), \(2p_Cp_I\), \(2p_Cp_T\), \(p_I^2\), \(2p_Ip_T\), \(p_T^2\)。
现假设随机捕了 \(n\) 只蛾子,其中深色 \(n_C\) 只、浅色 \(n_T\) 只,中间色 \(n_I\) 只,但是各基因型的频数不可观测:
| \(CC\) | \(CI\) | \(CT\) | \(II\) | \(IT\) | \(TT\) | |
|---|---|---|---|---|---|---|
| 不可观测 | \(n_{CC}\) | \(n_{CI}\) | \(n_{CT}\) | \(n_{II}\) | \(n_{IT}\) | \(n_{TT}\) |
| 观测 | \(n_C\) | \(n_I\) | \(n_T\) | |||
| 深色 | 中间色 | 浅色 | ||||
此时观测数据为 \(x=(n_C,n_I,n_T)\),而完全数据为 \(y=(n_{CC},n_{CI},n_{CT},n_{II},n_{IT},n_{TT})\),其中 \(n_{CC}+n_{CI}+n_{CT}=n_C\), \(n_{II}+n_{IT}=n_I\), \(n_{TT}=n_T\)。完全数据下的似然函数为 \[\begin{align*} \ln f(y\mid p)&=n_{CC}\ln p_C^2+n_{CI}\ln(2p_Cp_I)+n_{CT}\ln(2p_Cp_T)\\ &\quad +n_{II}\ln p_I^2+n_{IT}\ln(2p_Ip_T)+n_{TT}\ln p_T^2+\ln\frac{n!}{n_{CC}!n_{CI}!n_{CT}!n_{II}!n_{IT}!n_{TT}!}. \end{align*}\]
注意到 \[\begin{align*} N_{CC},N_{CI},N_{CT}\mid n_C,n_I,n_T,p&\sim MB\left(n_C,\frac{p_C^2}{1-(p_I+p_T)^2},\frac{2p_Cp_I}{1-(p_I+p_T)^2},\frac{2p_Cp_T}{1-(p_I+p_T)^2}\right),\\ N_{II},N_{IT}\mid n_C,n_I,n_T,p&\sim MB\left(n_I,\frac{p_I^2}{2p_Ip_T+p_I^2},\frac{2p_Ip_T}{2p_Ip_T+p_I^2}\right). \end{align*}\]
从而在E-M算法的E步,对完全似然函数取期望得到 \[\begin{align*} Q(p\mid p^{(t)})&=n_{CC}^{(t)}\ln p_C^2+n_{CI}^{(t)}\ln(2p_Cp_I)+n_{CT}^{(t)}\ln(2p_Cp_T)\\ &\quad +n_{II}^{(t)}\ln p_I^2+n_{IT}^{(t)}\ln(2p_Ip_T)+n_{TT}^{(t)}\ln p_T^2+k(n_C,n_I,n_T,p^{(t)}), \end{align*}\] 其中 \[\begin{align*} n_{CC}^{(t)}&=\mathbb E[N_{CC}\mid n_C,n_I,n_T,p^{(t)}]=n_C\cdot\frac{(p_C^{(t)})^2}{1-(p_I^{(t)}+p_T^{(t)})^2},\\ n_{CI}^{(t)}&=\mathbb E[N_{CI}\mid n_C,n_I,n_T,p^{(t)}]=n_C\cdot\frac{2p_C^{(t)}p_I^{(t)}}{1-(p_I^{(t)}+p_T^{(t)})^2},\\ n_{CT}^{(t)}&=\mathbb E[N_{CT}\mid n_C,n_I,n_T,p^{(t)}]=n_C\cdot\frac{2p_C^{(t)}p_T^{(t)}}{1-(p_I^{(t)}+p_T^{(t)})^2},\\ n_{II}^{(t)}&=\mathbb E[N_{II}\mid n_C,n_I,n_T,p^{(t)}]=n_I\cdot\frac{(p_I^{(t)})^2}{2p_I^{(t)}p_T^{(t)}+(p_I^{(t)})^2},\\ n_{IT}^{(t)}&=\mathbb E[N_{IT}\mid n_C,n_I,n_T,p^{(t)}]=n_I\cdot\frac{2p_I^{(t)}p_T^{(t)}}{2p_I^{(t)}p_T^{(t)}+(p_I^{(t)})^2},\\ n_{TT}^{(t)}&=\mathbb E[N_{TT}\mid n_C,n_I,n_T,p^{(t)}]=n_T, \end{align*}\] 而最后一项与 \(p\) 无关。
在E-M算法的M步,注意到 \(p_C+p_I+p_T=1\),于是关于 \(p_C\) 和 \(p_I\) 求导并令导数为零可解得迭代公式 \[\begin{align*} p_C^{(t+1)}&=\frac{2n_{CC}^{(t)}+n_{CI}^{(t)}+n_{CT}^{(t)}}{2n},\\ p_I^{(t+1)}&=\frac{2n_{II}^{(t)}+n_{IT}^{(t)}+n_{CI}^{(t)}}{2n},\\ p_T^{(t+1)}&=\frac{2n_{TT}^{(t)}+n_{IT}^{(t)}+n_{CT}^{(t)}}{2n}. \end{align*}\]
因此,使用以上结论便可以进行E-M算法。
moth <- function(p, n.obs) {
n <- sum(n.obs)
nc <- n.obs[1]; ni <- n.obs[2]; ntt <- nt <- n.obs[3]
pct <- pit <- ptt <- rep(0, 20)
pct[1] <- p[1]
pit[1] <- p[2]
ptt[1] <- 1 - p[1] - p[2]
for (i in 2:20) {
pc.old <- pct[i-1]
pi.old <- pit[i-1]
pt.old <- ptt[i-1]
den <- pc.old^2 + 2 * pc.old * pi.old + 2 * pc.old * pt.old
ncc <- nc * pc.old^2 / den
nci <- nc * 2 * pc.old * pi.old / den
nct <- nc * 2 * pc.old * pt.old / den
nii <- ni * pi.old^2 / (pi.old^2 + 2 * pi.old * pt.old)
nit <- ni * 2 * pi.old * pt.old / (pi.old^2 + 2 * pi.old * pt.old)
pct[i] <- (2 * ncc + nci + nct) / (2 * n)
pit[i] <- (2 * nii + nit + nci) / (2 * n)
ptt[i] <- (2 * ntt + nit + nct) / (2 * n)
}
return(list(pct = pct, pit = pit, ptt = ptt))
}
n.obs <- c(85, 196, 341)
p <- c(1/3, 1/3)
a <- moth(p, n.obs)
pct <- a$pct; pit <- a$pit; ptt <- a$ptt
rcc <- sqrt((diff(pct)^2 + diff(pit)^2) / (pct[-20]^2 + pit[-20]^2))
rcc <- c(0, rcc)
d1 <- (pct[-1] - pct[20]) / (pct[-20] - pct[20])
d1 <- c(d1, 0)
d2 <- (pit[-1] - pit[20]) / (pit[-20] - pit[20])
d2 <- c(d2, 0)
cbind(pct, pit, ptt, rcc, d1, d2)[1:10,]## pct pit ptt rcc d1 d2
## [1,] 0.33333333 0.3333333 0.3333333 0.000000e+00 0.04250214 0.3365890
## [2,] 0.08199357 0.2374062 0.6806002 5.706852e-01 0.03693257 0.1876547
## [3,] 0.07124895 0.1978696 0.7308814 1.631212e-01 0.03672683 0.1777993
## [4,] 0.07085204 0.1903604 0.7387876 3.575602e-02 0.03671927 0.1762412
## [5,] 0.07083746 0.1890227 0.7401398 6.586043e-03 0.03671899 0.1759459
## [6,] 0.07083693 0.1887869 0.7403762 1.168320e-03 0.03671898 0.1758875
## [7,] 0.07083691 0.1887454 0.7404177 2.058004e-04 0.03671898 0.1758758
## [8,] 0.07083691 0.1887381 0.7404250 3.620522e-05 0.03671966 0.1758735
## [9,] 0.07083691 0.1887368 0.7404263 6.367857e-06 0.03673582 0.1758730
## [10,] 0.07083691 0.1887366 0.7404265 1.119945e-06 0.03702319 0.17587297.5.2 指数族E-M算法
当完全数据是来自指数分布族中的某个分布时,其密度可以写为 \(f(y\mid\theta)=c(\theta)\exp\{\theta^\textsf{T}s(y)\}h(y)\),其中 \(\theta\) 为自然参数向量,\(s(y)\) 为充分统计量的向量。此时E步得到\[Q(\theta\mid\theta^{(t)})=k+\ln c(\theta)+\int\theta^\textsf{T}s(y)f_{Z|X}(z\mid x,\theta^{(t)})\text{d}z,\] 其中 \(k\) 为与 \(\theta\) 无关的数。在M步中,令 \(Q\) 对 \(\theta\) 的导数为零,整理得到\[\mathbb E_Y[s(Y)\mid\theta]=-\dfrac{c'(\theta)}{c(\theta)}=\int s(y)f_{Z|X}(z\mid x,\theta^{(t)})\text{d}z.\] 最大化 \(Q\) 相当于解上述等式。
7.5.3 混合模型E-M算法
考虑如下正态混合问题:\[f(x\mid\theta)=\sum_{i=1}^kp_if_i(x),\] 其中 \(p_i>0\),\(\sum\limits_{i=1}^kp_i=1\),\(f_i(x)\) 为正态分布 \(N(\mu_i,\sigma^2)\) 的密度。于是 \(\theta=(\pmb p,\pmb\mu,\sigma^2)\) 为待估参数,其中 \(\pmb p=(p_1,\dots,p_{k-1})\),\(\pmb\mu=(\mu_1,\dots,\mu_k)\)。
设观测数据为 \(\pmb x=(x_1,\dots,x_n)\),缺失数据为 \(\pmb z=(z_1,\dots,z_n)\),其中 \(z_j=(z_{1j},\dots,z_{kj})\),其分量 \(z_{ij}=(z_j)_i=1\) 当且仅当 \(x_j\) 来自于 \(f_i\)。于是完全数据 \(\pmb y=(\pmb x,\pmb z)\) 下的对数似然函数为 \[\begin{align*} l(\theta\mid\pmb y)&=\ln\prod_{j=1}^nf(x_j,z_j)=\ln\prod_{j=1}^n\prod_{i=1}^k[p_if_i(x_j)]^{z_{ij}}\\ &=\sum_{i=1}^k\sum_{j=1}^nz_{ij}\ln p_i-\frac{1}{2}\sum_{i=1}^k\sum_{j=1}^nz_{ij}\left[\ln\sigma^2+\frac{(x_j-\mu_i)^2}{\sigma^2}\right]+C. \end{align*}\] 此时E步得到\[Q(\theta\mid\theta^{(t)})=\sum_{i=1}^k\sum_{j=1}^nz_{ij}^{(t)}\ln p_i-\frac{1}{2}\sum_{i=1}^k\sum_{j=1}^nz_{ij}^{(t)}\left[\ln\sigma^2+\frac{(x_j-\mu_i)^2}{\sigma^2}\right]+C,\] 其中\[z_{ij}^{(t)}=\mathbb E(Z_{ij}\mid\pmb x,\theta^{(t)})=\mathbb P(Z_{ij}=1\mid\pmb x,\theta^{(t)})=\dfrac{p_i^{(t)}f_i(x_j)}{\sum_{i=1}^kp_i^{(t)}f_i(x_j)}.\] 在M步中,最大化 \(Q(\theta\mid\theta^{(t)})\) 最终可得 \[\begin{align*} p_i^{(t+1)}=\frac{1}{n}\sum_{j=1}^nz_{ij}^{(t)},\quad\mu_i^{(t+1)}=\frac{\sum_{j=1}^nz_{ij}^{(t)}x_j}{\sum_{j=1}^nz_{ij}^{(t)}},\quad(\sigma^2)^{(t+1)}=\frac{1}{n}\sum_{i=1}^k\sum_{j=1}^nz_{ij}^{(t)}(x_j-\mu_i^{(t+1)})^2. \end{align*}\]
7.5.4 方差的估计
在极大似然的框架下,E-M算法用以寻求一个极大似然估计,但不能自动给出极大似然估计的协方差阵的一个估计。而我们知道在一些正则条件下,极大似然估计满足渐近正态性\[\sqrt{n}(\hat{\theta}-\theta)\rightarrow N(0,I^{-1}(\theta)),\] 其中 \(I(\theta)\) 为Fisher信息阵。因此极大似然估计 \(\hat{\theta}\) 的协方差阵的一个自然估计就是 \([nI(\hat{\theta})]^{-1}\)。
注意到 \(I(\theta)=-\mathbb E\dfrac{\partial\ln f(X\mid\theta)}{\partial\theta\partial\theta^\textsf{T}}\),因此若记样本 \(x=(x_1,\dots,x_n)\),则对数似然函数为\[l(\theta\mid x)=\sum_{i=1}^n\ln f(x_i\mid\theta).\] 从而Fisher信息阵 \(I(\theta)\) 可以通过计算观测信息(对数似然函数的Hessian阵)\[-l''(\hat{\theta}\mid x)=-\sum_{i=1}^n\dfrac{\partial\ln f(x_i\mid\theta)}{\partial\theta\partial\theta^\textsf{T}}\Big|_{\theta=\hat{\theta}}\]来估计。
但这里的似然是基于观测数据的似然,往往不容易计算,下面介绍Louis方法。注意到\[\ln f_X(x\mid\theta)=\ln f_Y(y\mid\theta)-\ln f_{Z|X}(z\mid x,\theta),\] 因此两边关于 \(Z\mid X=x,\theta^{(t)}\) 取期望得\[\ln f_X(x\mid\theta)=Q(\theta\mid\theta^{(t)})-H(\theta\mid\theta^{(t)}),\] 其中 \(H(\theta\mid\theta^{(t)})=\mathbb E[\ln f_{Z|X}(Z\mid x,\theta)\mid X=x,\theta^{(t)}]\),因此\[-l''(\theta\mid x)=-H''(\theta\mid\omega)|_{\omega=\theta}+Q''(\theta\mid\omega)|_{\omega=\theta},\] 即\[\hat{i}_X(\theta)=\hat{i}_Y(\theta)-\hat{i}_{Z|X}(\theta),\] 这里 \(\hat{i}_X(\theta)\) 为观测信息,\(\hat{i}_Y(\theta)\) 和 \(\hat{i}_{Z|X}(\theta)\) 分别称为完全信息和缺失信息。可以证明\[\hat{i}_{Z|X}(\theta)=\textsf{Var}\left[\frac{\partial\ln f_{Z|X}(Z\mid x,\theta)}{\partial\theta}\right].\] 如果完全信息和缺失信息难以解析计算,则可以通过MC方法来估计。
例如,假定完全数据 \(Y_1,\dots,Y_n\overset{\text{i.i.d.}}{\sim}Exp(\lambda)\),而观测数据是右删失的,即只能观测到 \(x=(x_1,\dots,x_n)\),其中 \(x_i=(\min\{y_i,c_i\},\delta_i)\),\(c_i\) 为删失水平,\(\delta_i=1\) 当且仅当 \(y_i\leq c_i\)。
显然完全数据的似然函数为 \(l(\lambda\mid y)=n\ln\lambda-\lambda\sum\limits_{i=1}^ny_i\),因此 \[\begin{align*} Q(\lambda\mid\lambda^{(t)})&=n\ln\lambda-\lambda\sum_{i=1}^n\mathbb E[Y_i\mid X_i=x_i,\lambda^{(t)}]\\ &=n\ln\lambda-\lambda\sum_{i=1}^n\left[y_i\delta_i+(c_i+1/\lambda^{(t)})(1-\delta_i)\right]\\ &=n\ln\lambda-\lambda\sum_{i=1}^n[y_i\delta_i+c_i(1-\delta_i)]-C\lambda/\lambda^{(t)}, \end{align*}\] 其中 \(C=\sum\limits_{i=1}^n(1-\delta_i)\)。因此 \(-Q''(\lambda\mid\lambda^{(t)})=n/\lambda^2\)。
一个删失事件 \(Z_i\) 的未观测到的结果有密度 \(f_{Z_i|X}(z_i\mid x,\lambda)=\lambda\exp\{-\lambda(z_i-c_i)\}\pmb 1_{\{z_i>c_i\}}\),因此\[\dfrac{\partial\ln f_{Z|X}(Z\mid x,\lambda)}{\partial\lambda}=\frac{C}{\lambda}-\sum_{i:\delta_i=0}(Z_i-c_i).\] 注意到 \(Z_i-c_i\) 服从指数分布,因此上式的方差\[\hat{i}_{Z|X}(\lambda)=\sum_{i:\delta_i=0}\textsf{Var}(Z_i-c_i)=\frac{C}{\lambda^2}.\] 因此应用Louis方法,即有\[\hat{i}_X(\lambda)=\frac{n-C}{\lambda^2}.\]
7.5.5 E-M的变种
- E步的变种
如果E步中的条件期望 \(Q(\theta\mid\theta^{(t)})=\mathbb E[l(\theta\mid X,Z)\mid X=x,\theta^{(t)}]\) 难以解析计算,则可以通过MC方法来近似。
Wei and Tanner (1990) 提出第 \(t\) 次迭代的E步可以通过如下两步来替代:
- 从条件分布 \(f_{Z|X}(z\mid x,\theta^{(t)})\) 中抽取 i.i.d. 样本 \(Z_1^{(t)},\dots,Z_{m_t}^{(t)}\),每个 \(Z_j^{(t)}\) 都是缺失数据 \(Z\) 的一个观测。这样 \(Y_j=(x,Z_j)\) 表示一个补齐的完整数据。
- 计算 \(\displaystyle\hat{Q}^{(t+1)}(\theta\mid\theta^{(t)})=\dfrac{1}{m_t}\sum_{j=1}^{m_t}\ln f_Y(Y_j^{(t)}\mid\theta)\)。
推荐的策略是在初期的E-M迭代中使用较小的 \(m_t\),并随着迭代的进行逐渐增大 \(m_t\),以减少在 \(\hat{Q}\) 中引入的MC波动性。
- M步的变种
如果最大化不能用解析的方式得到,可以考虑使用优化方法。Lange提出单步的Newton法替代M步,从而可以近似取得最大值而不用真正的精确求解。M步用下面替代 \[\begin{align*} \theta^{(t+1)}&=\theta^{(t)}-Q''(\theta\mid\theta^{(t)})^{-1}|_{\theta=\theta^{(t)}}Q'(\theta\mid\theta^{(t)})|_{\theta=\theta^{(t)}}\\ &=\theta^{(t)}-Q''(\theta\mid\theta^{(t)})^{-1}|_{\theta=\theta^{(t)}}l'(\theta^{(t)}\mid x). \end{align*}\]
这个梯度算法和完全的E-M算法对 \(\hat{\theta}\) 有相同的收敛速度。