Chapter 10 Applications of Multivariate Calculus
In Chapter 9, we introduced multivariable functions and notions of differentiation. In this chapter, we present several applications of multivariate calculus.
10.1 Change of Coordinates
In lots of situations, one may need a change of coordinates, which in general could be a nonlinear transformation. In this section, we focus on the familiar example of the change of coordinates from polar coordinates (\(\vec{x}= (r, \theta)\)) to cartesian (\(\vec{x} = (x, y)\)) and vice versa to illustrate the concepts. We generalise these results at the end of the section.
Let \(x = x(r, \theta)\) and \(y = y(r, \theta)\), we have: \[x = r\cos{\theta}, \quad y = r \sin{\theta}. \] Conversely, we have for \(r = r(x, y)\) and \(\theta = \theta(x, y)\): \[r = \sqrt{x^2 + y^2}, \quad \theta = \arctan{(\frac{y}{x})}.\] Using total differentiation, we can obtain a relationship between the vectors of infinitesimal change \(\vec{dx}\) and \(\vec{dr}\). \[\begin{eqnarray*} dx = \left( \dfrac{\partial x}{\partial r}\right)_\theta dr + \left( \dfrac{\partial x}{\partial \theta}\right)_r d\theta, \\ dy = \left( \dfrac{\partial y}{\partial r}\right)_\theta dr + \left( \dfrac{\partial y}{\partial \theta}\right)_r d\theta. \end{eqnarray*}\] We can write this in vector-matrix form as \[\begin{bmatrix} dx\\ dy \end{bmatrix} = \begin{bmatrix} \left( \dfrac{\partial x}{\partial r}\right)_\theta & \left( \dfrac{\partial x}{\partial \theta}\right)_r\\ \left( \dfrac{\partial y}{\partial r}\right)_\theta & \left( \dfrac{\partial y}{\partial \theta}\right)_r \end{bmatrix} \begin{bmatrix} dr\\ d\theta \end{bmatrix}.\] By defining matrix \(J\) known as Jacobian of the transformation as below we can write this relationship as \(\vec{dx} = J \vec{dr}\) in short. \[J = \begin{bmatrix} \left( \dfrac{\partial x}{\partial r}\right)_\theta & \left( \dfrac{\partial x}{\partial \theta}\right)_r\\ \left( \dfrac{\partial y}{\partial r}\right)_\theta & \left( \dfrac{\partial y}{\partial \theta}\right)_r \end{bmatrix} = \begin{bmatrix} \cos{\theta} & -r\sin{\theta}\\ \sin{\theta} & r\cos{\theta} \end{bmatrix}.\]
Similarly for the polar to cartesian transformation we have: \[\begin{eqnarray*} dr = \left( \dfrac{\partial r}{\partial x}\right)_y dx + \left( \dfrac{\partial r}{\partial y}\right)_x dy \\ d\theta = \left( \dfrac{\partial \theta}{\partial x}\right)_y dx + \left( \dfrac{\partial \theta}{\partial y}\right)_x dy \end{eqnarray*}\] In vector-matrix form we can writh this using matrix \(K\) defined below as \(\vec{dr} = K\vec{dx}\): \[K = \begin{bmatrix} \left( \dfrac{\partial r}{\partial x}\right)_y & \left( \dfrac{\partial r}{\partial y}\right)_x\\ \left( \dfrac{\partial \theta}{\partial x}\right)_y & \left( \dfrac{\partial \theta}{\partial y}\right)_x \end{bmatrix} = \begin{bmatrix} \cos{\theta} & \sin{\theta}\\ -\frac{\sin{\theta}}{r} & \frac{\cos{\theta}}{{r}} \end{bmatrix}.\] It is evident that \(K\), the Jacobian of the transformation from polar to cartersian is equal to the inverse of \(J\), the Jacobian of the transformation from cartesian to polar. \[K = J^{-1}.\]
Application 1: Infinitesimal element of length
Consider the curve \(y(x)\), the infinitesimal element of length \(ds\), along this curve is \[ds^2 = dx^2 + dy^2\] What is the infinitesimal element of length in polar coordinates? Given we have \(\vec{dx} = J\vec{dr}\), we have: \[ds^2 = (dx)^2 + (dy)^2 = \begin{bmatrix} dx & dy \end{bmatrix}\begin{bmatrix} dx \\ dy \end{bmatrix} = \begin{bmatrix} dr & d\theta \end{bmatrix}J^TJ\begin{bmatrix} dr \\ d\theta \end{bmatrix}=(dr)^2 + r^2(d\theta)^2.\]
Application 2: Infinitesimal element of area in polar coordinate
Infinitesimal element of area is useful in taking integrals of functions of two variables (\(f(x, y)\)) over a domain in the \((x, y)\) plane. In cartesian coordinates we have: \[dA = dxdy.\] We note that letting \(\vec{dx} = dx \hat{i}\) and \(\vec{dy} = dy \hat{j}\) and using the fact that the area of a parallelogram is equal to the magnitude of the cross-product of vectors spanning its edges, we can also write \(dA\) as: \[dA = \lVert\vec{dx}\times\vec{dy}\rVert = \lVert \text{det}\begin{bmatrix}\hat{i} & \hat{j} & \hat{k}\\ dx & 0 & 0\\ 0 & dy & 0 \end{bmatrix}\rVert.\] What is area element for a general transformation? Consider a general transformation in two-dimensions: \[ x = x(u, v) \quad \text{and} \quad y = y(u, v).\] We have: \[\begin{bmatrix} dx \\ dy \end{bmatrix} = J \begin{bmatrix} du \\ dv \end{bmatrix},\] where \(J\) is the Jacobian of the transformation. We therefore have for \(\vec{du}\) and \(\vec{dv}\) in cartesian coordinates: \[\vec{du} = J\begin{bmatrix} du \\ 0 \end{bmatrix}, \quad \vec{dv} = J\begin{bmatrix} 0 \\ dv \end{bmatrix}.\] Using the cross-product rule for the area of the parallelogram, we have: \[dA' = \lVert \vec{du} \times \vec{dv} \rVert = \lvert \text{det}J \rvert du dv.\] For the polar coordinate we obtain:
\[dA' = \lvert \text{det} J \rvert drd\theta = rdrd\theta.\] Note that some texts do not use prime on the transformed area element, although \(dA\) and \(dA'\) are not mathematically equal (one can easily check that \(dxdy \ne rdrd\theta\)). However, there is a conceptual equivalence between \(dA\) and \(dA'\).
This result generalizes to higher dimensions for a volume element. Given a general transformation \(u\) in \(n\) dimensions we have: \[\vec{dx}_{n\times 1} = J_{n \times n} \,\vec{du}_{n \times 1},\] where \(J\) is the Jacobian of the transformation. The infinitesimal volume element in cartesian coordinates is \(dV = \prod_{i=1}^{n} dx_i\). For the volume element in the transformed coordinates we have \[dV' = \lvert\text{det}J\rvert\prod_{i=1}^n du_i.\]
10.2 Partial Differential Equations (PDEs)
Analogous to an ordinary differential equation (ODE), one can define a partial differential equation or PDE with \(f(\vec{x})\), \(\vec{x} \in \mathbb{R}^n\) satisfying: \[f(x_1, \cdots, x_n, f, \dfrac{\partial f}{\partial x_1}, \cdots, \dfrac{\partial f}{\partial x_n}, \dfrac{\partial^2 f}{\partial x_i x_j}, \cdots) = 0.\]
Consider the following 2 dimensional examples. 1. Laplace Equation for \(u(x, y)\) (relevant to multiple areas of physics including fluid dynamics): \[\frac{\partial^2u}{\partial x^2} + \frac{\partial^2u}{\partial y^2} = 0.\] 2. Wave Equation for \(u(x, t)\) (describing the dynamics of a wave with speed \(c\) in one spatial dimension and time): \[\frac{\partial^2u}{\partial x^2} -\frac{1}{c^2} \frac{\partial^2u}{\partial y^2} = 0.\] Our discussion of PDEs here will be very brief, but this topic is a major part of your multivariable calculus course and one of the applied elective courses in the second year. If you would like to have a sneak preview and for some cool connections to the Fourier series you saw last term, you can check out this video.
Transforming a PDE under a change of coordinates
We again consider the example of transformation from cartesian to polar coordinates: \[u(x, y) \quad \longleftrightarrow \quad u(r, \theta),\] with \(J\) being Jacobian of the transformation. Using total differentiation we have:
\[\begin{align*} du & = \left(\frac{\partial u}{\partial x}\right)_y dx + \left(\frac{\partial u}{\partial y}\right)_y dy \\ & = \left(\frac{\partial u}{\partial x}\right)_y\left[\left(\frac{\partial x}{\partial r}\right)_\theta dr + \left(\frac{\partial x}{\partial \theta}\right)_r d\theta\right] + \left(\frac{\partial u}{\partial y}\right)_y \left[\left(\frac{\partial y}{\partial r}\right)_\theta dr + \left(\frac{\partial y}{\partial \theta}\right)_r d\theta\right] \\ & = \left[\left(\frac{\partial u}{\partial x}\right)_y\left(\frac{\partial x}{\partial r}\right)_\theta + \left(\frac{\partial u}{\partial y}\right)_y \left(\frac{\partial y}{\partial r}\right)_\theta \right]dr + \left[\left(\frac{\partial u}{\partial x}\right)_y\left(\frac{\partial x}{\partial \theta}\right)_r + \left(\frac{\partial u}{\partial y}\right)_y \left(\frac{\partial y}{\partial \theta}\right)_r\right]d\theta. \end{align*}\] Now, by equating the terms in the above and the total derivative of \(u(r, \theta)\), and also using the definition of \(J\), we obtain the following: \[\begin{bmatrix} \left(\frac{\partial }{\partial r}\right)_\theta \\ \left(\frac{\partial }{\partial \theta}\right)_r \end{bmatrix} u(r, \theta)= J^T \begin{bmatrix} \left(\frac{\partial }{\partial x}\right)_y \\ \left(\frac{\partial }{\partial y}\right)_x \end{bmatrix} u(x, y).\]
Laplace equation in Cartesian coordinates is: \[\dfrac{\partial^2 u}{\partial x^2} + \dfrac{\partial^2 u}{\partial y^2} = 0.\] In polar coordinates we have: \[\begin{align*} \dfrac{\partial}{\partial x}\left[ u\right] &= \dfrac{\partial u}{\partial r}\dfrac{\partial r}{\partial x} + \dfrac{\partial u}{\partial \theta}\dfrac{\partial \theta}{\partial x}\\ &=\left[\cos{\theta} \frac{\partial}{\partial r} - \frac{\sin{\theta}}{r}\frac{\partial}{\partial \theta} \right]u. \end{align*}\]
Now taking second derivative we have: \[\begin{align*} \dfrac{\partial^2}{\partial x^2}\left[ u\right] &= \left[\cos{\theta} \frac{\partial}{\partial r} - \frac{\sin{\theta}}{r}\frac{\partial}{\partial \theta} \right]\left[\cos{\theta} \frac{\partial}{\partial r} - \frac{\sin{\theta}}{r}\frac{\partial}{\partial \theta} \right]u \\ & = \cos^2\theta \dfrac{\partial^2 u}{\partial r^2} + \dfrac{2\cos \theta \sin \theta}{r^2} \dfrac{\partial u}{\partial \theta} - \dfrac{2\cos \theta \sin \theta}{r} \dfrac{\partial^2 u}{\partial r \partial \theta} + \dfrac{\sin^2 \theta}{r} \dfrac{\partial u}{\partial r} + \dfrac{\sin^2 \theta}{r^2}\dfrac{\partial^2 u }{\partial \theta^2}. \end{align*}\]
Similarly, we have: \[\dfrac{\partial^2}{\partial y^2}\left[ u\right] = \sin^2\theta \dfrac{\partial^2 u}{\partial r^2} - \dfrac{2\cos \theta \sin \theta}{r^2} \dfrac{\partial u}{\partial \theta} + \dfrac{2\cos \theta \sin \theta}{r} \dfrac{\partial^2 u}{\partial r \partial \theta} + \dfrac{\cos^2 \theta}{r} \dfrac{\partial u}{\partial r} + \dfrac{\cos^2 \theta}{r^2}\dfrac{\partial^2 u }{\partial \theta^2}.\]
Finally, we have: \[\dfrac{\partial^2 u}{\partial x^2} + \dfrac{\partial^2 u}{\partial y^2} = \dfrac{\partial^2 u}{\partial r^2} + \frac{1}{r}\dfrac{\partial u}{\partial r} + \frac{1}{r^2}\dfrac{\partial^2 u}{\partial \theta^2} = 0.\] For example, if one looking for function \(u(r)\) (with no dependence on \(\theta\)) fulfilling the Laplace equation, we could solve the following ODE: \[\frac{d^u}{dr^2} + \frac{1}{r} \frac{du}{dr} = 0.\]
10.3 Exact ODEs
The concept of total differentiation provides an alternative method for solving first order nonlinear ODEs. Consider the given first order ODE:
\[\dfrac{dy}{dx} = \dfrac{-F(x, y)}{G(x, y)}.\]
If we have a solution of the ODE in implicit form \(u(x, y) = 0\), assuming \(u\) is continuous with continuous derivatives. For total derivative of \(u\) we have: \[ du = \left(\frac{\partial u}{\partial x}\right)_y dx + \left(\frac{\partial u}{\partial y}\right)_y dy = 0 \quad \Rightarrow \quad \frac{dy}{dx} = \frac{-\left(\frac{\partial u}{\partial x}\right)_y}{\left(\frac{\partial u}{\partial y}\right)_y}.\] For the solution \(u(x, y) = 0\) to exist then we need the RHS of the above equation to be equal to the RHS of the ODE, we are trying to solve. This will be the case if \[F = \left(\frac{\partial u}{\partial x}\right)_y \quad \text{and} \quad G = \left(\frac{\partial u}{\partial y}\right)_y.\] But, if that is the case, due to the symmetry of the partial second mixed derivatives, we should have: \[\frac{\partial u^2}{\partial y\partial x} = \frac{\partial u^2}{\partial x\partial y} \quad \Rightarrow \quad \frac{\partial F}{\partial y} = \frac{\partial G}{\partial x}.\] This is known as the condition of integrability of the ODE and if it is satisfied then there exists \(u(x, y)\), where \[F = \left(\frac{\partial u}{\partial x}\right)_y \quad \text{and} \quad G = \left(\frac{\partial u}{\partial y}\right)_y,\] and then \(u(x, y) = 0\) is a solution of the first order ODE. We call this kind of ODE exact.
Letting \[F(x, y) = 2xy +\cos x \cos y \quad \text{and} \quad G(x, y) = x^2 - \sin x \sin y.\] We can check the condition of integrability and see the ODE is exact: \[\frac{\partial F}{\partial y} = \frac{\partial G}{\partial x} = 2x - \cos{x} \sin{y},\] since the ODE is exact, we can look for a solution in implicit form \(u(x, y) = 0\) such that:
\[F(x, y) = \dfrac{\partial u}{\partial x} \quad \text{and} \quad G(x, y) = \dfrac{\partial u}{\partial y}.\] We can do that in two steps. Firstly, we have: \[\left(\dfrac{\partial u}{\partial x}\right)_y = 2xy + \cos{x}\cos{y} \quad \] Integrating with respect to \(x\) and assuming the constant of intgration could depend on \(y\), we obtain: \[u = yx^2 + \cos{y}\sin{x} + f(y).\] Now in the second step, we use \[G(x, y) = \dfrac{\partial u}{\partial y} = x^2 - \sin{y}\sin{x} \quad \Rightarrow \quad \frac{df}{dy} = 0.\] This implies \(f\) is a constant, so we obtain the general solution \(y(x)\) of the ODE in implicit form: \[ u(x, y) = yx^2 + \cos{y}\sin{x} + c = 0.\]
When the ODE is not exact, sometimes we can find a function (an integrating factor) that will make the equation exact. Given:
\[F(x, y)dx + G(x, y)dy = 0,\]
is not exact, we look for a function \(\lambda(x)\) or \(\lambda(y)\) such that:
\[\lambda F(x,y)dx + \lambda G(x, y) dy = 0,\] is exact. Note that an integrating factor can in general be a function of both \(x\) and \(y\), but in this case we cannot find an explicit solution for \(\lambda\), and it is for this reason we can not solve very many ODEs.
Letting \(F = xy -1\) and \(G = x^2 - xy\), we see that the ODE is not exact as: \[\frac{\partial F}{\partial y} \ne \frac{\partial G}{\partial x}.\]
So, we will try to find a \(\lambda(x)\) (or \(\lambda(y)\) that will make the ODE exact). We need to find \(\lambda(x)\) such that:
\[\dfrac{\partial [\lambda(x)(xy-1)]}{\partial y} = \dfrac{\partial [\lambda(x)(x^2 - xy)]}{\partial x}.\] After simplification we obtain: \[(x - y)\left[\frac{d\lambda}{dx}x + \lambda\right] = 0.\] As we obtain an ODE for \(\lambda(x)\) (that does not depend on \(y\)), an integrating factor of the form \(\lambda(x)\) exists and can be obtained by solving this ODE to be: \[\lambda = \frac{c}{x}.\]
Now we can solve the exact ODE that is obtained (left as a quiz):
\[(y - \dfrac{1}{x})dx + (x - y)dy = 0.\]
10.4 Sketching functions of two variables
Similar to the sketching of functions of one variable, we will use the following steps in sketching a function of two variables \(f(x, y)\):
- Check continuity and find singularities.
- Find asymptotic behaviour \[\lim\limits_{x, y \rightarrow \pm \infty} f(x, y) \quad \text{and} \quad \lim\limits_{\vec{x} \rightarrow \vec{x}_{sing}} f(\vec{x}).\]
- Obtain some level curves, for example \(f(\vec{x}) = 0\).
- Find stationary points: minimum, maximum, saddle points
Stationary points for functions of two variables
Reminder that for a function of one variable \(f(x)\), we find stationary points by setting the first derivative to zero: \[f(x^*) = 0.\] Then, using Taylor expansion of \(f(x)\) near \(x^*\), we see that one can use the sign of the second derivative of \(f(x)\) at \(x^*\) to decide if the stationary point is minimum (if \(\frac{d^2f}{dx^2}(x^*)>0\)) or maximum (if \(\frac{d^2f}{dx^2}(x^*)<0\)).
Using a similar approach for the functions of two variables \(f(x, y)\), we have stationary points are the points where tangent plane at \(x^*\) is parallel to \((x, y)\) plane: \[\frac{\partial f}{\partial x} (\vec{x}^*) = \frac{\partial f}{\partial y} (\vec{x}^*) = 0.\] Then, the type of stationary point can be determined using the Taylor expansion around the stationary point \(\vec{x^*}\) and by the Hessian matrix. \[f(\vec{x}^* + \Delta \vec{x}) = f(\vec{x}^*) + \left[ \dfrac{\partial f}{\partial x}(\vec{x}^*) \quad \dfrac{\partial f}{\partial y}(\vec{x}^*) \right] \Delta \vec{x} + \dfrac{1}{2} \Delta \vec{x}^T\begin{bmatrix} \dfrac{\partial^2 f}{\partial^2 x}(\vec{x}^*) & \dfrac{\partial^2 f}{\partial x \partial y}(\vec{x}^*) \\ \dfrac{\partial^2 f}{\partial y \partial x}(\vec{x}^*) & \dfrac{\partial^2 f}{\partial^2 y}(\vec{x}^*) \end{bmatrix}\Delta \vec{x}.\] Given the fact that the first partial derivatives of \(f(\vec{x})\) are zero at the stationary points, we have: \[f(\vec{x}^* + \Delta \vec{x}) - f(\vec{x}^*) = \dfrac{1}{2}\Delta\vec{x}^TH(\vec{x}^*)\Delta\vec{x}.\] Under the assumption of continuity, we have the symmetry of the second mixed partial derivatives: \[\frac{\partial^2 f}{\partial y\partial x} = \frac{\partial^2 f}{\partial x \partial y},\] therfore the Hessain is symmetric (\(H = H^T\)), which implies that \(H\) is diagonalizable and it has real eigenvalues \(\lambda_1\) and \(\lambda_2\). So, there exists a similarity transformation \(V\) that diagonalise the Hessian: \[V^{-1}HV = \Lambda = \begin{bmatrix} \lambda_1 & 0 \\ 0 & \lambda_2 \end{bmatrix}.\] Also as \(H\) is symmetric, we have \(V^{-1} = V^T\). So, we have: \[f(\vec{x}^* + \Delta \vec{x}) - f(\vec{x}^*) = \dfrac{1}{2}\Delta\vec{x}^T\left[ V((\vec{x}^*)\Lambda(\vec{x}^*)V^T(\vec{x}^*)\right]\Delta\vec{x}.\] Now, if we let \(\Delta\vec{z} = V^T(\vec{x}^*) \Delta\vec{x}\), we have: \[\Delta f = f(\vec{x}^* + \Delta \vec{x}) - f(\vec{x}^*) = \dfrac{1}{2} \Delta \vec{z}^T\Lambda(\vec{x}^*)\Delta \vec{z} = \dfrac{1}{2}\left[ (\Delta z_1)^2\lambda_1 + (\Delta z_2)^2\lambda_2\right].\] Given this expression, we can use the sign of the eigenvalues to classify the stationary points.
If \(\lambda_1, \lambda_2 \in \mathbb{R}^+\), we have \(\Delta f > 0\) as we move away from the stationary point, suggesting \(\vec{x}^*\) is a minimum.
If \(\lambda_1, \lambda_2 \in \mathbb{R}^-\), we have \(\Delta f < 0\) as we move away from the stationary point, suggesting \(\vec{x}^*\) is a maximum.
If \(\lambda_1 \in \mathbb{R}^+\) and \(\lambda_2 \in \mathbb{R}^-\), we classify \(\vec{x}^*\) is a saddle point, since \(\Delta f\) can be positive or negative depending the direction of \(\Delta \vec{x}\).
We note that, we could use the trace (\(\tau\)) and determinant \(\Delta\) of the matrix \(H\) to know the sign of the eigenvalues with explicityly calculating the eigenvalues as done in section 7.3 in the analysis of the 2D linear ODEs. In particular, \(\Delta > 0, \tau>0\) (\(\Delta > 0, \tau<0\)) suggests eigenvalues are positive (negative) and we have a minima (maxima). \(\Delta < 0\) indicates a saddle point stationary point.
We note the function is continuous and there are no singularities. The asymptotic behavior is that \(u(x, y) \rightarrow \pm \infty\) as \(x, y \rightarrow \pm \infty\).
Next, we find the level curves at zero
\[u(x, y) = 0 \quad \Rightarrow \quad x = y \quad \text{and} \quad x^2 + y^2 - 1 = 0\]
In the next step, we obtain the stationary points.
\[\dfrac{\partial u}{\partial x}(\vec{x}^*) = \dfrac{\partial u}{\partial y}(\vec{x}^*) = 0\]
\[\dfrac{\partial u}{\partial x} = (x^2 + y^2 - 1) + 2x(x - y) = 0,\]
\[\dfrac{\partial u}{\partial y} = -(x^2 + y^2 - 1) + 2y(x - y) = 0.\]
Adding these two equations we obtain \(x^* = y^*\) or \(x^* = -y^*\).
\(x^* = y^* \quad \Rightarrow \quad 2{x^*}^2 - 1 = 0 \quad \Rightarrow \quad P_1 = (\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}), \quad P_2 = (-\frac{1}{\sqrt{2}}, -\frac{1}{\sqrt{2}}).\)
\(x^* = -y^* \quad \Rightarrow \quad 6{x^*}^2 - 1 = 0 \quad \Rightarrow \quad P_3 = (\frac{1}{\sqrt{6}}, -\frac{1}{\sqrt{6}}), \quad P_4 = (-\frac{1}{\sqrt{6}}, \frac{1}{\sqrt{6}}).\)
We classify the stationary points using the Hessain:
\[H(\vec{x}) = \begin{bmatrix} 6x-2y & 2y-2x \\ 2y - 2x & 2x - 6y \end{bmatrix}\] Now we use the determinant (\(\Delta\)) and trace (\(\tau\)) of matrix \(H\) at each stationary point to classify each stationary point:
\[P_1 = (\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}) \, \Rightarrow \, H(P_1) = \begin{bmatrix} 4\frac{1}{\sqrt{2}} & 0 \\ 0 & - 4 \frac{1}{\sqrt{2}} \end{bmatrix} \, \Rightarrow \, \Delta <0 \, \Rightarrow \, P_1 \text{ is a saddle point.}\] \[P_2 = (-\frac{1}{\sqrt{2}}, -\frac{1}{\sqrt{2}}) \, \Rightarrow \, H(P_2) = \begin{bmatrix} -4\frac{1}{\sqrt{2}} & 0 \\ 0 & 4 \frac{1}{\sqrt{2}} \end{bmatrix} \, \Rightarrow \, \Delta <0 \, \Rightarrow \, P_2 \text{ is a saddle point.}\] \[P_3 = (\frac{1}{\sqrt{6}}, -\frac{1}{\sqrt{6}}) \, \Rightarrow \, H(P_3) = \begin{bmatrix} \frac{8}{\sqrt{6}} & -\frac{4}{\sqrt{6}} \\ -\frac{4}{\sqrt{6}} & \frac{8}{\sqrt{6}} \end{bmatrix} \, \Rightarrow \, \Delta >0, \tau>0 \, \Rightarrow \, P_3 \text{ is a minimum.}\] \[P_4 = (-\frac{1}{\sqrt{6}}, \frac{1}{\sqrt{6}}) \, \Rightarrow \, H(P_4) = \begin{bmatrix} -\frac{8}{\sqrt{6}} & \frac{4}{\sqrt{6}} \\ \frac{4}{\sqrt{6}} & -\frac{8}{\sqrt{6}} \end{bmatrix} \, \Rightarrow \, \Delta >0, \tau<0 \, \Rightarrow \, P_4 \text{ is a maximum.}\]
Given the location and stability of the stationary points, we complete our sketch of
\[u(x,y) = (x-y)(x^2 + y^2 -1),\] as seen in Figure 10.1, by sketching some level curves, specifying the sign of the funcion and the location of the stationary points.
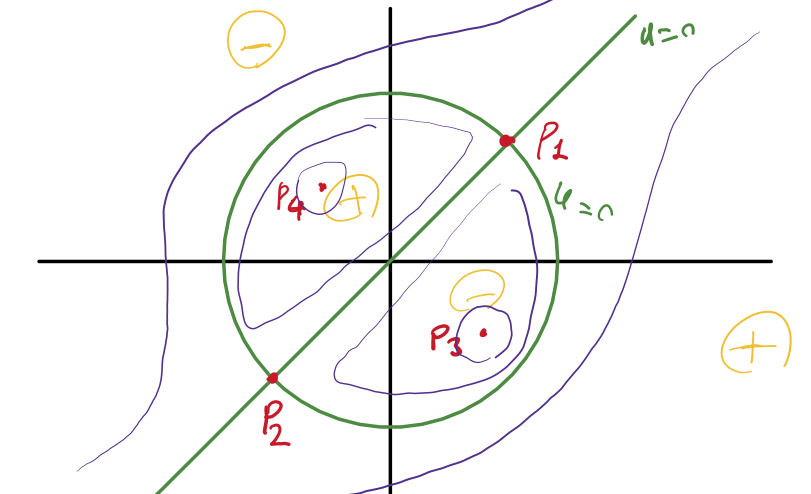
Figure 10.1: The contour plot and sketch of function \(u(x,y) = (x-y)(x^2 + y^2 -1)\)