4.3 Generation of a synthetic Radio Network

In our research we are very interested in different effects originating from the Radio Network specification. Therefore, we will implement many parameters that can be tuned and toggled for further research. The current choices of the parameter values are grounded on exploratory and theoretical research.

We generate a radio network, which is composed of three layers. The layers follow the pop.area.kind variable - layer 1 (Rural) spans over the Rural, Suburban and Urban tiles, layer 2 (Suburban) spans over the Suburban and Urban tiles and layer 3 (Urban) is spanned over the Urban tiles.

Important features and parameters of the generated radio network:

• The layers follow a hexagon shape with cell towers located in the respective centroid of each hexagon

• Towers vary in distance to each other of the same layer, i.e. how far/close are towers of the same layer located to each other: layer 1 = 27,000m; layer 2 = 7000m; layer 3 = 900m (-> the more urbanized, the closer the towers are too each other -> denser coverage). Furthermore, hexagon independent rotation in reference to the first layer is executed: layer 2 = 35 degrees; layer 3 = 70 degrees

• Each cell tower location is jittered in order to break the symmetry. The jitter amount depends on the layer: layer 1 = 5000m, layer 2 = 1000m, layer 3 = 400m.

• Each tower contains three antennas pointing into 120 degree differing directions.

• We assume a circular coverage. The layer determines the coverage diameter of an antenna: layer 1 = 15,000m; layer 2 = 2500m; layer 3 = 500m.

• Each tile of the focus area is sufficiently covered by at least one antenna and the antennas’ coverage areas are allowed to overlap.

Parameters concerning the device to cell association are specified in the next subsection.

To operationalize this, we first define some helper objects that carry the specifications of the parameters and functions that help with specifiying. Furthermore, we create a layer object, layers, that contains three independent versions of our focus area, one for each layer. Each of these data frames contains the spatial area which the layer dependent network is covering. For this we span a regular hexagonal shape grid over these areas and introduce the mentioned rotation to layer 2 and layer 3.

census.classified.final.sf <- readRDS("C:/Users/Marco/Vysoká škola ekonomická v Praze/Tony Wei Tse Hung - YAY/working objects/census.classified.final.sf.rds")
census.geo.body <- readRDS("C:/Users/Marco/Vysoká škola ekonomická v Praze/Tony Wei Tse Hung - YAY/working objects/shape.focusarea.rds")

set.seed(3)
# Three region / layer types
type <- list("Rural" = c("Rural", "Suburban", "Urban"),
             "Suburban" = c("Suburban", "Urban"),
             "Urban" = c("Urban"))
layer.base <- list("Rural" = census.classified.final.sf, "Suburban" = census.classified.final.sf, "Urban" = census.classified.final.sf) %>% 
  map2(., type, ~filter(.x, pop.area.kind %in% .y))


area.kind <- list("Rural" = "Rural", "Suburban" = "Suburban", "Urban" = "Urban")
tower.dist <- list("Rural" = 8000, "Suburban" = 5000, "Urban" = 900) # relation to radius (qm)
rotation.degree <- list("Rural" = 0, "Suburban" = 35, "Urban" = 70)
jitter <- list("Rural" = 2000, "Suburban" = 1000, "Urban" = 400)
coverage.centroid.dist <- list("Rural" = 5000, "Suburban" = 2800, "Urban" = 500) # same as radius
coverage.radius <- c("Rural" = 5000, "Suburban" = 2800, "Urban" = 500)
# Focus area
bb.focus.vec <- c(xmin = 4400000, xmax = 4500000,
                  ymin = 2700000, ymax = 2900000)

# functions
rotation = function(a){
  r = a * pi / 180 #degrees to radians
  matrix(c(cos(r), sin(r), -sin(r), cos(r)), nrow = 2, ncol = 2)
} 

layer_network_generate = function(x, tower.dist, rotation.degree){
  layer.geo <- x %>% 
    st_make_grid(cellsize = tower.dist, 
                 square = F, # hexagon 
                 flat_topped = T) %>%  # different cell size (qm)
    st_geometry()
  
  layer.centroid <- st_centroid(layer.geo)
  layer <- (layer.geo - layer.centroid) * rotation(rotation.degree) + layer.centroid # rotate by 35 degrees
  return(layer)
  
}

# Generate layers
layers <- pmap(list(layer.base, tower.dist, rotation.degree), 
              ~layer_network_generate(x = ..1, tower.dist = ..2, rotation.degree = ..3)) %>% 
  set_names(c("Layer.1", "Layer.2", "Layer.3"))

We use a hexagonal structure to place towers across our focus area. This is a quite realistic setup for cell towers. Each hexagon corresponds to one tower which is originally placed in the centroid of the respective hexagon. In order to exclude symmetrical structure, we implement some randomness in the exact location of the cell towers.

# Generate 3 antennas per tower and coverage areas
coverage.areas.tower <- layers %>%
  map2(., jitter, ~st_jitter(st_centroid(.x), .y)) %>%
  map(~st_coordinates(.)) %>%
  map(~as_tibble(.)) %>%
  # map_at(c("Layer.1"), ~bind_rows(., manually.towers.rural)) %>% # only needed if additional antennas are added retrospectively
  # map_at(c("Layer.2"), ~bind_rows(., manually.towers.suburban)) %>% 
  map(~dplyr::select(., X.tow = X, Y.tow = Y)) %>% 
  map2(., c("RT", "ST", "UT"), ~mutate(.x, tower.ID = paste0(.y, 1:n())))

coverage.layer1 <- coverage.areas.tower[[1]] %>% # Layer 1
  st_as_sf(coords = c("X.tow", "Y.tow"), crs = 3035) 
 
layers.plot <- layers[[1]] %>% 
  st_as_sf(crs = 3035) %>%  
  ggplot() + 
  geom_sf(linetype = "dotted") + 
  geom_sf(data = coverage.layer1, aes(color = "#4273C5"), shape = 17) + 
  scale_color_identity(name = "", 
                       labels = c("Jittered tower location"), 
                       guide = "legend") + 
  labs(x = NULL, y = NULL,
       title = "Tower locations in Layer 1") +
  theme(axis.text.x = element_text(angle = 90, hjust = 1))

layers.plot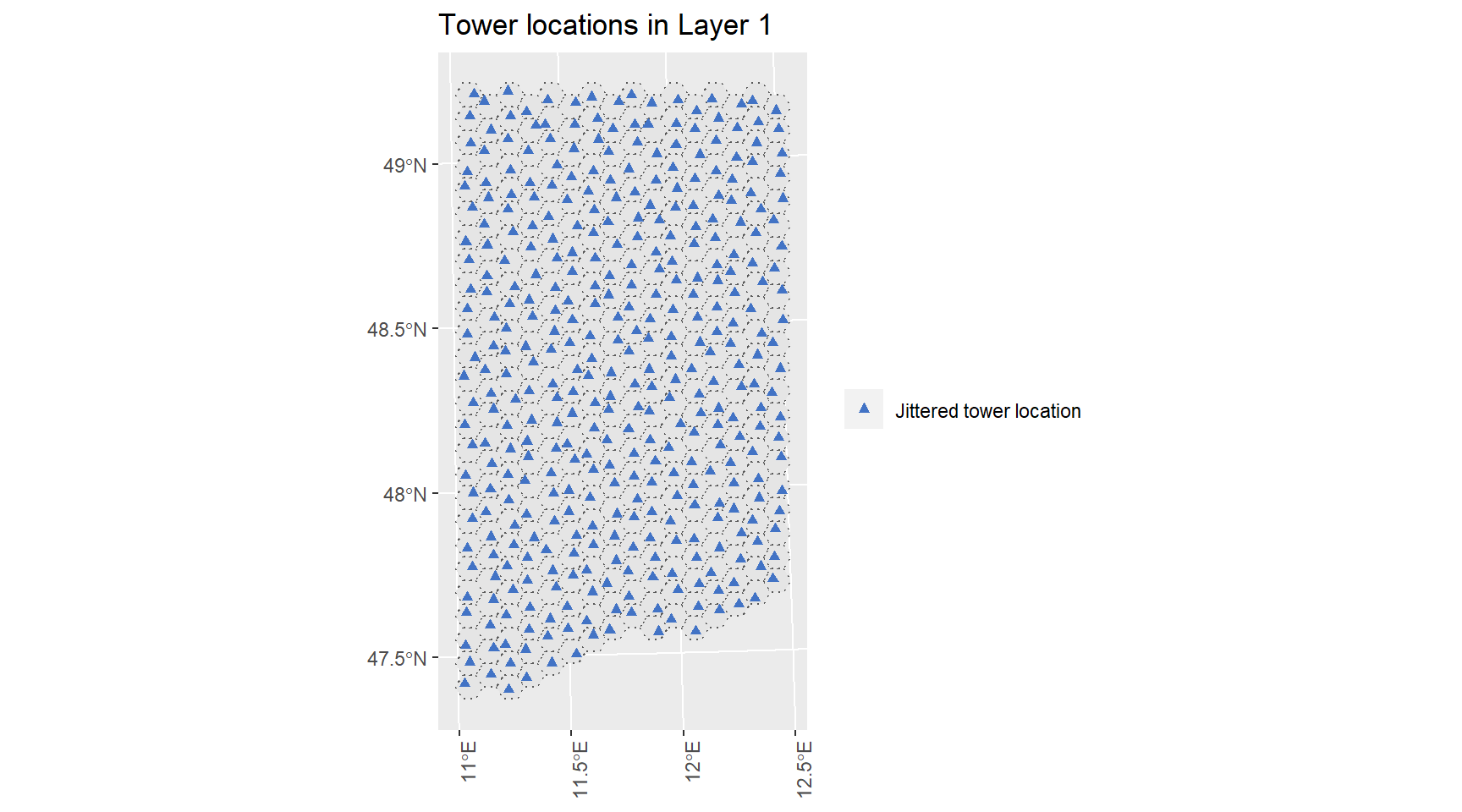

Figure 4.3: …

This example visualizes the tower locations for layer 1. The actual location deviates slightly from the centroid in order to break the symmetry of the underlying hexagonal structure. We can also see from this plot that the hexagonal grid spans over the complete focus area. Next we need to place three antennas on each tower for each layer and specify their coverage area. The setup of a tower with its corresponding antennas is in every layer the same: Three antennas per tower, pointing into 120 degree differing directions. The animated visualization exemplifies this for any generic tower.

knitr::include_graphics("https://raw.githubusercontent.com/R-ramljak/MNO_Eurostat/master/Gifs/antenna%20animation.gif")

Figure 4.4: …

We end up with a data frame of the following format:

coverage.areas.final <- coverage.areas.tower %>% 
  map(~slice(., rep(1:n(), each = 3))) %>%
  map(~group_by(., tower.ID)) %>%
  map(~mutate(., antenna.ID = paste(tower.ID, "A", 1:3, sep = "."))) %>%
  map(~ungroup(.)) %>%
  map(~mutate(., antenna.kind = str_sub(antenna.ID, -1))) %>%
  map2(., coverage.centroid.dist, ~mutate(.x,
                                          X.ant.help = case_when(antenna.kind == "1" ~ X.tow - .y * 0,
                                                                 antenna.kind == "2" ~ X.tow + .y * 0.77,
                                                                 antenna.kind == "3" ~ X.tow - .y * 0.77),
                                          Y.ant.help = case_when(antenna.kind == "1" ~ Y.tow - .y * 1, # meter distance apart
                                                                 antenna.kind == "2" ~ Y.tow + .y * 0.77,
                                                                 antenna.kind == "3" ~ Y.tow + .y * 0.77))) %>%
  # map(~mutate(., X.ant = X.ant.help,
  #             Y.ant = Y.ant.help)) %>% 
  map(~st_as_sf(., coords = c("X.ant.help", "Y.ant.help"))) %>%
  map(~mutate(., antenna.centroid = geometry)) %>% 
  map2(., coverage.radius, ~st_buffer(.x, .y)) %>% # radius coverage are per antenna
  map2(., coverage.radius, ~mutate(.x, coverage.radius = .y)) %>% # 
  map(~st_sf(., crs = 3035)) %>%
  map(~st_crop(., bb.focus.vec)) %>%
  map(~st_set_agr(., "aggregate")) %>% # clean up
  map2_dfr(., area.kind, ~mutate(., area.kind = .y)) %>% 
  st_intersection(census.geo.body)

## Warning: attribute variables are assumed to be spatially constant throughout all
## geometries

## Warning: attribute variables are assumed to be spatially constant throughout all
## geometries

## Warning: attribute variables are assumed to be spatially constant throughout all
## geometries

## Warning: attribute variables are assumed to be spatially constant throughout all
## geometries

rm(layer.base)

# saveRDS(coverage.areas.final, file = "C:/Users/Marco/Vysoká škola ekonomická v Praze/Tony Wei Tse Hung - YAY/working objects/coverage.areas.final.rds")
coverage.areas.final <- readRDS("C:/Users/Marco/Vysoká škola ekonomická v Praze/Tony Wei Tse Hung - YAY/working objects/coverage.areas.final.rds")

coverage.areas.final %>% 
  datatable()

## Warning in instance$preRenderHook(instance): It seems your data is too big
## for client-side DataTables. You may consider server-side processing: https://
## rstudio.github.io/DT/server.html

The table above presents the structure of the radio network object, coverage.areas.final. The data frame contains information on the antenna level. Each antenna has a unique ID, which also reveals the corresponding Layer. We know the location of the respective tower and the location of the antenna’s coverage area centroid, (coverage area centroid).

The following table presents the number of towers and the number of antennas of each layer. Furthermore, it indicates the coverage area in square kilometers. The number of antennas is not always a perfect factor of 3 as the coverage areas are cropped according to the focus area. This means if the complete coverage area of an antenna lies outside of the focus area it is discarded.

tile.count <- census.classified.final.sf %>%  
  st_drop_geometry() %>% 
  group_by(pop.area.kind) %>%  
  summarise(area.in.sq.km = n() / 100) %>% 
  arrange(desc(pop.area.kind)) %>% 
  mutate(area.in.sq.km = case_when(pop.area.kind == "Rural" ~ cumsum(area.in.sq.km),
                                   pop.area.kind == "Suburban" ~ cumsum(area.in.sq.km),
                                   pop.area.kind == "Urban" ~ cumsum(area.in.sq.km))) %>% 
  arrange(pop.area.kind)

## `summarise()` ungrouping output (override with `.groups` argument)

coverage.areas.final %>%  
  st_drop_geometry() %>%  
  group_by(area.kind, tower.ID) %>%  
  summarise(n.antenna = n(), .groups = "drop") %>%  
  ungroup() %>%  
  group_by(area.kind) %>%  
  summarise(n.tower = n(), 
            n.antenna = sum(n.antenna), .groups = "drop") %>%  
  left_join(tile.count, by = c("area.kind" = "pop.area.kind")) %>%  
  dplyr::select(layer = area.kind, n.tower, n.antenna, area.in.sq.km) %>%  
  datatable()

As described in the parameter list above, Rural areas are covered only by layer 1, Suburban areas are covered by layer 1 and 2 and the Urban areas are covered by all three layers. The average distance between multiple towers of the same layer decreases in layer 2 and layer 3 compared to layer 1. This leads to denser networks within these layers represented by the higher numbers of towers and therefore higher numbers of antennas in layer 2 and 3, given their area. The reason for this is that any generic antenna can only offer signal service to a limited amount of number of mobile phones. To cover all cell phones in more urbanized areas a denser radio cell network is needed in these areas.

The following figures present the actual geographic coverage of each layer for the focus area.

coverage.area.plot <- coverage.areas.final %>%  
  ggplot() + 
  geom_sf(aes(col = area.kind), fill = NA) + 
  facet_grid(cols = vars(area.kind)) + 
  ggtitle("") + 
    scale_color_ptol(breaks = c("Rural", "Suburban", "Urban"), "Layer") +
  labs(x = NULL, y = NULL, title = "Coverage per layer") +
  theme(axis.text.x = element_text(angle = 90, hjust = 1))

coverage.area.plot

Figure 4.5: The circles represent the coverage area of each antenna per layer. The signal density increases with increasing population density.

The figure above visualizes the possibility of overlapping coverage areas - with antennas of the same tower, as well as across towers of the same or another layer.

Finally, we can compare our true geographic population distribution and our generated radio network.

# Implement shape of focus area

pop.dist.map.data <- census.classified.final.sf %>% 
  group_by(pop.area.kind) %>% 
  summarise(geometry = st_union(geometry))
# saveRDS(pop.dist.map.data, "C:/Users/Marco/Vysoká škola ekonomická v Praze/Tony Wei Tse Hung - YAY/Estimates/Plot.files/pop.dist.map.area.kind.data.rds")

true.pop.geo.plot <- true.pop.data %>% 
  ggplot() +
  geom_sf(aes(fill = mobile, color = mobile)) +
  scale_fill_ptol(name = "# Mobile phones") +
  scale_color_ptol(guide = F) +
  labs(x = "", y = "", title = "True population value in size categories") +
  theme(axis.text.x = element_text(angle = 90, hjust = 1))

pop.dist.map.plot <- pop.dist.map.data %>% 
  ggplot() + 
  geom_sf(aes(fill = pop.area.kind, color = pop.area.kind), show.legend = F) + 
  scale_fill_ptol(breaks = breaks.first) + 
  scale_color_ptol(breaks = breaks.first, guide = F) + 
  ggtitle("Geographic distribution") + 
  theme(axis.text.x = element_text(angle = 90, hjust = 1))
# saveRDS(pop.dist.map.plot, "C:/Users/Marco/Vysoká škola ekonomická v Praze/Tony Wei Tse Hung - YAY/Estimates/Plot.files/pop.dist.map.plot.rds")

coverage.area.full.plot <- coverage.areas.final %>% 
  ggplot() +
  geom_sf(aes(col = area.kind), fill = NA) +
  ggtitle("Full coverage") +
    scale_color_ptol(breaks = breaks.first, "Layer") +
  theme(axis.text.x = element_text(angle = 90, hjust = 1))
 
pop.dist.map.plot
coverage.area.full.plot

Figure 4.6: The figure on the left shows the geographical distribution of the tiles classified into the three layers based on the spatial clustering. On the right side, the coverage per layer is represented. The full coverage corresponds to the population density.

The figure on the right presents the full network structure. By comparing the network structure to the geographic distribution we can see that full and partially overlapping coverage is granted for all areas and that the network layering structure follows suit with the true geographical population density (i.e. urban areas have more coverage).

The radio network generation marks the next important interim result in the Generation of our Toy World. We now have radio network implemented into our geography and that covers to a sufficient degree all tiles. However, this does not guarantee that all units in the population can actually connect, and therefore be counted, to an antenna. We will introduce the parameter of signal strength as this describes the differing coverage intensity, dependent on how far a mobile phone is from the coverage area centroid. This will be handlded in the next part, device to cell (antenna) association.