Chapter 7 Probability
Get Started
This chapter provides a brief look at some of the important terms and definitions related to the concept of probability. To follow along, you should load the following data sets: anes20.rda, which you’ve worked with in previous chapters, and grades.rda, a data set summarize final grades over several semesters from a course I teach on data analysis. You should also make sure to attach the libraries for the following R packages: descr, DescTools, and Hmisc.
Probability
You probably use the language of probability in your everyday life. Whether we are talking or thinking about the likelihood, odds, or chance that something will occur, you are using probabilistic language. At its core, probability is about whether something is likely or unlikely to happen.
Probabilities can be thought of as relative frequencies that express how often a given outcome (X) occurs, relative to the number of times it could occur:
\[P(X)=\frac{\text{Number X outcomes}}{\text{Number possible X outcomes}}\]
Probabilities range from 0 and 1, with zero meaning an event never happens and 1 meaning the event always happens. As you move from 0 to 1, the probability of an event occurring increases. When the probability value is equal to .50, there is an even chance that the event will occur. This connection between probabilities and everyday language is summarized below in Figure 7.1. It is also common for people to use the language of percentages when discussing probabilities, e.g., 0% to 100% range of possible outcomes. For instance, a .75 probability that something will occur might be referred to as a 75% probability that the event will occur.
[Figure****** 7.1 ******about here.]
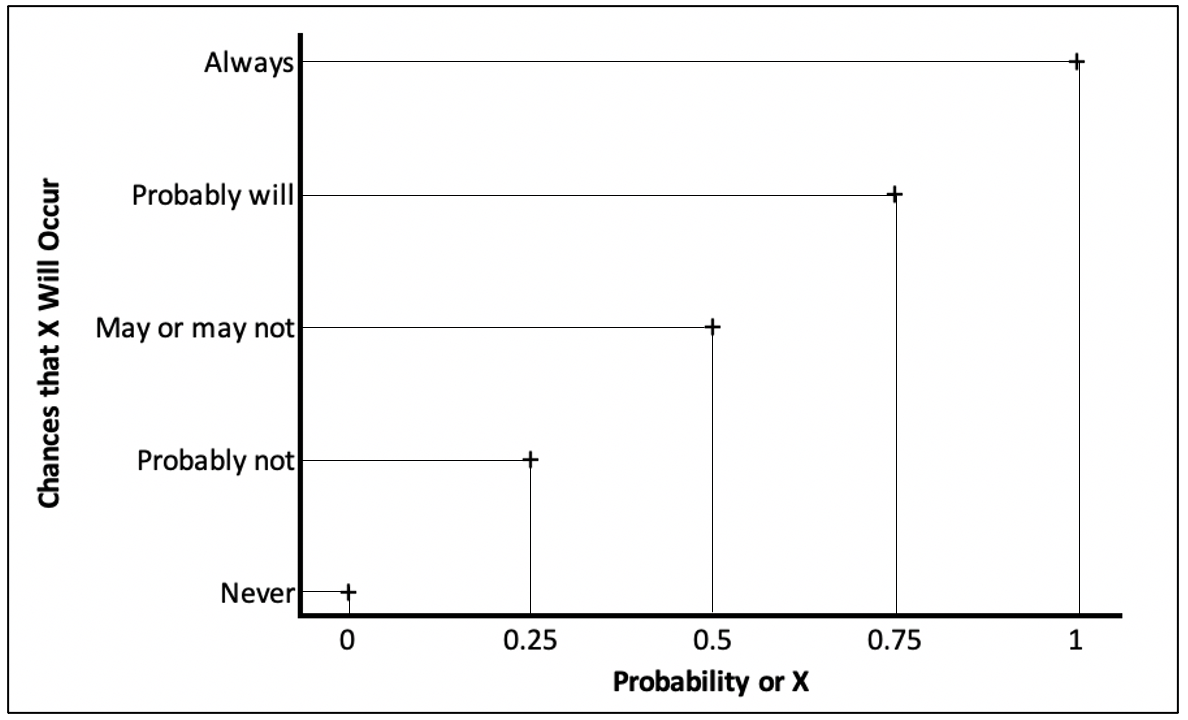
Figure 7.1: Substantive Meaning of Probability Values
Consider this example. Suppose we want to know the probability that basketball phenom and NBA Champion Giannis Antetokounmpo, of the Milwaukee Bucks, will make any given free-throw attempt. We can use his performance from the 2020-2021 regular season as a guide. Giannis (if I may) had a total of 581 free-throw attempts (# of possible outcomes) and made 398 (number of X outcomes) . Using the formula from above, we get: \[P(success)=\frac{389}{581} = .685\]
The probability of Giannis making any given free-throw during the season was .685. This outcome is usually converted to a percentage and known as his free-throw percentage (68.5%).
Is this a high probability or a low probability? Sometimes, the best way to evaluate probabilities is comparatively; in this case, that means comparing Giannis’ outcome to others. If you compared Giannis to me, he would seem like a free-throw superstar, but that is probably not the best standard for evaluating a professional athlete. Instead, you could also compare him to the league average for the 2020-2021 season (.778), or his own average in the previous year (.633). By making these comparisons, we are contextualizing the probability estimate, so we can better understand its meaning in the setting of professional basketball.
It is also important to realize that this probability estimate is based on hundreds of “trials” and does not rule out the possibility of “hot” or “cold” shooting streaks. For instance, Giannis made 4 of his 11 free throw attempts in Game 5 against the Phoenix Suns (.347) and was 17 of 19 (.897) in series clinching Game 6. In those last two games, he was 21 of 30 (.70), just a wee bit higher than his regular season average.
Theoretical Probabilities
It is useful to distinguish between theoretical and empirical probabilities. Theoretical probabilities can be determined, or solved, on logical grounds. There is no need to run experiments or gather data to estimate these probabilities. Sometimes these are referred to as a priori (think of this as something like “based on assumptions”) probabilities.
Consider the classic example of a coin toss. There are two sides to a coin, “Heads” and “Tails,” so if we assume the coin is fair (not designed to favor one side or the other), then the probability of getting “Heads” on a coin flip is ½ or .5. The probability of coming up “Heads” on the next toss is also .50 because the two tosses are independent, meaning that one toss does not affect subsequent tosses.
Likewise,
We can estimate the probability of rolling a 4 on a fair six-sided die with sides numbered 1 through 6. Since 4 is one of six possibilities, the probability is 1/6, or .167.
The same idea applies to estimating the probability of drawing an Ace from a well-shuffled deck of cards. Since there are four Aces out of the 52 cards, the probability is 4/52, or .077.
The same for drawing a Heart from a well-shuffled deck of cards. Since there are 13 cards for each suit (Hearts, Diamonds, Clubs, and Spades), the probability is 13/52, or .25.
What about the probability of drawing an Ace of Hearts from a deck of cards? There is only one Ace of Hearts in the 52-card deck, so the probability is 1/52, or .019. Note that this is the probability of an Ace (.077) multiplied times the probability of a Heart (.25).
Sometimes, these probabilities may appear to be at odds with what we see in the real world, especially when we have a small sample size. Think about the flip of a coin. Theoretically, unless the coin is rigged, \(P(H)=P(T)=.50\). So, if we flip the coin 10 times, should we expect 5 Heads and 5 Tails? If you’ve ever flipped a coin ten times in a row, you know that you don’t always end up with five “Heads” and five “Tails.” But, in the long run, with many more than ten coin flips, the outcomes of coin tosses converge on \(P(H)=.50\). I illustrate the idea of long run expected values below using small and large samples of coin tosses and rolls of a die.
Large and Small Sample Outcomes
The graph shown below in Figure 7.2 illustrates the simulated18 coin toss outcomes using different numbers of coin tosses, ranging from ten to two-thousand tosses. In the first four simulations (10, 20, 60, and 100 tosses), the results are not very close to expected outcome (50% “Heads”), ranging from 30% to 58%. However, for the remaining ten simulations (150 to 2000 tosses), the results are either almost exactly on target or very slightly different from the expected outcome.
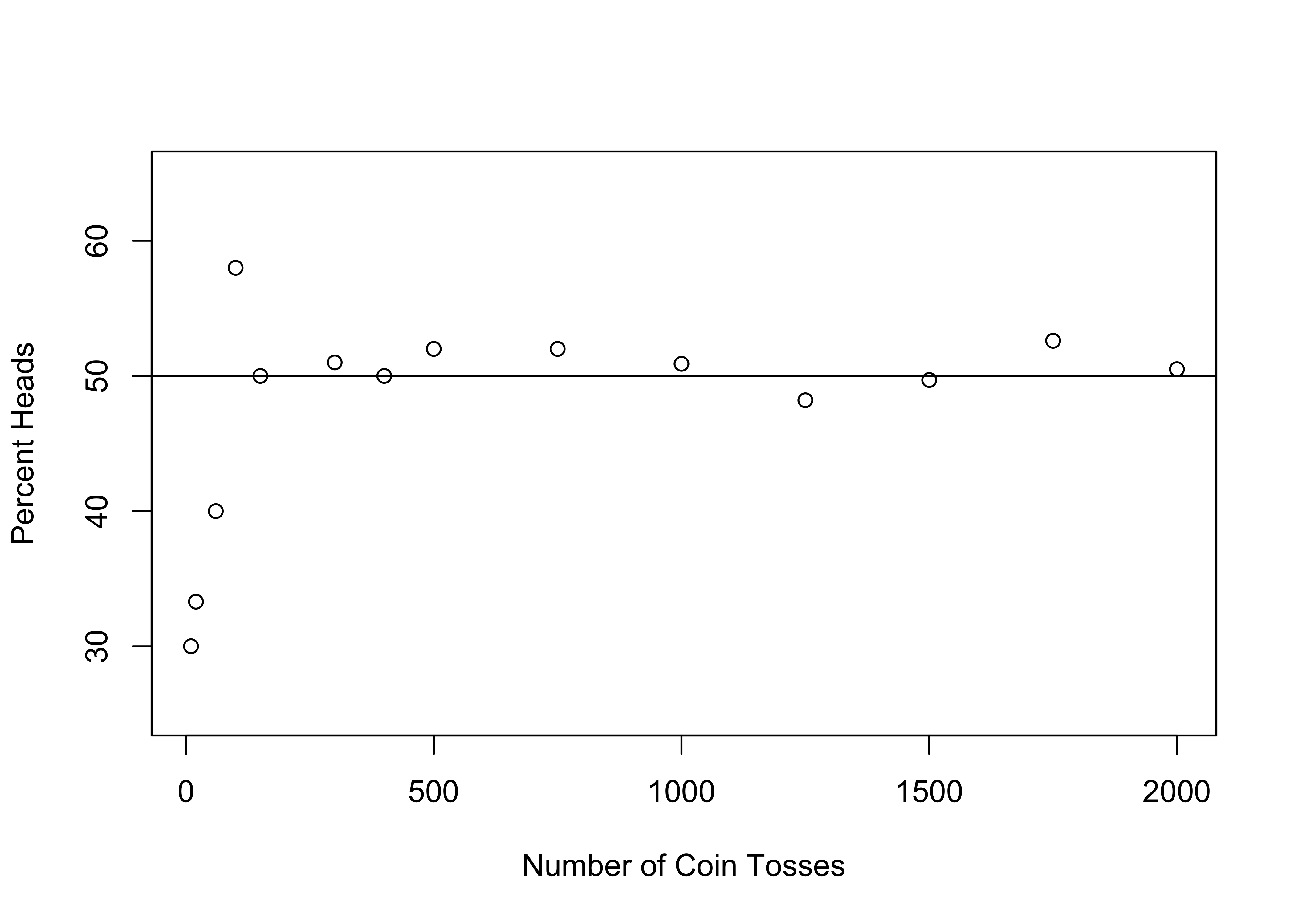
Figure 7.2: Simulated Results from Large and Small Coin Toss Samples
[Figure** 7.2 **about here]
We can work through the same process for rolling a fair six-sided die, where the probability of each of the six outcomes is 1/6=.167. The results in Figure 7.3 summarize the outcomes of rolling a six-sided die 100 times (on the left) and 2000 times (on the right), using a solid horizontal line to indicate the expected value (.167). Each of the six outcomes should occur approximately the same number of times. On the left side, based on just 100 rolls of the die, the outcomes deviate quite a bit from the expected outcomes, ranging from .08 of outcomes for the number 3, to .21 of outcomes for both numbers 2 and 4. This is not what we expect from a fair, six-sided die. But if we increase the number of rolls to 2000 (right side of Figure 7.3, we see much more consistency across each of the six numbers on the die, and all of the proportions are very close to .167, ranging from .161 for the number 1, to .175 for the number 4.
[Figure** 7.3 **about here]
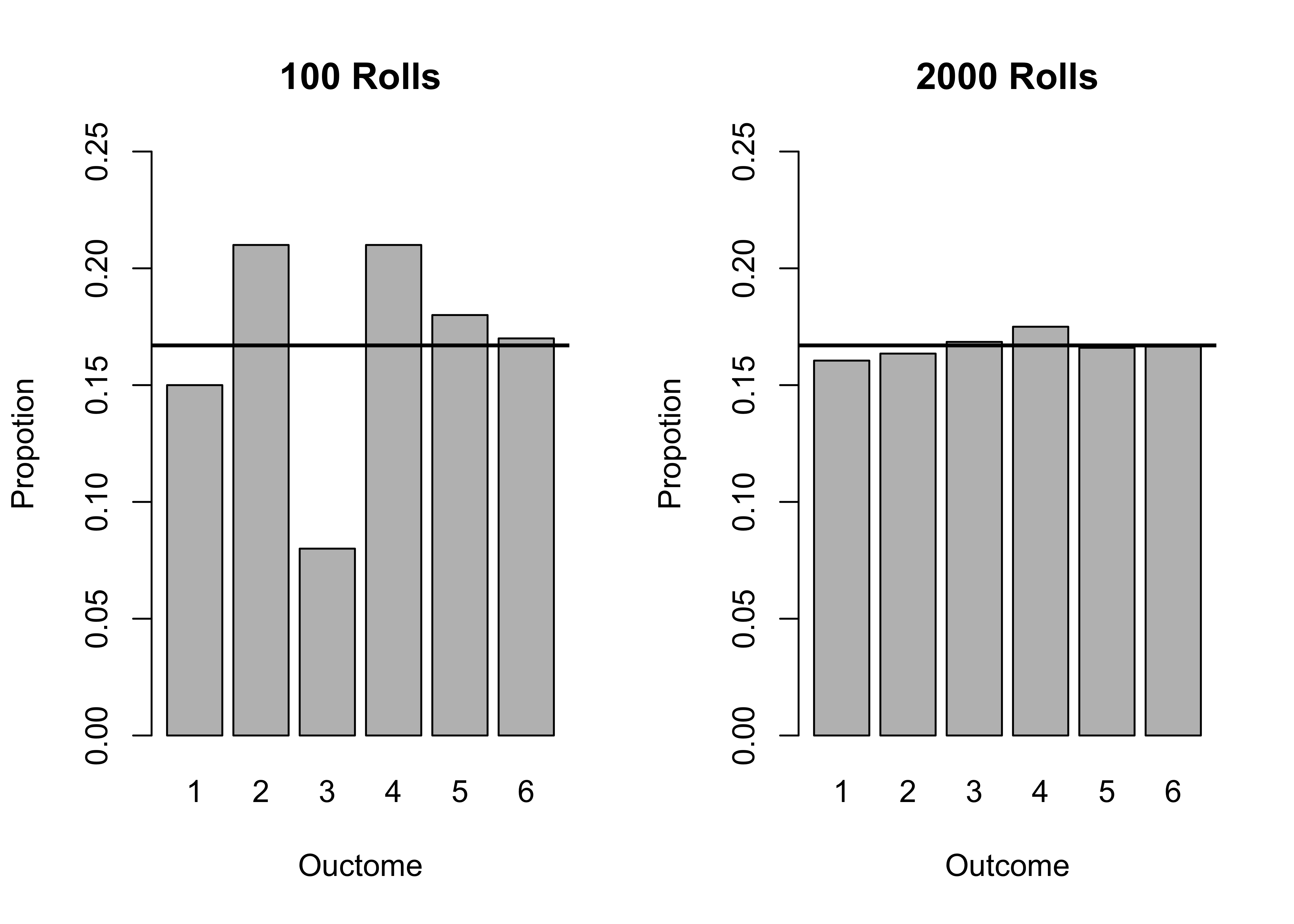
Figure 7.3: Simulated Results from Large and Small Samples of Die Rolls
The coin toss and die rolling simulations are important demonstrations of the Law of Large Numbers: If you conduct multiple trials or experiments of a random event, the average outcome approaches the theoretical (expected) outcome as the number of trials increases and becomes large.
This idea is very important and comes into play again in Chapter 8.
Empirical Probabilities
Empirical probability estimates are based on observations of the relative occurrence of events in the past, as we discussed in the opening example. These probabilities are also sometimes referred to as posterior probabilities because they cannot be determined, or solved, on logical grounds; we need data from past experiences in order to estimate them.
For instance:
We know from earlier that the probability of Giannis making any given free throw during the 2020-2021 season was \(P(success)\) = (389/581) = .685, based on observed outcomes from the season.
From the past several semesters of teaching data analysis, I know that 109 of 352 students earned a grade in the B range, so the \(P(B)=109/352=.31\).
Brittney Griner, the center for the Phoenix Mercury, made 248 of the 431 shots she took from the floor in the 2021 season, so the probability of her making a any shot she took during that season was \(P(Swish)=248/431=.575\).
Joe Biden won the presidential election in 2020 with 51.26% of the popular vote, so the probability that a 2020 voter drawn at random voted for Biden is .5126.
To arrive at these empirical probabilities, I used data from the real world and observed the relative occurrence of different outcomes. These probabilities are the relative frequencies expressed as proportions.
Empirical Probabilities in Practice
We can also use the results of joint frequency distributions to estimate the probabilities of different outcomes occurring, either separately or at the same time. Let’s look at a joint frequency table (cross tabulation) for vote choice and level of education in the 2020 U.S. presidential election, using data from the ANES.
First, we need to prepare that variables by modifying and collapsing some category labels.
#Create Vote variable
anes20$vote<-factor(anes20$V202073)
#Collapse levels to Biden, Trump, Other
levels(anes20$vote)<-c("Biden", "Trump", "Other", "Other",
"Other", "Other","Other", "Other",
"Other")
#Create education variable
anes20$educ<-ordered(anes20$V201511x)
#Edit the levels so they fit in the table
levels(anes20$educ)<-c("LT HS", "HS", "Some Coll",
"4yr degr", "Grad degr")Now, we can get a crosstabulation of both vote choice and education level.
#Get a crosstab of vote by education, using a weight, no plot
crosstab(anes20$vote, anes20$educ,weight=anes20$V200010b, plot=F)You should note the addition of weight=anes20$V200010b in the command line for the crosstab. Often, despite best efforts at drawing a good sample, some sample characteristics differ significantly from known population characteristics. Using sample weights is a way to align certain sample characteristics with their known values in the population. The idea is to assign less weight to over-represented characteristics and more weight to under-represented characteristics. The ANES uses a complex weighting method that corrects for sampling bias related to sex, race, education, size of household, region, and other characteristics. The weighting information is activated using anes20$V200010b. We won’t use the weight function in most cases, but it does help improve the accuracy of the vote margins a bit (though not perfectly).
Each row in the table represents an outcome for vote choice, and each column represents a different level of educational attainment. Each of the interior cells in the table represents the intersection of a given row and column. At the bottom of each column and the end of each row, we find the row and column totals, also known as the marginal frequencies. These totals are the frequencies for the dependent and independent variables (note, however, that the sample size is now restricted to the 5183 people who gave valid responses to both survey questions).
Cell Contents
|-------------------------|
| Count |
|-------------------------|
======================================================================
anes20$educ
anes20$vote LT HS HS Some Coll 4yr degr Grad degr Total
----------------------------------------------------------------------
Biden 124 599 741 801 518 2783
----------------------------------------------------------------------
Trump 117 644 770 493 232 2256
----------------------------------------------------------------------
Other 10 20 47 47 20 144
----------------------------------------------------------------------
Total 251 1263 1558 1341 770 5183
======================================================================From this table we can calculate a number of different probabilities. To calculate the vote probabilities, we just need to divide the raw vote (row) totals by the sample size:
Note that even with the sample weights applied, these estimates are not exactly equal to the population outcomes (.513 for Biden and .468 for Trump). Some part of this is due to sampling error, which you will learn more about in the next chapter.
We can use the column totals to calculate the probability that respondents have different levels of education.
Intersection of Two Probabilities
Sometimes, we are interested in the probability of two things occurring at the same time, the intersection of two probabilities represented as \(P(A\cap B)\). If the events are independent, such as the \(P(Ace)\) and \(P(Heart)\), which we looked at earlier, then \(P(A\cap B)\) is equal to \(P(A) * P(B)\). By independent, we mean that the probability of one outcome occurring is not affected by another outcome. In the case of drawing an Ace of Hearts, the suit and value of cards are independent, because each suit has the same thirteen cards. Similarly, coin tosses are independent because the outcome of one toss does not affect the outcome of the other toss.
Suppose that we are interested in estimating the probability of a respondent being a Trump voter AND someone whose highest level of education is a high school diploma or equivalent, the intersection of Trump and HS (\(P(\text{Trump}\cap \text{HS}\)). Vote choice and education levels in the table below are not independent of each other, so we can’t use the simple multiplication rule to calculate the intersection of two probabilities.19. Although we can’t use the multiplication rule, we can use the information in the joint frequency distribution, focusing on that part of the table where the Trump row intersects with the HS column. We take the number of respondents in the Trump/HS cell (644) and divide it by the total sample size (5183).
The Union of Two Probabilities
Sometimes, you might want to estimate the probability of one event OR another happening, the union of two probabilities, represented as \(P(A\cup B)\). For instance, we can estimate the probability of Trump OR HS occurring (the union of Trump and HS) by adding the probability of each event occurring and then subtracting the intersection of the two events:
\[P(Trump\cup HS)= P(Trump)+P(HS)-P(Trump \cap HS)\]
\[P(Trump\cup HS)= .4353+.2437-.1243 = .5547\]
Why do we have to subtract \(P(Trump\cap HS)\)? If we didn’t, we would be double counting the 644 people in the Trump/HS cell since they are in both the Trump row and HS column.
Of course, you can also get \(P(Trump\cup HS)\) by focusing on the raw frequencies in the joint frequency table: add the total number of Trump voters (2256) to the total number of people in the HS column (1263), subtract the total number of respondents in the cell where the Trump row intersects that HS column (644) and divide the resulting number (2875) by the total number of respondents in the table (5183):
Conditional Probabilities
These probabilities are well and good, but let’s face it, sometimes they are not terribly interesting on their own, at least in the current example. They don’t tell much of a story on their own. They tell us how likely it is that certain outcomes will occur, but not about how the outcomes of one variable might affect the outcomes of the other variable. From my perspective, it is far more interesting to learn how the probability of voting for Trump or Biden varies across levels of educational attainment. In other words, does educational attainment seem to have an impact on vote choice? To answer this, we need to ask something like, ‘What is the probability of voting for Trump, GIVEN that a respondent’s level of educational attainment is a high school degree or equivalent?’ and ‘how does that compare with the probability of voting for Trump GIVEN other levels of education?’ These sorts of probabilities are referred to as conditional probabilities because they are saying the probability of an outcome on one variable is conditioned by, or depends upon the outcome of another variable. This is what we mean when we say that two events are not independent–that the outcome on one depends upon the outcome on the other.
Let’s start with the probability of voting for Trump given that someone is in the HS category on educational attainment: \(P(Trump\mid HS)\). There are two ways to calculate this using the data we have. First, there is a formula based on other probability estimates:
\[P(Trump\mid HS)=\frac{P(Trump\cap HS)}{P(HS)}\] \[(Trump\mid HS)=\frac{.12425}{.24368}=.5099\]
A more intuitive way to get this result, if you are working with a joint frequency distribution, is to divide the total number of respondents in the Trump/HS cell by the total number of people in the HS column: \(\frac{644}{1263} =.5099\). By limiting the frequencies to the HS column, we are in effect calculating the probability of respondents voting for Trump given that high school equivalence is their highest level of education. Using the raw frequencies has the added benefit of skipping the step of calculating additional probabilities.
Okay, so the probability of someone voting for Trump in 2020, given their level of educational attainment was a high school degree is .5099. So what? Well, first, we note that this is higher than the overall probability of voting for Trump (\(P(Trump)=.4353\)), so we know that having a high school level of educational attainment is associated with a higher than average probability of casting a Trump vote. We can get a broader sense of the impact of educational attainment on the probability of voting for Trump by calculating the other conditional probabilities:
What this shows us is a very clear relationship between educational attainment and vote choice in the 2020 presidential election. Specifically, voters in the lowest three educational attainment categories had a somewhat higher than average probability of casting a Trump vote, while voters in the two highest educational attainment groups had a substantially lower probability of casting a Trump vote. People whose highest level of educational attainment is a high school degree had the highest probability of supporting President Trump’s reelection (.5099), while those with graduate degrees had the lowest probability (.3013). Although the pattern is not perfect, generally, as education increases, the probability of voting for Trump decreases.
The Normal Curve and Probability
The normal distribution can also be used to calculate probabilities, based on what we already know about the relationship between the standard deviation and the normal curve. In the last chapter, when we calculated areas to the right or left of some z-score, or between two z-scores, we were essentially calculating the probability of outcomes occurring in those areas.
For instance, if we know that 68% of all values for a normally distributed variable lie within 1 standard deviation from the mean, then we know that the probability of a value, chosen at random, being within 1 standard deviation of the mean is about .68. What about the probability of a value being within 2 standard deviations of the mean? (about .95) More than 2 standard deviations from the mean? (about .05) These cutoff points are familiar to us from Chapter 6.
We can use the normal distribution to solve probability problems with real world data. For instance, suppose you are a student thinking about enrolling in my Political Data Analysis class and you want to know how likely it is that a student chosen at random would get a grade of A- or higher for the course (at least 89% of total points). Let’s further suppose that you know the mean (75.12) and standard deviation (17.44) from the previous several semesters. What you want to know is, based on data from previous semesters, what is the probability of any given student getting an overall score of 89 or better?
In order to solve this problem, we need to make the assumption that course grades are normally distributed, convert the target raw score (89) into a z-score, and then calculate the probability of getting that score or higher, based on the area under the curve to the right of that z-score. Recall that the formula for a z-score is:
\[Z_i=\frac{x_i-\bar{x}}{S}\]
In this case \(x_i\) is 89, the score you need to earn in order to get at least an A-, so:
\[Z_{89}=\frac{89-75.15}{17.44}=\frac{13.85}{17.44}=.7942\]
We know that \(Z_{89}=.7942\), so now we need to calculate the area to the right of .7942 standard deviations on a normally distributed variable:
#Get area to the right of z=.7942
pnorm(.7942, lower.tail = F)[1] 0.2135395The probability of a student chosen at random getting a grade of A- or higher is about .2135. You could also interpret this as meaning that the expectation is that about 21.35% of students will get a grade of A- or higher.
Again, it is important to recognize that this probability estimate is based on assumptions we make about a theoretical distribution, even though we are interested in estimating probabilities for an empirical variable. As discussed in Chapter 6, the estimates derived from a normal distribution are usually in the ballpark of what you find in empirical distributions, provided that the empirical distribution is not too oddly shaped. Since we have the historical data on grades, we can get a better sense of how well our theoretical estimate matches the overall observed probability of getting at least an A-, based on past experiences (empirical probability).
#Let's convert the numeric scores to letter grades (with rounding)
grades$A_Minus<-ordered(cut2(grades$grade_pct, c(88.5)))
#assign levels
levels(grades$A_Minus)<-c("LT A-", "A-/A")
#show the frequency distribution for the letter grade variable.
freq(grades$A_Minus, plot=F)grades$A_Minus
Frequency Percent Cum Percent
LT A- 276 78.41 78.41
A-/A 76 21.59 100.00
Total 352 100.00 Not Bad! Using real-world data, and collapsing the point totals into two bins, we estimate that the proportion of students earning a grade of A- or higher is .216. This is very close to the probability estimate based on assuming a theoretical normal distribution (.214).
There is one important caveat: this bit of analysis disregards the fact that the probability of getting an A- is affected by a number of factors, such as effort and aptitude for this kind of work. If you have no other information about any given student, your best guess is that they have about a .22 probability of getting an A- or higher. Ultimately, it would be better to think about this problem in terms of conditional probabilities, whereby \(P(\text{A-})\) is affected by other variables. Do you imagine that the probability of getting a grade of the A- or higher might be affected by how much time students are able to put into the course? Maybe those who do all of the reading and spend more time on homework have a higher probability of getting a grade in the A-range. In other words, to go back to the language of conditional probabilities, we might want to say that the probability of getting a grade in the A-range is conditioned by student characteristics.
Next Steps
The material in this and the next two chapters is essential to understanding one of the important concepts from Chapter 1, the idea of level of confidence in statistical results. In the next chapter, we expand upon the idea of the Law of Large numbers by exploring related concepts such as sampling error, the Central Limit Theorem, and statistical inference. Building on this content, Chapter 9 kicks off a several-chapters-long treatment of hypothesis testing, beginning with testing hypotheses about the differences in mean outcomes between two groups. The upcoming material is a bit more abstract than what you have read so far, and I think you will find the shift in focus interesting. My sense from teaching these topics for several years is that this is also going to be new material for most of you. Although this might make you nervous, I encourage you to look at it as an opportunity!
Exercises
Concepts and Calculations
- Use the table below, showing the joint frequency distribution for attitudes toward the amount of attention given to sexual harassment (a recoded version of
anes20$V202384) and vote choice for this problem.
Cell Contents
|-------------------------|
| Count |
|-------------------------|
=============================================================
anes20$harass
anes20$vote Not Far Enough About Right Too Far Total
-------------------------------------------------------------
Biden 1385 1108 293 2786
-------------------------------------------------------------
Trump 402 984 869 2255
-------------------------------------------------------------
Other 61 51 33 145
-------------------------------------------------------------
Total 1848 2143 1195 5186
=============================================================Estimate the following probabilities:
\(P(Too\> Far)\)
\(P(About\>Right)\)
\(P(Not\>Far \> Enough)\)
\(P(Trump\cap Not\>Far \> Enough)\)
\(P(Trump\cup Not\>Far \> Enough)\)
\(P(Trump\mid Too\> Far)\)
\(P(Trump\mid About\> Right)\)
\(P(Trump\mid Not\>Far \> Enough)\)
Using your estimates of the conditional probabilities, summarize how the probability of voting for President Trump was related to how people felt about the amount of attention given to sexual harassment.
I flipped a coin 10 times and it came up Heads only twice. I say to my friend that the coin seems biased toward Tails. They say that I need to flip it a lot more times before I can be confident that there is something wrong with the coin. I flipped the coin 1000 times, and it came up Heads 510 times. Was my friend right? What principle is involved here? In other words, how do you explain the difference between 2/10 on my first set of flips and 510/1000 on my second set?
In an analysis of joint frequency distribution for vote choice and whether people support or oppose banning assault-style rifles in the 2020 election, I find that \(P(Biden)=.536\) and \(P(Oppose)=.305\). However, when I apply the multiplication rule (\((P(Biden)*P(Oppose)\)) to find \(P(Biden\cap Oppose)\) I get .1638, while the correct answer is .087. What did I do wrong? Why didn’t the multiplication rule work?
Identify each of the following as a theoretical or empirical probability.
- The probability of drawing a red card from a deck of 52 playing cards.
- The probability of being a victim of violent crime.
- The probability that 03 39 44 54 62 19 is the winning Powerball combination.
- The probability of being hospitalized if you test positive for COVID-19.
- The probability that Sophia Smith, of the Portland Thorns FC, will score a goal in any given match in which she plays.
The table below is a crosstabulation of two variables from the anes20 data set, respondent age and respondent opinion on whether business owners should be allowed to refuse services to same sex couples. After calculating the conditional probabilities, describe how age affects the probability that respondents chose the first option, “Should be allowed to refuse.”
Cell Contents
|-------------------------|
| Count |
|-------------------------|
================================================================================
PRE: SUMMARY: Respondent age
PRE: Services to same sex coupls 18-29 30-44 45-60 61-75 76+ Total
--------------------------------------------------------------------------------
Allowed to Refuse 388 932 1036 1135 401 3892
--------------------------------------------------------------------------------
Required to Provide 612 1068 1020 971 286 3957
--------------------------------------------------------------------------------
Total 1000 2000 2056 2106 687 7849
================================================================================R Problems
- Use the code below to create a new object in R called “coin” and assign two different outcomes to the object, “Heads” and “Tails”. Double check to make sure you’ve got this right.
coin <- c("Heads", "Tails")
coin- Next, you need to use R to simulate the results of tossing a coin ten times. Copy and run the code below to randomly choose between the two outcomes of “coin” (“Heads” and “Tails”) ten times, saving the outcomes in a new object,
coin10. These outcomes represent the same thing as ten coin tosses. Usetable(coin10)to see how many “Heads” and “Tails” outcomes you have from the ten coin tosses. Is the outcome you got close to the 5 Heads/5 Tails you should expect to see?
#Take a random sample of outcomes from ten tosses
coin10<-sample(coin, 10, rep=T)
table(coin10)- Now, repeat the R commands in Question 2 nine more times, recording the number of heads and tails you get from each simulation. Show your results and sum up the number of “Heads” outcomes from the ten simulations. If the probability of getting “Heads” on any given toss is .50, then you should have approximately 50 “Heads” outcomes. Discuss how well you results match the expected 50/50 outcome. Also, comment on the range of outcomes–some close to 50/50, some not at all close–you got across the ten simulations.
By “simulated,” I mean that I created an object named “coin” with two values, “Heads” and “Tails” (coin <- c(“Heads”, “Tails”)) and told R to choose randomly from these two values and store the results in a new object, “coin10”, where the “10” indicates the number of tosses (coin10=sample(coin, 10, rep=T)). The frequencies of the outcomes for object “coin10” can be used to show the number of “Heads” and “Tails” that resulted from the ten tosses. I then used the same process to generate results from larger samples of tosses.↩︎
You will see in just a bit, in the section on conditional probabilities, that the probabilities of candidate outcomes are not the same across levels of education↩︎