Chapter 16 Multiple Regression
Getting Started
This chapter expands the discussion of regression analysis to include the use of multiple independent variables in the same model. To follow along in R, you should load the countries2 data set and attach the libraries for the DescTools and stargazer packages.
Multiple Regression
To this point, we have findings from three simple regression models that offer different potential explanations for cross-national variation in life expectancy: differences in fertility rate and in levels of education are both strongly related to differences in life expectancy, while there is no apparent relationship between size of population and life expectancy. However, we know from the discussion of partial correlations in Chapter 14 that the fertility rate and mean years of education are highly correlated with each other and overlap somewhat in accounting of variation in life expectancy. Because of the degree to which these two variables are correlated with each other, it is highly likely that the results from the simple regression model overestimate their independent effect on the dependent variable.
Just as we were able to extend the discussion from Pearson’s r to partial correlations to account for overlapping influences in Chapter 14, we can extend the regression model to include several independent variables to accomplish the same goal. With multiple regression analysis, we can use a linear model to consider the impact of each independent variable on the dependent variable, controlling for the influence of all of the other independent variables, as well as how the independent variables are related to each other.
Multiple regression extends the simple model by adding independent variables:
\[y_i= a + b_1x_{1i}+ b_2x_{2i}+ \cdot \cdot \cdot + b_kx_{ki} + e_i\]
Where:
\({y}_i\) = the predicted value of the dependent variable
\(a\) = the sample constant (aka the intercept)
\(x_{1i}\) = the value of x1
\(b_1\) = the partial slope for the impact of x1, controlling for the impact of other variables
\(x_{2i}\) = the value of x2
\(b_2\) = the partial slope for the impact of x2, controlling for the impact of other variables
\(k\)= the number of independent variables
\(e_i\) = error term; the difference between the predicted and actual values of y (\(y_i-\hat{y}_i\)).
The formulas for estimating the constant and slopes for a model with two independent variables are presented below:
\[b_1=\left (\frac{s_y}{s_1} \right) \left (\frac{r_{y1}-r_{y2}r_{12}}{1-r^2_{12}} \right) \]
\[b_2=\left (\frac{s_y}{s_2}\right)\left(\frac{r_{y2}-r_{y1}r_{12}}{1-r^2_{12}}\right)\]
\[a=\bar{Y}-b_1\bar{X}_1-b_2\bar{X}_2\] We won’t calculate the constant and slopes here, but I want to point out that they are based on the relationship between each of the independent variables and the dependent variable and also the interrelationships among the independent variables. You should recognize the right side of the formula for \(b\) as very similar to the formula for the partial correlation coefficient. This illustrates that the partial regression coefficient is doing the same thing that the partial correlation does: it provides an estimate of the impact of one independent variable while controlling for how it is related to the other independent variables AND for how the other independent variables are related to the dependent variable. The primary difference is that the partial correlation summarizes the strength and direction of the relationship between x and y, controlling for other specified variables, while the partial regression slope summarizes the expected change in y for a unit change in x, controlling for other specified variables and can be used to predict outcomes of y. As independent variables are added to the model, the level of complexity for calculating the slopes increases, but the basic principle of isolating the independent effects of multiple independent variables remains the same.
To get multiple regression results from R, you add the independent variables to the linear model function, using the “+” sign to separate them. Also, since you are listing multiple variables from the same data set, you can save some space and effort by adding data=DataSetName to the command and then just listing the variable names, instead of using DataSetName$Variable for each variable. 41
#Note the "+" sign before each additional variable.
#See footnote for information about "na.action"
fit<-lm(data=countries2, lifexp~fert1520 +
mnschool+ log10(pop19_M), na.action=na.exclude)
summary(fit)
Call:
lm(formula = lifexp ~ fert1520 + mnschool + log10(pop19_M), data = countries2,
na.action = na.exclude)
Residuals:
Min 1Q Median 3Q Max
-14.920 -2.297 0.302 2.674 9.632
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 75.468 2.074 36.38 < 2e-16 ***
fert1520 -3.546 0.343 -10.34 < 2e-16 ***
mnschool 0.750 0.140 5.36 0.00000026 ***
log10(pop19_M) 0.296 0.340 0.87 0.38
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 3.77 on 179 degrees of freedom
(12 observations deleted due to missingness)
Multiple R-squared: 0.748, Adjusted R-squared: 0.743
F-statistic: 177 on 3 and 179 DF, p-value: <2e-16The raw R output is shown above, so you can see that it changes very little when you add variables. The stargazer output is shown below.
#Use 'stargazer' to produce a table for the three-variable model
stargazer(fit, type="text",
dep.var.labels=c("Life Expectancy"),
covariate.labels = c("Fertility Rate",
"Mean Years of Education",
"Log10 Population"))
===================================================
Dependent variable:
---------------------------
Life Expectancy
---------------------------------------------------
Fertility Rate -3.546***
(0.343)
Mean Years of Education 0.750***
(0.140)
Log10 Population 0.296
(0.340)
Constant 75.468***
(2.074)
---------------------------------------------------
Observations 183
R2 0.748
Adjusted R2 0.743
Residual Std. Error 3.768 (df = 179)
F Statistic 176.640*** (df = 3; 179)
===================================================
Note: *p<0.1; **p<0.05; ***p<0.01This output looks a lot like that from the individual models, except now we have the coefficients for each of the independent variables in a single model.
Here’s how I would interpret the results:
Two of the three independent variables are statistically significant: fertility rate has a negative impact on life expectancy, and educational attainment has a positive impact. The p-values for the slopes of these two variables are less than .01. Population size has no impact on life expectancy.
For every additional unit of fertility rate, life expectancy is expected to decline by 3.546 years, controlling for the influence of other variables. So, for instance, if two countries are the same on all other variables, but one country’s fertility rate is one unit higher than the other, we would predict life expectancy to be 3.546 years lower in the country with the higher fertility rate than in the other country.
For every additional year of mean educational attainment, life expectancy is predicted to increase by .75 years, controlling for the influence of other variables. If two countries are the same on all other variables, but one country’s mean years of education is one unit higher than the other, we would predict life expectancy to be .75 years higher in the country with the higher level of education than in the other country.
Together, these three variables explain 74.8% of the variation in country-level life expectancy.
You can also write this out as a linear equation, if that helps you with interpretation:
\[\hat{\text{lifexp}}= 75.468-3.546(\text{fert1520})+.75(\text{mnschool})-.296(\text{log10(pop)})\]
It is also important to note that the slopes for fertility and level of education are much smaller than they were in the bivariate (one independent variable) models, reflecting the consequence of controlling for overlapping influences. For fertility rate, the slope changed from -4.911 to -3.546, a 28% decrease; while the slope for education went from 1.839 to .75, a 59% decrease in impact. This is to be expected when two highly correlated independent variables are put in the same multiple regression model.
One thing you might have noticed about this discussion of findings is that it includes both a discussion of general findings and a discussion of specific statistics. I have found that this approach generally works well.
Missing Data. When working with multiple regression, or any other statistical technique that involves using multiple variables at the same time, it is important to pay attention to the number of missing cases. Missing cases occur on any given variable when cases do not have any valid outcomes. We discussed this a bit earlier in the book in the context of public opinion surveys, where missing data might occur because people refuse to answer questions or do not have an opinion to offer. When working with aggregate cross-national data, as we are here, missing outcomes usually occur because the data are not available for some countries on some variables. For instance, some countries may not report data on some variables to the international organizations (e.g., World Bank, United Nations, etc.) that are collecting data, or perhaps the data gathering organizations collect certain types of data from certain types of countries but not for others.
This is a more serious problem for multiple regression than simple regression because multiple regression uses “listwise” deletion of missing data, meaning that if a case is missing on one variable it is dropped from the analysis. This is why it is important to pay attention to missing data as you add more variables to the model. It is possible that one or two variables have a lot of missing data and you could end up making generalizations based on a lot fewer data points than you realize. The output reported in stargazer format reports the number of observations (183) but does not report the number of missing cases. The raw R output reports the number of missing as “12 observations deleted due to missingness.” There are relatively few missing data points, but it is important to monitor the number of observations as you add independent variables.
Assessing the Substantive Impact
Sometimes, calculating predicted outcomes for different combinations of the independent variables can give you a better appreciation for the substantive importance of the model. We can use the model estimates to predict the value of life expectancy for countries with different combinations of outcomes on these variables. To do this, you need to plug in the values of the independent variables, multiplying them times their respective slopes, and then add the constant, similar to the calculations made in Chapter 15 (Table 15.2). Consider two hypothetical countries that have very different (but realistic) outcomes on fertility and education but are the same on population:
| Country | Fertility Rate | Mean Education | Logged Population |
|---|---|---|---|
| Country A | 1.8 | 10.3 | .75 |
| Country B | 3.9 | 4.9 | .75 |
Country B has a higher fertility rate and lower value on educational attainment than Country A, so we expect it to have an overall lower predicted outcome on life expectancy. Let’s plug in the numbers and see what we get.
For Country A:
\(\hat{y}= 75.468 -3.546(1.8) +.75(10.3) +.296(.75) = 77.03\)
For Country B:
\(\hat{y}= 75.468 -3.546(3.9) + .75(4.9) +.296(.75) = 65.54\)
The predicted life expectancy in Country A is almost 11.5 years higher than in Country B, based on differences in fertility and level of education. Given the gravity of this dependent variable—how long people are expected to live—this is a very meaningful difference. It is important to understand that the difference in predicted outcomes would be much narrower if the model did not fit the data as well as it does. If fertility and education levels were not as strongly related to life expectancy, then differences in their values would not predict as substantial differences in life expectancy.
Model Accuracy
Adjusted R2. The interpretation and importance of the R2 statistic in multiple regression is much the same as in simple regression, with a couple of minor differences. First, in multiple regression, the R2 for any given model describes how well the group of variables explains variation in the dependent variable, not the explanatory power of any single variable. Second, especially when focusing on differences in R2 values across different models, it is important to take into account the number of variables in the models. In the current example, the new model R2 (.748) appears to be an improvement over the strongest of the bi-variate models (fertility rate), which had an R2 of .711. However, with multiple regression analysis, the R2 value will increase every time a variable is added to the model, even if only by some slight magnitude. Given this, it is important to determine whether there was a real increase in the R2 value of the life expectancy model beyond what could be expected simply due to adding two variables. One way to address this is to “adjust” the R2 to take into account the number of variables in the model. The adjusted R2 value can then be used to assess the fit of the model.
The formula for the adjusted R2 is:
\[R^2_{adj}= 1-(1-R^2) \left(\frac{N-1}{N-k-1}\right)\]
Here, \(N-K-1\) is the degrees of freedom for the regression model, where N=sample size (183), and K=number of variables (3). One thing to note about this formula is that the impact of additional variables on the value of R2 is greatest when the sample size is relatively small. As N increases, the difference between R2 and adjusted R2 for additional variables grows smaller.
For the model above, with the R2 value of .7475 (carried out four places to the right of the decimal):
\[R^2_{adj}= 1-(.2525) \left(\frac{182}{179}\right)=.743\]
This new estimate is slightly smaller than the unadjusted R2, but still represents a real improvement over the strongest of the bivariate models, in which the adjusted R2 was .710. Usually, when discussing model fit, people refer to the R2 of the model rather than the adjusted R2. This is fine, especially because the two are usually close in value, but it is important to report the adjusted R2 in the table of results so readers can evaluate it alongside the original R2.
Root Mean Squared Error. The R2 (or adjusted R2) statistic is a nice measure of the explanatory power of the models, and a higher R2 for a given model generally means less prediction error, within the context of that model. However, the R2 statistic does not tell us exactly how much error there is in the model estimates. For instance, the results above tell us that the model explains about 74% of the variation in life expectancy, but that piece of information does not speak to the typical error in prediction (\((y_1-\hat{y})^2\)). Yes, the model reduces error in prediction by quite a lot, but how much error is there, on average? For that, we can use a different statistic, the Root Mean Squared Error (RMSE). The RMSE reflects the typical error in the model; it is the square root of the mean squared error:
\[RMSE=\sqrt{\frac{\sum(y_i-\hat{y})^2}{N-k-1}}\]
The sum of squared residuals (error) constitutes the numerator, and the model degrees of freedom constitute the denominator. Let’s run through these calculations for the regression model.
#Calculate squared residuals using the saved residuals from "fit"
residsq <- residuals(fit)^2
#Sum the squared residuals, add "na.rm" because of missing data
sumresidsq<-sum(residsq, na.rm=T)
sumresidsq[1] 2541.9#Divide the sum of squared residuals by N-K-1 and take the square root
RMSE=sqrt(sumresidsq/179)
RMSE[1] 3.7684The resulting RMSE can be taken as the typical prediction error. For the model above, RMSE= 3.768. This appears in the regression table as “Residual Std Error: 3.768 (df = 179)”
One drawback to RMSE is that “3.768” has no standard meaning. Whether it is a lot or a little error depends on the scale of the dependent variable. For a dependent variable that ranges from 1 to 15, this could be a substantial amount of error. However, for a variable like life expectancy, which ranges from about 52 to 85, this is not much error. The best use of the RMSE lies in comparison of error across models that use the same dependent variable. For instance, the RMSE values for the Fertility, Education, and Population regression results in Chapter 15 were 4.032, 4.738, and 7.423, respectively. The RMSE for the multiple regression model is smaller than any of the individual models.
Both the R2 and RMSE are valuable tools for evaluating the level of error in regression models. Best practice is to use each of them for what they can tell you.
Predicted Outcomes
It is useful to think of the strength of the model in terms of how well its predictions correlate overall with the dependent variable. In the initial discussion of the simple bivariate regression model, I pointed out that the square root of the R2 is the correlation between the independent and dependent variables. We can think of the multiple regression model in a similar fashion: the square root of R2 is the correlation (Multiple R) between the dependent variable and the predictions from the regression model. By this, I mean that Multiple R is literally the correlation between the observed values of the dependent variable (y) and the values predicted by the regression model (\(\hat{y}\)).
In the example shown below, predicted outcomes are generated based on the three-variable model, and a scatterplot of the predicted and actual outcomes is provided to gain an appreciation for how well the model explains variation in the dependent variable. First, let’s generate predicted outcomes (yhat) for all observations, based on their values of the independent variables, using information stored in fit.
#Use information stored in "fit" to predict outcomes
countries2$yhat<-(predict(fit)) The scatterplot illustrating the relationship between the predicted and actual values of life expectancy is presented below.
#Use predicted values as an independent variable in the scatterplot
plot(countries2$yhat,countries2$lifexp,
xlab="Predicted Life Expectancy",
ylab = "Actual Life Expectancy")
#Plot the regression line
abline(lm(countries2$lifexp~countries2$yhat))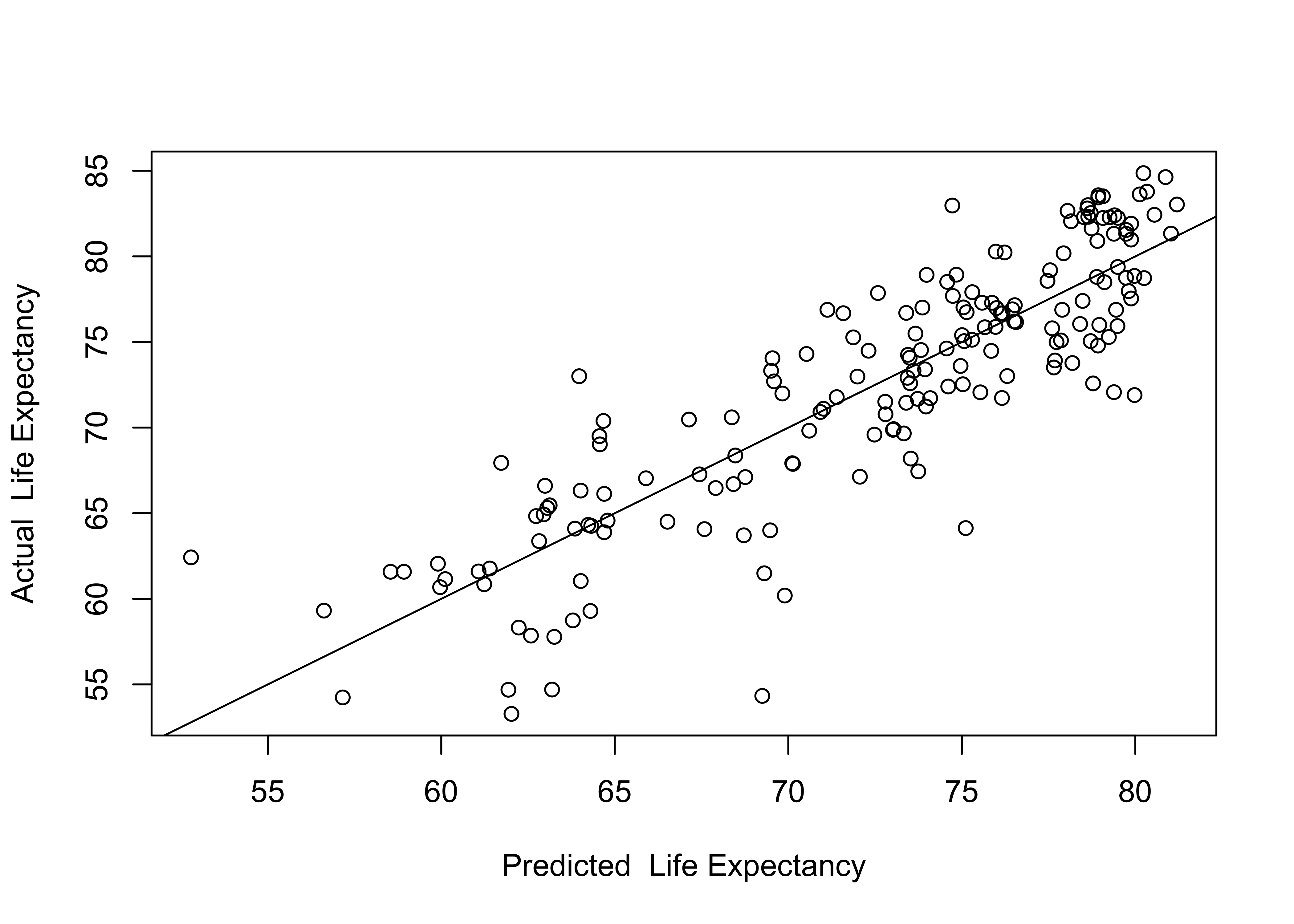
Here we see the predicted values along the horizontal axis, the actual values on the vertical axis, and a fitted (regression) line. The key takeaway from this plot is that the model fits the data fairly well. The correlation (below) between the predicted and actual values is .865, which, when squared, equals .748, the R2 of the model.
#get the correlation between y and yhat
cor.test(countries2$lifexp, countries2$yhat)
Pearson's product-moment correlation
data: countries2$lifexp and countries2$yhat
t = 23.1, df = 181, p-value <2e-16
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
0.82270 0.89713
sample estimates:
cor
0.86458 In addition to plotting the predicted and actual data points, you might want to identify some of the observations that are relative outliers (that don’t fit the pattern very well). In the scatterplot shown above, there are no extreme outliers but there are a few observations whose actual life expectancy is quite a bit less than their predicted outcome. These observations are the farthest below the prediction line. Changing the plot command so that it lists the country code for each country, allows us to identify these and any other outliers.
plot(countries2$yhat,countries2$lifexp,
xlab="Predicted Life Expectancy",
ylab = "Actual Life Expectancy",
cex=.001)
abline(lm(countries2$lifexp~countries2$yhat))
text(countries2$yhat,countries2$lifexp, countries2$ccode, cex=.6) 
Based on these labels, several countries stand out as having substantially lower than predicted life expectancy: Central African Republic (CEB), Lesotho (LSO), Nigeria (NGA), Sierra Leone (SLE), South Africa (ZAF), and Swaziland (SWZ). This information is particularly useful if it helps you identify patterns that might explain outliers of this sort. For instance, if these countries shared an important characteristic that we had not yet put in the model, we might be able to improve the model by including that characteristic. In this case, the first thing that stands out is that these are all sub-Saharan African countries. At the same time, predictions for most sub-Saharan African countries are closer to the regression line, and one of the countries that stands out for having higher than expected life is expectancy is Niger (NER), another sub-Saharan African country. While it is important to be able to identify the data points and think about what the outliers might represent, it is also important to focus on broad, theoretically plausible explanations that might contribute to the model in general and could also help explain the outliers. One thing that is missing in this model that might help explain differences in life expectancy is access to health care, which we will take up in the next chapter.
Revisiting Presidential Votes in the states
In this section, I use the presidential vote data from Chapter 15 to review how to use and interpret the results of a multiple regression model. The dependent variable is Joe Biden’ percent of the two-party vote in the states (states20$d2pty20), and the independent variables are the percent of the state population who are white males (states20$whitemale), the percent of the non-agricultural work force who are unionized (states20$union), and a dichotomous variable identifying whether the state is in South (1) or non-South (0) (states20$south). The expectations are that Biden support is negatively related to the percent white male in the population and the southern region indicator, and positively related to the percent of the workforce who are unionized.
Interpreting Dichotomous Independent Variables
You might have noticed that one of the independent variables, south, is not quite like the others. Both whitemale and union are continuous numeric variables, whereas south is dichotomous variable scored 0 and 1 to indicate the presence of a qualitative characteristic, the southern region of the country. In Chapter 4 (measures of central tendency), we discussed treating dichotomous indicators of qualitative outcomes as numeric variables that indicate the presence or absence of some characteristic; in this case, that characteristic is being a southern state.
In order to appreciate what kind of information dichotomous variables provide, let’s take a look at the simple mean difference in Biden’s percent of the two-party vote between 13 southern and 27 non-southern states, using the compmeans command. Remember, non-southern states are scored 0 and southern states are scored 1 on this variable.
#Get group means
compmeans(states20$d2pty20,states20$south, plot=F)Warning in compmeans(states20$d2pty20, states20$south, plot = F): Warning:
"states20$south" was converted into factor!Mean value of "states20$d2pty20" according to "states20$south"
Mean N Std. Dev.
0 50.969 37 10.8849
1 42.643 13 7.0943
Total 48.804 50 10.6293Here, we see that the mean Democratic percent in southern states in 2020 was 42.64%, compared to 50.97% in non-southern states, for a difference of 8.33 points. Of course, we can add a bit more to this analysis by using the t-test for the difference:
#Get t-test or region-based difference in "d2pty20"
t.test(states20$d2pty20~states20$south,var.equal=T)
Two Sample t-test
data: states20$d2pty20 by states20$south
t = 2.56, df = 48, p-value = 0.014
alternative hypothesis: true difference in means between group 0 and group 1 is not equal to 0
95 percent confidence interval:
1.797 14.855
sample estimates:
mean in group 0 mean in group 1
50.969 42.643 The t-score for the difference is 2.56, and the p-value is .014 (< .05), so we conclude that there is a statistically significant difference between the two groups.
Now, let’s take a look at a simple regression model to see that we can get exactly the same kind if information through regression analysis.
#Run regression model
south_demo<-lm(data=states20, d2pty20~south)
#View regression results
stargazer(south_demo, type="text",
dep.var.labels = "Biden % of Two-party Vote",
covariate.labels = "Southern State (0,1)")
================================================
Dependent variable:
---------------------------
Biden % of Two-party Vote
------------------------------------------------
Southern State (0,1) -8.326**
(3.247)
Constant 50.969***
(1.656)
------------------------------------------------
Observations 50
R2 0.120
Adjusted R2 0.102
Residual Std. Error 10.072 (df = 48)
F Statistic 6.574** (df = 1; 48)
================================================
Note: *p<0.1; **p<0.05; ***p<0.01The most important thing to get about using dichotomous independent variables is that it does not make sense to interpret the value of b (-8.33) as a slope in the same way we might think of a slope for a numeric variable with multiple categories. There are just two values to the independent variable, 0 (non-south) and 1 (south), so statements like “for every unit increase in south, Biden vote drops by 8.33 points” sound a bit odd. Instead, the slope is really saying that the expected level of support for Biden in the south is 8.33 points lower than his support in the rest of the country. Let’s plug in the values of the independent variable to illustrate this.
When South=0: \(\hat{y}=50.97-8.33(0)= 50.97\)
When South=1: \(\hat{y}=50.97-8.33(1)= 42.64\)
These numbers should look familiar to you, as this is exactly what we saw in the compmeans results: the mean for southern states is 42.64, while the mean for other states is 50.97, and the difference between them (-8.33) is equal to the regression coefficient for south. Also, the t-score and p-value associated with the slope for the south variable in the regression model are exactly the same as in the t-test model.
What this illustrates is that when using a dichotomous independent variable, the “slope” captures the mean difference in the predicted value of the dependent variable between the two categories of the independent variable and the results are equivalent to a difference of means test. In fact, in a bi-variate model like this, the slope for a dichotomous variable like this is really just an addition to or subtraction from the intercept for cases scored 1; for cases scored 0 on the independent variable, the predicted outcome is equal to the intercept.
Next Steps
It’s hard to believe we are almost to the end of this textbook. It wasn’t so long ago that you were looking at bar charts and frequencies, perhaps even having a bit of trouble getting the R code for those things to work. You’ve certainly come a long way since then!
You now have a solid basis for using and understanding regression analysis, but there are just a few more things you need to learn about in order to take full advantage of this important analytic tool. The next chapter takes up issues related to making valid comparisons of the relative impact of the independent variables, problems created when the independent variables are very highly correlated with each other or when the relationship between the independent and dependent variables does not follow a linear pattern. Then, Chapter 18 provided a brief overview of a number of important assumptions that underlie the regression model. It’s exciting to have gotten this far, and I think you will find the last few topics interesting and important additions to what you already know.
Exercises
Concepts and Calculations
- Answer the following questions regarding regression model below, which focuses on multiple explanations for county-level differences in internet access, using a sample of 500 counties. The independent variables are the percent of the county population living below the poverty rate, the percent of the county population with advanced degrees, and the logged value of population density (logged because density is highly skewed).
=====================================================
Dependent variable:
---------------------------
% With Internet Access
-----------------------------------------------------
Poverty Rate (%) -0.761***
(0.038)
Advanced Degrees (%) 0.561***
(0.076)
Log10(Population Density) 2.378***
(0.398)
Constant 79.817***
(0.922)
-----------------------------------------------------
Observations 500
R2 0.604
Adjusted R2 0.602
Residual Std. Error 5.686 (df = 496)
F Statistic 252.530*** (df = 3; 496)
=====================================================
Note: *p<0.1; **p<0.05; ***p<0.01- Interpret the slope for poverty rate.
- Interpret the slope for advanced degrees.
- Interpret the slope for the log of population density.
- Evaluate the fit of the model in terms of explained variance.
- What is the typical error in the model? Does that seem like a small or large amount of error?
- Use the information from the model in Question #1, along with the information presented below to generate predicted outcomes for two hypothetical counties, County A and County B. Just to be clear, you should use the values of the independent variable outcomes and the slopes and constant to generate your predictions.
| County | Poverty Rate | Adv. Degrees | Log10(Density) | Prediction? |
|---|---|---|---|---|
| A | 19 | 4 | 1.23 | |
| B | 11 | 8 | 2.06 |
- Prediction of County A:
- Prediction of County B:
- What did you learn from predicting these hypothetical outcomes that you could not learn from the model output?
- The table below contains the results of a multiple regression model that uses the Democratic Party feeling thermometer as the dependent variable, and age, sex, race, and number of LGBTQ rights supported are the independent variables.
===============================================================
Dependent variable:
------------------------------
Democratic Feeling Thermometer
---------------------------------------------------------------
Age 0.179***
(0.019)
Race (White=1, Other=0) -19.035***
(0.718)
Sex (Female=1, Other=0) 4.390***
(0.633)
#LGBTQ Rights Supported (0 to 5) 10.096***
(0.205)
Constant 13.604***
(1.350)
---------------------------------------------------------------
Observations 7,422
R2 0.304
Adjusted R2 0.303
Residual Std. Error 27.021 (df = 7417)
F Statistic 809.390*** (df = 4; 7417)
===============================================================
Note: *p<0.1; **p<0.05; ***p<0.01- Interpret the slope for age.
- Interpret the slope for race
- Interpret the slope for sex.
- Interpret the slope for support for LGBTQ rights.
- Evaluate the fit of the model in terms of explained variance.
- What is the typical error in the model? Does that seem like a small or large amount of error? Explain.
- Based on the model results in the previous question, what is the predicted Democratic Party feeling thermometer rating for each of the following:
A 35-year-old White man who supports 0 out of 5 LGBTQ rights.
A 35-year-old non-White woman who supports 4 out of five LGBTQ rights.
R Problems
I’m trying to extend the Biden vote share regression model used earlier in this chapter to include a couple of additional independent variables but I can’t get it to run. Check out the code I used (below) and let me know what I’ve done wrong. Produce a nicely organized table of results using
stargazer. (Hint: there are two errors)Votes<-lm(data=states20, d2pty20~whitemale+ union south+ vep_turnout20+ early_pct)Building on the regression models from the R problems in the last chapter, use the
states20data set and run a multiple regression model with infant mortality (infant_mort) as the dependent variable, and per capita income (PCincome2020), the teen birth rate (teenbirth), and percent low birth weight birthslowbirthwtas the independent variables. Store the results of the regression model in an object calledrhmwrkand produce a nicely organized table usingstargazer, one that replaced the R variable names with descriptive labels.
- Based on the results of this regression model, discuss the determinants of infant mortality in the states. Pay special attention to the direction and statistical significance of the slopes, and to all measures of model fit and accuracy.
- Use the following command to generate predicted values of infant mortality in the states from the regression model produced in problem #1.
#generate predicted values
states20$yhat<-predict(rhmwrk)- Now, produce a scatterplot of predicted and actual levels of infant mortality and replace the scatterplot markers with state abbreviations (see Chapter 15 homework). Make sure this scatterplot includes a regression line showing the relationship between predicted and actual values.
- Generally, does it look like there is a good fit between the model predictions and the actual levels of infant mortality? Explain.
- Identify states that stand out as having substantially higher or lower than expected levels of infant mortality. Do you see any pattern among these states?
na.action=na.excludeis included in the command because I want to add some of the hidden information fromfit(predicted outcomes) to thecountries2data set after the results are generated that we will use later. Without adding this to the regression command, R would skip all observations with missing data when generating predictions and the rows of data for the predictions would not match the appropriate rows in the original data set. This is a bit of a technical point. Ignore it if it makes no sense to you.↩︎