Chapter 5 Measures of Central Tendency
Get Ready
In this chapter, we move on to examining measures of central tendency. The techniques learned here complement and expand upon the material from Chapter 3, providing a few more options for describing how the outcomes of variables are distributed. In order to follow along in this chapter, you should load the anes20 and states20 data sets and attach the libraries for the following packages: DescTools and descr.
Central Tendency
While frequencies tell us a lot about the distribution of variables, we are also interested in more precise measures of the general tendency of the data. Do the data tend toward a specific outcome? Is there a “typical” value? What is the “expected” value? Measures of central tendency provide this information. There are a number of different measures of central tendency, and their role in data analysis depends in part on the level measurement for the variables you are studying.
Mode
The mode is the category or outcome that occurs most often, and it is most appropriate for nominal data because it does not require that the underlying variable be quantitative in nature. That said, the mode can sometimes provide useful information for ordinal and numeric data, especially if those variables have a limited number of categories.
Let’s look at an example of the mode by using Religious affiliation, a nominal-level variable that is often tied to important social and political outcomes. The frequency below shows the outcomes from anes20$denom, an eight-category recoded version of the original twelve-category variable measuring religious affiliation (anes20$V201435).
#Create new variable for religious denomination
anes20$denom<-anes20$V201435
#Reduce number of categories by combine some of them
levels(anes20$denom)<-c("Protestant", "Catholic", "OtherChristian",
"OtherChristian", "Jewish", "OtherRel",
"OtherRel", "OtherRel","Ath/Agn", "Ath/Agn",
"SomethingElse", "Nothing")#Checkout the new variable
freq(anes20$denom, plot=F)PRE: What is present religion of R
Frequency Percent Valid Percent
Protestant 2113 25.519 25.778
Catholic 1640 19.807 20.007
OtherChristian 267 3.225 3.257
Jewish 188 2.271 2.294
OtherRel 163 1.969 1.989
Ath/Agn 796 9.614 9.711
SomethingElse 1555 18.780 18.970
Nothing 1475 17.814 17.994
NA's 83 1.002
Total 8280 100.000 100.000From this table, you can see in both the raw frequency and percent columns that “Protestant” is the modal category (recognizing that this category includes a number of different religions). Let’s think about how this represents the central tendency or expected outcome of this variable. With nominal variables such as this, the concept of a “center” doesn’t hold much meaning, strictly speaking. However, if we are a bit less literal and take “central tendency” to mean something more like the typical or expected outcome, it makes more sense.
Think about this in terms of guessing the outcome, and you need information that will minimize your error in guessing (this idea will also be important later in the book). Suppose you have all 8197 valid responses on separate strips of paper in a great big hat, and you need to guess the religious affiliation of each respondent, using the coding scheme from this variable. What’s your best guess as pull each piece of paper out of the hat? It turns out that your best strategy is to guess the modal category, “Protestant,” for all 8197 valid respondents. You will be correct 2113 times and wrong 6084 times. That’s a lot of error, but no other guess will give you less error, because “Protestant” is the most likely outcome. In this sense, the mode is a good measure of the “typical” outcome for nominal data.
Besides using the frequency table, you can also get the mode for this variable using the Mode command in R:
#Get the modal outcome, Note the upper-case M
Mode(anes20$denom)[1] NA
attr(,"freq")
[1] NAOops, this result doesn’t look quite right. That’s because many R functions don’t know what to do with missing data and will report NA instead of the information of interest. We get this error message because there are 83 missing cases for this variable (see the frequency). This is fixed in most cases by adding na.rm=T to the command line, telling R to remove the NAs from the analysis.
#Add "na.rm=T" to account for missing data
Mode(anes20$denom, na.rm=T)[1] Protestant
attr(,"freq")
[1] 2113
8 Levels: Protestant Catholic OtherChristian Jewish OtherRel ... NothingThis confirms that “Protestant” is the modal category, with 2113 respondents, and also lists all of the levels. In many cases, I prefer to get the mode from a frequency table because it provides a more complete picture of the variable, showing, for instance, that while “Protestant” is the modal category, “Catholic” is a very close second.
While the mode is the most suitable measure of central tendency for nominal-level data, it can be used with ordinal and interval-level data. Let’s look at two variables we’ve used in earlier chapters, spending preferences on programs for the poor (anes20$V201320x12), and state abortion restrictions (states20$abortion_laws):
#Mode for spending on aid to the poor
Mode(anes20$V201320x, na.rm=T)[1] 3. Kept the same
attr(,"freq")
[1] 3213
5 Levels: 1. Increased a lot 2. Increased a little ... 5. Decreasaed a lot#Mode for # Abortion restrictions
Mode(states20$abortion_laws)[1] 10
attr(,"freq")
[1] 12Here, we see that the modal outcome for spending preferences is “Kept the same”, with 3213 respondents, and the mode for abortion regulations is 10, which occurred twelve times. While the mode does provide another piece of information for these variables, there are better measures of central tendency for working with ordinal or interval/ratio data, especially continuous numeric variables, for which the mode is unlikely to provide much useful information. However, the mode is the preferred measure of central tendency for nominal data.
Median
The median cuts the sample in half: it is the value of the outcome associated with the observation at the middle of the distribution when cases are listed in order of magnitude. Because the median is found by ordering observations from the lowest to the highest value, the median is not an appropriate measure of central tendency for nominal variables.
If the cases for an ordinal or numeric variable are listed in order of magnitude, we can look for the point that cuts the sample exactly in half. The value associated with that observation is the median. For instance, if we had 5 observations ranked from lowest to highest, the middle observation would be the third one (two above it and two below it), and the median would be the value of the outcome associated with that observation. Just to be clear, the median in this example would not be 3, but the value of the outcome associated with the third observation.
Here is a useful formula for finding the middle observation:
\[\text{Middle Observation}={\frac{n+1}{2}}\]
where n=number of cases
If n is an odd number, then the middle is a single data point. If n is an even number, then the middle is between two data points and you should use the mid-point between those two values as the median. Figure 5.1 illustrates how to find the median, using hypothetical data for a small sample of cases.
[Figure** 5.1 **about here]
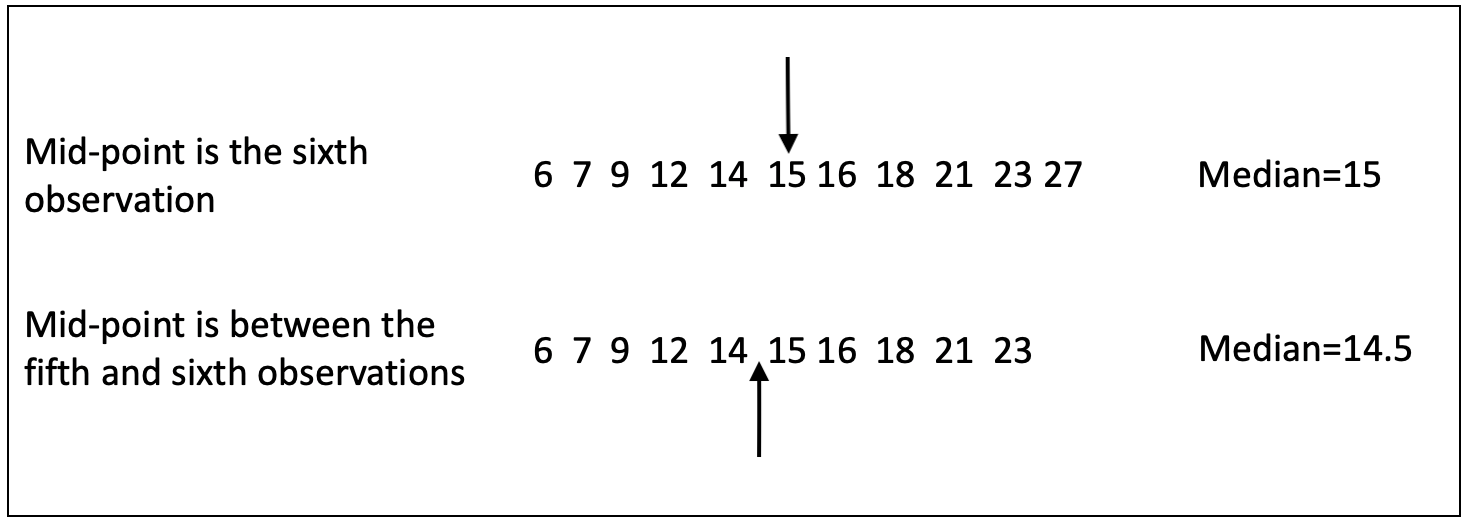
Figure 5.1: Finding the Median with Odd and Even Numbers of Cases
In the first row of data, the sixth observation perfectly splits the sample, with five observations above it and five below. The value of the sixth observation, 15, is the median. In the second row of data, there is an even number of cases (10), so the middle of the distribution is between the fifth and sixth observations, with values of 14 and 15, respectively. The median is the mid-point between these values, 14.5.
Now, let’s look at this with some real-world data, using the abortion laws variable from the states20 data set. There are 50 observations, so the mid-point is between the 25th and 26th observations ((50+1)/2). Obviously, we can get R to just show us the median, but it is instructive at this point to find it by “eyeballing” the data. All fifty observations for states20$abortion_laws are listed below in order of magnitude. The value associated with the 25th observation is 9, as is the value associated with the 26th observation. Since these are both the same, the median outcome is 9.
#Use "sort" to view outcomes in order of magnitude
sort(states20$abortion_laws) [1] 1 2 3 3 4 4 4 5 5 5 5 5 6 6 6 6 6 6 7 7 7 8 8 8 9
[26] 9 9 9 9 9 9 10 10 10 10 10 10 10 10 10 10 10 10 11 11 12 12 12 13 13We could also get this information more easily:
#Get the median value
median(states20$abortion_laws)[1] 9To illustrate the importance of listing the outcomes in order of magnitude, check the list of outcomes for states20$abortion_law when the data are listed in alphabetical order, by state name:
#list abortion_laws without sorting from lowest to highest
states20$abortion_laws [1] 8 8 11 10 5 2 4 6 10 9 5 11 5 12 9 13 10 10 4 6 5 10 9 9 12
[26] 7 10 7 3 7 6 4 9 9 10 13 3 9 6 10 10 10 12 10 1 8 5 6 10 6If you took the mid-point between the 25th (12) and 26th (7) observations, you would report a median of 9.5. While this is close to 9, by coincidence, it is incorrect.
Let’s turn now to finding the median value for spending preferences on programs for the poor (anes20$V201320x). Since there are over 8000 observations for this variable, it is not practical to list them all in order, but we can do the same sort of thing using a frequency table. Here, I use the Freq command because I am particularly interested in the cumulative percentages.
# Use 'Freq' to get cumulative %
Freq(anes20$V201320x) level freq perc cumfreq cumperc
1 1. Increased a lot 2'560 31.1% 2'560 31.1%
2 2. Increased a little 1'617 19.7% 4'177 50.8%
3 3. Kept the same 3'213 39.1% 7'390 89.8%
4 4. Decreased a little 446 5.4% 7'836 95.3%
5 5. Decreasaed a lot 389 4.7% 8'225 100.0%What we want to do now is use the cumulative percent to identify the category associated with the 50th percentile, the middle of the distribution. In this case, you can see that the cumulative frequency for the category “Increased a little” is 50.8%, meaning the middle observation (50th percentile) is in this category, so this is the median outcome.
We can check this with the median command in R. One little quirk here is that R requires numeric data to calculate the median. That’s fine. All we have to do is tell R to treat the values as if they were numeric, replacing the five levels with values 1,2,3,4 and 5.
#Get the median, treating the variable as numeric
median(as.numeric(anes20$V201320x), na.rm=T)[1] 2This confirms that the median outcome is the second category, “Increased a little”.
The Mean
The Mean is usually represented as \(\bar{x}\) and is also referred to as the average, or the expected value of the variable, and is a good measure of the typical outcome for numeric data. The term “typical” outcome is interesting in this context because the mean value of a variable may not exist as an actual outcome.
The best way to think about the mean as a measure of typicality is somewhat similar to the discussion of the mode as your best guess if you want to minimize error in predicting the outcomes in a nominal variable. The difference here is that since the mean is used with numeric data, we don’t judge accuracy in a dichotomous right/wrong fashion; instead, we can judge accuracy in terms of how close the mean is to each outcome. For numeric data, the mean is closer overall to the actual values than any other guess you could make. In this sense, the mean represents the typical outcome better than any other statistic.
The formula for the mean is:
\[\bar{x}=\frac{\sum_{i=1}^n x_i}{n}\]
This reads: take the sum of the values of all observations (the numerical outcomes) of x, and divide that by the total number of valid observations (observations with real values). This formula highlights an important way in which the mean is different from both the median and the mode: it is based on information from all of the values of x, not just the middle value (the median) or the value that occurs most often (the mode). This makes the mean a more encompassing statistic than either the median or the mode.
Using this formula, we could calculate the mean number of state abortion restrictions (states20$abortion_laws) something like this:
\[\frac{1+2+3+3+4+4+\cdot\cdot\cdot\cdot+11+12+12+12+13+13}{50}\]
We don’t actually have to add up all fifty outcomes manually to get the numerator. Instead, we can tell R to sum up all of the values of x:
#Sum all of the values of 'abortion_laws'
sum(states20$abortion_laws)[1] 394So the numerator is 394. We divide through by the number of cases (50) to get the mean:
#Divide the sum or all outcomes by the number of cases
394/50[1] 7.88\[\bar{x}=\frac{394}{50} = 7.88\]
Of course, it is simpler, though not quite as instructive, to have R tell us the mean:
#Tell R to get the mean value
mean(states20$abortion_laws)[1] 7.88A very important characteristic of the mean is that it is the point at which the weight of the values is perfectly balanced on each side. It is helpful to think of the outcomes as numeric variables distributed according to their weight (value) on a plank resting on a fulcrum, with fulcrum placed at the mean of the distribution, the point at which both sides are perfectly balanced (see Figure 5.2. If the fulcrum is placed at the mean, the plank will not tip to either side, but if it is placed at some other point (the median, for instance), then the weight will not be evenly distributed and the plank will tip to one side or the other.
[Figure** 5.2 **about here]
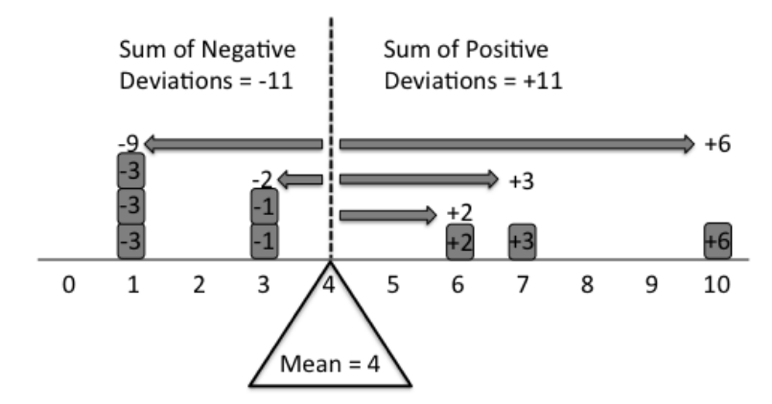
Figure 5.2: The Mean Perfectly Balances a Distribution
*Source: https://stats.stackexchange.com/questions/200282/explaining-mean-median-mode-in-laymans-terms
A really important concept here is the deviation of the values of x from the mean of x, represented as \(x_i-\bar{x}\). For instance, the deviation from the mean number of abortion restrictions (7.88) for a state like Alabama, with 8 abortion restrictions on the books is .12 units (8-7.88), and for a state like Colorado, with 2 restrictions on the books, the deviation is -5.88 (2-7.88). For any numeric variable, the distance between the mean and all values greater than the mean is perfectly offset by the distances between the mean and all values lower than the mean.
This means that summing up all of the deviations from the mean (\(\sum_{i=1}^n{x_i-\bar{x}}\)) is always equal to zero. This point is important for understanding what the mean represents, but it is also important for many other statistics that are based on the mean.
We can check this balance property in R. First, we express each observation as a deviation from the means.
##Subtract the mean of x from each value of x
dev_mean=(states20$abortion_laws- mean(states20$abortion_laws))
#Print the mean deviations
dev_mean [1] 0.12 0.12 3.12 2.12 -2.88 -5.88 -3.88 -1.88 2.12 1.12 -2.88 3.12
[13] -2.88 4.12 1.12 5.12 2.12 2.12 -3.88 -1.88 -2.88 2.12 1.12 1.12
[25] 4.12 -0.88 2.12 -0.88 -4.88 -0.88 -1.88 -3.88 1.12 1.12 2.12 5.12
[37] -4.88 1.12 -1.88 2.12 2.12 2.12 4.12 2.12 -6.88 0.12 -2.88 -1.88
[49] 2.12 -1.88As expected, some deviations from the mean are positive, and some are negative. Now, if we take the sum of all deviations, we get:
#Sum the deviations of x from the mean of x
sum(dev_mean)[1] 5.329071e-15That’s a funny looking number. Because of the length of the resulting number, the sum of the deviations from the mean is reported using scientific notation. In this case, the scientific notation is telling us we need to move the decimal point 15 places to the left, resulting in .00000000000000532907. Not quite exactly 0, due to rounding, but essentially 0.
Note, that the median does not share this “balance” property; if we placed a fulcrum at the median, the distribution would tip over because the positive deviations do not balance perfectly by the negative deviations, as shown here:
#Sum the deviations of x from the median of x
sum(states20$abortion_laws- median(states20$abortion_laws))[1] -56The negative deviations from the median outweigh the positive by a value of 56.
Dichotomous Variables
Here’s an interesting bit of information that will be useful in the future: for dichotomous variables with all values scored either 0 or 1, the mean of the variable is the proportion of cases in category 1. Let’s take an example from one of the indicator variables we created in Chapter 4. There, we used the following code to covert anes20$V201415, a qualitative variable based on a survey question about whether gays and lesbians should be allowed to adopt children, into a numeric question scored 0 and 1:
#Code from Chapter 4. Create indicator for "adoption" variable
anes20$lgbtq4<-as.numeric(anes20$V201415 == "1. Yes")If we look at the outcomes for both variables, we can see that the 6554 respondents (80.4%) who said “Yes” on anes20$V201415 are assigned a value of 1 on anes20$lgbtq4, and the 1598 (19.6%) respondents who said “No” are assigned a value of 0.
freq(anes20$V201415, plot=F)PRE: Should gay and lesbian couples be allowed to adopt
Frequency Percent Valid Percent
1. Yes 6554 79.155 80.4
2. No 1598 19.300 19.6
NA's 128 1.546
Total 8280 100.000 100.0freq(anes20$lgbtq4, plot=F)anes20$lgbtq4
Frequency Percent Valid Percent
0 1598 19.300 19.6
1 6554 79.155 80.4
NA's 128 1.546
Total 8280 100.000 100.0We now have a dichotomous numeric variable that distinguishes between those who think gays and lesbians should be allowed to adopt and those who think they should not. We can use the formula presented earlier to calculate the mean of this variable. Since the value 0 occurred 1598 times, and the value 1 occurred 6554 times, the mean is equal to
\[\bar{x}=\frac{(0*1598)+(1*6554)}{8152}=\frac{6554}{8152}=.80397\] We can verify this with R:
#Get the mean of the indicator variable
mean(anes20$lgbtq4, na.rm=T)[1] 0.8039745The mean of this dichotomous variable is the proportion in category 1. This should always be the case with similar dichotomous variables. This may not seem very intuitive to you at this point, but it will be very useful to understand it later on.
You might be questioning at this point how we can treat what seems like a nominal variable—whether people favor or oppose allowing gays and lesbians to adopt children—as a numeric variable. The way I like to think about this is that this variable measures the presence (1) or absence (0) of a characteristic, supporting adoption by gays and lesbians. In cases like this, you can think of the 0 value as a genuine zero point, indicating that the respondent does not have the characteristic you are measuring. Since the value 1 indicates having a unit of the characteristic, we can treat this variable as numeric. However, it is important to always bear in mind what the variable represents and that there are only two outcomes, 0 and 1. This becomes especially important in later chapters when we discuss using these types of variables in regression analysis.
Mean, Median, and the Distribution of Variables
As a general rule, the mean is most appropriate for interval/ratio level variables, and the median is most appropriate for ordinal variables. However, there are instances when the median might be a better measure of central tendency for numeric data, almost always because of skewness in the data. Skewness occurs in part as a consequence of one of the virtues of the mean. Because the mean takes into account the values of all observations, whereas the median does not actually emphasize “values” but uses the ranking of observations, the mean can be influenced by extreme values that “pull” it away from the middle of the distribution. Consider the following simple example, using five observations from a hypothetical variable:
In this case, the mean and the median are the same. Now, watch what happens is we change the value 5 to 18, a value that is substantially higher than the rest of the values:
The median is completely unaffected by the extreme values but the mean is. The median and some other statistics are what we call robust statistics because their value is not affected by the weight of extreme outcomes. In some cases, the impact of extreme values is so great that it is better to use the median as a measure of central tendency when discussing numeric variables. The data are still balanced around the mean, and the mean is still your “best guess” (smallest error in prediction), but in terms of looking for an outcome that represents the general tendency of the data, it may not be the best option in some situations.
In general, when the mean is significantly higher than the median, this is a sign that the distribution of values is right (or positively) skewed, due to the influence of extreme values at the high end of the scale. This means that the extreme values are pulling the mean away from the middle of the observations. When the mean is significantly lower than the median, this indicates a left (or negatively) skewed distribution, due to some extreme values at the low end of the scale. When the mean and median are the same, or nearly the same, this could indicate a bell-shaped distribution, but there are other possibilities as well. When the mean and median are the same, there is no skew.
Figure 5.3 provides caricatures of what these patterns might look like. The first graph shows that most data are concentrated at the low (left) end of the x-axis, with a few very extreme observations at the high (right) end of the axis pulling the mean out from the middle of the distribution. This is a positive skew. The second graph shows just the opposite pattern: most data at the high end of the x-axis, with a few extreme values at the low (left) end dragging the mean to the left. This is a negatively skewed distribution.
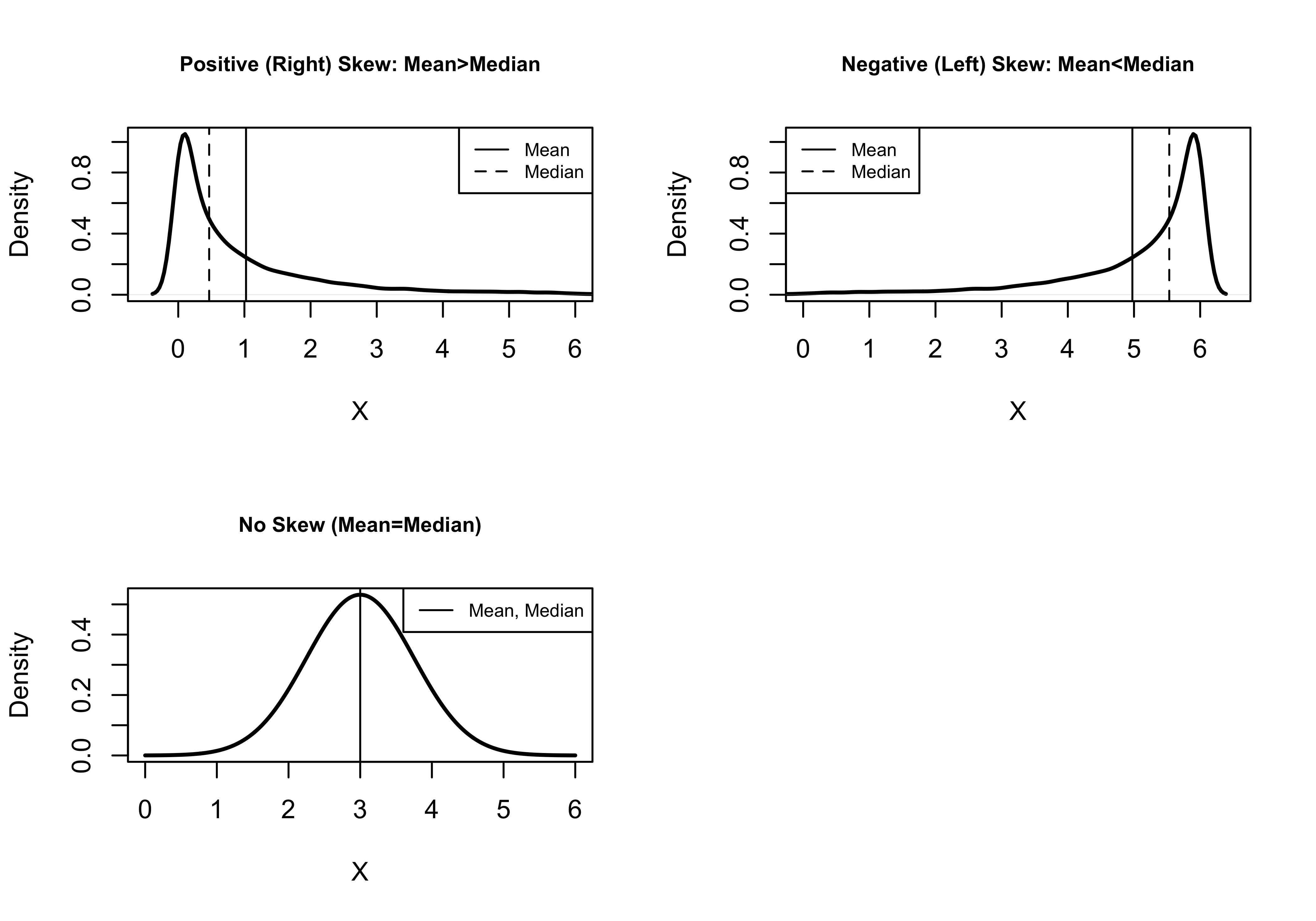
Figure 5.3: Illustrations of Different Levels of Skewness
[Figure** 5.3 **about here]
Finally, the third graph shows a perfectly balanced, bell-shaped distribution, with the mean and the median equal to each other and situated right in the middle of the distribution. There is no skewness in this graph. This bell-shaped distribution is not the only way type of distribution with no skewness13, but it is an important type of distribution that we will take up later.
It has been my experience that once students hear that the median might be preferred over the mean when there is a significant difference between them, they tend to default to using the median whenever it is at all different from the mean. There will almost always be some difference between the mean and the median, so automatically defaulting to the median is not good practice. My best advice is that the mean should be your first choice. If, however, there is evidence that the mean is heavily influenced by extreme observations (see below), then you should also use the median. Of course, it doesn’t hurt to present both statistics, as more information is usually good information.
Let’s see what this looks like when using real-world data, starting with abortion laws in the states (states20$abortion_laws).
#get mean and median for 'abortion_laws'
mean(states20$abortion_laws)[1] 7.88median(states20$abortion_laws)[1] 9The mean is a bit less than the median, so we might expect to see signs of negative (left) skewness in the density plot.
plot(density(states20$abortion_laws),
xlab="# Abortion Restrictions in State Law",
main="")
#Insert vertical lines for mean and median
abline(v=mean(states20$abortion_laws))
abline(v=median(states20$abortion_laws), lty=2) #use dashed line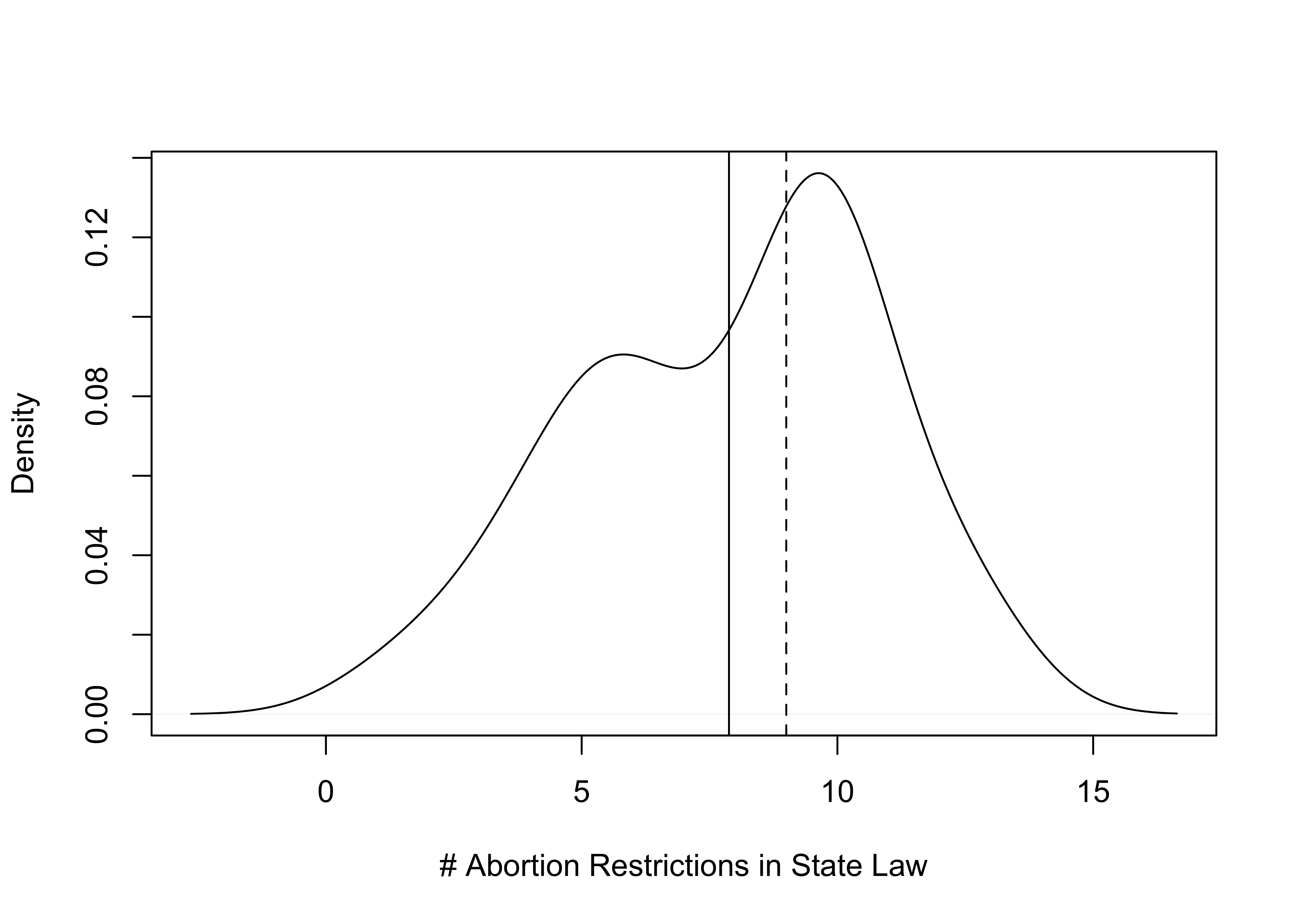
Here, we see the difference between the mean (solid line) and the median (dashed line) in the context of the full distribution of the variable, and the graph shows a distribution with a bit of negative skew. The skewness does not appear to be severe, but it is visible to the naked eye. Note that you get the same impression if you use a histogram:
hist(states20$abortion_laws,
xlab="# Abortion Restrictions in State Law",
main="")
#Insert vertical lines for mean and median
abline(v=mean(states20$abortion_laws))
abline(v=median(states20$abortion_laws), lty=2) #use dashed line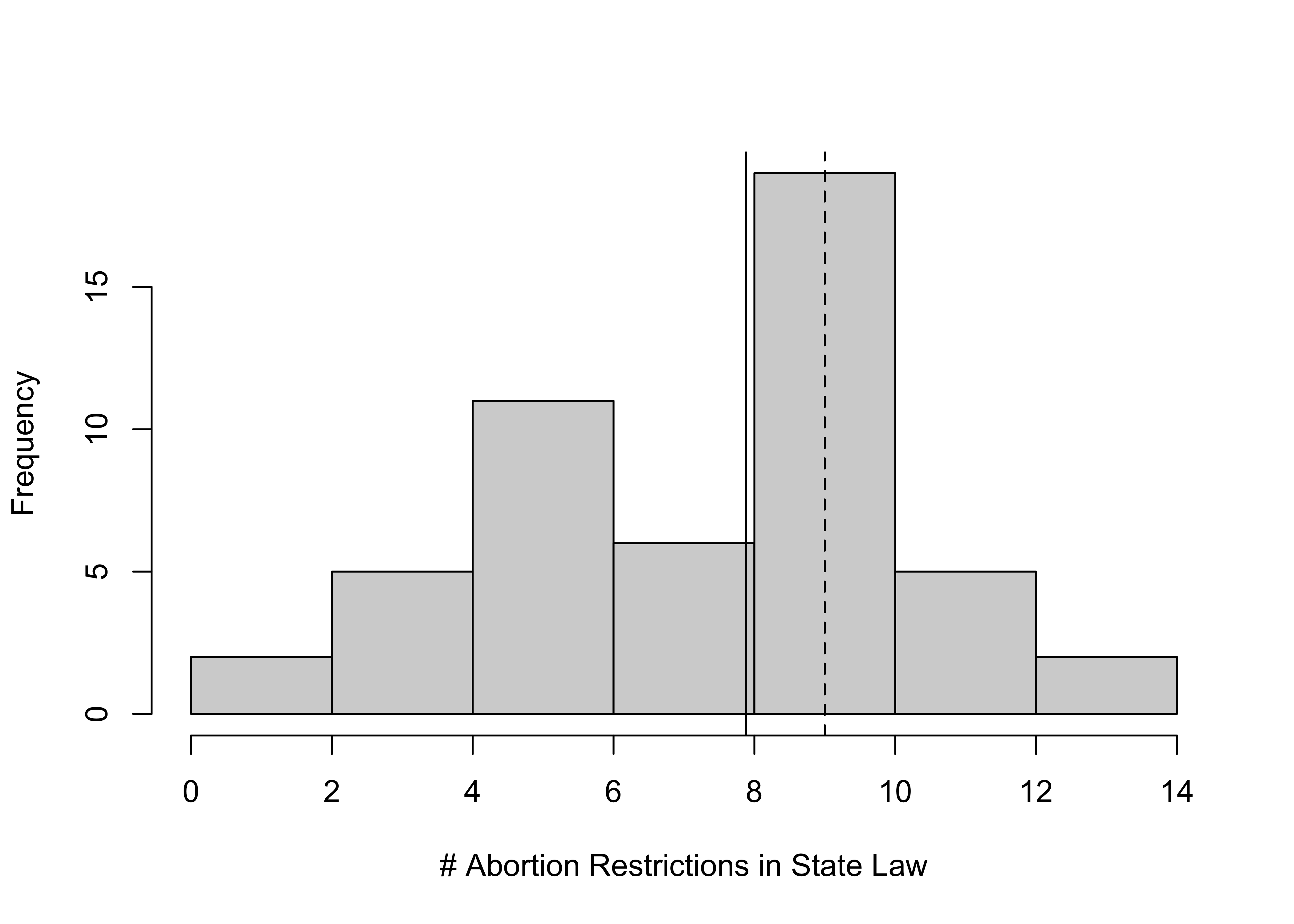
An R code digression. The density plot above includes the addition of two vertical lines, one for the mean and one for the median. To add these lines, I used the abline command. This command allows you to add lines to existing graphs. In this case, I want to add two vertical lines, so I use v= to designate where to put the lines. I could have put in the numeric values of the mean and median (v=7.88 and v=9), but I chose to use have R calculate the mean and median and insert the results in the graph (v=mean(states20$abortion_laws) and v=median(states20$abortion_laws)). Either way would get the same result. Also, note that for the median, I added lty=2 to get R to use “line type 2”, which is a dashed line. The default line type (1) is a solid line, which is used for the mean.
Now, let’s take a look at another distribution, this time for a variable we have not looked at before, the percent of the state population who are foreign-born (states20$fb). This is an increasingly important population characteristic, with implications for a number of political and social outcomes.
mean(states20$fb)[1] 7.042median(states20$fb)[1] 4.95Here, we see a bit more evidence of a skewed distribution. Since the mean is greater than the median, it is reasonable to expect to see some positive skewness. The density plot (below) supports this expectation and looks somewhat more like a skewed distribution than in the example using state abortion laws.
#Density plot for % foreign-born
plot(density(states20$fb),
xlab="Percent foreign-born",
main="")
#Add lines for mean and median
abline(v=mean(states20$fb))
abline(v=median(states20$fb), lty=2) #Use dashed line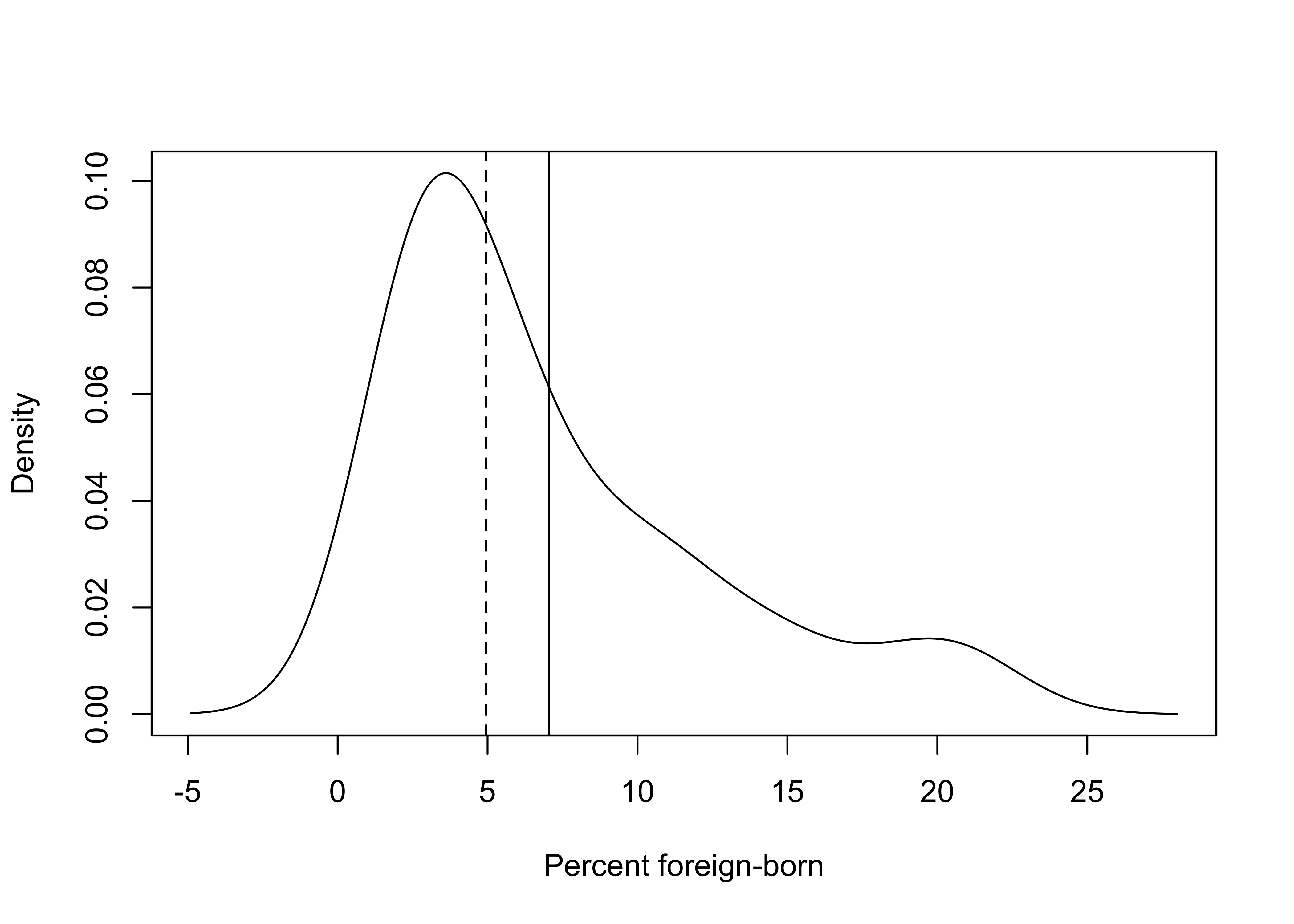
Finally, as a counterpoint to these skewed distributions, let’s take a look at the distribution of percent of the two-party vote for Joe Biden in the 2020 election:
mean(states20$d2pty20)[1] 48.8044median(states20$d2pty20)[1] 49.725Here, there is very little difference between the mean and the median, and there appears to be almost no skewness in the shape of the density plot (below).
plot(density(states20$d2pty20),
xlab="% of Two-Party Vote for Biden",
main="")
abline(v=mean(states20$d2pty20))
abline(v=median(states20$d2pty20), lty=2)
What’s interesting here is that the distance between the mean and median for Biden’s vote share (.92) is not terribly different than the distance between the mean and the median for the number of abortion laws (1.12). Yet there is not a hint of skewness in the distribution of votes, while there is clearly some negative skew to abortion laws. This, of course, is due to the difference in scale between the two variables. Abortion laws range from 1 to 13, while Biden’s vote share ranges from 27.5 to 68.3, so relative to the scale of the variable, the distance between the mean and median is much greater for abortion laws in the states than it for Biden’s share of the two-party vote in the states. This illustrates the real value of examining a numeric variable’s distribution with a histogram or density plot alongside statistics like the mean and median. Graphs like these provide context for those statistics.
Skewness Statistic
Fortunately, there is a skewness statistic that summarizes the extent of positive or negative skew in the data. There are several different methods for calculating skewness. The one used in R is based on the direction and magnitude of deviations from the mean, relative to the amount of variation in the data.14 The nice thing about the skewness statistic is that there are some general guidelines for evaluating the direction and seriousness of skewness:
- A value of 0 indicates no skew to the data.
- Any negative value of skewness indicates a negative skew, and positive values indicate positive skew.
- Values lower than -2 and higher than 2 indicate extreme skewness that could pose problems for operations that assume a relatively normal distribution.
Let’s look at the skewness statistics for the three variables discussed above.
#Get skew for three variables (upper-case S in "Skew" command)
Skew(states20$abortion_laws)[1] -0.3401058Skew(states20$fb)[1] 1.202639Skew(states20$d2pty20)[1] 0.006792623These skewness statistics make a lot of sense, given the earlier discussion of these three variables. There is a little bit of negative skew (-.34) to the distribution of abortion restrictions in the states, a more pronounced level of (positive) skewness to the distribution of the foreign-born population, and no real skewness in the distribution of Biden support in the states (.007). None of these results are anywhere near the -2,+2 cut-off points discussed earlier, so these distributions should not pose any problems for any analysis that uses these variables.
Log Transformations
Quite often, you will be using variables whose distributions look a lot like the three shown above, maybe a bit skewed, but nothing too outrageous. Occasionally, though, you will come across variables with severe skewness that can be detected visually and by using the skewness statistic. As a point of reference, consider the three distributions shown earlier in Figure 5.3, one with what appears to be severe positive skewness (top left), one with severe negative skewness (top right), and one with no apparent skewness (bottom left). The values of the skewness statistics for these three distributions are 4.25, -4.25, and 0, respectively.
In some instances, the skewness is so excessive, often due to just a few extreme outliers, that it can create serious problems for calculating some statistics. In many of these cases, it make sense to transform the data so the extreme outliers do not have an out-sized effect on statistical results. One variable like this that is used in later chapters measures country-level population size in 2019, in millions of people (countries2$pop19_M). As you can see in the histogram below, this variable’s distribution is heavily influenced by a few extreme outliers.
hist(countries2$pop19_M, breaks=13,
xlab = "Population (Millions)",
ylab = "Number of Countries",
main = "")
Skew(countries2$pop19_M)[1] 8.320391The vast majority of countries fall in the first bin (0 to 100,000, anchored by Nauru at 10,800 people), and a handful more are in the next three bins (the U.S. the highest in this group 329 Million), and then China and India are at the far right end of the scale, coming in at about 1.4 Billion population each. The skewness statistic reflects this distribution with a value of 8.3.
One useful way to minimize the impact of the extreme values is to take logged values of each observation. Log transformations like this have many uses. In this instance, we want to minimize the impact of extreme values. Later, in Chapter 17, you will see how to use logged values to model certain types of relationships in regression analysis. Here, I will use a log(10) transformation. This means that all of the original values are transformed into their logged values, using a base of 10. A logged value is nothing more than the power to which you have to raise your log base (in this case, 10) in order to get the original raw score. For instance, for the U.S., the log10 of population is 2.517, since \(10^{2.52} = 329\), the log10 of population for China is 3.1565 because \(10^{3.1565}=1434\), and so on. The code below shows how to get log10 values and how to translate logged values back to the original values.
log10(329)[1] 2.517196log10(1434)[1] 3.15654910^2.517196[1] 329.000110^3.156549[1] 1434The result of the transformation is that relatively extreme values are brought closer to the middle, and the resulting distribution is usually easier to deal with. Check out the histogram below, which shows the log-transformed distribution.
hist(log10(countries2$pop19_M),
xlab = "Log10 of Population (Millions)",
ylab = "Number of Countries",
main = "")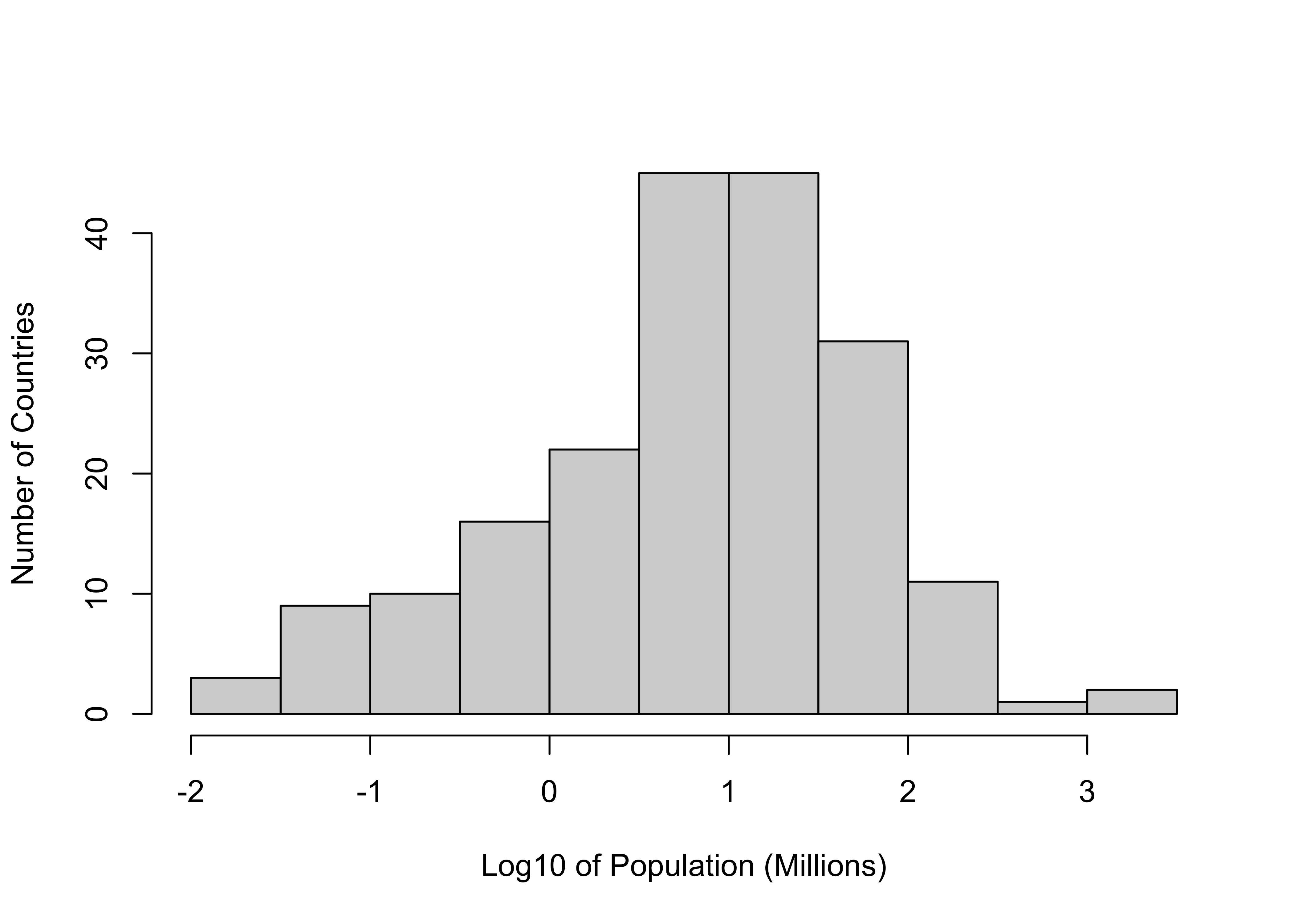
There will be more discussion of this transformation later, but for now here are a couple of other things to know.
This only works for variables with positive values. Taking log transformations of variables with negative or zero values will produce missing data.
In the histogram command, I used
(log10(countries2$pop19_M), where I told R to transform the original variable and use it in the histogram. Alternatively, you could create a transformed version of the variable (countries2$lg10_pop<-countries2$pop19_M) and use that variable in the histogram or elsewhere. Both approaches work.
Adding Legends to Graphs
The vertical lines for the mean and median used in the graphs shown above are useful visual aids for understanding how those variables are distributed. Importantly, these lines were explained in the text, but there was no identifying information provided in the graphs themselves. When presenting information like this in a formal setting (e.g., on the job, for an assignment, or for a term paper), it is usually expected that you provide a legend with your graphs that identifies what the lines represent (see Figure 5.3 as an example). This can be a bit complex, especially if there are multiple lines in your graph. In the current case, however, it is not terribly difficult to add a legend.
This code is added below to the density plot command used to generate the density plot for states20$fb:
#Create a legend to be put in the top-right corner, identifying
#mean and median outcomes with solid and dashed lines, respectively
legend("topright", legend=c("Mean", "Median"), lty=1:2)The first bit ("topright") is telling R where to place the legend in the graph. In this case, I specified topright because I know that is where there is empty space in the graph. You can specify top, bottom, left, right, topright, topleft, bottomright, or bottomleft, depending on where the legend fits the best. The second piece of information, legend=c("Mean", "Median"), provides names for the two objects being identified, and the last part, lty=1:2, tells R which line types to use in the legend (the same as in the graph). Let’s add this to the command lines for the density plot for states20$fb and see what we get.
plot(density(states20$fb),
xlab="Percent foreign-born",
main="")
abline(v=mean(states20$fb))
abline(v=median(states20$fb), lty=2)
#Add the legend
legend("topright", legend=c("Mean", "Median"), lty=1:2)
This extra bit of information fits nicely in the graph and aids in interpreting the pattern in the data.
Sometimes, it is hard to get the legend to fit well in a graph space. When this happens, you need to tinker a bit to get a better fit. There are some fairly complicated ways to achieve this, but I favor trying a couple of simple things first: try different locations for the legend, reduce the number of words you use to name the lines, or add the cex command to reduce the overall size of the legend. When using cex, you might start with cex=.8, which will reduce the legend to 80% of its original size, and then change the value as needed to make the legend fit.
Next Steps
The next chapter builds on the discussion of descriptive statistics by focusing on something we’ve dealt with tangentially in this chapter: measuring variability in the data. The measures of central tendency discussed here chapter are important descriptive tools, but they also are essential for calculating and understanding many other statistics, including measures of dispersion, which we take up in Chapter 6. Following that, we spend a bit of time on the more abstract topics of probability and statistical inference. These things might sound a bit intimidating, but you will be ready for them when you get there.
Exercises
Concepts and Calculations
Let’s return to the list of variables used for exercises in Chapters 1 & 3. Identify what you think is the most appropriate measure of central tendency for each of these variables. Choose just one measure for each variable
- Course letter grade
- Voter turnout rate (votes cast/eligible voters)
- Marital status (Married, divorced, single, etc)
- Occupation (Professor, cook, mechanic, etc.)
- Body weight
- Total number of votes cast in an election
- #Years of education
- Subjective social class (Poor, working class, middle class, etc.)
- Poverty rate
- Racial or ethnic group identification
Below is a list of voter turnout rates in twelve Wisconsin Counties during the 2020 presidential election. Calculate the mean, median, and mode for the level of voter turnout in these counties. Which of these is the most appropriate measure of central tendency for this variable? Why? Based on the information you have here, is this variable skewed in either direction? Explain.
| Wisconsin County | % Turnout |
|---|---|
| Clark | 63 |
| Dane | 87 |
| Forrest | 71 |
| Grant | 63 |
| Iowa | 78 |
| Iron | 82 |
| Jackson | 65 |
| Kenosha | 71 |
| Marinette | 71 |
| Milwaukee | 68 |
| Portage | 74 |
| Taylor | 70 |
- The following table provides the means and medians for four different variables from the
states20data set. Use this information to offer your best guess as to the level and direction of skewness in these variables. Explain your answer. Make sure to look at thestates20codebook first, so you know what these variables are measuring.
| Variable Name | Mean | Median |
|---|---|---|
| obesity | 29.9 | 30.10 |
| Cases10k | 421.9 | 453.9 |
| PerPupilExp | 12,720 | 11,826 |
| metro | 64.2 | 68.5 |
- The table below shows responses to a question from the
anes20that asked if respondents agreed or disagreed that “immigrants are good for America’s Economy.” What are the mode and median for this variable? Explain your answer.
POST: CSES5-Q05c: Out-group attitudes: immigrants good for America's economy
Frequency Percent Valid Percent
1. Agree strongly 1870 22.585 25.418
2. Agree somewhat 2770 33.454 37.651
3. Neither agree nor disagree 1876 22.657 25.500
4. Disagree somewhat 605 7.307 8.223
5. Disagree strongly 236 2.850 3.208
NA's 923 11.147
Total 8280 100.000 100.000The table below shows the logged (base 10) values of the cumulative number of COVID-19 cases in five different states by the end of August 2021. Use this information to calculate the raw number of cases for each state. Comment on the difference in the impression you get about the differences in the prevalence of COVID-19 cases between the two columns of numbers. (Hint: See footnote #4)
State Log10(Cases) Number of Cases Vermont 4.419 Montana 5.102 Arkansas 5.653 Pennsylvania 6.113 California 6.643
R Problems
Use R to report all measures of central tendency that are appropriate for each of the following variables: The feeling thermometer rating for the National Rifle Association (
anes20$V202178), Latinos as a percent of state populations (states20$latino), party identification (anes20$V201231x), and region of the country where ANES survey respondents live (anes20$V203003). Where appropriate, also discuss potential skewness.Using one of the numeric variables listed in the previous question, create a density plot that includes vertical lines showing the mean and median outcomes, and add a legend. (Depending on which variable you use, you may have to add
na.rm=Tto the density command). Describe what you see in the plot.Get a histogram of
states20$pop2020and describe its distribution. Then get a histogram of the logged (base 10) values ofstates20$pop2020and describe its distribution.
The original version of this variable is used here instead of the transformed version (
anes20$poor_spnd), just in case you weren’t assigned Chapter 4, or didn’t save the transformations you made there.↩︎For instance, a U-shaped distribution, or any number of multi-modal distributions could have no skewness.↩︎
\(Skewness=\frac{(x_{i}-\bar{x})^3}{n*{S^3}}\), where n= number of cases, and S=standard deviation↩︎