from sympy import symbols, Eq, solve7 เงินกู้และการผ่อนชำระหนี้ (Loans and Amortization)
7.1 รูปแบบการชำระหนี้ (Loan Repayment Models)
ในคณิตศาสตร์การเงิน การชำระหนี้แบบผ่อนชำระมีหลายรูปแบบ ซึ่งแต่ละรูปแบบมีโครงสร้างการชำระที่แตกต่างกัน แต่โดยทั่วไปแล้ว
ผู้กู้จ่ายงวดเท่ากันทุกงวด (Level Payment Loan)
ผู้กู้จ่ายเงินต้นคงที่ ส่วนดอกเบี้ยลดลงเรื่อย ๆ (Principal Repayment Loan)
การชำระหนี้แบบบอลลูน (Balloon Loan) : ผู้กู้จ่ายเฉพาะดอกเบี้ยหรือจ่ายน้อยช่วงต้น แล้วจ่ายก้อนใหญ่ (balloon) ในงวดท้าย
จำนวนรายงวดที่ต้องจ่ายก็จ่าย สามารถหาได้จาก สูตรการคำนวณในบทที่ 3 โดยที่ยอดผ่อนจ่ายรายงวดคือ \[L=R\cdot a_{\overline{n}|i}\rightarrow R=\dfrac{L}{a_{\overline{n}|i}}\] โดยที่
\(L\) = เงินกู้เริ่มต้น (loan amount)
\(R\) = จำนวนเงินที่จ่ายรายงวด
\(i\) = อัตราดอกเบี้ยต่อช่วง
\(n\) = จำนวนงวดทั้งหมด
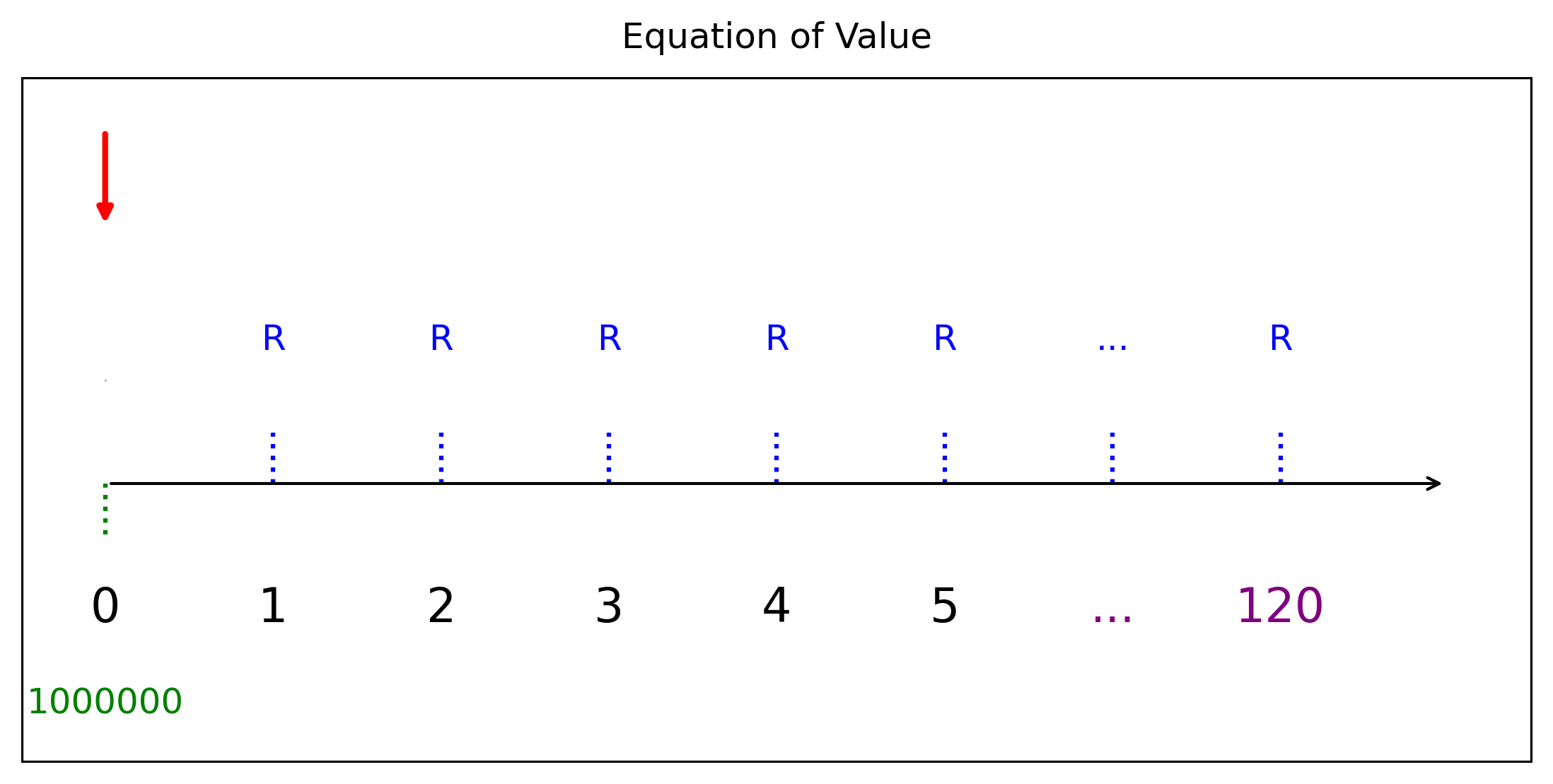
สมมุติกู้ยืมเงิน 1 ล้านบาท ด้วยอัตราดอกเบี้ย \(i^{(12)}=0.06\) ผ่อนชำระทุกสิ้นเดือน เป็นเวลา 10 ปี ต้องผ่อนเดือนละเท่าไหร่
อัตราดอกเบ้ียต่อเดือนคือ \(i =i^{(12)}/12=0.06/12=0.005\) สมการแห่งมูลค่าคือ \[1,000,000=R\cdot a_{\overline{120}|i}, = 0.005\]
# นิยามตัวแปร
L,R, i, n, k, = symbols('L R i n k' , positive=True)
a_ni = symbols('a_ni')
i = 0.005
v = 1 / (1 + i)
n = 120
L = 1e6
a_ni =(1-v**n)/i
eq = Eq(L,R*a_ni)
sol =solve(eq, R)
sol[11102.0501941652]ต้่องผ่อนเดือนละ 11,102.05 เป็นเวลา 10 ปี แต่ปกติผผู้ให้กู หรือ ผู้กู้อาจจะผ่อนจ่ายเพิ่มขึ้นอีกเล็กน้อย เช่น 11,200 11,110 หรือ 11,103 บาท ซึ่งผลของการผ่อนมากขึ้นอีกเล็กน้อยจะทำให้การชำระหนี้หมดเร็วขึ้นไปอีก เพราะส่งผลให้งวดสุดท้ายจ่ายเงินเป็นจำนวนทึ่ลดลง โดยจะมีหนี้เหลือเท่าไหร่ ในงวดสุดท้าย หรืองวดสุดท้ายต้องจ่ายเท่าไหร่เพื่อปิดหนี้ จะกล่าวถึงในหัวข้่อถัดไป
7.2 ยอดเงินคงค้าง (Outstanding Balance)
ณ งวดใด ๆ ของการชำระหนี้ เราสามารถแยก ยอดคงค้าง (Outstanding Balance) ได้ 2 วิธี
7.2.1 วิธีมองไปข้างหน้า (Prospective Method)
ในแนวคิดของ วิธีมองไปข้างหน้า การคำนวณยอดคงค้าง ณ งวดที่ \(k\) คือการพิจารณามูลค่าปัจจุบันของงวดชำระหนี้ที่เหลืออยู่ทั้งหมดตั้งแต่งวดที่ \(k+1\) ไปจนถึงงวดสุดท้าย \(n\) โดยคิดลดด้วยอัตราดอกเบี้ย \(i\)
สูตรในการคำนวณยอดคงค้าง ณ งวดที่ \(k\) คือ
\[ B_k = R \cdot a_{\overline{n - k}|i} \]
โดยที่
\(B_k\) คือ ยอดคงค้างของเงินกู้ ณ จุดสิ้นสุดของงวดที่ \(k\)
\(R\) คือ จำนวนเงินที่ต้องจ่ายในแต่ละงวด (ค่างวดเท่ากันทุกงวด)
\(a_{\overline{n-k}|i}\) คือ มูลค่าปัจจุบันของการชำระเงินจำนวน \(R\) ทั้งหมดที่เหลืออีก \(n-k\) งวด โดยคิดลดด้วยอัตราดอกเบี้ย \(i\)
กล่าวอีกนัยหนึ่ง ยอดคงค้าง ณ งวดที่ \(k\) เท่ากับ มูลค่าปัจจุบันของค่างวดที่เหลืออยู่ในอนาคต ทั้งหมด ณ เวลานั้น
7.2.2 วิธีมองย้อนกลับ (Retrospective Method)
ในแนวคิดของ วิธีมองย้อนกลับ การคำนวณยอดคงค้าง ณ งวดที่ \(k\) คือการพิจารณามูลค่าที่สะสมของเงินกู้เริ่มต้นจนถึงงวดที่ \(k\) แล้วหักด้วยมูลค่าที่สะสมของการชำระเงินที่ได้จ่ายไปแล้วจนถึงงวดที่ \(k\) โดยคิดรวมดอกเบี้ยที่สะสมในแต่ละงวด
สูตรในการคำนวณยอดคงค้าง ณ งวดที่ \(k\) คือ \[ B_k = L(1+i)^k - R \cdot s_{\overline{k}|i} \] โดยที่
\(B_k\) คือ ยอดคงค้างของเงินกู้ ณ จุดสิ้นสุดของงวดที่ \(k\)
\(L\) คือ จำนวนเงินกู้เริ่มต้น
\(i\) คือ อัตราดอกเบี้ยต่อช่วง
\(R\) คือ จำนวนเงินที่ต้องจ่ายในแต่ละงวด (ค่างวดเท่ากันทุกงวด)
\(s_{\overline{k}|i}\) คือ มูลค่าที่สะสมของการชำระเงินจำนวน \(R\) ทั้งหมดที่ได้จ่ายไปแล้วใน \(k\) งวด โดยคิดรวมดอกเบี้ยที่สะสมในแต่ละงวด
กล่าวอีกนัยหนึ่ง ยอดคงค้าง ณ งวดที่ \(k\) เท่ากับ มูลค่าที่สะสมของเงินกู้เริ่มต้น จนถึงงวดที่ \(k\) หักด้วย มูลค่าที่สะสมของการชำระเงินที่ได้จ่ายไปแล้ว จนถึงงวดที่ \(k\)
ตัวอย่างที่ 1 นายสมชายกู้เงินจำนวน \(L = 10{,}000\) บาท โดยชำระคืนเป็นรายปี จำนวนเงินงวดละ \(R = 2{,}638.55\) บาท เป็นเวลา 5 ปี ที่อัตราดอกเบี้ย \(i = 8\%\) ต่อปี (ค่างวดเท่ากันทุกงวด) จงหายอดคงค้างของเงินกู้ ณ สิ้นปีที่ 3
วิธีทำ:
เหลือจำนวนงวดที่ต้องชำระอีก 2 งวด ด้วยวิธีมองไปข้างหน้า \[X= 2504.56\cdot a_{\overline{2}|0.08}\]
i,v, n, X, a_n = symbols('i v n X a_n', positive = True)
i = 0.08
v = 1/(1+i)
n = 2
a_n = (1-v**n)/i
X = 2504.56*a_n
X4466.293552812076ดังนั้นเมื่อชำระงวดที่ 3 แล้วจะเหลือหนี้ 4,705.23 บาท
- ใช้วิธีคิดแบบมองย้อนกลับ
สมการมูลค่า คือ \[10000\cdot(1+i)^3 = 2504.56\cdot s_{\overline{3}|i}+X, i=.08\]
i, n, X, s_n = symbols('i n X s_n', positive = True)
i = 0.08
n = 3
s_n = ((1+i)**n - 1)/i
eq = Eq(1e4*(1+i)**n, 2504.56*s_n + X)
eq\(\displaystyle 12597.12 = X + 8130.80358400001\)
แก้สมการ
solution = solve(eq,X)
solution[0].evalf(6)\(\displaystyle 4466.32\)
ทั้งสองวิธีแตกต่างกันเล็กน้อย เนื่องจากเลขทศนิยมของรายงวดที่จ่ายไม่ใช่ตัวเลขจริง เนื่องใช้ทดนิยมเพียงสองตำแหน่ง
ตัวอย่างที่ 2 บริษัทแห่งหนึ่งกู้เงินจำนวน \(L = 50{,}000\) บาท ชำระคืนทุกไตรมาส (ปีละ 4 ครั้ง) เป็นเวลา 3 ปี รวมทั้งหมด 12 งวด ที่อัตราดอกเบี้ย \(i^{(4)} = 6\%\) ต่อปี หรือ \(i = \frac{0.06}{4} = 0.015\) ต่อไตรมาส ชำระงวดละ \(R = 4{,}348.50\) บาท
คำถาม: หายอดคงค้างของเงินกู้ ณ สิ้นงวดที่ 5
ถ้าจะใช้วิธีมองไปข้างหน้า ต้องแน่ใจก่อนว่า 4348.50 ที่ชำระ 12 งวดมีมูลค่าปัจจุบันเท่ากับ 50,000 บาท
i, v, n, R, a_n = symbols('i v n R a_n', positive = True)
i = 0.015
v = 1/(1+i)
n = 12
a_n = (1-v**n)/i
R = 50000/a_n
R4583.9996453114845จะพบว่า ไม่สามารถใช้วิธีมองไปข้างหน้าได้ ต้องใช้วิธีมองย้อนกลับ
เทียบกับตัวอย่างที่ผ่านมาสมการแห่งมูลค่าคือ \[X = 50000\cdot (1+i)^5-4348.5\cdot s_{\overline{5}|i},~i =0.015\]
i,n, s_n, X = symbols('i n s_n X', positive = True)
i =0.015
n = 5
s_n = ((1+i)**n-1)/i
X = 50000*(1+i)**5-4348.5*s_n
X31459.567468138554หลังจากชำระงวดที่ 5 มียอดหนี้คงเหลือเท่ากับ 31.459.57 บาท
ตัวอย่างที่ 3 กู้เงิน 1 ล้าน ด้วยอัตราดอกเบี้ย 6% ต่อปีเปลี่ยนแปลงทุกเดือน โดยมีการชำระทุกสิ้นเดือน เป็นเวลา 6 ปี เมื่อชำระครบแล้ว 3 ปีเหลือหนี้เท่าไหร่ หลังจากนั้นถ้าต้องการชำระหนี้ให้หมดเร็วขึ้น 1 ปีท ต้องชำระหนี้งวดละเท่าไหร่
ผ่อนเป็นเวลา 6 ปีมีจำนวนงวดเท่ากับ 72 งวด อัตราดอกเบี้ยต่องวด(เดือน) \(i =i^{(12)}/12=0.006/12=0.005\)
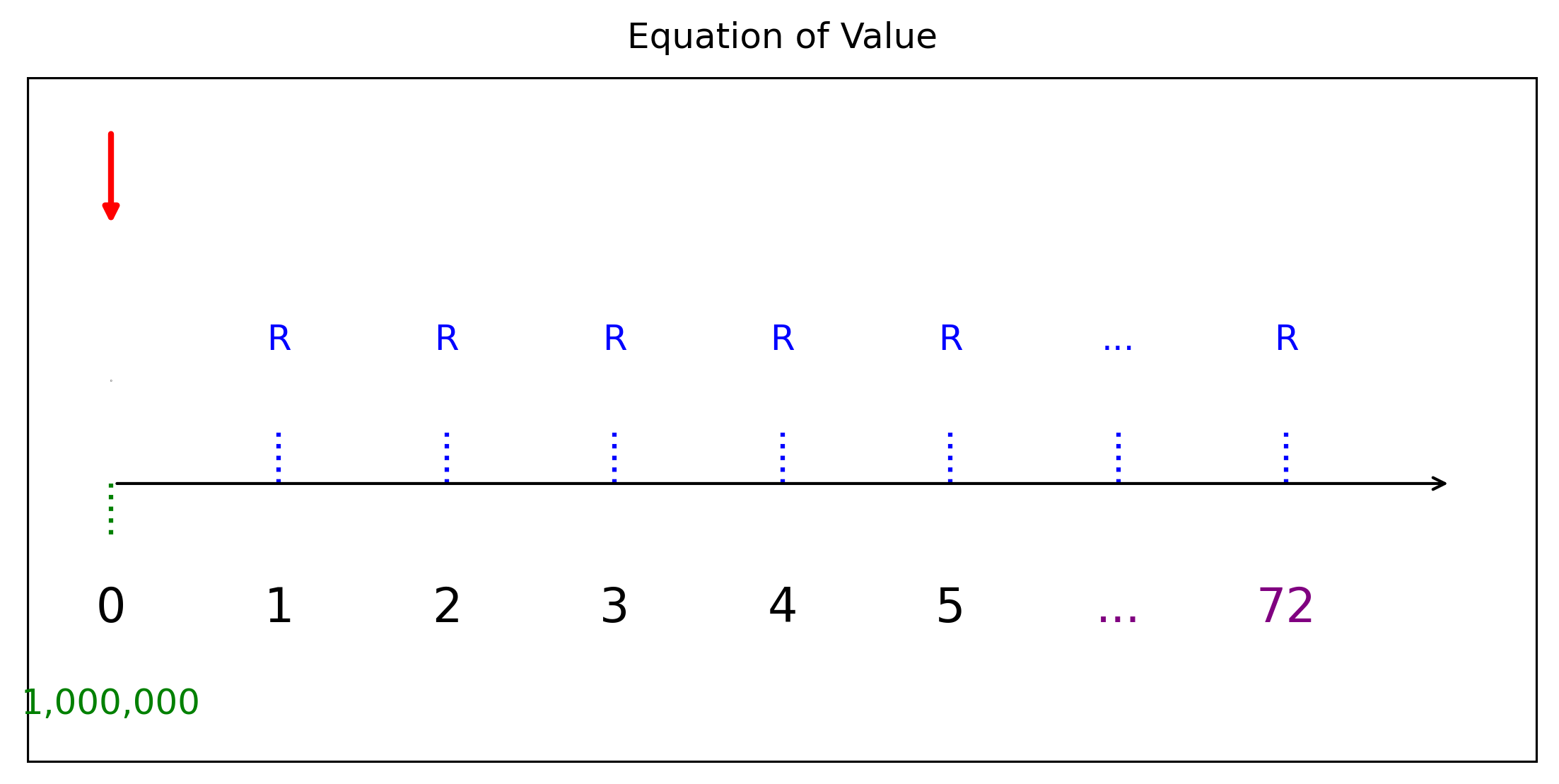 สมการแห่งมูลค่าคือ \(1,000,000 = R\cdot a_{\overline{72}|i}\) หรือ \[R =1,000,000/a_{\overline{72}|i}, i =0.005\]
สมการแห่งมูลค่าคือ \(1,000,000 = R\cdot a_{\overline{72}|i}\) หรือ \[R =1,000,000/a_{\overline{72}|i}, i =0.005\]
i,n, v, a_n, R = symbols('i n v a_n R', positive = True)
i = 0.005
n = 72
v = 1/(1+i)
a_n = (1-v**n)/i
R = 1e6/a_n
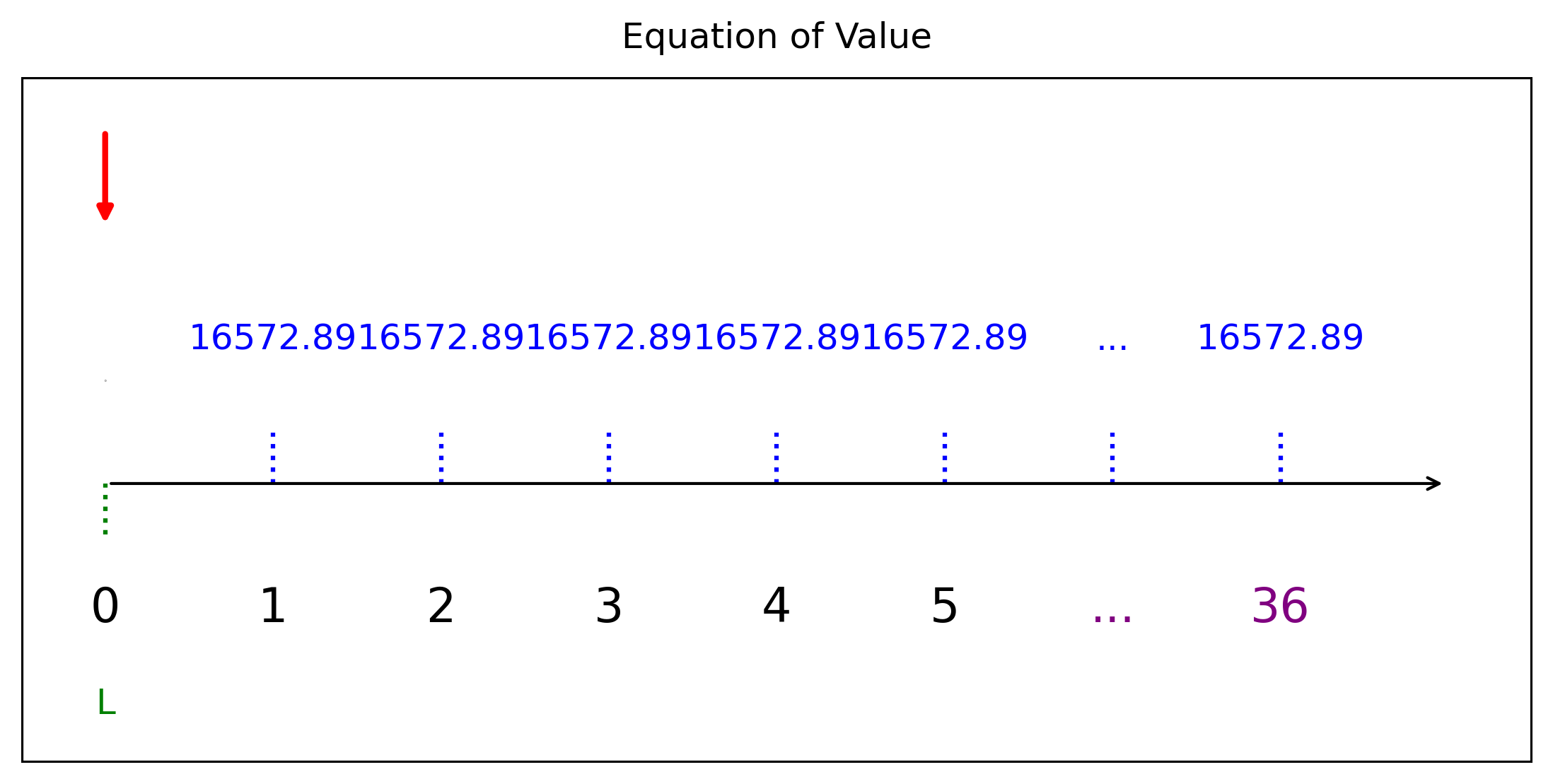
R16572.88789347258ต้องผ่อนชำระ เดือนละ 16,572.89 บาท ต่อเดือน ดังนั้นเมืผ่อนชำระไปแล้ว 3 ปี เหลือหนี้ที่ต้องชำระอีก 36 คือ
สมการแห่งมูลค่าคือ \[L=16572.89\cdot a_{\overline{36}|i}\]
i, n, v, L, a_n = symbols('i n v L a_n', positive = True)
i = 0.005
n = 36
v = 1/(1+i)
a_n = (1-v**n)/i
L = 16572.89*a_n
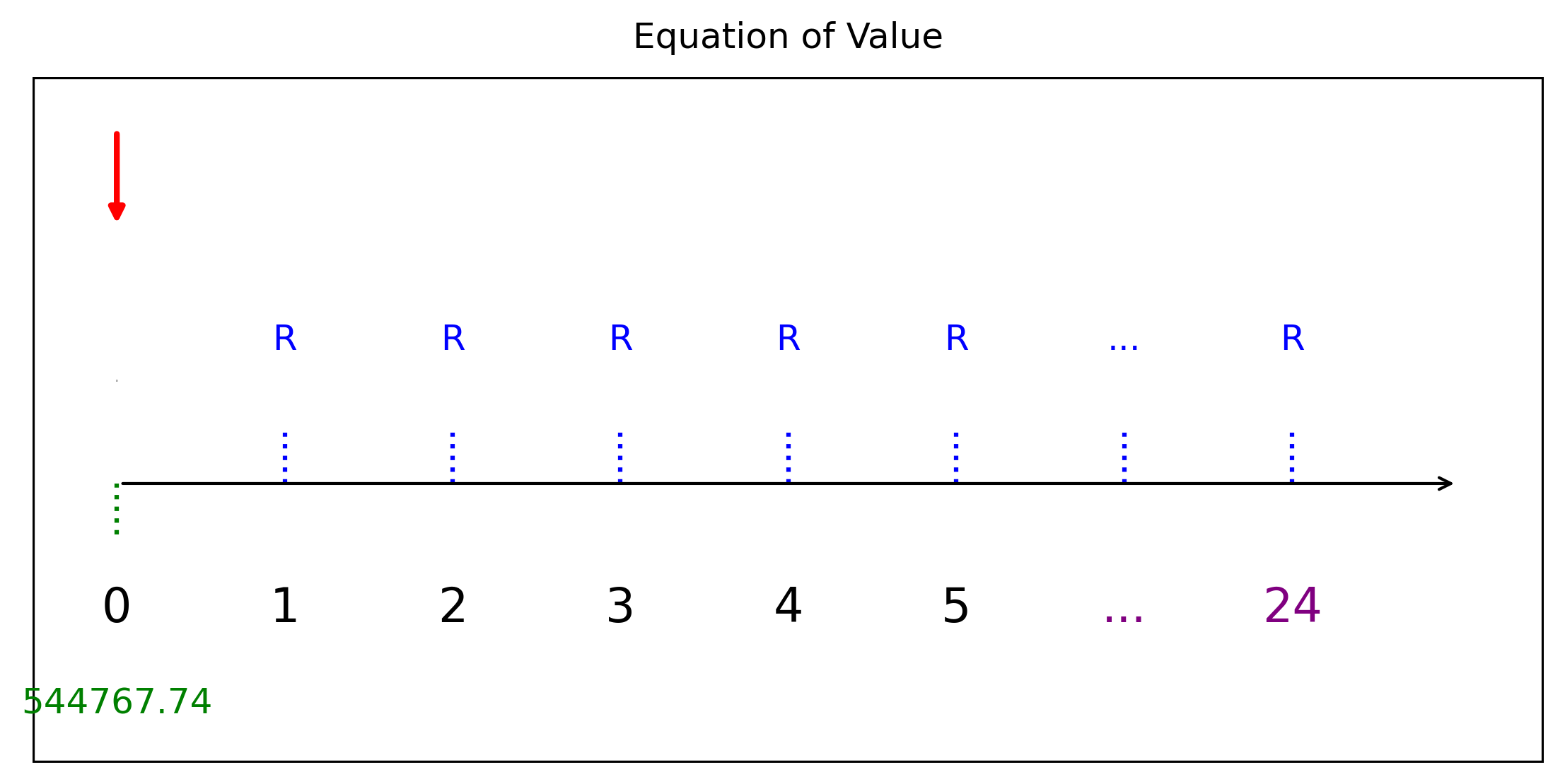
L544767.736321554ดังนั้นถ้าต้องการให้หนี้หมดเร็วขี้น 1 ปี ต้องผ่อนอีก 24 งวด
สมการแห่งมูลค่าคือ \[R = 544767.74/a_{\overline{24}|i},~ i =0.005\]
i,n, v, a_n, R = symbols('i n v a_n R', positive = True)
i = 0.005
n = 24
v = 1/(1+i)
a_n = (1-v**n)/i
R = 544767.74/a_n
R24144.438682815817ต้่องผ่อนชำระเป็นเงิน 24,144.44 บาท เพื่อหมดหนี้เร็วขึ้น 1 ปี
7.3 ตารางการชำระหนี้ (Amortization Schedule)
เป็นเครื่องมือที่ใช้แสดงรายละเอียดของการชำระคืนเงินกู้ในแต่ละงวด โดยตารางประกอบด้วยคอลัมน์สำคัญที่อธิบายได้ดังนี้
| งวดที่ \(k\) | ค่างวด \(R\) | ดอกเบี้ย \(I_k\) | เงินต้น \(P_k\) | ยอดคงค้าง \(B_k\) |
|---|---|---|---|---|
| 1 | … | … | … | … |
| 2 | … | … | … | … |
| … | … | … | … | … |
งวดที่ \(k\) หมายถึง ลำดับของการชำระหนี้ เช่น งวดที่ 1, 2, 3,… จนถึงงวดสุดท้าย เป็นการบ่งบอกว่าการชำระหนี้นี้เกิดขึ้นในช่วงเวลาใดของแผนการชำระหนี้
ค่างวด \(R\) คือ จำนวนเงินที่ต้องชำระในแต่ละงวด ซึ่งมักจะเป็นจำนวนเท่ากันทุกงวด (ในกรณีของเงินกู้แบบงวดคงที่) ค่างวดนี้ประกอบด้วย ดอกเบี้ย และ เงินต้น
ดอกเบี้ย \(I\_k\) คือ จำนวนดอกเบี้ยที่ต้องจ่ายในงวดที่ \(k\) โดยคำนวณจากยอดคงค้างของเงินกู้ในช่วงต้นงวดก่อนการชำระ สูตรที่ใช้คือ \[ I_k = i \cdot B_{k-1} \] โดยที่ \(B_{k-1}\) คือยอดคงค้างก่อนการชำระในงวดที่ \(k\) และ \(i\) คืออัตราดอกเบี้ยต่อช่วงเวลา
เงินต้น \(P\_k\) คือ ส่วนของค่างวดที่นำไปชำระเงินต้น ซึ่งหาได้จากการนำค่างวดหักด้วยดอกเบี้ย \[ P_k = R - I_k \] เงินต้นส่วนนี้จะทำให้ยอดคงค้างลดลงในแต่ละงวด
ยอดคงค้าง \(B\_k\) คือ ยอดเงินกู้ที่เหลืออยู่หลังจากการชำระหนี้ในงวดที่ \(k\) แล้ว คำนวณโดยการนำยอดคงค้างก่อนหน้าหักด้วยเงินต้นที่ชำระในงวดนั้น \[ B_k = B_{k-1} - P_k \] ยอดคงค้างนี้จะลดลงเรื่อย ๆ จนเหลือศูนย์ในงวดสุดท้าย
เนื่องจากซิมไพ ใช้สำหรับการคำนวณเชิงสัญลักษณ์เป็นหลัก ถ้าต้่องการตารางการผ่อนชำระ จำเป็นต้องบันทึกการคำนวณในอยู่ของตาราง (data frame) โดยใช้ชุดคำสั่ง panda ในไพธอน เข้าช่วย
ขั้นตอนคือ
ใช้
SymPyสร้างสูตร symbolic เช่น ดอกเบี้ย, เงินต้น, ยอดคงค้างใช้
pandasสร้าง ตารางการชำระหนี้ (Amortization Schedule) ที่แสดงค่าจริงจากการแทนค่าตัวแปร
ตัวอย่าง เงินกู้ \(L = 10,000\), ดอกเบี้ย \(i = 8\%\) ต่อปี, งวดละ \(R = 2,504.56\), จำนวน 5 งวด
from sympy import N
# --- กำหนด symbol สำหรับคำนวณเชิงสัญลักษณ์ ---
L, i, R = symbols('L i R')
B_prev, B_curr, I_k, P_k = symbols('B_prev B_curr I_k P_k')
# --- ค่างวดที่แทนค่าจริง ---
L_val = 10000
i_val = 0.08 # 8% = 0.08
R_val = 2504.56
n_periods = 5import pandas as pd
# --- เตรียมตารางใน pandas ---
amort_table = pd.DataFrame(columns=["งวดที่", "ค่างวด R", "ดอกเบี้ย I_k",
"เงินต้นP_k", "ยอดคงค้าง B_k"])
# --- ค่าเริ่มต้นยอดคงค้างก่อนงวดแรก ---
B_prev_val = L_val
for k in range(1, n_periods + 1):
# สร้างสมการดอกเบี้ยและเงินต้นเชิงสัญลักษณ์
I_k_expr = i * B_prev
P_k_expr = R - I_k_expr
B_k_expr = B_prev - P_k_expr
# แทนค่าคำนวณจริง
I_k_val = N(I_k_expr.subs({i: i_val, B_prev: B_prev_val}))
P_k_val = N(P_k_expr.subs({R: R_val, i: i_val, B_prev: B_prev_val}))
B_curr_val = N(B_k_expr.subs({R: R_val, i: i_val, B_prev: B_prev_val}))
# เติมข้อมูลในตาราง
amort_table.loc[k-1] = [k, round(R_val, 2), round(I_k_val, 2), round(P_k_val, 2),
round(B_curr_val, 2)]
# อัปเดตยอดคงค้างสำหรับรอบถัดไป
B_prev_val = B_curr_val
## แสดงตาราง
amort_table| งวดที่ | ค่างวด R | ดอกเบี้ย I_k | เงินต้นP_k | ยอดคงค้าง B_k | |
|---|---|---|---|---|---|
| 0 | 1 | 2504.56 | 800.000000000000 | 1704.56 | 8295.44 |
| 1 | 2 | 2504.56 | 663.64 | 1840.92 | 6454.52 |
| 2 | 3 | 2504.56 | 516.36 | 1988.20 | 4466.32 |
| 3 | 4 | 2504.56 | 357.31 | 2147.25 | 2319.06 |
| 4 | 5 | 2504.56 | 185.52 | 2319.04 | 0.03 |
7.4 ฟังก์ชัน N ในซิมไพ
ชุดคำสั่งซิมไพ ฟังก์ชัน N() หรือ evalf() ใช้สำหรับ ประเมินค่าตัวเลข (numerical evaluation) ของนิพจน์เชิงสัญลักษณ์ (symbolic expression)
| ฟังก์ชัน | ความหมาย | ตัวอย่าง |
|---|---|---|
N(expr) |
ประเมินค่านิพจน์ให้เป็นค่าทศนิยม | N(1/3)\(\rightarrow\) 0.333333333333333 |
expr.evalf() |
เขียนอีกแบบหนึ่งของ N(expr) |
(pi).evalf()\(\rightarrow\) 3.14159265358979 |
N(expr, n) |
กำหนดจำนวนหลักทศนิยม | N(pi, 50) \(\rightarrow\) ประเมินค่าพาย 50 หลัก |
from sympy import N, pi, sqrt
# ตัวอย่างทั่วไป
N(1/3) #$\rightarrow$ 0.333333333333333
N(pi) #$\rightarrow$ 3.14159265358979
N(sqrt(2)) #$\rightarrow$ 1.41421356237310
N(pi, 30) #$\rightarrow$ 3.14159265358979323846264338328
# ใช้กับสมการซับซ้อน
from sympy import symbols
x = symbols('x')
expr = (pi + sqrt(2)) / 3
N(expr) #$\rightarrow$ ค่าทศนิยมของนิพจน์เมื่อต้องการ “ค่าจริง” จากนิพจน์ที่ยังคงเป็นสัญลักษณ์
ใช้ในสมการทางคณิตศาสตร์การเงิน เช่น ค่างวด, มูลค่าเงิน, PV, FV
ใช้ก่อนนำค่าที่คำนวณได้ไป แสดงผล, เขียนลง DataFrame, หรือ plot
7.4.1 การใช้ฟังก์ชันเพื่อแยกเงินต้นและดอกเบี้ย
from sympy import symbols, Function, Eq, solve, Rational, simplify
# นิยามตัวแปร
L, i, n, k = symbols('L i n k', positive=True)
v = 1 / (1 + i)
# ค่างวด R
R = simplify(L * i / (1 - v**n)) # หรือ L / (1 - v**n) * i
# ยอดคงค้างแบบ prospective ณ งวดที่ k
B_k = simplify(R * (1 - v**(n - k)) / i)
# ดอกเบี้ยงวดที่ k
I_k = simplify(i * B_k.subs(k, k - 1))
# เงินต้นงวดที่ k
P_k = simplify(R - I_k)ตัวอย่าง กู้เงิน 10,000 บาท จ่าย 5 งวด ดอกเบี้ย 6% ต่อปี (0.06 ต่อปี), ผ่อนชำระปีละครั้ง
# ตัวอย่างการแทนค่า
R_val = R.subs({L: 10000, i: 0.06, n: 5}).evalf()
B3_val = B_k.subs({L: 10000, i: 0.06, n: 5, k: 3}).evalf()
I3_val = I_k.subs({L: 10000, i: 0.06, n: 5, k: 3}).evalf()
P3_val = P_k.subs({L: 10000, i: 0.06, n: 5, k: 3}).evalf()หรือ จะใช้ชุดคำสั่ง numpy ร่วมกับ panda ก็ได้
import numpy as np
import pandas as pd
# กำหนดค่าตัวแปร
L = 10000 # เงินกู้เริ่มต้น
i = 0.08 # อัตราดอกเบี้ยต่อปี
R = 2504.56 # ค่างวด
n = 5 # จำนวนงวด
# เตรียมข้อมูลงวด 1 ถึง n
k = np.arange(1, n + 1)
# ดอกเบี้ยแต่ละงวด: I_k = i * B_{k-1}
# ใช้ vector trick: สร้าง B_k ทีละงวดจาก recursive
B = np.zeros(n + 1) # รวม B0 ถึง B5
I = np.zeros(n)
P = np.zeros(n)
B[0] = L # ยอดเงินเริ่มต้นก่อนงวดที่ 1
for t in range(n):
I[t] = i * B[t]
P[t] = R - I[t]
B[t+1] = B[t] - P[t]
# ตัด B0 และ B_{n+1}
B_k = B[1:]
# รวมเป็น DataFrame
df = pd.DataFrame({
"งวดที่": k,
"ค่างวด R": np.full(n, R),
"ดอกเบี้ย I_k": np.round(I, 2),
"เงินต้น P_k": np.round(P, 2),
"ยอดคงค้าง B_k": np.round(B_k, 2)
})
df| งวดที่ | ค่างวด R | ดอกเบี้ย I_k | เงินต้น P_k | ยอดคงค้าง B_k | |
|---|---|---|---|---|---|
| 0 | 1 | 2504.56 | 800.00 | 1704.56 | 8295.44 |
| 1 | 2 | 2504.56 | 663.64 | 1840.92 | 6454.52 |
| 2 | 3 | 2504.56 | 516.36 | 1988.20 | 4466.32 |
| 3 | 4 | 2504.56 | 357.31 | 2147.25 | 2319.06 |
| 4 | 5 | 2504.56 | 185.52 | 2319.04 | 0.03 |
7.5 เงินกู้ที่มีการชำระก้อนสุดท้ายขนาดใหญ่ (Balloon Payment Loan)
เงินกู้ที่มีการชำระก้อนสุดท้ายขนาดใหญ่ (Balloon Payment Loan) คือ เงินกู้ที่ผู้กู้จะจ่ายค่างวดในแต่ละงวดต่ำกว่าปกติ โดยจะมี “ยอดก้อนใหญ่” (balloon) ที่ต้องชำระในงวดสุดท้ายหรือช่วงท้ายของสัญญา
ลักษณะสำคัญ
ผู้กู้ชำระดอกเบี้ยหรือเฉพาะบางส่วนของเงินต้นในงวดต้น ๆ
งวดสุดท้ายต้องจ่าย “ยอดก้อนใหญ่” ที่รวมเงินต้นที่ยังคงค้าง
นิยมใช้ในกรณีที่
ผู้กู้มีรายรับไม่สม่ำเสมอ
คาดว่าจะมีรายได้ก้อนใหญ่ในอนาคต
ต้องการลดภาระค่างวดในช่วงเริ่มต้น
ตัวแปรและสมการที่เกี่ยวข้อง
\(L\) คือยอดเงินกู้เริ่มต้น
\(i\) คืออัตราดอกเบี้ยต่อปี
\(B\) คือยอด balloon payment
\(R\) คือค่างวดที่ชำระรายงวด (หากมี)
\(n\) คือจำนวนงวดทั้งหมด
7.5.1 กรณีจ่ายเฉพาะดอกเบี้ย (Interest-only)
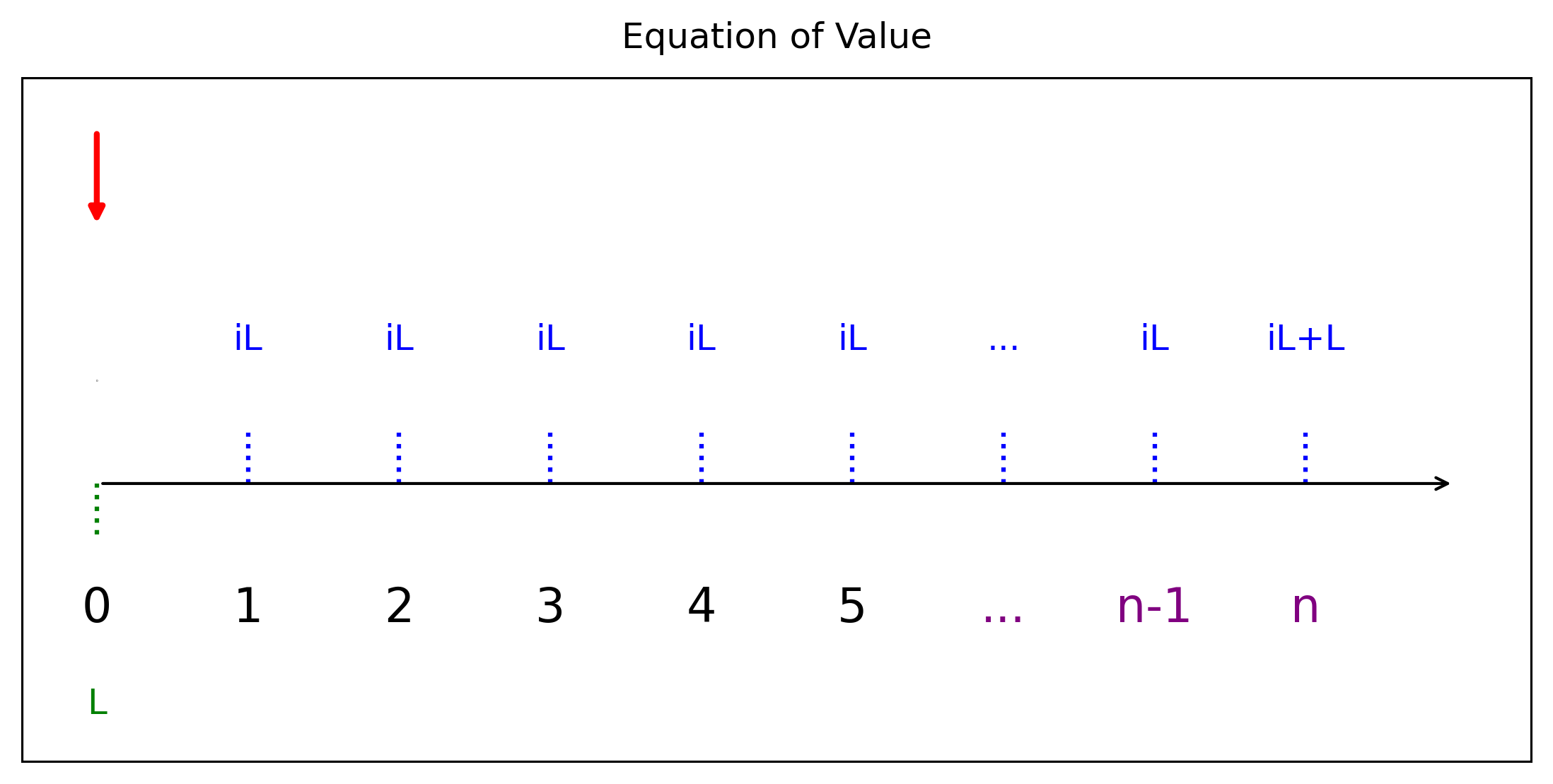 \[L =iL\cdot a_{\overline{n}|i}+ L\cdot v^n\]
\[L =iL\cdot a_{\overline{n}|i}+ L\cdot v^n\]
ผู้กู้ชำระเพียงดอกเบี้ย \(iL\) ทุกงวดเป็นเวลา \(n - 1\) งวด แล้วชำระยอด \(L + iL\) ในงวดสุดท้าย
งวดที่ 1 ถึง \(n - 1\) ชำระ \(iL\)
งวดที่ \(n\) ชำระ \(iL + L\)
7.5.2 กรณีมีบางส่วนของเงินต้น
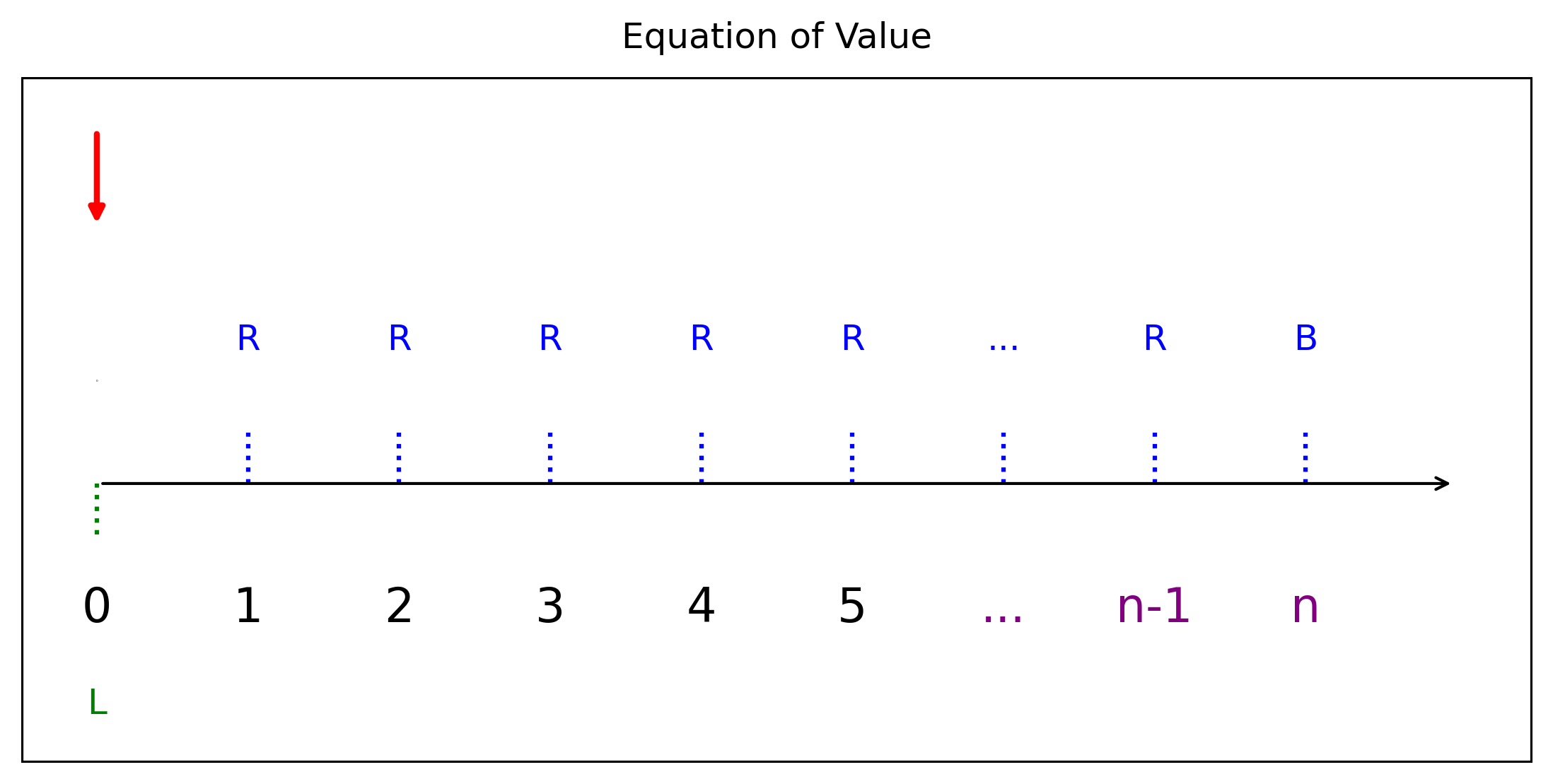
ในบางกรณีผู้กู้จ่ายทั้งดอกเบี้ยและเงินต้นเล็กน้อยในแต่ละงวด และมี balloon payment \(B\) ณ งวดสุดท้าย \[L = R \cdot a_{\overline{n-1}|i}+B\cdot v^n\]
ตัวอย่าง Interest-Only + Balloon
นาย A กู้เงิน 100,000 บาท ดอกเบี้ย 6% ต่อปี เป็นเวลา 5 ปี เลือกชำระแบบจ่ายเฉพาะดอกเบี้ยรายปี และชำระคืนเต็มจำนวนในปีที่ 5
ดังนั้น
ปี 1–4 จ่าย \(100,000 \times 0.06 = 6,000\) บาท
ปี 5 จ่าย \(6,000 + 100,000 = 106,000\) บาท
ตัวอย่าง Partial Principal + Balloon
กู้เงิน 100,000 บาท ดอกเบี้ย 6% ต่อปี ผ่อน 4 ปีโดยจ่ายงวดละ 10,000 บาท และจ่าย balloon payment ในปีที่ 5 จงหาขนาด balloon payment \(B\) \[L = R \cdot a_{\overline{4}|i} + B\cdot v^5\]
B, L, R, i, n , v, a_n = symbols('B L R i n v a_n')
i = 0.06
v = 1/(1+i)
n = 4
L = 1e5
R = 1e4
a_n = (1-v**4)/i
eq = Eq(L, R*a_n+B*v**5)
Sol = solve(eq, B)
Sol[0].evalf(7)\(\displaystyle 87451.63\)
งวดสุดท้ายต้องใช้จ่ายเท่ากับ \(87,451.63\) บาท
7.6 แบบฝึกหัดท้ายบท
จงอธิบายความแตกต่างระหว่างการผ่อนชำระแบบต้นเงินลดลง (decreasing balance) และค่างวดคงที่ (level payment loan) พร้อมยกตัวอย่างการใช้งานจริง
จงเขียนสูตรสำหรับค่างวดเงินกู้รายงวด \(R\) เมื่อทราบจำนวนงวด \(n\), อัตราดอกเบี้ยต่อปี \(i\), และยอดเงินกู้ \(L\) ด้วยซิมไพโดยใช้ฟังก์ชัน Sum()
ถ้าคุณกู้เงิน 100,000 บาท ที่ดอกเบี้ย 6% ต่อปี เป็นเวลา 5 ปี โดยผ่อนชำระรายปีแบบค่างวดคงที่ จงหายอดคงค้างหลังจ่ายไป 2 ปี
จากข้อ 3. จงแสดงตารางการผ่อนชำระเงินกู้ 3 ปีแรก โดยแยกดอกเบี้ยและเงินต้นของแต่ละงวด
จงวาดไดอะแกรมแสดงกระแสเงินสดของผู้กู้ (draw cash flow diagram) สำหรับเงินกู้ 3 ปี พร้อมอธิบาย
ให้นักเรียนเขียนโค้ดโดยใช้ซิมไพ เพื่อคำนวณยอดคงค้างหลังจ่ายงวดที่ 2 ของเงินกู้ 50,000 บาท ที่จ่ายรายเดือน 24 งวด
ถ้าอัตราดอกเบี้ยเปลี่ยนจาก 6% เป็น 8% หลังจากงวดที่ 3 จงคำนวณยอดคงค้าง ณ สิ้นงวดที่ 4 ด้วยซิมไพและสร้างตารางการผ่อนชำระ
อธิบายความหมายของ Balloon Payment พร้อมยกตัวอย่างการใช้จริง และคำนวณค่างวดถ้าเงินกู้ 100,000 บาท จ่าย 4 งวดเท่ากัน + จ่ายก้อนสุดท้ายก้อนใหญ่
อธิบายแนวคิดของการรีไฟแนนซ์ และคำนวณว่าถ้าคุณรีไฟแนนซ์เงินกู้หลังจาก 2 ปี จะประหยัดได้เท่าไรถ้าอัตราดอกเบี้ยลดลง
จงคำนวณดอกเบี้ยรวมที่จ่ายตลอดอายุเงินกู้ 5 ปี ที่ค่างวดละ 10,000 บาทต่อเดือน ถ้าต้องจ่ายดอกเบี้ยที่ \(i^{(12)}=6\%\) ต่อปี
มียอดเงินกู้ 60,000 บาท ผ่อน 10 งวด ดอกเบี้ย 7% ต่อปี จงหาว่าในงวดที่ 4 ชำระเงินต้นเท่าไร