from sympy import symbols, expand
x = symbols('x')
expr = (x + 1)**3
expand(expr)1 การติดตั้งโปรแกรมและการใช้งานซิมไพเบื้องต้น
ถ้าไม่ต้องการติดตั้งโปรแกรมภาษาไพธอนในเครื่องคอมพิวเตอร์ หรือผู้อ่านใช้ iPad หรือ tablet อื่นๆ ผู้อ่านสามารถใช้ภาษาไพธอนและซิมไพได้จาก
https://jupyter.org/ หรือ https://colab.google/ ก็ได้
โดยไม่ต้องติดตั้งโปรแกรมที่เกี่ยวข้องลงในคอมพิวเตอร์
1.1 ติดตั้งไพธอนสาม (Python3)
ตรวจสอบว่าเครื่องคอมพิวเตอร์มีไพธอนหรือไม่ โดยพิมพ์ใน command line สำหรับ WINDOWS และใน terminal สำหรับ MAC OS หรือ LINUX
python3 --versionถ้ายังไม่มี
- macOS ดาวน์โหลดจาก https://www.python.org/downloads/macos/ หรือสามารถติดตั้งผ่าน Homebrew
brew install pythonWindows ดาวน์โหลดจาก https://www.python.org/downloads/ อย่าลืมเลือก “Add Python to PATH”
LINUX(สาย ubuntu) ติดตั้งผ่าน terminal
sudo apt update
sudo apt install python3 python3-pip -y- สร้าง Virtual Environment (แนะนำ)
python3 -m venv sympy-env
source sympy-env/bin/activate # บน macOS / Linux
sympy-env\Scripts\activate.bat # บน WindowsVirtual Environment (สภาพแวดล้อมเสมือน) คือเครื่องมือในภาษาไพธอนที่ใช้สร้างสภาพแวดล้อมเฉพาะตัวสำหรับโปรเจกต์หนึ่ง ๆ ซึ่งแยกออกจากไพธอนและไลบรารีหลักที่ติดตั้งไว้ในเครื่องเพื่อให้สามารถ
แยกไลบรารี แต่ละโปรเจกต์สามารถใช้เวอร์ชันของไลบรารีที่ต่างกันได้โดยไม่ชนกัน
หลีกเลี่ยงปัญหา dependency conflict โปรเจกต์ A อาจใช้
sympy==1.7.1ส่วนโปรเจกต์ B ใช้sympy==1.12ทำงานร่วมกับทีมได้ง่ายขึ้น สามารถแนบ
requirements.txtแล้วให้คนอื่นติดตั้งไลบรารีตามที่คุณใช้ได้ไม่รบกวนระบบหลัก ไพธอนและไลบรารีในเครื่องยังคงปลอดภัยจากการเปลี่ยนแปลงในแต่ละโปรเจกต์
1.1.1 ติดตั้งซิมไพ และ Jupyter Notebook
ก่อนเริ่มต้นใช้งานซิมไพ ซึ่งเป็นไลบรารีในภาษาไพํอนสำหรับการคำนวณเชิงสัญลักษณ์ (symbolic computation) และ Jupyter Notebook ซึ่งเป็นเครื่องมือยอดนิยมในการเขียนและรันโค้ดไพธอนในรูปแบบอินเทอร์แอกทีฟ ผู้ใช้จำเป็นต้องติดตั้งโปรแกรมทั้งสองผ่านคำสั่งในเทอร์มินัล (Terminal) หรือ Command Prompt ดังนี้
pip3 install sympy notebookpip3คือคำสั่งสำหรับติดตั้งแพ็กเกจในไพธอนsympyคือไลบรารีสำหรับการคำนวณเชิงสัญลักษณ์ เช่น การแก้สมการ หาค่าอนุพันธ์ อินทิกรัล และอื่น ๆnotebookคือแพ็กเกจสำหรับติดตั้ง Jupyter Notebook ซึ่งเป็นเครื่องมือที่ช่วยให้สามารถเขียนโค้ด คำอธิบาย และดูผลลัพธ์ในหน้าต่างเดียวกัน
เมื่อดำเนินการติดตั้งเสร็จเรียบร้อยแล้ว ผู้ใช้สามารถเริ่มต้นเขียนสมการทางคณิตศาสตร์โดยใช้ซิมไพ ได้ทันทีใน Jupyter Notebook
1.1.2 ทดสอบว่าทุกอย่างใช้งานได้
เริ่มใช้งาน Jupyter notebook ใน ternimal หรือ command line โดยการพิมพ์
jupyter notebookjupyter notebook ก็จะพร้อมใช้งานสำหรับการคำนวณเชิงสัญลักษณ์ด้วยซิมไพ
สามารถทดลองการใช้งาน โดยการประมวลผลคำสั่งต่อไปนี้
และถ้าใช้ jupyter notebook โดยตรงจะได้ผลลัพธ์ทางหน้าหน้าจอ \[x^3+3x^2+3x+1\]
แต่ถ้าผ่านอ่านใช้ quarto ในโปรแกรม RStudio จะได้ผลลัพธ์ทางหน้าจอคือ
x**3 + 3*x**2 + 3*x + 1และเมื่อทำการประมวลปลออกมาเป็นเอกสารต่างๆ จะได้สมการที่ถูกต้องสวยงามไม่แตกต่างทั้งจาก jupyter notebook
1.2 สรุปคำสั่งหลักสำหรับการใช้งานซิมไพ
# ติดตั้ง Python (ถ้ายังไม่มี)
brew install python # สำหรับ macOS
# สร้าง virtual environment
python3 -m venv sympy-env
source sympy-env/bin/activate
# ติดตั้ง SymPy และ Jupyter
pip3 install sympy notebook
# เรียกใช้งาน Jupyter Notebook
jupyter notebookการคำนวณเชิงสัญลักษณ์ (symbolic mathematics) โดยใช้ชุดคำสั่งซิมไพสำหรับผู้ที่มีพื้นฐานภาษาไพธอน เช่น การแก้สมการ การหาอนุพันธ์ การอินทิเกรต พีชคณิตเชิงเส้น สมการเชิงอนุพันธ์ ฯลฯ
from sympy import Symbol
## เช่นการสร้างตัวแปรสัญลักษณ์การจ่ายรายงวด
a_n = Symbol('a_{\\overline{x}|i}')
a_n\(\displaystyle a_{\overline{x}|i}\)
1.3 ทำไมเลือกใช้ซิมไพ
สามารถคำนวณเชิงสัญลักษณ์ เหมือน Mathematica หรือ Maxima หรือ Maple
เหมาะสำหรับการทำงานด้วย Jupyter Notebook หรือ Google Colab
สามารถทำร่วมกับชุดคำสั่งอื่นๆ ที่สำคัญต่อไปได้ เช่น Numpy Panda Mathplotlib เป็นต้น
สามารถสร้างเอกสาร เช่น รายงาน หรือไลด์ หรือเวบไซต์ ร่วมกับ markdown หรือ Quarto ได้เป็นอย่างดี
สามารถแสดงผลแบบเชิงสัญลักษณ์ทางคณิตศาสตร์ต่างๆ ได้เป็นอย่างดี
1.4 การกำหนดสัญลักษณ์ด้วยคำสั่ง symbols
คำสั่ง symbols ในซิมไพเป็นคำสั่งพื้นฐานที่ สำคัญมาก เพราะใช้ในการสร้าง ตัวแปรเชิงสัญลักษณ์ (symbolic variables) ซึ่งเป็นหัวใจของการคำนวณเชิงสัญลักษณ์ เช่น การแก้สมการ, การอนุพันธ์, อินทิกรัล, การแทนค่า ฯลฯ
ความหมายของคำสั่ง symbols
from sympy import symbols
x = symbols('x')คำสั่งนี้หมายถึง สร้างตัวแปรสัญลักษณ์ชื่อว่า \(x\)
เป็นวัตถุ (object) ของชนิด Symbol ที่ซิมไพใช้แทน “ตัวแปรทางคณิตศาสตร์” เหมือนที่เราใช้ในสมการจริงๆ
ซิมไพไม่ใช้ตัวแปรแบบไพธอนทั่วไป เช่น x = 5 แต่ใช้ x = symbols('x') เพื่อบอกว่า “ฉันต้องการใช้ \(x\) เป็นตัวแปรในสมการ/สูตร”
ความสำคัญของคำสั่ง symbols()
| วัตถุประสงค์ | อธิบาย |
|---|---|
| 1. สร้างตัวแปรเชิงสัญลักษณ์ | เหมือน \(x, y, z\) ในคณิตศาสตร์ |
| 2. ใช้ในสมการ | ใช้สร้าง, แก้, หรือแปลงสมการ |
| 3. ใช้ในการคำนวณขั้นสูง | เช่นการหาอนุพันธ์, อินทิกรัล, ลิมิต, พีชคณิตเชิงเส้น เป็นต้น |
| 4. ควบคุมสมบัติตัวแปร | เช่นมีคุณสมบัติเป็นจำนวนบวก, จำนวนจริง หรือจำนวนเต็ม |
| 5. รองรับเวกเตอร์/แมทริกซ์/อนุกรม | ใช้ได้ทั้งการตัวแปรแบบรายตัวหรือหลายตัวพร้อมกัน |
from sympy import symbols
# สร้างตัวแปรเชิงสัญลักษณ์ชื่อ x ให้มีค่าเท่ากับ x
x = symbols('x')หรือหลายตัว:
from sympy import symbols
# สร้างตัวแปรเชิงสัญลักษณ์ชื่อ x y และ z ให้มีค่าเท่ากับ x y และ z ตามลำดับ
x, y, z = symbols('x y z')หรือเป็นลำดับ ลิสต์/เมตริกซ์ของตัวแปร
from sympy import symbols
a = symbols('a1:6') # ได้ a1, a2, ..., a5
a(a1, a2, a3, a4, a5)1.5 การกำหนดสมมุติฐานให้ตัวแปรเชิงสัญลักษณ์ (assumptions)
ซิมไพรองรับสมมุติฐานที่ช่วยลดความซับซ้อนของนิพจน์ หรือข่วยในเวลาต้องการแก้สมการหาคำตอบ
หากไม่กำหนดสมมุติฐาน ซิมไพจะให้เป็นค่าไม่ทราบแน่ชัด
การกำหนดสมมุติฐานที่เหมาะสมช่วยให้ simplify, solve, limit, และการพิสูจน์เชิงสัญลักษณ์ต่าง ๆ แม่นยำขึ้น
a = symbols('a', positive = True) # a > 0
b = symbols('b', real = True, positive = True) # b เป็นจำนวนจริง บวก
c = symbols('c', integer = True) # c เป็นจำนวนเต็ม
d = symbols('d', nonzero = True) # d ไม่เท่ากับ 0
e = symbols('d')ตรวจสอบว่า a เป็นจำนวนเต็มบวกใช่หรือไม่?
a.is_positiveTrueหรือ b เป็นจำนวนจริงบวกใช่หรือไม่?
b.is_realTrueb.is_positiveTrueถ้าไม่กำหนดสมมุติฐานเช่น ตัวแแปรเชิงสัญลักษณ์ e
e.is_real # เป็นจำนวนเต็มใช่หรือไม่?e.is_complex # เป็นจำนวนเชิงซ้อนใช่หรือไม่?จะไม่ได้คำตอบออกมา ว่าเป็นจริงหรือเท็จ
1.5.1 ตัวอย่างสมมุติฐานที่ใช้ได้
| สมมุติฐาน | ความหมาย |
|---|---|
real = True |
เป็นจำนวนจริง |
positive = True |
> 0 |
negative = True |
< 0 |
nonzero = True |
\(\neq\) 0 |
integer = True |
เป็นจำนวนเต็ม |
odd = True, even = True |
เป็นเลขคี่, เลขคู่ |
finite = True |
ไม่เป็นอินฟินิตี้ |
prime = True |
เป็นจำนวนเฉพาะ |
1.5.2 การสร้างสัญลักษณ์ภาษากรีก
สัญลักษณ์หรือตัวแปรต่างๆ ในทางคณิตศาสตร์มักใช้ใช้่ตัวอักษรกรีซในการสื่อความหมาย และซิมไพอนุญาติให้เราสามารถใช้ตัวอักษรกรีกได้โดยใช้ชื่อของสัญลักษณ์โดยตรง เช่น
## ตัวแปรเชิงสัญลักษณ์ภาษากรีซ
alpha, beta, gamma, lam, mu, nu, pi = symbols('alpha beta gamma lambda mu nu pi')ซิมไพรองรับการแสดงผลเป็นอักษรกรีกอัตโนมัติเมื่อใช้ pretty(), LaTeX, หรือ notebook rendering
| พิมพ์ว่า | ได้เป็นสัญลักษณ์ |
|---|---|
alpha |
\(\alpha\) |
beta |
\(\beta\) |
lam |
\(\lambda\) |
mu |
\(\mu\) |
nu |
\(\nu\) |
pi |
\(\pi\) |
ตัวอย่างใช้งานและผลลัพธ์ทางหน้าจอหรือเอกสาร
alpha + beta - gamma/lam + mu + nu/pi\(\displaystyle \alpha + \beta - \frac{\gamma}{\lambda} + \mu + \frac{\nu}{\pi}\)
1.6 การหลีกเลี่ยงการใช้บางชื่อเป็นตัวแปร
ถูกใช้เป็นชื่อฟังก์ชันหรือคลาสของซิมไพเอง
เป็นคำสงวน (reserved keywords) ในไพธอน
อาจทำให้เกิด conflict หรือพฤติกรรมผิดพลาดโดยไม่รู้ตัว
ชื่อที่ควรหลีกเลี่ยงในซิมไพโดยเฉพาะ
| ชื่อ | เหตุผล |
|---|---|
I |
แทนหน่วยจินตภาพ \(i = \sqrt{-1}\) |
E |
แทนค่าคงที่ \(e \approx 2.718\) |
pi |
ค่าคงที่ \(\pi\) |
oo |
Infinity (\(\infty\)) |
zoo |
Complex infinity |
NaN |
Not a Number |
S |
ตัวช่วยเรียกค่าคงที่ เช่น S(1)/2 |
Eq, solve, diff, integrate, symbols, expand, ฯลฯ |
เป็นฟังก์ชันหลักของซิมไพ |
ถ้าเขียน I = symbols('I') \(\rightarrow\) จะทำให้ I ไม่ใช่ \(\sqrt{-1}\) อีกต่อไป และอาจทำให้การคำนวณเชิง complex ผิดพลาด
ชื่อที่เป็น reserved keywords ของไพธอน (ห้ามใช้)
เช่น:
if, else, while, for, in, def, class, return, lambda, True, False, Noneห้ามสร้างตัวแปรชื่อ lambda
lambda = symbols('lambda') # SyntaxErrorผลลัพธ์
File "<string>", line 1
lambda = symbols('lambda') # SyntaxError
^
SyntaxError: invalid syntax)แต่สามารถใช้ชื่อใกล้เคียงได้
lambda_ = symbols('lambda_') # สามารถทำได้
lambda_\(\displaystyle \lambda_{}\)
ชื่อที่ใช้ในชุดคำสั่งหรือไลบรารีอื่น เช่น NumPy, matplotlib
ถ้าเราต้องใช้หลายไลบรารีร่วมกัน (เช่น NumPy, Pandas, matplotlib) ก็ควรหลีกเลี่ยงชื่อต่อไปนี้เช่นกัน:
| ชื่อ | ความเสี่ยง |
|---|---|
sum, min, max, range |
เป็น built-in function ของ Python |
list, dict, set |
ชื่อชนิดข้อมูล |
np, pd, plt |
ชื่อย่อ (alias) ของไลบรารี |
วิธีป้องกันตัวแปรซ้อนชื่อสำคัญ
ใช้ suffix เช่น
_var,_sym,_valใช้ underscore
_เช่นlambda_,I_,pi_ใช้
dir()เพื่อตรวจสอบว่าชื่อนั้นถูกใช้แล้วหรือไม่
'I' in dir() # ถ้า True แสดงว่ามี object ชื่อ I แล้วถ้าต้องการสร้างสัญลักษณ์หลายตัว เช่น \(\lambda, \mu, \sigma\) ที่ชื่อซ้อนกับค่าพิเศษเหล่านี้อาจใช้ lambda_ mu_sym หรือ sigma_sym
1.7 สัญลักษณ์ที่มี “ยกกำลัง” หรือ “ตัวห้อย”
x_t = symbols('x_t') # ตัวห้อย
x_t\(\displaystyle x_{t}\)
i_m = symbols('i^{(m)}') # ตัวยก
i_m\(\displaystyle i^{(m)}\)
ผู้อ่านจะเข้าใจภาษา LaTeX เบื้องต้นเกี่ยวกับเขียนสมการก่อน จะทำให้เข้าใจหลักของ การสร้างตัวแปรเชิงสัญลักษณ์ด้วยซิมไพได้เข้าใจมากยิ่งขึ้น
1.8 สัญลักษณ์พื้นฐานที่ใช้ในคณิตศาสตร์การเงิน
ในการศึกษาวิชาคณิตศาสตร์การเงิน การใช้ สัญลักษณ์ทางคณิตศาสตร์ มีความสำคัญอย่างยิ่ง เนื่องจากช่วยให้สามารถเขียนสูตรและแบบจำลองต่าง ๆ ได้อย่างกระชับ ชัดเจน และเป็นสากล โดยเฉพาะอย่างยิ่งในการวิเคราะห์เรื่องดอกเบี้ย มูลค่าเงินตามเวลา เงินงวด (Annuities) และเงินสำรอง (Reserves)
หัวข้อนี้จึงรวบรวมสัญลักษณ์พื้นฐานที่ใช้กันอย่างแพร่หลายในการคำนวณทางการเงิน เช่น
อัตราดอกเบี้ย (เช่น \(i\), \(d\))
ค่าคิดลด (\(v\))
จำนวนงวดและระยะเวลา (\(n, m\))
มูลค่าปัจจุบันและมูลค่าในอนาคต (\(PV, FV\))
เงินงวดและทุนตั้งต้น (\(A, P, F, S\))
การกำหนดสัญลักษณ์ด้วยภาษาไพธอนด้วยชุดคำสั่งซิมไพยังช่วยให้สามารถคำนวณเชิงสัญลักษณ์ได้ ซึ่งเหมาะทั้งสำหรับการเรียน การสอน และการสร้างแบบจำลองเชิงทฤษฎีและเชิงปฏิบัติ
1.8.1 อัตราดอกเบี้ย และมูลค่าเงิน
ในการคำนวณทางการเงิน อัตราดอกเบี้ยและการวัดมูลค่าของเงินในช่วงเวลาต่าง ๆ ถือเป็นพื้นฐานสำคัญที่ใช้ในการวิเคราะห์ เช่น การคำนวณดอกเบี้ย มูลค่าปัจจุบัน (Present Value) หรือมูลค่าในอนาคต (Future Value) ของเงิน
เพื่อความสะดวกในการเขียนสมการและทำงานเชิงสัญลักษณ์ เราสามารถกำหนดสัญลักษณ์ที่สำคัญได้ดังนี้
from sympy import symbols
# อัตราดอกเบี้ย
i = symbols('i', positive=True) # i: effective
i_m = symbols('i^{(m)}', positive=True) # i^{(m)}: nominal interest rate (m ครั้งต่อปี)
r = symbols('r', positive=True) # r: nominal interest rate m -> oo
d = symbols('d', positive=True) # d: effective discount rate
d_m = symbols('d^{(m)}', positive=True) # i: nominal discount rate
# อัตราต่อช่วง
m = symbols('m', integer=True, positive=True) # จำนวนงวดต่อปี
# ปัจจัยมูลค่าปัจจุบัน / อนาคต
v = symbols('v', positive=True) # v = 1/(1+i)
n = symbols('n', positive=True) # n ปี
# มูลค่าปัจจุบันและอนาคต
PV, FV = symbols('PV FV') # Present Value / Future Value
# ปริมาณเงินหรือจำนวนเงิน
A, P, F, S = symbols('A P F S') # Annuity, Principal, Future, Sinking fund1.8.2 มูลค่าปัจจุบันและอนุกรม
ในคณิตศาสตร์การเงิน การคำนวณมูลค่าปัจจุบันของเงินงวด (annuity) และมูลค่าในอนาคตของเงินงวด เป็นหัวข้อหลักที่สำคัญ โดยทั่วไปจะมีสัญลักษณ์เฉพาะที่ใช้เรียกสูตรมาตรฐาน เช่น \(a_{\overline{n}|i}\), \(s_{\overline{n}|i}\), \(\ddot{a}_{\overline{n}|i}\), \(\ddot{s}_{\overline{n}|i}\) เป็นต้น
เงินงวดสิ้นงวด (Ordinary Annuity)
สัญลักษณ์ a_n ใช้แทนค่าปัจจุบันของเงินงวดสิ้นงวดจำนวน \(n\) งวด โดยมีอัตราดอกเบี้ย \(i\) ต่อช่วง ค่าของมันคำนวณจากสูตร
# ปัจจัยมูลค่าปัจจุบันของเงินงวดสิ้นงวด อย่างย่อ
a_n = symbols('a_n') # a_n = (1 - v^n)/iสัญลักษณ์ \(a_{\overline{n}|i}\) คือรูปแบบเต็มที่ใช้กันในเอกสารทางการเงิน เพื่อแสดงว่าเป็นมูลค่าปัจจุบันของอนุกรมเงินงวดสิ้นงวด
# หรือสร้างสัญลักษณ์เต็มรูปแบบ
a_n = symbols('a_{\\overline{n}|i}')
a_n # แสดงผลลัพธ์\(\displaystyle a_{\overline{n}|i}\)
สัญลักษณ์ s_n ใช้แทน มูลค่าในอนาคต (Future Value) ของเงินงวดสิ้นงวดจำนวน \(n\) งวด
# สัญลักษณ์อย่างย่อ
s_n = symbols('s_n') # s_n = ((1+i)^n - 1)/iสัญลักษณ์ \(s_{\overline{n}|i}\) คือรูปแบบเต็มของมูลค่าในอนาคตของอนุกรมเงินงวดสิ้นงวด
# หรือ สร้างสัญลักษณ์เต็มรูปแบบ
s_n = symbols('s_{\\overline{n}|i}')
s_n # แสดงผลลัพธ์\(\displaystyle s_{\overline{n}|i}\)
เงินงวดต้นงวด (Annuity Due)
สัญลักษณ์ a_n_due แทนมูลค่าปัจจุบันของเงินงวดต้นงวด โดยแต่ละงวดจ่ายต้นงวดแทนที่จะเป็นสิ้นงวด
# สัญลักษณ์อย่างย่อ
a_n_due = symbols('a_n_due') # เงินรายงวด ต้นงวดสัญลักษณ์ \(\ddot{a}_{\overline{n}|i}\) คือรูปแบบมาตรฐานของมูลค่าปัจจุบันของเงินงวดต้นงวด ซึ่งต่างจากกรณีสิ้นงวดเพียงแค่คูณเพิ่มด้วย \(1 + i\)
# สัญลักษณ์เต็ม
a_n_due = symbols('\\ddot{a}_{\\overline{n}|i}')
a_n_due\(\displaystyle \ddot{a}_{\overline{n}|i}\)
s_n_due ใช้แทนมูลค่าในอนาคตของอนุกรมที่จ่ายต้นงวด
# สัญลักษณ์อย่างย่อ
s_n_due = symbols('s_n_due')\(\ddot{s}_{\overline{n}|i}\) คือรูปแบบเต็มของมูลค่าในอนาคตของเงินงวดต้นงวด ใช้ในกรณีที่เราสนใจผลรวมเงินสะสมที่ปลายงวดสุดท้าย
# สัญลักษณ์เต็ม
s_n_due = symbols('\\ddot{s}_{\\overline{n}|i}')
s_n_due\(\displaystyle \ddot{s}_{\overline{n}|i}\)
1.8.3 เงินงวดชำระไม่เท่ากัน
นอกจากเงินงวดที่มีจำนวนคงที่ทุกงวด (level annuity) ซึ่งใช้บ่อยในการคำนวณเบี้ยประกันหรือเงินสำรอง เรายังพบกับกรณีที่ จำนวนเงินงวดเปลี่ยนแปลงในแต่ละงวด เช่น
เงินงวด เพิ่มขึ้นทีละจำนวนคงที่ เช่น เพิ่มขึ้น 1 หน่วยทุกงวด (Arithmetic Increasing Annuity)
เงินงวด เพิ่มขึ้นแบบทบต้น เช่น เพิ่มขึ้น 5% ทุกงวด (Geometric Increasing Annuity)
เราสามารถกำหนดสัญลักษณ์แทนกรณีเหล่านี้ไว้ล่วงหน้า เพื่อใช้ในสูตรและสมการต่าง ๆ ดังนี้
# เงินงวดเพิ่มขึ้นตามเลขคณิต/เรขาคณิต
Ia_n = symbols('Ia_n') # เงินงวดเพิ่มขึ้น 1 หน่วย/งวด (Arithmetic)
Ga_n = symbols('Ga_n') # เงินงวดเพิ่มขึ้นแบบ geometric1.8.4 Yield และ Internal Rate of Return (IRR)
ในโลกของการเงินและการลงทุน การประเมินผลตอบแทนจากการลงทุนระยะยาว เช่น พันธบัตร ประกันชีวิตแบบมีเงินปันผล หรือการลงทุนในสินทรัพย์ทางการเงินอื่น ๆ จำเป็นต้องใช้แนวคิด อัตราผลตอบแทนภายใน (IRR) หรือ ผลตอบแทนของพันธบัตร (YTM)
IRR (Internal Rate of Return) คือ อัตราดอกเบี้ยที่ทำให้มูลค่าปัจจุบันของกระแสเงินสดเท่ากับศูนย์
YTM (Yield to Maturity) คือ อัตราผลตอบแทนที่ผู้ลงทุนจะได้รับหากถือพันธบัตรจนครบกำหนด
การกำหนดตัวแปรสัญลักษณ์เหล่านี้จะช่วยให้เขียนสมการคำนวณกระแสเงินสดในลักษณะทั่วไปได้อย่างยืดหยุ่น
IRR = symbols('IRR', positive=True)
YTM = symbols('YTM', positive=True)1.9 การเปลี่ยนฟังก์ชันสัญลักษณ์เป็นฟังก์ชันเชิงตัวเลข
สาเหตุที่ต้องการแปลงฟังก์ชันเชิงสัญลักษณ์เป็นฟังก์ชันเชิงตัวเลขก็เพื่อใช้สำหรับการวาดแผนภาคหรือกราฟที่สวยงามกว่าในการวาดกราฟด้วยซิมไพ ดังตัวอย่างต่อไปนี้
from sympy import symbols, lambdify
import numpy as np
import matplotlib.pyplot as plt
# สร้างตัวแปรเชิงสัญลักษณ์ t
t = symbols('t')
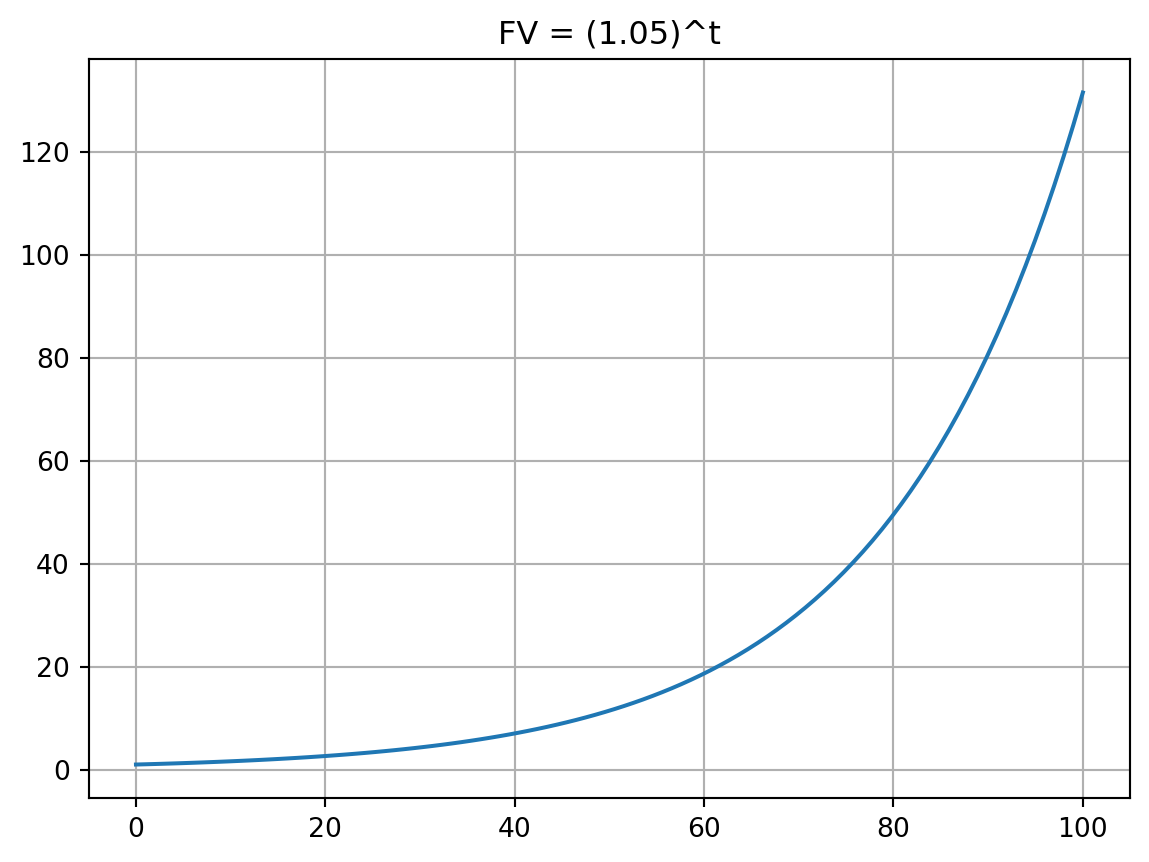
# เงินสะสมของดอกเบี้ยทบต้นที่อัตราดอกเบี้ย 5% ณเวลาที่ t
expr = (1.05)**t
# แปลงเป็นฟังก์ชัน Python (numerical FV =(1.05)^t
FV = lambdify(t, expr, modules=['numpy'])
# สร้าง array เริ่มจากจุด 0 ไปถึง 100 จำนวน 100 จุด
T = np.linspace(0, 100, 100)
Fv = FV(T)
# สร้างกราฟ
plt.plot(T, Fv)
plt.title('FV = (1.05)^t')
plt.grid(True)
plt.show()from sympy import symbols, Lambda, simplify
# สร้างตัวแปรสัญลักษณ์
i, t, n = symbols('i t n', positive=True)
# นิยามฟังก์ชันคณิตศาสตร์การเงินแบบ symbolic ด้วย Lambda
pv = Lambda((i, t), 1 / (1 + i)**t) # Present Value: PV(i, t)
fv = Lambda((i, t), (1 + i)**t) # Future Value: FV(i, t)
a_n = Lambda((i, n), (1 - (1 + i)**(-n)) / i) # Present value of ordinary annuity
# Present value of annuity-due
a_n_due = Lambda((i, n), ((1 - (1 + i)**(-n)) / i) * (1 + i))
s_n = Lambda((i, n), ((1 + i)**n - 1) / i) # Future value of ordinary annuity
# Future value of annuity-due
s_n_due = Lambda((i, n), (((1 + i)**n - 1) / i) * (1 + i)) # ทดสอบแสดงนิยาม
print('PV(i, t) =', simplify(pv(i, t)))
print('FV(i, t) =', simplify(fv(i, t)))
print('a_n(i, n) =', simplify(a_n(i, n)))
print('a_n_due(i, n) =', simplify(a_n_due(i, n)))
print('s_n(i, n) =', simplify(s_n(i, n)))
print('s_n_due(i, n) =', simplify(s_n_due(i, n)))PV(i, t) = (i + 1)**(-t)
FV(i, t) = (i + 1)**t
a_n(i, n) = 1/i - 1/(i*(i + 1)**n)
a_n_due(i, n) = (i + 1)**(1 - n)*((i + 1)**n - 1)/i
s_n(i, n) = ((i + 1)**n - 1)/i
s_n_due(i, n) = (i + 1)*((i + 1)**n - 1)/iLambda() และ lambdify() ดูคล้ายกัน แต่ทำงานต่างกัน อย่างสิ้นเชิง
สรุปเปรียบเทียบ
| ฟังก์ชัน | Lambda() (ของ SymPy) |
lambdify() (ของ SymPy) |
|---|---|---|
| ประเภท | symbolic function | numeric function wrapper |
| การประเมินค่า | ยังคงอยู่ในโลกสัญลักษณ์ (symbolic) | แปลงเป็น ฟังก์ชัน Python ปกติ (หรือ NumPy) |
| ใช้กับอะไร | งาน symbolic เช่นนิยามฟังก์ชันในสูตร | งาน plotting, คำนวณตัวเลข, หรือใช้ร่วมกับ NumPy |
| Return type | sympy.Lambda |
ฟังก์ชัน Python (def หรือ lambda แบบ runtime) |
Lambda()นิยามฟังก์ชันเชิงสัญลักษณ์ (symbolic)
from sympy import symbols, Lambda
x = symbols('x')
f = Lambda(x, x**2 + 1)f # ค่าx ส่งไปยังฟังก์ชัน f = x^2+1\(\displaystyle \left( x \mapsto x^{2} + 1 \right)\)
f(x) # ใส่ตัวแปรเชิงสัญลักษณ์ x เข้าไปในฟังก์ชัน f\(\displaystyle x^{2} + 1\)
f(3) # ใส่เลข 3 ลงไปยังฟังก์ชัน 3\(\displaystyle 10\)
f(3) ทำงานได้เพราะ 3 ถูกแปลงเป็น symbolic Integer(3) โดยอัตโนมัติ
lambdify()แปลงเป็นฟังก์ชัน Python/NumPy สำหรับคำนวณจริง
from sympy import lambdify
f_num = lambdify(x, x**2 + 1)
f_num <function _lambdifygenerated(x)>f_num(x)\(\displaystyle x^{2} + 1\)
f_num(3)10ใช้กับ np.linspace(), plotting, numerical methods ได้ทันที
x_vals = np.linspace(-10, 10, 5)
print(f_num(x_vals))[101. 26. 1. 26. 101.]แต่ ถ้าเป็นฟังก์ชันที่สร้างจาก Lambda จะไม่สามารถใช้งานได้
f(x_vals) ผู้เขียนไม่ได้แสดงค่าความผิดพลาด (error) ในหนังสือนี้เนื่องจากเป็นความที่ยาวเกินไป ให้ผู้อ่านลองเขียนคำสั่งและดูผลที่เกิดขึ้น
ฟังก์ชัน f ที่สร้างขึ้นไม่รองรับอาเรย์ x_vals ทำให้ไม่สามารถวัดวาดกราฟด้วย matplotlib ได้
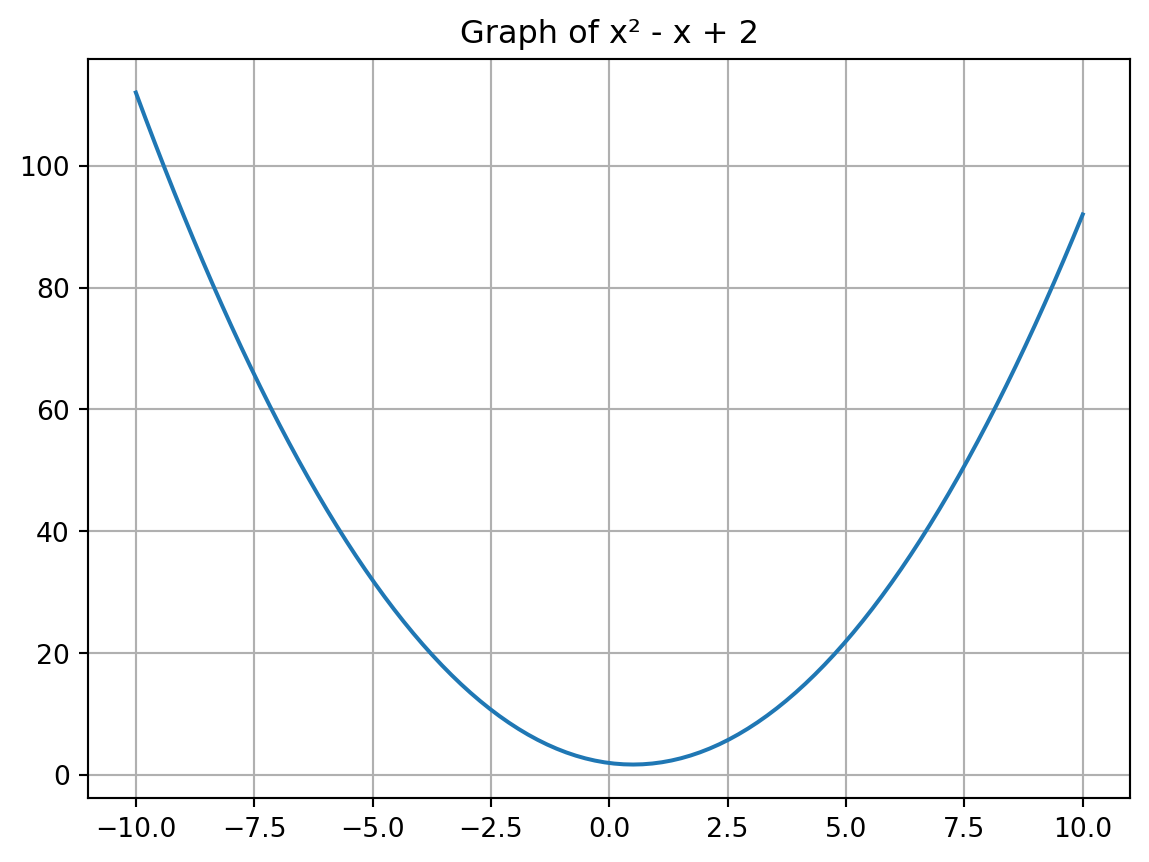
# Lambda แบบ numeric สำหรับ plot
expr = x**2 -x +2
f_num = lambdify(x, expr, 'numpy')
x_vals = np.linspace(-10, 10, 100)
y_vals = f_num(x_vals)
plt.plot(x_vals, y_vals)
plt.title('Graph of x² - x + 2')
plt.grid()
plt.show()สำหรับฟังก์ชันที่ซิมไพอื่นๆ ที่เกี่ยวข้องจะทยอยนำเสนอในบทต่อๆ ไป